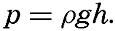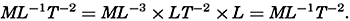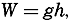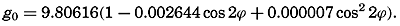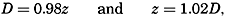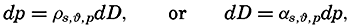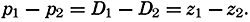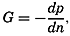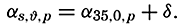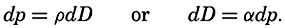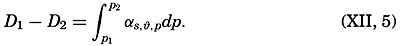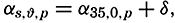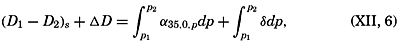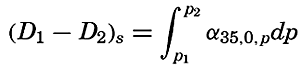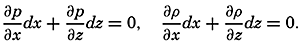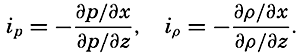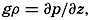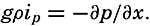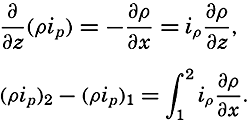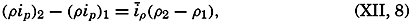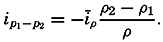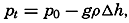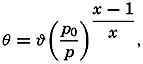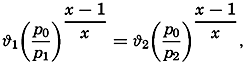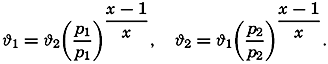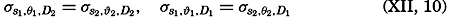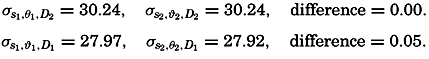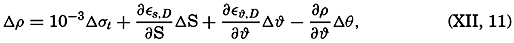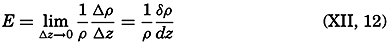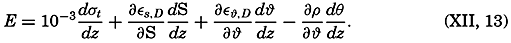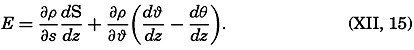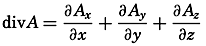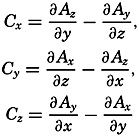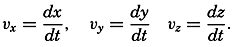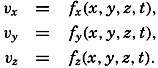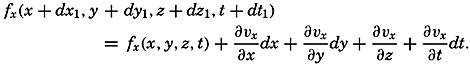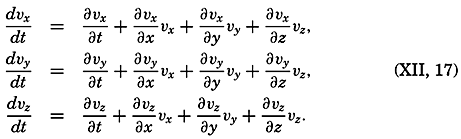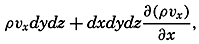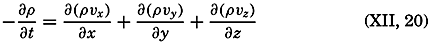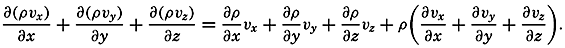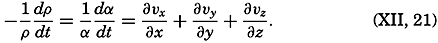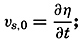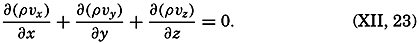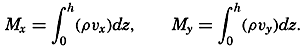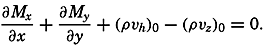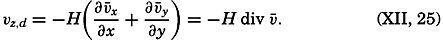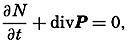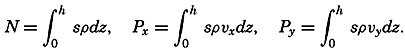---

XII. Statics and Kinematics ^[PDF]

STATICS

Units and Dimensions

In the preceding chapters, different units have been introduced without strict definitions, but now it is necessary to define both units and dimensions. The word “dimension” in the English language is used with two different meanings. In everyday language, the term “dimensions of an object” refers to the size of the object, but in physics “dimensions” mean the fundamental categories by means of which physical bodies, properties, or processes are described. In mechanics and hydrodynamics, these fundamental dimensions are mass, length, and time, denoted by M, L, and T. When using the word “dimension” in this sense, no indication of numerical magnitude is implied, but the concept is emphasized that any physical characteristic or property can be described in terms of certain categories, the dimensions. This will be clarified by examples on p. 402.

Fundamental Units. In physics the generally accepted units of mass, length, and time are gram, centimeter, and second; that is, quantities are expressed in the centimeter-gram-second (c.g.s.) system. In oceanography, it is not always practicable to retain these units, because, in order to avoid using large numerical values, it is convenient to measure depth, for instance, in meters and not in centimeters. Similarly, it is often practical to use one metric ton as a unit of mass instead of one gram. The second is retained as the unit of time. A system of units based on meter, ton, and second (the m.t.s. system) was introduced by V. Bjerknes and different collaborators (1910). Compared to the c.g.s. system the new units are 1 m = 10² cm, 1 metric ton = 10⁶ g, 1 sec = 1 sec. For thermal processes, the fundamental unit, 1°C, should be added.

Unfortunately, it is not practical to use even the m.t.s. system consistently. In several cases it is of advantage to adhere to the c.g.s. system in order to make results readily comparable with laboratory results that are expressed in such units, or because the numerical values are more conveniently handled in the c.g.s. system. When measuring horizontal

---

distances, on the other hand, it is preferable to use larger units such as kilometers, statute miles, or nautical miles. In oceanography it is therefore always necessary to indicate the units in which any quantity is measured.

Derived Units. Units in mechanics other than mass, M, length, L, and time, T, can be expressed by the three dimensions, M, L, and T, and by the unit values adopted for these dimensions. Thus, velocity has the dimension length divided by time, which is written as LT⁻¹ and is expressed in centimeters per second or in meters per second. Velocity, of course, can be expressed in many other units, such as nautical miles per hour (knots), or miles per day, but the dimensions remain unaltered. Acceleration is the time change of a velocity and has the dimensions LT⁻². Force is mass times acceleration and has dimensions MLT⁻².

Table 60 shows the dimensions of a number of the terms that will be used. Several of the terms in the table have the same dimensions, but the concepts on which the terms are based differ. Work, for instance, is defined as force times distance, whereas kinetic energy is defined as mass times the square of a velocity, but work and kinetic energy both have the dimensions ML²T⁻². Similarly, one and the same term can be defined differently, depending upon the concepts that are introduced. Pressure, for instance, can be defined as work per unit volume, ML²T⁻²L⁻³ = ML⁻¹T⁻², but is more often defined as force per unit area, MLT⁻²L⁻² = ML⁻¹T⁻².

In any equation of physics, all terms must have the same dimensions, or, applied to mechanics, in all terms the exponents of the fundamental

---

dimensions, M, L, and T, must be the same. It is inaccurate, for instance, to state that the acceleration of a body is equal to the sum of the forces acting on a body, because acceleration has dimensions LT⁻², whereas force has dimensions MLT⁻². The correct statement is that the acceleration of a body is equal to the sum of the forces per unit mass acting on a body. An example of a correct statement is the expression for the pressure exerted by a column of water of constant density, ρ, and of height, h, at a locality where the acceleration of gravity is g: In this case the dimensions on both sides of the equality sign are

Some of the constants that appear in the equations of physics have dimensions, and their numerical values will therefore depend upon the particular units that have been assigned to the fundamental dimensions, whereas other constants have no dimensions and are therefore independent of the system of units. Density has dimensions ML⁻³, but the density of pure water at 4° has the numerical value 1 (one) only if the units of mass and length are selected in a special manner (grams and centimeters or metric tons and meters). On the other hand, the specific gravity, which is the density of a body relative to the density of pure water at 4°, has no dimensions (ML⁻³/ML⁻³) and is therefore expressed by the same number, regardless of the system of units that is employed.

The Fields of Gravity, Pressure, and Mass

Level Surfaces. Coordinate surfaces of equal geometric depth below the ideal sea surface are useful when considering geometrical features, but in problems of statics or dynamics that involve consideration of the acting forces, they are not always satisfactory. Because the gravitational force represents one of the most important of the acting forces, it is convenient to use as coordinate surfaces the level surfaces, defined as surfaces that are everywhere normal to the force of gravity. It will presently be shown that these surfaces do not coincide with surfaces of equal geometric depth.

It follows from the definition of level surfaces that, if no forces other than gravitational are acting, a mass can be moved along a level surface without expenditure of work and that the amount of work expended or gained by moving a unit mass from one surface to another is independent of the path taken.

The amount of work, W, required for moving a unit mass a distance, h, along the plumb line is

---

where g is the acceleration of gravity. Work per unit mass has dimensions L²T⁻², and the numerical value depends therefore only on the units used for length and time. When the length is measured in meters and the time in seconds, the unit of work per unit mass is called a dynamic decimeter (Bjerknes and different collaborators, 1910).

In the following, the sea surface will be considered a level surface. The work required or gained in moving a unit mass from sea level to a point above or below sea level is called the gravity potential, and in the m.t.s. system the unit of gravity potential is thus one dynamic decimeter.

The practical unit of the gravity potential is the dynamic meter, for which the symbol D is used. When dealing with the sea the vertical axis is taken as positive downward. The geopotential of a level surface at the geometrical depth, z, is therefore, in dynamic meters,

The geometrical depth in meters of a given level surface, on the other hand, is

The acceleration of gravity varies with latitude and depth, and the geometrical distance between standard level surfaces therefore varies with the coordinates. At the North Pole the geometrical depth of the 1000-dynamic-meter surface is 1017.0 m, but at the Equator the depth is 1022.3 m, because g is greater at the Poles than at the Equator. Thus, level surfaces and surfaces of equal geometric depth do not coincide. Level surfaces slope relative to the surfaces of equal geometric depth, and therefore a component of the acceleration of gravity acts along surfaces of equal geometrical depth.

The topography of the sea bottom is represented by means of isobaths—that is, lines of equal geometrical depth—but it could be presented equally well by means of lines of equal geopotential. The contour lines would then represent the lines of intersection between the level surfaces and the irregular surface of the bottom. These contours would no longer be at equal geometric distances, and hence would differ from the usual topographic chart, but their characteristics would be that the amount of work needed for moving a given mass from one contour to another would be constant. They would also represent the new coast lines if the sea level were lowered without alterations of the topographic features of the bottom, provided the new sea level would assume perfect hydrostatic equilibrium and adjust itself normal to the gravitational force.

Any scalar field can similarly be represented by means of a series of topographic charts of equiscalar surfaces in which the contour lines

---

represent the lines of intersection of the level surfaces with the equiscalar surface. Charts of this character will be called geopotential topographic charts, or charts of geopotential topography, in contrast to topographic charts in which the contour lines represent the lines along which the depth of the surface under consideration is constant.

The Field of Gravity. The fact that gravity is the resultant of two forces, the attraction of the earth and the centrifugal force due to the earth's rotation, need not be considered, and it is sufficient to define gravity as the force that is derived empirically by pendulum observations. Furthermore, it is not necessary to take into account the minor irregular variations of gravity that detailed surveys reveal, but it is enough to make use of the “normal” value, in meters per second per second, which at sea level can be represented as a function of the latitude, ϕ, by Helmert's formula:

Thus, the normal value at the poles is 9.83205, and at the Equator it is 9.78027. The normal value of g increases with depth, according to the formula From formula (XII, 1) one obtains in dynamic meters the geopotential that corresponds to a given depth, z: or from (XII, 2) the depth corresponding to a given value of D: In the first approximation, meaning that the numbers which represent the depth in meters deviate only by about 2 per cent from the numbers which represent the geopotential in dynamic meters. Extensive use will be made of this numerical agreement between the two units, but it must always be borne in mind that a dynamic meter is a measure of work per unit mass, and not a measure of length. The conversion factors, 0.98 and 1.02, are therefore not pure numbers, but the former has the dimensions LT⁻² and the latter has the dimensions L⁻¹T².

The field of gravity can be completely described by means of a set of equipotential surfaces corresponding to standard intervals of the gravity potential. These are at equal distances if the geopotential is

---

used as the vertical coordinate, but, if geometric depth is used, the distance between the equipotential surfaces varies. If the field is represented by equipotential surfaces at intervals of one dynamic decimeter, it follows from the definition of these surfaces that the numerical value of the acceleration of gravity is the reciprocal of the geometric thickness in meters of the unit sheets.

The Field of Pressure. The distribution of pressure in the sea can be determined by means of the equation of static equilibrium:

Here, k is a numerical factor that depends on the units used, and ρ_{s, ϕ p} is the density of the water (p. 56).

The hydrostatic equation will be discussed further in connection with the equations of motion (p. 440). At this time it is enough to emphasize that, as far as conditions in the ocean are concerned, the equation, for all practical purposes, is exact.

Introducing the geopotential expressed in dynamic meters as the vertical coordinate, one has 10dD = gdz. When the pressure is measured in decibars (defined by 1 bar = 10⁶ dynes per square centimeter), the factor k becomes equal to 1/10, and equation (XII, 3) is reduced to

where α _{s, ϕ, p} is the specific volume.

Because ρ_{s, ϕ, p}and α_{s, ϕ, p} differ little from unity, a difference in pressure is expressed in decibars by nearly the same number that expresses the difference in geopotential in dynamic meters, or the difference in geometric depth in meters. Approximately,

The pressure field can be completely described by means of a system of isobaric surfaces. Using the geopotential as the vertical coordinate, one can present the pressure distribution by a series of charts showing isobars at standard level surfaces or by a series of charts showing the geopotential topography of standard isobaric surfaces. In meteorology, the former manner of representation is generally used on weather maps, in which the pressure distribution at sea level is represented by isobars. In oceanography, on the other hand, it has been found practical to represent the geopotential topography of isobaric surfaces.

The pressure gradient is defined by

where n is directed normal to the isobaric surfaces (p. 156). The pressure

---

gradient has the character of a force per unit volume, because pressure has the dimensions of a force per unit area. The dimension of a pressure is ML⁻¹ T⁻² = MLT⁻² × L⁻², and the dimension of a pressure gradient is ML⁻² T⁻² = MLT⁻² × L⁻³. Multiplying the pressure gradient by the specific volume, M⁻¹L³, one obtains a force per unit mass of dimensions LT⁻².

The pressure gradient has two principal components: the vertical, directed normal to the level surfaces, and the horizontal, directed parallel to the level surfaces. When static equilibrium exists, the vertical component, expressed as force per unit mass, is balanced by the acceleration of gravity. This is the statement which is expressed mathematically by means of the equation of hydrostatic equilibrium. In a resting system the horizontal component of the pressure gradient is not balanced by any other force, and therefore the existence of a horizontal pressure gradient indicates that the system is not at rest or cannot remain at rest. The horizontal pressure gradients, therefore, although extremely small, are all-important to the state of motion, whereas the vertical are insignificant in this respect.

It is evident that no motion due to pressure distribution exists or can develop if the isobaric surfaces coincide with level surfaces. In such a state of perfect hydrostatic equilibrium the horizontal pressure gradient vanishes. Such a state would be present if the atmospheric pressure, acting on the sea surface, were constant, if the sea surface coincided with the ideal sea level and if the density of the water depended on pressure only. None of these conditions is fulfilled. The isobaric surfaces are generally inclined relative to the level surfaces, and horizontal pressure gradients are present, forming a field of internal force.

This field of force can also be defined by considering the slopes of isobaric surfaces instead of the horizontal pressure gradients. By definition the pressure gradient along an isobaric surface is zero, but, if this surface does not coincide with a level surface, a component of the acceleration of gravity acts along the isobaric surface and will tend to set the water in motion, or must be balanced by other forces if a steady state of motion is reached. The internal field of force can therefore be represented also by means of the component of the acceleration of gravity along isobaric surfaces (p. 440).

Regardless of the definition of the field of force that is associated with the pressure distribution, for a complete description of this field one must know the absolute isobars at level surfaces or the absolute geopotential contour lines of isobaric surfaces. These demands cannot possibly be met. One reason is that measurements of geopotential distances of isobaric surfaces must be made from the actual sea surface, the topography of which is unknown. It will be shown that all one can do is to determine the pressure field that would be present if the pressure

---

distribution depended only upon the distribution of mass in the sea. This part of the total pressure field will be called the relative field of pressure, but it cannot be too strongly emphasized that the total field of pressure is composed of this relative field and, in addition, a field that is maintained by external forces such as atmospheric pressure and wind.

In order to illustrate this point a fresh-water lake will be considered which is so small that horizontal differences in atmospheric pressure can be disregarded and the acceleration of gravity can be considered constant. Let it first be assumed that the water is homogeneous, meaning that the density is independent of the coordinates. In this case, the distance between any two isobaric surfaces is expressed by the equation

This equation simply states that the geometrical distance between isobaric surfaces is constant, and it defines completely the internal field of pressure. The total field of pressure depends, however, upon the configuration of the free surface of the lake. If no wind blows and if no stress is thus exerted on the free surface of the lake, perfect hydrostatic equilibrium exists, the free surface is a level surface, and, similarly, all other isobaric surfaces coincide with level surfaces. On the other hand, if a wind blows across the lake, the equilibrium will be disturbed, the water level will be lowered at one end of the lake, and water will be piled up against the other end. The free surface will still be an isobaric surface, but it will now be inclined relative to a level surface. The relative field of pressure, however, will remain unaltered as represented by equation (XII, 4), meaning that all other isobaric surfaces will have the same geometric shape as that of the free surface.

One might continue and introduce a number of layers of different density, and one would find that the same reasoning would be applicable. The method is therefore also applicable when one deals with a liquid within which the density changes continually with depth. By means of observations of the density at different depths, one can derive the relative field of pressure and can represent this by means of the topography of the isobaric surfaces relative to some arbitrarily or purposely selected isobaric surface. The relative field of force can be derived from the slopes of the isobaric surface relative to the selected reference surface, but, in order to find the absolute field of pressure and the corresponding absolute field of force, it is necessary to determine the absolute shape of one isobaric surface.

These considerations have been set forth in great detail because it is essential to be fully aware of the difference between the absolute field of pressure and the relative field of pressure, and to know what types of data are needed in order to determine each of these fields.

---

The Field of Mass. The field of mass in the ocean is generally described by means of the specific volume as expressed by (p. 57)

The field of the specific volume can be considered as composed of two fields, the field of α_{35, 0,p} and the field of δ.

The former field is of a simple character. The surfaces of α_35,0,p coincide with the isobaric surfaces, the deviations of which from level surfaces are so small that for practical purposes the surfaces of α_35,0,p can be considered as coinciding with level surfaces or with surfaces of equal geometric depth. The field of α_35,0,p can therefore be fully described by means of tables giving α_35,0,p as a function of pressure and giving the average relationships between pressure, geopotential and geometric depths. Since this field can be considered a constant one, the field of mass is completely described by means of the anomaly of the specific volume, δ, the determination of which was discussed on p. 58.

The field of mass can be represented by means of the topography of anomaly surfaces or by means of horizontal charts or vertical sections in which curves of δ = constant are entered. The latter method is the most common. It should always be borne in mind, however, that the specific volume in situ is equal to the sum of the standard specific volume, α_35,0,p at the pressure in situ and the anomaly, δ.

The Relative Field of Pressure. It is impossible to determine the relative field of pressure in the sea by direct observations, using some type of pressure gauge, because an error of only 0.1 m in the depth of a pressure gauge below the sea surface would introduce errors greater than the horizontal differences that should be established. If the field of mass is known, however, the internal field of pressure can be determined from the equation of static equilibrium in one of the forms

In oceanography the latter form has been found to be the more practical, but all reasoning applies equally well to results deduced from the former.

Integration of the latter form gives

Because one can write where and is called the standard geopotential distance between the isobaric

---

surfaces p₁ and p₂, and where is called the anomaly of the geopotential distance between the isobaric surfaces p₁ and p₂, or, abbreviated, the geopotential anomaly.

Equation (XII, 6) can be interpreted as expressing that the relative field of pressure is composed of two fields: the standard field and the field of anomalies. The standard field can be determined once and for all, because the standard geopotential distance between isobaric surfaces represents the distance if the salinity of the sea water is constant at 35 ‰ and the temperature is constant at 0°C. The standard geopotential distance decreases with increasing pressure, because the specific volume decreases (density increases) with pressure, as is evident from table 7H in Bjerknes (1910), according to which the standard geopotential distance between the isobaric surfaces 0 and 100 decibars is 97.242 dynamic meters, whereas the corresponding distance between the 5000-and 5100-decibar surfaces is 95.153 dynamic meters.

The standard geopotential distance between any two standard isobaric surfaces is, on the other hand, independent of latitude, but the geometric distance between isobaric surfaces varies with latitude because g varies.

Because in the standard field all isobaric surfaces are parallel relative to each other, this standard field lacks a relative field of horizontal force. The relative field of force, which is associated with the distribution of mass, is completely described by the field of the geopotential anomalies. It follows that a chart showing the topography of one isobaric surface relative to another by means of the geopotential anomalies is equivalent to a chart showing the actual geopotential topography of one isobaric surface relative to another. The practical determination of the relative field of pressure is therefore reduced to computation and representation of the geopotential anomalies, but the absolute pressure field can be found only if one can determine independently the absolute topography of one isobaric surface.

In order to evaluate equation (XII, 7), it is necessary to know the anomaly, δ, as a function of absolute pressure. The anomaly is computed from observations of temperature and salinity, but oceanographic observations give information about the temperature and the salinity at known geometrical depths below the actual sea surface, and not at known pressures. This difficulty can fortunately be overcome by means of an artificial substitution, because at any given depth the numerical value of the absolute pressure expressed in decibars is nearly the same as the numerical value of the depth expressed in meters, as is evident from the following corresponding values:

---

Thus, the numerical values of geometric depth deviate only 1 or 2 percent from the numerical values of the standard pressure at that depth. This agreement is not accidental, but has been brought about by the selection of the practical unit of pressure, the decibar.

It follows that the temperature at a pressure of 1000 decibars is nearly equal to the temperature at a geometric depth of 990 m, or the temperature at the pressure of 6000 decibars is nearly equal to the temperature at a depth of 5875 m. The vertical temperature gradients in the ocean are small, especially at great depths, and therefore no serious error is introduced if, instead of using the temperature at 990 m when computing δ, one makes use of the temperature at 1000 m, and so on. The difference between anomalies for neighboring stations will be even less affected by this procedure, because within a limited area the vertical temperature gradients will be similar. The introduced error will be nearly the same at both stations, and the difference will be an error of absolutely negligible amount. In practice one can therefore consider the numbers that represent the geometric depth in meters as representing absolute pressure in decibars. If the depth in meters at which either directly observed or interpolated values of temperature and salinity are available is interpreted as representing pressure in decibars, one can compute, by means of the tables in the appendix, the anomaly of specific volume at the given pressure. By multiplying the average anomaly of specific volume between two pressures by the difference in pressure in decibars (which is considered equal to the difference in depth in meters), one obtains the geopotential anomaly of the isobaric sheet in question expressed in dynamic meters. By adding these geopotential anomalies, one can find the corresponding anomaly between any two given pressures. An example of a complete computation is given in table 61.

Certain simple relationships between the field of pressure and the field of mass can be derived by means of the equations for equiscalar surfaces (p. 155) and the hydrostatic equation. In a vertical profile the isobars and the isopycnals are defined by

The inclinations of the isobars and isopycnals are therefore By means of the hydrostatic equation

---

one obtains

From the two latter equations it follows that If the density distribution is represented by means of unit sheets (p. 156), the integral on the right-hand side can be evaluated where ī_p means the average inclination of unit sheets. The isobaric surface p₁ lies above the surface p₂, because the vertical axis is positive downward. The inclination of the upper isobaric surface relative to the lower, i_p1−p2, therefore, when an average value of the density is introduced,

---

is Using the specific volume anomaly and making the specific volume equal to unity, one obtains approximately Because δ decreases with depth, δ₁ - δ₂ is positive, and the inclination of one isobaric surface relative to another is of opposite sign to the inclination of the δ surfaces (p. 449). This rule permits a rapid estimate of the relative inclinations of isobaric surface in a section in which the field of mass has been represented by δ curves.

Profiles of isobaric surfaces based on the data from a series of stations in a section must evidently be in agreement with the inclination of the δ curves, as shown in a section and based on the same data, but this obvious rule often receives little or no attention.

Relative Geopotential Topography of Isobaric Surfaces. If simultaneous observations of the vertical distribution of temperature and salinity were available from a number of oceanographic stations within a given area, the relative pressure distribution at the time of the observations could be represented by a series of charts showing the geopotential topography of standard isobaric surfaces relative to one arbitrarily or purposely selected reference surface. From the preceding it is evident that these topographies are completely represented by means of the geopotential anomalies.

In practice, simultaneous observations are not available, but in many instances it is permissible to assume that the time changes of the pressure distribution are so small that observations taken within a given period may be considered simultaneous. The smaller the area, the shorter must be the time interval within which the observations are made. Figs. 110, p. 454 and 204, p. 726, represent examples of geopotential topographies. The conclusions as to currents which can be based on such charts will be considered later.

Charts of geopotential topographies can be prepared in two different ways. By the common method, the anomalies of a given surface relative to the selected reference surface are plotted on a chart and isolines are drawn, following the general rules for presenting scalar quantities. In this manner, relative topographies of a series of isobaric surfaces can be prepared, but the method has the disadvantage that each topography is prepared separately.

By the other method a series of charts of relative topographies is prepared stepwise, taking advantage of the fact that the anomaly of geopotential thickness of an isobaric sheet is proportional to the average

---

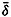specific volume anomaly, [Equation], in the isobaric sheet. Thus, if the thickness of the isobaric sheet is 100 decibars, δDp1p1-100 = 100δ. Consequently, curves of 100δ represent the topography of the surface p = p1 − 100 relative to the surface p = p1, and one can proceed as follows: The topography of the surface ps − 200, where ps is the selected reference surface, is constructed by means of curves of equal values of the specific volume anomaly in the sheet ps to ps − 100. The topography of the surface ps − 200 relative to the surface ps − 100 is constructed by means of the specific volume anomalies in the sheet ps − 100 to ps − 200, and by graphical addition of these two charts (V. Bjerknes and collaborators, 1911) the topography of the surface ps − 200 relative to the surface ps is found. This process can be repeated, and by successive constructions of charts and specific volume anomalies and by graphical additions, the entire fields of mass and pressure can be represented.

This method is widely used in meteorology, but is not commonly employed in oceanography because, for the most part, the different systems of curves are so nearly parallel to each other that graphical addition is cumbersome. The method is occasionally useful, however, and has the advantage of showing clearly the relationship between the distribution of mass and the distribution of pressure. It especially brings out the geometrical feature that the isohypses of the isobaric surfaces retain their form when passing from one isobaric surface to another only if the anomaly curves are of the same form as the isohypses. This characteristic of the field is of great importance to the dynamics of the system.

Character of the Total Field of Pressure. From the above discussion it is evident that, in the absence of a relative field of pressure, isosteric and isobaric surfaces must coincide. Therefore, if for some reason one isobaric surface, say the free surface, deviates from a level surface, then all isobaric and isosteric surfaces must deviate in a similar manner. Assume that one isobaric surface in the disturbed condition lies at a distance Δh cm below the position in undisturbed conditions. Then all other isobaric surfaces along the same vertical are also displaced the distance Δh from their undisturbed position. The distance Δh is positive downward because the positive z axis points downward. Call the pressure at a given depth at undisturbed conditions p₀. Then the pressure at disturbed conditions is p_t = p₀ − Δp, where Δp = gρΔh and where the displacement Δh can be considered as being due to a deficit or an excess of mass in the water column under consideration.

The above considerations are equally valid if a relative field of pressure exists. The absolute distribution of pressure can always be completely determined from the equation

---

and would therefore be fully known if one could determine Δh, the vertical displacement of the isobaric surfaces due to excess or deficit of mass in the column under consideration. An added horizontal field of force is present when this vertical displacement varies from one locality to another, in which case the absolute isobaric surfaces slope in relation to the isobaric surfaces of the relative field. The added field can be called the slope field, and this analysis thus leads to the result that the total field of pressure is composed of the internal field and the slope field. This distinction is helpful when discussing the character of the currents.

Significance of σ_t Surfaces

The density of sea water at atmospheric pressure, expressed as σ_t = (ρ_s,ϕ,0 − 1) × 10³, is often computed and represented in horizontal charts or vertical sections. It is therefore necessary to study the significance of σ_t surfaces, and in order to do so the following problem will be considered: Can water masses be exchanged between different places in the ocean space without altering the distribution of mass?

The same problem will first be considered for the atmosphere, assuming that this is a perfect, dry gas. In such an atmosphere the potential temperature means the temperature which the air would have if it were brought by an adiabatic process to a standard pressure. The potential temperature, θ, is

where ϕ is the temperature at the pressure p, p₀ is the standard pressure, and κ = 1.4053 is the ratio of the two specific heats of an ideal gas (c_p/c_v). In a dry atmosphere in which the temperature varies in space and in which the vertical gradient differs from the gradient at adiabatic equilibrium, it is always possible to define surfaces of equal potential temperature. One characteristic of these surfaces is that along such a surface air masses can be interchanged without altering the distribution of temperature and pressure and, thus, without altering the distribution of mass.

Consider two air masses, one of temperature ϕ₁ at pressure p₁, and one of temperature ϕ₂ at pressure p₂. If both have the same potential temperature, it follows that

or

---

The latter equations tell that if the air mass originally characterized by ϕ₂, p₂ is brought adiabatically to pressure p₁, its temperature has been changed to ϕ₁, and, similarly, that the air mass which originally was characterized by ϕ₁, p₁ attains the temperature ϕ₂ if brought to pressure p₂. Thus, no alteration of the distribution of mass is made by an exchange, and such an exchange has no influence either on the potential energy of the system or on the entropy of the system. In an ideal gas the surfaces of potential temperature are therefore isentropic surfaces.

With regard to the ocean, the question to be considered is whether surfaces of similar characteristics can be found there. Let one water mass at the geopotential depth D₁ be characterized by salinity S₁ and temperature ϕ₁, and another water mass at geopotential depth D₂ be characterized by salinity S₂ and temperature ϕ₂. The densities in situ of these small water masses can then be expressed as σ_s1,ϑ1,D1 and σ_s²,ϑ2,D2.

Now consider that the mass at the geopotential depth D₁ is moved adiabatically to the geopotential depth D₂. During this process the temperature of the water mass will change adiabatically from ϕ₁ to θ₁ and the density in situ will be σ_s1,θ1,D2. Moving the other water mass adiabatically from D₂ to D₁ will change its temperature from ϕ₂ to θ₂. If the two water masses are interchanged, the conditions

must both be fulfilled if the distribution of mass shall remain unaltered. These conditions can be fulfilled, however, only in the trivial case that S₁ = S₂, ϕ₁ = ϕ₂, and D₁ = D₂. This is best illustrated by a numerical example. Assume the values These values represent conditions encountered in the Atlantic Ocean, but at a distance of about 50° of latitude.

The adiabatic change in temperature between the geopotential depths of 200 and 700 dyn meters is 0.09°, and thus θ₁ = 13.82, θ₂ = 8.01. By means of the Hydrographic Tables of Bjerknes and collaborators, one finds

Thus, the conditions (XII, 10) are not both fulfilled and the two water masses cannot be interchanged without altering the distribution of mass.

It should also be observed that the mixing of two water masses that are at the same depth and are of the same density in situ, but of different temperatures and salinities, produces water of a higher density. If, at D = 700 dyn meters, equal parts of water S₁ = 36.01 ‰, ϕ₁ = 13.82°,

---

and S₂ = 34.60 ‰, ϕ₂ = 8.10°, respectively, are mixed, the resulting mixture will have a salinity S = 35.305 ‰, and a temperature ϕ = 10.96°. The density in situ of the two water masses was identical (σ_s,ϕ,D = 30.24), but the resulting mixture has a higher density, 30.29. Similarly, if equal parts of the water masses S₁ = 36.01 ‰, ϕ₁ = 13.73°, D₁ = 200 dyn meters, and S₂ = 34.60 ‰, ϕ₂ = 8.01°, and D₂ = 200 dyn meters are mixed, the density in situ of the mixture will be 27.98, although the densities of the two water masses were 27.97 and 27.92, respectively.

This discussion leads to the conclusion that in the ocean no surfaces exist along which interchange or mixing of water masses can take place without altering the distribution of mass and thus altering the potential energy and the entropy of the system (except in the trivial case that isohaline and isothermal surfaces coincide with level surfaces). There must exist, however, a set of surfaces of such character that the change of potential energy and entropy is at a minimum if interchange and mixing takes place along these surfaces. It is impossible to determine the shape of these surfaces, but the σ_t surfaces approximately satisfy the conditions. In the preceding example, which represents very extreme conditions, the two water masses were lying nearly on the same σ_t surface (σ_t1, = 27.05, σ_t2 = 26.97).

Thus, in the ocean, the σ_t surfaces can be considered as being nearly equivalent to the isentropic surfaces in a dry atmosphere, and the σ_t surfaces may therefore be called quasi-isentropic surfaces. The name implies only that interchange or mixing of water masses along σ_t surfaces brings about small changes of the potential energy and of the entropy of the body of water.

Stability

The change in a vertical direction of σ_t is nearly proportional to the vertical stability of the system. Assume that a water mass is displaced vertically upward from the geopotential depth D₂ to the geopotential depth D₁. The difference between the density of this mass and the surrounding water (see p. 57) will then be

where Δσ_t, ΔS, and Δϕ represent the variations of σt, S and ϕ between the geopotentials D₁ to D₂, and where Δθ represents the adiabatic change of temperature. The water mass will evidently remain at rest in the new surroundings if Δρ = 0; it will sink back to its original place if Δρ is positive, because it is then heavier than the surroundings; and will rise if Δρ is negative, because it is then lighter than the surroundings. The acceleration of the mass will be proportional to Δρ/ρ. The reasoning remains unaltered if we introduce geometric depths instead of geopotential. If the acceleration due to displacement along the short

---

vertical distance Δz is proportional to Δρ/ρ, then the acceleration due to displacement along a vertical distance of unit length must be proportional to Δρ/ρΔz. Hesselberg (1918) has called the term the “stability.” Omitting the factor 1/ρ, which differs little from unity, one obtains, by means of equation (XII, 11), where dθ/dz is the adiabatic change of temperature per unit length. This term is small, and, because the ε terms and the vertical gradients of salinity and temperature also are small, it follows that, approximately,

Hesselberg and Sverdrup (1914–15) have published tables by means of which the terms of equation (XII, 13) are found, and give an example based on observations in the Atlantic Ocean on May, 1910, in lat. 28°37′N, long. 19°08′W (Helland-Hansen, 1930). This example is reproduced in

---

table 62, in which the exact values of the stability are given under the heading 10⁸E, and the approximate values, obtained by means of equation (XII, 14), under the heading 10⁵dσ_t/dz. The two values agree fairly well down to a depth of 1400 m. The negative values above 50 m indicate instability.

Hesselberg and Sverdrup have also computed the order of magnitude of the different terms in equation (XII, 13) and have shown that dσ_t/dz is an accurate expression of the stability down to a depth of 100 m, but that between 100 and 2000 m the terms containing ε may have to be considered, and that below 2000 m all terms are important. The following practical rules can be given:

1. Above 100 m the stability is accurately expressed by means of 10⁻³dσ_t/dz.

2. Below 100 m the magnitude of the other terms of the exact equation (XII, 13) should be examined if the numerical value of 10⁻³dσ_t/dz is less than 40 × 10⁻⁸.

The stability can also be expressed in a manner that is useful when considering the stability of the deep water:

If the salinity does not vary with depth (dS/dz = 0), as is often the case in the deep water, Of the quantities in this equation, ∂ρ/∂ϕ is negative, dθ/dz is positive, and dϕ/dz is negative if the temperature decreases with depth, but positive if the temperature increases. The stratification will always be stable if the temperature decreases with depth or increases more slowly than the adiabatic, but indifferent equilibrium exists if dϕ/dz = dθ/dz, and instability is found if dϕ/dz > dθ/dz.

KINEMATICS

Vector Fields

A vector field can be completely represented by means of three sets of charts, one of which shows the scalar field of the magnitude of the vector and two of which show the direction of the vector in horizontal and vertical planes. It can also be fully described by means of three sets of scalar fields representing the components of the vector along the principal coordinate axes (V. Bjerknes and different collaborators, 1911). In oceanography, one is concerned mainly with vectors that are horizontal, such as velocity of ocean currents—that is, two-dimensional vectors.

---

These can be completely represented by means of two sets of charts, or one chart with two sets of curves—vector lines, which at all points give the direction of the vector, and equiscalar curves, which give the magnitude of the vector. Fig. 95 shows a schematic example of an arbitrary two-dimensional vector field that is represented by means of vectors of indicated direction and magnitude and by means of vector lines and equiscalar curves of magnitude.

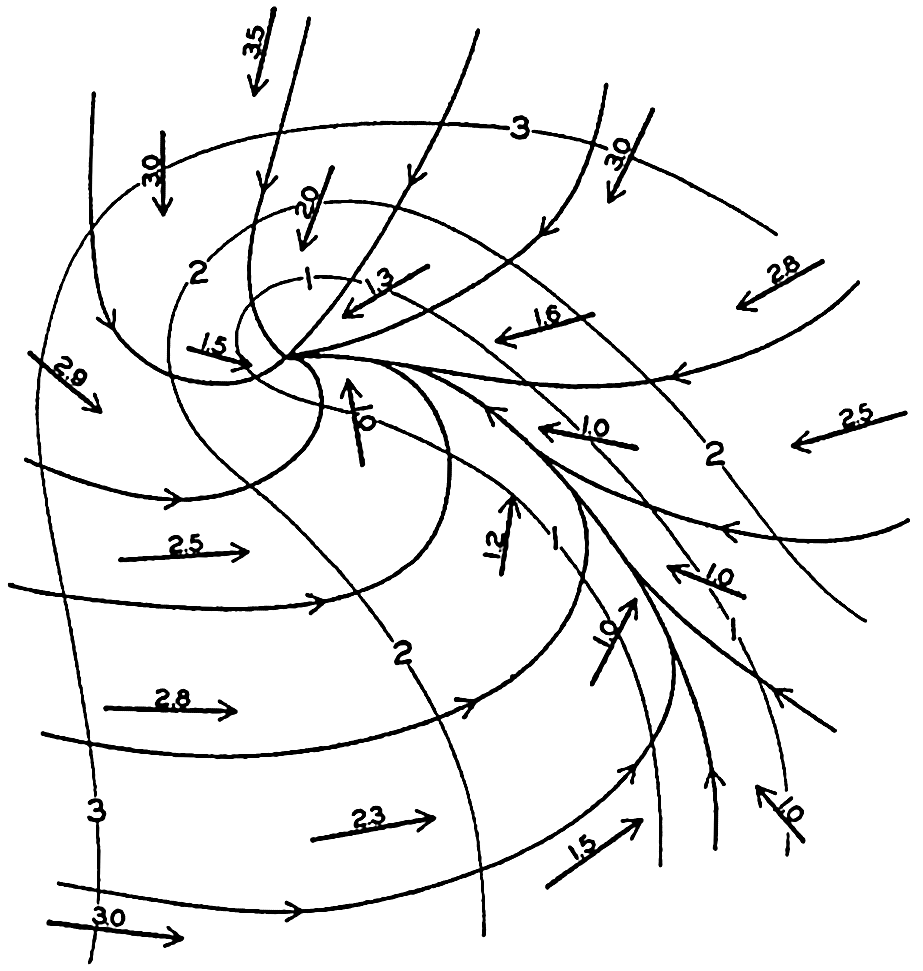
Vector lines cannot intersect except at singular points or lines, where the magnitude of the vector is zero. Vector lines cannot begin or end within the vector field except at singular points, and vector lines are continuous.

The simplest and most important singularities in a two-dimensional vector field are shown in fig. 96: These are (1) points of divergence (fig. 96A and C) or convergence (fig. 96B and D), at which an infinite number of vector lines meet; (2) neutral points, at which two or more vector lines intersect (the example in fig. 96E shows a neutral point of the first order in which two vector lines intersect—that is, a hyperbolic point); and (3) lines of divergence (fig. 96F) or convergence (fig. 96G), from which an infinite number of vector lines diverge asymptotically or to which an infinite number of vector lines converge asymptotically.

---

The significance of these singularities in the field of motion will be explained below.

It is not necessary to enter upon all the characteristics of vector fields or upon all the vector operations that can be performed, but two important vector operations must be mentioned.

Assume that a vector A has the components A_x, A_y, and A_z. The scalar quantity

is called the divergence of the vector.

---

The vector which has the components

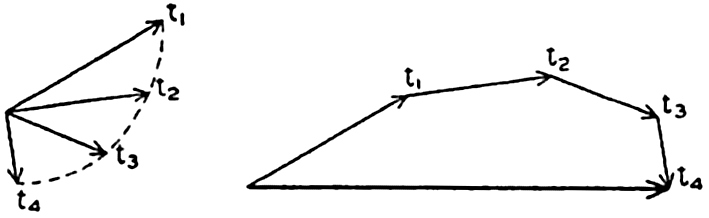
is called the curl, or the vorticity, of the vector A. Divergence and vorticity of fields of velocity or momentum have definite physical interpretations.

Two representations of a vector that varies in space and time will also be mentioned. A vector that has been observed at a given locality during a certain time interval can be represented by means of a central vector diagram (fig. 97). In this diagram, all vectors are plotted from the same point, and the time of observation is indicated at each vector. Occasionally the end points of the vector are joined by a curve on which the time of observation is indicated and the vectors themselves are omitted. This form of representation is commonly used when dealing with periodic currents such as tidal currents. A central vector diagram is also used extensively in pilot charts to indicate the frequency of winds from given directions. In this case the direction of the wind is shown by an arrow, and the frequency of wind from that direction is shown by the length of the arrow.

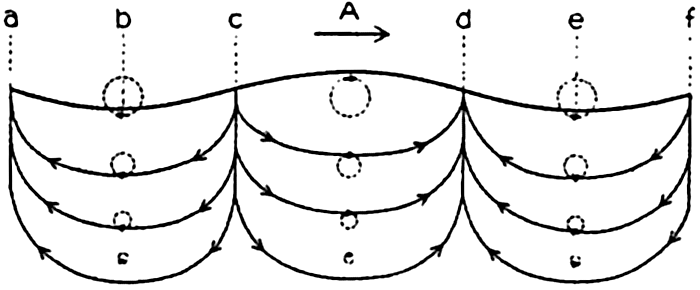
If it can be assumed that the observations were made in a uniform vector field, a progressive vector diagram is useful. This diagram is constructed by plotting the second vector from the end point of the first, and so on (fig. 97). When dealing with velocity, one can compute the displacement due to the average velocity over a short interval of time. When these displacements are plotted in a progressive vector diagram, the resulting curve will show the trajectory of a particle if the velocity field is of such uniformity that the observed velocity can be considered representative of the velocities in the neighborhood of the place of observation. The vector that can be drawn from the beginning of the first vector to the end of the last shows the total displacement in the entire time interval, and this displacement, divided by the time interval, is the average velocity for the period.

---

The Field of Motion and the Equation of Continuity

The Field of Motion. Among vector fields the field of motion is of special importance. Several of the characteristics of the field of motion can be dealt with without considering the forces which have brought about or which maintain the motion, and these characteristics form the subject of kinematics.

The velocity of a particle relative to a given coordinate system is defined as ν = dr/dt, where dr is an element of length in the direction in which the particle moves. In a rectangular coordinate system the velocity has the components

The velocity field can be completely described by the Lagrange or by the Euler method. In the Lagrange method the coordinates of all moving particles are represented as functions of time and of a threefold multitude of parameters that together characterize all the moving particles. From this representation the velocity of each particle, and, thus, the velocity field, can be derived at any time.

The more convenient method by Euler will be employed in the following. This method assumes that the velocity of all particles of the fluid has been defined. On this assumption the velocity field is completely described if the components of the velocity can be represented as functions of the coordinates and of time:

The characteristic difference between the two methods is that Lagrange's method focuses attention on the paths taken by all individual particles, whereas Euler's method focuses attention on the velocity at each point in the coordinate space. In Euler's method it is necessary, however, to consider the motion of the individual particles in order to find the acceleration. After a time dt, a particle that, at the time t, was at the point (x,y,z) and had the velocity components f_x(x,y,z,t), and so on, will be at the point (x + dx, y + dy, z + dz), and will have the velocity components f_x(x + dx, y+ dy, z + dz, t + dt), and so on. Expanding in Taylor's series, one obtains

The change in velocity in the time dt—that is, the acceleration of the

---

individual particles under consideration—will therefore have the components

Thus, one has to deal with two time derivatives: the individual time derivative, which represents the acceleration of the individual particles, and the local time derivative, which represents the time change of the velocity at a point in space and is called the local acceleration. The last terms in equation (XII, 17) are often combined and called the field acceleration.

The above development is applicable not only when considering the velocity field, but also when considering any field of a property that varies in space and time (p. 157). The velocity field is stationary when the local time changes are zero:

It should be observed that, when the individual acceleration vanishes—that is, when the velocity field is stationary only if the field acceleration also disappears.

The Equation of Continuity. Consider a cube of volume dxdydz. The mass of water that in unit time flows in parallel to the x axis is equal to pv_xdydz, and the mass that flows out is equal to

supposing that both ρ and ν_x vary in the direction of the x axis. The net outflow per unit time and per unit volume in the direction of the x axis is, therefore, ∂(ρν_x)/∂x Similarly, the corresponding net outflow along the y and z axes is ∂)ρν_y)/∂y and ∂(ρν_z)/∂z, respectively. The net outflow from a cube of unit volume is the sum of these terms, but this outflow per unit time must also equal the decrease of the density per unit time, -∂ρ/∂t. The condition

---

must therefore always be fulfilled in order to maintain the continuity of the system. This fundamentally important equation is called the equation of continuity. It tells that the local loss of mass, represented by -∂ρ/∂t, equals the divergence of the specific momentum (p. 420).

Now:

By means of equation (XII, 17), therefore, The term on the left-hand side represents the rate of expansion of the moving element. In this form the equation of continuity states that the rate of expansion of the moving element equals the divergence of the velocity.

The equation of continuity is not valid in the above form at a boundary surface because no out- or inflow can take place there. In a direction normal to a boundary a particle in that surface must move at the same velocity as the surface itself. If the surface is rigid, no component normal to the surface exists and the velocity must be directed parallel to the surface. The condition

where n is directed normal to the boundary surface and dn/dt is the velocity of the boundary surface in this direction, represents the kinematic boundary condition, which at the boundary takes the place of the equation of continuity.

Application of the Equation of Continuity. At the sea surface the kinematic boundary condition must be fulfilled. Designating the vertical displacement of the sea surface relative to a certain level of equilibrium by η, and taking this distance positive downward, because the positive z axis is directed downward, one obtains

that is, the vertical velocity at the sea surface is equal to the time change of the elevation of the sea surface. If the sea surface remains stationary, one has ν_z,0 = 0. If the bottom is level, one has, similarly, ν_z,h = 0, where h is the depth to the bottom.

With stationary distribution of mass (∂ρ/∂t = 0) the equation of continuity is reduced to

---

The total transport of mass through a vertical surface of unit width reaching from the surface to the bottom has the components

Multiplying equation (XII, 23) by dz and integrating from the surface to the bottom, one obtains Here, ν_z,h = 0, and at stationary sea level ν_z,0 = 0. Thus, the equation is reduced to or, when the sea level remains stationary, the transport between the surface and the bottom is free of divergence.

When dealing with conditions near the surface, one can consider the density as constant and can introduce average values of the velocity components 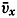[Equation] and 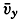[Equation] within a top layer of thickness H. With these simplifications, one obtains, putting ν_z,0 = 0,

If H is small enough, the average velocity will not differ much from the surface velocity. Since a negative vertical velocity represents an ascending motion, and a positive vertical velocity represents a descending motion, equation (XII, 25) states that at a small distance below the surface ascending motion is encountered if the surface currents are diverging, and descending if the surface currents are converging. This is an obvious conclusion, because, with diverging surface currents, water is carried away from the area of divergence and must be replaced by water that rises from some depth below the surface, and vice versa. Thus, conclusions as to vertical motion can be based on charts showing the surface currents.

For this purpose, it is of advantage to write the divergence of a two-dimensional vector field in a different form:

where dl is an element of length in the direction of flow and where Δn represents the distance between neighboring stream lines. If the velocity is constant along the stream lines (∂ν/∂l = 0), the flow is divergent when the distance between the stream lines increases (dΔn/dl > 0), and convergent when the distance decreases (dΔn/dl > 0). When, on the

---

other hand, the distance between the stream lines remains constant (dΔn/dl = 0), the divergence depends only upon the change of velocity along the stream lines. Increasing velocity (∂ν/∂l > 0) means divergence accompanied by ascending motion below the surface if this surface remains stationary, and decreasing velocity (∂ν/∂l < 0) means convergence associated with descending motion below the surface.

The equation of continuity is applicable not only to the field of mass but also to the field of a dissolved substance that is not influenced by biological activity. Let the mass of the substance per unit mass of water be s. Multiplying the equation of continuity by s and integrating from the surface to bottom, one obtains, if the vertical velocity at the surface is zero,

where Under stationary conditions the local time change is zero, and one has

These equations have already been used in simplified form in order to compute the relation between inflow and outflow of basins (p. 147). Other simplifications have been introduced by Knudsen, Witting, and Gehrke (Krümmel, 1911, p. 509–512).

Stream Lines and Trajectories. The vector lines showing the direction of currents at a given time are called the stream lines, or the lines of flow. The paths followed by the moving water particles, on the other hand, are called the trajectories of the particles. Stream lines and trajectories are identical only when the motion is stationary, in which case the stream, lines of the velocity field remain unaltered in time, and a particle remains on the same stream line.

The general difference between stream lines and trajectories can be illustrated by considering the type of motion in a traveling surface wave. The solid lines with arrows in fig. 98 show the stream lines in a cross section of a surface wave that is supposed to move from left to right, passing the point A. When the crest of the wave passes A, the motion of the water particles at A is in the direction of progress, but with decreasing

---

velocities downward. At the troughs of the wave, at b and e, the motion is in the opposite direction. Between A and b there is, therefore, a divergence with descending motion, and between A and e there is a convergence with ascending motion. The surface will therefore sink at c and rise at d, meaning that the wave will travel from left to right. When the point c reaches A, there will be no horizontal motion of the water, but as b passes A the motion will be reversed. Thus, the pattern of stream lines moves from left to right with the velocity at which the wave proceeds.

It is supposed that the speed at which the wave travels is much greater than the velocity of the single water particles that take part in the wave motion. On this assumption a water particle that originally was located below A will never be much removed from this vertical and will return after one wave period to its original position. The trajectories of such particles in this case are circles, the diameters of which decrease with increasing distance from the surface, as shown in the figure. It is evident that the trajectories bear no similarity to the stream lines.

Representations of the Field of Motion in the Sea

Trajectories of the surface water masses of the ocean can be determined by following the drift of floating bodies that are carried by the currents. It is necessary, however, to exercise considerable care when interpreting the available information about drift of bodies, because often the wind has carried the body through the water. Furthermore, in most cases, only the end points of the trajectory are known—that is, the localities where the drift commenced and ended. Results of drift-bottle experiments present an example of incomplete information as to trajectories. As a rule, drift bottles are recovered on beaches, and a reconstruction of the paths taken by the bottles from the places at which they were released may be very hypothetical. The reconstruction may be aided by additional information in the form of knowledge of distribution of surface temperatures and salinities that are related to the currents, or by information obtained from drift bottles that have been picked up at sea. Systematic drift-bottle experiments have been conducted, especially in coastal areas that are of importance to fisheries.

Stream lines of the actual surface or subsurface currents must be based upon a very large number of direct current measurements. Where the velocity is not stationary, simultaneous observations are required. Direct measurements of subsurface currents must be made from anchored vessels, but this procedure is so difficult that no simultaneous measurements that can be used for preparing charts of observed subsurface currents for any area are available.

Numerous observations of surface currents, on the other hand, have been derived from ships' logs. Assume that the position of the vessel at

---

noon of any day has been fixed by astronomical observations (point A in fig. 99). From point A the course is set for point B, which, at the average speed of the vessel, should be reached in twenty-four hours. The following day, astronomic observations show, however, that the vessel has not reached point B, which would be the position by dead reckoning, but is at the position B′. It is then assumed that the displacement BB′ is due to a current which on an average has the direction B to B′ and the velocity BB′/24 knots if the distance BB′ is given in nautical miles. Current velocities observed in this manner are given either in knots or in nautical miles per day. Direction and velocity are uncertain if the displacement is small, because an astronomical fix is usually not accurate within 1 or 2 nautical miles, and the accuracy of a position by dead reckoning is as a rule less. Little weight can be given to displacements of 5 miles or less in twenty-four hours.

The data on surface currents obtained from ships' logs cannot be used for construction of a synoptic chart of the currents, because the number of simultaneous observations is far too small. Data for months, quarter years, or seasons have been compiled, however, from many years' observations, although even these are unsatisfactory for presentation of the average conditions because such data are not evenly distributed over large areas but are concentrated along trade routes. In some charts the average direction in different localities is indicated by arrows, and where strong currents prevail the average speed in nautical miles per day is shown by a number. In other charts the surface flow is represented by direction roses in which the number at the center of the rose represents the percentage of no current, the lengths of the different arrows represent the percentage of currents in the direction of the arrows, and the figures at the ends of the arrows represent the average velocity in miles per day of currents in the indicated direction. These charts contain either averages for the year or for groups of months.

On the basis of such charts, average surface currents during seasons or months have in some areas been represented by means of stream lines and equiscalar curves of velocity. The principle advantage of this representation is that it permits a rapid survey of the major features and that it brings out the singularities of the stream lines, although in many instances the interpretation of the data is uncertain and the details of the chart will depend greatly upon personal judgment.

---

In drawing these stream lines it is necessary to follow the rules concerning vector lines (p. 419). The stream lines cannot intersect, but an infinite number of stream lines can meet in a point of convergence or divergence or can approach asymptotically a line of convergence or diverge asymptotically from a line of divergence.

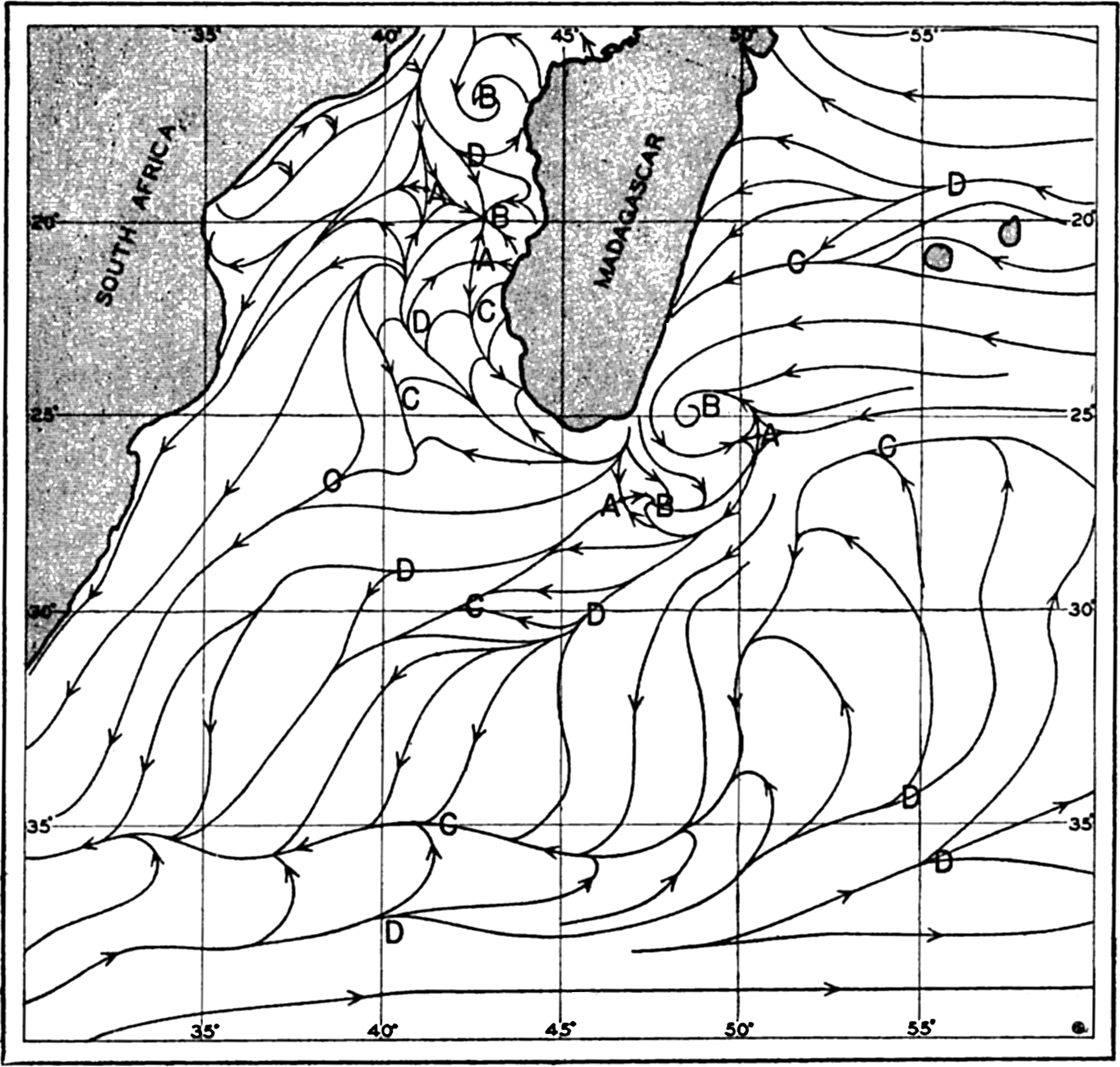
As an example, stream lines of the surface flow in July off southeast Africa and to the south and southeast of Madagascar are shown in fig. 100. The figure is based on a chart by Willimzik (1929), but a number of the stream lines in the original chart have been omitted for the sake of simplification. In the chart a number of the characteristic singularities of a vector field are shown. Three hyperbolic points marked A appear, four points of convergence marked B are seen, and a number of lines of convergence marked C and lines of divergence marked D are present. The stream lines do not everywhere run parallel to the coast, and the representation involves the assumption of vertical motion at the coast, where the horizontal velocity, however, must vanish.

---

The most conspicuous feature is the continuous line of convergence that to the southwest of Madagascar curves south and then runs west, following lat. 35°S. At this line of convergence, the Subtropical Convergence, which can be traced across the entire Indian Ocean and has its counterpart in other oceans, descending motion must take place. Similarly, descending motion must be present at the other lines of convergence, at the points of convergence, and at the east coast of Madagascar, whereas ascending motion must be present along the lines of divergence and along the west coast of Madagascar, where the surface waters flow away from the coast. Velocity curves have been omitted, for which reason the conclusions as to vertical motion remain incomplete (see p. 425). Near the coasts, eddies or countercurrents are indicated, and these phenomena often represent characteristic features of the flow and remain unaltered during long periods.

As has already been stated, representations of surface flow by means of stream lines have been prepared in a few cases only. As a rule, the surface currents are shown by means of arrows. In some instances the representation is based on ships' observation of currents, but in other cases the surface flow has been derived from observed distribution of temperature and salinity, perhaps taking results of drift-bottle experiments into account. The velocity of the currents may not be indicated or may be shown by added numerals, or by the thickness of the arrows. No uniform system has been adopted (see Defant, 1929), because the available data are of such different kinds that in each individual case a form of representation must be selected which presents the available information in the most satisfactory manner. Other examples of surface flow will be given in the section dealing with the currents in specific areas.

Bibliography

Bjerknes, V., and different collaborators. 1910. Dynamic meteorology and hydrography. Pt. I. Statics. Carnegie Inst. Washington, Pub. no. 88, 146 pp. + tables, 1910.

Bjerknes, V., and different collaborators. 1911. Dynamic meteorology and hydrography. Pt. II. Kinematics. Carnegie Inst. Washington, Pub. no. 88, 175 pp., 1911.

Defant, A.. 1929. Dynamische Ozeanographie. Naturwissenschaftliche Monographien und Lehrbücher, Bd. 9, III, 222 pp., 1929. Berlin.

Helland-Hansen, B.. 1930. “Physical oceanography and meteorology. Michael Sars North Atlantic Deep-Sea Exped., 1910” . Rept. Sci. Results, v. 1, art. 2, 217 pp., 1930.

Hesselberg, Th.. 1918. “Über die Stabilitätsverhältnisse bei vertikalen Verschiebungen in der Atmosphäre und im Meer” . Ann. d. Hydr. u. Mar. Meteor., p. 118–29, 1918.

Hesselberg, Th., and H. U. Sverdrup. 1915. Die Stabilitätsverhältnisse des Seewassers bei vertikalen Verschiebungen. Bergens Museums Aarbok 1914–15, No. 15, 16 pp., 1915.

Willimzik, M.1929. “Die Strömungen im subtropischen Konvergenzgebiet des Indischen Ozeans. Berlin, Universität” . Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 14, 27 pp., 1929.