The Water Masses of the Oceans
TheT-S Diagram. Water masses can be classified on the basis of their temperature-salinity characteristics, but density cannot be used
The corresponding temperature and salinity values in a water column are found to arrange themselves according to depth. The depths of the observed values can be entered along the T-S curve, which then will also give information as to variation of temperature and salinity with depth.
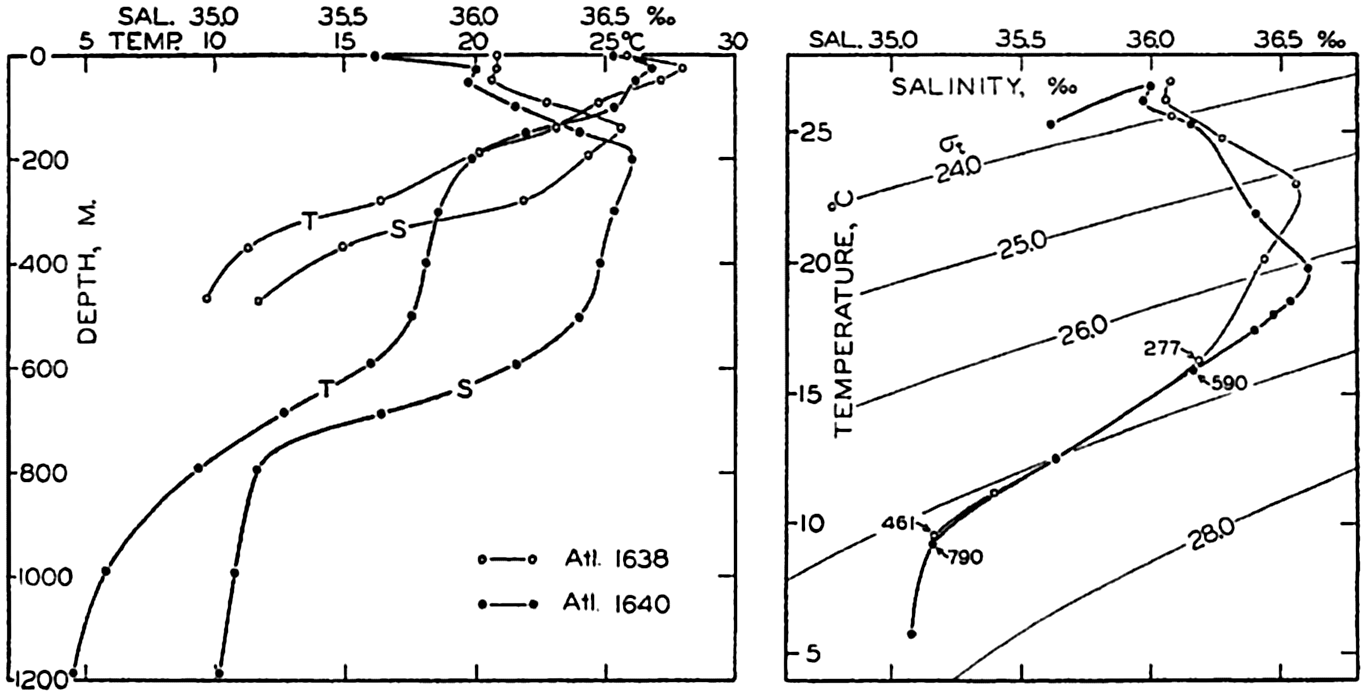
Left: Temperature and salinity at Atlantis stations 1638 and 1640 in the Gulf Stream off Onslow Bay plotted against depth. Right: The same data plotted in a T-S diagram in which σt-curves have been entered.
Since the density of the water at atmospheric pressure, which is expressed by means of σt (p. 56), depends only on temperature and salinity, curves of equal values of σt can be plotted in the T-S diagram. If a sufficiently large scale is used, the exact σt value corresponding to any combination of temperature and salinity can be read off and, if a small scale is used, as is commonly the case, approximate values can be obtained. The slope of the observed T-S curve relative to the σt curves gives immediately an idea of the stability of the stratification (p. 417).
A T-S diagram is shown on the right in fig. 34. On the left in the same figure the observed temperatures and salinities at the Atlantis stations 1638 and 1640 in the Gulf Stream off Onslow Bay are plotted
The T-S diagram has become one of the most valuable tools in physical oceanography. By means of this diagram characteristic features of the temperature-salinity distribution are conveniently represented and anomalies in the distribution are easily recognized. The diagram is also widely used for detecting possible errors in the determination of temperature or salinity (p. 358).
Water Masses and Their Formation. Following Helland-Hansen's original suggestion, a water mass is defined by a T-S curve, but in exceptional cases it may be defined by a single point in a T-S diagram; that is, by means of a single temperature and a single salinity value. These exceptional cases are encountered in basins where homogeneous water is present over a wide range of depth. A water type, on the other hand, is defined by means of single temperature and salinity values, but a given water type is generally present along a surface in the sea and has no thickness. Only in the exceptional cases that were referred to are the terms “water type” and “water mass” interchangeable, but in oceanographic literature the terms have been used loosely and without the distinction that has been introduced here.
In many areas the T-S curves are straight lines or can be considered as composed of several pieces of straight lines. Elementary considerations show that a linear relation between temperature and salinity must result if the water types that can be defined by the end points of the straight line mix in different proportions. Similarly, a curved T-S relation may result from the mixing of three different types of water. Fig. 35 illustrates in two simple cases how progressive mixing alters the temperature-salinity relation. These considerations are of a formalistic nature, but have in many instances led to the concept that certain water types exist and that the T-S relations that are observed represent the end results of mixing between the types. This concept presupposes that the water types (often referred to as water masses) are continually renewed, because, if that were not the case, processes of mixing would ultimately lead to the formation of homogeneous water. It is possible, however, to account for the character of the T-S curves in the ocean by considering other processes.
In the first place it should be observed that a water mass of uniform temperature and salinity is rarely formed in the open ocean. In high latitudes, where convection currents in winter may reach to the bottom, most of the deep and bottom water will not be uniform, because in some
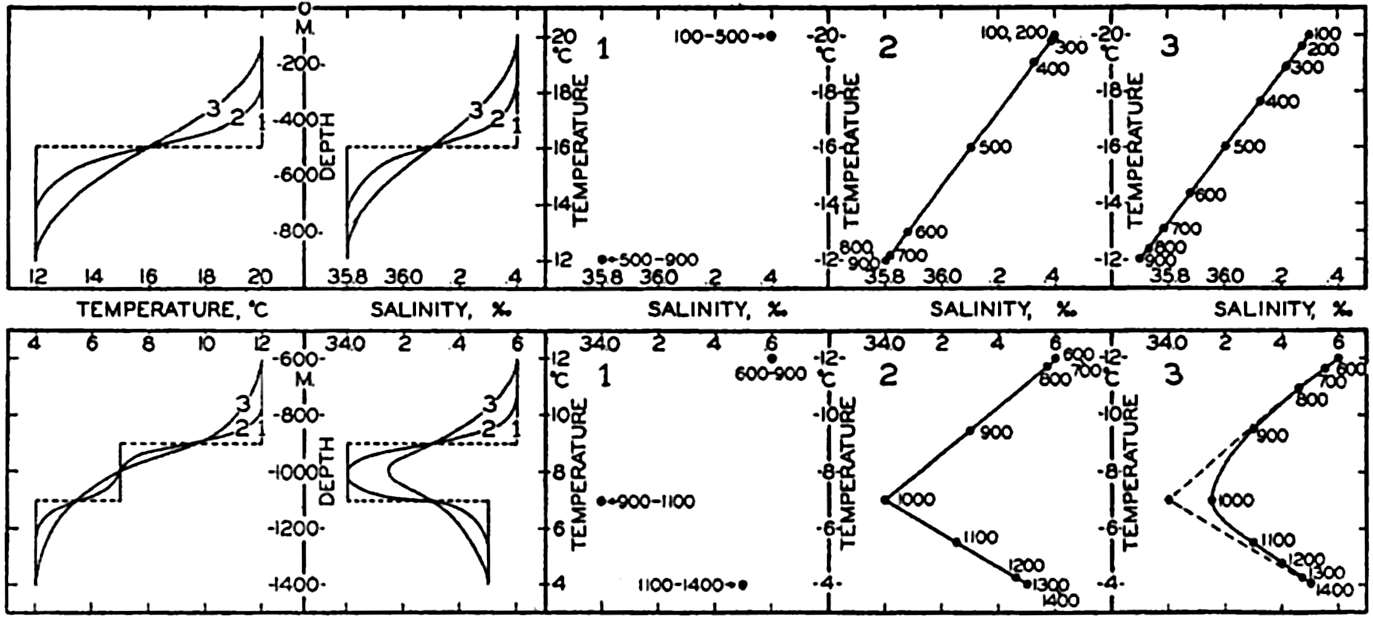
Diagrammatic representation of results of vertical mixing of water types. To the left the results of mixing are shown by temperatures and salinities as functions of depth, and to the right are shown in three T-S diagrams the initial water types (1) and the T-S relations produced by progressive mixing (2 and 3).
However, a similar T-S relationship can be established by different processes, as illustrated in the lower part of fig. 36. It is here assumed that two water types, a and b, are formed at the surface and sink along their characteristic σt surfaces. It is furthermore assumed that at subsurface depths mixing takes place between these two water types, whereas near the surface external processes influence the distribution of temperature and salinity so that there the different curves cross each other. In these circumstances one obtains a T-S relation at subsurface depths that is similar to the one found in the previous example, but along the sea surface an entirely different T-S relation may exist. The processes of mixing, in this case, must take place across σt surfaces in order to establish the T-S relation, but at subsurface depths mixing along σt surfaces is not excluded. At present it is impossible to decide what processes are of the greater importance.
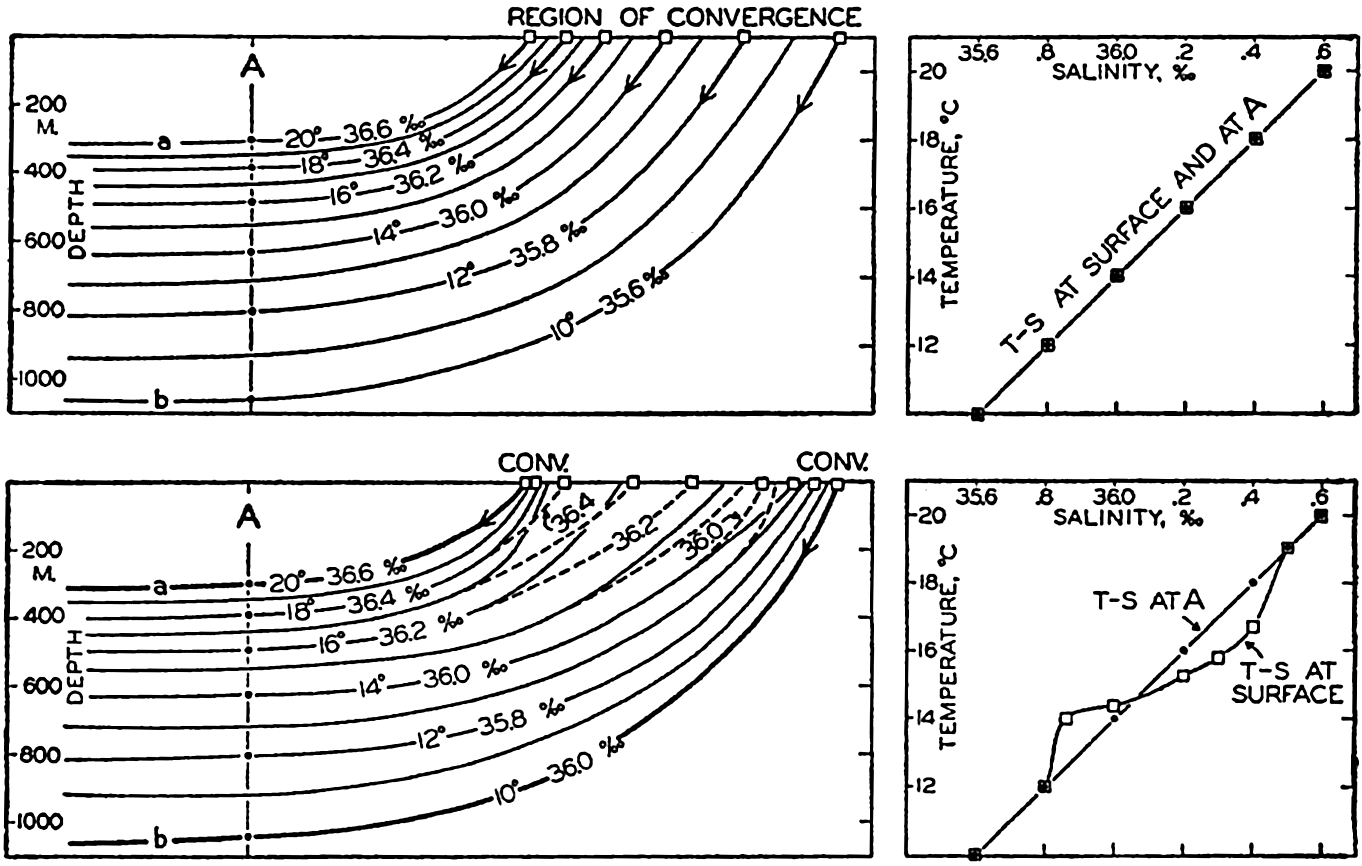
Upper: Schematic representation of the formation of a water mass by sinking along σt surfaces (which coincide with the parallel temperature and salinity surfaces) in a region of convergence. The diagram to the right demonstrates that the vertical T-S relation of the water mass agrees with the horizontal T-S relation at the surface in the region of convergence. Lower: Schematic representation of the formation of a water mass by sinking of water types at two convergences and by subsequent mixing. The diagram to the right illustrates that in this case the vertical T-S relation of the water mass need not agree with the horizontal T-S relation at the surface between the convergences.
The point to bear in mind is that the waters of the oceans all attained their original characteristics when the water was in contact with the atmosphere or subject to heating by absorption of radiation in the surface layers, and that in course of time these characteristics may become greatly changed by mixing. This mixing can either be lateral—that
An example of lateral mixing between water masses is found off the coast of California (Sverdrup and Fleming, 1941), where the water which flows north close to the coast has a T-S relation that differs greatly from that of the water flowing south at some distance from the coast (fig. 199, p. 713). Between these two water masses are found waters of an intermediate character which could not possibly have been formed by vertical mixing and which must have been formed by lateral mixing, probably along σt surfaces. An example of modification of a water mass by vertical mixing is found in the South Atlantic, where the Antarctic intermediate water flows north. This water, near its origin, is characterized by a low salinity minimum, but the greater the distance from the Antarctic Convergence the less pronounced is this minimum (fig. 210, p. 748). The change probably cannot be accounted for by lateral mixing, but Defant (1936) has shown that it can be fully explained as a result of vertical mixing.
Wüst (1935) has introduced a different method for the study of the spreading out and mixing of water types, the “Kernschicht-methode,” which can be translated “the core method.” By the “core” of a layer of water is understood that part of the layer within which temperature or salinity, or both, reach extreme values. Thus, in the Atlantic Ocean, the water that flows out from the Mediterranean has a very high salinity and can be traced over large portions of the Atlantic Ocean by means of a secondary salinity maximum which decreases in intensity with increasing distance from the Strait of Gibraltar. The layer of salinity maximum is considered as the core of the layer in which the Mediterranean water spreads, and the decrease of the salinity within the core is explained as the result of processes of mixing. In this case a certain water type, the Mediterranean water, enters the Atlantic Ocean and loses its characteristic values, owing to the mixing, but can be traced over long distances. The spreading of the water can also be described by means of a T-S curve, one end point of which represents the temperature and salinity at the source region and the other end point of which represents the temperature and salinity in the region where the last trace of this particular water disappears. Having defined such a T-S curve, one can directly read off from the curve the percentage amount of the original water type that is found in any locality. The core method has proved very successful in the Atlantic Ocean and is particularly applicable in cases in which a well-defined water type spreads out from a source region.