Distribution of Conservative Concentrations in the Sea

The discussion has so far been of a purely formalistic nature. If one goes a step further and considers the processes that maintain or tend

---

to alter distributions, it is of advantage to introduce the term concentration to describe any constituent that is present in a measurable amount in a given volume of sea water. Thus, heat content, total salt (which can be represented with sufficient accuracy by salinity), amount of a given compound, and dissolved oxygen or other gases can be given as concentrations, and the same applies to floating organisms. A concentration is a scalar quantity that is continuous in time and space, and the distribution can therefore be represented by means of fields whose characteristics have been dealt with.

The processes that tend to modify the concentrations can be divided into two groups: external processes, which are active only at the boundary surfaces of the fluid, and internal processes, which are active anywhere in the fluid. The external processes are of importance in determining the concentrations at the boundaries, and the internal processes, together with the boundary values, determine the distribution throughout the fluid.

By conservative concentrations are meant concentrations that are altered locally, except at the boundaries, by processes of diffusion and advection only. Heat content and salinity are two outstanding examples of conservative concentrations. Consider a cube the surfaces of which are of unit area and are normal to the coordinate axes. Through the two surfaces that are normal to the x axis, diffusion leads to a transport in unit time of (A_x/ρ)₁(∂ s/∂ x)₁ and (A_x/ρ)₂(∂ s/∂ x)₂, respectively, where both the coefficient, A_x, and the derivative, ∂ s/∂ x, may vary in the x direction. The coefficient of diffusion enters here in the “kinematic” form (p. 470) as A / ρ, where A is the eddy diffusivity, because concentrations have been defined as amounts per unit volume. The difference per unit length of these transports, ∂/∂ x[(A_x/ρ)(∂ s/∂ x)], represents the net change of concentration in the unit volume due to diffusion. In the presence of a current in the x direction, there will also be a net change of concentration due to advection. The concentration that a current of velocity, v_x, transports through a unit surface in unit time is equal to sv_x, and, if this transport changes in the direction of flow, the concentration per unit volume is altered by —∂(sv_x)/∂ x. Similar considerations are applicable to transport through the other surfaces of the cube, and the combined local change of concentration, therefore, is the sum of terms representing diffusion and advection:

The last term can be written

---

but in an incompressible fluid the sum of the terms in parentheses is equal to zero (p. 424). Sea water can be considered as incompressible; therefore, or, in words: Local time change of concentration equals the effect of diffusion minus effect of advection.

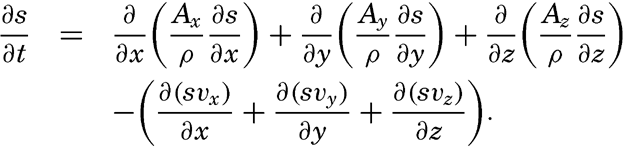
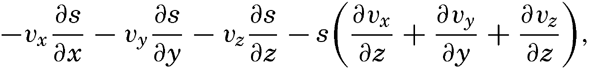
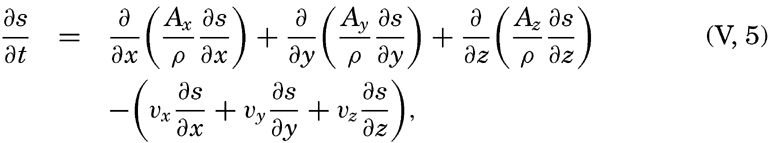
Taking equation (V, 4) into consideration, one obtains

or, in words: Individual time change of concentration equals effect of diffusion.

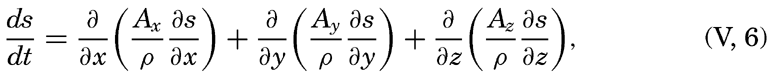
In practice these equations must be greatly simplified. Consider, for example, a two-dimensional system in which the velocity is directed along the x axis, in which diffusion in the x direction can be neglected, and in which it can be assumed that the coefficient of vertical diffusion, A / ρ, is constant. For such a system the condition for a stationary distribution of s, (∂ s/∂ t = 0), is reduced to

This equation has been used by Defant (1929) and Thorade (1931) for studying the character of stationary distributions and by Defant (1936) for computing the ratio A / v_x from observed distributions.

As another example, consider a uniform field for which ∂ s/∂ t=ds/dt and assume that A_x = A_y = 0. The above equations are then reduced to

which represents the equation of temperature conduction (p. 135). It may be observed that temperature is not a concentration according to the above definition, but since the temperature is proportional to the heat content, cpϑ, of a unit volume, s can mean temperature.

Other simplifications of the equations can be made, depending upon the nature of the problem under consideration (Montgomery, 1939, Sverdrup, 1939).