Density of Sea Water

The density of any substance is defined as the mass per unit volume. Thus, in the c.g.s. system, density is stated in grams per cubic centimeter. The specific gravity is defined as the ratio of the density to that of distilled water at a given temperature and under atmospheric pressure. In the c.g.s. system the density of distilled water at 4°C is equal to unity. In oceanography, specific gravities are now always referred to distilled water at 4°C and are therefore numerically identical with densities. In oceanography the term density is generally used, although, strictly speaking, specific gravity is always considered.

The density of sea water depends upon three variables: temperature, salinity, and pressure. These are indicated by designating the density by the symbol ρ_s,ϑ,p, but, when dealing with numerical values, space is saved by introducing σ_s,ϑ,p which is defined in the following manner:

Thus, if ρ_s,ϑ,p = 1.02575, σ_s,ϑ,p = 25.75.

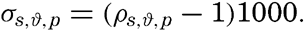
The density of a sea-water sample at the temperature and pressure at which is was collected, ρ_s,ϑ,p is called the density in situ, and is generally expressed as σ_s,ϑ,p. At atmospheric pressure and temperature ϑ°C, the corresponding quantity is simply written σ_t, and at 0° it is written σ₀. The symbol ϑ will be used for temperature except when writing σ_t, where, following common practice, t stands for temperature.

At atmospheric pressure and at temperature of 0°C the density is a function of the salinity only, or, as a simple relationship exists between salinity and chlorinity, the density can be considered a function of chlorinity. The International Commission, which determined the relation between salinity and chlorinity and developed the standard technique for determinations of chlorinity by titration, also determined the density of sea water at 0° with a high degree of accuracy, using pycnometers. From these determinations the following relation between (σ₀ and chlorinity was derived:

Corresponding values of σ₀, chlorinity, and salinity are given in Knudsen's Hydrographical Tables for each 0.01 ‰ Cl

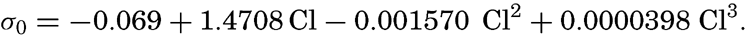
In order to find the density of sea water at other temperatures and pressures, the effects of thermal expansion and compressibility on the density must be known. The coefficient of thermal expansion has been determined in the laboratory under atmospheric pressure, and

---

according to these determinations the density under atmospheric pressure and at temperature ϑ° can be written in the form The quantity D is expressed as a complicated function of σ₀ and temperature, and is tabulated in Knudsen's Hydrographical Tables. Since the values of σ_t are widely used in dynamical oceanography, tables for computing σ_t directly from temperature and salinity have been prepared by McEwen (1929) and Matthews (1932). A special slide rule for the same purpose has been devised by Sund (1929). Knudsen's tables also contain a tabulation of D as a function of σ_t and temperature, by means of which σ₀ can be found if σ_t is known (σ₀ = σ_t + D). This table is useful for obtaining the salinity of a water sample the density of which has been directly determined at some known temperature (p. 53).

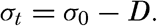
The effect on the density of the compressibility of sea water of different salinities and at different temperatures and pressures was examined by Ekman (1908), who established a complicated empirical formula for the mean compressibility between pressures 0 and p decibars (quoted in V. Bjerknes and Sandström, 1910). From this formula, correction terms have been computed which, added to the value of σ_t, give the corresponding value σ_s,ϑ,p for any value of pressure.

Computation of Density and Specific Volume in Situ. Tables from which the density in situ, ρ_s,ϑ,p could be obtained directly from the temperature, salinity, and pressure with sufficiently close intervals in the three variables would fill many large volumes, but by means of various artifices convenient tables have been prepared. Following the procedure of Bjerknes and Sandström (1910), one can write

The first four terms can be expressed by σ_t, which can readily be determined by the methods outlined above, and the remaining terms represent the effects of the compressibility. When dealing with density it is desirable, for reasons that will be explained later (p. 402), to introduce the dynamic depth, D, as the independent variable instead of the pressure, p, and to write The ∊ terms in this equation have been tabulated by Bjerknes and Sndström (1910) and by Hesselberg and Sverdrup (1914).

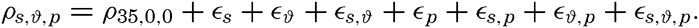
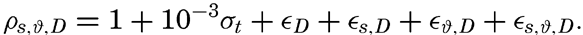
Instead of the density, ρ_s,ϑ,p, its reciprocal value, the specific volume in situ, α_s,ϑ,p is generally used in dynamic oceanography. In order to avoid writing a large number of decimals, the specific volume is commonly expressed as an anomaly, δ, defined in the following way:

---

where α_35,0,p is the specific volume of water of salinity 35 ‰, at 0°C, and at pressure p in decibars. The anomaly depends on the temperature, salinity, and pressure, and hence can be expressed as It should be observed that the anomaly, by definition, does not contain a term δ_p, which would represent the effect of pressure at temperature 0° and salinity 35 ‰. The reason for this is explained on page 409. Of the above terms the last one, δ_s,ϑ,p is so small that it can always be neglected. Thus, five terms are needed for obtaining δ, and these were tabulated by Bjerknes and Sandström. If σ_t has already been computed, the terms that are independent of pressure can be combined as Δ_s,ϑ, (Sverdrup, 1933).

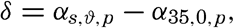
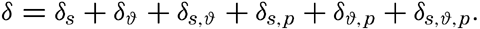
The value of Δ_s,ϑ, = δ_s + δ_ϑ + δ_{s, ϑ} is easily obtained from σ_t because

and Hence Thus, in practice, The values for these three terms are given in the appendix in small tables from which one can obtain the specific volume anomaly in situ of any water sample when its temperature, salinity, σ_t and the pressure are known. In these tables the terms are entered with one extra decimal place in order to avoid any accumulation of errors due to rounding-off of figures, and also in order to facilitate preparation of exact graphs that may be used instead of the tabulation, or for the preparation of tables in which the arguments are entered at such close intervals that interpolation becomes easy or unnecessary.

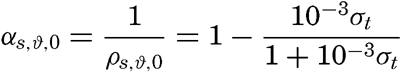
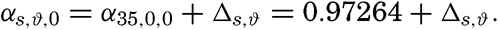
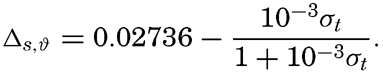
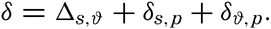
The procedure that is followed in calculating the density or specific volume in situ can be summarized as follows. For a given water sample the temperature, salinity, and depth at which it was collected must be known. For reasons stated elsewhere it can be assumed that the numerical value of the pressure in decibars is the same as that of the depth in meters. From the temperature and salinity the value σ_t is obtained from Knudsen's Tables or from graphs or tables prepared from this source, (McEwen, 1929; Matthews, 1932). With the values of σ_t temperature, salinity, and pressure the specific volume anomaly is computed by means of the tables given in the appendix. If the absolute value of the specific volume is required, the anomaly must be added to

---

the appropriate value of α_35,0,p,ϑ, given in the appendix. In this table are given the specific volume of water of 35 ‰ and 0° at various pressures in decibars. The absolute density in situ can then be obtained as the reciprocal of the specific volume.

Another set of tables for computing the specific volume in situ has been prepared by Matthews (1938), who, in our notations, defines the anomaly as δ′ = α_s,ϑ,p − α_34,85,0,p. Thus, he refers the anomalies to water of salinity 34.85 ‰, for which σ₀ = 28.00. The difference, δ − δ′ = α_34,85,0,p − α_35,0,p, depends upon the pressure:

Before comparing numerical values of the specific volume anomalies published in different reports, it is necessary to know on what tables the reported values are based.

Use of Knudsen's Hydrographical Tables. A certain point concerning the use of Knudsen's Hydrographical Tables should be kept in mind. Although they have been shown to hold very well over the normal range of the concentration of sea water, they are not necessarily valid for highly diluted or concentrated sea water. The tables are based on the careful examination of a series of samples collected from various regions. The dilute samples used were taken in the Baltic Sea, where dilution sometimes reduces the chlorinity to about 1 ‰, and where the river water that is mainly responsible for the dilution contains relatively large quantities of dissolved solids. This is shown by the fact that the equation relating salinity to chlorinity shows a salinity of 0.03 ‰ for zero chlorinity, and according to Lyman and Fleming (1940) the total dissolved solids corresponding to this figure are probably of the order of 0.07 ‰. Thus, empirically, the salinity of sea water can be expressed by an equation of the type

where the numerical value of a depends upon the composition of the diluted samples used for establishing the relation. If 1 kg of water of high salinity, S, is diluted by adding n kilograms of distilled water, the salinity of the dilution will be S_D = S/(n + l), and the chlorinity of the diluted sample will be Cl/(n + 1). According to Knudsen's Tables this sample, however, has a salinity S_K = a + b Cl/(n + 1). The difference between this and the true salinity is S_K − S_D = a[n/(n + l)], meaning that, if after dilution the chlorinity were determined by titration and the salinity were taken from Knudsen's Tables, it would be too high. Knudsen's Tables would therefore also give too great a density. As an example, let us assume that 1 kg of water of salinity 35 ‰ and chlorinity 19.375 ‰ is diluted by adding 9 kg of distilled water, reducing the

---

chlorinity to 1.938 ‰. Knudsen's Tables give for this chlorinity a salinity of 3.53 ‰, whereas the “true” salinity would be 3.50 ‰. Similarly, Knudsen's Tables would give a σ₀ equal to 2.78, whereas the true value should be 2.75. At low concentration, chlorinities computed from direct density determinations, and vice versa, may therefore be in error. For example, “chlorinities” of sea ice computed from density measurements made on the melt water were consistently smaller than those determined by titration (p. 219), and in this case the diluting water was essentially distilled water. The restricted application of the Cl : S : density relations to highly diluted water occurring naturally or prepared in the laboratory should always be kept in mind.