Currents Related to the Field of Pressure
Relative Currents and Slope Currents. The above considerations are all general and are valid regardless of the character of the pressure field. When discussing the latter (p. 413) it was pointed out that the total pressure field could always be considered as composed of two parts: the relative field of pressure due to the field of mass, and the slope field due to actual piled-up masses: pt = p − Δp, where pt is the total pressure and p is the relative pressure, and where the last term represents a correction due to piled-up masses. With the pressure in decibars, Δp = gρΔh/10, where Δh represents the thickness of the removed or added mass in meters, and is positive when mass is removed, because the positive z axis is directed downward.
The total pressure gradient, therefore, has the components
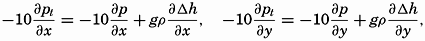
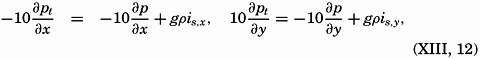
Introducing equation (XIII, 12) in the equation of motion, considering that pt has previously been written p, and omitting the frictional terms, one obtains
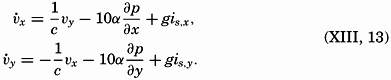
In the first approximation, therefore, writing νx = νp,x + νs,x and νy = νp,y + νs,y, one obtains
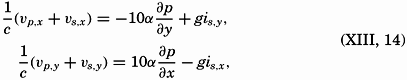
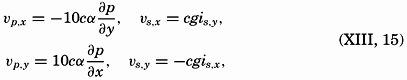
These equations mean that the current can be considered as composed of two parts: one which is dependent on the relative field of pressure and will be called the relative current, and one which depends on the added slope of the free surface and will be called the slope current. Ekman has called the relative current the convection current, but this term, as pointed out by Ekman, is liable to cause confusion because, in meteorology, convection currents mean ascending and descending currents and not horixontal flow.
Of these two types of currents, only the relative current can be derived from observations of density, because only the relative field of pressure can be determined from such observations. Any added slope of the isobaric surfaces due to actual piling up of mass in certain instances can be derived from precise leveling along coasts, but in general it cannot be observed. It is of great importance to bear these facts in mind in order to avoid erroneous conclusions.
The character of the slope current is readily seen. Equations (XIII, 15) state that the velocity is always directed at right angles cum sole relative to the slope. As the slope is independent of the depth, the same therefore applies to the velocity. Thus, if slope currents exist, they are uniform from top to bottom, in contrast to the relative currents, which vary with depth.
In the equations which, on the above assumptions, determine the relative current, the geometric or the geopotential slope of the relative isobaric surfaces can be introduced (p. 440):
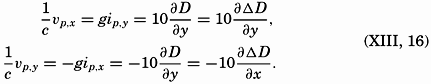
Currents in Stratified Water. Some of the outstanding relationships between the distribution of mass and the velocity field are brought out by considering two water masses of different density, ρ and ρ′, where ρ is greater than ρ′. In the absence of currents, the boundary surface between the two water masses is a level surface, the water mass of lesser density, ρ′, lying above the denser water. On the other hand, if the water of density ρ′ moves at a uniform velocity ν′ and the water of greater density moves at another uniform velocity ν, the boundary must slope. For the sake of simplicity it will be assumed that both water masses move in the direction of the y axis and that the acceleration of gravity g can be considered constant. The dynamic boundary condition (p. 441) then takes the form
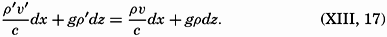
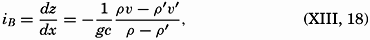

As an extreme case, consider two water masses, one of salinity 34.00 ‰ and temperature 20°, and one of salinity 35.00‰ and temperature 10°, and assume that the velocity of the former is 0.5 m/sec. Neglecting the effect of pressure on density, one obtains
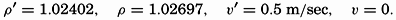
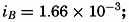
The slopes of the isobaric surfaces are much smaller. Inserting the numerical values in equation (XIII, 19), one obtains
Isobaric surfaces and currents within a wedge of water which extends over resting water of greater density.
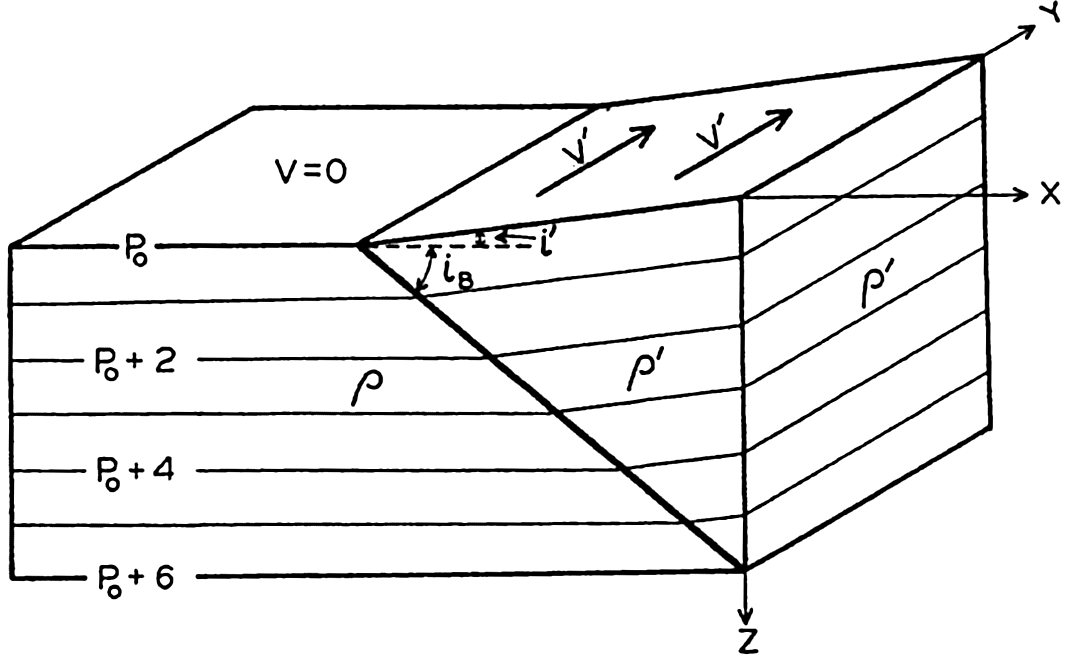
As another example, consider the case in which the current in the upper layer is limited to a band L. In this case, perfect static equilibrium must exist in the regions of no currents, and there the boundary between the two water masses must be horizontal, but in the region where the water of low density flows with a velocity ν′, the boundary surface must slope, the steepness of the slope being determined by equation (XIII, 18). These conditions are shown schematically by the block diagram in fig. 106, in which it is supposed that the denser water reaches the surface on the left-hand side of the current. This figure brings out an important relationship between the current and the distribution of mass: The current flows in such a direction that the water of low density is on the right-hand side of the current, and the water of high density is on the left-hand
Other examples could be added (Defant, 1929b), but the two which have been given here demonstrate sufficiently the relation between the currents and the distribution of mass in stratified water.
In the ocean a discontinuous transition from one type of water to another is never found, but in several regions a transition takes place in such a short distance that for practical purposes the layer of transition can be considered as a boundary surface. In such cases, equation (XIII, 18) can be used for computing the relative currents in a direction parallel to the boundary surface. Certain simplifications can be introduced, because ρ and ρ′ always differ so little that (ρν − ρ′ν′) can be replaced by 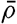 (ν − ν′). Therefore, the relative velocity can be computed by means of the equations
(ν − ν′). Therefore, the relative velocity can be computed by means of the equations
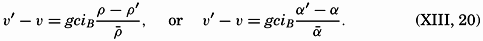
Isobaric surfaces and curreants within water which in part extends as a wedge over resting water of greater density.
The relative slope of the isobaric surfaces (XIII, 19) can also be expressed by means of the slope of a boundary layer:
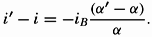
The above equation can be derived in a different manner. In fig. 106, it has been assumed that the isobaric surfaces that lie completely in the
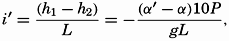
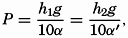
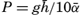 . With this value, one obtains
. With this value, one obtains
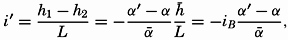
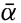 /L equals the slope of the boundary surface.
/L equals the slope of the boundary surface.Where the isobaric surfaces slope, a current must flow in a direction at right angles to the slope, and with such velocity that the component of gravity acting along the slope is balanced by the deflecting force of the earth's rotation:
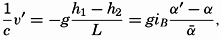
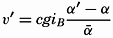

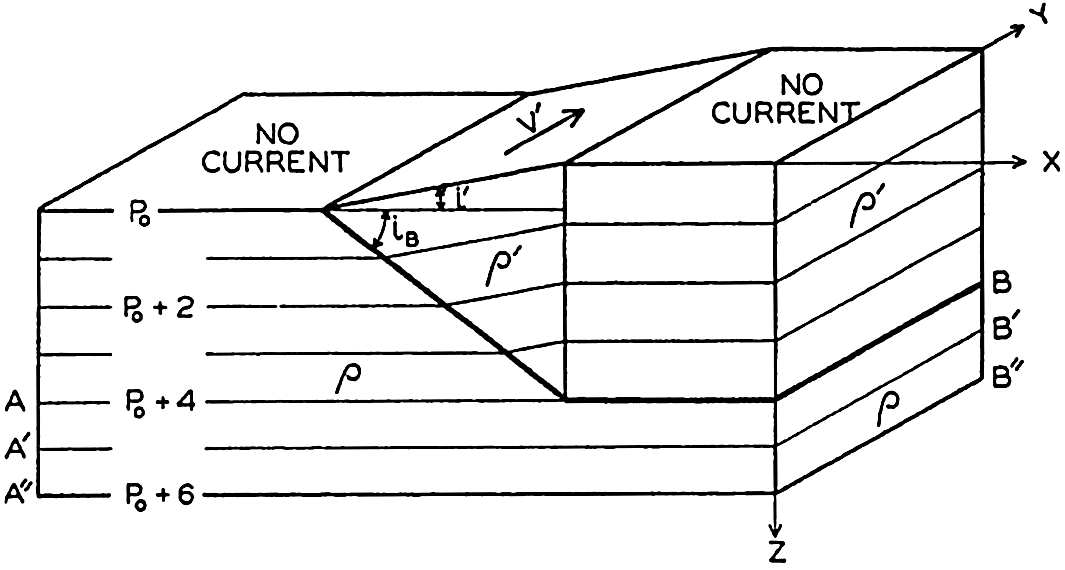
Currents in Water in Which the Density Increases Steadily with Depth. The discussion in the preceding paragraph leads directly to corresponding formulae in the general case in which the density of the water increases steadily with depth. The relative velocity has, as previously, the numerical value ν1 − ν2 = cgip1−p2, where ip1−p2 is the inclination of the isobaric surface p1 relative to the isobaric surface p2.
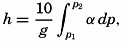
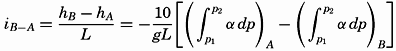
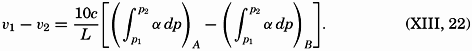
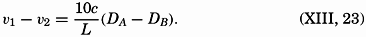
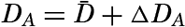 and
and 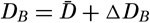 (p. 408), the equation is reduced to
(p. 408), the equation is reduced to
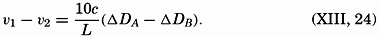
By means of the relations between the field of pressure and the field of mass, which were derived on p. 410, one similarly obtains (Werenskiold, 1937)

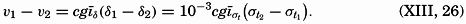
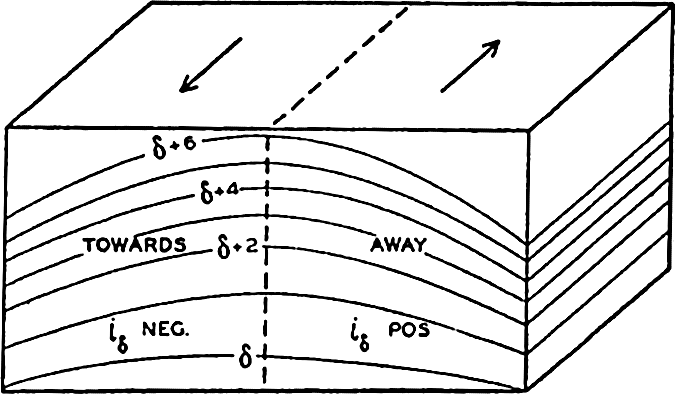
Equations (XIII, 26) are of practical importance because they facilitate a rapid survey of the relative currents at right angles to a section in which the field of mass has been represented by means of the anomalies, δ, or by means of σt curves. The inclination of a curve is positive when the curve slopes downward from left to right, because the positive z axis points downward (see fig. 107). Since “pressure”
In the Northern Hemisphere the current at one depth relative to the current at a greater depth flows away from the reader if, on an average, the δ or σt curves in a vertical section slope downward from left to right in the interval between the two depths, and toward the reader if the curves slope downward from right to left. In the Southern Hemisphere the current flows toward the reader if the curves slope downward from left to right, and away from the reader if the curves slope downward from right to left.
Schematic representation of a field of mass and of the direction of the currents which must be present if the field shall remain stationary (Northern Hemisphere).
These rules make possible an orientation as to the direction of the relative currents by a glance at a δ or σt section and a rapid computation of the approximate velocities.
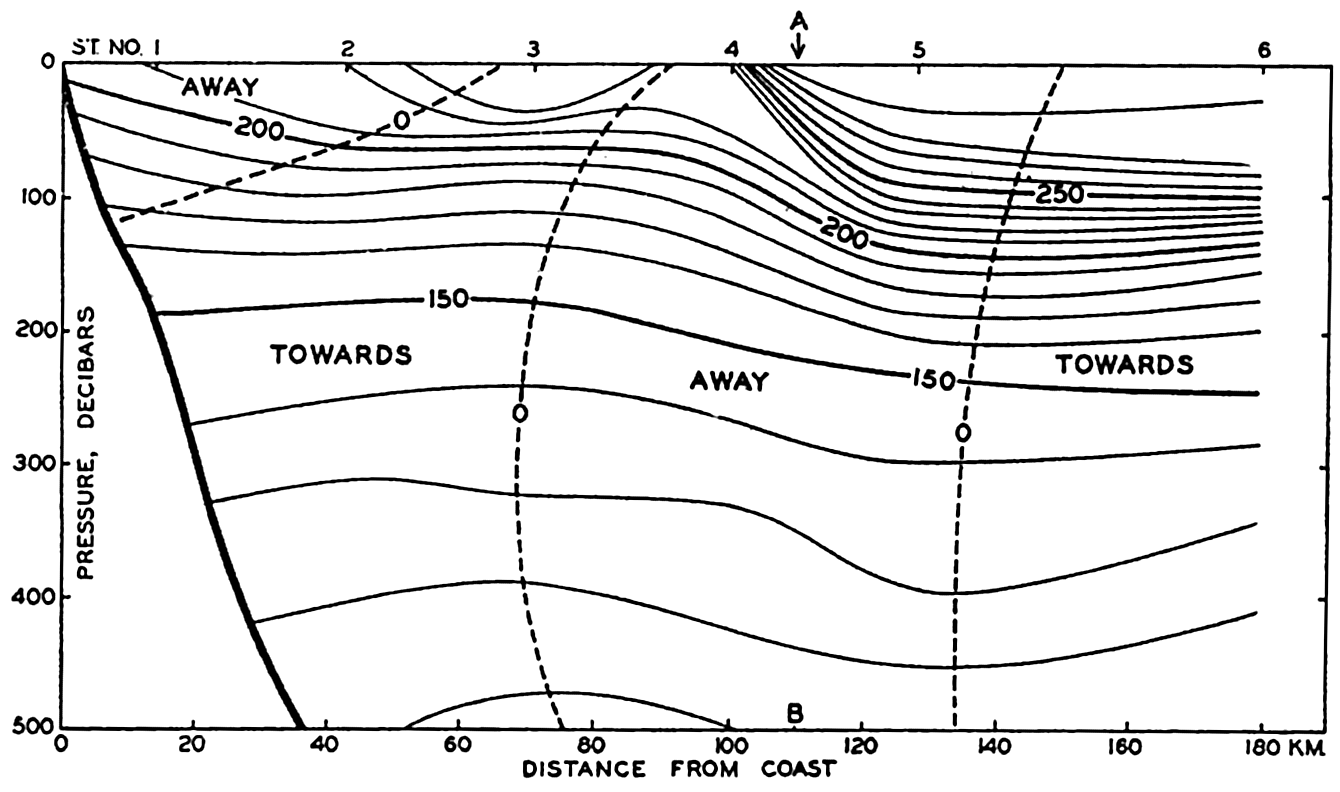
Specific volume anomalies in a vertical section at right angles to the coast of California in lat, 34.5°N, and direction of corresponding currents above 500 decibars.
Fig. 108 gives an example of a section at right angles to the coast of California in lat. 34.5°N. The section runs in the direction northeast-southwest, and the reader looks southeast. In the section, δ curves are entered at intervals of 10 × 10−5. The velocity relative to the
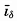 is approximately zero between them and the 500-decibar surface. To the right the relative current is directed toward the reader, and to the left it is also directed toward the reader except within the upper layer. In the middle a strong current is directed away from the reader, toward the southeast. Along the line A-B,
is approximately zero between them and the 500-decibar surface. To the right the relative current is directed toward the reader, and to the left it is also directed toward the reader except within the upper layer. In the middle a strong current is directed away from the reader, toward the southeast. Along the line A-B,
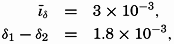
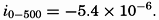
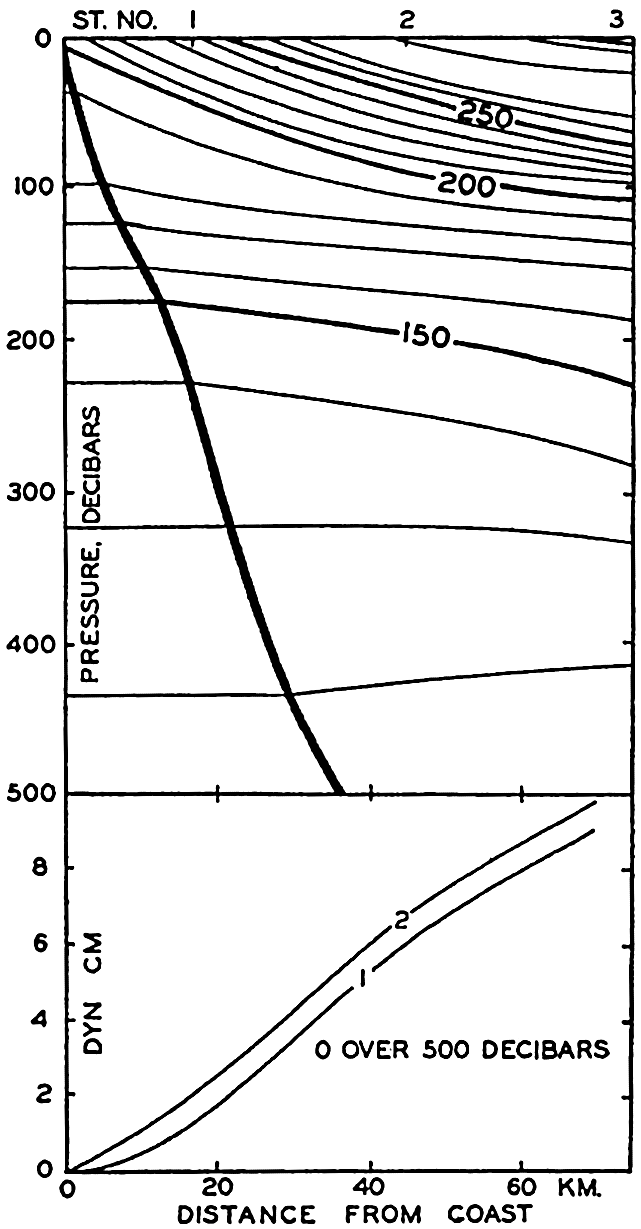
Upper. Specific volume anomalies in a vertical section at right angles to the coast of California in lat. 34.5°N. Lower. Profiles of sea surface computed (1) by continuing the anomaly curves horizontally from the point where they intersect the sea bottom, or (2) by assuming that the slope of the anomaly curves at the bottom determines the slope of the isobaric surface (see text).
Fig. 108 brings out a difficulty that is encountered when dealing with conditions in a section which extends into shallow water. In the figure the δ curves have been drawn to the solid line that represents the contour line of the bottom. Formula (XIII, 26), for computing the slope of the free surface relative to the slope of the 500-decibar surface, is applicable, however, only where the depth to the bottom is greater than 500 m, and loses its meaning if the depth to the bottom is less. The question then arises as to how the inclination of the free surface shall be computed when the depth to the bottom is less than the depth of the standard isobaric surface to which the inclination is referred. At the suggestion of Nansen, Helland-Hansen (1934) introduced a method which is actually based on the assumption that along the bottom both the
A similar method has been proposed by Jacobsen and Jensen (1926), but their formula introduces the additional assumptions that the profile of the bottom of the sea is a straight line and that the δ curves are parallel and at equal distances.
The assumption that the velocity vanishes at the bottom is probably always correct because of the influence of friction, but it is doubtful if the slope of the isobaric surface vanishes. As another approximation, one can apply the equation ip = −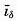 (δ1 − δ2) (p. 412), introducing the slope of the δ surfaces where they cut the bottom and taking the difference δ1 − δ2 along the bottom. In the lower part of fig. 109 the profile of the free surface is shown as computed by means of the two assumptions. The difference in this case is very small and, even under extreme conditions, will never be very significant.
(δ1 − δ2) (p. 412), introducing the slope of the δ surfaces where they cut the bottom and taking the difference δ1 − δ2 along the bottom. In the lower part of fig. 109 the profile of the free surface is shown as computed by means of the two assumptions. The difference in this case is very small and, even under extreme conditions, will never be very significant.
No general rule can be given as to what method should be preferred. One may encounter conditions in which the assumption that the slope of the isobaric surface vanishes at the bottom is justified, and in such cases Helland-Hansen's method should be used, but in other instances, where it may appear improbable that the slope of the isobaric surface is zero near the bottom, the last-mentioned method should be preferred.
Practical Method for Computing Relative Currents. The formulae that have been dealt with in the last chapter are applicable to computation of currents at right angles to a vertical section. In order to derive a method for computing the currents in space, it is necessary only to return to equation (XIII, 16), which states that in the absence of friction and acceleration the velocity must be such that the deflecting force of the earth's rotation balances the component of gravity acting along an isobaric surface. It is now desirable to drop the assumption that the acceleration of gravity can be considered constant and to use the geopotential slope of isobaric surfaces instead of the geometric slope. It follows from equation (XIII, 16) that, on the assumptions made, the direction of the velocity will be normal to the slope of the isobaric surfaces—that is, parallel to the contour lines of the topography of the surfaces. The magnitude of the velocity will be inversely proportional to the distance between the contour lines, the factor of proportionality depending upon the latitude. The whole problem of presenting the
As has already been stated (p. 412), oceanographic observations can give information only as to the relative topographies, and therefore only as to the relative velocities. When using the term “relative velocity,” one should bear in mind that the absolute velocities (referred to the rotating earth) are not obtained by adding a constant value to the relative velocities, but that the value which has to be added in order to obtain the absolute velocities varies from one point to another, depending upon the unknown slope of the isobaric surface that has been used as a reference surface.
The contour lines of the isobaric surfaces represent the stream lines of the relative motion, but they are not, as a rule, identical with trajectories even if the reference surface is sufficiently level so that the computed velocities represent the absolute motion. If such is the case, the contour lines will be trajectories only if the motion is stationary—that is, if ∂ν/∂t = 0 (p. 157). Because it has been assumed that dv/dt = 0, it follows that the conditions
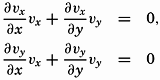
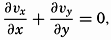
It is also of great importance to remember that equations (XIII, 16) and (XIII, 22) express nothing as to cause or effect. They do not state that the current is present because the distribution of mass is such and such. Nor do they state that the distribution of mass shows certain
The computation of the geopotential distances between isobaric surfaces has already been discussed, and the whole problem of computing ocean currents would therefore be very simple if (1) simultaneous observations of temperature and salinity at different depths were available from a number of stations so that relative topographies could be constructed, (2) accelerations could be neglected, (3) frictional forces could be neglected, and (4) periodic changes in the distribution of mass as related to internal waves (p. 601) were negligible.
Simultaneous observations from a number of stations are never available, and the question therefore arises as to whether charts based on stations that have been occupied within a certain time interval can be considered as approximately representing a synoptic situation. This question can be examined by repeated surveys of the same area. Such surveys have shown that conditions vary in time, but so slowly that the main features of a certain topography are represented correctly by nonsimultaneous observations that have been taken within a reasonably short time interval. Results of repeated surveys are found in the publications of the U. S. Coast Guard presenting the work of the International Ice Patrol off the Grand Banks of Newfoundland, where a small area has been covered in less than a week and where cruises have been repeated at intervals of three to four weeks. In these intervals of time the details of the relative topography have changed greatly, but the main features have changed much more slowly. Similar surveys have been conducted off southern California by the Scripps Institution of Oceanography (Sverdrup and staff, 1942).
Fig. 110 shows the results of two cruises off the coast of southern California in 1940. The upper chart shows the topography of the surface relative to the 500-decibar surface according to observations between April 4 and 14, and the lower chart shows the corresponding topography on April 22 to May 3. The stations upon which the charts are based are shown as dots. The time interval between the cruises was about sixteen days, and, although the main features were similar, the details were greatly changed. Thus, in lat. 33°40′N, long. 120°W, the computed surface current on the first cruise was 36 cm/sec toward N 80°E, whereas on the second cruise it was 14 cm/sec toward S 30°E. In the time interval between the two cruises the average local acceleration was therefore 2.5 × 10−5 cm/sec2 toward S 57°W, but, compared to the acting forces, this is a small quantity. On the first cruise the numerical value of the geopotential slope of the surface was 294 × 10−5 cm/sec2, and on the second it was 117 × 10−5 cm/sec2. The total acceleration is generally of the same order of magnitude as the local acceleration, and was therefore also small. Even in these cases the stream lines of the flow approximately coincided with the contour lines, although the distribution of mass was changing continuously, and the combination of observations taken during ten days led to a somewhat distorted picture of the topography.
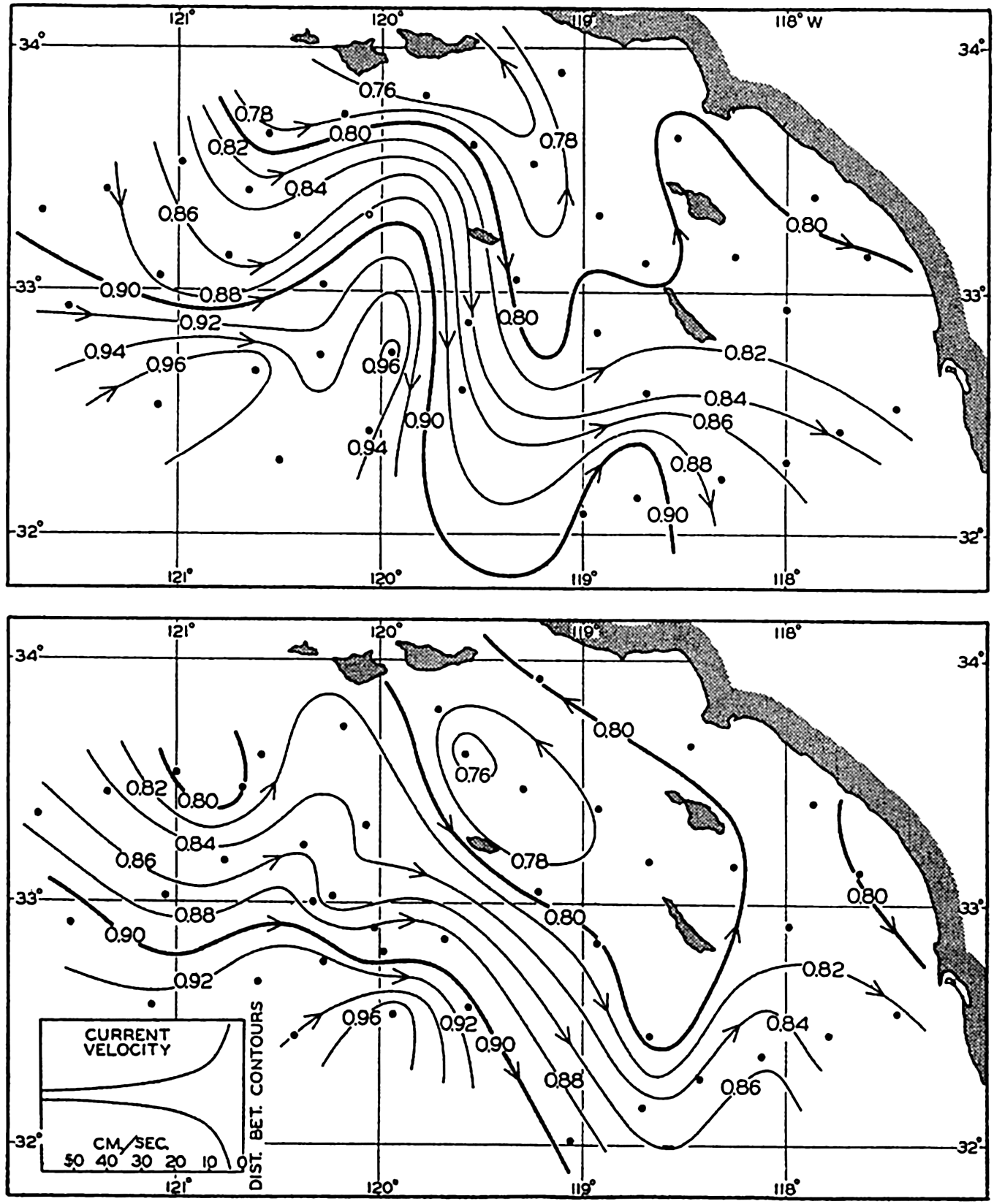
Geopotential topography of the sea surface in dynamic meters referred to the 500-decibar surface according to observations off southern California on April 4 to 14, 1940 (upper), and on April 22 to May 3, 1940 (lower).
As a rule, it can be stated that the smaller the area the more nearly simultaneous must observations be in order to permit conclusions as to currents. On the other hand, when dealing with ocean-wide conditions, observations from different years can be combined.
The second assumption, that the motion is not accelerated, is evidently not fulfilled when dealing with a smaller area within which conditions change rapidly, but, according to the above numerical example, no serious errors are introduced if one is satisfied with an approximate value of velocity. The assumption will be more closely correct when large-scale conditions are considered.
The third assumption, that the frictional forces can be disregarded, must also be approximately correct, as is evident from agreement obtained between computed surface currents and surface currents that are derived from ships' logs or from the results of experimentation with drift bottles. The fourth assumption is nearly correct where the accelerations are small. It can be stated therefore that the computations which have been outlined can be expected to render an approximately correct pictures of the relative velocities that are associated with the distribution of mass.
Absolute Currents Associated with the Field of Mass. In the discussion so far, we have considered only the relative currents associated with the relative field of pressure, but the ultimate goal must be to determine the absolute current. The problem of determining absolute currents can be dealt with in two steps. In the first place, one can consider whether there are reasons to assume that the absolute currents are determined completely by the internal distribution of mass. If this question is answered in the affirmative, one can decide what reference surface should be used in order to find the absolute motion.
The first question can be approached in the following manner: If the distribution of mass remains stationary, the flow must always be parallel to the isopycnals, because, if this condition is not fulfilled, the distribution of mass will be altered by the motion. On the assumptions made, the flow is always parallel to the isobars, and it follows, therefore, that under stationary conditions isopycnals and isobars must be parallel at all levels. It also follows that the isobars and isopycnals at one level must be parallel to those at all other levels (p. 157). This rule is identical with the “law of the parallel solenoids” of Helland-Hansen and Ekman (Ekman, 1923). The absolute motion that must be considered when dealing with distortion of the field of mass depends, however, on the total field, and this total field must evidently have the same geometrical shape as the internal field if the law of the parallel solenoid shall be fulfilled. The total field is composed of the internal and the slope fields (p. 413); consequently, these fields must coincide if the law of the parallel
The study of large-scale conditions in the ocean has shown that over large areas the isotherms and isohalines, and, consequently, the isopycnals, are parallel at different levels and that their direction coincides with the direction of the relative isobars or with the contour lines of the isobaric surfaces. This empirical result strongly supports the view that the large-scale currents are mainly determined by the internal distribution of mass. Even in small areas a similar arrangement is often found, but many exceptions are encountered there which clearly demonstrate that stationary conditions do not exist, and which may be interpreted as indicating that the details of the absolute currents are not determined by the distribution of mass.
The next question that arises is whether it is possible in the ocean to determine a surface along which the velocity is zero, so that absolute velocities are found when the relative motion is referred to this surface. Such a surface need not be an isobaric surface but may have any shape.
One school of oceanographers points out that the deep waters of the oceans are nearly uniform and that in the deep water the isopycnal surfaces are nearly horizontal. It is therefore assumed that in the deep water the isobaric surfaces are also nearly horizontal and that absolute currents are found if the reference level is placed at a sufficiently great depth.
A second school of oceanographers claims that the distribution of oxygen in the ocean must be closely related to the type of motion, and especially that the layer or layers of minimum oxygen content that are found over large areas must represent layers of minimum horizontal motion. Consumption of oxygen takes place at all levels, owing to biological processes, and it is reasoned that minimum oxygen content is found where the replenishment of oxygen by horizontal flow is at a minimum because of weak motion. Rossby (1936a) and Iselin (1936), among others, have drawn attention to the fact, which has been clearly demonstrated by Dietrich (1937a), that this conception may lead to peculiar results concerning the currents. In the Gulf Stream, with the 2000-decibar surface as reference surface, one finds flow in the direction of the Gulf Stream from the sea surface to a depth of 2000 m, whereas, by selecting the oxygen minimum layer as reference surface, one finds that the flow in the direction of the Gulf Stream is limited to the upper layers, while at greater depths the current flows in the opposite direction with velocities that increase toward the bottom. The latter type of flow appears unreasonable, and therefore the oxygen minimum layer in that case cannot be a layer of no motion.
Another argument may also be advanced against assigning dynamic significance to the oxygen minimum layer (Sverdrup, 1938a). As has already been stated with regard to this layer as a layer of minimum motion, it is argued that the low oxygen content is due to a slow replenishment of oxygen by horizontal flow. It must be borne in mind, however, that in the ocean the distribution of oxygen is nearly stationary, meaning that at any point the amount of oxygen which in a given time is brought into a given volume by physical processes, such as diffusion and horizontal flow, must exactly equal the amount which in the same time and volume is consumed because of biological processes. Therefore, if the oxygen minimum layer represents a layer of minimum replenishment, it must also represent a layer of minimum consumption, and this requirement leads to certain conceptions concerning the biological conditions in the ocean which at present appear arbitrary. From this point of view, it does not appear permissible to make use of the oxygen distribution when drawing conclusions as to the character of the currents, although cases exist in which a minimum oxygen layer may lie close to a surface of no motion (p. 161).
A third method has been employed by Defant (1941), who points out that in the Atlantic Ocean the relative distances between isobaric surfaces remain nearly constant within certain intervals of depth. He assumes that a surface of no motion lies within this interval, and arrives in this manner at a consistent picture of the shape of the reference surface in the Atlantic and at results which are in good agreement with those obtained by considering the equation of continuity.
A fourth method is based on the equation of continuity, but this method has so far been little used because it requires comprehensive data. The application can be illustrated by considering the currents of such an ocean as the South Atlantic. It is evident that the net transport of water (p. 465) through any cross section of the South Atlantic between South Africa and South America must be zero, because water cannot permanently be removed from the North Atlantic or be accumulated in that ocean, which is practically a closed bay. In the South Atlantic a surface of no motion must therefore be selected so that the flow to the north above that surface equals the flow to the south below the same surface (p. 465). Similarly, the surface of no motion has to be selected in other regions in such a manner that one arrives at a consistent picture of the currents, taking into account the continuity of the system and the fact that subsurface water masses retain their character over long distances. Examples of such pictures are shown in figs. 187 and 205. Hidaka (1940) has computed absolute currents by another application of the equations of continuity in the form div P = 0, div M = 0 (p. 426). This and similar methods should be more widely used.
Slope Currents. Variations of Sea Level. The fact that over large areas of the open oceans the law of parallel solenoids is nearly fulfilled indicates, as has already been stated, that no large-scale slope currents exist, but the absence of such currents does not exclude the possibility that slope currents may be found within small areas, particularly in coastal regions. It is probable that converging winds may lead to an actual piling up of water in certain areas, and diverging winds to a removal of water from other areas, thus creating slopes that may give rise to currents at all levels between the surface and the bottom. This type of slope current may be more readily developed near coasts, where piling up takes place against the solid boundary. So far, only indirect evidence exists for the occurrence in the open ocean of such slope currents, and this evidence will be dealt with later (p. 678).
Under the discussion of the general character of the distribution of pressure (p. 407) it was mentioned that the absolute topography of the free surface of a lake might be determined by means of very accurate measurements of the water level along the shores of the lake. This method has actually been used for studying the influence of the wind on the slope of the sea surface in such landlocked bodies of water as the Gulf of Bothnia (Palmén and Laurila, 1938). Similarly, it might seem possible to obtain an idea of the absolute topography of the ocean surface by exact leveling along the coasts, but this procedure encounters the difficulty that lines of precision leveling cannot be carried from one continent to the other. Precision leveling along the coasts of the United States has been completed, however, although as yet the interpretation of most of the results appears doubtful.
According to these results (Bowie, 1936) the mean sea level along the coast of the Gulf of Mexico generally drops eastward, but along the Atlantic coast of the United States the mean sea level rises to the north (table 81, p. 677). If friction can be disregarded and if slope currents do not exist, the differences in sea level should be completely accounted for by the differences in the average density of the water off the coast, provided that minor corrections for differences in atmospheric pressure have been applied. A study of the distribution of density (Dietrich, 1937b, Montgomery, 1938) shows that in the Gulf of Mexico the decrease of mean sea level toward the east is in good agreement with the density distribution. However, the rise toward the north along the two coasts cannot be accounted for in this manner. Dietrich (1937b) arrives at the conclusion that the rise along the Atlantic coast is due to frictional influence, and he states that a rise of the mean sea level along a coast in the direction of flow of the main current off the coast must be present where the addition of kinetic energy to the current is less than the destruction of kinetic energy by friction. Ekman (1939), however, expresses doubt as to the correctness of Dietrich's conclusion, and the
On the Pacific coast the mean sea level is horizontal between San Diego and San Francisco. To the north of San Francisco the sea level appears to rise, but this conclusion is based on records of sea level at the mouth of the Columbia River (Fort Stevens), where the outflow of fresh water may account for the higher sea level, and, further to the north, on records of sea level at great distances from the open coast. The rise toward the north is therefore not well established.
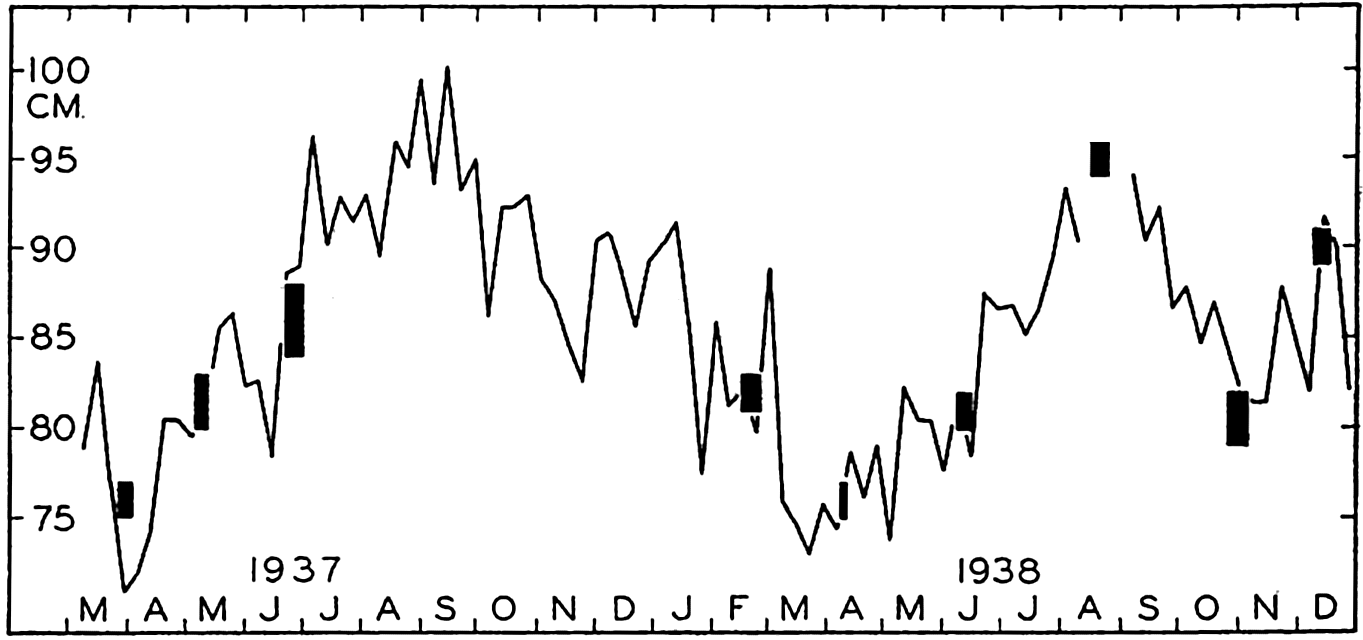
Variations of sea level at La Jolla, California, according to tidal records (curve), and according to observed variations in density above a depth of 500 m (columns).
Sea level on the Pacific coast is about 50 cm higher than on the Atlantic coast, and this difference may perhaps be related to the lower average density of Pacific water.
Variations in the average density of water columns appear capable of accounting for local variations in sea level, as is demonstrated by recent studies of Montgomery (1938) and LaFond (1939). The curve in fig. 111 (LaFond, 1939) shows weekly averages of sea level according to tidal records at La Jolla, California, and the black columns represent the sea level at La Jolla as extrapolated from charts showing the topography of the surface relative to the 500-decibar surface as derived from cruises in 1937 and 1938. The 500-decibar surface was used as reference because near the coast water of uniform density was encountered below a depth of 500 m. Columns have been entered instead of dots because extrapolation of the contour lines as far as the coast is uncertain. The height of the columns gives the probable limits within which sea level on the coast should lie, and the width corresponds to the length in time of the cruises. The agreement between the variations of sea level as
Off a coast near which the density of the coastal water may vary owing to external influences (whereas the density of the oceanic water remains relatively constant), the variations in sea level have direct bearing on the slope of the sea surface toward or away from the coast. Variation in sea level can thus be interpreted in terms of slope of sea surface—that is, in terms of a coastal current. Similarly, if a current flows between an island and a coast, there must be a difference in sea level across the current. Simultaneous registrations of sea level on the island and on the coast may be very helpful in detecting changes of the slope and, thus, in changes in the velocity of the current. For the purpose of detecting such changes, the Woods Hole Oceanographic Institution, with the cooperation of the U. S. Coast and Geodetic Survey, has established a permanent tidal station on Cat Cay, one of the Bimini Islands, which lies on the southeastern side of the Strait of Florida. The records at this station will be compared to those at Key West and Miami, Florida. It can be expected that these studies, which deal with variations in the slope, will amplify the knowledge of the total field of pressure.
Bjerknes' Theorem of Circulation. The general formula for computing ocean currents from the slope of the isobaric surfaces, ν =−gci, was derived by H. Mohn in 1885, but Mohn did not discriminate sharply between the slope due to internal distribution of mass and the slope due to external factors. Furthermore, the oceanographic observations at the time when Mohn presented his theory were not sufficiently accurate for computation of the relative field of pressure. Owing to these circumstances, and also to others depending on certain characteristics of the theory that have recently been explained by Ekman (1939), Mohn's formula received no attention. The corresponding formula for computation of currents associated with the relative distribution of pressure,
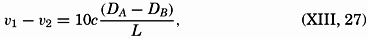
Bjerknes makes use of the term “circulation along a closed curve.” Consider a closed curve that is formed by moving particles of a fluid. The velocity of each particle has a component νs along the curve, and
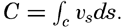 .
.If friction is neglected, the time change of the circulation can easily be found from the equations of motion, because
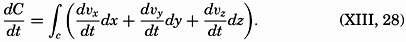
Consider, first, conditions in a coordinate system that is at rest and assume that gravity is the only external force. The integral of the component of gravity along a closed curve is always zero, because it represents the work performed against gravity in moving a particle along a certain path back to the starting point. There remains, therefore, only

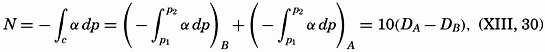
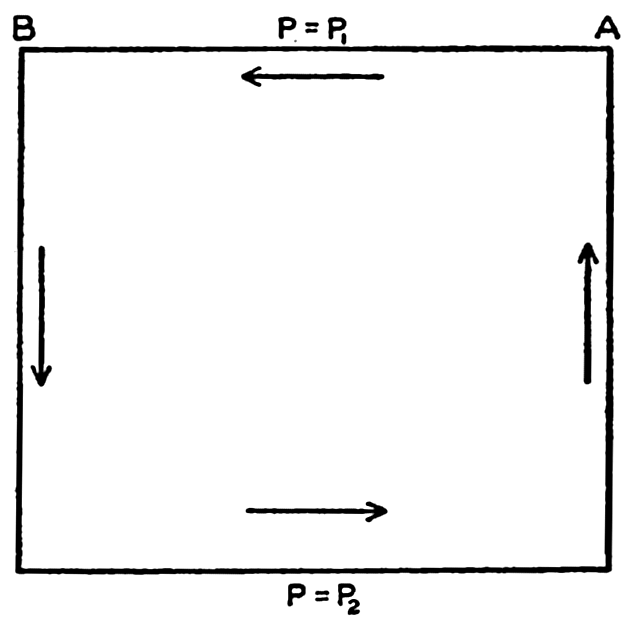
Location in the pressure field of a curve along which the time change of circulation is examined.
If the circulation relative to the earth is considered, the deflecting force has to be taken into account. According to Bjerknes, this is done by writing
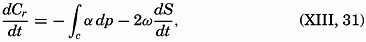
Consider the same curve as before, and assume that the upper line, p = p1, moves at a velocity ν1 at right angles to the line A−B, whereas the lower line, p = p2, moves at a velocity ν2, and let the distance A−B be called L. Then the time change of the projection on the equator plane is
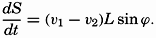
Assume now that the circulation is constant (dC/dt = 0). It then follows that the velocity difference, ν1 − ν2, must be expressed by the equation
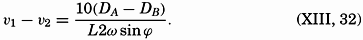
*In the literature, some confusion exists as to the signs in these equations. The above signs are consistent with the coordinates used. The relative velocity is positive; that is, the relative current is directed away from the reader if A lies to the right of B and if DA is greater than DB.
The complete theorem of circulation contains a great deal more than the simple statement expressed by equation (XIII, 32), but so far it has not been possible to make more use in oceanography of Bjerknes' elegant formulation of one of the fundamental laws governing the motion of nonhomogeneous fluids.
Transport by Currents. The volume transport by horizontal currents has the components
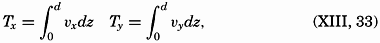
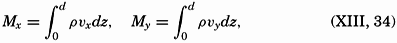
The absolute volume transport can be computed only if the absolute velocities are known, but the volume transport by relative currents can be derived from the distribution of mass. By means of equations (XIII, 16), one obtains
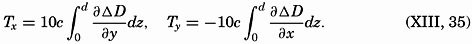

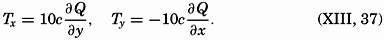
The quantity Q is easily computed, because ΔD is always determined if velocities are to be represented.
It should be observed that in practice the numbers that represent the geometric depths are also considered as representing the pressures in decibars (p. 410). In computing Q the integration is therefore carried to the pressure p decibars and the depth d meters, which are both expressed by the same number, but a small systematic error is thereby introduced. Jakhelln (1936) has examined this error and has shown that the customary procedure leads to Q values that are systematically 1 per cent too small, but this error is negligible.
Curves of equal values of Q can be drawn on a chart, and these curves will bear the same relation to the relative volume transport that the curves of ΔD bear to the relative velocity, provided that the derivations of Q are taken as positive in the direction of decrease. Therefore, the direction of the volume transport above the depth to which the Q values are referred will be parallel to the Q lines, and numerical values will be proportional to the gradient of the Q lines. The factor of proportionality will depend upon the latitude, however; between two Q lines that indicate transport to the north, the transport will increase in the direction of flow, whereas, between two Q lines indicating transport to the south, the transport will decrease in the direction of flow. Taking this fact into account, one can construct curves between which the transport is constant, but these curves will no longer be exactly parallel to the direction of the transport. Within a small area the deviation will be imperceptible, but within a larger area it will be considerable.
Between two stations A and B (A lying to the right), at distance L, the volume transport is
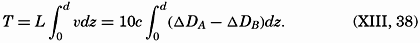
It is not necessary to develop corresponding equations for the mass transport, because this can be derived with sufficient accuracy from the volume transport by multiplication with an average density (Ekman, 1929, 1939; Jakhelln, 1936).
Convenient formulae for the computation of the transport of a coastal current have been developed by Werenskiold (1937) on the assumption that the isosteres rise toward the surface and intersect the surface at some distance from the coast (see fig. 113).
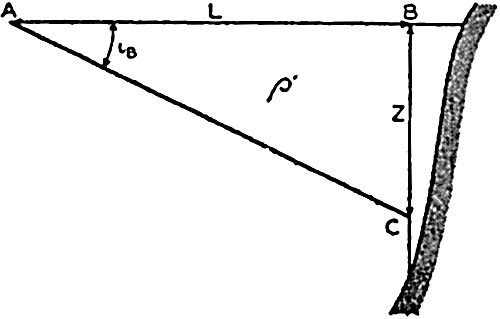
Schematic representation of hydrographic conditions off a coast.
If there are only two layers of homogeneous water, the transport is easily found. If the water of greatest density is at rest, the velocity in the area ABC (fig. 113) is
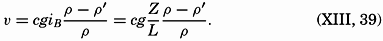
The volume transport apparently has been computed from observations at only the one station at which the depth to the boundary surface is Z, but the assumption that at and beyond the distance L the homogeneous, denser water reaches surfaces is equivalent to assuming that conditions at a second station at or beyond L are known. Owing to this circumstance, it is readily seen that the boundary surface can have any shape, because it has already been shown that the transport between two stations depends only upon the distribution of density at the two stations and is independent of the distribution of density between the stations.
For currents in water within which the density varies continually with depth, Werenskiold arrives at the formula
A consideration of computed transport and of the continuity of the system is helpful, under certain conditions, in separating currents flowing one above the other. The average transport through a vertical section that represents the opening to a basin must be zero, because water cannot accumulate in the basin, nor can it continue to flow out of the basin. Observations at stations at the two sides of such a section may, however, show transport in or out if the velocity along the bottom is assumed to be zero. However, this assumption would be wrong, and a depth of no motion must be determined in such a manner that the transport above and below that depth are equal. This depth can be found by plotting the difference ΔDA − ΔDB against depth, computing the average value of the difference between the surface and the bottom, and reading from the curve the depth at which that average value is found. This depth is then the average depth of no motion, and the transports above and below that depth are in opposite directions.
Determination of the depth above and below which the transport between two stations, A and B, is equal.
The procedure is illustrated in fig. 114, in which is plotted the difference ΔDA − ΔDB at Meteor stations 46 off South America and 23 off South Africa, both in about latitude 29°S. Assuming no current at a depth of 3500 m, one would obtain a transport to the north proportional to the area ABC, or equal to 44.5 million m3/sec. Such a transport to the north is impossible, and the velocity must therefore be zero at some other depth. The average value of ΔDA − ΔDB is 0.090 dynamic meters, and this value is found at a depth of 1325 m. If this depth is selected as a depth of no motion, the transport to the north becomes proportional to the area DBE and equal to 20.7 million m3/sec, and below 1325 m the transport is directed to the south, is proportional to the area ECF, and is also equal to 20.7 million m3/sec. The transport above the depth of no motion can be written in the form
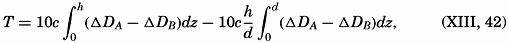
Only the average depth of no motion can be determined in this manner. Generally, the depth of no motion is not constant, but the inclination can be found by studying the distribution of temperature and salinity in the section. It is rational to assume that a surface of no motion coincides with isothermal and isohaline surfaces, and that therefore, in a section, the depth of no motion follows the isotherms and isohalines. On that assumption, one finds that in the example which has been discussed the depth of no motion rises from about 1450 m off South America to about 1200 m off South Africa.
Deflections of a current when passing a ridge, the profile of which is shown at the bottom. Left. Deflection of a current in homogeneous water, due to friction (Ekman). Right. Deflection of a relative current (see fig. 116).
The Influence of Bottom Topography on Ocean Currents. Ekman (1923, 1927, 1932) has examined the effect of the bottom topography on currents, taking into account the rotation of the earth. He arrived at the conclusion that in low latitudes the currents tend to flow east-west, independent of the slope of the bottom, but that in middle and high latitudes the currents tend to follow the bottom contours. These conclusions are verified by experience. Ekman also found that a current will be deflected cum sole when entering shallower water and contra solem when entering deeper water, and that these deflections are independent of the absolute depth to the bottom. The curvature of the stream lines is greatest where the change in slope is greatest, and when crossing a ridge the stream lines will therefore have the form shown in fig. 115, left.
In his examination, Ekman assumed homogeneous water and the presence of a slope current within which the velocities are independent of depth except within a layer that is influenced by bottom friction (p. 499). The effect of the bottom topography on relative currents in non-homogeneous water has not been examined, but qualitatively the character of the modifications is easily seen. Consider first, in the Northern Hemisphere, a relative current which in an ocean of constant depth reaches nearly to the bottom (fig. 116). Within such a current the deepest isopycnic or isosteric surfaces are horizontal, but above the
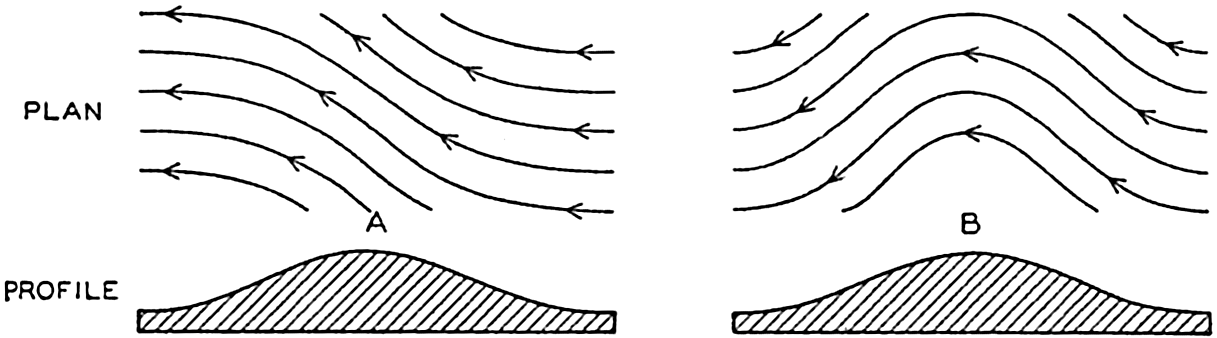
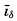 (δ1 − δ2) expresses the relation between the slope of the isobaric surface, ip, and the average slope of the δ surfaces,
(δ1 − δ2) expresses the relation between the slope of the isobaric surface, ip, and the average slope of the δ surfaces, 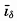 (p. 412). This distribution of mass and pressure is illustrated on the right-hand side of the perspective diagram in fig. 116, where it is supposed that the isosteric surface δ = δ1 coincides with a level surface.
(p. 412). This distribution of mass and pressure is illustrated on the right-hand side of the perspective diagram in fig. 116, where it is supposed that the isosteric surface δ = δ1 coincides with a level surface.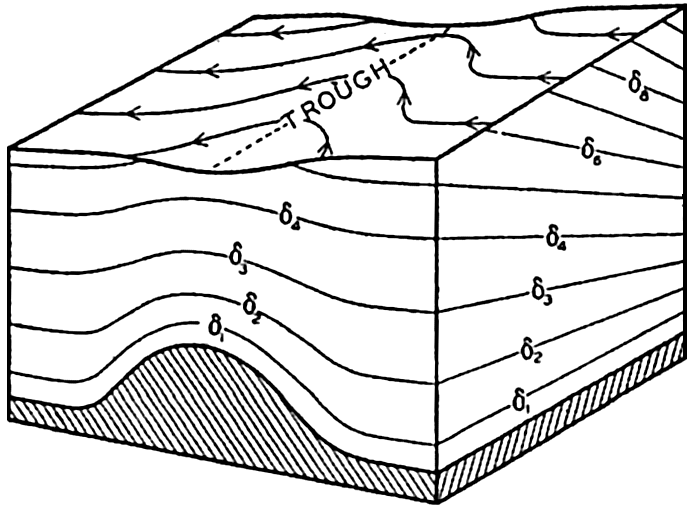
Perspective diagram showing the deformation of the sea surface when a relative current reaching nearly to the bottom crosses a submarine ridge.
When this current approaches a submarine ridge over which the water must flow, the δ surfaces must rise, as shown in the diagram. Accordingly, the distribution of mass is altered in the direction of flow in such a manner that the δ surfaces slope upward when approaching the ridge and downward after passing the ridge. The isobaric surfaces are altered correspondingly and must slope downward when the current approaches the ridge and upward after it has passed; that is, a low-pressure trough develops along the ridge, but this trough rises from left to right relative to an observer who looks in the direction of flow, because the lighter water remains on the right-hand side (fig. 116). Consequently, the isohypses of the isobaric surfaces, which were straight lines over the even bottom, bend to the right when the current approaches the ridge and to the left when it has passed. In the Southern Hemisphere the bends will be in opposite directions, and, in general, a deep current is therefore deflected from its straight course when crossing a ridge, the deflection being to the right in the Northern Hemisphere and to the left in the Southern. The maximum deflection in this case is directly over the ridge, as shown in fig. 115.
In the schematic representation in fig. 116 the δ surfaces at intermediate depths—say, the surfaces marked δ3 and δ4—must evidently show a ridge above the bottom ridge and must at the same time slope from left to right. The σt surfaces must have a similar form. As an example of such influence of the bottom topography on the field of mass, fig. 117 shows the topography of the surface σt = 27.7 in the region where
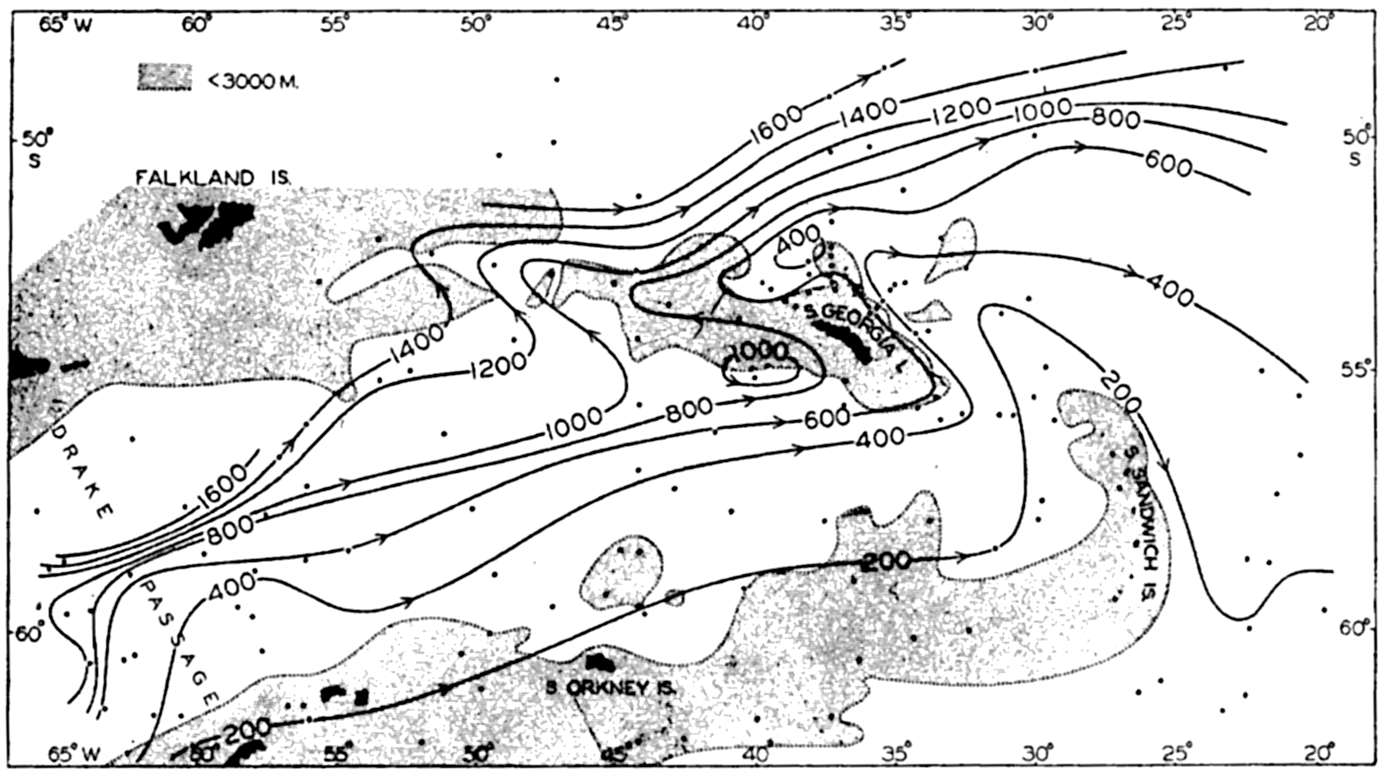
Topography of the surface σt = 27.7 in the area from the Drake Passage to the east of South Sandwich Islands.
Qualitative examples other than the one shown in fig. 116 can easily be prepared. Thus, the current must flow around a peak rising from the sea bottom, and this flow will result in a widening of the distance between the stream lines above the peak and perhaps in the development of a cyclonic eddy. The discussions by Wüst (1940) and Neumann (1940) of conditions around the Altair dome in the North Atlantic confirm these conclusions.
The above reasoning is purely qualitative. If the quantitative effect of the bottom topography is to be examined, it is necessary to consider that the equation of continuity and the equations of stationary motion and stationary distribution of mass must be satisfied. No quantitative computations have been made, but it can be pointed out that stationary distribution of mass requires that the law of the parallel solenoids be fulfilled (p. 455). Hence the isohypses of all isobaric