KINEMATICS
Vector Fields
A vector field can be completely represented by means of three sets of charts, one of which shows the scalar field of the magnitude of the vector and two of which show the direction of the vector in horizontal and vertical planes. It can also be fully described by means of three sets of scalar fields representing the components of the vector along the principal coordinate axes (V. Bjerknes and different collaborators, 1911). In oceanography, one is concerned mainly with vectors that are horizontal, such as velocity of ocean currents—that is, two-dimensional vectors.
Representation of a two-dimensional vector field by vectors of indicated direction and magnitude and by vector lines and equiscalar curves.
Vector lines cannot intersect except at singular points or lines, where the magnitude of the vector is zero. Vector lines cannot begin or end within the vector field except at singular points, and vector lines are continuous.
The simplest and most important singularities in a two-dimensional vector field are shown in fig. 96: These are (1) points of divergence (fig. 96A and C) or convergence (fig. 96B and D), at which an infinite number of vector lines meet; (2) neutral points, at which two or more vector lines intersect (the example in fig. 96E shows a neutral point of the first order in which two vector lines intersect—that is, a hyperbolic point); and (3) lines of divergence (fig. 96F) or convergence (fig. 96G), from which an infinite number of vector lines diverge asymptotically or to which an infinite number of vector lines converge asymptotically.
It is not necessary to enter upon all the characteristics of vector fields or upon all the vector operations that can be performed, but two important vector operations must be mentioned.
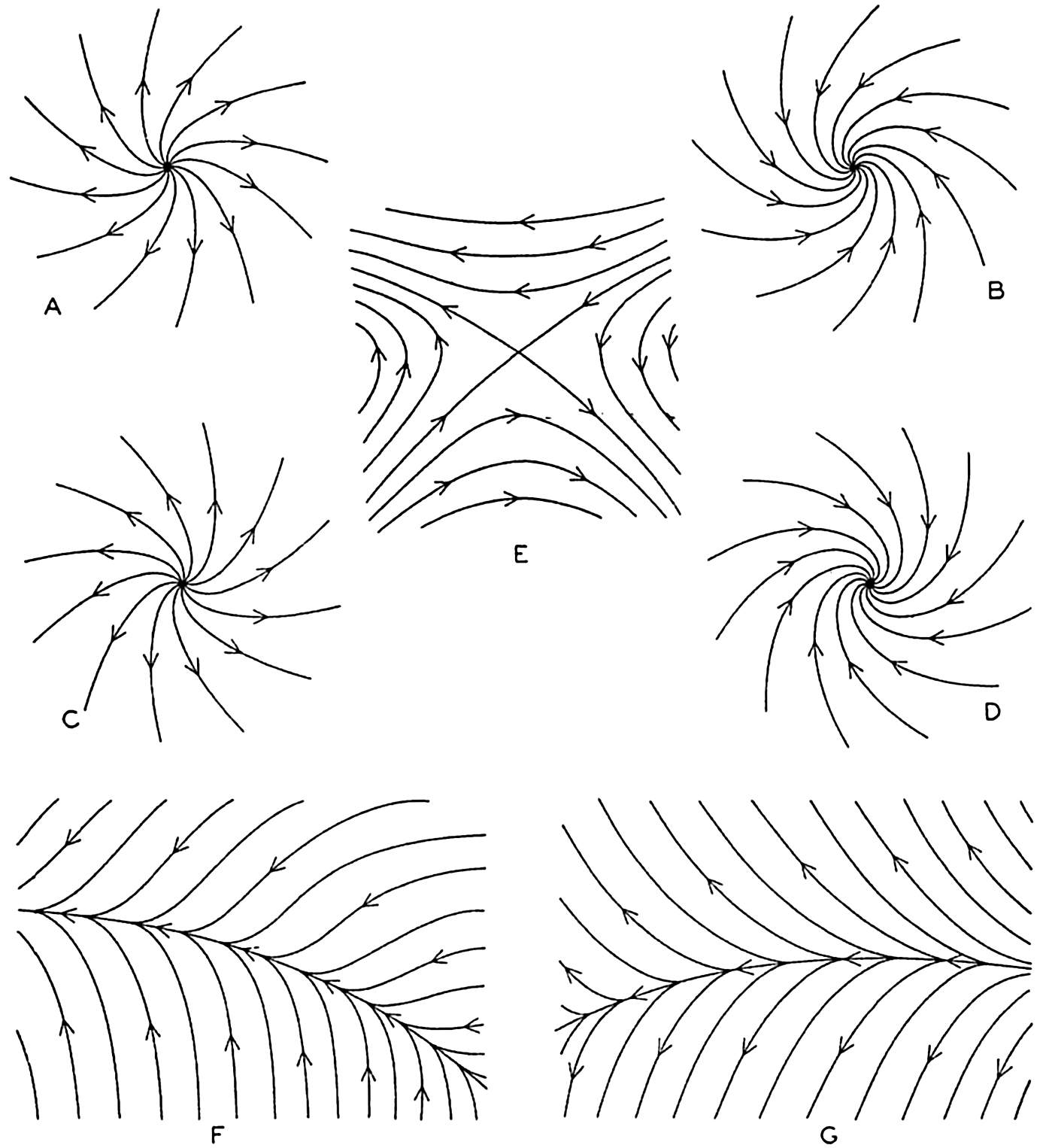
Singularities in a two-dimensional vector field. A and C, points of divergence; B and D, points of convergence; E, neutral point of first order (hyperbolic point); F, line of convergence; and G, line of divergence.
Assume that a vector A has the components Ax, Ay, and Az. The scalar quantity
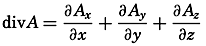
The vector which has the components
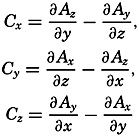
Two representations of a vector that varies in space and time will also be mentioned. A vector that has been observed at a given locality during a certain time interval can be represented by means of a central vector diagram (fig. 97). In this diagram, all vectors are plotted from the same point, and the time of observation is indicated at each vector. Occasionally the end points of the vector are joined by a curve on which the time of observation is indicated and the vectors themselves are omitted. This form of representation is commonly used when dealing with periodic currents such as tidal currents. A central vector diagram is also used extensively in pilot charts to indicate the frequency of winds from given directions. In this case the direction of the wind is shown by an arrow, and the frequency of wind from that direction is shown by the length of the arrow.
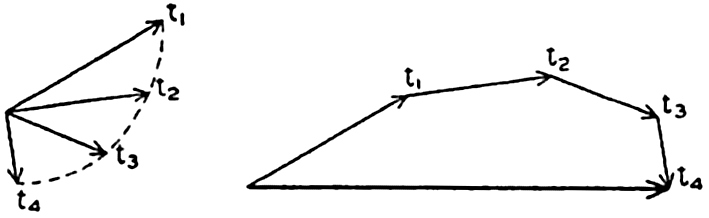
Time variation of a vector represented by a central vector diagram (left) and a progressive vector diagram (right).
If it can be assumed that the observations were made in a uniform vector field, a progressive vector diagram is useful. This diagram is constructed by plotting the second vector from the end point of the first, and so on (fig. 97). When dealing with velocity, one can compute the displacement due to the average velocity over a short interval of time. When these displacements are plotted in a progressive vector diagram, the resulting curve will show the trajectory of a particle if the velocity field is of such uniformity that the observed velocity can be considered representative of the velocities in the neighborhood of the place of observation. The vector that can be drawn from the beginning of the first vector to the end of the last shows the total displacement in the entire time interval, and this displacement, divided by the time interval, is the average velocity for the period.
The Field of Motion and the Equation of Continuity
The Field of Motion. Among vector fields the field of motion is of special importance. Several of the characteristics of the field of motion can be dealt with without considering the forces which have brought about or which maintain the motion, and these characteristics form the subject of kinematics.
The velocity of a particle relative to a given coordinate system is defined as ν = dr/dt, where dr is an element of length in the direction in which the particle moves. In a rectangular coordinate system the velocity has the components
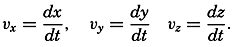
The velocity field can be completely described by the Lagrange or by the Euler method. In the Lagrange method the coordinates of all moving particles are represented as functions of time and of a threefold multitude of parameters that together characterize all the moving particles. From this representation the velocity of each particle, and, thus, the velocity field, can be derived at any time.
The more convenient method by Euler will be employed in the following. This method assumes that the velocity of all particles of the fluid has been defined. On this assumption the velocity field is completely described if the components of the velocity can be represented as functions of the coordinates and of time:
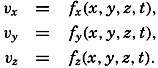
The characteristic difference between the two methods is that Lagrange's method focuses attention on the paths taken by all individual particles, whereas Euler's method focuses attention on the velocity at each point in the coordinate space. In Euler's method it is necessary, however, to consider the motion of the individual particles in order to find the acceleration. After a time dt, a particle that, at the time t, was at the point (x,y,z) and had the velocity components fx(x,y,z,t), and so on, will be at the point (x + dx, y + dy, z + dz), and will have the velocity components fx(x + dx, y+ dy, z + dz, t + dt), and so on. Expanding in Taylor's series, one obtains
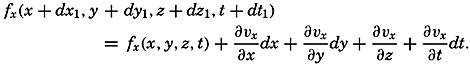
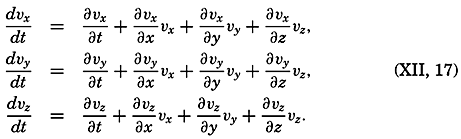
Thus, one has to deal with two time derivatives: the individual time derivative, which represents the acceleration of the individual particles, and the local time derivative, which represents the time change of the velocity at a point in space and is called the local acceleration. The last terms in equation (XII, 17) are often combined and called the field acceleration.
The above development is applicable not only when considering the velocity field, but also when considering any field of a property that varies in space and time (p. 157). The velocity field is stationary when the local time changes are zero:


The Equation of Continuity. Consider a cube of volume dxdydz. The mass of water that in unit time flows in parallel to the x axis is equal to pvxdydz, and the mass that flows out is equal to
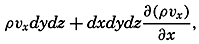
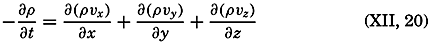
Now:
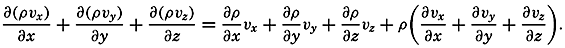
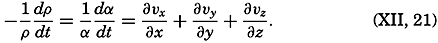
The equation of continuity is not valid in the above form at a boundary surface because no out- or inflow can take place there. In a direction normal to a boundary a particle in that surface must move at the same velocity as the surface itself. If the surface is rigid, no component normal to the surface exists and the velocity must be directed parallel to the surface. The condition

Application of the Equation of Continuity. At the sea surface the kinematic boundary condition must be fulfilled. Designating the vertical displacement of the sea surface relative to a certain level of equilibrium by η, and taking this distance positive downward, because the positive z axis is directed downward, one obtains
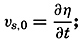
With stationary distribution of mass (∂ρ/∂t = 0) the equation of continuity is reduced to
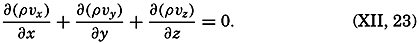
The total transport of mass through a vertical surface of unit width reaching from the surface to the bottom has the components
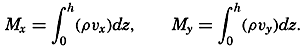
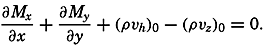

When dealing with conditions near the surface, one can consider the density as constant and can introduce average values of the velocity components 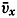 and
and 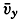 within a top layer of thickness H. With these simplifications, one obtains, putting νz,0 = 0,
within a top layer of thickness H. With these simplifications, one obtains, putting νz,0 = 0,
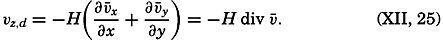
For this purpose, it is of advantage to write the divergence of a two-dimensional vector field in a different form:

The equation of continuity is applicable not only to the field of mass but also to the field of a dissolved substance that is not influenced by biological activity. Let the mass of the substance per unit mass of water be s. Multiplying the equation of continuity by s and integrating from the surface to bottom, one obtains, if the vertical velocity at the surface is zero,
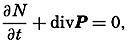
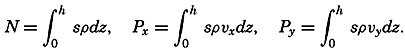

These equations have already been used in simplified form in order to compute the relation between inflow and outflow of basins (p. 147). Other simplifications have been introduced by Knudsen, Witting, and Gehrke (Krümmel, 1911, p. 509–512).
Trajectories (full drawn lines) and stream lines (dashed lines) in a progressive surface wave.
Stream Lines and Trajectories. The vector lines showing the direction of currents at a given time are called the stream lines, or the lines of flow. The paths followed by the moving water particles, on the other hand, are called the trajectories of the particles. Stream lines and trajectories are identical only when the motion is stationary, in which case the stream, lines of the velocity field remain unaltered in time, and a particle remains on the same stream line.
The general difference between stream lines and trajectories can be illustrated by considering the type of motion in a traveling surface wave. The solid lines with arrows in fig. 98 show the stream lines in a cross section of a surface wave that is supposed to move from left to right, passing the point A. When the crest of the wave passes A, the motion of the water particles at A is in the direction of progress, but with decreasing
It is supposed that the speed at which the wave travels is much greater than the velocity of the single water particles that take part in the wave motion. On this assumption a water particle that originally was located below A will never be much removed from this vertical and will return after one wave period to its original position. The trajectories of such particles in this case are circles, the diameters of which decrease with increasing distance from the surface, as shown in the figure. It is evident that the trajectories bear no similarity to the stream lines.
Representations of the Field of Motion in the Sea
Trajectories of the surface water masses of the ocean can be determined by following the drift of floating bodies that are carried by the currents. It is necessary, however, to exercise considerable care when interpreting the available information about drift of bodies, because often the wind has carried the body through the water. Furthermore, in most cases, only the end points of the trajectory are known—that is, the localities where the drift commenced and ended. Results of drift-bottle experiments present an example of incomplete information as to trajectories. As a rule, drift bottles are recovered on beaches, and a reconstruction of the paths taken by the bottles from the places at which they were released may be very hypothetical. The reconstruction may be aided by additional information in the form of knowledge of distribution of surface temperatures and salinities that are related to the currents, or by information obtained from drift bottles that have been picked up at sea. Systematic drift-bottle experiments have been conducted, especially in coastal areas that are of importance to fisheries.
Stream lines of the actual surface or subsurface currents must be based upon a very large number of direct current measurements. Where the velocity is not stationary, simultaneous observations are required. Direct measurements of subsurface currents must be made from anchored vessels, but this procedure is so difficult that no simultaneous measurements that can be used for preparing charts of observed subsurface currents for any area are available.
Numerous observations of surface currents, on the other hand, have been derived from ships' logs. Assume that the position of the vessel at
Determination of surface currents by difference between positions by fixes and dead reckoning.
The data on surface currents obtained from ships' logs cannot be used for construction of a synoptic chart of the currents, because the number of simultaneous observations is far too small. Data for months, quarter years, or seasons have been compiled, however, from many years' observations, although even these are unsatisfactory for presentation of the average conditions because such data are not evenly distributed over large areas but are concentrated along trade routes. In some charts the average direction in different localities is indicated by arrows, and where strong currents prevail the average speed in nautical miles per day is shown by a number. In other charts the surface flow is represented by direction roses in which the number at the center of the rose represents the percentage of no current, the lengths of the different arrows represent the percentage of currents in the direction of the arrows, and the figures at the ends of the arrows represent the average velocity in miles per day of currents in the indicated direction. These charts contain either averages for the year or for groups of months.
On the basis of such charts, average surface currents during seasons or months have in some areas been represented by means of stream lines and equiscalar curves of velocity. The principle advantage of this representation is that it permits a rapid survey of the major features and that it brings out the singularities of the stream lines, although in many instances the interpretation of the data is uncertain and the details of the chart will depend greatly upon personal judgment.
In drawing these stream lines it is necessary to follow the rules concerning vector lines (p. 419). The stream lines cannot intersect, but an infinite number of stream lines can meet in a point of convergence or divergence or can approach asymptotically a line of convergence or diverge asymptotically from a line of divergence.
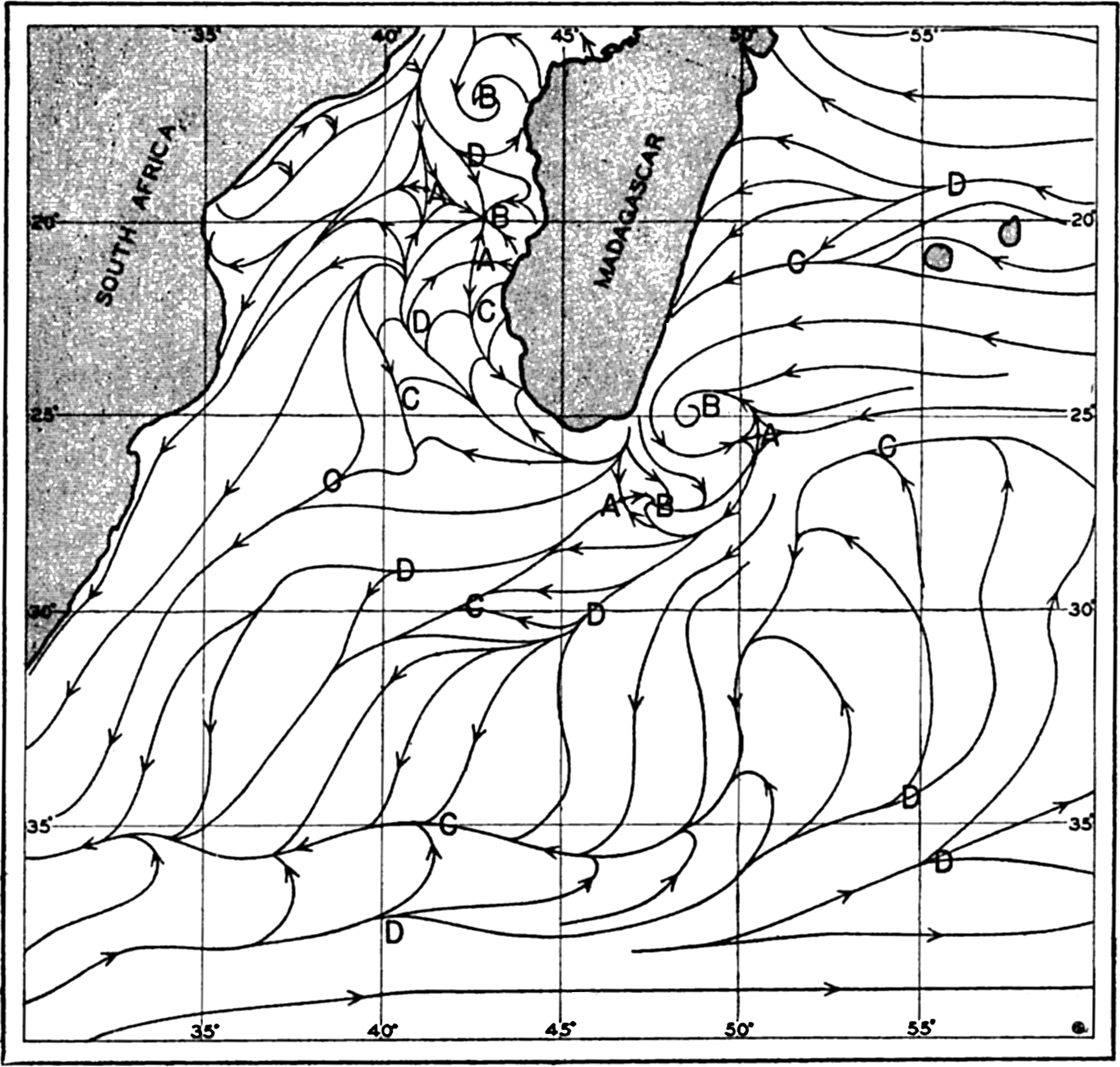
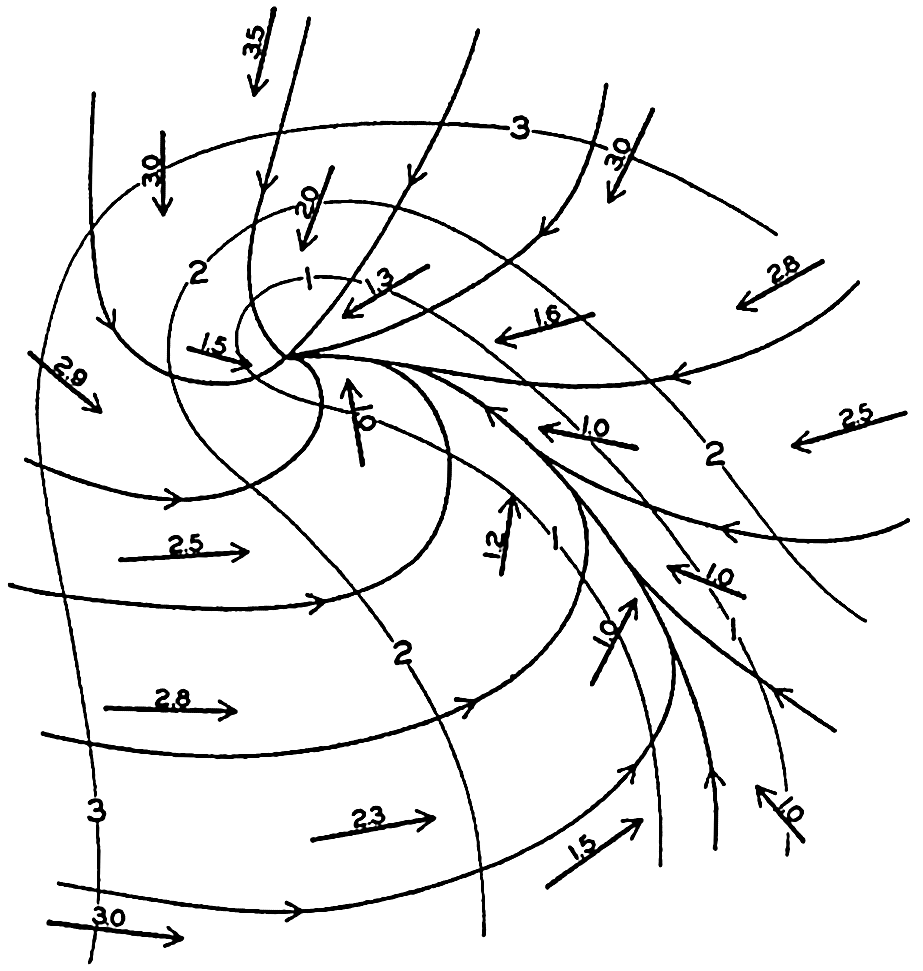
Stream lines of the surface currents off southeastern Africa in July (after Wilimzik).
As an example, stream lines of the surface flow in July off southeast Africa and to the south and southeast of Madagascar are shown in fig. 100. The figure is based on a chart by Willimzik (1929), but a number of the stream lines in the original chart have been omitted for the sake of simplification. In the chart a number of the characteristic singularities of a vector field are shown. Three hyperbolic points marked A appear, four points of convergence marked B are seen, and a number of lines of convergence marked C and lines of divergence marked D are present. The stream lines do not everywhere run parallel to the coast, and the representation involves the assumption of vertical motion at the coast, where the horizontal velocity, however, must vanish.
The most conspicuous feature is the continuous line of convergence that to the southwest of Madagascar curves south and then runs west, following lat. 35°S. At this line of convergence, the Subtropical Convergence, which can be traced across the entire Indian Ocean and has its counterpart in other oceans, descending motion must take place. Similarly, descending motion must be present at the other lines of convergence, at the points of convergence, and at the east coast of Madagascar, whereas ascending motion must be present along the lines of divergence and along the west coast of Madagascar, where the surface waters flow away from the coast. Velocity curves have been omitted, for which reason the conclusions as to vertical motion remain incomplete (see p. 425). Near the coasts, eddies or countercurrents are indicated, and these phenomena often represent characteristic features of the flow and remain unaltered during long periods.
As has already been stated, representations of surface flow by means of stream lines have been prepared in a few cases only. As a rule, the surface currents are shown by means of arrows. In some instances the representation is based on ships' observation of currents, but in other cases the surface flow has been derived from observed distribution of temperature and salinity, perhaps taking results of drift-bottle experiments into account. The velocity of the currents may not be indicated or may be shown by added numerals, or by the thickness of the arrows. No uniform system has been adopted (see Defant, 1929), because the available data are of such different kinds that in each individual case a form of representation must be selected which presents the available information in the most satisfactory manner. Other examples of surface flow will be given in the section dealing with the currents in specific areas.