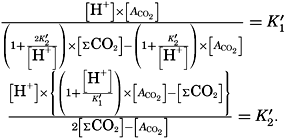
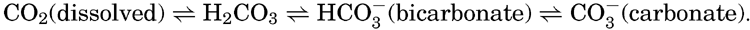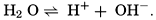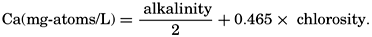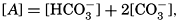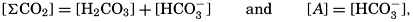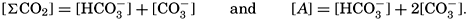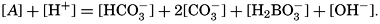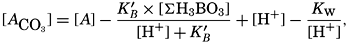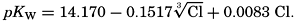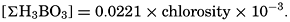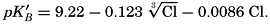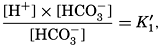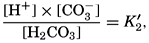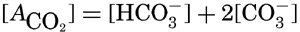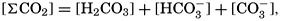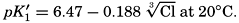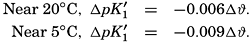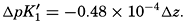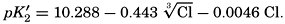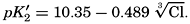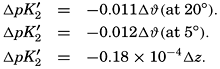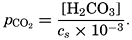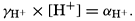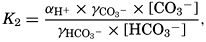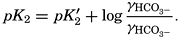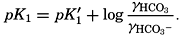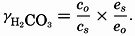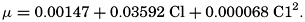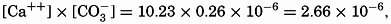The Carbon Dioxide System
Although an extensive literature exists concerning the carbon dioxide system in sea water, publications prior to about 1929 are now chiefly of historic interest. The solution of the problems involved awaited not only the development of suitable analytical methods for the determination of the total carbon dioxide and the various forms in which it is present in sea water, but also the development of the theory and methods for studying the hydrogen ion concentration and certain general theories in physical chemistry. In the brief discussion to follow, only the salient features of the contemporary theories will be presented. These may be adequate for many purposes, but the investigations are not yet closed. Methods of analysis require further refinements, and in many cases fundamental constants must be more accurately determined.
Early investigators studying the carbon dioxide in sea water attempted to apply methods similar to those used for fresh water, where the carbon dioxide is largely present as free carbon dioxide that can be driven off by boiling, by applying a vacuum, or by bubbling through the water a stream of CO2-free gas. The use of such methods on sea water gave variable and conflicting results. It was later found that in order to drive off all the CO2 a strong acid must be added to the water, indicating that at least part of the carbon dioxide was present as the carbonate or bicarbonate of some basic cation. Methods were then developed for the determination of the total carbon dioxide and also for measuring the quantity present as carbonate and bicarbonate ions. It is now considered that the CO2 can exist in the following forms in sea water and that under any given set of conditions equilibria will prevail:
If the gases in sea water are driven off by some suitable method, the CO2 present as dissolved gas will be removed and the equilibria will be displaced until virtually all of the free CO2 and carbonic acid are removed and the bicarbonate is all converted to carbonate. If a strong acid isFrom the foregoing discussion it can be seen that the total CO2 in sea water does not follow Henry's law for the solution of gases in inert solutions. Nevertheless, the partial pressure of the carbon dioxide in sea water in contact with the atmosphere will tend to establish equilibrium with that in the air. If the pressure is increased the amount in solution will be greater, and if it is reduced the quantity of CO2 will decrease. The quantity present in a sample of water in equilibrium with a given carbon dioxide pressure will depend on the concentration of carbon dioxide bound base and the temperature and salinity of the water sample. If these factors are kept constant, the partial pressure of CO2 can be used as a measure of the total carbon dioxide content of the water.
Hydrogen Ion Concentration (pH) of Sea Water. Sea water is normally alkaline. Since both the H+ and OH− ions play parts in the equilibria, any understanding of the carbon dioxide system requires knowledge of their concentrations. Pure distilled water dissociates into hydrogen and hydroxyl ions:
The ionic product [H+] × [OH−], when the concentrations are expressed in chemical equivalents per liter, varies somewhat with temperature, but at 25°C is 10−14 (p. 198). In pure water or in any solution that contains equal concentrations of H+ and OH− ions, the solution is said to be neutral. If the concentration of H+ is in excess of OH−, the solution is acid, and if less it is alkaline. The ionic product is a known function of the temperature and salt concentrations; hence, if [H+] or [OH−] is known, the other can readily be calculated. For expressing the hydrogen ion concentration, a logarithmic scale is commonly used, where pH is the logarithm of the reciprocal of the hydrogen ion concentration expressed as normality; that is, as equivalents per liter,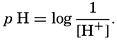 [Equation]. Thus, a neutral solution has a pH of approximately 7, an acid solution a pH less than 7, and an alkaline solution a pH greater than 7. It should be noted that a unit change in pH corresponds to a tenfold change in the hydrogen ion and hydroxyl ion concentrations.
[Equation]. Thus, a neutral solution has a pH of approximately 7, an acid solution a pH less than 7, and an alkaline solution a pH greater than 7. It should be noted that a unit change in pH corresponds to a tenfold change in the hydrogen ion and hydroxyl ion concentrations.The hydrogen ion concentration, or pH, of a solution may be determined in various ways, but all are essentially either electrometric or
Certain organic compounds classed as indicators have the property of changing color over a given range of hydrogen ion concentration. So-called bicolor indicators have one color when in an “acid” solution and another color when in an “alkaline” solution. For any indicator the color change takes place over a definite range in pH, and, at the hydrogen ion concentration that is numerically equal to the dissociation constant of the indicator, equal quantities of both color phases are present in the solution. The range in pH for which various indicators can be used is described by Clark (1928), who also gives in detail the methods for preparing the indicators. For sea water, cresol red and phenol red are generally used, as they cover the pH range normally found in the sea. When working in high pH ranges, bromthymol blue is commonly used.
Three important properties of pH indicators must be known before they can be applied to sea water: the dissociation constant of the indicator, the effect of temperature upon this value, and the salt error. The presence of neutral ions in the solution has a pronounced effect upon the color and, hence, upon the apparent pH as determined by indicators. This is known as the salt error. In general, neutral salts increase the apparent dissociation constant of the indicator, and therefore give low pH readings. In practice a carefully controlled quantity of an indicator solution is added to a sample of sea water, and either the color developed is compared to a set of tubes containing the equivalent quantity of indicator in solutions of known pH or the sample is examined in a bicolorimeter. The accepted colorimetric technique used for determining the pH of sea-water samples and the correction to be applied for salt error and temperature effects are described by Buch (1937) and by Buch and Nynäs (1939). Because of the effects of changes in temperature and pressure upon the dissociation constants of carbonic acid (p. 200) the measured pH of a sea-water sample will differ from the pH in situ. The magnitude of the temperature correction is given by Buch (1937), and the effect of pressure upon the pH has been studied by Buch and Gripenberg (see Buch et al, 1932).
The pH encountered in the sea is between about 7.5 and 8.4. That is, the hydrogen ion concentration ranges from 32 × 10−9 to 4 × 10−9
Alkalinity and Carbon Dioxide Components. The total amount of carbon dioxide in sea water, present either as free gas or bound, may be determined gasometrically after a strong acid has been added to the water to break up the carbonate compounds. Such a method has been described by Greenberg, Moberg, and Allen (1932). In order to determine the carbon dioxide components—namely, the amounts present as carbonic acid (including the free CO2), bicarbonate, and carbonate—titrations must be made. For a given sample of sea water the amount of a strong acid (usually HCl about 0.01 normal) necessary to reduce the pH to about 4.5 is independent of the total CO2. This amount of acid is required to set free the weak acids whose anions have been bound against basic cations. It is therefore not only a measure of the quantity of anions of weak acids in the sample, but also of the cations balanced against them. This quantity, when expressed as the number of milliequivalents of hydrogen ions (mg-atoms of H+) necessary to set free the ions of weak acids in a volume of water which at 20° has a volume of 1 L, is known as the alkalinity. This quantity has also been referred to as the titratable base, excess base, titration alkalinity, and buffer capacity. The term alkalinity has been adopted as the standard designation by the International Association of Physical Oceanography (1939). It should be noted that the term as here defined has no relation to the hydroxyl ion concentration or to the fact that sea water is normally alkaline.
A number of methods have been suggested for determining the alkalinity, and these have been summarised by Thompson and Robinson (1932) and Gripenberg (1937b). In general, they follow one of two techniques. Either the titration is carried out in the presence of the carbon dioxide, in which case the end point is taken at about 4.5, or the carbon dioxide is driven off. In the latter case a higher pH, about
The alkalinity bears a fairly constant relation to the chlorinity. The alkalinity: chlorosity factor for surface water has been determined by a number of workers and found to be close to 0.120 when the alkalinity is expressed in terms of milligram-atoms. The designation specific alkalinity that has been used in some cases is obtained by dividing the alkalinity, as mg-atoms/L, by the chlorinity, in g/kg, but such a mixed ratio should not be used. In water from greater depths the ratio may be somewhat higher than that given above, approaching an upper limit of 0.125 near the sea floor (Wattenberg, 1933). In brackish water the ratio may be increased tremendously if the river water is high in bound carbonate compounds. When the alkalinity: chlorosity factor is to be used as an index in studies of industrial pollution, the “normal” change in the ratio with concentration must first be established in samples of sea water diluted with unpolluted river water. Observations by Moberg and Revelle (1937) and by Wattenberg (1936) have shown that in oceanic water the increase in the Ca:Cl factor with depth is equivalent to the rise in the alkalinity:Cl factor. This indicates that changes in the alkalinity and calcium are of common origin—namely, precipitation or solution of CaCO3. Further material concerning the regional variations in the alkalinity: chlorosity factor is given on p. 208.
Because variations in the alkalinity: chlorosity factor in oceanic water are associated with corresponding changes in the calcium: chlorosity factor, the calcium content of the water may be computed from the alkalinity by the following expression:
This procedure for estimating calcium has been followed by Wattenberg (for example, Wattenberg, 1936).It may be seen that the alkalinity: chlorosity factor of 0.1205 is the same as the HCO3−:Cl factor given in table 35, when the bicarbonate is expressed as milligram-atoms of carbon per liter. The reason for this identity is that, in preparing the table, it was assumed that the pH of the water was such that only bicarbonate ions were present and, hence, would be equivalent to the alkalinity.
In discussions of the carbon dioxide system in sea water, the concentrations of the components have commonly been given in millimoles per liter. These are numerically identical with concentrations given as mg-atoms/L of carbon.
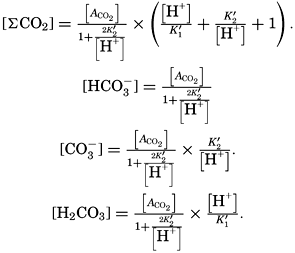
Salts of weak acids containing the following elements are known to occur in sea water: carbon, boron, phosphorus, arsenic, and silicon. Of these, salts of carbonic and boric acid only are present in sufficient concentrations to affect the magnitude of the alkalinity. For the present, we shall neglect the boric acid, which does not affect the alkalinity determination and which has to be considered in the carbonate system only at higher pH's. The alkalinity may then be taken as a measure of the concentration of bicarbonate and carbonate ions, and
where the brackets indicate molar concentrations—that is, gram-atoms of carbon per liter. The [H2CO3] may be determined by titration with sodium hydroxide and the [CO3−] by titration with acid, using carefully controlled end points. The method is described by Greenberg, Moberg, and Allen (1932). It is shown later that the concentration of either H2CO3 or CO3− will be negligible when the other is present in significant quantities. Therefore we may write: or By substituting in these equations the measured quantities, the other components may be obtained.Studies of the carbon dioxide system based on measurements made by these methods have been reported by Greenberg, Moberg, and Allen (1932) and Moberg, Greenberg, Revelle, and Allen (1934). In fig. 38 are shown vertical distribution curves for the carbon dioxide components, total carbon dioxide calculated from the titrations and by direct gasometric measurements, and the alkalinity at a station off the coast of southern California. The total CO2 obtained by the two methods agrees very well and shows a general increase with depth. In the upper layers there is an appreciable amount of CO3−, but this decreases to zero at 200 m, and below this level H2CO3 occurs in quantities which increase with depth. The alkalinity is indicated for the upper 200 m, below which it corresponds, of course, to the curve showing the amount of HCO3−. The increase of alkalinity with depth may be partly due to the biological precipitation of CaCO3 in the upper layers, but in this area it is principally associated with the increasing salinity.
We shall now proceed to a discussion of the laws governing the equilibria between the various carbon dioxide components, the alkalinity,
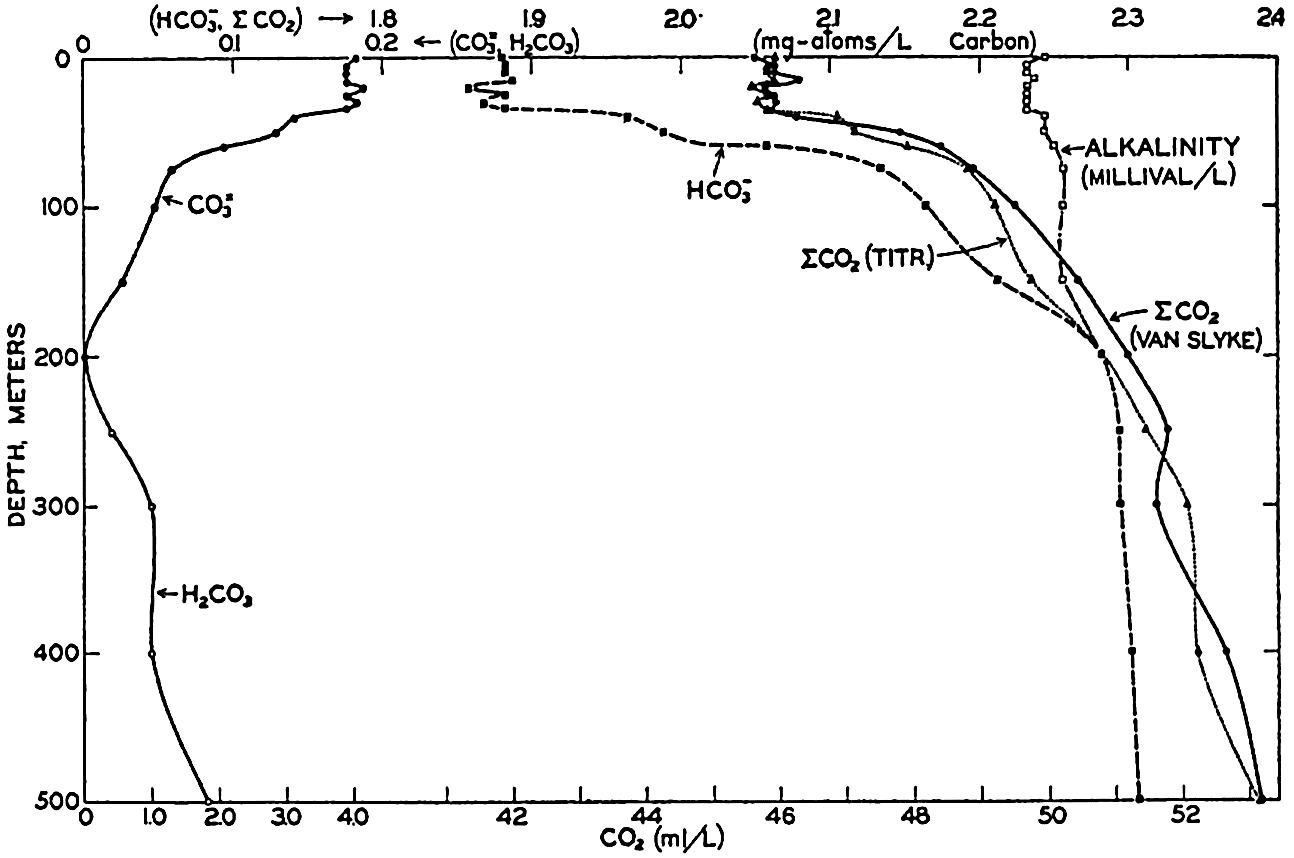
Vertical distribution of the alkalinity and carbon dioxide components off southern California.
[Full Size]
If we indicate the portion of the base (alkalinity) directly bound to the carbon dioxide components as ACO2, the relationship may be written (Buch, 1933a,b)
where all concentrations are in gram-atoms per liter. K′B is the apparent first dissociation constant of boric acid in sea water at the particular temperature and salinity prevailing, and KW is the ionic concentration product of water, [H+] × [OH−], under similar conditions. According to Buch (1938) the ionic product in sea water at 20° can be computed from the following equation: pKW decreases by about 0.035 for each l-degree rise in temperature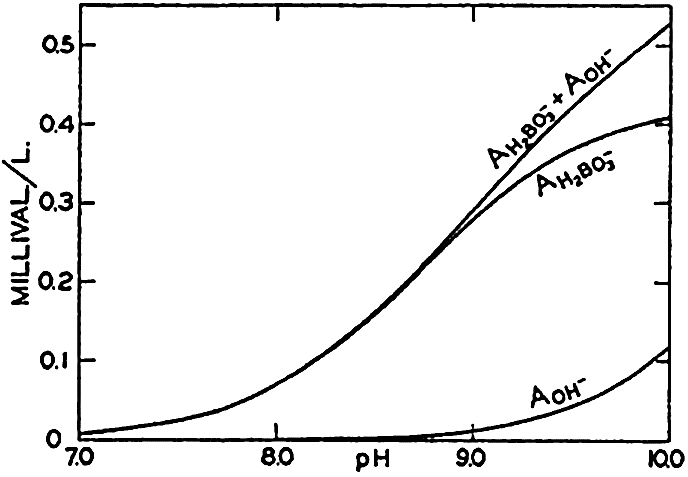
Concentrations of hydroxidebound (AOH−) and borate-bound (AH2BO3−) base as a function of pH in water of Cl = 19.00 ‰ at 20°C.
[Full Size]
The equation for the first dissociation constant of carbonic acid is
and for the second: where the brackets indicate molar concentrations. By introducing the relationships and it is possible to eliminate HCO3− and CO3− from the above equations and obtain them in the following form: Extensive investigations have been carried out to determine the magnitudes of K1′ and K2′. These studies have been reported by Buch, Harvey, Wattenberg, and Gripenberg (1932), and by Moberg, Greenberg, Revelle, and Allen (1934). Buch and others have followed up the work,The effect of hydrostatic pressure, as expressed by means of the depth Δz in meters, on the first dissociation constant is
Buch (1938) found that the second dissociation constant of carbonic acid in sea water at 20°C may be computed from the following equation:Over the normal range of chlorinity in sea water a simpler expression is adequate—namely,
The temperature and pressure corrections are For any given set of conditions, as expressed by means of temperature, salinity, pressure, alkalinity, and pH, the values of ACO2 and K′1 and K′2′ can be calculated. From these the total carbon dioxide and its various components can be computed from the following equations (Revelle, 1934): In fig. 40 are shown the variations in the carbon dioxide components with pH, calculated from the equations given above for sea water ofThe partial pressure of carbon dioxide is related to the amount of free CO2 + H2CO3 (indicated as H2CO3; see p. 190) in the solution:
The value of cs (p. 191) depends upon the temperature and salinity and the units used for expressing the concentration and partial pressure.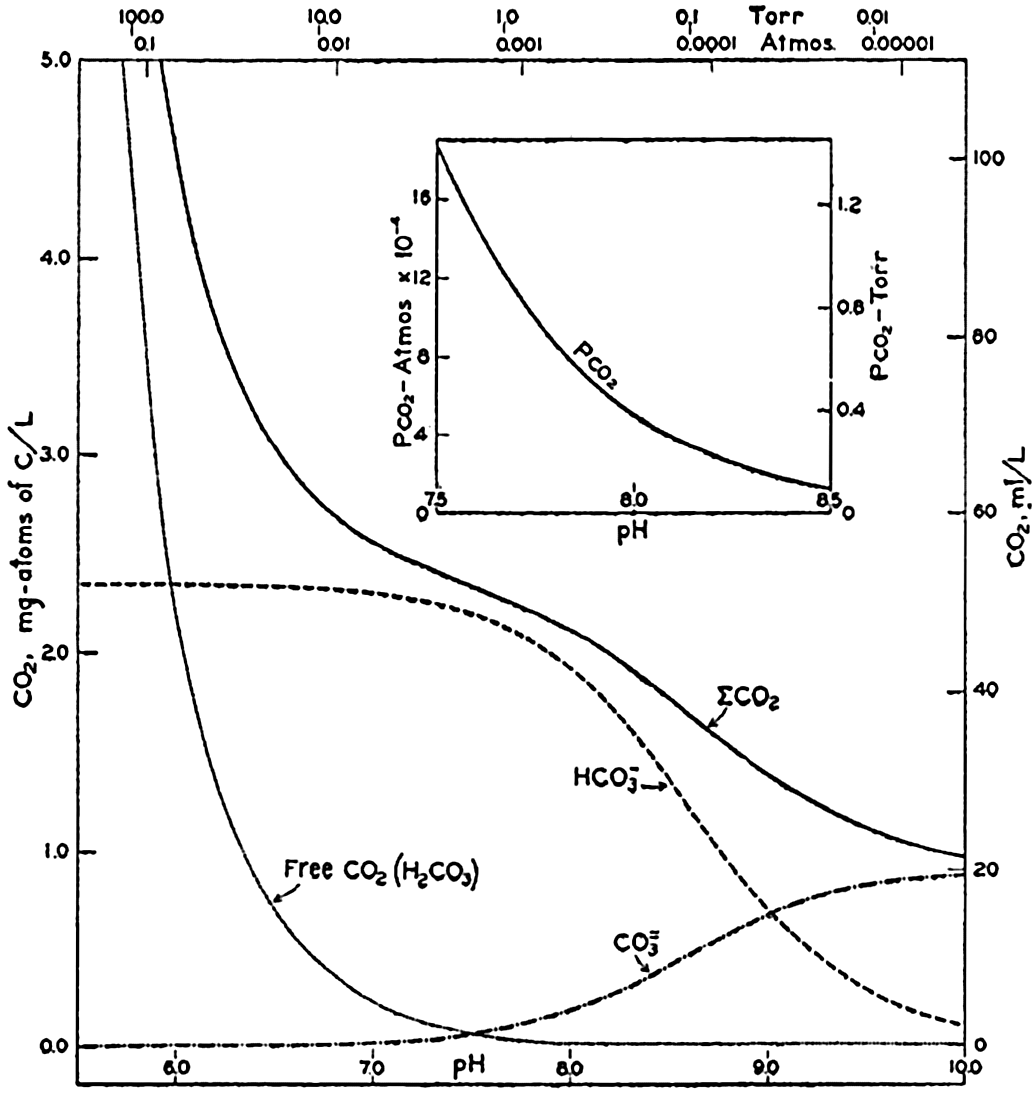
Carbon dioxide components in sea water of Cl = 19.00 ‰ at 20°C as a function of pH and the partial pressure of carbon dioxide.
[Full Size]
In fig. 41 are shown curves for cs at different temperatures and chlorinities, where they represent the amount of H2CO3, in milligram atoms of carbon per liter of sea water, in solution under the designated conditions when the partial pressure of CO2 is 1 physical atmosphere (760 Torr). At 20° and 19 ‰ Cl, cs, is 34.2. That is, a partial pressure of one atmosphere of CO2 would be in equilibrium with a solution containing 34.2 milligram-atoms of carbon as free CO2 + H2CO3. The data are from Buch et al (1932).
The variations in pco2 with the other components is shown in fig. 40. The range is from less than 0.01 to greater than 100 Torr (0.1 × 10−4 to 1000 × 10−4 atm). The relationship over the pH range normally encountered in sea water is shown in the inset diagram in fig. 40. Between pH 7.5 and 8.3, pco2 decreases from 1.4 to 0.15 Torr (18.0 to 2.0 × 10−4 atm). The average partial pressure of CO2 in the air is about 0.23 Torr; hence surface sea water of Cl = 19.0 ‰ at 20° will have a pH of 8.2 if it is in equilibrium with the atmosphere.
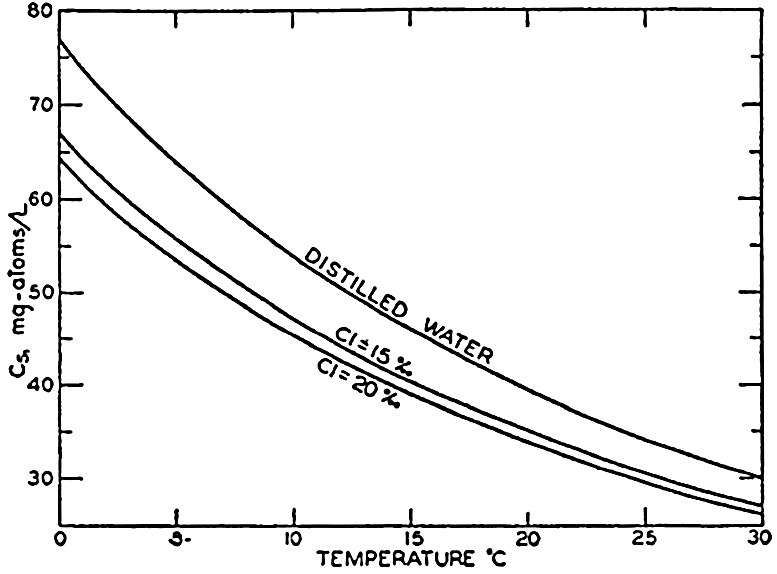
Absorption coefficient (cs) of carbon dioxide in sea water as a function of temperature and chlorinity.
[Full Size]
Sea water is a very favorable medium for the development of photosynthetic organisms. It not only contains an abundant supply of Co2, but removal or addition of considerable amounts results in no marked changes of the partial pressure of CO2 and the pH of the solution, both of which are properties of importance in the biological environment (p. 268). If the CO2 available for photosynthesis is assumed to be H2CO3 + ½HCO3−, 0.48 mg-atoms of carbon per liter may be removed from water of Cl = 19 ‰ with an increase of the pH from 7.5 to only 8.5. In distilled water or in an inert salt solution of zero akalinity initially at pH 7.5, the total CO2 would be about one seventh of that amount.
Buffer Action of Sea Water. If a small quantity of a strong acid or base is added to pure water, there are tremendous changes in the numbers of H+ and OH− ions present, but the changes are small if the acid or base is added to a solution containing a weak acid and its salts or a weak base and its salts. This repression of the change in pH is known as buffer action, and such solutions are called buffer solutions. Sea water contains carbonic and boric acids and their salts and is, therefore, a buffer solution. Let us consider only the carbonate system. Carbonate and bicarbonate salts of strong bases, such as occur in sea water, tend to hydrolyze, and there are always both H+ and OH− ions in the solution. If an acid is added, carbonate is converted to bicarbonate and the bicarbonate to carbonic acid, but, as the latter is a weak acid (only slightly dissociated), relatively few additional hydrogen ions are set free. Similarly, if a strong base is added, the amount of carbonate increases, but the OH− ions formed in the hydrolysis of the carbonate increase only slightly. The buffering effect is greatest when the hydrogen
Cycle of CO2 Between Sea and Atmosphere. Investigations of the partial pressure of CO2 in the ocean and the atmosphere have been made by Krogh (1904) and Buch (1939a,b). The following internal changes will increase or decrease the pCO2 in the surface layer:
| Increase pco2 | Decrease pco2 |
|---|---|
| 1. Rise in temperature | 1. Decrease in temperature |
| 2. Rise in salinity (evaporation) | 2. Decrease in salinity |
| 3. Respiration | 3. Photosynthesis |
| 4. Precipitation of CaCO3 | 4. Solution of CaCO3 |
| 5. Deep water brought to surface |
The partial pressure of CO2 in the surface water can be computed with sufficient accuracy when the temperature, salinity, alkalinity, and pH are known, but, before a better understanding of the CO2 exchange between the sea and the atmosphere can be obtained, a far more comprehensive study of the partial pressure of the atmospheric CO2 must be made. Buch (1939b) has reported a number of direct observations on the CO2 content of the air which indicate that polar air is relatively low in CO2 (pCO2 = 0.23 Torr), compared to continental and tropical air (pCO2 = 0.25 Torr). It has been suggested that in low latitudes the air is enriched with CO2 from the ocean and that the general atmospheric circulation carries the CO2 into high latitudes. There it again dissolves in the sea water, which in time brings it back toward the Equator.
Activity of Ions in Sea Water. The apparent first and second dissociation constants of carbonic acid and the first dissociation constant of boric acid in sea water are larger than in distilled water and increase with increasing salinity. That is, the strength of these acids appears to be greater in solutions containing salts. These phenomena can be accounted for on the theory of activity introduced by Lewis and Randall (1923) and developed mathematically by Debye and Hückel. In a solution containing a mixture of electrolytes, such as sea water, there is a mutual interference of the ions, so that their activity or ability to participate independently in some reaction is much reduced. Most chemical determinations measure the total concentration of some ion and not its activity; however, certain physical measurements show the activity. For example, electromotive force determinations involve the activity of the hydrogen and other ions. Similarly, the measurement of the vapor pressure of a solution of a nonvolatile compound is an indication of the activity of the solvent. The activity will be less than that of the pure solvent under similar conditions. The partial pressure of dissolved gases is a measure of their activity.
The activity coefficient γ is related to the activity α of an ion as in the following example:
Hence, αH+ is the activity of the hydrogen ions expressed as gram-atoms per liter and [H+] is the stoichiometric concentration.In the studies of the carbon dioxide system in sea water, the total CO2, alkalinity, and carbon dioxide components are measured chemically, and hence the values represent the stoichiometric values and not the activities. On the other hand, the hydrogen ion concentration is determined colorimetrically or electrometrically, and these methods yield the activity of hydrogen ions directly. Therefore, in the equations relating the CO2 components αH+ could have been inserted instead of [H+]. The dissociation constants have been referred to as apparent dissociation constants, in contrast to the thermodynamic constants that would be obtained at infinite dilution, where the activity coefficients (γ) are unity. The apparent dissociation constants are indicated by the symbol prime (′)—for example, K′2. For carbonic acid the thermodynamic second dissociation constant can be written
and this is related to the apparent dissociation constant (Moberg et al, 1934): Similarly, The value of γ H2Co3 depends upon the relative solubility of CO2 in pure water and in sea water at the same temperature and upon the activity of the water in the two cases: The subscript o indicates values at infinite dilution, and the subscript s the values at the concentration under consideration. The values of co and cs can be obtained from fig. 41, and es and eo, (the vapor pressures) can be computed (p. 67).From the empirical equations relating pK′1 and pK′2 to the temperature and chlorinity, we know that at 20° and zero chlorinity the thermodynamic values are pK1 = 6.47 and pK2 = 10.288, and, at 19.00 ‰ Cl, pK'1 = 5.97 and pK'2 = 9.02. By substituting these values and γH2CO3
Empirical equations have been presented which relate pK′1 and pK′2 to the cube root of the chlorinity. It has been shown (Buch et al, 1932, Moberg et al, 1934) that these equations are generally valid for salt solutions other than sea water if the ionic strength is used instead of chlorinity as a measure of concentration. The ionic strength (μ) of a solution is obtained by first multiplying the concentration of each individual type of ion, in moles per kilogram of solvent water, by the square of its valence, and then taking half the sum of these products (Lewis and Randall, 1923, p. 373). Lyman and Fleming (1940) have shown that the ionic strength of sea water in the normal range of concentration may be computed from the expression
Moberg et al (1934) have summarized the pertinent data, but no satisfactory expressions have yet been developed to show the manner in which the activity coefficients of the different ions in sea water change with concentration.Solubility of CaCO3. The solubility of an electrolyte, such as calcium carbonate, may be expressed by a solubility product. The solubility product is identical with the ionic product (if concentrations are expressed as moles per liter) when the solution is in equilibrium with the solid salt and, therefore, saturated. The value of the solubility product depends upon temperature, the concentration of other ions (salinity), and the hydrostatic pressure. If, under a given set of conditions, the ionic product is less than the solubility product, the solution is undersaturated; if the ionic product is greater the solution is supersaturated, and if suitable nuclei are present, precipitation will proceed until the ionic product equals the solubility product.
The solubility product of CaCO3(KCaCO3) in distilled water at 20° is 5.0 × 10−9. In sea water of chlorinity 19.00 ‰ and at the same temperature, the calcium content is 10.23 mg-atoms/L, and at pH 8.2 the carbonate ion concentration is 0.26 mg-atoms/L of carbon. Therefore the ionic product is
which is 530 times greater than the solubility product in distilled water. If solubility data for distilled water are to be applied to sea water, it isIt is therefore necessary to determine empirically the concentrations of Ca++ and CO−3 that can exist in contact with solid CaCO3. Working at 30° and increasing the CO−3 content by lowering the total CO2, Revelle and Fleming (1934) obtained precipitation of CaCO3 as aragonite needles and spherulites. The calcium content of the solution was determined directly, and the CO−3 was calculated from measurements of the pH, alkalinity, and chlorinity. The average of three experiments gave K'CaCO3 = 2.4 × 10−6 at 30°C. Wattenberg has carried out a number of studies on the solubility of calcium carbonate in sea water. His general procedure was to add CaCO3 crystals to sea water, and in some instances to increase the pCO2 The sea-water samples were then placed in sealed flasks and agitated until equilibrium was established. The calcium content of the water was calculated from the alkalinity measurements (p. 196), and the CO3 was obtained with the aid of pH determinations. Wattenberg and Timmerman (1936) give the following values for the apparent solubility product in sea water of Cl = 18.5 to 19.5 ‰:
| Temperature, °C | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| K′CaCO3 | 8.1 | 7.9 | 7.4 | 6.8 | 6.2 | 5.5 | 4.7 | 3.8 × 10−7 |
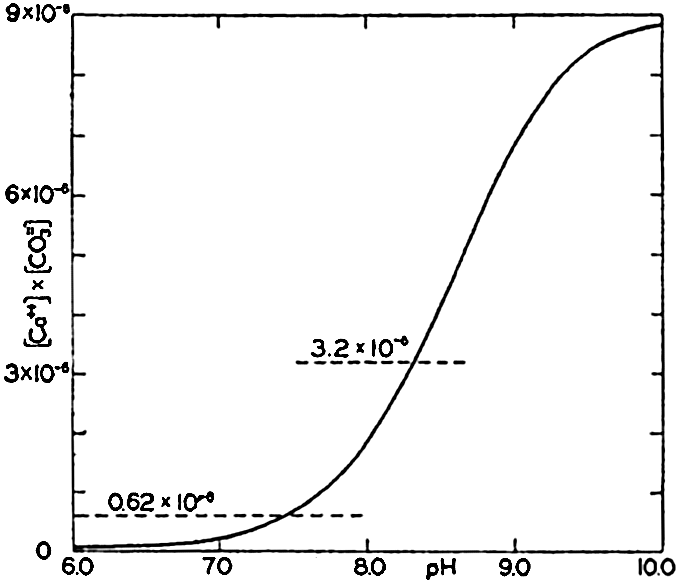
Ionic product [Ca++l × [CO3−] in sea water of Cl = 19.00 ‰ at 20°C as a function of pH. The horizontal lines indicate the solubility product according to Wattenberg (0.62 × 10−6 and according to Revelle and Fleming (3.2 × 10−6).
[Full Size]
At 30° Wattenberg's value is only one fifth of that obtained by Revelle and Fleming. No satisfactory explanation of this difference has yet been offered. In fig. 42 the ionic product in sea water of Cl = 19.00 ‰ at 20° is plotted against pH. The value of K'CaCO3, for this temperature obtained by Wattenberg—namely, 0.62 × l0−6—would indicate that supersaturation exists at all pH's above about 7.5. Surface water in equilibrium with the atmosphere has a pH of about 8.2 and would be
Smith (1940) has investigated the calcium carbonate deposition that takes place in the shallow waters overlying the Bahama Banks. He found the alkalinity to be much reduced, and from measurements he computed the ionic product, [Ca++] × [CO3−]. Minimum values of the product that he considers approach the solubility product were found to fall between the values of Revelle and Fleming and those of Wattenberg.
According to Wattenberg (1936), K'CaCO3 at 20° changes with the chlorinity in the following way:
| Cl, ‰ | 0 | 5 | 10 | 15 | 20 |
| K′CaCO3 | 0.05 | 1.8 | 4.0 | 5.0 | 6.2 × 10−7 |
That is, in sea water the apparent solubility product of CaCO3 increases with chlorinity and decreases with temperature.
Revelle (1934) and Wattenberg (1936) consider that hydrostatic pressure has no significant effect upon the value of K'CaCO3. However, it should be remembered that, because of changes in the dissociation constants of carbonic acid, pressure does modify the relative amounts of HCO3 and CO−3 in the water. Hence, water that is saturated at the surface will be slightly undersaturated if subjected to hydrostatic pressure, even if the total CO2 and calcium contents remain unaltered. Conversely, bottom water saturated with CaCO3 will be supersaturated when brought to the surface.
Although our knowledge of the values of K′CaCO3 under different conditions is incomplete and uncertain, it is possible to show the effect of changes in the conditions upon the ionic product, thus obtaining an understanding of those agencies that will favor precipitation or solution. Revelle (1934) has shown that, in surface water, increase of the salinity and the temperature, and decrease of the pco2—that is, the total CO2 content—all tend to increase the ionic product and therefore favor precipitation. The salinity effect is relatively small, and hence areas of high or rising temperature and of active photosynthesis will be those where precipitation of CaCO3 is most likely to occur. Opposite conditions will favor solution.
In the deep water the range in temperature and salinity is small, and therefore the variations in pCO2 will have the most pronounced effect. According to Wattenberg's studies (1933) the deep waters of the Atlantic Ocean are virtually saturated with calcium carbonate. Areas overlying red clay show slight undersaturation, and those overlying calcareous deposits (globigerina ooze) show either saturation or slight supersaturation.
Certain types of calcareous sedimentary material, both recent and fossil, do not show any evidence of organic origin. These are sometimes considered to be “chemical” deposits. In certain areas, microorganisms undoubtedly play an important part in establishing conditions that result in the incidental precipitation of carbonates. In tropical seas, this process may occur in shoal-water areas, coral reefs, lagoons, and mangrove swamps (Field, 1932). Although microorganisms can produce conditions favoring the precipitation of calcium carbonate, it is considered that they are effective agents in this process only in and on the sediments in the environments listed above. Smith (1940) has found that over the Great Bahama Bank CaCO3 is precipitated, under conditions of heating and excessive evaporation, on nuclei supplied by the sediments. The finely divided CaCO3 in certain deep-sea sediments is thought to arise from the break-down of the shells of foraminifera (p. 982) and not from precipitation in situ.
Distribution of Alkalinity, pH, and Carbon Dioxide Components. In the preceding discussion it has been assumed that the alkalinity: chlorosity factor is constant, and the value 0.1205 (milliequivalents per unit Cl) has been used in computations. This is in agreement with the average of a large number of observations made by Wattenberg (1933) in the Atlantic Ocean and those reported by Revelle (1936) for the upper layers of the Pacific Ocean. Wattenberg's value is commonly given as the specific alkalinity—namely, as milliequivalents per unit chlorinity, in which case it is 0.123. A number of different methods (p. 195) have been employed for measuring alkalinity, but there is no definite proof that they all yield similar values. Hence, it is difficult to compare the results obtained from various parts of the oceans by different workers. However, the findings of Wattenberg (1933), Mitchell and Rakestraw (1933), and Revelle (1936) all show that there is a somewhat higher alka1inity:chlorosity factor in the deeper water than there is in the surface layers. The increase in the factor usually amounts to about 0.005. Wattenberg examined a number of water samples collected immediately over the bottom, and in these he found an even larger factor. The low values in the surface waters are ascribed to removal of calcium carbonate by organisms possessing calcareous skeletons. Smith (1940) has suggested that, at least in certain localities, there may be inorganic precipitation if suitable nuclei are present when
The pH of sea water in contact with the air will vary between about 8.1 and 8.3, depending upon the temperature and salinity of the water and the partial pressure of carbon dioxide in the atmosphere. In areas of great dilution lower values may occur. At subsurface levels, where exchange of carbon dioxide with the atmosphere is impossible, the pH will vary with the extent to which the CO2 content of the water is modified by biological activity. In the euphotic zone, higher pH's are usually found; below this they decrease to a minimum corresponding in general to the layer of minimum oxygen content, and then increase again toward the bottom. Although variations in the salinity affect the pH, the predominant factor is the total carbon dioxide content or its partial pressure.
Unfortunately, differences in technique and in the constants used in arriving at pH's from colorimetric measurements make it difficult to compare the results of different workers. The most extensive studies made on the distribution of pH in the oceans are those of the Meteor (Wattenberg, 1933) in the Atlantic Ocean and those of the Carnegie in the Pacific Ocean. The distributions of pH and dissolved oxygen along a longitudinal profile in the eastern Atlantic Ocean are shown in fig. 43. The rather close similarity of the isolines can easily be seen, and similar patterns would be given by the partial pressure and total CO2 content, although in this case the relations would be inverse ones. The temperature

Distribution of pH and dissolved oxygen in the eastern part of the Atlantic Ocean. The locations of the sections are shown in the map on the left-hand side. The vertical and horizontal scales are different in the two sections. (After Wattenberg.)
[Full Size]