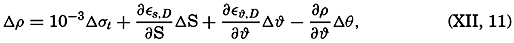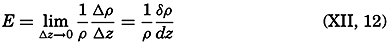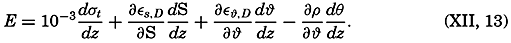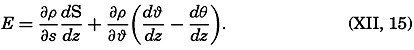Stability
The change in a vertical direction of σt is nearly proportional to the vertical stability of the system. Assume that a water mass is displaced vertically upward from the geopotential depth D2 to the geopotential depth D1. The difference between the density of this mass and the surrounding water (see p. 57) will then be
where Δσt, ΔS, and Δϕ represent the variations of σt, S and ϕ between the geopotentials D1 to D2, and where Δθ represents the adiabatic change of temperature. The water mass will evidently remain at rest in the new surroundings if Δρ = 0; it will sink back to its original place if Δρ is positive, because it is then heavier than the surroundings; and will rise if Δρ is negative, because it is then lighter than the surroundings. The acceleration of the mass will be proportional to Δρ/ρ. The reasoning remains unaltered if we introduce geometric depths instead of geopotential. If the acceleration due to displacement along the short| Depth (m) | Temp. (°C) | Salinity (‰) | σt | 108E | 105(dσt/dz) |
| 0 | 19.2 | 36.87 | 26.42 | ||
| 10 | .31 | .85 | .38 | −440 | −400 |
| 25 | .34 | .83 | .35 | −150 | −200 |
| 50 | .24 | .79 | .34 | −13 | −40 |
| 75 | 18.65 | .79 | .49 | 610 | 600 |
| 100 | .24 | .78 | .58 | 390 | 375 |
| 150 | 17.50 | .56 | .61 | 34 | 60 |
| 200 | 16.45 | .40 | .73 | 270 | 240 |
| 300 | 14.52 | .02 | .88 | 160 | 150 |
| 400 | 13.08 | 35.77 | .99 | 120 | 110 |
| 500 | 11.85 | .64 | 27.13 | 150 | 140 |
| 600 | 10.80 | .54 | .25 | 130 | 120 |
| 800 | 9.09 | .39 | .43 | 100 | 90 |
| 1000 | 8.01 | .37 | .58 | 89 | 75 |
| 1200 | 7.27 | .42 | .74 | 84 | 80 |
| 1400 | 6.40 | .35 | .80 | 48 | 30 |
| 2000 | 4.52 | .15 | .87 | 39 | 12 |
| 3000 | 2.84 | 34.92 | .86 | 11.2 | −1 |
| 4000 | 2.43 | .90 | .87 | 7.6 | 1 |
| 5000 | 2.49 | .90 | .87 | 1.3 | 0 |
Hesselberg and Sverdrup (1914–15) have published tables by means of which the terms of equation (XII, 13) are found, and give an example based on observations in the Atlantic Ocean on May, 1910, in lat. 28°37′N, long. 19°08′W (Helland-Hansen, 1930). This example is reproduced in
Hesselberg and Sverdrup have also computed the order of magnitude of the different terms in equation (XII, 13) and have shown that dσt/dz is an accurate expression of the stability down to a depth of 100 m, but that between 100 and 2000 m the terms containing ε may have to be considered, and that below 2000 m all terms are important. The following practical rules can be given:
Above 100 m the stability is accurately expressed by means of 10−3dσt/dz.
Below 100 m the magnitude of the other terms of the exact equation (XII, 13) should be examined if the numerical value of 10−3dσt/dz is less than 40 × 10−8.
The stability can also be expressed in a manner that is useful when considering the stability of the deep water:
If the salinity does not vary with depth (dS/dz = 0), as is often the case in the deep water, Of the quantities in this equation, ∂ρ/∂ϕ is negative, dθ/dz is positive, and dϕ/dz is negative if the temperature decreases with depth, but positive if the temperature increases. The stratification will always be stable if the temperature decreases with depth or increases more slowly than the adiabatic, but indifferent equilibrium exists if dϕ/dz = dθ/dz, and instability is found if dϕ/dz > dθ/dz.