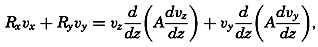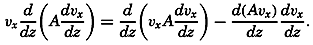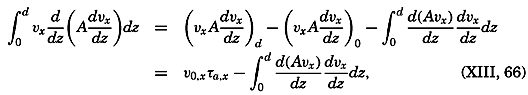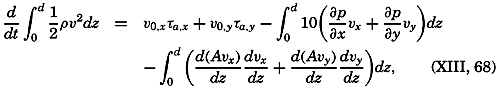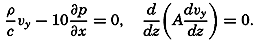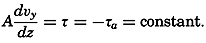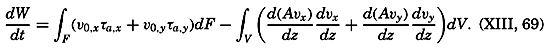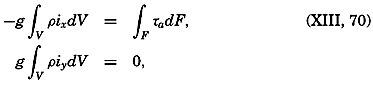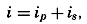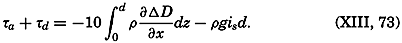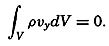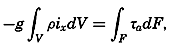Friction
General Consideration of Friction. Two of the fundamental concepts concerning friction in a fluid are (1) that shearing stresses are produced when layers are slipping relative to each other, and (2) that the shearing stresses acting on a unit area are proportional to the rate of shear normal to the surface on which the stress is exerted: τ = μdv/dn. The factor of proportionality, μ, is called the dynamic viscosity of the fluid.
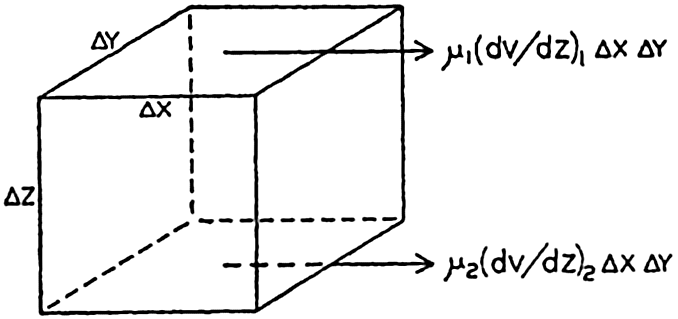
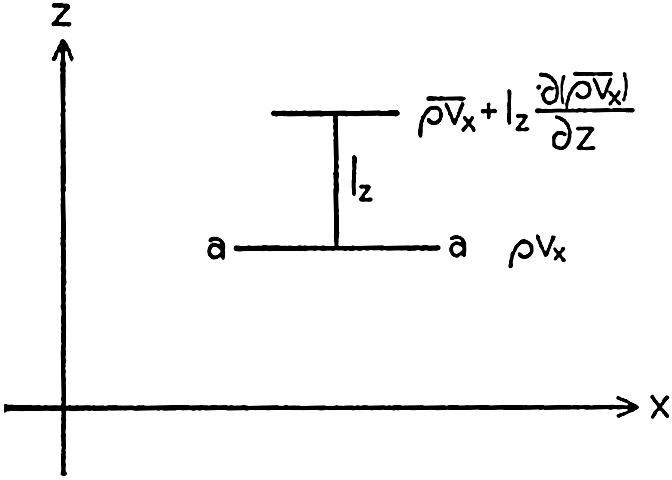
Frictional forces per unit volume are equal to the differences between shearing stresses exerted on opposite sides of a cube of unit dimensions. Consider a cube of side length Δz (fig. 118) in a fluid moving only in the direction of the x axis, and let the rate of shear at the upper and lower surfaces of the cube be (dv/dz)1 and (dv/dz)2, respectively. The shearing stress per unit area of the upper surface is then τ1 = (μdv/dz)1, and the total stress acting on the upper surface is
Similarly, the shearing stress exerted on the lower surface is The force acting on the cube is equal to (τ1 − τ2)ΔxΔy, and the force per unit volume isIn classical hydrodynamics the dynamic viscosity, μ, is considered a characteristic property of the fluid—namely, the property that resists angular deformation. Being a characteristic property, the magnitude of μ is independent of the state of motion, but it varies, as a rule, with the temperature of the fluid. Within wide limits it is independent of the pressure. The dynamic viscosity has the dimensions ML−1T−1, whereas the kinematic viscosity, defined as ν = μ/ρ, has the dimensions L2T−1. A table of the dynamic viscosity of sea water is given on p. 69.
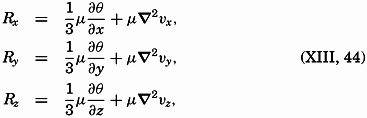
The derivation of the general frictional terms that must be taken into account when dealing with motion in space is given in the general textbooks on hydrodynamics or fluid mechanics which are listed at the end of this chapter. The complete theory requires the introduction of both shearing and normal stresses, and leads, if μ is considered constant, to the expressions for the frictional terms:
where and where the operation ∇2 means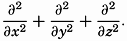 [Equation].
[Equation].When these terms are added to the equations of motion (XIII, 1), and if the terms depending upon the divergence of the velocity are omitted, one obtains the Navier-Stokes equation of motion (for example, Lamb, 1932), which in greatly simplified form has found application to problems in fluid mechanics. The theory that leads to the development of the Navier-Stokes equation excludes, however, the possibility of local fluctuations in velocity and presupposes that the fluid moves in layers, or laminae. This type of motion is called “laminar flow,” but is probably never encountered in the ocean. The Navier-Stokes equations find, therefore, no application to oceanographic problems and have been mentioned here only as an approach to the problem of fluid resistance
Turbulence. Laminar flow, in which sheets of fluid move in an orderly manner is, as has already been stated, not known to occur in the ocean. The ocean currents are, instead, characterized by numerous eddies of different dimensions by which small fluid masses are constantly carried into regions of different velocity. It is this completely irregular type of motion which is called turbulent flow, and the process by which a rapid exchange of fluid masses is maintained is called turbulence.
The very character of turbulent flow is such that rapid fluctuations of velocity take place in all localities, and no steady state of motion exists if attention is paid to the individual particles of the fluid. It might therefore appear hopeless to arrive at a theory that takes full account of the complicated character of the actual motion, but the problem has, nevertheless, been attacked with considerable success by using statistical methods. The velocity at any given point in space can always be considered as the vector sum of two different velocities: 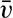 [Equation], which represents the average velocity at that point during a long period of time, and ν′ which represents the added “turbulent” velocity. At any given time the actual velocity components can therefore be written
[Equation], which represents the average velocity at that point during a long period of time, and ν′ which represents the added “turbulent” velocity. At any given time the actual velocity components can therefore be written
After such a segregation is made, the whole pattern of flow can be considered as composed of two systems, one representing the average flow, which may be steady or accelerated, according to the acting forces, and one representing the irregular turbulent motion, which is superimposed upon the average flow and whose nature is not known at any given time. The former system, the average flow, is of interest when dealing with the ocean currents, but knowledge of the superimposed turbulent flow is necessary for studying the extent to which the turbulent flow modifies the apparent viscosity.
Frictional Stresses Due to Turbulent Motion. It is not possible here to present the complete development of the frictional terms. Interested readers are referred to general textbooks on hydrodynamics or fluid mechanics (for example, Lamb, 1932, Rouse, 1938), but a few important points must be brought out here. Owing to the very character of the turbulent motion, small fluid masses are carried back and forth across any given surface, and a mass coming from a region of high velocity has, when entering a region of low velocity, a momentum which is greater than that of the surrounding particles. If this fluid mass assumes approximately the velocity of the surroundings, it loses momentum, and, similarly, a small fluid mass that comes from a region of low velocity into one of high velocity gains momentum. Thus, where a
Reynolds first derived expressions for the stresses due to momentum transport, and since then the theory of turbulence has been further developed, notably by L. Prandtl, G. I. Taylor, and Th. v. Kármán. The method of attack which so far has found the greatest application to oceanographic problems is based on Prandtl's introduction of the mixing length. Consider that the average flow is in the direction of the x axis and that 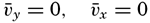 [Equation]. Then
[Equation]. Then
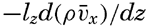 [Equation] between the average original momentum of the small fluid masses
[Equation] between the average original momentum of the small fluid masses 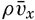 [Equation] and the average momentum at the locality where exchange takes place. The momentum given off per unit time must be proportional to the average numerical value of the vertical velocity of the small fluid masses, which is
[Equation] and the average momentum at the locality where exchange takes place. The momentum given off per unit time must be proportional to the average numerical value of the vertical velocity of the small fluid masses, which is 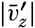 [Equation]. Therefore, the rate of momentum transport, M, will be
where k is a factor of proportionality. This factor can be absorbed in
[Equation]. Therefore, the rate of momentum transport, M, will be
where k is a factor of proportionality. This factor can be absorbed in
Prandtl's theory also leads to another definition of Az:
and according to von Kármán's statistical theory, where K0 is a nondimensional factor of proportionality which has the character of a universal constant and has been found to be equal to nearly 0.4.The above considerations lead to the result that
The notation τxz means that the stress acts in the direction of the x axis and along a surface that is normal to the z axis.Equation (XIII, 50) is similar to the equation τ = μdv/dn (p. 69). The coefficient Az has the same dimensions as the dynamic viscosity μ and is called the eddy viscosity. However, a fundamental difference exists between the two quantities. The dynamic viscosity is independent of the state of motion and is a characteristic property of the fluid, comparable to the elasticity of a solid body, but the eddy viscosity depends upon the state of motion and is not a characteristic physical property of the fluid. The numerical value of the eddy viscosity varies within very wide limits according to the type of motion, and, as far as ocean currents are concerned, only the order of magnitude of Az has been ascertained.
It should be observed that the eddy viscosity can be introduced without paying any attention to the mixing length or any other statistical quantity that describes the character of the turbulence. Because in a
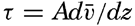 [Equation], where
[Equation], where 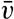 [Equation] stands for the mean motion and where A evidently must depend upon the character of the turbulence. This notation was used by Ekman (1905) in his classical discussion of wind currents, in which the eddy viscosity was first introduced analytically under the name “virtual viscosity” when dealing with oceanographic problems.
[Equation] stands for the mean motion and where A evidently must depend upon the character of the turbulence. This notation was used by Ekman (1905) in his classical discussion of wind currents, in which the eddy viscosity was first introduced analytically under the name “virtual viscosity” when dealing with oceanographic problems.For the sake of completeness, it may be added that the expression for the stress should also contain the term 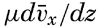 [Equation], but this can always be neglected, because μ is very small compared to A. Oceanographic data give values of A ranging between 1 and 1000 g/cm/sec, whereas μ is about 0.015 (table 16, p. 69).
[Equation], but this can always be neglected, because μ is very small compared to A. Oceanographic data give values of A ranging between 1 and 1000 g/cm/sec, whereas μ is about 0.015 (table 16, p. 69).
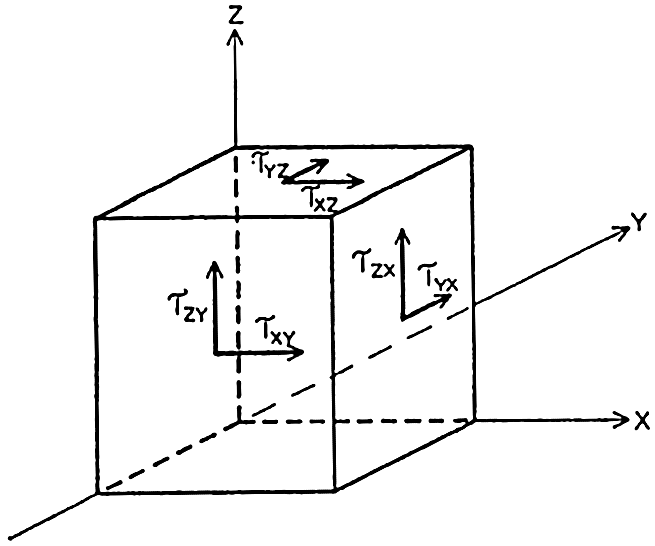
The discussion of the shearing stresses due to turbulent exchange of momentum can now be extended by dropping the assumption that the motion takes place in the direction of the x axis only, because the reasoning is equally correct if the average velocity has a component in the direction of the y axis. The stress in the direction of the y axis on a surface normal to the z axis, τyz, is
Dropping the assumption that 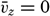 [Equation] = 0 and that the average velocity does not vary in a horizontal direction leads to the introduction of four new shearing stresses (fig. 120):
[Equation] = 0 and that the average velocity does not vary in a horizontal direction leads to the introduction of four new shearing stresses (fig. 120):
Here the coefficients of eddy viscosity may be defined as before:
partial differentials are used because it is no longer assumed that the velocity varies only in the direction of the z axis.Frictional Forces Due to Turbulent Motion. The frictional force acting in the direction of the x axis is derived from the stresses τxz and τxy (fig. 120):
In order to arrive at frictional terms that are of importance when dealing with ocean currents, it will be assumed that (1) only the shearing stresses that have been discussed here are important, (2) the vertical velocity is so small that the gradients of the vertical velocity are negligible, and (3) the horizontal mixing length and the average horizontal turbulent velocities are independent of the direction of motion; that is, Ax = Ay = Ah. Writing simply νx instead of 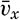 [Equation], and so on, one obtains the frictional terms in the form
[Equation], and so on, one obtains the frictional terms in the form
The above derivation is not an exact one, and therefore the equations that define the frictional forces in the ocean represent only approximations that appear satisfactory at the present stage of knowledge of ocean currents. When it becomes desirable to improve these expressions, it will be necessary to consult the treatment of the problem of fluid friction which is given in the textbooks on hydrodynamics or fluid mechanics listed at the end of this chapter.
In applying the expressions for the frictional forces, a further simplification is generally be introduced—namely, that the horizontal frictional forces can be disregarded. The concept of horizontal turbulence, however, has been introduced because horizontal or quasihorizontal turbulence appears to play an important part in large-scale processes of diffusion, although the dynamic significance is not yet clear.
If horizontal turbulence is neglected, the consideration of transport of momentum leads to the frictional terms
G. I. Taylor (1932) has introduced the assumption that, instead, the transport of vorticity should be considered. This assumption leads to the termsInfluence of Stability on Turbulence. No theory has been developed for the state of turbulence which at indifferent equilibrium or at stable stratification characterizes a given pattern of flow, except in the immediate vicinity of a solid boundary surface (p. 480), but it has been demonstrated that the turbulence as expressed by the eddy viscosity decreases with increasing stability. Thus, Fjeldstad (1936) found that he could obtain satisfactory agreement between observed and computed tidal currents in shallow water by assuming that the eddy viscosity was a function not only of the distance from the bottom but of the stability as well. He introduced A = f(z)/(1 + aE), where E is the stability and where the factor a is determined empirically.
The relation between eddy viscosity and eddy diffusion has been examined by Taylor (1931). Taylor's reasoning is based on the fact that, in the presence of turbulence, the kinetic energy of the system can be considered as composed of two parts: the kinetic energy of the mean motion, and the kinetic energy of the superimposed turbulent motion. In homogeneous water the latter is being dissipated by viscosity only, wherefore, if the turbulence remains constant, turbulent energy must enter a unit volume at the same rate at which it is dissipated. Where stable stratification is found (p. 92), part of the turbulent energy is also used for increasing the gravitational potential energy of the system. In this case the rate at which turbulent energy enters a unit volume, T, must equal the sum of the rate at which the potential energy increases, P, and the rate at which energy is dissipated by viscosity, D. It follows that, if the turbulence remains unaltered, one must have T > P.
Taylor shows that the rate at which turbulent energy enters a unit volume equals 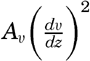 [Equation], where Av means the eddy viscosity, and that the rate at which the potential energy increases equals gEAs, where E is the stability (p. 416) and As is the eddy diffusivity. It follows that
[Equation], where Av means the eddy viscosity, and that the rate at which the potential energy increases equals gEAs, where E is the stability (p. 416) and As is the eddy diffusivity. It follows that
Taylor tested the correctness of this conclusion by measurements made by Jacobsen (1913) in Danish waters, where Jacobsen found values
According to Taylor's theory, turbulence can always be present, regardless of how great the stability is, but the type of turbulence must be such that the condition (XIII, 57) is fulfilled; that is, the rate at which the Reynolds stresses communicate energy to a region must be greater than the rate at which the potential energy of that region increases. It explains why observations in the ocean mostly give smaller values of As than of Av. A velocity gradient of 0.1 m/sec on 100 m is common where the stability is about 10−6 m−1, and with these values one obtains As < 0.1Av. Within layers of very great stability the velocity gradient is generally also great, but the value of As becomes even smaller than in the above example. Thus, below the Equatorial Countercurrent in the Atlantic the decrease of velocity in a vertical direction is 6.10−3 sec−1, and the stability is about 5.10−5 m−1 (Montgomery, 1939). With these values, one obtains As < 7.10−2 Av, or, if the eddy viscosity were equal to 10 g/cm/sec, the eddy diffusivity would be less than 0.7.
Thus the effect of stability on turbulence is twofold. In the first place, the turbulence is reduced, leading to smaller values of the eddy viscosity, and, in the second place, the type of the turbulence is altered in such a manner that the accompanying eddy diffusivity becomes smaller than the eddy viscosity. The latter change is explained by Jacobsen (1930) by assuming that elements in turbulent motion give off their momentum rapidly to their surroundings, but that other properties are exchanged slowly, and that before equalization has taken place the elements are moved to new surroundings by gravitational forces (p. 92). A possible influence of stability on lateral turbulence has not been examined, but it has been suggested by Parr (1936) that this kind of turbulence increases with increasing stability.
Horizontal Turbulence. The horizontal turbulence needs some further explanation because of the effect of the earth's rotation. Let it be assumed that the field of pressure is such that the deflecting force associated with the mean motion is balanced by the pressure gradient:
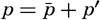 [Equation], one finds that the above equations must take the form
Here
[Equation], one finds that the above equations must take the form
Here 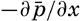 [Equation] and
[Equation] and 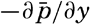 [Equation] represent the mean pressure gradients, and −∂p′/∂x and −∂p′/∂y represent local pressure gradients associated with the turbulent motion.
[Equation] represent the mean pressure gradients, and −∂p′/∂x and −∂p′/∂y represent local pressure gradients associated with the turbulent motion.Thus, superimposed upon the average field of pressure must be an irregular field. If the pressure distribution could be represented by means of the absolute geopotential topographies of isobaric surfaces (p. 413), these would show, besides certain major features that would characterize the mean motion, also a number of small “lows” and “highs,” troughs and ridges, which would represent the superimposed irregular pressure field. Detailed surveys during which the oceanographic stations have been spaced at intervals of 20 km or less have revealed that the relative distribution of pressure shows numerous irregularities of such nature. This fact strongly supports the conclusion that the horizontal motion associated with the pressure distribution is far from being uniform, but is characterized by numerous eddies that may have dimensions up to 20 km or more.
Boundary Friction. In oceanography the problem of frictional stresses at boundary surfaces can be dealt with in the same manner as the similar problem in fluid mechanics. Over an absolutely smooth surface
Over a rough surface, different conditions are encountered. Prandtl assumes that over such a surface the turbulent motion extends to the very surface, meaning that the mixing length has a definite value at the surface itself:
where z0 is called the roughness length and is related to the average height of the roughness elements. Equation (XIII, 48) gives or and Through integration, assuming ν = 0 at z = 0, one obtainsMeasurements of the velocity at two distances are needed in order to determine both τ and z0, and measurements at three or more levels are necessary in order to test the validity of the equation. So far, few measurements have been made so close to the bottom that they can be used for testing the application of these results to oceanographic conditions, but one example can be given. On November 15, 1937, Revelle and Fleming (unpublished data) measured tidal currents off the entrance to San Diego Harbor at 126, 51, and 21 cm above the bottom. Table 63 contains the average velocities and the stress at the bottom, if the bottom is assumed to be smooth or rough. Agreement is obtained only if the bottom is considered rough. The roughness length is found to be about 2.0 cm, and with this value the observations consistently give the same stress at the bottom. These observations indicate therefore that the above formulae, with von Kármán's constant, k0 = 0.4, are applicable to the currents directly above the sea bottom. In this case the value of the eddy viscosity would be A = 0.93 (z + z0); that is, at a distance of 1 m above the bottom the eddy viscosity would be 95 g/cm/sec.
| Distance from bottom, cm | 126 | 51 | 21 |
| Average velocity, cm/sec | 26.3 | 21.6 | 15.6 |
| Computed frictional stress, g/cm/sec2} Smooth bottom | 0.87 | 0.71 | 0.46 |
| Computed frictional stress, g/cm/sec2} Rough bottom, z0 = 2.0 cm | 5.8 | 6.2 | 6.0 |
The above results apply to a fluid in a state of indifferent equilibrium. Certain modifications must be introduced if the stratification is stable or unstable, but the character of these modifications is not fully understood. It can be stated only that under stable conditions the velocity profile at some distance from the surface can no longer be represented by a logarithmic law, but is better represented by a power law of the type Vz1/Vz2 = (z1/z2)n. However, very near the surface, the logarithmic law appears to be valid (Sverdrup, 1939b).
At the sea surface, different boundary conditions have to be considered. In the first place, it should be observed that the currents of the sea are always much slower than the air currents, the winds. Therefore the velocity of the air relative to that of the water can always be considered, with sufficient accuracy, equal to the velocity of the wind.
At the sea surface the stress that the wind exerts on the water, τa, must balance the stress that the water exerts on the air:
This equation implies that both A0 and (dv/dz)0 must differ from zero. Thus the eddy viscosity must have a definite value at the surface, meaning that the mixing length must have a definite value and that the surface cannot remain smooth, because a smooth surface would mean no mixing length there. A free surface can, however, be rough, but it is difficult to perceive that the mixing length can be great near the surface. Rossby and Montgomery (1935) introduced therefore an upper boundary layer within which the mixing length increased rapidly with increasing distance from the free surface, but it must be admitted that nothing definite is known as to the character of the turbulence at the free surface.When a current flows parallel to a coast, a lateral stress is exerted, and one may expect a horizontal velocity profile to develop which shows some similarity to the vertical profile near the bottom. The velocity profile must be related to the horizontal eddy viscosity and to the lateral stress, but this relation has not yet been examined.
Numerical Values of the Vertical and Lateral Eddy Viscosity and Eddy Diffusivity. For the determination of the eddy viscosity, Aν., in the ocean, it is necessary to know the frictional forces and the velocity gradients. The frictional forces cannot be determined directly, but may be obtained as the difference between other acting forces. The velocity gradients, however, can be obtained from directly obseryed currents. When dealing with wind currents, theories based on certain assumptions as to the character of the eddy viscosity are helpful (p. 492), and for considering currents close to the bottom, results from fluid mechanics make possible conclusions as to the eddy viscosity from current measurements only (p. 480). The uncertainties of the correct application of theories, the difficulties in making current measurements in the open ocean, and the even greater difficulties in determining the acting forces, all introduce great uncertainties in the numerical values of the eddy viscosity which have so far been determined.
Table 64 contains results of such determinations. The specific methods used cannot be discussed here, but some of them will be mentioned later on. All values are from regions of moderate or strong currents that have been measured with considerable accuracy, or they have been derived from the effect of wind currents on the surface layer. The values range from nearly zero up to 7500 g/cm/sec, but some consistency in the variations can be seen. At the very bottom, small values are always found; at greater distances from the bottom, great values are associated with strong currents and small stability or with strong currents and great stability. On the North Siberian Shelf the eddy viscosity approached a small value in a thin layer of very great stability within which the tidal currents reached their maximum values.
| Locality | Layer | Av in g/cm/sec | Av derived from | Authority |
| All oceans | surface | [a]Av = 1.02 W3 (W<6m/sec) | homogeneous layer | Thorade, 1914 |
| Av = 4.3 W2 (W >6m/sec) | Thickness of upper | Ekman, 1905 | ||
| North Siberian Shelf | 0 to 60 m | 0−1000 | Tideal currents | Sverdrup, 1926 |
| North Siberian Shelf | 0 to 60 m | 10−400 | Tidal currents | Fjeldstad, 1936 |
| North Siberian Shelf | 0 to 22 m | Wind currents | Fjeldstad, 1929 | |
| North Sea | 0 to 31 m | 75−1720 | Strong tidal currents | Thorade, 1928 |
| Danish waters | 0 to 15 m | [c] 1.9−3.8 | All currents | Jacobsen, 1913 |
| Kuroshio | 0 to 200 m | [d] 680−7500 | All currents | Suda, 1936 |
| Japan Sea | 0 to 200 m | 150−1460 | All currents | Suda, 1936 |
| Off San Diego, Calif | near bottom | [e] 93(z + 0.02) | Tidal currents | Revelle and Fleming, ms. |
By computations that are based on equation (V, 5), p. 159, in a simplified form, the eddy diffusivity, As can be derived from observed time and space variations of temperature, salinity, oxygen content, or other properties. In some cases the currents need not be known, but in other cases only the ratio As/v can be determined, where ν is the velocity of the currents (p. 159). If this velocity can be estimated, an approximate value of As can be found. Temperature, salinity, and oxygen content can be measured much more easily and with greater accuracy than currents, and data for studying the eddy diffusion are therefore more readily obtained. As a consequence, many more determinations of eddy diffusivity have been made, and the results show greater consistency.
Table 65 contains a summary of values derived from observations in different oceans and at different depths between the surface and the bottom. The values range from 0.02 up to 320 g/cm/sec, but by far the greater number of values lie between 3 and 90. The range is therefore smaller than the apparent range of the eddy viscosity. The highest value, 320 g/cm/sec, was found in a homogeneous surface layer, within which one can expect the eddy diffusivity to equal the eddy viscosity. This value is the only one which is as great, probably, as the corresponding eddy viscosity; otherwise, the eddy diffusivity is smaller, in agreement with the fact that generally stable stratification is encountered. From the remarks in the table, it is evident that the eddy diffusivity increases with increasing velocity of the currents and decreases with increasing stability, in agreement with the preceding considerations.
The results of a few determinations of lateral eddy coefficients are given in table 66. The values of the coefficients have been derived by bold assumptions and can be considered as indicating only the order of magnitude. The fact that this order of magnitude depends upon the size of the area from which observations are available probably explains why the value from the California Current is much smaller than the values from the Atlantic Ocean, where conditions within much larger regions have been considered. The latter values, which have been obtained partly from observations at or near the surface and partly from observations at great depth, agree remarkably well. No relation appears between the average velocity of the currents and the eddy coefficients or between the stability and the coefficients. Similarly, from the meager evidence, the eddy viscosity and eddy diffusivity appear to be equal. Therefore, the processes of lateral turbulence seem to be entirely different from those of vertical turbulence, but it should be borne in mind that the study of lateral turbulence in the ocean is at its very beginning.
| Locality | Layer | As in g/cm/sec | Remarks | Authority |
| Equatorial Atlantic Ocean | 0 to 50 m | 320 | Homogeneous water, moderate currents | Defant, 1932 |
| Bay of Biscay | 0 to 100 m | 2–16 | Moderate stability, weak currents | Fjeldstad, 1933 |
| Danish waters | 0 to 15 m | 0.02–0.6 | Great stability, moderate currents | Jacobsen, 1913 |
| Kuroshio | 0 to 200 m | 30–80 | Moderate stability, strong currents | Sverdrup et al, 1942 |
| Kuroshio | 0 to 400 m | 7–90 | Moderate stability, strong currents | Suda, 1936 |
| Japan Sea | 0 to 200 m | 1–17 | Moderate to small stability, moderate currents | Suda, 1936 |
| California Current | 0 to 200 m | 30–40 | Moderate stability, weak currents | McEwen, 1919 |
| Arctic Ocean | 200 to 400 m | 20–50 | Small stability, weak currents | Sverdrup, 1933 |
| South Atlantic Ocean | 400 to 1400 m | 5–10 | Moderate stability, weak currents | Defant, 1936 |
| Equatorial Atlantic Ocean | 600 to 2000 m | 8 | Moderate stability, weak currents | Seiwell, 1935 |
| Caribbean Sea | 500 to 700 m | 2.8 | Moderate stability, weak currents | Seiwell, 1938 |
| South Atlantic Ocean | 3000 m to bottom | 4 | Homogeneous water, weak currents | Defant, 1936 |
| South Atlantic Ocean | Near bottom | 4 | Homogeneous water, weak currents | Wattenberg, 1935 |
| Locality | Layer | Av,h or As,h in g/cm/sec | Remarks | Authority |
| Northwestern North Atlantic Ocean | Surface | As,h 4 × 108 | Strong currents | Neumann, 1940 |
| Atlantic Equatorial Countercurrent | 0 to 200 m | Av,h 7 × 107 | Great stability, moderate currents | Montgomery and Palmén, 1940 |
| 0 to 200 m | As,h 4 × 107 | Montgomery, 1939 | ||
| South Atlantic Ocean | 2500 to 4000 m | As,h 1 × 108 | Small stability, weak currents | Sverdrup, 1939a |
| California Current | 200 to 400 m | As,h 2 × 106 | Moderate stability, weak currents, small area | Severdrup and Fleming, 1941 |
The Energy Equation When Friction Is Taken into Consideration. Because explicit terms for the components of the frictional forces have been introduced, the total power of the frictional forces can be computed. Disregarding the effect of horizontal turbulence, the power of the frictional forces per unit volume is
where A has been written instead of Az. Now Therefore because at the bottom the velocity is assumed to be zero and because at the surface the stress balances the stress exerted by the wind (equation (XIII, 65), p. 481).The integral on the right-hand side represents the loss per unit time and unit surface area of kinetic energy due to the vertical turbulence (the dissipation). If A were constant, the integral would be reduced to
which is the form obtained from the general dissipation function (Lamb, 1932, p. 579) on the assumptions that have been made concerning the character of the motion. The latter integral is always positive, and the corresponding integral on the right-hand side of (XIII, 66) is also always positive, because the two factors under the integral sign will nearly always have the same sign.The first term on the right-hand side, ν0,τa, represents the power per unit area (ML2T−3 × L−2) which is exerted by the stress of the wind.
The energy equation can now be written in the form
Some general conclusions can be drawn from this equation. In the first place, it is seen that the change of the kinetic energy may be positive or negative; that is, the energy transmitted to the water from the atmosphere may be greater or smaller than the loss due to motion across isobars and dissipation. Furthermore, if the kinetic energy remains unaltered and the stress of the wind is zero, energy must be gained by motion across the isobars; that is, the average motion must be from high to low pressure, because the dissipation is always positive. On the other hand, if the first integral vanishes, the dissipation equals the power of the stress of the wind. The first integral can disappear, either because the term (∂p/∂x)vx + (∂p/∂y)vy is zero at all depths, or because the term is negative at some depths and positive at others. In the former case the motion is parallel to the isobars. Furthermore, if stationary conditions are assumed, the isobars at one level must be parallel to the isobars at another level (p. 455). If the horizontal x axis is placed in the direction of the pressure gradient, the equations of motion are reduced to
The latter equation can be integrated directly, giving Thus, the assumed conditions can exist only if the stress remains constant, but this condition is not fulfilled when dealing with the ocean currents. It is probable that A decreases with depth, meaning that dv/dz would have to increase with depth, but such an increase is contrary to experience. The assumption of stationary conditions therefore is not fulfilled if a stress is exerted on the surface. On the other hand, the term under discussion may disappear, because it is negative at some depths and positive at others. This situation, however, would mean that motion must take place across the isobars, which is incompatible with stationary conditions. The conclusion is that stationary conditions cannot exist in the ocean if a wind blows, but this conclusion has been arrived at because the thermodynamic terms have been omitted. The considerations must be based on the energy equation, which is obtained by combining the dynamic with the thermodynamic (p. 441). For a closed system in a stationary state, one obtainsThe energy equations have so far received but little attention in oceanographic work, and further theoretical considerations and applications to specific problems appear desirable.
Other conclusions as to the effect of the stress of the wind can be based directly upon an integration of the equations of motion. Consider a closed space in which stationary conditions exist, and assume that the motion is nowhere accelerated. In such a system the transport through any cross section must be zero. Therefore, if the positive x axis is placed in the direction of the wind, one obtains, by multiplying the equations of motion by dxdydz and integrating over the entire volume,
where ix and iy are the slopes of the isobaric surfaces. Thus, under assumed conditions, the component of gravity acting horizontally on the body of water balances the stress exerted by the wind on the surface. If the closed space is rectangular in form, if ix and iy are constant, and if the water is homogeneous, one obtains where d is the depth to the bottom. The negative sign enters because the z axis is positive downward.The formula is valid only if the depth to the bottom is so great that the velocity gradient at the bottom is zero, because only on this assumption does the stress at the bottom vanish. If this condition is not fulfilled, one obtains
where τd is the stress at the bottom.In nonhomogeneous water, one can write
where ip is the slope of the isobaric surfaces due to distribution of mass and is is the added slope due to piled-up mass. Introducing geopotential slopes (p. 440), one obtainsAll of the above equations become modified if horizontal stresses and frictional forces related to such stresses are considered, but so far these modifications have not been examined. Rossby (1936a), however, has pointed out that the stress of the wind exerts an anticyclonic torque on the surface of the different oceans and that lateral stresses must provide the balancing cyclonic torque, because the bottom stresses are probably negligible. Studies by Montgomery and Palmén (1940) support this conclusion, but the problem deserves further attention.
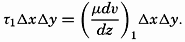
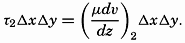
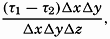

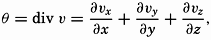
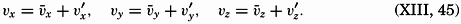
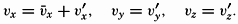
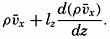
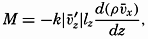






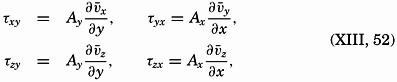
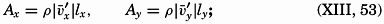
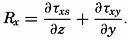
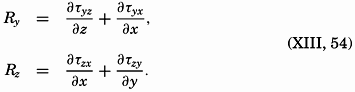
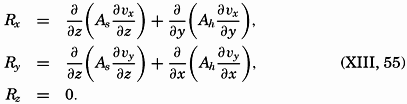
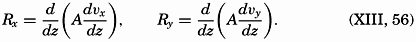
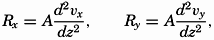

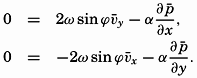
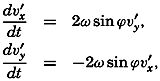
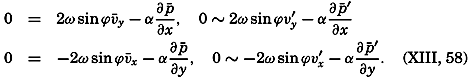
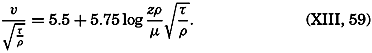

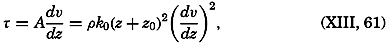
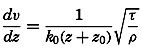

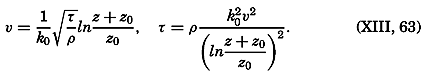
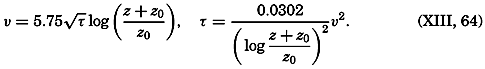
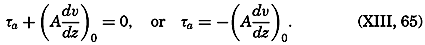
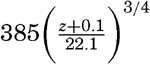 [
[