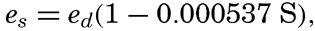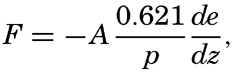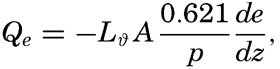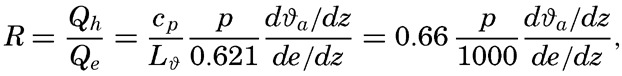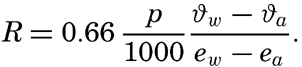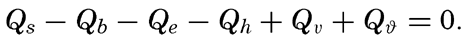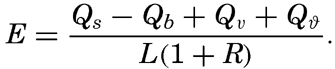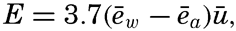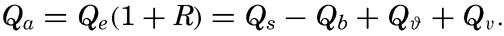Evaporation from the Sea
The Process of Evaporation. The vapor tension at a flat surface of pure water depends on the temperature of the water. The salinity decreases the tension slightly, the empirical relation between vapor tension and salinity being (p. 66)
where es is the vapor tension over sea water, ed is the vapor tension over distilled water of the same temperature, and S is the salinity in parts per mille. In the open ocean the relation is approximately es = 0.98 ed. Table 29 contains the vapor tension in millibars over water of salinity 35.00 ‰ and at the stated temperatures.Air in which the vapor tension is less than that over water of the same temperature is undersaturated with moisture, and air in which the vapor tension exactly equals that over a water surface of the same temperature is saturated with moisture. In absolutely pure air the vapor pressure can be above the saturation value, but generally the air contains “nuclei” on which the vapor is condensed when the vapor tension reaches the value corresponding to that over water of the same temperature. Under these conditions the vapor tension in the air cannot be further increased, and in meteorology one therefore uses the
| Temperature (°C) | Vapor pressure (mb) | Temperature (°C) | Vapor pressure (mb) |
|---|---|---|---|
| −2 | 5.19 | 18 | 20.26 |
| −1 | 5.57 | 19 | 21.57 |
| 0 | 5.99 | 20 | 22.96 |
| 1 | 6.44 | 21 | 24.42 |
| 2 | 6.92 | 22 | 25.96 |
| 3 | 7.43 | 23 | 27.59 |
| 4 | 7.98 | 24 | 29.30 |
| 5 | 8.56 | 25 | 31.12 |
| 6 | 9.17 | 26 | 33.01 |
| 7 | 9.83 | 27 | 35.02 |
| 8 | 10.52 | 28 | 37.13 |
| 9 | 11.26 | 29 | 39.33 |
| 10 | 12.05 | 30 | 41.68 |
| 11 | 12.88 | 31 | 44.13 |
| 12 | 13.76 | 32 | 46.71 |
| 13 | 14.70 | ||
| 14 | 15.69 | ||
| 15 | 16.74 | ||
| 16 | 17.85 | ||
| 17 | 19.02 |
In discussing the process of evaporation it is more rational to consider not the vapor pressure but the specific humidity, f—that is, the mass of water vapor per unit mass of air. The amount of water vapor, F, which per second is transported upward through a surface of cross section 1 cm2 is, then, – Adf/dz, where A is the eddy conductivity and – df/dz is the vertical gradient of the specific humidity, which is positive when the specific humidity decreases with height. If the vapor pressure, e, is introduced, the equation becomes approximately
The ratio between the amounts of heat given off to the atmosphere as sensible heat (p. 114) and used for evaporation is
The last expression is obtained by introducing cp = 0.240 and L = 585. Thus, the ratio R depends mainly upon the ratio between the temperature and humidity gradients in the air at a short distance from the sea surface. These gradients are difficult to measure but can be replaced approximately by the difference in temperature and vapor pressure at the sea surface and the corresponding values in the air at a height of a few meters: This ratio was derived in a different manner by Bowen (1926), and is often referred to as the “Bowen ratio.”Values of the ratio R can be computed from climatological charts of the oceans, but a comprehensive study has not been made. Calculations based on data contained in the Atlas of Climatic Charts of the Oceans, published by the U. S. Weather Bureau (1938), show that the ratio varies from one part of the ocean to the other. As a rule, the ratio is small in low latitudes, where it remains nearly constant throughout the year, but is greater in middle latitudes, where it reaches values up to 0.5 in winter and in some areas drops to –0.2 in summer. A negative value indicates that heat is conducted from the atmosphere to the sea. On an average, the value for all oceans appears to lie at about 0.1, meaning that about 10 per cent of the heat surplus that the oceans receive by radiation processes is given off as sensible heat, whereas about 90 per cent is used for evaporation (p. 115).
There are certain points regarding the character of the evaporation which need to be emphasized. If the water is warmer than the air, the vapor pressure at the sea surface remains greater than that in the air, and evaporation can always take place and will be greatly facilitated in these circumstances because the turbulence of the air will be fully developed owing to the unstable stratification of the very lowest layers (p. 92). It must therefore be expected that the greatest evaporation occurs when cold air flows over warm water. If the air is much colder
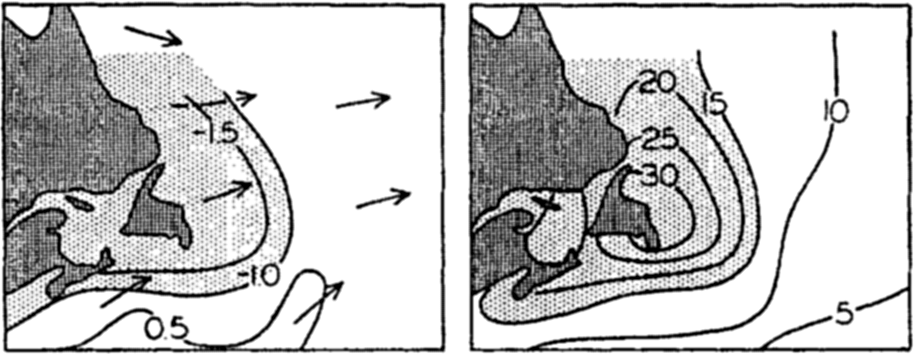
Left: The difference, air minus sea-surface temperature, and the prevailing wind-direction over the Grand Banks of Newfoundland in March, April, and May. Right: Percentage frequency of fog in the same months.
[Full Size]
When the sea surface is colder than the air, evaporation can take place only if the air is not saturated with water vapor. In this case turbulence is reduced and evaporation must stop when the vapor content of the lowest layer of the atmosphere has reached such a value that the vapor pressure equals that at the sea surface. If warm, moist air passes over a colder sea surface, the direction of transport will be reversed and condensation will take place on the sea surface in such a way that heat is brought to the surface and not carried away from it. Owing to the fact that this process can take place only when the air is warmer than the sea and that then turbulence is greatly reduced, one can expect that condensation of water vapor on the sea will not be of great importance, but it should be borne in mind that this process can and does take place when conditions are right. In these circumstances, contact with the sea and conduction lower the air temperature to the dew point for a considerable distance above the sea surface. Condensation takes place in the air and fog is formed, “advection” fog that is commonly encountered over the sea. The relation between the frequency of fog or mist and the difference between sea-surface and air temperatures are well illustrated by charts in the Atlas of Climatic Charts of the Oceans (1938). As an example, fig. 26 shows the frequency of fog, the difference between air and sea-surface temperature, and the prevailing wind direction over the Grand Banks of Newfoundland in March, April, and May. It can be concluded that in spring, when the water is colder than the air, no
In middle and higher latitudes the sea surface in winter is mostly warmer than the air, and hence one must expect the evaporation then to be at its maximum. This conclusion appears contrary to common experience that evaporation from heated water is greater than that from cold water, but the contradiction is only apparent, because greatest evaporation always occurs when a water surface is warmer than the air above it, which is exactly what happens in winter.
Observations and Computations of Evaporation. Present knowledge of the amount of evaporation from the different parts of the oceans is derived partly from observations and partly from computations based on consideration of the heat balance.
Observations have been made by means of pans on board ship, but such observations give values of the evaporation from the sea surface that are too high, partly because the wind velocity is higher at the level of the pan than at the sea surface, and partly because the difference between vapor pressure in the air and that of the evaporating surface is greater at the pan than at the sea surface. Analyzing the decrease of the wind velocity and the increase of the vapor pressure between the average level of pans used on shipboard and a level a few centimeters above the sea surface, Wüst (1936) arrived at the conclusion that the measured values had to be multiplied by 0.53 in order to represent the evaporation from the sea surface.
In computing the evaporation on the basis of the heat balance, one has to begin with the equation (p. 101)
Introducing the ratio R = Qh/Qe, and converting the evaporation, E, into centimeters by dividing Qe by the latent heat of vaporization, L, one obtains In this form the equation representing the heat balance has found wide application for computation of evaporation. The result gives the evaporation in centimeters during the time intervals to which the values Qs, and so on, apply, provided these are expressed in gram calories.A second method for computing the evaporation from the oceans has been suggested by Sverdrup (1937), who, on the basis of results in fluid mechanics as to the turbulence of the air over a rough surface, established a formula for the evaporation, using in part constants that had been determined by laboratory experiments and in part constants that were obtained from the character of the variation of vapor pressure with
The exact formulae are not well suited for numerical computation, but at wind velocities between 4 and 12 m/sec, the mean annual evaporation in centimeters can be found approximately from the simple relation
where ēw represents the average vapor pressure in millibars at the sea surface as derived from the temperature and salinity of the sea, ēa represents the average vapor pressure in the air at a height of 6 m above the sea surface, and ū is the average wind velocity in meters per second at the same height.Average Annual Evaporation from the Oceans. On the basis of pan measurements conducted in different parts of the ocean, Wüst (1936) found that the average evaporation from all oceans amounts to 93 cm/year, and he considers this value correct within 10 to 15 per cent. W. Schmidt (1915) computed the evaporation by means of the preceding equation for E, in which the terms Qϑ and Qv can be omitted in considering the oceans as a whole. Schmidt introduced high values of R, and on the basis of the available data as to incoming radiation and back radiation he found a total evaporation of 76 cm/year. A revision based on more recent measurements of radiation (Mosby, 1936) and use of R = 0.1 resulted in a value of 106 cm/year. The latter value represents an upper limit, and may be 10 to 15 per cent too high, whence it appears that Wüst's result is nearly correct.
It is of interest in this connection to give some figures regarding the relation between evaporation and precipitation over the oceans, the land areas, and the whole earth (according to Wüst, 1936). The total evaporation from the oceans amounts to 334,000 km3/year, of which 297,000 km3 returns to the sea in the form of precipitation, and the difference, 37,000 km3, must be supplied by run-off, since the salinity of the oceans remains unchanged. The total amount of precipitation falling on the land is 99,000 km3, of which amount a little over one third, 37,000 km3, is supplied by evaporation from the oceans and 62,000 km3 is supplied by evaporation from inland water areas or directly from the moist soil. For the sake of comparison it may be mentioned that the capacity of Lake Mead, above Boulder Dam, is 45 km3.
Evaporation in Different Latitudes and Longitudes. From pan observations at sea, Wüst has derived average values of the evaporation from the different oceans in different latitudes (table 30, p. 123). By means of the energy equation one can compute similar annual values, assuming that the net transport of heat by ocean currents can be neglected. Such a computation has been carried out for the Atlantic
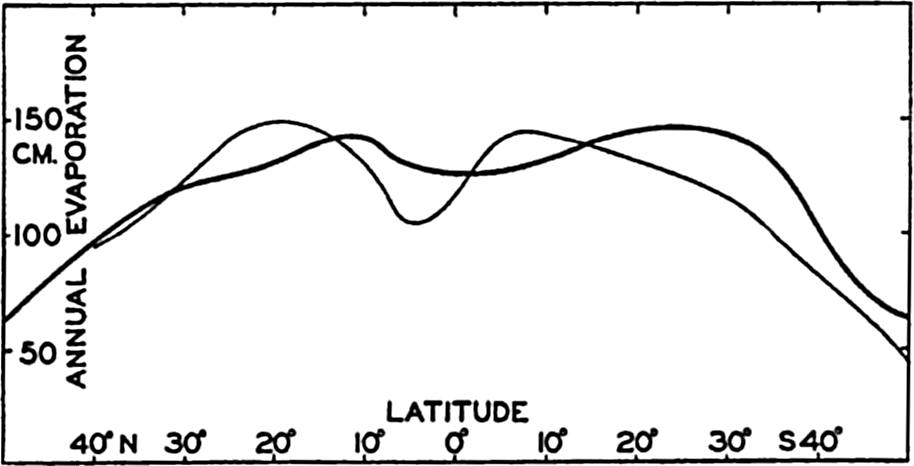
Annual evaporation from the Atlantic Ocean between latitudes 50°N and 50°S. Thin curve based on observations (Wüst, 1936) and heavy curve on computations, using the energy equation.
[Full Size]
It appears that the average annual values of the evaporation in different latitudes are well established, but the evaporation also varies from the eastern to the western parts of the oceans and with the seasons. These variations are of great importance to the circulation of the atmosphere, because the supply of water vapor that later on condenses and gives off its latent heat represents a large portion of the supply of energy. So far, none of the details are known, but it is possible that approximate values of the evaporation from different parts of the ocean and in different seasons can be found by means of the method proposed by Sverdrup (1937) and used by Jacobs (1942).
Annual Variation of Evaporation. The character of the annual variation of evaporation can be examined by means of the energy equation (Sverdrup, 1940):
The quantity Qϑ can be computed if the annual variation of temperature due to processes of heating and cooling is known at all depths where such annual variations occur. The annual variation of temperature at the surface has been examined, but only few data are available from subsurface depths, the most reliable being those which have been compiled by Helland-Hansen (1930) from an area in the eastern North Atlantic with its center in 47°N and 12°W (p. 132). The radiation income in that area can be obtained from Kimball#x0027;s data (1928), the back radiation can be found by means of the diagram in fig. 25, and the transport by currents, Qv, can be neglected. In fig. 28A are represented the annual variation of the net surplus of radiation, Qr, the annual variation of the amount of heat used for changing the temperature of the water, Qϑ, and the difference between these two amounts, Qa, which represents the total amount of heat given off to the atmosphere. The greater part of the last amount is used for evaporation, and the curve marked Qa represents, therefore, approximately the annual variation of the evaporation, which shows a maximum in the fall and early winter, a secondary minimum in February, followed by a secondary maximum in March, and a low minimum in summer. In June and July no evaporation takes place. The total evaporation during the year is about 80 cm.
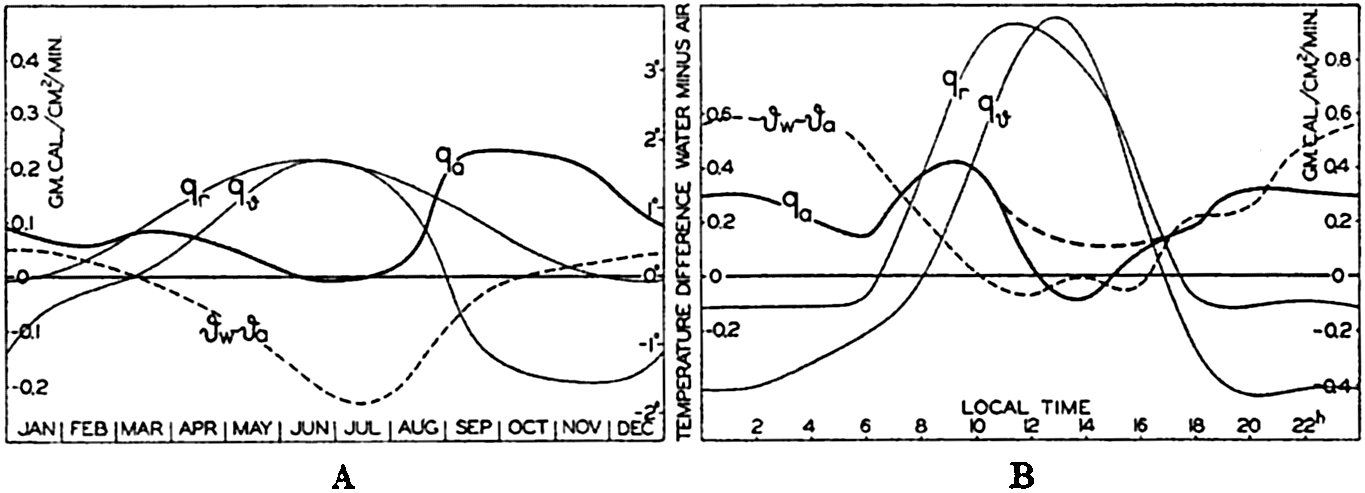
(A) Annual variation in the total amount of heat, qa, given off to the atmosphere in an area of the North Atlantic (about 47°N, 12°W). (B) Corresponding diurnal variation near the Equator in the Atlantic Ocean. (For explanation of symbols, see text.)
[Full Size]
This example illustrates a method of approach that may be applied, but so far the necessary data for a more complete study are lacking. The result that the evaporation is at a minimum in summer and at a maximum in fall and early winter is in agreement with the conclusions that were drawn when discussing the process of evaporation in general.
| Latitude | Atlantic Ocean | Indian Ocean | Pacific Ocean | All Oceans | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S (‰) | E (cm/yr) | P (cm/yr) | E – P (cm/yr) | S (‰) | E (cm/yr) | P (cm/yr) | E – P (cm/yr) | S (‰) | E (cm/yr) | P (cm/yr) | E – P (cm/yr) | S (‰) | E (cm/yr) | P (cm/yr) | E – P (cm/yr) | |
| 40°N | 35.80 | 94 | 76 | 18 | 33.64 | 94 | 93 | 1 | 34.54 | 94 | 93 | 1 | ||||
| 35 | 36.46 | 107 | 64 | 43 | 34.10 | 106 | 79 | 27 | 35.05 | 106 | 79 | 27 | ||||
| 30 | 36.79 | 121 | 54 | 67 | 34.77 | 116 | 65 | 51 | 35.56 | 120 | 65 | 55 | ||||
| 25 | 36.87 | 140 | 42 | 98 | 35.00 | 127 | 55 | 72 | 35.79 | 129 | 55 | 74 | ||||
| 20 | 36.47 | 149 | 40 | 110 | (35.05) | (125) | (74) | (51) | 34.88 | 130 | 62 | 68 | 35.44 | 133 | 65 | 68 |
| 15 | 35.92 | 145 | 62 | 83 | (35.07) | (125) | (73) | (52) | 34.67 | 128 | 82 | 46 | 35.09 | 130 | 82 | 48 |
| 10 | 35.62 | 132 | 101 | 31 | (34.92) | (125) | (88) | (37) | 34.29 | 123 | 127 | − 4 | 34.72 | 129 | 127 | 2 |
| 5 | 34.98 | 105 | 144 | − 39 | (34.82) | (125) | (107) | (18) | 34.29 | 102 | (177) | (-75) | 34.54 | 110 | 177 | − 67 |
| 0 | 35.67 | 116 | 96 | 20 | 35.14 | 125 | 131 | − 6 | 34.85 | 116 | 98 | 18 | 35.08 | 119 | 102 | 17 |
| 5°S | 35.77 | 141 | 42 | 99 | 34.93 | 121 | 167 | − 46 | 35.11 | 131 | 91 | 40 | 35.20 | 124 | 91 | 33 |
| 10 | 36.45 | 143 | 22 | 121 | 34.57 | 99 | 156 | − 57 | 35.38 | 131 | 96 | 35 | 35.34 | 130 | 96 | 34 |
| 15 | 36.79 | 138 | 19 | 119 | 34.75 | 121 | 83 | 38 | 35.57 | 125 | 85 | 40 | 35.54 | 134 | 85 | 49 |
| 20 | 36.54 | 132 | 30 | 102 | 35.15 | 143 | 59 | 84 | 35.70 | 121 | 70 | 51 | 35.69 | 134 | 70 | 64 |
| 25 | 36.20 | 124 | 40 | 84 | 35.45 | 145 | 46 | 99 | 35.62 | 116 | 61 | 55 | 35.69 | 124 | 62 | 62 |
| 30 | 35.72 | 116 | 45 | 71 | 35.89 | 134 | 58 | 76 | 35.40 | 110 | 64 | 46 | 35.62 | 111 | 64 | 47 |
| 35 | 35.35 | 99 | 55 | 44 | 35.60 | 121 | 60 | 61 | 35.00 | 97 | 64 | 33 | 35.32 | 99 | 64 | 35 |
| 40 | 34.65 | 81 | 72 | 9 | 35.10 | 83 | 73 | 10 | 34.61 | 81 | 84 | − 3 | 34.79 | 81 | 84 | − 3 |
| 45 | 34.19 | 64 | 73 | − 9 | 34.25 | 64 | 79 | − 15 | 34.32 | 64 | 85 | − 21 | 34.14 | 64 | 85 | − 21 |
| 50 | 33.94 | 43 | 72 | − 29 | 33.87 | 43 | 79 | − 36 | 34.16 | 43 | 84 | − 41 | 33.99 | 43 | 84 | − 41 |
Diurnal Variation of Evaporation. The diurnal variation of evaporation can be examined in a similar manner, but at the present time suitable data are available only at four Meteor stations near the Equator in the Atlantic Ocean (Defant, 1932; Kuhlbrodt and Reger, 1938). In fig. 28B the curves marked Qr and Qϑ correspond to the similar curves in fig. 28A, and the difference between these, Qa, shows the amount of heat lost during twenty-four hours, which is approximately proportional to the evaporation. The diurnal variation of evaporation in the Tropics appears to have considerable similarity to the annual variation in middle latitudes, and is characterized by a double period with maxima in the late forenoon and the early part of the night and minima at sunrise and in the early afternoon hours. It is possible that the afternoon minimum appears exaggerated, owing to uncertainties as to the absolute values of Qr and Qϑ. The total diurnal evaporation was 0.5 cm, but the sky was nearly clear on the four days that were examined and the average diurnal value is therefore smaller. The double diurnal period of evaporation appears to be characteristic of the Tropics, but in middle latitudes a single period with maximum values during the night probably dominates.