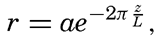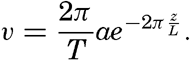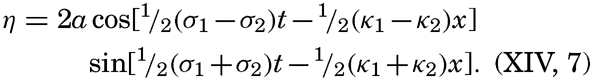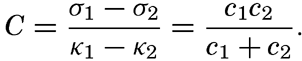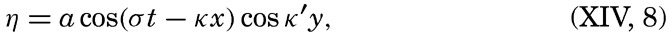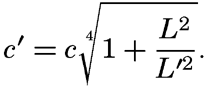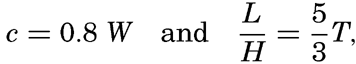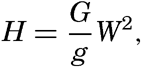Surface Waves
Origin of Surface Waves. It is evident to the most casual observer that surface waves are created by wind, but only recently, in a work by H. Jeffreys, has a successful physical explanation of the process been presented (Defant, 1929, Thorade, 1931). Jeffreys avails himself of the fact that in air in turbulent flow, eddies are formed on the lee side of obstacles. If a strong wind blows against an isolated house, an eddy is formed in the same manner that eddies are formed behind stones in a river. The result is that the wind exerts a pressure on the windward side of the house, but on the lee side there will be suction. Similarly, when the wind blows over a sequence of waves, eddies will be formed on the lee side of the waves, for which reason the pressure of the wind will be greater on the windward slopes than on the slopes that are sheltered by the crests. This condition can prevail, however, only if the waves travel at a velocity that is smaller than the speed of the wind. On the basis of these arguments, Jeffreys finds that waves may increase only if
Here W is the velocity of the wind, c is the velocity of the waves, v is the kinematic viscosity of the water, g is the acceleration of gravity, ρ and ρ′ are the densities of the water and the air, respectively, and s is a non-dimensional numerical coefficient that Jeffreys calls the “sheltering coefficient.” It should be observed that in his reasoning Jeffreys takes into account both the turbulent character of the wind and the viscosity of the water. His theory therefore must be expected to give results in better agreement with actual conditions than earlier theories based on the concepts of classical hydrodynamics, which neglect turbulence and viscosity.The term on the right-hand side of equation (XIV, 5) is always positive. The product on the left-hand side must therefore always be positive and can exceed the right-hand term only if the wave velocity differs sufficiently both from zero and from the wind velocity. For any given wind velocity, there can be only a limited range of possible wave velocities. It is readily seen that at a given wind velocity the right-hand side of (XIV, 5) is at a maximum when c = ⅓W. Therefore, unless
there will be no values of c that satisfy the condition.Equation (XIV, 6) determines the velocity of the weakest wind which can raise any waves, and this weakest wind could be determined if the sheltering coefficient were known. Jeffreys has not been able to make
The velocity of the smallest possible waves should be one third of the limiting wind velocity, or about 37 cm/sec, and according to the theory the corresponding wave length must be 8.8 cm (p. 525). Thus, measurements of the smallest waves can be used for testing the correctness of the theory, but measurement of such small wave lengths is very difficult and no exact observations have been made. Jeffreys finds that the length of the shortest waves observed by him lies in the neighborhood of the theoretical value. On the other hand, Scott Russell reported in 1844 that he had measured surface waves of a length of only 5 cm, and the smallest waves measured by Cornish are only about 2.5 cm long. The problem of the generation of surface waves is therefore not satisfactorily solved, but the approach by Jeffreys is in better agreement with observations than is any previous attempt.
It should be added that if only the forces due to surface tension and gravity are considered, waves should not be formed until the wind velocity passes the limit of 6.7 m/sec, and if only the stress of the wind on the surface and gravity are taken into account, the limiting wind velocity will be about 4.8 m/sec. Experience shows that these values are far too high, and the turbulent character of the wind must therefore be of the greatest importance.
Form and Characteristics. In physics the general picture of surface waves is that of sequences of rhythmic rise and fall which appear to progress along the surface when progressive waves are concerned, or which appear stationary if standing waves are being considered. The actual appearance of the surface of the open sea, however, is mostly in the sharpest contrast to that of rhythmic regularity. If a wind blows, waves of all different sizes are present, varying in form from long, gently sloping ridges to waves of short and sharp crests. Superimposed on the gentler waves, which may or may not run in the direction of the wind, series of deformations of the surface appear which, from the point of view of physics, can be termed “waves” only by stretching the definition.
If the sea surface were characterized by an unbroken series of waves of the same amplitude, a chart of the topography of the surface would contain nothing but a series of straight lines showing the alternating wave
Topography of the sea surface derived from stereophotogrammetric pictures of the sea surface taken on board the Meteor on January 23, 1926, in lat. 59°S, long. 63°4′ W. The state of the sea was recorded as 6, waves as advancing from WSW, wind WSW 7 (Beaufort).
[Full Size]
The most striking characteristic of the picture is not a regular sequence of waves but a great irregularity in topography. A relation to the direction of the wind is evident, however, because the wind was blowing at nearly right angles to the prevailing direction of the contour lines of the surface, but, instead of a long wave crest running at right angles to the wind direction, there are two separate heights, one of which is very steep. This irregular appearance, the “cross sea” (Kreuz See) is more common in the open ocean than the swells with long crests, which are more conspicuous near the coast, where series of long waves may roll against the beach in rhythmic sequence.
In spite of the irregular appearance of the sea, it is possible to apply the terms wave period, wave height, and wave length, because some of the waves will be more conspicuous than others and their characteristics can be observed. As has already been stated, the general theory of waves on the surface of the sea leads to a simple formula for the wave velocity:
Of the three interrelated quantities, c, T, and L, the wave period T can probably be most easily determined by using the method which was proposed by Cornish (1934) and which consists in recording the time intervals between appearances of a well-defined patch of foam at a sufficient distance from the ship. The same method can be used on the coast, where, in addition, the interval between breakers can be accurately timed. A simple device for recording the movement of a floater on a rotating drum has been used with success at the end of the Scripps Institution of Oceanography pier (Shepard and La Fond, 1940). At sea the wave length is mostly estimated on the basis of the ship's length, but this procedure leads to uncertain results, because it is often difficult to locate both crests of the wave relative to the ship and because of disturbances due to the waves created by the movement of the ship. The most satisfactory measurements are made from a ship that is hove to. Another method consists in letting out a floater as a wave crest passes the stern of the ship and recording both the length of line paid out when the floater reappears on the crest and the angle that the line forms with the heading of the ship. The velocity of the wave can be found by recording the time needed for the wave to run a measured distance along the ship. If the period is also determined, the wave length is found from the simple formula L = cT.
A large number of measurements have been made at sea in order to establish the relationship between the wave period, the wave length, and the wave velocity. Critical examination of the methods employed has been made, especially by Cornish (1912, 1934), and a number of average results have been compiled by different authors. Table 68 contains one of the compilations made by Krümmel, from which it is evident that the observed values are in fair agreement with the theoretical expectation.
The longest wave periods observed at sea rarely exceed the value of 13.5 sec, which Cornish reports from the Bay of Biscay. It has been established, however, that the swell reaching the shore may have much longer periods and correspondingly longer wave lengths and greater velocities of progress. The longest period that Cornish has observed is about 22.5 sec, corresponding to a wave length in deep water of about
The theory of waves leads not only to a relation between velocity of progress and the wave length, but also to results concerning the profile of the wave. These results are based on the concepts of classical hydrodynamics and have been derived from the hydrodynamic equations, omitting friction but taking the boundary conditions into consideration. In an ideal fluid the free surface of the waves, according to Stokes' results of 1847 (Lamb, 1932), very nearly take the shape of a trochoid—that is, the curve which is formed by the motion of a point on a disk when this disk rolls along a level surface. If the amplitude is small compared to the wave length, the trochoid approaches in shape a sine curve, but at great amplitude the crests become narrower and the troughs longer. Gerstner's theory of 1802 leads exactly to the trochoid form, but Stokes has pointed out that this theory is not in complete agreement with the concepts of classical hydrodynamics.
| Region | Wave velocity, m/sec | Wave length, m | Wave period, sec | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Observed | Computed from | Observed | Computed from | Observed | Computed from | ||||
|
|
|
|
|
| ||||
| Atlantic Ocean | |||||||||
| Trade wind region | 11.2 | 10.8 | 10.5 | 65 | 70 | 61 | 5.8 | 6.0 | 6.2 |
| Indian Ocean | |||||||||
| Trade wind region | 12.6 | 13.1 | 13.7 | 96 | 88 | 104 | 7.6 | 7.3 | 6.9 |
| South Atlantic Ocean | |||||||||
| West wind region | 14.0 | 15.5 | 17.1 | 133 | 109 | 163 | 9.5 | 8.6 | 7.8 |
| Indian Ocean | |||||||||
| West wind region | 15.0 | 15.2 | 13.7 | 114 | 125 | 104 | 7.6 | 8.0 | 8.3 |
| China Sea | 11.4 | 11.9 | 12.4 | 79 | 72 | 86 | 6.9 | 6.6 | 6.3 |
| Western Pacific Ocean | 12.4 | 13.6 | 14.7 | 102 | 85 | 121 | 8.2 | 7.5 | 6.9 |
Stokes's results lead to the conclusion that at increasing amplitude the wave form deviates more and more from the trochoid. Studies of the stability of waves by Michell (Lamb, 1932) show that the wave becomes unstable if the angle formed by the crest approaches 120°, and that the smallest ratio of height to length is 1:7 (fig. 130). The velocity of progress of these waves is no longer independent of the height; in the case
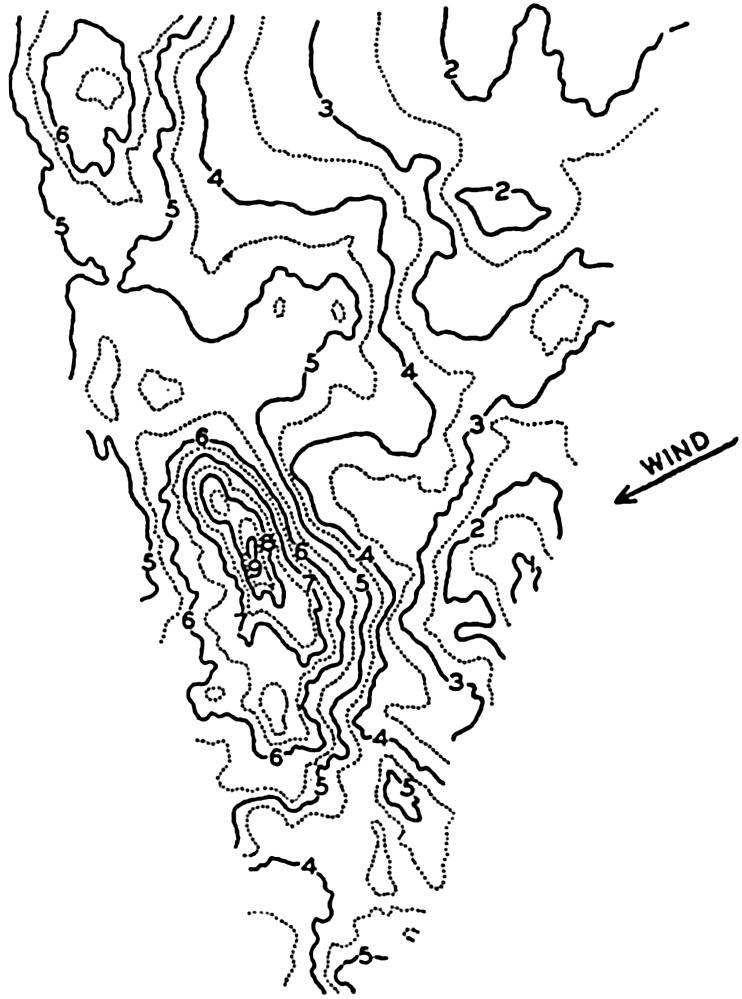
Accurate measurements of actual wave profiles would be very desirable in order to examine the correctness of the above-mentioned theoretical conclusions. Such actual measurements can be based on photogrammetric pictures, but so far only a few such pictures have been evaluated. Fig. 131 (Schumacher, 1928) shows two profiles of the wave the topography of which was presented in fig. 129 and two profiles of other waves that were photographed on the Meteor Expedition. In the figure the trochoids are entered as dashed lines, and it is seen that these curves can hardly be considered as fitting the actual profiles with any degree of accuracy.
Profiles of waves (vertical scale 5 × horizontal scale) of waves derived from stereophotogrammetric pictures taken on the Meteor. The two lower profiles refer to the wave shown in fig. 129; the two upper profiles refer to waves photographed on July 7, 1926. The waves proceed from right to left. The dashed curves represent trochoids.
[Full Size]
The wave theory also leads to certain conclusions concerning the character of motion of individual water particles. In a wave that has
| Wave characteristics | Velocity of particles in cm/sec at stated depths | ||||||
|---|---|---|---|---|---|---|---|
| Period length (sec) | Velocity of progress (cm/sec) | Length (m) | Height (m) | 0 m | 2 m | 20 m | 100 m |
| 2 | 312 | 6.2 | 0.25 | 39 | 5.2 | 0.0 | 0.0 |
| 4 | 624 | 25 | 1.00 | 79 | 49 | 0.5 | 0.0 |
| 6 | 937 | 56 | 2.00 | 105 | 85 | 11.3 | 0.0 |
| 8 | 1249 | 100 | 5.00 | 196 | 173 | 55.6 | 0.4 |
| 10 | 1561 | 156 | 7.00 | 220 | 203 | 99.0 | 4.2 |
| 12 | 1873 | 225 | 10.00 | 211 | 199 | 114.0 | 12.9 |
| 14 | 2185 | 306 | 12.00 | 273 | 262 | 180.0 | 35.0 |
| 16 | 2498 | 396 | 10.00 | 197 | 190 | 143.0 | 40.6 |
| 18 | 2810 | 506 | 8.00 | 140 | 136 | 109.0 | 40.5 |
| 20 | 3122 | 624 | 5.00 | 78 | 76 | 63.0 | 28.4 |
No measurements are available of the actual motion of water particles in waves. Experience in submarines has shown, however, that the wave motion decreases rapidly with increasing depth. Vening Meinesz has availed himself of this fact and has been able to conduct observations of gravity at sea on board a submarine, making use of pendulums, which can be employed only when the motion of the vessel is small.
As a consequence of the decrease of the particle velocity with depth a small transport of water takes place in the direction of progress. A water particle moves in the direction of progress when it is above its mean depth, and in the opposite direction when it is below its mean depth, but, owing to the decrease of velocity with depth, it moves somewhat faster in the direction of progress than in the opposite direction. Consequently, after having completed one revolution in its orbit, the particle does not return to the point from which it started, but is advanced somewhat in the direction of progress, meaning that an actual transport of water takes place in this direction even in the absence of wind (see U.S. Beach Erosion Board, 1941.)
The irregular appearance of the surface is not accounted for by the theories that have been mentioned so far, but a somewhat better understanding of the pattern of waves is obtained when one takes into account the phenomenon of interference. Two surface waves that travel in the same direction can then be represented by the equations
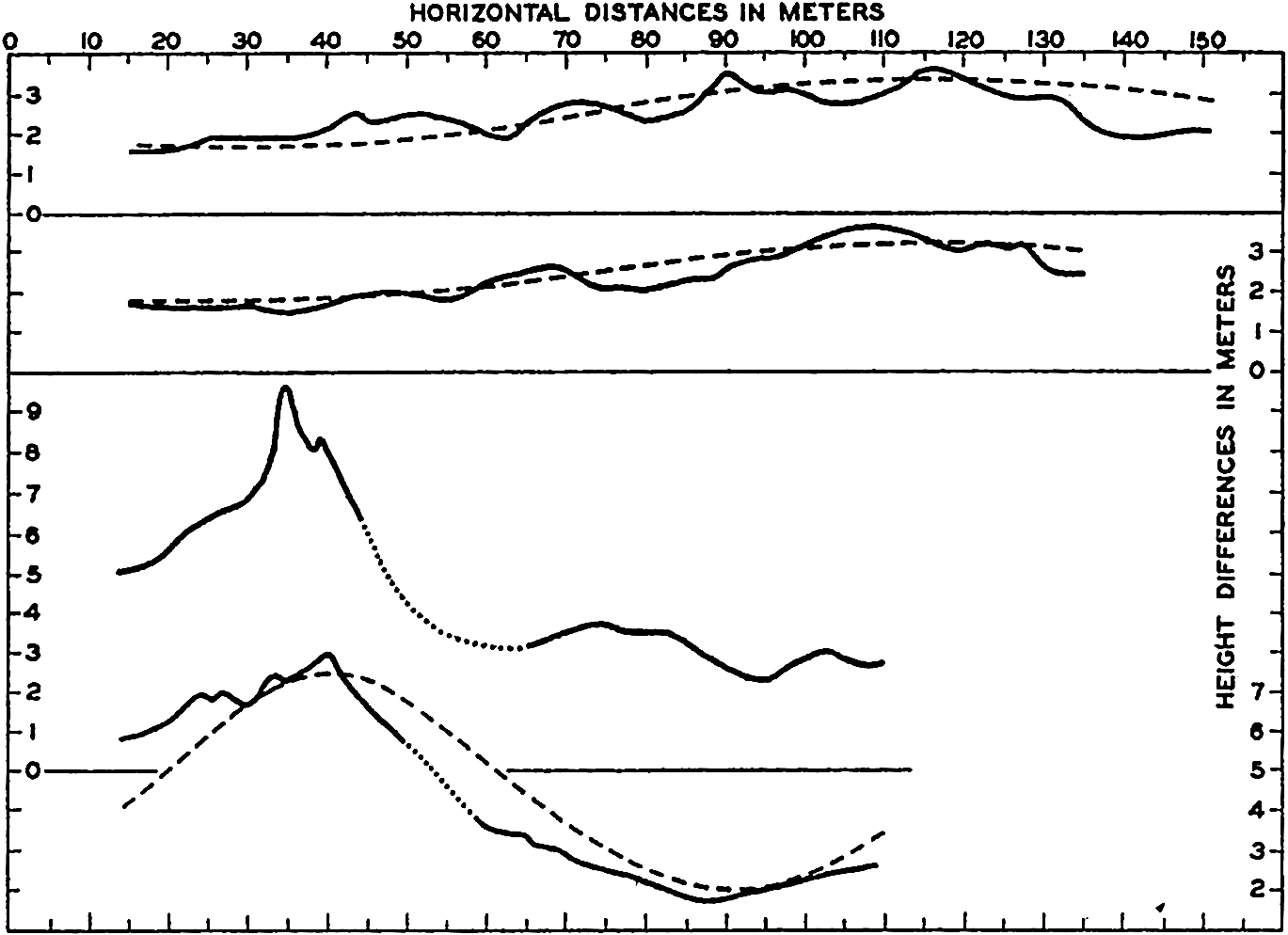
and the actual appearance of the surface is obtained by adding the displacements due to the two individual waves. If the amplitudes are equal, one obtains If the wave lengths differ by a small amount only, this new equation represents a wave whose length is the average of the two waves of which it is composed but whose amplitude varies between zero and 2a. At the locality where the two waves are in phase, the amplitudes are added, and a wave appears that has twice the amplitude of the two original waves, but, where the waves are in opposite phase, the amplitudes cancel.
Upper curve: Record of waves at the end of the Scripps Institution pier, showing interference. Middle curve: Computed pattern of wave interference. Lower curve: Example of the ordinary type of records of waves at the Scripps Institution pier, showing very complicated conditions.
[Full Size]
The upper curve in fig. 132, which is a reproduction of a record obtained at the end of the Scripps Institution of Oceanography pier, represents an example of interference of waves of nearly the same period length but of different amplitudes. In the middle portion of the figure are shown two sine curves, one of period 9.6 sec and amplitude 0.75 m, and one of period 8.7 sec and amplitude 0.32 m. The heavy curve presents the wave pattern that would result by interference between the two, and it is seen that this corresponds roughly to the observed pattern. The discrepancies are accounted for partly by the fact that the
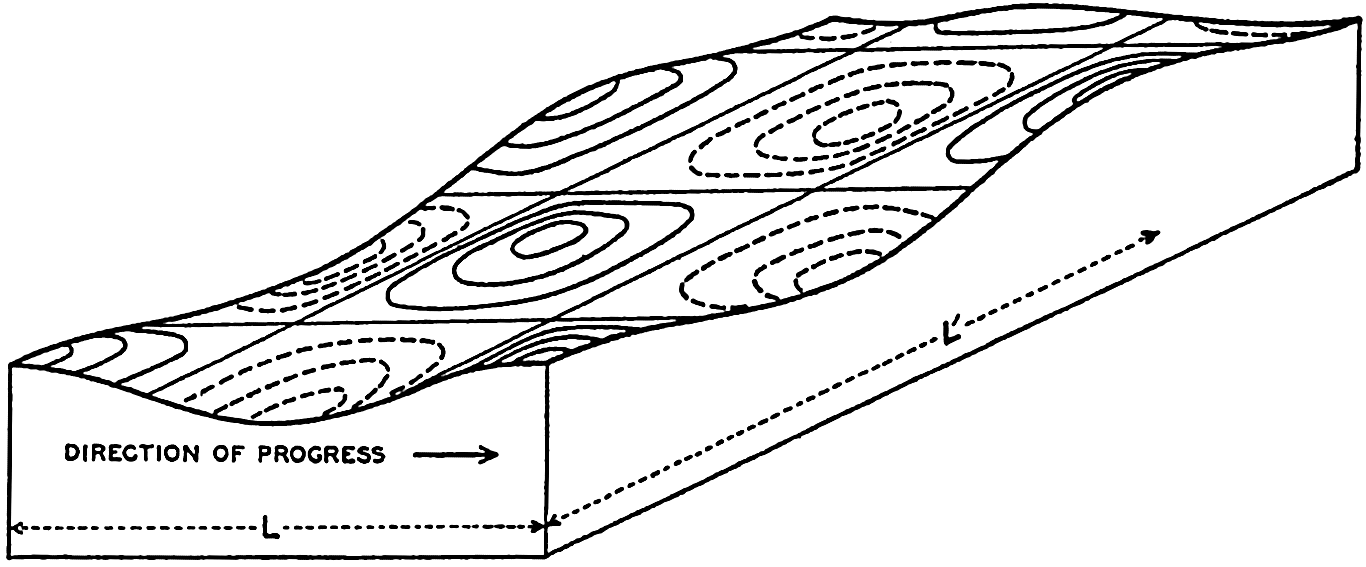
These considerations help to explain the occurrence of a sequence of high waves followed by a sequence of low ones, but they do not explain the irregular pattern of waves that is called “cross sea.” Progress towards explaining the typical cross sea, however, has been made by H. Jeffreys (Defant 1929). The waves that have been dealt with so far he called long crested, because the crest of the wave is long compared to the wave length. Mathematically speaking, it is assumed that the wave crests are of infinite length (see equation XIV, 2). Jeffreys has introduced the so-called short-crested waves, which can also travel without altering from and therefore belong to the group of waves that are theoretically possible. These waves can be represented by
where L′ = 2π/κ′ represents the length of the crests (fig. 133). This formula defines a series of waves that travel at a somewhat greater speed than the long-crested ones:According to Jeffreys, the first waves that are generated by the weakest winds must be long crested, but, when the wind increases in velocity, short-crested waves can be formed. The explanation here is that the
In table 68, only wave velocity, wave length, and wave period are listed, with no information as to the wave height. A large number of measurements of wave heights has been made by different methods which, although uncertain, are considered more accurate than the measurements of wave lengths. The wave height can be found if a location on board ship can be selected at which the tops of the waves appear level with the horizon, in which case the wave height is equal to the eye height of the observer above the water line. Another method is based on the records of a delicate barometer, and still another that gives very accurate results makes use of photogrammetric measurements.
The greatest wave heights observed in most oceans are about 12 m. Cornish gives a very vivid description of waves of such height during a storm that he experienced in the Bay of Biscay in December, 1911. On the day preceding the gale a heavy swell with a period of 11.4 sec and an average height of about 6 m came from the northwest. The wind, which had blown as a breeze from the southwest, changed during the night to west-northwest and increased in the morning to a strong gale with velocities up to 23 m/sec. The period of the waves increased to 13.5 sec, corresponding to a length of 310 m and a velocity of progress of 21 m/sec, while the wave height increased to 12 m. There are many accounts of similar large waves. In a hurricane in the North Atlantic in December, 1922, when the wind velocity probably exceeded 45 m/sec, one of the officers of the Majestic reported waves that averaged more than 20 m in height and reached a maximum height of up to 30 m. It is probable, however, that these great wave heights refer to occasional peaks of water that may shoot up to elevations considerably above the general wave height. In the region of the prevailing westerlies of the Antarctic Ocean, wave heights up to 14 or 15 m have been observed relatively often, but the average wave height lies much below these values.
The observations quoted regarding maximum wave height and wave length all refer to conditions far from land. Near the shore, waves created directly by wind do not reach such heights, but the height will depend upon the stretch of water across which the wind has blown—namely, upon the fetch of the wind. Stevenson (Cornish, 1934) has combined the average data into the simple formula h = ⅓ 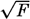 [Equation], where h is the greatest observed wave height in meters and F is the fetch of the wind in kilometers. This formula is valid for small bodies of water, and is
[Equation], where h is the greatest observed wave height in meters and F is the fetch of the wind in kilometers. This formula is valid for small bodies of water, and is
Growth and Dissipation of Surface Waves. In order to explain some of the phenomena concerned here, it is necessary to consider the energy of the waves. This energy can be computed by considering that it is present partly as potential energy and partly as kinetic energy. The computation leads to the result that for long-crested waves the energy per unit area of the sea surface is approximately equal to ½gρa2, where g is the acceleration of gravity, ρ is the density of the water, and a is the amplitude of the wave. For short-crested waves the energy per unit area of sea surface is approximately one half of this amount.
The energy of the waves is transmitted to them by the wind, and, according to Jeffreys, the processes that lead to the generation of waves are also of fundamental importance to their further development. When the wind velocity increases, the pressure exerted on the windward side of the wave will be greater than that on the lee side. Consequently, the waves will increase in height as their energy increases. The energy considerations do not lead to any limit of height to which the waves can grow, but the wave theory itself as developed by Michell (see p. 527) shows that the height cannot exceed about one seventh of the wave length. Thus, if energy is constantly imparted to the waves by the wind without an increase of the wave length, the crests will break and the sea will become covered with whitecaps. However, the longer the wave, the greater height it can reach and thus the greater amount of energy it can absorb from the wind. The wind is able to produce waves of different length, but the shorter will rapidly reach their maximum height and break, whereas the longer will continue to grow. Jeffreys therefore concludes that, “when the waves have travelled a long distance, with the wind blowing them all the time, the longest waves will tend to predominate, simply because they can store more energy.”
However, there is also a limit to the length that waves can attain, because the velocity of progress of the waves increases with increasing wave length and because the wind cannot impart further energy to the waves if they travel at a speed that is as great as or greater than the wind velocity. At a given wind velocity the longest-possible waves will therefore be those that travel at a velocity somewhat below the wind velocity. According to Cornish the speed of the fully developed waves, on an average, is eight tenths of the speed of the wind, but it should be borne in mind that the observed wind velocity depends upon the height at which it is measured. Information is still lacking as to the relation between the velocity of the wind directly over the sea surface and the velocity of the waves.
It also follows that the greatest wave velocity cannot exceed the velocity of the wind that created the waves, assuming that a surface wave continues to proceed at a constant speed after leaving a region of strong winds. Theories developed by Poisson and Cauchy (Lamb, 1932), however, lead to the conclusion that the wave length and therefore the velocity of progress and the period of a surface wave increase in course of time. The velocity of progress of the swell reaching the coast, according to these theories, should be greater than the velocity of the waves that were directly created by the wind. Krümmel (1911) quotes a single observation that may support these conclusions, whereas Cornish (1934) emphasizes the fact that no breakers have been observed of such period lengths that their velocity of progress in deep water would exceed observed wind velocities. Breakers with a period of 20 sec, corresponding to a velocity of progress of about 30 m/sec, were observed on the coast of the English Channel on December 29, 1898, and Cornish points out that prior to the arrival of these breakers a gale had been reported in mid-Atlantic in which the force of the wind had probably exceeded 35 m/sec, which was about 5 m/sec greater than the speed of the waves. He considers it probable that these waves were formed within the area of the gale and traveled for a long distance at their original speed.
Cornish also points out that in the open ocean the existence of long swells can be obscured if shorter waves of greater height are present at the same time. He illustrates his point by a graph similar to the one shown in fig. 134. It is here assumed that two waves are present: one long swell, curve A, and one wave that has only one third the period of the swell but twice the amplitude, curve B. By interference of these two waves, the surface takes the appearance shown by the heavy curve C. An observer would get the impression in this case that the waves present were of the same period as the shortest waves but of variable height, a phenomenon which is often recorded. The long swell may therefore very well be obscured by shorter waves.
A number of studies have dealt with the relation between the wind velocity and the maximum wave height, and between the steepness of the waves and their velocity of progress. In instances in which the quantities to be correlated have not been directly measured, use is made of the equations (p. 525), which give the theoretical relations between wave velocity, wave length, and wave period.
Cornish's empirical results regarding the highest waves can be summarized as follows:
where W is the wind velocity. By means of the equations on p. 525, one obtains H = 0.48 W, which states that the highest wave heights are proportional to the wind velocity. Zimmerman's empirical results (Patton and Marmer, 1932) are L = 10.62 H4/3 = 3.55 W4/3, giving H = 0.44 W, in good agreement with the results of Cornish as to the relation between wave height and wind. Krümmel, on the other hand, arrives at the conclusion that the maximum wave heights are greater than those corresponding to a linear relationship, and Rossby and Montgomery (1935) have for theoretical reasons suggested a formula of the type where G is a nondimensional constant. Introducing G = 0.3, they find that this formula fits the available data fairly well at high wind velocities.The steepness of the waves is generally expressed by means of the ratio of wave length to wave height, L/H, which is inversely proportional to the steepness but can be used as a measure. Cornish's relations lead to the formula L/H = 0.85 W, but this formula is evidently not valid at wind velocities much below 10 m/sec, because the steepest possible waves have a ratio L/H = 7. Zimmerman's values give L/H = 8.1 W⅓. These two results are in qualitative agreement, because both indicate an increase of the ratio L/H with increasing wind velocity. They are also in agreement with Jeffrey's explanation of the growth of waves, according to which one must expect L/H to be greatest for the longest waves. Schott, on the other hand, found that the ratio L/H decreased with increasing wind velocity, but Krümmel (1911), in discussing a large number of observations by Paris, found the ratio to be constant. The ratio between the length and the height of the waves appears to vary between 10 and 20 m when a fresh wind blows, but in the case of the swell the ratio may lie between 30 and 100. Observations from lakes indicate that there the ratio varies between 10 and 12.
A similar confusion exists regarding the relation between wave velocity and wind velocity. As already stated, Cornish found c = 0.8 W, but from Zimmerman's relation it follows that c = 2.35 W⅔. According to the latter equation the wave velocity is greater than that of the wind up to a wind velocity of 13.2 m/sec, and it is smaller when the wind is above that value, in disagreement with energy considerations, which
All these discrepancies indicate that wave height, wave profile, and velocity of progress are not dependent upon the wind velocity alone at the time of observation, but may also depend upon the length of time the wind has blown, the state of the sea when the wind started blowing, and the dimensions of the area over which the wind blows. Comprehensive observations are needed for clearing up these questions.
It has been mentioned (p. 532) that the wave height depends upon the fetch of the wind, and that for small bodies of water a simple empirical relationship has been established between maximum wave heights and the dimensions of the body. This formula is valid to a distance of 1000 to 1500 kilometers, at which the maximum wave height characteristic of the open ocean, about 12 m, may be reached. The fact that greater wave heights are rarely observed may be due to the circumstance that the wind systems mostly have dimensions smaller than 1500 kilometers, so that in the open ocean the actual fetch of the wind will be, at most, 1500 km, or it may be that a longer fetch of the wind tends more toward increasing the length of the waves than toward increasing their height.
The differences in energy of long-crested and short-crested waves and of large and small waves have to be considered in the discussion of what happens to waves when the wind stops blowing. Owing to the smaller energy per unit area the short-crested waves will be destroyed more rapidly by friction, and the largest of the long-crested waves stand the best chance of surviving for a long time. It is also probable that the dissipation of energy is more rapid within the steeper waves, for which reason the steeper and shorter waves will be destroyed more rapidly than the longer and less steep. Thus, one should expect that, outside of the region in which the wind blows, long-crested swells will become more and more dominating, and at considerable distances from the wind areas only long-crested swells will be present. These conclusions are in good agreement with observed conditions.
Waves Near the Coast. Breakers. When waves approach the coast, a number of things happen. In the first place it is conspicuous that the short-crested cross sea disappears at some distance from the coast and that mainly long-crested rollers reach the beaches. Jeffreys has been able to show that this transformation is associated with the change in form and dissipation of energy that take place when surface waves enter shallow water. One of the characteristic deformations which take place is that, when the depth decreases, originally symmetrical waves become unsymmetrical, the front of the waves becomes steeper, and, finally, the waves break. This effect is more pronounced in the case of the short-crested waves, and the latter will, therefore, break at a greater
Another effect of the decrease of depth is related to a decrease of the wave velocity. The part of the wave that first approaches the coast is slowed down, but the outer portion of the wave still advances with great velocity, wherefore the direction of the wave front is turned, and a wave that approaches the coast at an angle may be turned in such a way that the wave front becomes nearly parallel to the coast.
Still another effect is related to the fact that when approaching shallow coastal waters the waves are transformed into types which are intermediate between surface waves and long waves (p. 519). The waves of long period take on some of the characteristics of long waves at a greater distance from the coast than do those of short period. Consequently the movement of the water particles of the long-period waves will reach to the bottom at a greater distance from the coast, although the height of these waves may be smaller than that of the short-period waves. This circumstance may have considerable bearing on sand movement caused by waves in shallow water.
The breaking of the wave is primarily related to change in the velocity of progress when the wave reaches shallower water (see Defant, 1929). As a consequence of this change, the wave front becomes increasingly steeper until it breaks. Friction may also play a part.
When a wave breaks near the shore, another wave type, known as a wave of translation, may develop. This wave, which was discovered and studied by Russell (Lamb, 1932), is characterized by having only a crest and no trough. The motion of water particles is only in the direction of progress, and the water particles are therefore displaced forward as the wave passes. It is formed when a mass of water is suddenly added to still water, and may therefore be produced as the crest of a breaking wave topples over and crashes down on the water surface in front. This wave type is unimportant in the open sea, but may be prominent on a shallow coast.
Certain phenomena that appear to be associated with breakers are not yet understood. The existence of undertow has not been satisfactorily explained, and is doubted by some observers (Shepard and La Fond, 1939). The rip currents which flow away from the coast through the breakers and which may carry swimmers far out from the beach also have not been fully explained, but it is probable that these currents are associated with surface transport of water against the beach by the waves (Shepard et al, 1941).
The destructive effect of breakers has been the subject of intensive studies, particularly by engineers, but cannot be discussed here. Interested readers are referred to some of the general works that are included in the list of literature.
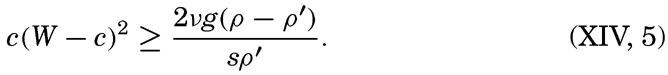

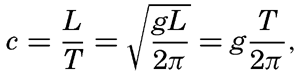
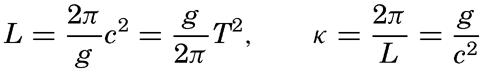
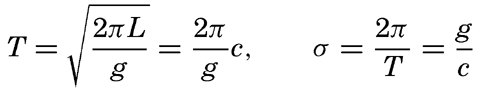
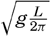 [
[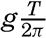 [
[ [
[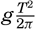 [
[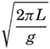 [
[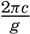 [
[