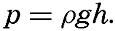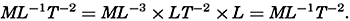Units and Dimensions

In the preceding chapters, different units have been introduced without strict definitions, but now it is necessary to define both units and dimensions. The word “dimension” in the English language is used with two different meanings. In everyday language, the term “dimensions of an object” refers to the size of the object, but in physics “dimensions” mean the fundamental categories by means of which physical bodies, properties, or processes are described. In mechanics and hydrodynamics, these fundamental dimensions are mass, length, and time, denoted by M, L, and T. When using the word “dimension” in this sense, no indication of numerical magnitude is implied, but the concept is emphasized that any physical characteristic or property can be described in terms of certain categories, the dimensions. This will be clarified by examples on p. 402.

Fundamental Units. In physics the generally accepted units of mass, length, and time are gram, centimeter, and second; that is, quantities are expressed in the centimeter-gram-second (c.g.s.) system. In oceanography, it is not always practicable to retain these units, because, in order to avoid using large numerical values, it is convenient to measure depth, for instance, in meters and not in centimeters. Similarly, it is often practical to use one metric ton as a unit of mass instead of one gram. The second is retained as the unit of time. A system of units based on meter, ton, and second (the m.t.s. system) was introduced by V. Bjerknes and different collaborators (1910). Compared to the c.g.s. system the new units are 1 m = 10² cm, 1 metric ton = 10⁶ g, 1 sec = 1 sec. For thermal processes, the fundamental unit, 1°C, should be added.

Unfortunately, it is not practical to use even the m.t.s. system consistently. In several cases it is of advantage to adhere to the c.g.s. system in order to make results readily comparable with laboratory results that are expressed in such units, or because the numerical values are more conveniently handled in the c.g.s. system. When measuring horizontal

---

distances, on the other hand, it is preferable to use larger units such as kilometers, statute miles, or nautical miles. In oceanography it is therefore always necessary to indicate the units in which any quantity is measured.

Derived Units. Units in mechanics other than mass, M, length, L, and time, T, can be expressed by the three dimensions, M, L, and T, and by the unit values adopted for these dimensions. Thus, velocity has the dimension length divided by time, which is written as LT⁻¹ and is expressed in centimeters per second or in meters per second. Velocity, of course, can be expressed in many other units, such as nautical miles per hour (knots), or miles per day, but the dimensions remain unaltered. Acceleration is the time change of a velocity and has the dimensions LT⁻². Force is mass times acceleration and has dimensions MLT⁻².

Table 60 shows the dimensions of a number of the terms that will be used. Several of the terms in the table have the same dimensions, but the concepts on which the terms are based differ. Work, for instance, is defined as force times distance, whereas kinetic energy is defined as mass times the square of a velocity, but work and kinetic energy both have the dimensions ML²T⁻². Similarly, one and the same term can be defined differently, depending upon the concepts that are introduced. Pressure, for instance, can be defined as work per unit volume, ML²T⁻²L⁻³ = ML⁻¹T⁻², but is more often defined as force per unit area, MLT⁻²L⁻² = ML⁻¹T⁻².

In any equation of physics, all terms must have the same dimensions, or, applied to mechanics, in all terms the exponents of the fundamental

---

dimensions, M, L, and T, must be the same. It is inaccurate, for instance, to state that the acceleration of a body is equal to the sum of the forces acting on a body, because acceleration has dimensions LT⁻², whereas force has dimensions MLT⁻². The correct statement is that the acceleration of a body is equal to the sum of the forces per unit mass acting on a body. An example of a correct statement is the expression for the pressure exerted by a column of water of constant density, ρ, and of height, h, at a locality where the acceleration of gravity is g: In this case the dimensions on both sides of the equality sign are

Some of the constants that appear in the equations of physics have dimensions, and their numerical values will therefore depend upon the particular units that have been assigned to the fundamental dimensions, whereas other constants have no dimensions and are therefore independent of the system of units. Density has dimensions ML⁻³, but the density of pure water at 4° has the numerical value 1 (one) only if the units of mass and length are selected in a special manner (grams and centimeters or metric tons and meters). On the other hand, the specific gravity, which is the density of a body relative to the density of pure water at 4°, has no dimensions (ML⁻³/ML⁻³) and is therefore expressed by the same number, regardless of the system of units that is employed.