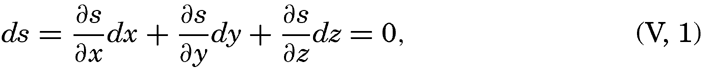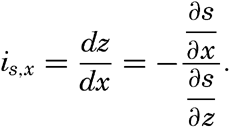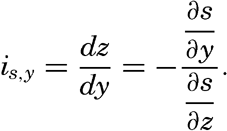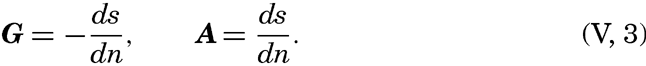Scalar Fields
It cannot be too strongly emphasized that the ocean is three-dimensional and that the distribution of properties or the type of motion must be represented in space. For this purpose a convenient system of coordinates is needed. Any point in the ocean can be designated by means of its geographic latitude and longitude and its depth below sea level, but if one deals with a small area one may consider the surface of the earth within that area as flat, and can introduce ordinary rectangular coordinates with the horizontal axes at sea level and the vertical axis positive downward. By “sea level” is meant not the actual sea level but an ideal sea level, which is defined as a surface along which no component of gravity acts. The difference between the actual and the ideal sea level will be further explained when dealing with the distribution of pressure (p. 406).
The location in the ocean space of any given surface is completely determined if in every latitude and longitude one knows the depth of the surface below the ideal sea level. In a chart this surface can be represented by means of lines of equal depth below sea level (isobaths), which together render it picture of the topography of the surface. Thus, the topography of the sea bottom is shown by isobaths drawn at selected intervals of depth.
The quantities that must be considered when dealing with the sea are either scalars or vectors. A scalar quantity is a physical quantity whose measure is completely described by a number, that depends on the selected system of units. Pressure, temperature, salinity, density, and oxygen content can be mentioned as examples of scalar quantities. A vector is a physical quantity that is completely described by magnitude and direction. The velocity of a particle, the acceleration of a particle, and the forces acting on a particle are examples of vectors.
The magnitude of a vector, such as the numerical value of the velocity of a particle, is a scalar quantity. A vector can be represented by means of its components along the axes of a coordinate system, and these components are scalar quantities.
A continuous fluid is characterized, at every point in the space which it occupies, by a number of different properties. The space distribution of one particular property is called the field of that property. The field is called a scalar field if the property is a scalar quantity, and a vector field if the quantity is a vector. In the ocean there are scalar fields such as the pressure field, the temperature field, and the density field, and there are vector fields such as the velocity field, the acceleration field, and so on.
The term field was first applied to a vector field in order to describe the distribution of electromagnetic forces. Every student of physics has seen the magnetic field of force demonstrated by means of iron filings placed on a card above a magnet, but this experiment brings out only certain characteristics of the field. It shows the direction of the magnetic forces in one single plane, but it does not show the space distribution or the magnitude of the force of the field.
A scalar field is completely represented by means of equiscalar surfaces—that is, surfaces along which the scalar quantity has the same numerical value. The temperature field in the ocean, for instance, would be completely described if one knew exactly the form of the isothermal surfaces, and, similarly, the pressure field would be fully represented if one knew the form of the isobaric surfaces. However, it is impracticable to prepare space models that show the actual configuration of isothermal surfaces or other equiscalar surfaces in the ocean, and it would be impossible to publish such representations. For practical purposes one must select other forms of representation. One widely used method is to show the lines of intersection between equiscalar surfaces and the coordinate surfaces. A chart showing the distribution of temperature at sea level is an example of such representation. In this case the sea level represents one of the principal coordinate surfaces, and the isotherms represent the lines at which the surfaces of equal temperature in the sea intersect the sea surface. Similarly, a chart showing the distribution of temperature at a depth of 1000 m shows the lines along which the isothermal surfaces intersect the 1000-m surface, whereas the temperature distribution in a vertical section shows the lines along which the isothermal surfaces intersect the vertical plane that is under consideration.
A series of horizontal charts of isotherms in surfaces at different distances below sea level give a representation of the temperature field in the ocean, and a series of vertical sections showing isotherms give another representation of the same field.
On the other hand, one can make use of an entirely different method of representation. Instead of showing the lines along which the isothermal surfaces intersect a coordinate surface, one can represent the isothermal surface itself and can show the lines along which the coordinate surfaces at different distances below sea level intersect that surface. Such a
These topographic charts would represent charts of absolute topography, because it is assumed that the depths below the ideal sea level are known. This ideal sea level, however, is a fictitious level that cannot be determined by observations, and all measurements have to be made from the actual sea level. In practice, therefore, the topography of a surface in the ocean will not represent the absolute topography but a relative topography referred to the unknown shape of the actual sea surface. In many instances one need not take the difference between absolute and relative topography into account, because it generally amounts to less than 1 m. For instance, it can be neglected when one deals with isothermal surfaces, because the change in temperature on a fraction of a meter is generally negligible. When dealing with the isobaric surfaces, on the other hand, as will be explained in detail when discussing the field of pressure, one must discriminate sharply between absolute and relative topographies.
These matters have been set forth explicitly, because it is essential to bear in mind that one must always consider distribution in space, which can be fully described by means of equiscalar surfaces. These, however, may have highly complicated forms.
The mathematical definition of an equiscalar surface can be written
where s is the scalar quantity under consideration (temperature, pressure, density, and so forth), ∂ s/∂ x · dx is the change of the scalar on the distance dx, ∂ s/∂ y · dy is the change on the distance dy, and ∂ s/∂ z · dz is the change on the distance dz. Along the equiscalar surface the total change must be zero, as expressed by (V, 1).In a vertical section in the x-z plane the equiscalar curves are similarly defined by
From the latter equation the slope of the equiscalar surfaces in the x-direction is obtained:So far, the discussion has dealt with equiscalar surfaces in general. In practice, one may select these surfaces so that there is a constant difference between the value of the variable at any two surfaces. These surfaces are called standard equiscalar surfaces. In the case of temperature, the isothermal surfaces might be selected for every one degree of temperature; in the case of salinity, the isohaline surfaces might be selected for every 0.1 ‰, and so on. These surfaces would divide the space into thin layers characterized by a constant difference of the quantity at the two boundary surfaces of every layer. Such layers are called equiscalar sheets. It should be noted that the scalar is not constant within this sheet but has a constant average value. It is evident that the thickness of these sheets represents the rate at which the scalar varies in a direction at right angles to the equiscalar surfaces. Where the sheets are thin the variation is great, but where the sheets are thick the variation is small. The rate of variation can be represented by means of a vector whose direction is normal to the equiscalar surface and whose magnitude is inversely proportional to the thickness of the sheet. The vector representing the rate of decrease is generally called the gradient (temperature gradient, pressure gradient), and the vector representing the rate of increase is called the ascendant. If the scalar is called s, then the gradient, G, and the ascendant, A, are defined by the equations
Vectors are printed in bold-face type.If the field is represented by means of a sufficient number of surfaces, these surfaces will completely define the gradients and ascendants that are characteristic of the distribution. Thus, the special vector fields of gradients and ascendants are entirely described by means of systems of equiscalar surfaces, but other vector fields cannot be described in that manner. Vector fields will be dealt with in chapter XII.