The Heat Budget of the Earth as a Whole
For the earth as a whole, the total amount of heat that is received during one year from the sun at the limit of the atmosphere must exactly balance the total amount that in the same period is lost by reflection and by radiation into space. Otherwise, the temperature of the atmosphere and the oceans would change. The radiation from the hot sun is called short-wave radiation, because the wave lengths which reach the limit of the earth's atmosphere lie roughly between 0.38 μ and 2.5 μ, whereas the dark-heat radiation which is emitted by all objects at ordinary temperatures is called long-wave radiation, being of wave lengths between 5 μ and 20 μ. The part of the short-wave radiation that is reflected is of no importance to the heat budget of the earth, and therefore the amount of short-wave radiation that is absorbed by the atmosphere, the oceans, and the land must exactly balance the long-wave radiation into space from the entire system. A small part of the heat that the atmosphere receives is transformed into kinetic energy which by friction is transformed back again to heat and ultimately lost into space by radiation. Thus, the transformation of heat to kinetic energy does not lead to any net gain of heat but serves to maintain the circulations of the atmosphere and the oceans.
As is customary procedure, the amounts of heat will be given in gram calories and not in units of work such as ergs or joules. The conversion factors are: 1 gram calorie = 4.183 × 107 ergs = 4.183 joules.
In lower latitudes, heat received by radiation is greater than heat lost by back radiation and reflection, whereas in higher latitudes the gain is less than the loss. Table 24 contains values of heat received and lost by processes of radiation and reflection in different latitudes. The third column, containing the differences between the two quantities, shows that there is an annual net gain of heat in the equatorial regions and a net loss in the polar regions. The mean annual temperatures in different latitudes on the earth remain unchanged from one year to another, showing that within the atmosphere and the oceans there must be a transport of heat from lower to higher latitudes which exactly equals the difference
The transport of heat from lower to higher latitudes takes place partly by air currents (winds) and partly by ocean currents. In meteorological literature it is generally assumed that the transport by ocean currents is negligible (Bjerknes et al, 1932), although the question has not been thoroughly examined. It can be shown that the assumption is correct when dealing with averages for the whole earth, but in some regions the transport by ocean currents is of considerable importance.
| Latitude (°) | Heat received (g cal/cm2/min) | Heat lost (g cal/cm2/min) | Surplus or deficit (g cal/cm2/min) | Heat transport across parallels of latitude (1016 g cal/min) | Heat transport across every centimeter of parallels of latitude (107 g cal/cm/min) |
|---|---|---|---|---|---|
| 0 | 0.339 | 0.300 | 0.039 | 0.00 | 0.00 |
| 10 | 0.334 | 0.299 | 0.035 | 1.59 | 0.40 |
| 20 | 0.320 | 0.294 | 0.026 | 2.94 | 0.78 |
| 30 | 0.297 | 0.283 | 0.014 | 3.58 | 1.07 |
| 40 | 0.267 | 0.272 | −0.005 | 3.96 | 1.30 |
| 50 | 0.232 | 0.258 | −0.026 | 3.34 | 1.32 |
| 60 | 0.193 | 0.245 | −0.052 | 2.40 | 1.20 |
| 70 | 0.160 | 0.231 | −0.071 | 1.20 | 0.88 |
| 80 | 0.144 | 0.220 | −0.076 | 0.32 | 0.46 |
| 90 | 0.140 | 0.220 | −0.080 | 0.00 | 0.00 |
The amount of heat transported in a north-south direction by a unit volume of ocean water is equal to cρϑvN, where c represents the specific heat, ρ the density, ϑ the temperature of the water, and vN the north-south component of velocity. The total transport through a certain section of the sea can be found by integration, but for the sake of simplicity
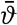 [Equation]ρTN, where
[Equation]ρTN, where 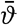 [Equation] represents the average temperature of the water and ρTN represents the mass of water passing north through the section in unit time. If the section is taken across an ocean, the mass transport to the north, ρTN, must equal the mass transport to the south, ρTS, but the heat transport may differ because the temperature of the water transported in one direction may be higher or lower than that of the water which is transported in the opposite direction. If these temperatures are designated by ϑN and ϑS, the net transport of heat will be c(ϑN − ϑS)ρT, where ρT now means the transport to the north and the south. As an example, we can apply these considerations to the North Atlantic Ocean along the parallel of 55°N. In the eastern Atlantic about 10 million m3/sec of warm water flow toward the north, and in the western Atlantic an equal volume of cold water is carried south by the Labrador Current and by the flow of the deep water (p. 684). With ϑN − ϑS = 5°, c = 1, ρ = 1, and T = 10 × 106 m3/sec, we find that the heat transport toward the north through latitude 55° in the Atlantic Ocean is about 0.3 × 1016 g cal/min. The total heat transport across the parallel of 55°N is about 3 × 1016 g cal/min; hence in the North Atlantic the fraction carried by the ocean currents is appreciable.
[Equation] represents the average temperature of the water and ρTN represents the mass of water passing north through the section in unit time. If the section is taken across an ocean, the mass transport to the north, ρTN, must equal the mass transport to the south, ρTS, but the heat transport may differ because the temperature of the water transported in one direction may be higher or lower than that of the water which is transported in the opposite direction. If these temperatures are designated by ϑN and ϑS, the net transport of heat will be c(ϑN − ϑS)ρT, where ρT now means the transport to the north and the south. As an example, we can apply these considerations to the North Atlantic Ocean along the parallel of 55°N. In the eastern Atlantic about 10 million m3/sec of warm water flow toward the north, and in the western Atlantic an equal volume of cold water is carried south by the Labrador Current and by the flow of the deep water (p. 684). With ϑN − ϑS = 5°, c = 1, ρ = 1, and T = 10 × 106 m3/sec, we find that the heat transport toward the north through latitude 55° in the Atlantic Ocean is about 0.3 × 1016 g cal/min. The total heat transport across the parallel of 55°N is about 3 × 1016 g cal/min; hence in the North Atlantic the fraction carried by the ocean currents is appreciable.This example represents an outstanding case of poleward transport of heat by ocean currents. In the Pacific Ocean a transport of comparable magnitude probably takes place in latitudes 30°N to 40°N, but in the southern oceans the north-south circulation and the corresponding temperature contrasts between currents flowing toward or away from the higher latitudes are smaller than those in the northern oceans. A detailed study of the transport of heat by ocean currents has not been made, but it seems certain that by far the major transport of heat is taken care of by the atmosphere.