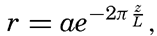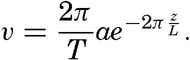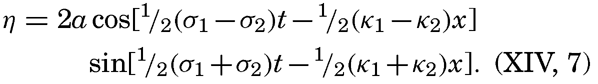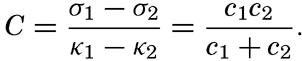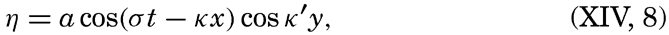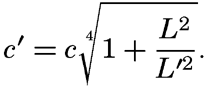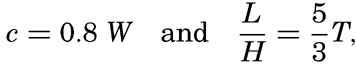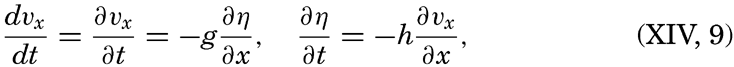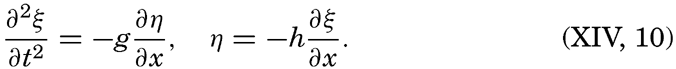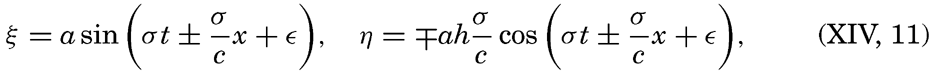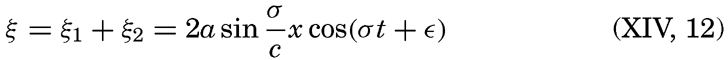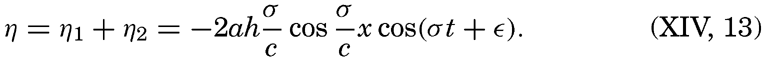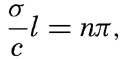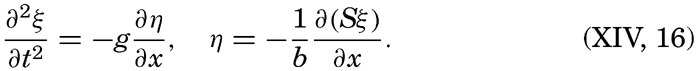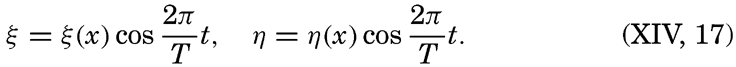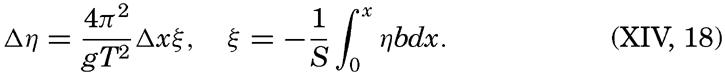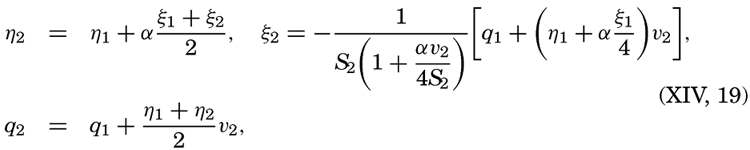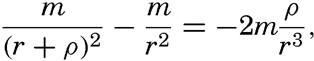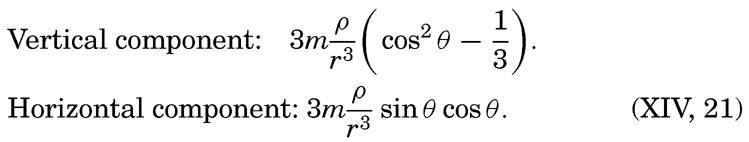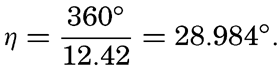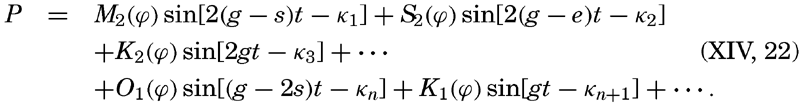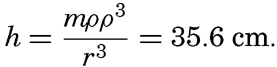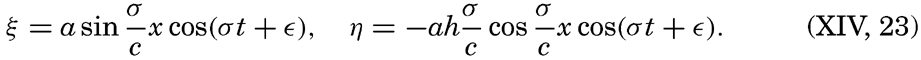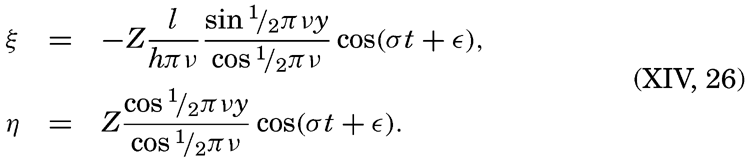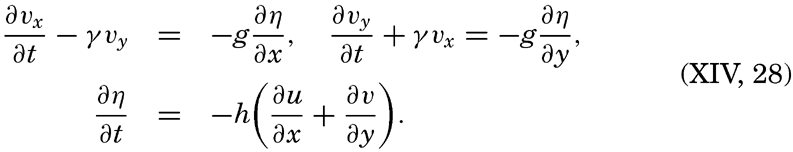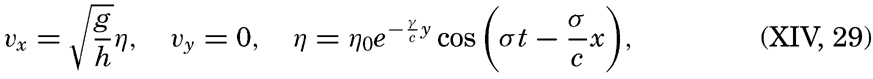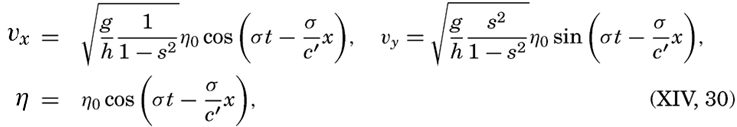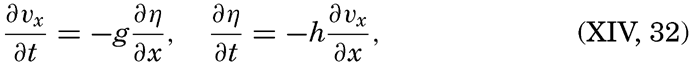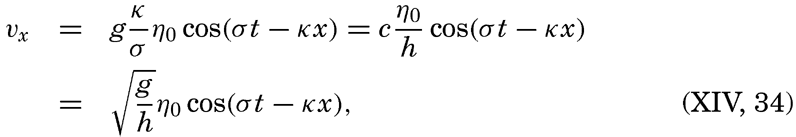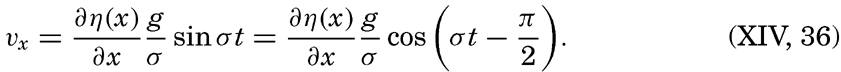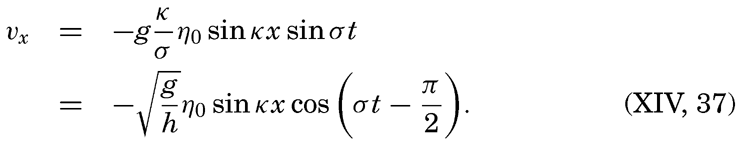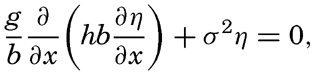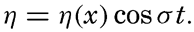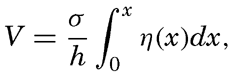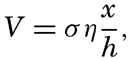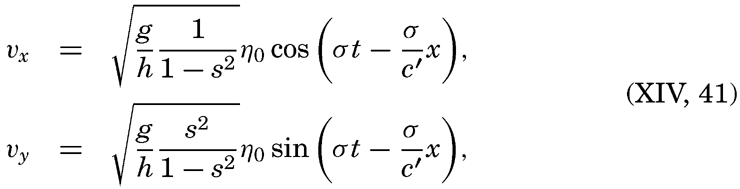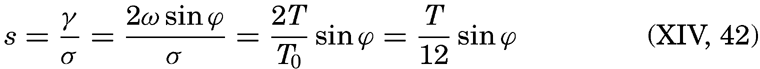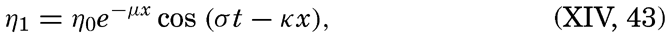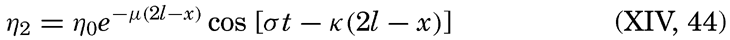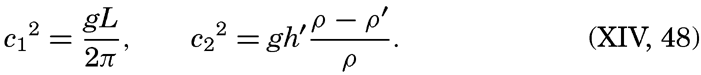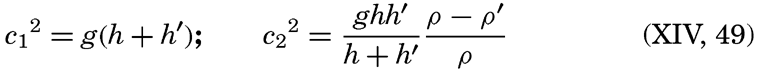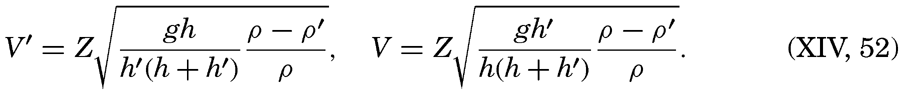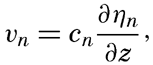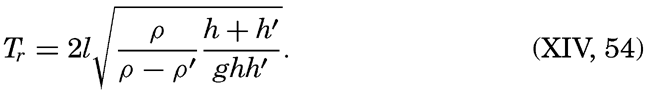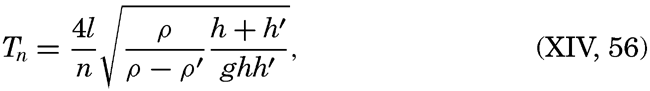XIV. Waves and Tides [PDF]
Introduction
The preceding sections have dealt with the types of motion in the ocean that bring about transport of water masses in a definite direction during a considerable length of time. They have also dealt with the random motion, the turbulence, which is superimposed upon the general flow. Besides these types, one has also to consider the oscillating motion characteristic of waves. In general, this motion manifests itself to the observer more by the rise and fall of the sea surface than by the motion of the individual water particles.
Waves have attracted attention since before the beginning of recorded history, and in recent years they have been the subject of extensive theoretical studies. Surveys of our knowledge as to the character of ocean waves have been presented by Cornish (1912, 1934), Krümmel (1911), Patton and Marmer (1932) and by Defant (1929). Lamb (1932) has discussed the hydrodynamic theories of waves, and Thorade (1931) has given a comprehensive review of the theoretical studies of ocean waves and has compiled a long list of literature covering the period from 1687 to 1930.
Our understanding of the waves of the ocean, how they are formed and how they travel, is as yet by no means complete. The reason is, in the first place, that actual observations at sea are so difficult that the characteristics of the waves cannot easily be determined. In the second place, the theories that serve to bring the observed sequence of events in nature into intimate connection with experience gained by other methods of study are still incomplete, particularly because most theories are based on classical hydrodynamics, which deal with wave motion in an idealized fluid. Here will be presented only a brief review of the best-established facts concerning waves and of some of the more outstanding theoretical accomplishments. Readers who wish to gain further insight are referred to some of the above-mentioned books.
In order to classify waves, it is necessary to introduce certain definitions. Wave height, H, is defined as the vertical distance from trough to crest, whereas wave amplitude, a, is one half of that distance (fig. 128).
For a wave the amplitude of which is small compared to the wave length, the height of the free surface, η, at a given locality can be represented by means of a simple harmonic function,
For a progressive wave of small amplitude, the variation in time and space of the free surface can be written A standing wave (fig. 128) can be considered as composed of two progressive waves traveling in opposite directions, and the term “velocity of progress” retains, therefore, a definite meaning.In wave motion, two types of velocity have to be considered: the velocity of progress of the wave itself and the velocity of the individual water particles. The water particles move back and forth, in circles, or
The rise and fall of the free surface can be ascribed to convergence and divergence of the horizontal motion of the water particles. Within a progressive wave (fig. 128, also fig. 98, p. 426) the horizontal flow at the wave crest is in the direction of progress, and at the trough it is opposite to the direction of progress. Convergence therefore takes place between the crest and the trough, and there the surface rises. Within a standing wave (fig. 128) the horizontal velocity is zero at every point at the time when the wave reaches its greatest height. During the following half period the horizontal velocity is directed from the crest to the trough, causing divergence below the crest and convergence below the trough, for which reason the crest will sink and the trough will rise. This process continues until the positions of the crest and of the trough become interchanged, and during the following half period the horizontal motion is reversed. The vertical velocity is always zero halfway between the crest and the trough, where the wave has nodes. The horizontal velocity is always zero at the crests and troughs, where the wave has antinodes or loops. Evidently a vertical wall can be inserted at the antinode without altering the character of the wave, because no horizontal motion exists at the antinode.
From a different point of view, waves can be classified as forced or free waves. A forced wave is a wave that is maintained by a periodic force, and the period of a forced wave must always coincide with the period of the force, regardless of the dimensions of the basin or of frictional influence. A free wave, on the other hand, represents one of the possible oscillations of a body of water if this body is set in motion by a sudden impulse. The period of a free wave depends on the dimensions of the basin and on the effect of friction. Later on, these types will be dealt with more fully.
When ocean waves are concerned, gravity and Corioli's force are the two important forces to be considered. For waves of a few centimeters in length the surface tension of the water has to be taken into account, but such waves are of no consequence in the sea. We shall therefore deal with gravity waves only and shall at first neglect Corioli's force.
A rational division of gravity waves into two classes can be made when considering the relation between wave velocity, wave length, and the depth to the bottom. The wave velocity can with sufficient accuracy be represented by means of the equation of classical hydrodynamics:
where h is the depth to the bottom. If the depth to the bottom exceeds about half a wave length, tanh 2π(h/L) can be put equal to unity, andIf, on the other hand, the depth is small compared to the wave length, tanh 2πh/L can be replaced by 2π;h/L, so that c = 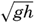 [Equation]. Thus, if the depth is small compared to the wave length, the velocity of the wave depends only on the depth to the bottom and is independent of the wave length. The latter waves are called long waves, whereas the former, the velocity of which is independent of depth, are called short waves, or surface waves. For water of any given depth the transition takes place within a narrow range of wave lengths, for which reason the classification is a very satisfactory one.
[Equation]. Thus, if the depth is small compared to the wave length, the velocity of the wave depends only on the depth to the bottom and is independent of the wave length. The latter waves are called long waves, whereas the former, the velocity of which is independent of depth, are called short waves, or surface waves. For water of any given depth the transition takes place within a narrow range of wave lengths, for which reason the classification is a very satisfactory one.
The physical reason for the difference between the surface waves and the long waves has been explained in simple words by H. Jeffreys (Cornish, 1934). Jeffreys points out that within surface waves the individual water particles near the surface move in circular orbits, but that the radii of these orbits, and therefore the velocities, decrease rapidly with depth. Theoretically the diameter of orbits at a depth of one half the wave length is only one twenty-third of the corresponding diameter at the surface. Regardless of the actual depth the character of the wave therefore remains unaltered if the depth to the bottom is greater than that short distance. Direct observations for substantiating this conclusion have not been made, but experience on submarines shows that in deep water a moderate wave motion decreases rapidly with depth and becomes negligible at a short distance below the surface, say at a depth of 30 m.
In shallow water the fact that no vertical motion can exist at the bottom modifies the character of the waves. At the bottom the motion can be only back and forth, and, if the depth is small compared to the wave length, the motion will remain nearly horizontal at all depths. Actually, the orbits of the single water particles will be flat ellipses that become more and more narrow when approaching the bottom, and at the bottom they degenerate into straight lines.
In a sea of variable depth the transition from short to long waves begins when the depth to the bottom becomes less than half the wave length, or where h < ½L. Since L = T2g/2π (p. 525) it is possible to establish a relation between the critical depth at which the transformation begins to take place and the wave period:
This formula is preferable to one containing the wave length, because theWaves of tidal period, on the other hand, always have the character of long waves. If the rotation of the earth is disregarded, their velocity of progress is equal to 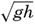 [Equation] = L/T if h/L is so small that tanh 2πh/L equals 2πh/L. The equation
[Equation] = L/T if h/L is so small that tanh 2πh/L equals 2πh/L. The equation 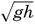 [Equation], = L/T can be written
[Equation], = L/T can be written
For waves of short periods the rotation of the earth can be disregarded, as can be shown by comparing the accelerations of the moving particles with Corioli's force. If Corioli's force is very small compared to the accelerations, it can be disregarded, because it is then negligible compared to the other forces, the resultant of which represents the accelerations.
Corioli's force is proportional to 2ω sin ϕ ν v, where ν is the horizontal velocity, and the acceleration, dv/dt, is proportional to (2π/T)v. The ratio between Corioli's force and the acceleration due to the wave motion is therefore proportional to (T/2π)2ω sin ϕ or to (T/Te)2 sin ϕ, where Te is the period of rotation of the earth. If the period is measured in hours, one can write (T/Te)2 sin ϕ = (T/12) sin ϕ. Now, 12/sin ϕ is equal to one half pendulum day (p. 437), and it can therefore be stated that the earth's rotation will be of importance to wave motion if the period of the wave approaches the length of one half pendulum day. For ocean surface waves the wave period T is always a very small fraction of half a pendulum day, for which reason the deflecting force is negligible beside the other forces, but long waves may be of tidal period, in which case the period length is of the same order of magnitude as a pendulum day, meaning that the deflecting force is of the same importance as other acting forces. Corioli's force will therefore be introduced when dealing with these waves.
Another noteworthy characteristic of surface waves is that below the depth to which motion of particles is perceptible the pressure remains constant when the waves pass. A pressure gauge placed on the bottom, if the depth were great enough, would not show any effect of surface waves, regardless of their height. The reason is that below the crest of the wave the acceleration is directed downward and will therefore counteract the effect of the acceleration of gravity, but below the trough the acceleration is directed upward and will be added to the acceleration
For waves of long periods the vertical accelerations, on the other hand, can be neglected, because the vertical displacements require a very long time. Consider a surface wave of period 10 sec and height 1 m, and a long wave of semidiurnal tidal period 44,700 sec and height 1 m. The ratio of the average vertical accelerations during the time when a water particle near the surface moves from its lowest to its highest position is inversely proportional to the square of the ratio of the wave periods, or in the wave of tidal period the vertical accelerations are about 5 × 10−8 times the vertical accelerations within the surface wave—that is, they are negligible. Consequently, when a long wave passes, the pressure at any given level is proportional to the height of the water, and a pressure gauge at the bottom gives a true record of the passing wave.
Some of the most outstanding characteristics of ocean surface waves and long waves can be summarized as follows:
| Surface Waves | Long Waves | |
|---|---|---|
| Character of wave. | Progressive, standing, forced or free. | Progressive, standing, forced or free. |
| Velocity of progress. | Dependent on wave length but independent of depth. | Dependent on depth but independent of wave length. |
| Movement of water particles in a vertical plane. | In circles, the radii of which decrease rapidly with increasing distance from the surface. Motion imperceptible at a depth which equals the wave length. In some types of surface waves the motion is in wide ellipses. | In ellipses which are so flat that practically the water particles are oscillating back and forth in a horizontal plane. Horizontal motion independent of depth. |
| Vertical displacement of water particles. | Decreases rapidly with increasing distance from the surface and becomes imperceptible at a depth which equals the wave length. | Decreases linearly from the surface to the bottom. |
| Distribution of pressure. | Below the depth of perceptible motion of the water particles the pressure is not influenced by the wave. | The wave influences the pressure distribution in the same manner at all depths. |
| Influence of the earth's rotation. | Negligible. | Cannot be neglected if the period of the wave approaches the period of the earth's rotation. The velocity of progress of the wave and the movement of the water particles are modified. |
In the following discussion the characteristics of the wave types of the oceans will be dealt with more fully.
Surface Waves
Origin of Surface Waves. It is evident to the most casual observer that surface waves are created by wind, but only recently, in a work by H. Jeffreys, has a successful physical explanation of the process been presented (Defant, 1929, Thorade, 1931). Jeffreys avails himself of the fact that in air in turbulent flow, eddies are formed on the lee side of obstacles. If a strong wind blows against an isolated house, an eddy is formed in the same manner that eddies are formed behind stones in a river. The result is that the wind exerts a pressure on the windward side of the house, but on the lee side there will be suction. Similarly, when the wind blows over a sequence of waves, eddies will be formed on the lee side of the waves, for which reason the pressure of the wind will be greater on the windward slopes than on the slopes that are sheltered by the crests. This condition can prevail, however, only if the waves travel at a velocity that is smaller than the speed of the wind. On the basis of these arguments, Jeffreys finds that waves may increase only if
Here W is the velocity of the wind, c is the velocity of the waves, v is the kinematic viscosity of the water, g is the acceleration of gravity, ρ and ρ′ are the densities of the water and the air, respectively, and s is a non-dimensional numerical coefficient that Jeffreys calls the “sheltering coefficient.” It should be observed that in his reasoning Jeffreys takes into account both the turbulent character of the wind and the viscosity of the water. His theory therefore must be expected to give results in better agreement with actual conditions than earlier theories based on the concepts of classical hydrodynamics, which neglect turbulence and viscosity.The term on the right-hand side of equation (XIV, 5) is always positive. The product on the left-hand side must therefore always be positive and can exceed the right-hand term only if the wave velocity differs sufficiently both from zero and from the wind velocity. For any given wind velocity, there can be only a limited range of possible wave velocities. It is readily seen that at a given wind velocity the right-hand side of (XIV, 5) is at a maximum when c = ⅓W. Therefore, unless
there will be no values of c that satisfy the condition.Equation (XIV, 6) determines the velocity of the weakest wind which can raise any waves, and this weakest wind could be determined if the sheltering coefficient were known. Jeffreys has not been able to make
The velocity of the smallest possible waves should be one third of the limiting wind velocity, or about 37 cm/sec, and according to the theory the corresponding wave length must be 8.8 cm (p. 525). Thus, measurements of the smallest waves can be used for testing the correctness of the theory, but measurement of such small wave lengths is very difficult and no exact observations have been made. Jeffreys finds that the length of the shortest waves observed by him lies in the neighborhood of the theoretical value. On the other hand, Scott Russell reported in 1844 that he had measured surface waves of a length of only 5 cm, and the smallest waves measured by Cornish are only about 2.5 cm long. The problem of the generation of surface waves is therefore not satisfactorily solved, but the approach by Jeffreys is in better agreement with observations than is any previous attempt.
It should be added that if only the forces due to surface tension and gravity are considered, waves should not be formed until the wind velocity passes the limit of 6.7 m/sec, and if only the stress of the wind on the surface and gravity are taken into account, the limiting wind velocity will be about 4.8 m/sec. Experience shows that these values are far too high, and the turbulent character of the wind must therefore be of the greatest importance.
Form and Characteristics. In physics the general picture of surface waves is that of sequences of rhythmic rise and fall which appear to progress along the surface when progressive waves are concerned, or which appear stationary if standing waves are being considered. The actual appearance of the surface of the open sea, however, is mostly in the sharpest contrast to that of rhythmic regularity. If a wind blows, waves of all different sizes are present, varying in form from long, gently sloping ridges to waves of short and sharp crests. Superimposed on the gentler waves, which may or may not run in the direction of the wind, series of deformations of the surface appear which, from the point of view of physics, can be termed “waves” only by stretching the definition.
If the sea surface were characterized by an unbroken series of waves of the same amplitude, a chart of the topography of the surface would contain nothing but a series of straight lines showing the alternating wave
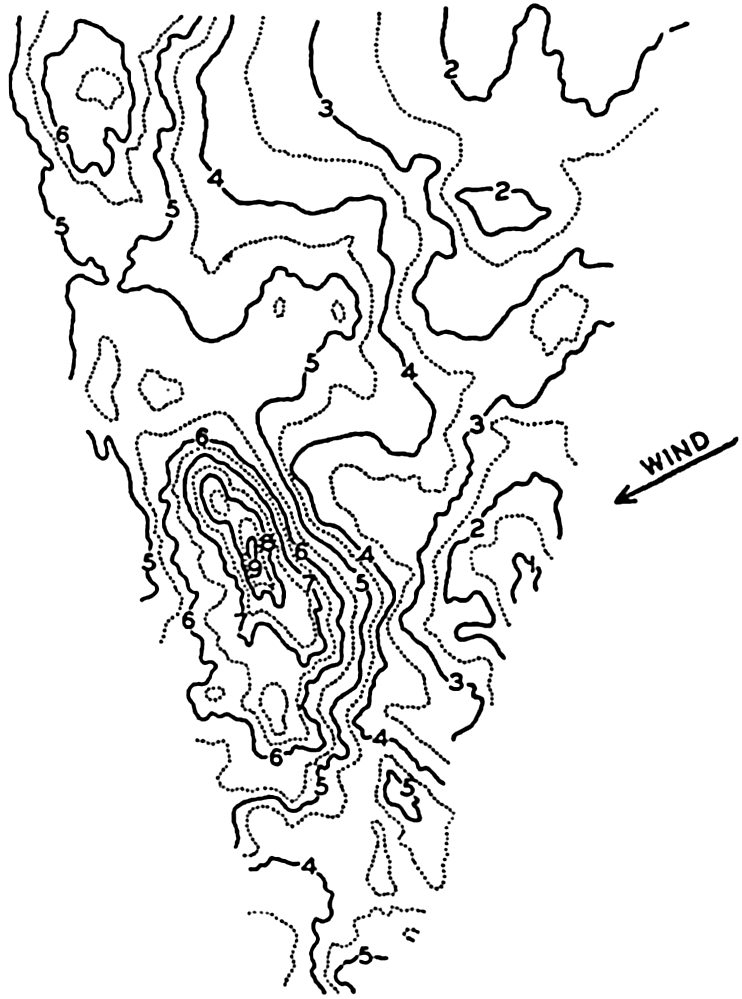
Topography of the sea surface derived from stereophotogrammetric pictures of the sea surface taken on board the Meteor on January 23, 1926, in lat. 59°S, long. 63°4′ W. The state of the sea was recorded as 6, waves as advancing from WSW, wind WSW 7 (Beaufort).
[Full Size]
The most striking characteristic of the picture is not a regular sequence of waves but a great irregularity in topography. A relation to the direction of the wind is evident, however, because the wind was blowing at nearly right angles to the prevailing direction of the contour lines of the surface, but, instead of a long wave crest running at right angles to the wind direction, there are two separate heights, one of which is very steep. This irregular appearance, the “cross sea” (Kreuz See) is more common in the open ocean than the swells with long crests, which are more conspicuous near the coast, where series of long waves may roll against the beach in rhythmic sequence.
In spite of the irregular appearance of the sea, it is possible to apply the terms wave period, wave height, and wave length, because some of the waves will be more conspicuous than others and their characteristics can be observed. As has already been stated, the general theory of waves on the surface of the sea leads to a simple formula for the wave velocity:
Of the three interrelated quantities, c, T, and L, the wave period T can probably be most easily determined by using the method which was proposed by Cornish (1934) and which consists in recording the time intervals between appearances of a well-defined patch of foam at a sufficient distance from the ship. The same method can be used on the coast, where, in addition, the interval between breakers can be accurately timed. A simple device for recording the movement of a floater on a rotating drum has been used with success at the end of the Scripps Institution of Oceanography pier (Shepard and La Fond, 1940). At sea the wave length is mostly estimated on the basis of the ship's length, but this procedure leads to uncertain results, because it is often difficult to locate both crests of the wave relative to the ship and because of disturbances due to the waves created by the movement of the ship. The most satisfactory measurements are made from a ship that is hove to. Another method consists in letting out a floater as a wave crest passes the stern of the ship and recording both the length of line paid out when the floater reappears on the crest and the angle that the line forms with the heading of the ship. The velocity of the wave can be found by recording the time needed for the wave to run a measured distance along the ship. If the period is also determined, the wave length is found from the simple formula L = cT.
A large number of measurements have been made at sea in order to establish the relationship between the wave period, the wave length, and the wave velocity. Critical examination of the methods employed has been made, especially by Cornish (1912, 1934), and a number of average results have been compiled by different authors. Table 68 contains one of the compilations made by Krümmel, from which it is evident that the observed values are in fair agreement with the theoretical expectation.
The longest wave periods observed at sea rarely exceed the value of 13.5 sec, which Cornish reports from the Bay of Biscay. It has been established, however, that the swell reaching the shore may have much longer periods and correspondingly longer wave lengths and greater velocities of progress. The longest period that Cornish has observed is about 22.5 sec, corresponding to a wave length in deep water of about
The theory of waves leads not only to a relation between velocity of progress and the wave length, but also to results concerning the profile of the wave. These results are based on the concepts of classical hydrodynamics and have been derived from the hydrodynamic equations, omitting friction but taking the boundary conditions into consideration. In an ideal fluid the free surface of the waves, according to Stokes' results of 1847 (Lamb, 1932), very nearly take the shape of a trochoid—that is, the curve which is formed by the motion of a point on a disk when this disk rolls along a level surface. If the amplitude is small compared to the wave length, the trochoid approaches in shape a sine curve, but at great amplitude the crests become narrower and the troughs longer. Gerstner's theory of 1802 leads exactly to the trochoid form, but Stokes has pointed out that this theory is not in complete agreement with the concepts of classical hydrodynamics.
| Region | Wave velocity, m/sec | Wave length, m | Wave period, sec | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Observed | Computed from | Observed | Computed from | Observed | Computed from | ||||
|
|
|
|
|
| ||||
| Atlantic Ocean | |||||||||
| Trade wind region | 11.2 | 10.8 | 10.5 | 65 | 70 | 61 | 5.8 | 6.0 | 6.2 |
| Indian Ocean | |||||||||
| Trade wind region | 12.6 | 13.1 | 13.7 | 96 | 88 | 104 | 7.6 | 7.3 | 6.9 |
| South Atlantic Ocean | |||||||||
| West wind region | 14.0 | 15.5 | 17.1 | 133 | 109 | 163 | 9.5 | 8.6 | 7.8 |
| Indian Ocean | |||||||||
| West wind region | 15.0 | 15.2 | 13.7 | 114 | 125 | 104 | 7.6 | 8.0 | 8.3 |
| China Sea | 11.4 | 11.9 | 12.4 | 79 | 72 | 86 | 6.9 | 6.6 | 6.3 |
| Western Pacific Ocean | 12.4 | 13.6 | 14.7 | 102 | 85 | 121 | 8.2 | 7.5 | 6.9 |
Stokes's results lead to the conclusion that at increasing amplitude the wave form deviates more and more from the trochoid. Studies of the stability of waves by Michell (Lamb, 1932) show that the wave becomes unstable if the angle formed by the crest approaches 120°, and that the smallest ratio of height to length is 1:7 (fig. 130). The velocity of progress of these waves is no longer independent of the height; in the case
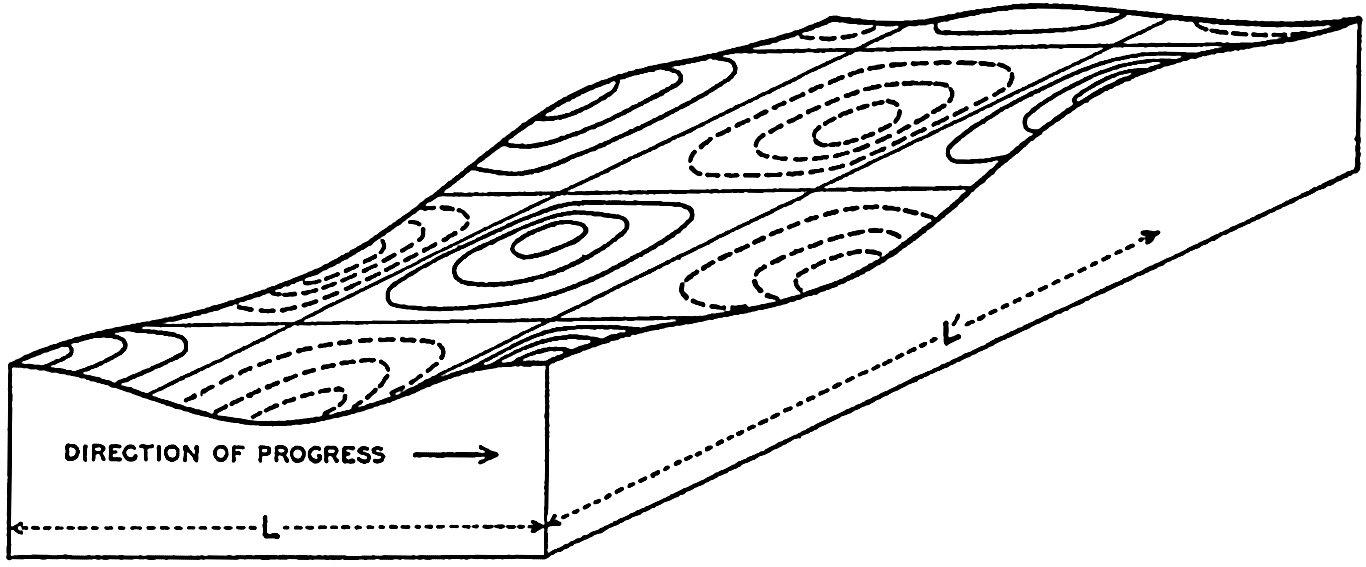
Accurate measurements of actual wave profiles would be very desirable in order to examine the correctness of the above-mentioned theoretical conclusions. Such actual measurements can be based on photogrammetric pictures, but so far only a few such pictures have been evaluated. Fig. 131 (Schumacher, 1928) shows two profiles of the wave the topography of which was presented in fig. 129 and two profiles of other waves that were photographed on the Meteor Expedition. In the figure the trochoids are entered as dashed lines, and it is seen that these curves can hardly be considered as fitting the actual profiles with any degree of accuracy.
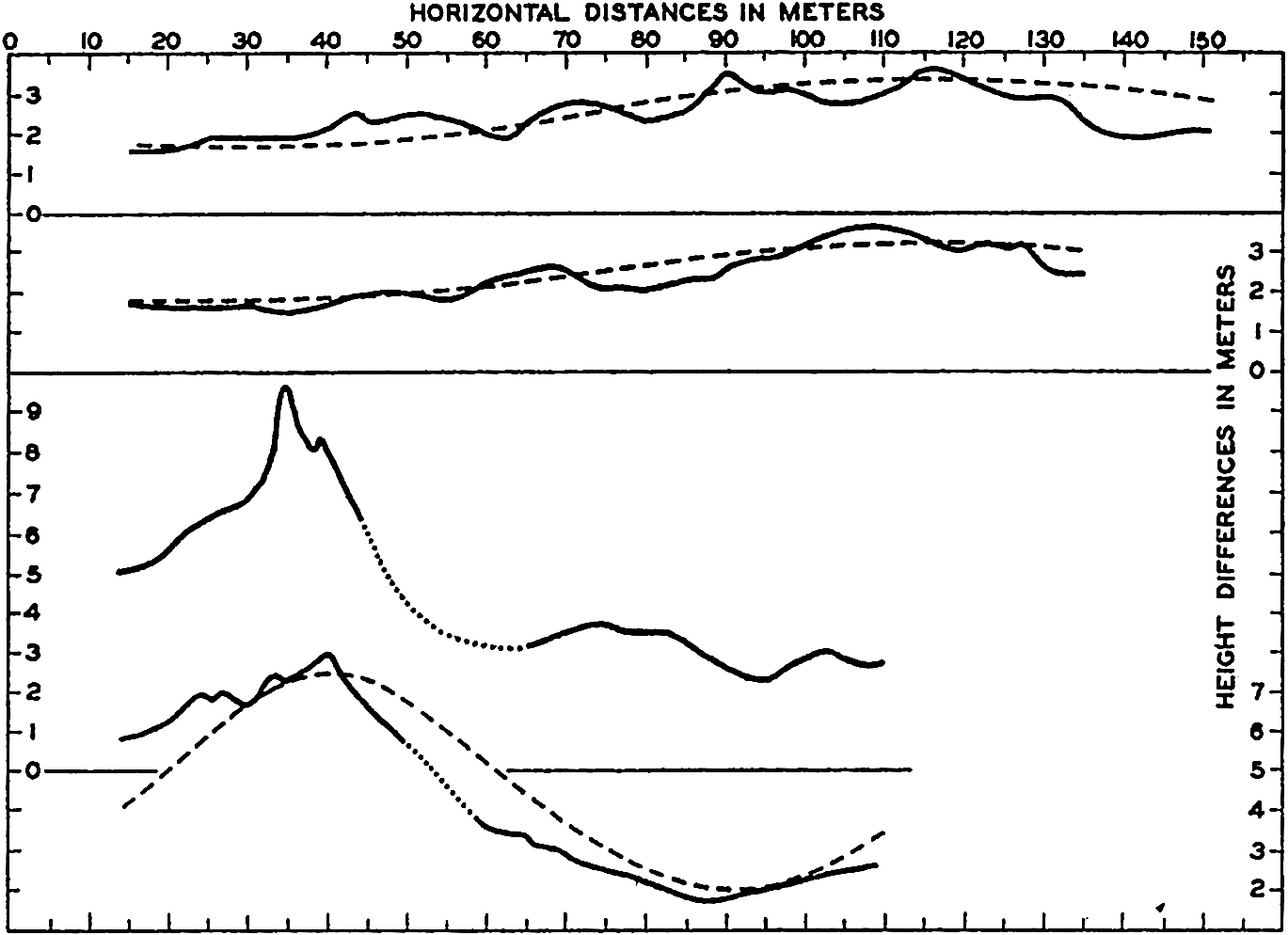
Profiles of waves (vertical scale 5 × horizontal scale) of waves derived from stereophotogrammetric pictures taken on the Meteor. The two lower profiles refer to the wave shown in fig. 129; the two upper profiles refer to waves photographed on July 7, 1926. The waves proceed from right to left. The dashed curves represent trochoids.
[Full Size]
The wave theory also leads to certain conclusions concerning the character of motion of individual water particles. In a wave that has
| Wave characteristics | Velocity of particles in cm/sec at stated depths | ||||||
|---|---|---|---|---|---|---|---|
| Period length (sec) | Velocity of progress (cm/sec) | Length (m) | Height (m) | 0 m | 2 m | 20 m | 100 m |
| 2 | 312 | 6.2 | 0.25 | 39 | 5.2 | 0.0 | 0.0 |
| 4 | 624 | 25 | 1.00 | 79 | 49 | 0.5 | 0.0 |
| 6 | 937 | 56 | 2.00 | 105 | 85 | 11.3 | 0.0 |
| 8 | 1249 | 100 | 5.00 | 196 | 173 | 55.6 | 0.4 |
| 10 | 1561 | 156 | 7.00 | 220 | 203 | 99.0 | 4.2 |
| 12 | 1873 | 225 | 10.00 | 211 | 199 | 114.0 | 12.9 |
| 14 | 2185 | 306 | 12.00 | 273 | 262 | 180.0 | 35.0 |
| 16 | 2498 | 396 | 10.00 | 197 | 190 | 143.0 | 40.6 |
| 18 | 2810 | 506 | 8.00 | 140 | 136 | 109.0 | 40.5 |
| 20 | 3122 | 624 | 5.00 | 78 | 76 | 63.0 | 28.4 |
No measurements are available of the actual motion of water particles in waves. Experience in submarines has shown, however, that the wave motion decreases rapidly with increasing depth. Vening Meinesz has availed himself of this fact and has been able to conduct observations of gravity at sea on board a submarine, making use of pendulums, which can be employed only when the motion of the vessel is small.
As a consequence of the decrease of the particle velocity with depth a small transport of water takes place in the direction of progress. A water particle moves in the direction of progress when it is above its mean depth, and in the opposite direction when it is below its mean depth, but, owing to the decrease of velocity with depth, it moves somewhat faster in the direction of progress than in the opposite direction. Consequently, after having completed one revolution in its orbit, the particle does not return to the point from which it started, but is advanced somewhat in the direction of progress, meaning that an actual transport of water takes place in this direction even in the absence of wind (see U.S. Beach Erosion Board, 1941.)
The irregular appearance of the surface is not accounted for by the theories that have been mentioned so far, but a somewhat better understanding of the pattern of waves is obtained when one takes into account the phenomenon of interference. Two surface waves that travel in the same direction can then be represented by the equations
and the actual appearance of the surface is obtained by adding the displacements due to the two individual waves. If the amplitudes are equal, one obtains If the wave lengths differ by a small amount only, this new equation represents a wave whose length is the average of the two waves of which it is composed but whose amplitude varies between zero and 2a. At the locality where the two waves are in phase, the amplitudes are added, and a wave appears that has twice the amplitude of the two original waves, but, where the waves are in opposite phase, the amplitudes cancel.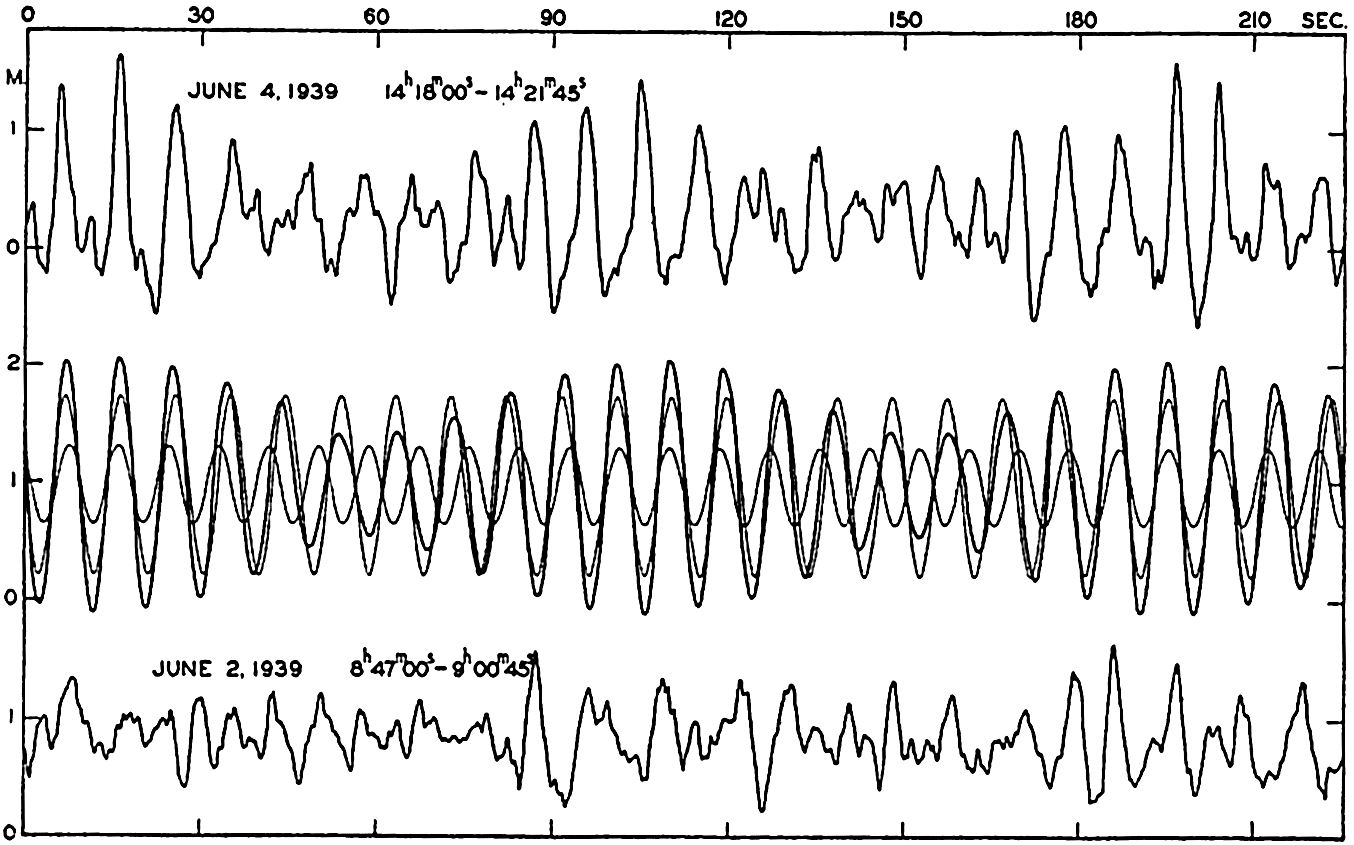
Upper curve: Record of waves at the end of the Scripps Institution pier, showing interference. Middle curve: Computed pattern of wave interference. Lower curve: Example of the ordinary type of records of waves at the Scripps Institution pier, showing very complicated conditions.
[Full Size]
The upper curve in fig. 132, which is a reproduction of a record obtained at the end of the Scripps Institution of Oceanography pier, represents an example of interference of waves of nearly the same period length but of different amplitudes. In the middle portion of the figure are shown two sine curves, one of period 9.6 sec and amplitude 0.75 m, and one of period 8.7 sec and amplitude 0.32 m. The heavy curve presents the wave pattern that would result by interference between the two, and it is seen that this corresponds roughly to the observed pattern. The discrepancies are accounted for partly by the fact that the
These considerations help to explain the occurrence of a sequence of high waves followed by a sequence of low ones, but they do not explain the irregular pattern of waves that is called “cross sea.” Progress towards explaining the typical cross sea, however, has been made by H. Jeffreys (Defant 1929). The waves that have been dealt with so far he called long crested, because the crest of the wave is long compared to the wave length. Mathematically speaking, it is assumed that the wave crests are of infinite length (see equation XIV, 2). Jeffreys has introduced the so-called short-crested waves, which can also travel without altering from and therefore belong to the group of waves that are theoretically possible. These waves can be represented by
where L′ = 2π/κ′ represents the length of the crests (fig. 133). This formula defines a series of waves that travel at a somewhat greater speed than the long-crested ones:According to Jeffreys, the first waves that are generated by the weakest winds must be long crested, but, when the wind increases in velocity, short-crested waves can be formed. The explanation here is that the
In table 68, only wave velocity, wave length, and wave period are listed, with no information as to the wave height. A large number of measurements of wave heights has been made by different methods which, although uncertain, are considered more accurate than the measurements of wave lengths. The wave height can be found if a location on board ship can be selected at which the tops of the waves appear level with the horizon, in which case the wave height is equal to the eye height of the observer above the water line. Another method is based on the records of a delicate barometer, and still another that gives very accurate results makes use of photogrammetric measurements.
The greatest wave heights observed in most oceans are about 12 m. Cornish gives a very vivid description of waves of such height during a storm that he experienced in the Bay of Biscay in December, 1911. On the day preceding the gale a heavy swell with a period of 11.4 sec and an average height of about 6 m came from the northwest. The wind, which had blown as a breeze from the southwest, changed during the night to west-northwest and increased in the morning to a strong gale with velocities up to 23 m/sec. The period of the waves increased to 13.5 sec, corresponding to a length of 310 m and a velocity of progress of 21 m/sec, while the wave height increased to 12 m. There are many accounts of similar large waves. In a hurricane in the North Atlantic in December, 1922, when the wind velocity probably exceeded 45 m/sec, one of the officers of the Majestic reported waves that averaged more than 20 m in height and reached a maximum height of up to 30 m. It is probable, however, that these great wave heights refer to occasional peaks of water that may shoot up to elevations considerably above the general wave height. In the region of the prevailing westerlies of the Antarctic Ocean, wave heights up to 14 or 15 m have been observed relatively often, but the average wave height lies much below these values.
The observations quoted regarding maximum wave height and wave length all refer to conditions far from land. Near the shore, waves created directly by wind do not reach such heights, but the height will depend upon the stretch of water across which the wind has blown—namely, upon the fetch of the wind. Stevenson (Cornish, 1934) has combined the average data into the simple formula h = ⅓ 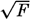 [Equation], where h is the greatest observed wave height in meters and F is the fetch of the wind in kilometers. This formula is valid for small bodies of water, and is
[Equation], where h is the greatest observed wave height in meters and F is the fetch of the wind in kilometers. This formula is valid for small bodies of water, and is
Growth and Dissipation of Surface Waves. In order to explain some of the phenomena concerned here, it is necessary to consider the energy of the waves. This energy can be computed by considering that it is present partly as potential energy and partly as kinetic energy. The computation leads to the result that for long-crested waves the energy per unit area of the sea surface is approximately equal to ½gρa2, where g is the acceleration of gravity, ρ is the density of the water, and a is the amplitude of the wave. For short-crested waves the energy per unit area of sea surface is approximately one half of this amount.
The energy of the waves is transmitted to them by the wind, and, according to Jeffreys, the processes that lead to the generation of waves are also of fundamental importance to their further development. When the wind velocity increases, the pressure exerted on the windward side of the wave will be greater than that on the lee side. Consequently, the waves will increase in height as their energy increases. The energy considerations do not lead to any limit of height to which the waves can grow, but the wave theory itself as developed by Michell (see p. 527) shows that the height cannot exceed about one seventh of the wave length. Thus, if energy is constantly imparted to the waves by the wind without an increase of the wave length, the crests will break and the sea will become covered with whitecaps. However, the longer the wave, the greater height it can reach and thus the greater amount of energy it can absorb from the wind. The wind is able to produce waves of different length, but the shorter will rapidly reach their maximum height and break, whereas the longer will continue to grow. Jeffreys therefore concludes that, “when the waves have travelled a long distance, with the wind blowing them all the time, the longest waves will tend to predominate, simply because they can store more energy.”
However, there is also a limit to the length that waves can attain, because the velocity of progress of the waves increases with increasing wave length and because the wind cannot impart further energy to the waves if they travel at a speed that is as great as or greater than the wind velocity. At a given wind velocity the longest-possible waves will therefore be those that travel at a velocity somewhat below the wind velocity. According to Cornish the speed of the fully developed waves, on an average, is eight tenths of the speed of the wind, but it should be borne in mind that the observed wind velocity depends upon the height at which it is measured. Information is still lacking as to the relation between the velocity of the wind directly over the sea surface and the velocity of the waves.
It also follows that the greatest wave velocity cannot exceed the velocity of the wind that created the waves, assuming that a surface wave continues to proceed at a constant speed after leaving a region of strong winds. Theories developed by Poisson and Cauchy (Lamb, 1932), however, lead to the conclusion that the wave length and therefore the velocity of progress and the period of a surface wave increase in course of time. The velocity of progress of the swell reaching the coast, according to these theories, should be greater than the velocity of the waves that were directly created by the wind. Krümmel (1911) quotes a single observation that may support these conclusions, whereas Cornish (1934) emphasizes the fact that no breakers have been observed of such period lengths that their velocity of progress in deep water would exceed observed wind velocities. Breakers with a period of 20 sec, corresponding to a velocity of progress of about 30 m/sec, were observed on the coast of the English Channel on December 29, 1898, and Cornish points out that prior to the arrival of these breakers a gale had been reported in mid-Atlantic in which the force of the wind had probably exceeded 35 m/sec, which was about 5 m/sec greater than the speed of the waves. He considers it probable that these waves were formed within the area of the gale and traveled for a long distance at their original speed.
Cornish also points out that in the open ocean the existence of long swells can be obscured if shorter waves of greater height are present at the same time. He illustrates his point by a graph similar to the one shown in fig. 134. It is here assumed that two waves are present: one long swell, curve A, and one wave that has only one third the period of the swell but twice the amplitude, curve B. By interference of these two waves, the surface takes the appearance shown by the heavy curve C. An observer would get the impression in this case that the waves present were of the same period as the shortest waves but of variable height, a phenomenon which is often recorded. The long swell may therefore very well be obscured by shorter waves.
A number of studies have dealt with the relation between the wind velocity and the maximum wave height, and between the steepness of the waves and their velocity of progress. In instances in which the quantities to be correlated have not been directly measured, use is made of the equations (p. 525), which give the theoretical relations between wave velocity, wave length, and wave period.
Cornish's empirical results regarding the highest waves can be summarized as follows:
where W is the wind velocity. By means of the equations on p. 525, one obtains H = 0.48 W, which states that the highest wave heights are proportional to the wind velocity. Zimmerman's empirical results (Patton and Marmer, 1932) are L = 10.62 H4/3 = 3.55 W4/3, giving H = 0.44 W, in good agreement with the results of Cornish as to the relation between wave height and wind. Krümmel, on the other hand, arrives at the conclusion that the maximum wave heights are greater than those corresponding to a linear relationship, and Rossby and Montgomery (1935) have for theoretical reasons suggested a formula of the type where G is a nondimensional constant. Introducing G = 0.3, they find that this formula fits the available data fairly well at high wind velocities.The steepness of the waves is generally expressed by means of the ratio of wave length to wave height, L/H, which is inversely proportional to the steepness but can be used as a measure. Cornish's relations lead to the formula L/H = 0.85 W, but this formula is evidently not valid at wind velocities much below 10 m/sec, because the steepest possible waves have a ratio L/H = 7. Zimmerman's values give L/H = 8.1 W⅓. These two results are in qualitative agreement, because both indicate an increase of the ratio L/H with increasing wind velocity. They are also in agreement with Jeffrey's explanation of the growth of waves, according to which one must expect L/H to be greatest for the longest waves. Schott, on the other hand, found that the ratio L/H decreased with increasing wind velocity, but Krümmel (1911), in discussing a large number of observations by Paris, found the ratio to be constant. The ratio between the length and the height of the waves appears to vary between 10 and 20 m when a fresh wind blows, but in the case of the swell the ratio may lie between 30 and 100. Observations from lakes indicate that there the ratio varies between 10 and 12.
A similar confusion exists regarding the relation between wave velocity and wind velocity. As already stated, Cornish found c = 0.8 W, but from Zimmerman's relation it follows that c = 2.35 W⅔. According to the latter equation the wave velocity is greater than that of the wind up to a wind velocity of 13.2 m/sec, and it is smaller when the wind is above that value, in disagreement with energy considerations, which
All these discrepancies indicate that wave height, wave profile, and velocity of progress are not dependent upon the wind velocity alone at the time of observation, but may also depend upon the length of time the wind has blown, the state of the sea when the wind started blowing, and the dimensions of the area over which the wind blows. Comprehensive observations are needed for clearing up these questions.
It has been mentioned (p. 532) that the wave height depends upon the fetch of the wind, and that for small bodies of water a simple empirical relationship has been established between maximum wave heights and the dimensions of the body. This formula is valid to a distance of 1000 to 1500 kilometers, at which the maximum wave height characteristic of the open ocean, about 12 m, may be reached. The fact that greater wave heights are rarely observed may be due to the circumstance that the wind systems mostly have dimensions smaller than 1500 kilometers, so that in the open ocean the actual fetch of the wind will be, at most, 1500 km, or it may be that a longer fetch of the wind tends more toward increasing the length of the waves than toward increasing their height.
The differences in energy of long-crested and short-crested waves and of large and small waves have to be considered in the discussion of what happens to waves when the wind stops blowing. Owing to the smaller energy per unit area the short-crested waves will be destroyed more rapidly by friction, and the largest of the long-crested waves stand the best chance of surviving for a long time. It is also probable that the dissipation of energy is more rapid within the steeper waves, for which reason the steeper and shorter waves will be destroyed more rapidly than the longer and less steep. Thus, one should expect that, outside of the region in which the wind blows, long-crested swells will become more and more dominating, and at considerable distances from the wind areas only long-crested swells will be present. These conclusions are in good agreement with observed conditions.
Waves Near the Coast. Breakers. When waves approach the coast, a number of things happen. In the first place it is conspicuous that the short-crested cross sea disappears at some distance from the coast and that mainly long-crested rollers reach the beaches. Jeffreys has been able to show that this transformation is associated with the change in form and dissipation of energy that take place when surface waves enter shallow water. One of the characteristic deformations which take place is that, when the depth decreases, originally symmetrical waves become unsymmetrical, the front of the waves becomes steeper, and, finally, the waves break. This effect is more pronounced in the case of the short-crested waves, and the latter will, therefore, break at a greater
Another effect of the decrease of depth is related to a decrease of the wave velocity. The part of the wave that first approaches the coast is slowed down, but the outer portion of the wave still advances with great velocity, wherefore the direction of the wave front is turned, and a wave that approaches the coast at an angle may be turned in such a way that the wave front becomes nearly parallel to the coast.
Still another effect is related to the fact that when approaching shallow coastal waters the waves are transformed into types which are intermediate between surface waves and long waves (p. 519). The waves of long period take on some of the characteristics of long waves at a greater distance from the coast than do those of short period. Consequently the movement of the water particles of the long-period waves will reach to the bottom at a greater distance from the coast, although the height of these waves may be smaller than that of the short-period waves. This circumstance may have considerable bearing on sand movement caused by waves in shallow water.
The breaking of the wave is primarily related to change in the velocity of progress when the wave reaches shallower water (see Defant, 1929). As a consequence of this change, the wave front becomes increasingly steeper until it breaks. Friction may also play a part.
When a wave breaks near the shore, another wave type, known as a wave of translation, may develop. This wave, which was discovered and studied by Russell (Lamb, 1932), is characterized by having only a crest and no trough. The motion of water particles is only in the direction of progress, and the water particles are therefore displaced forward as the wave passes. It is formed when a mass of water is suddenly added to still water, and may therefore be produced as the crest of a breaking wave topples over and crashes down on the water surface in front. This wave type is unimportant in the open sea, but may be prominent on a shallow coast.
Certain phenomena that appear to be associated with breakers are not yet understood. The existence of undertow has not been satisfactorily explained, and is doubted by some observers (Shepard and La Fond, 1939). The rip currents which flow away from the coast through the breakers and which may carry swimmers far out from the beach also have not been fully explained, but it is probable that these currents are associated with surface transport of water against the beach by the waves (Shepard et al, 1941).
The destructive effect of breakers has been the subject of intensive studies, particularly by engineers, but cannot be discussed here. Interested readers are referred to some of the general works that are included in the list of literature.
Long Waves
Standing Waves in Bays. Seiches. In bays, standing waves may develop which are similar to the oscillations in lakes. These waves are known as seiches, and were first studied by Forel (Defant, 1929; Thorade, 1931) in the Lake of Geneva. They are free oscillations of a period that depends upon the horizontal dimensions and the depth of the lake and upon the number of nodes of the standing wave. The wave length will be of the same order of magnitude as the length of the lake, and, as the length of a lake is usually great compared to the depth, the waves will have the character of long waves.
A long wave that proceeds in water of constant depth in the positive or negative x direction must satisfy the equations of motion and continuity in the form (p. 425 and p. 432)
if frictional forces and the deflecting force of the earth's rotation are neglected. Here dvx/dt has been replaced by ∂vx/∂t, because in the case of a long wave ∂vx/∂x, can be considered a small quantity. The vertical displacement of the surface is called η, and ∂η/∂x is therefore the inclination of the free surface. Introducing the horizontal displacement ξ, one has vx = ∂ξ/∂t, and the above equations take the form These equations are satisfied if where the velocity of progress of the wave, c = σ/k, is equal to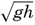 [Equation].
[Equation].Equations (XIV, 11) define two waves that progress in opposite directions. The equations of motion are therefore also satisfied by a superposition of two waves that proceed in opposite directions and for which the velocity of progress is c:
and For a free oscillation the antinodes of a wave in a closed basin must be located at the ends of the basin, where only vertical motion can exist.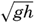 [Equation],
[Equation],
It is readily seen that n is the number of nodes of the standing wave. The standing wave of the longest period is the one that has only one node and the period
This relation, derived by J. R. Merian in 1828, is known as “Merian's formula.” In fig. 128, (p. 517), is shown a standing wave with two nodes.In applying this very simple theory to actual oscillations of the water in lakes, considerable modifications must be made, because the shape of a lake deviates very much from that of a rectangular basin of constant depth. Crystal (Defant, 1925) has developed the theory of standing waves in basins of different shapes, and more recently Defant (1925) has introduced a convenient method of determining the possible periods of oscillation in lakes by means of a numerical integration of the hydrodynamic equations. Defant's method can be directly applied to lakes or bays of any shape and permits the computation of periods, the relative magnitudes of vertical displacements, and the position of nodal lines. Defant's reasoning as presented in his book of 1929 will be briefly summarized here.
In a basin of variable width b, and variable cross-section area S, the equations of motion and of continuity can be written in the form
The vertical and horizontal displacements are supposed to vary periodically:
Replacing the differentials in equation (XIV, 16) by the small quantities Δξ and Δη, one obtains
These equations can be used for a stepwise computation of the displacements if it is possible to determine independently an approximate value of the period of the free oscillations. If then one cross section after another is considered, and if these cross sections are placed close together, it can be assumed that the changes of the displacement from one cross section to the next are linear, in which case equation (XIV, 18) can be written
where α = (4π2/gT2)Δx and where the quantities indicated by subscript 1 and subscript 2 represent the values for two successive sections, and where vi is the surface area of the sea between the sections i − 1 and i. The quantity q0 is equal to zero.The period T for any given basin can be computed in the following manner. First, an approximate value of T is found by means of formula (XIV, 15), introducing the average depth of the basin. The result is an approximate value of α. At the end of the basin at which the computation begins (x = 0), the horizontal displacement must be zero, and for the vertical displacement an arbitrary value can be selected. In this manner the boundary condition at the one end is fulfilled. By means of equation (XIV, 19), one can now, step by step, compute the displacements for all cross sections of the basin, and, if the approximate period that was derived by means of formula (XIV, 15) is correct for the simplest seiche, the computation must give the value ξ = 0 at the other end of the lake in order to fulfill the boundary condition. The computed value will usually differ from zero, and hence it is necessary to select another value of the period and to repeat the entire computation. If this new value does not lead to a correct result, one has to select a third one, but as a rule it is possible to select the first two values of the period in such a way that the correct one lies between them and can be determined by suitable interpolation. The final result will give relative values of the displacements and the exact locations of the nodal line. In a similar manner, one can find the period of an oscillation with two nodal lines and fix their location. Figure 135 shows the computed displacement of seiches in Garda Lake, according to Defant.
So far, only lakes have been considered. In a bay that is in open communication with a large body of water, horizontal flow can take place through the opening. For a rectangular bay the simplest form of a standing wave will be that which has a nodal line across the opening and
If the opening of the bay is very wide, it is necessary to introduce a correction that increases the period. The increase is 32 per cent, according to Rayleigh (Thorade, 1931), if the width of the bay equals the length, but is reduced to about 10 per cent if the width is one tenth of the length. Actual experimental verification of this theory has not been obtained.
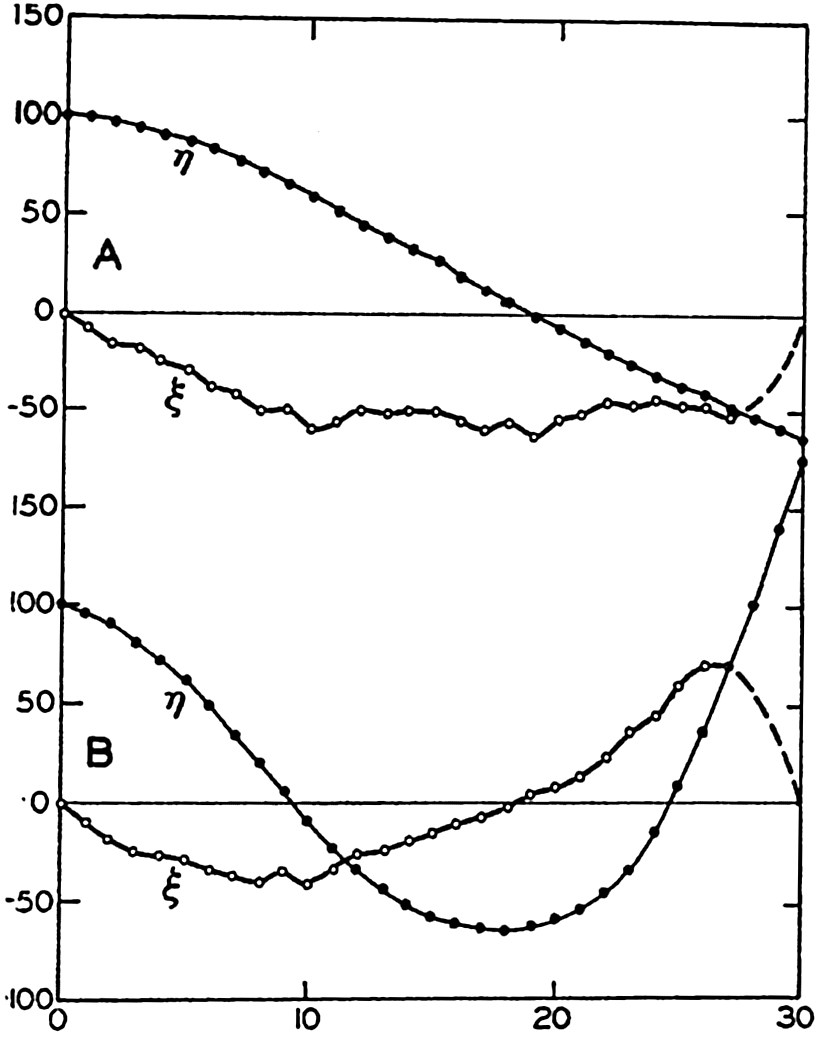
Oscillations of the Garda Lake, according to Defant. Relative values of the vertical and horizontal amplitudes are indicated by η and ξ. Upper curves marked A show the oscillation with one node of period T1 = 39.8 minutes; lower curves marked B show oscillation of two nodes of period T2 = 22.6 minutes.
[Full Size]
In a canal that is open at both ends, standing waves can also be present, but these must be such that nodal lines are located at the two openings of the canal. The longest possible period of a standing oscillation is therefore the same as the period of a lake of similar shape, but in a lake antinodes are located at the ends of the lake, whereas in a canal nodes are found at the ends.
The period and the character of the oscillation in bays or canals can be found by Defant's method, taking the proper boundary conditions into account. In a bay the vertical displacement must be equal to zero at the opening, and in a canal it must be equal to zero at both openings.
Seiches occur commonly in bays, as is evident from records of tidal gauges in such localities. Studies of oscillations in bays along the coast of Japan have been conducted by Honda, Terada, Yoshida, and Isitani
The causes of such oscillations are not fully understood. It should be observed, however, that only a small amount of energy is needed for producing standing oscillations in a body of water and for maintaining them. Very weak periodical variations in wind or barometric pressure may therefore produce seiches if these variations are of a period length corresponding to one of the possible free oscillations. It has also been shown by J. Proudman and A. T. Doodson (Defant, 1929) that a sudden change of wind or a rapid variation in pressure may cause oscillations that will gradually die out because of friction.
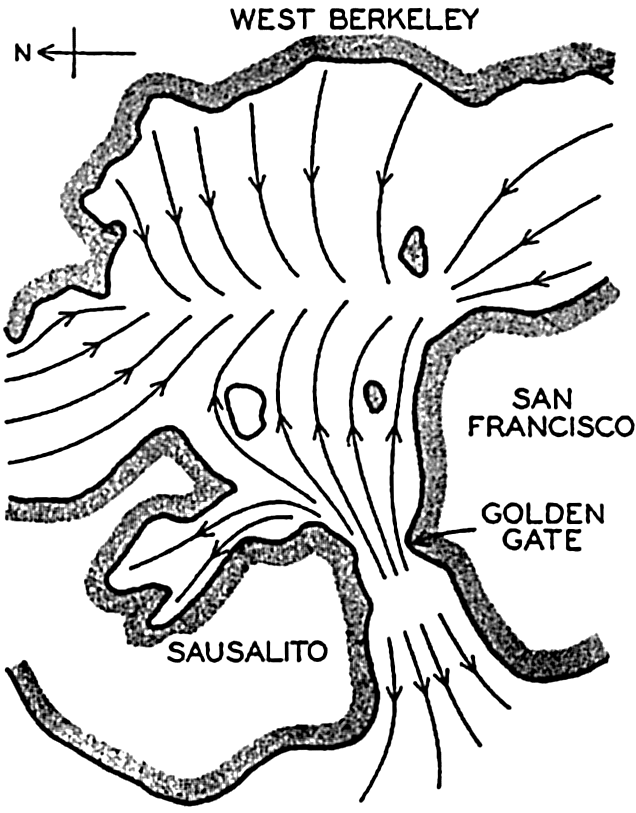
Oscillation with three nodes in San Francisco Bay, according to experiments by Honda, Terada, Yoshida, and Isitani.
[Full Size]
Seiches do not appear to be confined only to bays, but occur frequently on practically open coasts. As an example, Patton and Marmer (1932) mention that at Atlantic City, on the open coast of New Jersey, heavy winds will frequently bring about a seiche oscillation with a period of about 15 minutes. They assume that this seiche represents an oscillation of some part of the wide embayment of the coast between Nantucket Island and Cape Hatteras. The theory of such seiches has been developed by Hidaka (1935).
Destructive Waves. The waves that occasionally inundate low-lying coasts and cause enormous damage are considered here, although they are commonly known as “tidal waves.” However, they have nothing in common with the tides, but the name “tidal wave” has become so firmly established in the English language that the popular use will probably be continued in spite of the unfortunate confusion to which it gives rise. The destructive waves known as tidal waves are caused by
Waves in the sea caused by earthquakes are of two different types. In the first place a submarine earthquake may produce longitudinal oscillations that proceed at the velocity of sound waves. When reaching the surface, such longitudinal oscillations will be felt on board a ship as a shock that violently rocks the vessel. The shock may be so severe that the sailors believe their vessel has struck a rock, and several such reported “rocks” were indicated on early charts in waters where recent soundings have shown that the depth to the bottom is several thousand meters. There are many ship reports dealing with shock waves, particularly from regions in which seismological records show that submarine earthquakes are frequent. Explosion waves of this character usually occur as independent phenomena, but occasionally they are accompanied by the release of large amounts of gases that rise toward the surface and may lift the surface up like a dome, thus producing a transverse wave that behaves like any other gravitational wave. Observations of this kind of waves are rare, but it is possible that ships which have been lost at sea have been completely destroyed by such enormous disturbances. A wave of this nature spreads out from the place where it is formed and decreases in amplitude. By the time it reaches the coast, it has usually become so reduced that it does not cause much damage.
Destructive waves caused by earthquakes, dislocation waves, or “tsunamis” are in general associated with submarine landslides which directly create transverse waves. These waves may reach enormous dimensions both in the open sea and near the coasts, and they proceed as ordinary long gravitational waves. Many records exist of such waves which, near their origin, have caused enormous damage by completely inundating low-lying areas and which have subsequently traversed the entire Pacific or Atlantic Ocean. Thus, the great damage caused by the earthquake at Lisbon on November 1, 1755, was mainly due to the gigantic wave which was set up and which continued across the Atlantic Ocean, reaching the West Indies as a “tidal wave” 4 to 6 m high. In Japan, similar earthquake waves have on many occasions brought great destruction and have led to the loss of many lives. As an example, it may be mentioned that in 1703 more than 100,000 persons lost their lives when the coast of Awa was flooded. Among the most discussed waves are those that accompanied the eruption of the volcano Krakatao in the Sunda Strait on August 26 and 27, 1883. Several waves occurred after the different eruptions, and the highest ones caused great devastation on some of the East Indian Islands, where more than 36,000 persons lost their lives and where the waves in certain localities must have reached a
These waves proceed, as already stated, as long gravitational waves and their velocity of progress should therefore, over a uniform bottom, be equal to 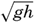 [Equation]. Where the depth to the bottom is variable, the velocity of progress will be somewhat less than
[Equation]. Where the depth to the bottom is variable, the velocity of progress will be somewhat less than 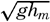 [Equation] where hm is the average depth, but it has been found that the velocity of progress is smaller than should be expected even if variations in depth are considered. In spite of this circumstance, the study of the rate of propagation of these waves served to give an idea of the average depth of the ocean prior to the time of deep-sea soundings. Thus, in 1856, A. D. Bache computed the average depth of the oceans to be about 4000 m, whereas Laplace had assumed an average depth of about 18,000 m.
[Equation] where hm is the average depth, but it has been found that the velocity of progress is smaller than should be expected even if variations in depth are considered. In spite of this circumstance, the study of the rate of propagation of these waves served to give an idea of the average depth of the ocean prior to the time of deep-sea soundings. Thus, in 1856, A. D. Bache computed the average depth of the oceans to be about 4000 m, whereas Laplace had assumed an average depth of about 18,000 m.
The period length of tsunamis varies between 15 and 60 minutes (Krümmel, 1911, Gutenberg, 1939). Where the depth to the bottom is 200 m, the velocity of progress of a long wave (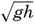 [Equation]) is 44.2 m/sec, and with a period length of 30 minutes the wave length is 79.5 km. The corresponding maximum particle velocity is independent of the wave period and equals
[Equation]) is 44.2 m/sec, and with a period length of 30 minutes the wave length is 79.5 km. The corresponding maximum particle velocity is independent of the wave period and equals  [Equation] η0/h (p. 565), where η0 is the amplitude of the wave and h is the depth to the bottom. With the above numerical values the maximum particle velocity becomes equal to 0.22η0. The energy of the wave per unit area of the surface is ½gη02, and, thus, equal to that of surface waves or tides of the same amplitude.
[Equation] η0/h (p. 565), where η0 is the amplitude of the wave and h is the depth to the bottom. With the above numerical values the maximum particle velocity becomes equal to 0.22η0. The energy of the wave per unit area of the surface is ½gη02, and, thus, equal to that of surface waves or tides of the same amplitude.
Destructive “waves” caused by wind are of an entirely different nature. In this case one has to deal, not with the effect of a wave, but instead with inundations which are caused by the ocean waters being swept up against the coast by violent storms. Abnormally high water levels caused by strong winds are frequent on many coasts, but fortunately the sea level rarely rises so much that great damage occurs. The most destructive storm “wave” known in the history of the United States is that which practically destroyed Galveston on September 8, 1900. A West Indian hurricane approached the coast of the Gulf of Mexico, where at Galveston the barometric pressure fell from 996.2 millibars, (29.42 inches) at noon to 964.4 millibars (28.48 inches) at 8:30 P.M. At the same time the wind velocity increased to 45 m/sec (100 miles per hour) at about 6:00 P.M., when the anemometer was broken to pieces. It has been estimated that the average wind velocity between 6:00 and 8:00 P.M. must have been about 55 m/sec, or 120 miles per hour. During the day of September 8 the water rose steadily but slowly until the wind had reached hurricane force, when a much more rapid rise took place. In the evening the water level was nearly 5 m (15 feet) above mean high
The hurricane that on September 21, 1938, struck the coast of New England brought an even higher water level in many localities, but did not cause so much loss of life. At Buzzard's Bay the highest water level ranged from 4 to 5 m above mean low water, and at Fall River it was reported that “the water came up rapidly in a great surge,” rising to about 6 m above normal. More than 600 persons lost their lives in the hurricane, and the property damage was estimated at $250,000,000 to $330,000,000, although only part of this damage was due to destructive waves (Tannehill, 1938).
Tides
The longest waves known in the ocean are those associated with the tidal movement, which manifests itself on the coast by the rhythmic rise and fall of the water and, particularly in sounds and narrow straits, by the regularly changing tidal currents. The wavelike character of the phenomenon is readily recognized by means of an automatic tide gauge, which records the actual sea level as a smooth curve with alternating maxima and minima. It is also recognized in connection with tidal currents in a strait, because these currents show a regularly alternating motion characteristic of waves. The rise and fall of the water and the accompanying currents should therefore be dealt with together, because they are only different manifestations of the same phenomenon. However, for practical reasons, it is of advantage to deal with them separately and, following common usage in English, to refer to the rise and fall of the water as the “tide,” and to the accompanying currents as “tidal currents.”
Since a knowledge of tides is of particular value to navigation, there exists an enormous literature dealing with the phenomenon, partly in the form of theoretical studies, partly in the form of extensive series of observations and discussions of them, and partly in the form of popular treatises. The tidal currents have also been dealt with extensively, although they are less readily observed than the tides and even more difficult to examine theoretically. The literature on tidal currents, however, is also very large. Only a brief outline of the tidal theories and of the character of tides and tidal currents will be presented here. (Reference made to Darwin, 1911; Krümmel, 1911; Marmer, 1932.)
Tide-Producing Forces. Tides are caused by the attraction of the moon and sun. In a given locality the tide is of a complicated character, but any tide can be shown to consist of a number of partial tides, each of which is related to the motion of the earth relative to the moon and the
Considering the moon and the earth only, let the mass of the earth be equal to unity, and the mass of the moon equal to m. The gravitational attraction of the moon at the center of the earth is then proportional to m/r2, where r is the distance from the center of the moon to the center of the earth (fig. 137). This distance remains constant, on an average, and the attraction of the moon on the earth must, therefore, on an average, be balanced by a centrifugal force that is directed away from the moon and is also proportional to m/r2.
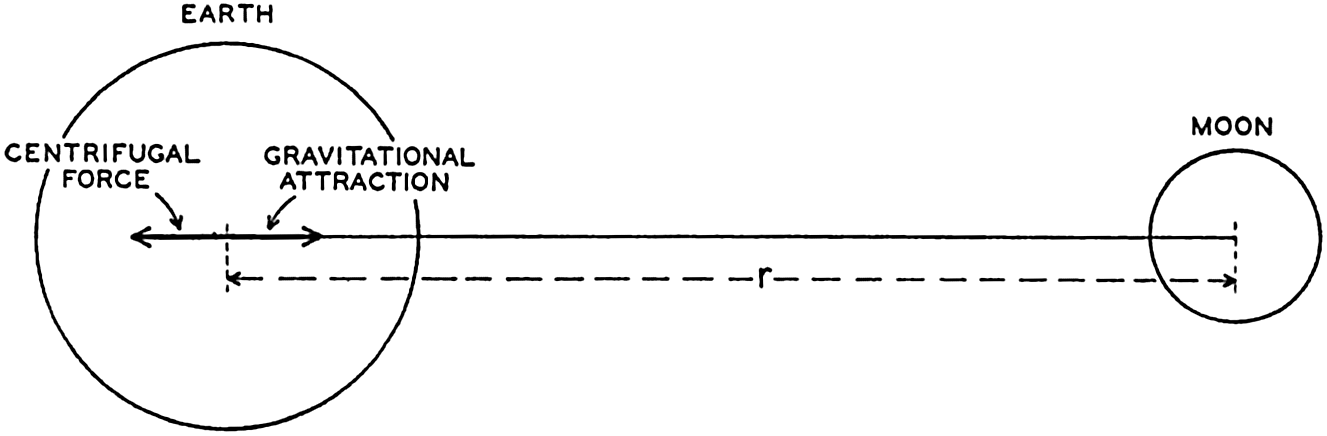
Schematic representation of the gravitational attraction between the earth and the moon and the centrifugal force which balances the attraction.
[Full Size]
The centrifugal force acting on any particle on the earth is the same, but the attraction of the moon varies. Consider a point at the surface of the earth lying on the line which joins the centers of the two bodies. At this point the attraction of the moon is proportional to m/(r − ρ)2, where ρ is the radius of the earth. The difference between the attraction of the moon at this point and the centrifugal force is proportional to m/(r − ρ)2 − m/r2, or to 2mρ/r3, because ρ/r is a small quantity. The numerical values are m = 1/81.45, r = 60.34ρ. Owing to this difference the moon's attraction tends to raise the surface of the earth at the point under consideration, but at the same point the attraction of the earth acts and is proportional to 1/ρ2. Thus the ratio between the disturbing force of the moon and the attraction of the earth is equal to 2mρ3/r3 = 1.176 × 10−7. The attraction of the earth, on the other hand, equals the acceleration of gravity, and thus the tide-producing force of the moon is only about 1.176 × 10−7 times the acceleration of gravity; that is, at the point under consideration the acceleration of gravity is reduced by the amount 0.000115 cm/sec2.
Consider next a point at the surface of the earth but opposite to the moon. At this point the attraction of the moon is less than the centrifugal force and is proportional to m/(r + ρ)2. The disturbing force is again found from the difference
Now take a point at the surface of the earth at right angles to the line joining the centers of the moon and of the earth. At this point the attraction of the moon is of the same magnitude as the attraction at the center of the earth, m/r2, but is directed, in fig. 138, along the line PM. The centrifugal force is parallel, however, to the line EM, and the resultant of these two forces is directed toward the center of the earth and is proportional to mp/r3. In this case the disturbing force leads to an increase in the acceleration of gravity of 0.00058 cm/sec2.
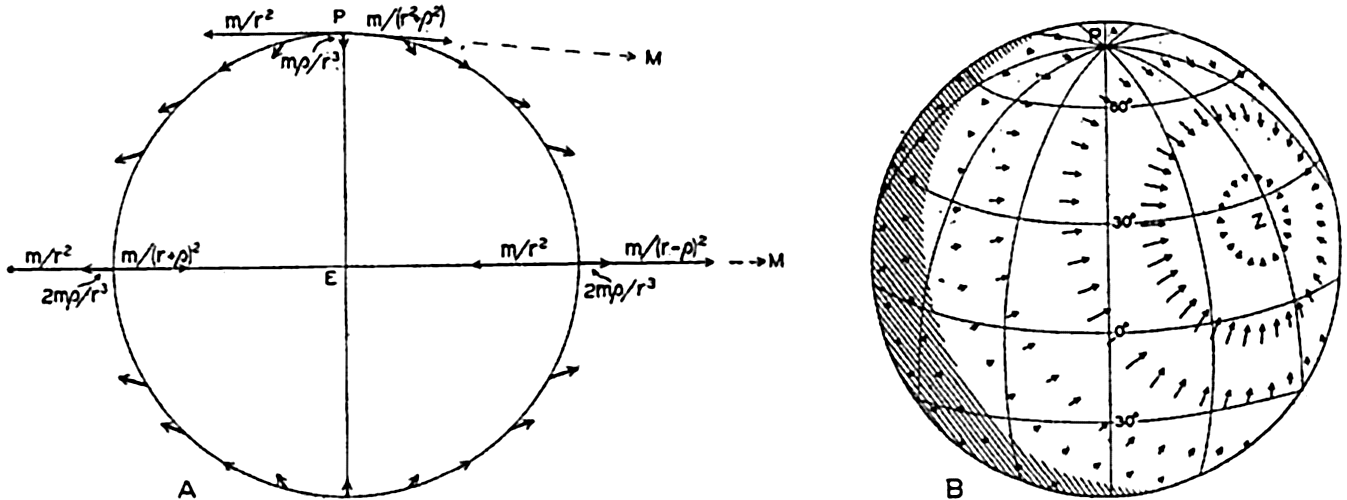
(A) Schematic representation of the tide-producing forces in a plane through the line joining the centers of the earth and the moon. (B) Distribution of horizontal tide-producing forces over the earth (according to G. H. Darwin). The moon is at zenith above the point marked Z.
[Full Size]
If a point were selected at random on the surface of the earth, one would find that generally the disturbing force forms an angle with the surface of the earth different from 90° and can therefore be considered as having a vertical component and a horizontal component along the earth's surface (fig. 138). The complete theory leads to the following equations for the vertical and horizontal components of the disturbing forces:
Here θ is the angle between the line joining the centers of the moon and the earth and the line from the center of the earth to the point on the earth's surface that is being considered. In fig. 138 are shown, according to G. H. Darwin (1911), the distribution of the horizontal componentsExactly similar reasoning can be applied if one considers the sun and the earth, but for numerical computations the mass of the sun and the distance between the sun and the earth must be entered. Using the same units as before, one finds that the mass of the sun is equal to 333,400 and that the distance is 23,484p. With these values, one finds that the maximum tide-producing force of the sun is only about 0.46 times that of the moon. The greater distance between the sun and the earth more than balances the effect of the greater mass of the sun.
By considerations of this nature, it is easily shown that no other heavenly body can produce tides on the earth. The closest planets are too small to have any effect, and the large planets are too far away.
The motion of the sun and the moon relative to the earth is so complicated that the system of tide-producing forces changes greatly in the course of time, but the patterns are repeated in regular sequence.
From the graphs in fig. 138 it is seen, for instance, that the field of the moon's tide-producing forces is symmetrical with respect to the poles of the earth if the moon stands above the Equator—that is, when the declination of the moon is zero. In this case, when the earth rotates around its axis, the components of the tide-producing forces will in all latitudes show two equally high maxima and two equally low minima during 24 lunar hours, a period that represents the time interval between two culminations of the moon, or 24.84 solar hours. To an observer on the earth the field of tide-producing forces appears to rotate around the earth in 12 lunar hours. The declination of the moon varies, however, during one month from about 28°S to about 28°N, meaning that at the greatest southern declination the moon passes through zenith in about lat. 28°S, and at the greatest northern declination the moon passes through zenith in about 28°N. In these positions of the moon the field of tide-producing forces is no longer symmetrical with respect to the poles of the earth. At the Equator the two diurnal maxima of the tide-producing forces still remain equal, but in all other latitudes one of the maxima will be less pronounced than the other during a complete revolution of the earth. To an observer on the earth the field appears to be composed of two fields, one that rotates twice in 24 lunar hours, and one that rotates once in the same time. Instead of continuing these reasonings, which would become very involved owing to the many variations in the relative positions of moon, sun, and earth, one can arrive at a complete picture by introducing a series of fictitious heavenly bodies that will each bring about a symmetrical field of tide-producing forces and by considering the total field as composed of all of these partial fields.
Assume first that there is an ideal moon that always remains in the equatorial plane and at any locality passes the upper meridian at intervals
Similarly, one could introduce other fictitious bodies, but the resultant angular velocities of the principal components of the tide-producing forces can all be derived from a small number of characteristic velocities:
The angular velocity of earth relative to the stars, g = 15.0411°.
The angular velocity of the rotation of the moon around the earth, s = 0.5490°.
The angular velocity of the movement of the long axis of the elliptic orbit of the moon, which completes one rotation in 8.85 years, p = 0.0046°.
The angular velocity of the motion of the earth around the sun, e = 0.04107°.
The angular velocities of the different components which together form the actual field of tide-producing forces can be obtained by combinations of these. Thus the angular velocity of the field due to the ideal moon that was first considered is 2(g − s) = 28.984°.
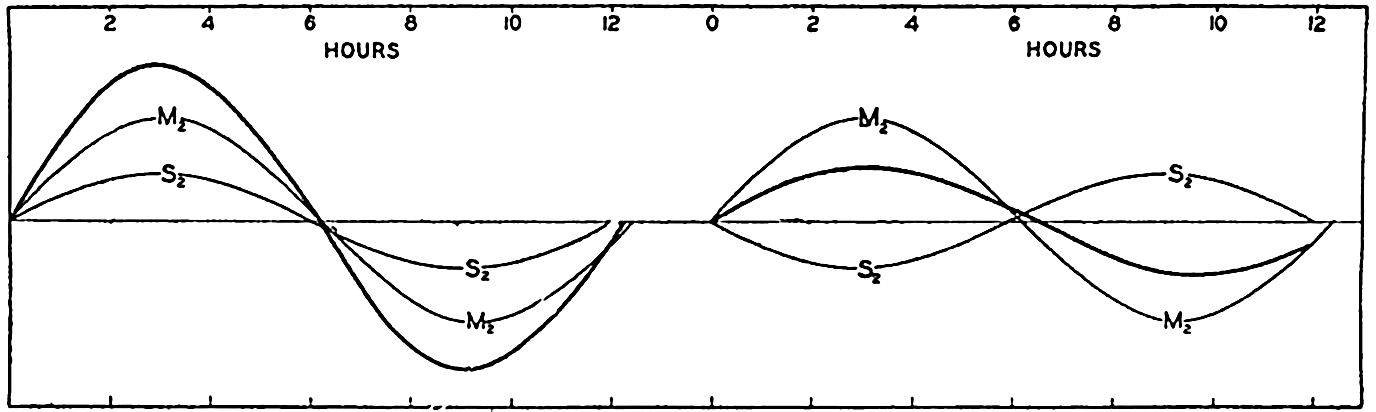
The complete analysis makes it possible to compute coefficients that are related to the intensities of these different partial fields. The significance of these coefficients will be explained. Analysis of tides shows that to these partial fields there are corresponding partial tides that have all received characteristic names and symbols. Table 70 contains the names of the more important semidiurnal, diurnal, and long-period partial tides, their symbols, their periods and angular velocities, and their so-called coefficients.
Thus, the components of the tide-producing forces in a given latitude can be represented by equations of the form
| Name of corresponding partial tide | Symbol | Period in hours | Angular velocity | Coefficient | |
|---|---|---|---|---|---|
| Symbol | In degrees per hour | ||||
| Semidiurnal: | |||||
| Principal lunar | M2 | 12.42 | 2(g − s) | 28.9841 | .4543 |
| Principal solar | S2 | 12.00 | 2(g − e) | 30.0000 | .2120 |
| Larger lunar elliptic | N2 | 12.66 | 2g − 3s + p | 28.4397 | .0880 |
| Luni-solar | K2 | 11.97 | 2g | 30.0821 | .0576 |
| Diurnal: | |||||
| Luni-solar | K1 | 23.93 | g | 15.0411 | .2655 |
| Principal lunar | O1 | 25.82 | g − 2s | 13.9430 | .1886 |
| Principal solar | P1 | 24.07 | g − 2e | 14.9589 | .0880 |
| Long-Period: | |||||
| Lunar fortnightly | Mf | 327.86 | 2s | 1.0980 | .0783 |
| Lunar monthly | Mm | 661.30 | s − p | 0.5444 | .0414 |
| Solar semi-annual | Ssa | 2191.43 | 2e | 0.0821 | .0365 |
Theories of Tides. In the preceding section the tide-producing forces were discussed, but no reference to the actual tides was made except in the content of table 70, in which were listed the partial tides corresponding to the more important tide-producing forces. Two different theories have been advanced as to how these forces can bring about tides, of which the first, the equilibrium theory, is mainly of historical interest and has been replaced by the dynamic theory. The equilibrium theory, which was first developed by Newton, is so often referred to, however, that its principles should be mentioned.
Assume first that the rotation of the earth relative to the moon is such that the same side of the earth always faces the moon. In this case the field of tide-producing forces, which was derived on p. 547 and shown in fig. 138, would remain stationary relative to the earth. The tide-producing forces would lead to a permanent reduction of the acceleration of gravity at the points of the earth nearest to and farthest away
Since the reduction of the acceleration of gravity at the points nearest to and farthest away from the moon is 2mρ/r3, the value of the acceleration of gravity is in the same units: 1/ρ2 − 2mρ/r3. This reduced value is found at a small distance h above the undisturbed surface, where the acceleration of gravity is 1/(ρ + h)2 = 1/ρ2 − 2h/ρ3. Therefore
If at the point nearest to and farthest away from the moon the undisturbed surface were raised to this height, there would be equilibrium, and the greatest elevations of the new equilibrium surface above the undisturbed surface would be 35.6 cm. Similarly, the greatest depressions would be half that amount, or 17.8 cm.The equilibrium theory assumes that these flood protuberances are actually formed and that the highest portions of the protuberances lie at the points nearest to and farthest away from the moon. However, the earth does not always have the same side turned toward the moon, but rotates relative to the moon once in 24.84 hours. Each flood protuberance therefore appears to travel once around the earth in 24.84 hours, and, because there are two protuberances, the time interval between the passages of flood protuberances will be 12.42 hours. Similar flood protuberances will be caused by the sun and by the irregularity of the motion of the moon and the sun, and the actual tides should appear as the combined result of such a series of protuberances, the heights of which would be proportional to the coefficients in table 70. The obvious criticism that can be directed at this theory is that the movement of a flood protuberance over the surface of the earth cannot take place unless water masses actually change position, but consideration of the movement of the water has been completely disregarded. Other objections to the theory need not be discussed here.
The dynamic theory is based on the fact that only the horizontal tide-producing forces are of importance to the movement of the water. The vertical tide-producing forces are unimportant because they can be considered as consisting of very small periodical variations of the acceleration of gravity. It has previously been shown that the distance between isobaric surfaces in the sea depends upon the acceleration of gravity, and it is evident that variations of the latter must lead to variations of the distances between isobaric surfaces. Where the depth to the bottom is
The general equations of the dynamic theory, which were developed by Lagrange, lead to problems mathematically so difficult that they have not yet been solved so far as the tides of the oceans are concerned. Instead, the application of the dynamic concept has followed two different lines. In the first place, the theory of tides in basins of defined geometrical shape has been developed, particularly by Proudman and Doodson; in the second place, tides in natural basins have been studied mainly by Sterneck and Defant by methods of numerical integration of the hydrodynamic equations. Both methods have helped toward an understanding of the observed phenomena, but here only the latter approach will be dealt with, because it leads to direct comparisons between theoretical results and observed conditions, and because it does not require any lengthy mathematical presentation.
Tides in relatively small bodies of water that are in communication with the open sea have much in common with seiches, and can therefore be discussed in much the same manner. The tides, however, differ from the seiches in the respect that they are forced oscillations of periods which must coincide with the periods of the impulses by which they are maintained, whereas the periods of the free oscillations depend only upon the geometrical shape of the bay.
The similarities and differences between tides and seiches are brought out by considering the oscillations in a long, rectangular bay of constant depth. Any wave in such a bay must fulfil the equations of motion and continuity. It was shown on p. 538 that, when the earth's rotation and friction are neglected, these equations are satisfied by
These equations must always hold, and, in addition, certain boundary conditions must be satisfied. These conditions depend upon whether one considers a free oscillation or an oscillation of the same period as an oscillation of the body of water with which the bay communicates, a cooscillation. In the case of a free oscillation in a bay of length l the boundary conditions were x = 0, ξ = 0, and x = l, ξ = 0, and from these
(A) Character of cooscillating tides in bays corresponding to different values of v. (B) Character of independent tides in bays corresponding to different values of v. (According to Defant.)
[Full Size]
For the independent tide which is produced directly by the tidal forces, it is necessary to add on the right-hand side of the equation of motion (XIV, 9) a periodic force: x = f cos (σt + ∊). With the boundary conditions x = y = 0, ξ = 0, and x = l, or y = 1, η = 0, one obtains
Again, resonance occurs if v = 1, 3, 5, …; otherwise the number of nodes depends on the value of v. Fig. 139B (Defant, 1925) shows the character of the independent tide corresponding to different values of v.So far, a rectangular bay of constant depth has been considered. For a bay of irregular shape and varying depth, one can start from the equations of motion and continuity in the form (XIV, 16) and can determine the character of the cooscillating and the independent tides by means of a numerical integration similar to the one developed by Defant (p. 539) for determining the free oscillation of the water in a basin (Defant, 1925). In all cases the character of the forced oscillation depends upon the relation of the period of the forced oscillation to that of the free. It can be shown that in general the increase of the range of the tide due to narrowing and shallowing is relatively small, and that very high tides at the ends of bays are, as a rule, a result of resonance.
In the preceding discussion, tide-producing forces have been considered which act in the direction of the long axis of the basin, and it has been assumed that at any given time the force is the same at all cross sections. If the basin is large, it may have to be taken into account that transverse forces exist, causing transverse oscillations, or that at a given time the force varies in the longitudinal direction.
The introduction of friction leads to further complications. In a free oscillation the period is increased by the effect of the friction, but the period of the forced oscillation must always remain equal to that of the force and cannot be altered by friction. The result is that no complete resonance can develop, because the greater the amplitude of the wave becomes, the greater is the effect of friction and the greater the increase of the period of the free oscillation. The ratio v can in these circumstances never remain at the value, 1, 3, 5, …, but can stay near one of these values.
Another effect of friction alters the character of the forced waves. In the absence of friction the cooscillating tide can be considered as a wave in a basin of constant depth which proceeds with constant amplitude and is totally reflected at the closed end of the bay. In the presence of friction the amplitude of the “incoming” wave decreases in the direction of progress, and the reflected wave has therefore a smaller amplitude
Even greater complications arise when the effect of the rotation of the earth is considered. Such consideration is necessary in most cases, since a comparison of the magnitude of the acting forces shows that the deflecting force cannot be neglected when dealing with tidal phenomena, because their period length is of the order of magnitude of a pendulum day (p. 520).
In order to get some idea of the modifications that arise owing to the rotation of the earth, it is necessary to return to the complete equations of motion and to consider not only the vertical and horizontal displacements, but also the horizontal velocities to which no attention has been paid so far. If the depth is constant, if friction is neglected, and if γ = 2ω sin ϕ, the equations of motion and continuity take the form
Two solutions of these equations can easily be written. Consider first an infinitely long canal of constant width b. If the x axis is placed in the direction of the canal, the boundary conditions y = 0, vy = 0, and y = b, vy = 0 must be fulfilled, because at the walls of the canal the motion can be in the x direction only. With these boundary conditions, one obtains in the Northern Hemisphere
where, as previously, c =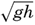 [Equation].
[Equation].This solution, which was first given by Lord Kelvin (Lamb, 1932), defines a wave, the Kelvin wave, which proceeds in the x direction with the velocity c and is characterized by great amplitudes on the right-hand side and by small amplitudes on the left-hand side. At high water, when the current flows in the direction of progress, the wave crest slopes down from right to left, and the component of gravity acting down that slope is exactly balanced by the deflecting force of the earth's rotation acting in the opposite direction. At low water the directions of the slope and the current are reversed. The forces again balance each other, and the
Another solution, given by Sverdrup (1927), is applicable to a wave that proceeds in an unlimited sea, provided that γ = 2ω sin ϕ can be considered constant:
where s = γ/σ and where nowThese equations define a wave that has horizontal crests like an ordinary long wave, but a velocity of progress that has been increased in the ratio 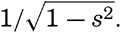 [Equation]. At the same time the motion of the water particles is no longer alternating back and forth, but is rotating, because, in addition to the velocities in the direction of progress (the longitudinal velocities), transverse velocities also exist. The ratio between the maximum longitudinal and transverse velocity is 1/s, and the latter reaches its maximum one fourth of a period after the longitudinal velocity was at its maximum. The character of these currents will be dealt with later, and attention will be focused here on the wave itself.
[Equation]. At the same time the motion of the water particles is no longer alternating back and forth, but is rotating, because, in addition to the velocities in the direction of progress (the longitudinal velocities), transverse velocities also exist. The ratio between the maximum longitudinal and transverse velocity is 1/s, and the latter reaches its maximum one fourth of a period after the longitudinal velocity was at its maximum. The character of these currents will be dealt with later, and attention will be focused here on the wave itself.
The velocity of progress of the wave becomes infinite when s = 1 and imaginary when s > 1. Now, s = γ/σ = (Tt/12) sin ϕ, where Tt is the period of the tide in hours. Thus, c becomes infinite when Tt = 12/sin ϕ, or, if sin ϕ = 1, when Tt = 12; that is, on a disk which rotates once in 24 hours, waves of this type cannot exist if the period of the wave is greater than half the period of rotation of the disk. Applied to the earth, the meaning is that waves of this type cannot exist if their period is longer than one half pendulum day. This result is not so significant as it appears to be, because the solution is valid only for an unlimited body of water, and on the rotating earth the limitation of the ocean will make impossible a complete development of this wave type. If a wave proceeds in the longitudinal direction of an ocean, the transverse velocities must vanish along the coasts, but may develop at some distance from the coast. The wave must be of an intermediate type between the Kelvin wave and the wave described here, and can be considered as composed of longitudinal and transverse oscillations, the nature of which cannot yet be expressed analytically.
In a narrow sea, transverse oscillations of the sea level will be present even if no conspicuous transverse currents are developed. The periodic
In the absence of transverse oscillations the tide will be zero along a nodal line, but in the presence of transverse oscillations the tide will vanish at a single point only. Points that have high or low water at the same hour can be joined by lines which are called cotidal lines. These cotidal lines all meet at a point where the tide vanishes, which is called an amphidromic point. An amphidromic point can be caused either by the effect of the earth's rotation or by the interference of two tidal waves.
If a standing oscillation exists in a bay, there are no cotidal lines, because high water occurs at the same time everywhere. However, when transverse oscillations are present which differ from the longitudinal by one quarter period, an amphidromic point is developed that lies on the original nodal line (fig. 140). To the right of the center, high water occurs at the time t = 0, to the left at the time t = ½T, and the other cotidal lines are spaced between these. Thus, the rotation of the cotidal lines around an amphidromic point that is caused by the earth's rotation is, in the Northern Hemisphere, counterclockwise (as shown in fig. 140), but it is clockwise in the Southern Hemisphere. This characteristic may be used for deciding whether or not an observed amphidromic point may be due to the rotation of the earth.
The methods of analysis that have been set forth here have been applied mainly by Sterneck and Defant to the tides in “adjacent seas,” such as the North Sea, the Adriatic Sea, the Red Sea, and others. In the case of the North Sea, from which numerous current measurements are available, other methods developed by Proudman and Defant have been used for deriving a complete picture. The considerations have even found application to the Atlantic Ocean, the principal tides of which have been studied by Sterneck and Defant. Their conclusions will be dealt with when the tidal currents are discussed. In the other oceans, application of the dynamic theories presents enormous difficulties and has not been attempted. The above reasonings are purely qualitative, but G. I. Taylor has succeeded in giving an exact solution for a bay of rectangular
A generalization of the observed conditions has been made by R. A. Harris (1894–1907), who divided the oceans into “oscillating areas,” the period of free oscillation of which would be about 12 or 24 lunar hours if they were enclosed by solid boundaries. The areas were selected so that the observed difference in the time of high water at both ends of the area would be approximately 6 or 12 hours. Within each area one or more nodal lines would be present. This division of the oceans into “oscillating areas” brings a surprising consistency in the otherwise confused picture of the tides, but, as pointed out by G. H. Darwin, it can hardly be accepted as a physical explanation because, among other factors, the rotation of the earth has been disregarded.
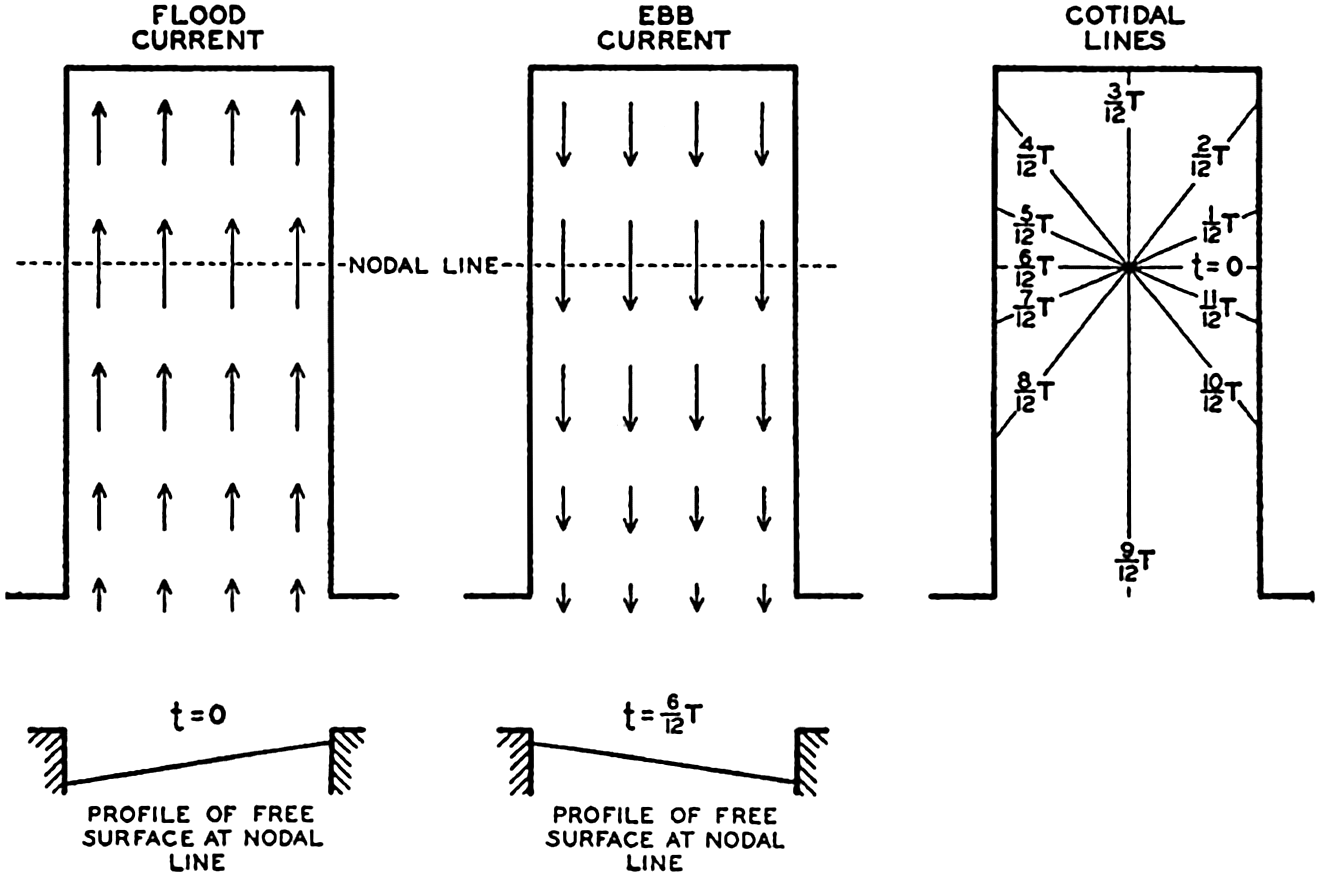
Schematic representation of transverse oscillations in a bay in the Northern Hemisphere leading to the development of an amphidromic point.
[Full Size]
The Character of the Tides. The tide-producing forces can be computed with great accuracy, but the response of the oceans to these forces is too complicated to be determined. Experience has shown, however, that the tides can be considered as composed mainly of a series of harmonic oscillations, or partial tides, having the periods of the tide-producing forces. To these terms must be added, in many localities, annual and semiannual terms which are not related to astronomical forces but which are ascribed to the effect of prevailing winds or changes of sea level due to heating and cooling (p. 459). These long-period tides
The most important tide-producing forces are those of nearly semi-diurnal and nearly diurnal period, for which reason the character of the tide in any locality depends mainly upon the relative heights and phase angles of the partial tides corresponding to these forces. Let us first consider the partial tides due to the semidiurnal lunar forces of a period 12.42 hours and to the semidiurnal solar force of a period of 12 hours. The former will give rise to two high waters and two low waters in 24.84 hours (one lunar day), and the latter to two high waters and two low waters in 24 hours (one ordinary day). Thus, the high water due to the moon will be retarded 0.84 hours every day, or about 50 minutes relative to that caused by the sun. After coinciding on a given day, the partial high waters will move apart, to coincide again when the lunar tide has been retarded 12 hours, or after 12/0.84 = 14.3 days. The semidiurnal tide will be great when the two partial tides coincide and small when they counteract each other (fig. 141). The large tides are called spring tides, and the small tides are called neap tides, and in a locality in which the semidiurnal components are dominating, spring and neap tides come at intervals of 14.3 days. Where the tides are of the semidiurnal type, the ratio between the ranges of the lunar and solar partial tides may be fairly close to the theoretical ratio 1:0.47 (table 70 p. 550), in which case the ratio between the ranges of spring and neap tides is fairly close to 1.47:0.53 = 2.77.
If the tides followed the tide-producing forces, the lunar and solar semidiurnal tides would coincide at full and new moon and would be opposite in phase at the quarters of the moon. In most localities the tides lag somewhat behind the tide-producing forces, and spring tides occur a day or two after full moon and a day or two after new moon. The time difference between the meridian passage of full or new moon and the occurrence of the highest high water is called the age of the tide, and is given in days.
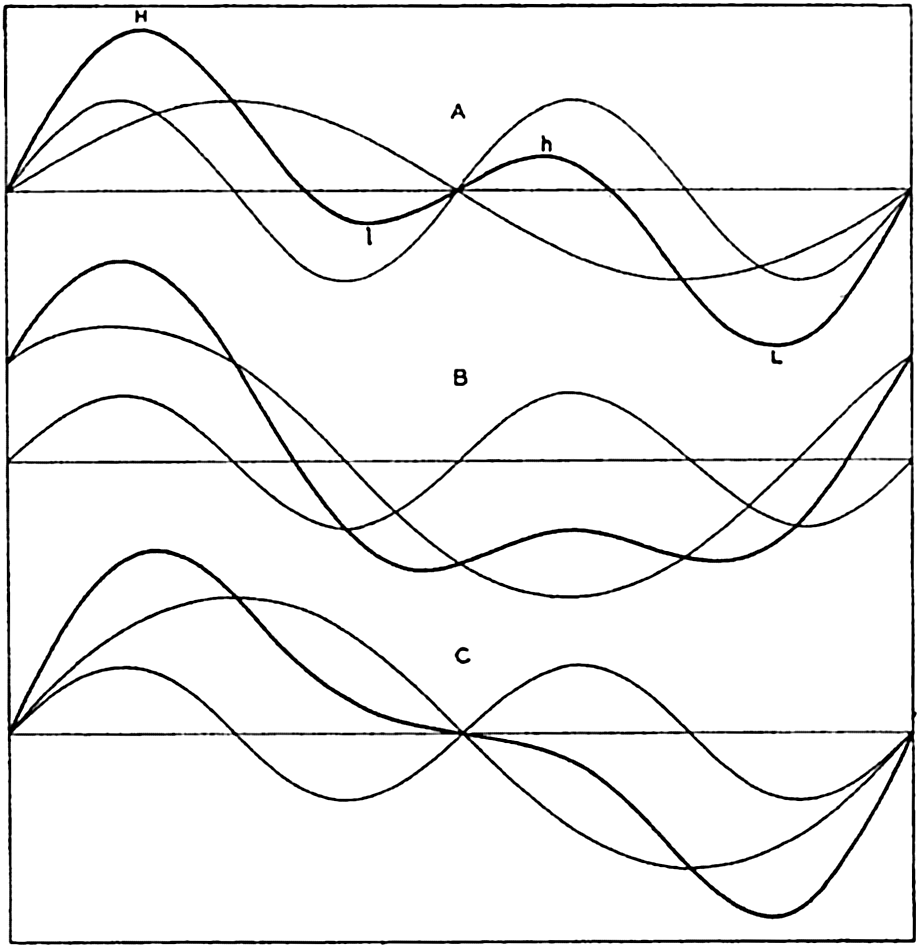
Examples of different types of tides resulting from simultaneous diurnal and semidiurnal tidal components.
[Full Size]
The close relation of the tide to the moon is also demonstrated by the fact that, where a semidiurnal tide prevails, high water always comes at nearly the same number of hours after the moon passes through the upper or lower meridian—that is, after the moon is due south or due north. The mean time difference between the meridian passage of the moon and the occurrence of the next high water is called the mean high water lunitidal interval, and is measured in hours.
Diurnal partial tides greatly complicate the picture, because the tide will depend upon the relative magnitudes of the semidiurnal and diurnal components and upon the time at which these components reach their maxima. Figure 142 illustrates a few possible combinations. Figure 142A shows an ordinary “mixed type” of tide in which one of the two high waters of the day is much higher than the other, and one of the
Figure 142B illustrates a case in which the inequality is found in the high waters only, the two low waters being equally low. Figure 142C illustrates a case in which only one high and one low water occur during the day, because the other high and low water melt together into a period of several hours with nearly constant water level. This particular phenomenon is called the “vanishing” tide.
The examples in fig. 142 were constructed by combining diurnal and semidiurnal tides of different heights and different phase angles. It is evident that different combinations lead to other tide curves in which the diurnal inequality of the tide appears more or less pronounced. The diurnal inequality of the tide varies during a month, because the distribution of the moon's tide-producing force over the earth varies with the declination of the moon. The tides that display the greatest diurnal inequalities are called the tropic tides, since they occur when the moon's declination is at its maximum or at its minimum—that is, when the moon is nearly above the Tropic of Cancer or of Capricorn.
Taking partial tides of other periods into account, and considering the fact that the tide-producing forces vary with the distance from the earth of the moon and the sun, one finds that a nearly unlimited number of possible types of tides exists and that, in any given locality, the type of the tide may change considerably during one month. As a rule, however, the tide has the same characteristics at neighboring stations on an open coast. Detailed information as to the character of the tides in different localities is found in several of the books listed at the end of this chapter.
Several terms used for describing the tide have been defined, but a few more must be added. Mean sea level is the plane about which the tide oscillates (Marmer, 1927). It is determined from tidal observations by averaging the tabulated hourly heights of the tide over a period of several years. Mean sea level does not coincide, as a rule, with an equipotential surface, because, where permanent currents are present, the sea surface always slopes at right angles to the current (p. 391). Mean sea level may also rise or drop along a coast, as is evident from results of precision leveling along the Atlantic coast of the United States (p. 677). Daily, weekly, monthly, and yearly sea level can be derived from observations during a day, a week, a month, or a year. For daily sea level, it is necessary to state how the average has been computed (see Marmer, 1927).
Mean high water is the average height of all high waters over several years, and, similarly, mean low water is the average height of all low waters over several years. The half-tide level lies exactly half way between mean high water and mean low water, and differs as a rule from mean sea level. In localities where the tide shows a considerable diurnal inequality, mean higher high water and mean lower low water are computed from the highest and lowest tides of each day.
In bays and in seas which communicate with the ocean through a relatively narrow opening, the tide may differ from that in the ocean, because the shape of the bay or the adjacent sea may favor the development of certain components of the tide. Modifications due to the rotation of the earth may also arise.
The tide in the English Channel represents an example of the latter modification. The tide there has in part the character of a progressive wave which enters the continental shelf from the Atlantic Ocean and which, as it advances, takes the appearance of a Kelvin wave, with small ranges on the left-hand side, the south coast of England, and great ranges on the right-hand side, the northwest coast of France. On the coast of France the Bay of St. Malo is particularly famous for its large tides, because in the inner part of the bay the range of the spring tide is up to 12 m (39 feet). This enormous range is in part attributed to the narrowing of the bay and the shoaling of the bottom.
The largest known tides occur in the Bay of Fundy, where, in Noel Bay, spring-tide ranges up to 15.4 m (50.5 feet) have been measured. However, this tide can be accounted for in a different manner. In the Bay of Fundy, high water occurs nearly simultaneously all around the bay and, furthermore, it has been found that the strongest tidal currents flow into the bay when the water is rising most rapidly, and out of the bay when the water is falling fastest. These features—the increase in the range of the tides toward the end of the bay, the simultaneous occurrence of high and low water all over the bay, and the maximum currents at mean water—all indicate that in the Bay of Fundy one has to deal with a standing wave.
The range of the tide is, however, not zero at the opening of the bay, for which reason the tide must be of the cooscillating type (fig. 139), and the great increase of the range toward the head of the bay must be due to resonance. An exact computation of the period of free oscillations of the waters of the Bay of Fundy has not been undertaken, but according to rough estimates this period lies between 13 and 11.6 hours (Defant, 1925). Such a period means that in the Bay of Fundy the ratio v = Tf/Tc (p. 553) is probably sufficiently close to unity to bring about resonance, but the increase of range toward the end of the bay may also be augmented by the narrowing and the shoaling of the upper part.
The tides in the Bay of Fundy are remarkable because of their great range, but the increase of the range from the opening to the end of the bay is not greater than in some other localities. The tides of the Adriatic Sea have been examined very thoroughly by Defant and Sterneck, who have found that there the cooscillating tide dominates. The longitudinal semidiurnal tide shows a node at a distance from the opening of about three quarters of the length of the sea, and inside the node the range of the semidiurnal tide increases rapidly. On the other hand, the range of the diurnal tides increases regularly from the opening toward the end, and is, at the end, about four times as great as the range at the opening. The range of the Bay of Fundy tide is also increased about fourfold from opening to end, and this increase represents therefore no exceptional case. By studying fig. 139 it is easily seen that the range of the cooscillating tide must increase from the opening to the end of a bay if the ratio v lies between 0 and 2, and that the increase must be the greater the closer v is to unity. In the Adriatic Sea the transverse oscillations due to the earth's rotation have also been studied, and excellent agreement has been obtained between observations and theory. Interested readers are referred to Defant (1925).
Attempts to represent the tides of a large area on charts encounter considerable difficulty, because the character of tides is known from coasts and islands only, and the data can be combined in many different ways. The first comprehensive representation was prepared by Whewell, who in 1833 published a map of the cotidal lines of all oceans (Marmer, 1926). As explained earlier (p. 557), cotidal lines are lines which join points having high water at the same time, referred to Greenwich or some other standard meridian. Later, charts of cotidal lines were prepared for several smaller areas, and for the Atlantic Ocean the cotidal lines of the semidiurnal and the diurnal tides have been plotted separately. Charts dealing with the partial tides are preferable, because the character of the cooscillating and independent partial tide of any body of water depends on the period of that tide. Similarly, charts showing the range of the tide have more rational meaning when they present partial tides, and charts of this nature have been prepared for some adjacent seas. When dealing with tidal ranges, one should use data from well-exposed stations, since the tide in bays and estuaries may be distorted.
Owing to the uncertainty involved in arriving at a general representation of the tides, it is often necessary to interpret the available data in a certain manner in order to arrive at a consistent picture. The most outstanding example of such interpretation is Harris's division of the oceans into “oscillating areas,” which was mentioned on p. 558. However,
Analysis and Prediction of Tides. Any observed tide curve can be represented, as has already been stated, by means of a series of harmonic terms, the periods of which correspond to the periods of the astronomical and meteorological tides (p. 550). This is true regardless of how complicated the tide is. The coefficients of the different terms can at any given localities be determined with great accuracy by means of harmonic analysis if sufficient data are available. Methods employed in harmonic analysis are described by Schureman (1924). Here it will be mentioned only that the harmonic analysis of tidal data is a complicated process, because many periods have to be considered, some of which differ but little in length. Methods have been developed, however, which permit fairly rapid calculations.
The tide curve can be reproduced with a high degree of accuracy if a sufficient number of harmonic terms have been evaluated. These terms can be used for computation of future tides, since the tide is one of the few geophysical phenomena that repeat themselves with nearly astronomical regularity. The process of computation consists in calculating the tide corresponding to each single term, using the empirically determined amplitudes and phase angles and finally adding the terms, thus constructing a predicted tide curve. The calculation and addition is now made by means of specially constructed tide-predicting machines for preparing tide tables. These machines are operated by the U. S. Coast and Geodetic Survey, Washington, D. C., the British Admiralty, London, and the Deutsche Seewarte, Hamburg. The tide tables, which are issued for each year, give advance information as to the time and height of high water and low water of all commercially important ports of the world. In addition, information is given as to the time difference between high water at principal ports and high water in neighboring localities.
A popular description of the tide-predicting machine of the U. S. Coast and Geodetic Survey is given by Marmer (1926), and a technical description is given by Schureman (1924). Experience has shown that the deviations of the actual tides from the predicted values are mostly small and are due to nonperiodic disturbances caused by winds and shifts in currents.
Tidal Currents
Tidal currents represent the motion of the water particles in the progressive or standing tide waves which on coasts and islands are recognized by the rise and fall of the tide. The tidal currents will therefore be of different character in different areas, depending upon the character
In order to discuss the general character of the tidal currents, it is necessary to repeat some of the equations that have been used previously. Disregarding friction and the rotation of the earth, placing the x-axis in the direction of progress of the tide wave, and assuming constant depth, one obtains the equations of motion and continuity in the form
where vx is the horizontal velocity, g is the acceleration of gravity, and η is the vertical displacement of the surface.For a progressive wave,
and therefore where c =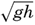 [Equation] is the velocity of progress of the wave.
[Equation] is the velocity of progress of the wave.Thus, the velocity reaches its maximum in the direction of progress at high tide (η = η0) and its maximum in the opposite direction at low tide (η = −η0). The tidal current is alternating, changing its direction every half period.
For a standing wave
wherefore The relation between the tide and the current is best recognized by considering a free-standing oscillation in a rectangular basin of constant depth, h. In this case η(x) = η0 cos kx, and therefore Thus the current is always zero at x = 0, and it is also zero at t = 0 and at t = ½T—that is, at the time of high and low water. It reaches itsThe total horizontal displacement during one half tidal period when the water flows in the same direction, if the maximum tidal current is called V, is
The displacement is also independent of depth.In order to get an idea of the corresponding velocities of the tidal currents and the maximum displacements, we shall consider the tide in a progressive wave of an amplitude (not range) of 100 cm. The corresponding maximum tidal currents in seas of different depths are shown in table 71.
| Semidiurnal tide | Depth (m) | ||||
|---|---|---|---|---|---|
| 100 | 500 | 1000 | 2000 | 4000 | |
| Maximum current {cm/sec | 31.3 | 14.0 | 9.9 | 7.0 | 4.9 |
| {knots | 0.61 | 0.27 | 0.19 | 0.14 | 0.10 |
| Maximum displacement {km | 4.4 | 2.0 | 1.4 | 1.0 | 0.7 |
| {nautical miles | 2.4 | 1.1 | 0.75 | 0.54 | 0.38 |
It appears from this table that in the open ocean the tidal currents cannot reach any appreciable velocities, but measurements demonstrate that the actual velocities are considerably higher than those tabulated, partly because the earth's rotation must be taken into account, and partly for reasons that as yet are unexplained. Before the effect of the earth's rotation is considered, tidal currents in waters of changing depth or changing width will be dealt with.
In a channel of rectangular cross section but variable depth, h, and width, b, the combination of the equations of motion and of continuity can be written (Lamb, 1932, p. 275)
whereFleming (1938) has used this equation for studying the tidal currents on a continental shelf related to a standing wave with a node line parallel to the coast. In this case, b is constant, and one obtains
where x is the distance from the coast and h is the depth. If the amplitude of the wave varies slowly with the distance from the coast, as may be expected if the continental shelf is wide and the water is not too shallow, the maximum velocity of the tidal current is approximately where x is the distance from the coast and h is the depth. It is assumed that x is small compared to the wave length.
Schematic cross section of a continental shelf showing that the ratio x/h is at a maximum near the border of the shelf.
[Full Size]
If the depth is constant, the velocity increases linearly with distance from the coast, but, if the slope of the bottom, x/h, is constant, the velocity is independent of the distance. Generally, the ratio x/h is not constant, and then the tidal currents reach a maximum at the distance x at which x/h is greatest. The profiles of many continental shelves are such that x/h is greatest near the border of the shelf (fig. 143), and the maximum tidal currents may therefore be expected near the border.
These considerations hold true not only in the case of a standing wave, but also, in general, if a transport of water toward the coast takes place during some part of the tidal period and away from the coast during some other part of the tidal period. Therefore they help to clarify some of the characteristics of tidal currents near coasts.
Another question of interest is that of tidal currents where the bottom topography is irregular, showing basins and submarine ridges and peaks. A basin is generally of small dimensions relative to the length of the tide wave (the semidiurnal tide wave is 4200 km long where the depth is 1000 m), and the tidal current, if existing, must therefore be in the same direction in the entire basin during one half tidal period, but such flow would necessitate the presence of ascending and descending motion of considerable velocity at the borders of the basin. If the depth of the basin below the general level of the sea bottom is 1 km and if the width of the area of ascending motion is 10 km, then the average ascending motion would have to be one tenth of the horizontal velocity. This type of flow would be possible in homogeneous
Variation in the width of bodies of water leads to other modifications of the tidal currents. Strong tidal currents through narrow sounds are readily accounted for by the fact that large amounts of water have to flow through these openings during each half tidal period. Consider a bay of surface area A square meters which is in communication with the open sea by an opening whose cross-section area is S square meters. Let the average range of the tide in the bay be 2η0 m. The total volume of water that flows into the bay in the time interval between low and high water is then A × 2η0 m3. The inflow, on the other hand, is equal to 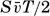 [Equation], where
[Equation], where  [Equation] is the average velocity during the half tidal period (T/2) in which inflow takes place. The maximum velocity during that time is π/2 times the average velocity, but the flow is not uniform through the cross section. Observations have shown that in mid-channel the velocity is about one third larger than the average velocity. Therefore, the maximum velocity of the tidal currents in mid-channel is approximately
[Equation] is the average velocity during the half tidal period (T/2) in which inflow takes place. The maximum velocity during that time is π/2 times the average velocity, but the flow is not uniform through the cross section. Observations have shown that in mid-channel the velocity is about one third larger than the average velocity. Therefore, the maximum velocity of the tidal currents in mid-channel is approximately
As a schematic example, let us consider a bay that has an area of 100 km2 and is in communication with the open sea through a channel that is only 200 m wide and 50 m deep. Let us assume that the range of the semidiurnal tide in the bay is 2 m. Then, in the time interval between high and low water (6.21 hours, or 22,356 seconds), 2 × 108 m3 of water must flow out through the channel, the cross section of which is 104 m2. The average current must therefore be
and the maximum current in mid-channel under the assumed conditions would reach a value of about 180 cm/sec, or 3.6 knots. Tidal currents of such velocity are not uncommon in sounds, and in many narrow straits tidal currents up to 10 knots or more occur at spring tide. Pilot books contain information as to the time and velocity of tidal currents in navigated passages and instructions as to the time when such passages can be made safely by different types of craft.If, in the above example, the opening had been 1 km wide and 100 m deep, the maximum currents at the center of the channel would have been only 0.36 knots. This clearly demonstrates that exceptionally strong tidal currents can be expected only in narrow sounds or inlets. Marmer (1926) has computed the tidal currents at the opening of the Bay of Fundy and found no higher maximum velocities than 1.59 knots, in spite of the tremendous range of the tide at the head of the bay. This result, which is in agreement with observations, clearly shows that strong tidal currents are not encountered at the opening of such bays as the Bay of Fundy, where the cross-section area of the opening is great compared to the surface area of the bay.
The tidal energy can be well illustrated by considering the number of horsepower which can theoretically be developed by tidal currents flowing through a narrow sound connecting a basin with the open sea. The average number of horsepower during one half tidal period, ½T, is equal to gρA2η02/T. With A = 100 km2 and 2η0 = 2 m one obtains 360,000 h.p., but even under the best of conditions only a small fraction of this amount can be actually utilized. Owing to the depth and the width of the opening through which the tidal currents flow, the energy is not concentrated as in a waterfall, but is distributed over a large surface. Furthermore, the tidal power has an intermittent character varying from zero to its maximum value in one quarter tidal period and reaching much higher maximum values at spring tide than at neap tide. This makes utilization on a large scale extremely difficult, but on a small scale tidal power is being used in a few river estuaries. Marmer (1926) computes that theoretically the tides in the Bay of Fundy can produce no less on an average than 200,000,000 h.p., but he adds that by the time the scheme
Neglecting the earth's rotation, the tidal currents are alternating if they are associated with a single standing or progressive tide wave; but if several tide waves are present, interference takes place which may give rise to rotary tidal currents, meaning that the tidal currents regularly change direction and velocity during one tidal period. If the velocities are plotted as vectors from one central point, the end points of the vector will describe a closed curve during one tidal period (fig. 144), and in the absence of other currents the vector sum will be zero.
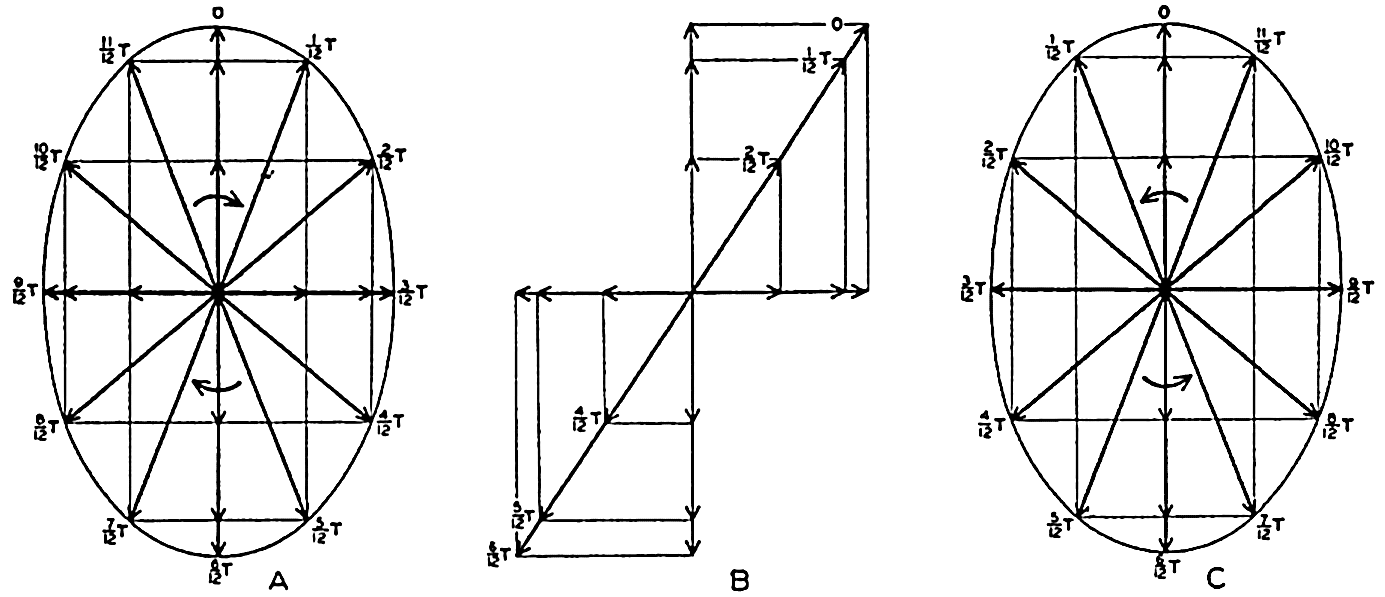
Examples of rotating currents produced by interference of tide waves progressing at right angles to each other and of different phases.
[Full Size]
As a simple case, let us consider the interference between two tidal waves which progress along the positive x and y axes. If the depth is constant, the alternating tidal currents corresponding to the two waves are at the point x = y = 0
where ∊ determines the phase difference between the currents at the time t = 0. Assume first ∊ = 0, meaning that the tidal currents in the x and y directions reach their maximum values at the same time (fig. 144B). In this case the resultant current will also be alternating and will form an angle α with the x axis, which is determined by tan α = η2/η1.Assume next ∊ = π/2, meaning that the maximum velocity in the direction of the negative y axis is reached one quarter period after the maximum velocity in the positive x direction. The result will be a current which rotates clockwise, the end points of the vectors representing
If ∊ = −π/2, similar reasoning leads to the conclusion that the current will turn counterclockwise as shown in fig. 144C. In general, interference of tide waves leads to rotating currents, the direction of rotation being clockwise or counterclockwise, depending upon the phase difference between the two interfering waves, and the ratio between the axes of the resulting ellipse depending upon the phase difference and the amplitudes of the waves.
Except in narrow sounds the observed tidal currents are mostly rotating. If these currents resulted from interference, one should expect to find clockwise or counterclockwise rotation to be equally frequent, but in the Northern Hemisphere, from which most observations are available, clockwise rotation is by far the more common. This fact indicates that the rotary currents are as a rule not caused by interference but by the effect of the rotation of the earth.
On p. 555 are given the equations of motion and continuity which apply to long waves, taking the rotation of the earth into account. Two integrals of these equations have been given—one by Lord Kelvin, which is applicable to a tidal wave in an infinitely long canal of constant width and depth:
and one by Sverdrup, which is applicable to conditions on a rotating disk of infinite dimensions: The former solution defines an alternating current which may be present in a narrow channel, provided that the amplitude of the tide wave varies across the channel according to the formula η = η0e−(γ/e)y. The latter solution defines a current which rotates clockwise in the Northern Hemisphere and counterclockwise in the Southern Hemisphere, that is, cum sole in both hemispheres. The end points of the vectors representing the tidal currents lie on an ellipse, the ratio of the axes of which is equal to s. When s = 1, the velocities become infinite, and at s > 1 they become imaginary. The solution has therefore no meaning unless s < 1. Now,Measurements at lightships have shown that rotating currents occur at a short distance from the coasts, and measurements from vessels anchored in deep water have demonstrated that rotating currents are as a rule present in the open sea. Most of these observations have been made in the Northern Hemisphere where, in nearly all instances, clockwise rotation of the tidal currents has been encountered, whereas a few observations in the Southern Hemisphere have shown counterclockwise rotation. These facts present the best support of the concept that, in general, the rotating tidal currents are due to the effect of the earth's rotation and not to interference, but in some cases interference may complicate the picture. An exact mathematical treatment of the tidal currents of the ocean, however, encounters the same difficulties as the exact development of the dynamic theories of the tides.
As already stated, tidal currents and tides represent two different manifestations of the same phenomenon. When dealing with the tides it was shown that in any locality the tide can be represented by means of a series of harmonic terms having the same periods as the periods of the tide-producing forces. The tidal currents can be represented in a similar manner, but if one deals with rotating currents it is necessary to consider separately two components of the current, say, the N-S and the E-W components. Tidal currents are much more difficult to observe exactly, however, mainly because other types of currents are as a rule superimposed on them, and a great number of data are needed in order to eliminate the superimposed currents and obtain a clear picture of the periodic tidal motion. It can be shown, however, that the tidal currents are closely related to the character of the tide.
It was mentioned that on the Atlantic coast of the United States the tide is of the semidiurnal type, the diurnal components being small. In agreement with this feature it has been found that off the Atlantic coast the tidal currents are also of the semidiurnal type, meaning that during 24 lunar hours the end points of vectors representing the tidal
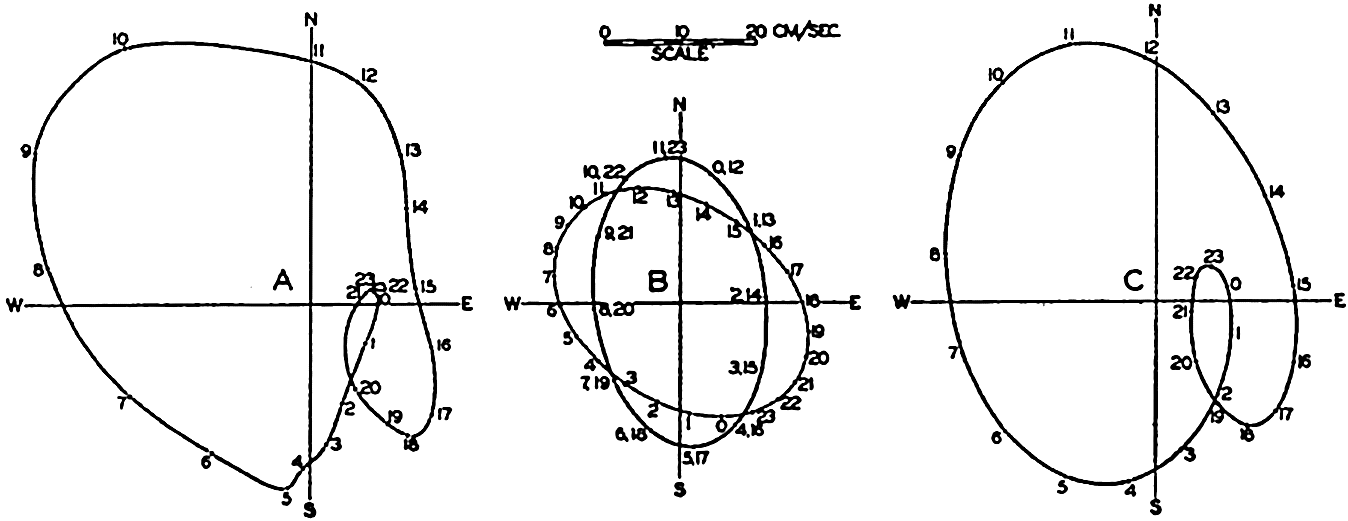
(A) Observed tidal currents at San Francisco light vessel. (B) Semidiurnal and diurnal tidal currents derived from the observations by harmonic analysis. (C) Tidal currents at the San Francisco light vessel computed from the semidiurnal and diurnal currents shown in B.
[Full Size]
On the Pacific coast of the United States the tides are of the mixed type and are characterized by a considerable diurnal inequality. Off that coast, complicated tidal currents are present and in course of a lunar day the end points of the vector representing hourly velocities and directions of the tidal flow describe curves that have no similarity to ellipses but that nevertheless result from the combination of several current ellipses corresponding to tides of different periods. In most instances a good approximation to the observed conditions is obtained by combining the different semidiurnal periods to one single period of length 12 lunar hours and the diurnal periods to a single diurnal period of length 24 lunar hours. This is illustrated in fig. 145, in which the left-hand diagram represents the average tidal currents (Marmer, 1926b) during 24 lunar hours at San Francisco light vessel, which is anchored in 31 m of water at a distance of nine nautical miles from the nearest coast. The representation corresponds to those in fig. 144 except that the arrows have been omitted and only the curve joining their end points is shown. The hours marked along this curve represent the lunar hours after the highest high water at San Francisco, the time of that high water being marked 0h. Harmonic analyses of the semidiurnal and diurnal tidal currents leads to the results which are represented in the middle part of the figure. The semidiurnal and diurnal currents both reach about the same maximum velocities, but the semidiurnal rotates twice in 24 lunar hours, whereas the diurnal rotates once. The diagram to the right has been derived by combining the two, and this diagram is sufficiently like the one to the left to demonstrate that the complicated pattern is mainly a
The periods of the tidal currents are in agreement with the periods of the tide, but no general relationship has been established between the velocities of the tidal currents and the height of the tide. The reason is that the velocities of the tidal currents depend not only upon the height of the tide but also upon the depth to the bottom, the slope of the bottom, and the effect of the earth's rotation. Theoretical consideration of all these variables has not yet been possible and observations of currents are too few to permit the establishment of empirical laws.
Effect of Friction on Tides and Tidal Currents
In shallow water the tide and the tidal currents will be modified by the friction to which the waters are subjected when moving over the bottom. This bottom friction influences the currents to a considerable distance from the boundary surface, owing to the turbulent character of the flow (p. 480).
The effect of friction on the tide can be illustrated by considering a co-oscillating tide in a bay of constant depth and width. In the absence of friction the tide will have the character of a standing wave that can be considered composed of two waves traveling in opposite direction, the incoming wave and the reflected wave. In the presence of friction the tide can still be considered as composed of two such waves, but the combination no longer results in a single standing oscillation because the amplitudes of both waves must decrease in their directions of progress. In general, it can be assumed that the amount of energy that is dissipated is always proportional to the total energy of the wave. If this is true, the friction leads to a logarithmic decrease of the amplitude, provided the depth is constant. Assume that the waves progress in the x direction, that the influence of friction begins at x = 0 and that reflection takes place at x = l. On these assumptions the amplitude of the incoming wave will be (Fjeldstad, 1929)
and of the reflected wave Here μ represents a coefficient of damping. The amplitude of the tide is found by adding η1 and η2, and the result can be written in the formFrom this equation it follows that the oscillation can be considered as brought about by two standing waves of phase difference π/2 or one quarter of a period (p. 552).
Let us consider a bay the length of which is ⅜ L, where L is the length of the wave in the bay. This means introducing l = ⅜ L, kl = ¾ π, and kx = 2πx/L. Let us furthermore assume that at the opening of the bay the tide can be represented by the equation η0 = Z cos σt, which means that at x = 0 the amplitude is Z and high water occurs at t = 0. In the absence of friction the standing wave in the bay will show a node at a distance of one quarter wave length from the opening, and inside of the node high water will occur at t = 6h if the period of the wave is 12h.
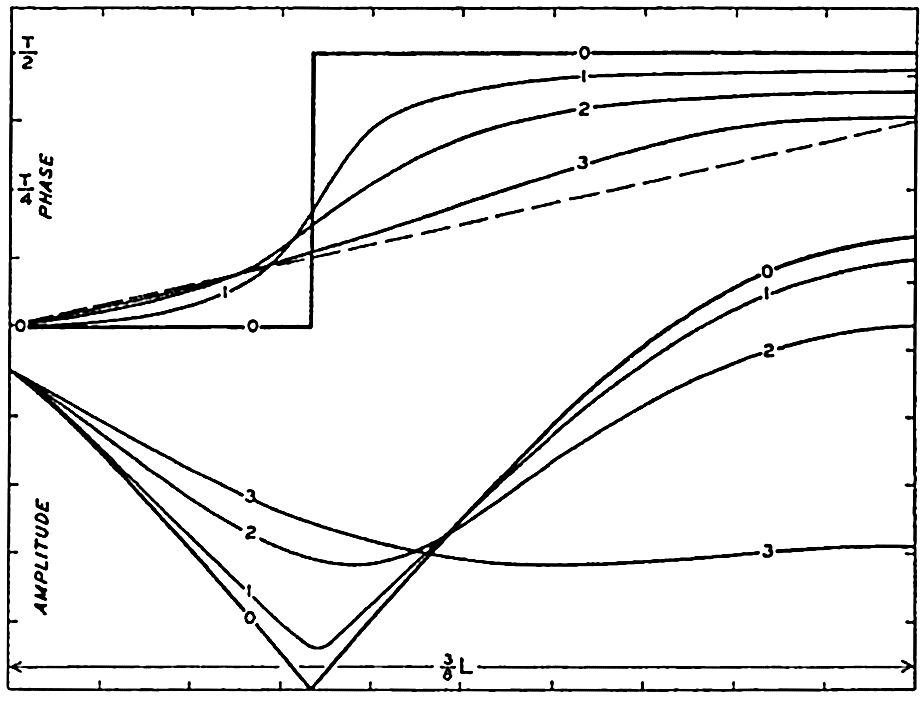
Effect of friction on amplitude and phase of the cooscillating tide in a bay, the length of which is 3/8 of the length of the tide wave.
[Full Size]
The variations along the length of the bay of amplitude and phase are shown in fig. 146, by the curves marked 0. The effect of friction will depend upon the value of μ and, in order to illustrate the effect, we introduce three numerical values μ = 8/(15L), μ = 4/(3L), and μ = 4/L, corresponding to a decrease of the amplitude of the tide wave to one half of its value on a distance equal to 1.17 L, 0.52 L, and 0.17 L, respectively. The corresponding variations along the length of the bay of amplitude and phase of the tide are shown in fig. 146 by the curves marked 1, 2, and 3. The dashed line in the upper part of the figure shows the change in phase on three eighths of a wave length of a progressive wave.
By means of fig. 146 three effects of friction are brought out: (1) the node at which the amplitude of the tide is zero disappears and, instead, a region with minimal range is found; (2) the abrupt change of phase disappears and is replaced by a gradual change; (3) the phase difference between the opening and the end of the bay is decreased and approaches
The most striking example of the influence of friction on tides is found on the wide shelf along the Arctic coast of eastern Siberia. There the tide wave reaches the shelf from the north after having entered the Polar Sea through the wide opening between Spitsbergen and Greenland and having crossed the deep portions of the Polar Sea. Between longitudes 150°E and 180°E the width of the North Siberian Shelf exceeds 300 miles and in the greater part of that area the depth of the water is between 20 and 40 meters. The sea is ice-covered nearly throughout the year and, owing to the resistance which the ice offers, the tidal currents are subjected to frictional influences from the ice on top as well as from the bottom. The total effect of friction is therefore so great that on the coast the tide nearly vanishes (Sverdrup, 1927, Fjeldstad, 1929 and 1936). The decrease of the amplitude when approaching the coast is brought out by the data in table 72, which shows the amplitude and phase of the term M2 near the border of the shelf and at two localities on the coast. Of these two localities, Ayon Island lies a little south of Four Pillar Island, but the tide wave reaches Four Pillar Island later because the direction of progress of the wave is altered near the coast owing to the configuration of the bottom (Sverdrup, 1927).
| Locality | Latitude N | Longitude E | M2 | ||
|---|---|---|---|---|---|
| Amplitude (cm) | Phase (degrees) | Difference in phase | |||
| Near border of shelf | 74°33′ | 167°10′ | 13.75 | 158 | 0 |
| Ayon Island | 69 52 | 167 43 | 1.78 | 347 | 189 |
| Four Pillar Island | 70 43 | 162 35 | 0.98 | 60 | 262 |
It is seen that the later the tide the smaller the amplitude is, and it can be readily verified that the logarithm of the amplitude is nearly a linear function of the phase difference, as should be expected if the wave length remained constant, because in that case μx = μLα/2π where α = kx represents the phase difference.
The fact that the tide practically vanishes on the coast shows that when crossing the wide shelf the energy of the incoming tide wave is
In several adjacent seas the effect of friction has been studied by H. Jeffreys, who used a method developed by G. I. Taylor and first applied to conditions in the Irish Sea. The principle is simply that under stationary conditions the net amount of tidal energy which is brought into an area must equal the amount which is lost in the same area by dissipation due to friction. Therefore a determination of the net amount of tidal energy which is brought into an area represents also a determination of the dissipation.
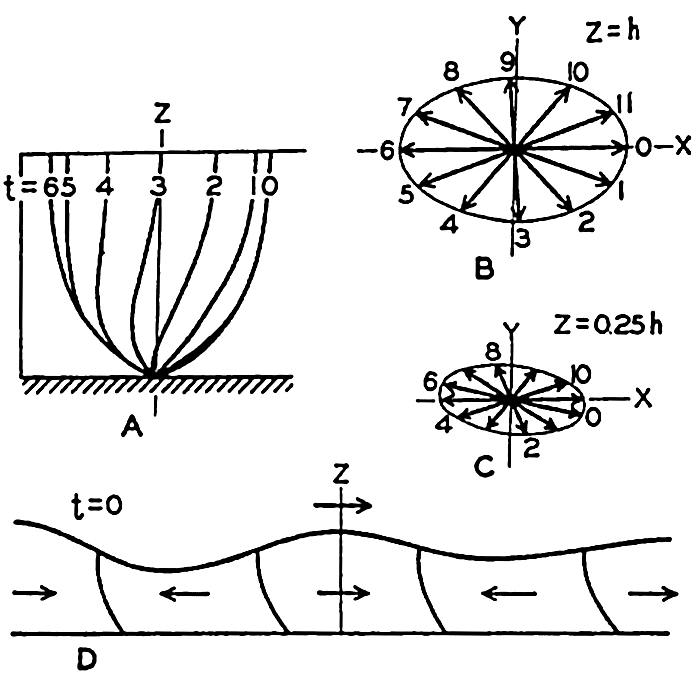
Combined influence of friction and the rotation of the earth on tidal currents in shallow water in the Northern Hemisphere (according to Sverdrup). For explanation, see text.
[Full Size]
These studies have found an interesting application. It appears to be established by astronomers that the speed of rotation of the earth is very slowly decreasing, so that during a century the length of the day increases on an average by about one thousandth of a second. This slowing up may be caused by the dissipation of tidal energy, because estimates of the dissipation give values which correspond to the energy needed for bringing about the observed change in the earth's period of rotation.
So far, we have considered the effect of friction on the tides. In order to study theoretically the effect of friction on tidal currents, it is necessary to add the frictional terms (p. 475) in the equations of motion applicable to long gravitational waves (p. 555), and to integrate the equations. Such integration was performed by Sverdrup (1927) on the assumption that only the vertical turbulence need be considered and that the coefficient of eddy viscosity was constant. The boundary conditions were that at the free surface the shearing stresses should be zero and at the bottom the velocity should be zero. The results give some idea about the effect of friction, although the assumption of a constant eddy viscosity is not in agreement with more recent results according to which the eddy viscosity near the bottom increases rapidly with increasing distance from the bottom.
The more important conclusions can be summarized as follows. Near the bottom there exists a “layer of frictional influence” the thickness of which depends upon the ratio s = (2T sin ϕ)/T0 and upon the value of the eddy viscosity, and above which the tidal currents have the
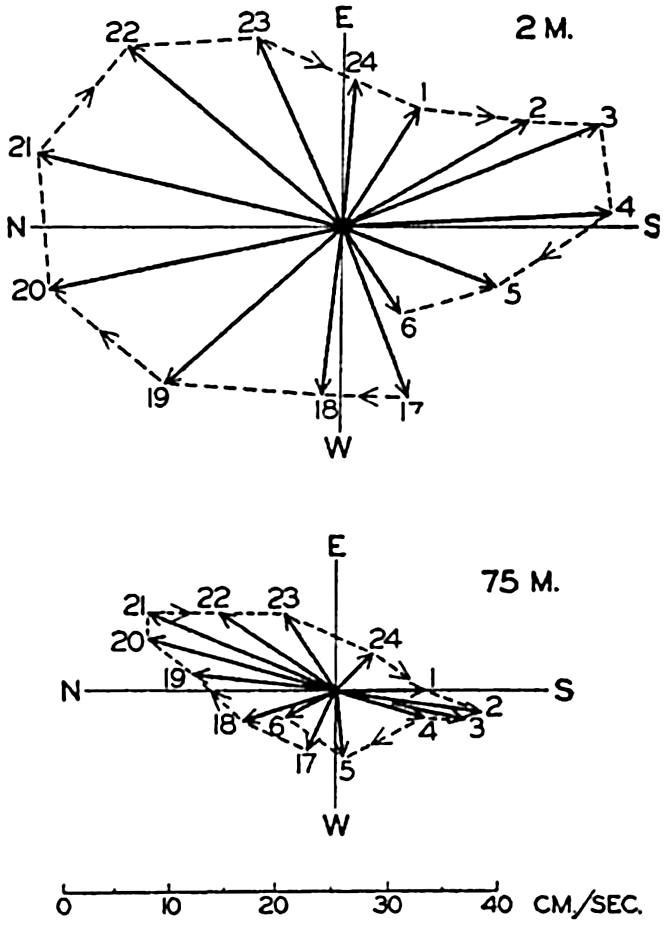
Tidal currents in the North Sea, lat. 58°17′N, long. 2°27′E, depth 80 m, demonstrating the effect of friction when approaching the bottom. Measurements by Helland-Hansen on August 7 and 8, 1906.
[Full Size]
Figure 148 shows an example of current measurements in the North Sea which appear to confirm the above conclusions. Other examples are found in Sverdrup's discussion (1927) of current measurements on the North Siberian Shelf, but in several of these cases it was necessary to take into account that the ice offered a resistance to the tidal motion and also that occasionally a nearly discontinuous increase in density at some depth brought complications. In the latter case an approximation could be obtained by introducing two layers of constant eddy viscosity separated by a layer of no eddy viscosity, the latter being the layer of very great stability.
The theoretical treatment of the subject has been expanded by Fjeldstad (1929, 1936) who has found integrals of the equations of wave motion in cases in which the eddy viscosity can be represented as a simple function
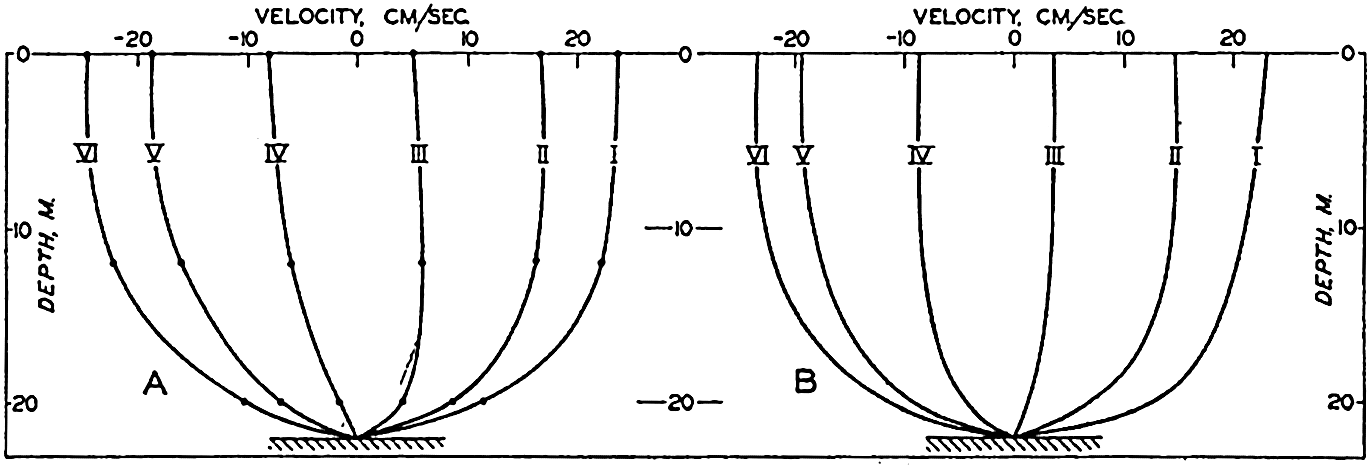
(A) Observed variations with depth of tidal currents at different lunar hours, according to measurements by Sverdrup on August 1, 1925, in lat. 76°36′N, long. 138°30′E. (B) Computed variation with depth of tidal currents, assuming an eddy viscosity which increases linearly from the bottom to the surface (according to Fjeldstad).
[Full Size]
At the bottom one should expect, from analogies with experimental work in laboratories (p. 479), that the eddy viscosity will be small, having a value which depends upon the roughness of the bottom and the “friction velocity.” Near the bottom the eddy viscosity should increase linearly with increasing distance, the increment being proportional to the friction velocity. At some greater distance from the bottom, stability of the stratification may influence the eddy viscosity, and in very shallow water the eddy viscosity must reach a maximum below the free surface and decrease to a small value at the very surface. In homogeneous shallow water it may be expected, however, that the introduction of an eddy viscosity which increases linearly from the bottom to the surface will give a good approximation because conditions close to the bottom exercise the greatest influence upon the character of the motion and because at some distance from the bottom the value of the eddy viscosity is of minor importance. This is illustrated by the example in fig. 149. To the left are represented the components of the tidal current in the direction of progress of the tide wave, at the time of maximum current at the surface (marked I) and at the five following tidal hours. The curves are based on observations at three depths—0, 12, and 20 m—on
Observations of tidal currents at different distances from the bottom and within the layer of frictional resistance are not available from many localities and the factual information as to the effect of friction on tidal currents is therefore meager. Measurements from the North Sea off the coast of Germany have been discussed by Thorade (1928), who has studied the influence of friction by a different method of attack. In the North Sea the gravitational forces can be directly determined because the slope of the surface due to the tide wave can at any time be derived from tidal observations at coastal stations. Furthermore, Corioli's force and the accelerations can be derived from the current measurements and the frictional forces can therefore be found by means of the equations of wave motion because all other terms in the equations are known. Thorade's results are, in general, in agreement with the conclusions which have been presented, but many details need further examination. It is of particular interest, however, to observe that on an average during one tidal period Thorade finds that the eddy viscosity is very small at the bottom, increases rapidly with increasing distance from the bottom, but decreases again when approaching the surface. The general character of this variation is in agreement with the above considerations as to the variation of the eddy viscosity.
The influence of friction on tidal currents is also evident from studies of the tidal currents in the Dover Straits by J. van Veen (1939). He finds there that the velocity distribution between the surface and the bottom can be represented by means of a function of the form v = az1/n where n equals about 5.2. This implies that the eddy viscosity is approximately proportional to z4.2/5.2, meaning that the increase is somewhat less than that corresponding to a linear law, but no conclusions can be drawn as to the numerical values of the coefficient.
The effect of lateral mixing on tidal currents has so far not been examined, but it is possible that friction arising from lateral turbulence is of importance close to coasts.
The Semidiurnal Tide of the Atlantic Ocean
A number of the theoretical considerations which have been set forth have been applied, particularly by Defant, towards explaining the tides of the Atlantic Ocean. Defant (1932) has dealt with both the semidiurnal and the diurnal tides, but in the following we shall consider mainly the semidiurnal tide.
The Atlantic Ocean and its continuation, the Norwegian Sea and the Polar Sea, can be considered as a long bay which is closed in the north, whereas in the south it is in open communication with the Antarctic Ocean. On the basis of this concept the tides of the Atlantic Ocean can be considered as composed of two parts, a cooscillating tide which is maintained by the tide of the Antarctic Ocean, and a free tide which is maintained by the direct effect of the tide-producing forces. Neglecting the rotation of the earth and the effect of friction, both the cooscillating and the free tide can be computed by means of the method of numerical integration which was presented on p. 539, taking into account that the energy of the part of the tide wave which enters the Norwegian Sea and the Polar Sea is completely dissipated on the shallow shelves of these areas and that for this reason no reflected wave returns from these areas (p. 577). Part of the entire tide wave will be reflected, however, and the resultant picture will have some similarity to that which was discussed when dealing with the effect of friction on the tide (p. 574).
The numerical computations involved are somewhat lengthy but have been carried through by Defant. The result, in agreement with the conclusions presented on p. 575, is that the semidiurnal tide of the Atlantic Ocean can be considered as composed of two standing oscillations having a phase difference of one quarter period or three lunar hours. The computation renders only the variation in amplitude and phase along the middle section of the Atlantic Ocean and, in order to obtain absolute values, it is necessary to introduce observed values from two localities. As such observations Defant selected the tidal data from the Azores in the North Atlantic Ocean and from Tristan da Cunha in the South Atlantic.
A check on the theory is obtained by comparing observed values of the amplitude and the phase of the semidiurnal tide at other islands of the Atlantic Ocean with the computed values, and a further check is possible by comparing theoretical phase angles along the central part of the Atlantic Ocean with those which can be derived from Sterneck's chart of cotidal lines for the diurnal tide. This chart, which is reproduced in fig. 150, is based not only upon data from islands but upon all available data on the coasts. The full-drawn lines in fig. 151 show Defant's computed values of the amplitude and phase of the semidiurnal tide along a line which approximately follows the center of the Atlantic Ocean.
The crosses indicate the amplitude or phase at the island stations, the names of which are shown in the figure, and the dashed line in fig. 151B indicates the change in phase according to Sterneck's map. The agreement between observations and computations is remarkably good, all of the crosses falling nearly on the computed curves. The discrepancy in the northern part of the North Atlantic Ocean between the computed phase and the phase as derived from Sterneck's map can be accounted for by the fact that the location of the amphidromic point to the south of Greenland is admittedly uncertain. The agreement speaks strongly in favor of Defant's concepts, and further evidence for the validity of his computations is obtained by an examination of the tidal currents as
(A) Computed variation of the amplitude of the semidiurnal tide along the central part of the Atlantic Ocean (according to Defant). Crosses indicate observations at islands. (B) Computed variation of the phase of the semidiurnal tide along the central part of the Atlantic Ocean (according to Defant). Crosses represent observations at islands, and dashed lines represent the variation according to Sterneck's map. (C) Computed variation of phase of the semidiurnal tidal currents along the central part of the Atlantic Ocean (according to Defant). Dots represent observed values.
[Full Size]
Certain discrepancies are revealed, however, if one compares the observed amplitudes of the tidal currents with the theoretical. Defant points out that the computed and observed velocities show similar variations with latitude if one subtracts from the observed velocities a latitude effect which can be ascribed to the earth's rotation. The latter was neglected when making the computation and must therefore be eliminated from the observed values. The correction which should be applied is due to the fact that on the rotating earth the velocity of the tidal current is
if v0 represents the corresponding velocity, neglecting the earth's rotation, and where s = (T sin ϕ)/12. (p. 571). In order to make a comparison between the computed and the observed values, the latter should be reduced by multiplication with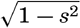 [Equation].
[Equation].After having done this, Defant finds that the character of the variation of the velocities agrees with the computed velocities, but the observed velocities are between two and three times greater than the computed. The computations give velocities of about 3 cm/sec, whereas the reduced observations give velocities of about 8 cm/sec. Defant suggests that this discrepancy arises because the direction of the tidal currents is not uniform through an entire cross section, as postulated by the theory, but another possible explanation is suggested on p. 595. Whether or not these explanations are accepted, the evidence in favor of Defant's theory is so great that his explanation of the semidiurnal tides of the Atlantic Ocean has to be given weight.
Concerning the character of the tidal currents it should be observed, furthermore, that the current measurements plainly show the effect of the earth's rotation. At all anchor stations the average semidiurnal current between the surface and the greatest depth of observation showed rotating currents, the direction of rotation being cum sole in 55 of 60 cases, including as cum sole four cases in which the current was practically alternating. The ratio between the major and minor axes of the current ellipses was on an average close to the theoretical value s = (T sin ϕ)/12 (p. 571). Thus, in mean latitude 36°18′, the observed ratio between the
Defant also computed the difference between the time of the maximum tidal current at the different anchor stations and the time of high water. He finds that in general high water occurs about one and a half hours before the maximum tidal current towards the north, and points out that this time difference should be zero if one had to deal with a progressive wave, and three hours if one had to deal with a standing wave. The fact that the time difference lies between these two values also shows that the semidiurnal tide of the Atlantic Ocean has neither the character of a progressive wave nor that of a standing wave, but is intermediate and can be regarded as brought about by superposition of several standing waves. It may especially be observed that in the South Atlantic Ocean the wave has nearly the character of a progressive wave, whereas in the North Atlantic Ocean the characteristics of a standing wave are more conspicuous.
The diurnal tide of the Atlantic Ocean is less well-known and Defant confines himself to a more summary treatment, the results of which indicate, however, that similar concepts are applicable in that case as well. It should be particularly pointed out that in the case of the diurnal wave the ratio between the axes of the current ellipses does not increase as rapidly as required by the simple theory on p. 571. According to this theory the current ellipse should degenerate in 30°N to a circle with infinite radius, and beyond 30°N diurnal waves of the simple character considered should no longer be possible. The observations show that the ratio between the axes of the diurnal current ellipses increases very slowly with increasing latitude, indicating that in relation to the diurnal wave the Atlantic Ocean cannot be considered as a wide ocean but as a bay or canal of moderate width. This conclusion may have bearing on future studies of the diurnal tides.
Similar treatment of the tides of other oceans has not yet been attempted and will encounter much greater difficulties. This is particularly true when considering the Pacific Ocean, which is so large that there the free tides must be of much greater importance.
Internal Waves
The waves which have been dealt with so far are characterized by maximum vertical displacements at the surface. For short waves the vertical displacement of the water particles decreases exponentially downwards, and for long waves the vertical displacement decreases linearly with depth, being zero at the bottom (p. 521). These waves will now be called ordinary waves. They are the only ones possible in homogeneous
The theory of the internal waves was first developed by Stokes (Lamb, 1932, p. 370) in the simple case of two layers of different density, and the general theory of progressive internal waves in heterogeneous water was developed by Fjeldstad (1933). Both theories have found application to oceanographic phenomena.
In a fluid consisting of two layers of infinite thickness, one lower layer of density p′ and one upper layer of density p′, waves at the boundary surface between the two layers will have a velocity of progress as given by
These waves are short waves because it is assumed that both layers of fluid are of infinite thickness, on which assumption the wave length L is always negligible compared to the thickness of the layers. If p′ means the density of the air and p the density of the water, the equation gives the velocity of progress of ordinary surface waves (p. 519), as p′ is very small relative to p. The surface waves which were dealt with on pp. 522–537 can therefore be considered as “internal” waves on the boundary between the air and the sea.When dealing with internal waves in water which has a free surface but consists of two homogeneous layers of different density, the kinematic and dynamic boundary conditions must be fulfilled both at the free surface and at the internal boundary surface, and the equation of continuity must be satisfied. This leads to a quadratic equation for c2 which, for short waves, has the approximate roots
assuming that the thickness of the lower layer h is great compared to the wave length. Here p represents the density of the lower layer and p′ and h′ represent density and thickness of the upper layer. If the wave length is great compared to h′, kh′ is a small quantity, coth kh′ can be replaced by 1/kh′, and equations (XIV, 47) are reduced toApplied to the ocean, this means that wherever there exists a thin top layer of water of small density, two types of waves are possible: the ordinary surface waves that progress with velocity c1; and the internal waves at the boundary between the light top layer and the heavier water underneath, that progress with velocity c2. Ekman (1904) has availed himself of this conclusion in order to explain the phenomenon known as “dead water.” In the time of the sailing vessels many captains reported that with a light breeze their vessels occasionally appeared to “stick” in the water, behaving sluggishly and making little headway. The experience was particularly common in Arctic waters in the presence of a thin top layer of nearly fresh water produced by melting of ice, and off rivers from which fresh water spread out. Slowly moving steamers have had similar experiences, but when their speed was increased to a few knots the unusual resistance disappeared. According to Ekman's theoretical studies and the results of his numerous experiments, this dead water is due to the fact that a slowly moving vessel may create internal waves at the lower boundary of a thin fresh-water layer the thickness of which is not much less nor much greater than the draft of the vessel. The energy otherwise applied towards overcoming the ordinary resistance of the water will now be used also for generating and maintaining internal waves, for which reason the vessel appears to “stick” in the water. The velocity of progress of internal waves as given by equation (XIV, 48) is, however, small. If the velocity of the vessel is greater than this small value, no internal waves are created and the vessel can proceed normally. With p − p′ = 0.025, nearly corresponding to a layer of fresh water on top of sea water of temperature 10°C and salinity 30 ‰, and with h′ = 400 cm, one obtains c2 = 100 cm/sec = 1.9 knots. These numerical values indicate that at a speed of a few knots no internal waves are created, which is in agreement with the general experience that dead water is not encountered at speeds above a few knots.
The short internal waves that have been dealt with so far may be present anywhere in the ocean, but escape observation on the high seas where the variation of density with depth is less conspicuous. In the open ocean long internal waves exist, however, and these have in recent years received much attention. When dealing with two layers and neglecting the effect of the earth's rotation the velocities of progress of the ordinary long wave and of the internal wave are obtained from the equations
It is assumed that p − p′ is a small quantity and that the wave length is long compared to the total depth, h + h′. Evidently c1 represents the velocity of progress of an ordinary long wave and need not be consideredThe internal wave is characterized by having its maximum amplitude at the boundary surface. At the free surface the amplitude of the internal wave does not entirely disappear but is reduced to
where the minus sign indicates that at the surface the phase is opposite to the phase at the boundary Z. At an internal boundary surface in the open sea the difference in density (p — p′) hardly ever exceeds 2 × 10−3, corresponding to, say, σt = 25.0 and σ t′ = 23.0. With this difference and with Z = 10 m, one obtains η0 = 2 cm, meaning that at the free surface the amplitude of the wave is so small that for all practical purposes it can be disregarded. At the bottom, no motion normal to the bottom can exist and there the vertical displacement must also disappear. In the simple case under consideration the amplitude of the internal wave increases linearly from the free surface to the boundary surface and decreases linearly from the boundary surface to the bottom (fig. 152B). The change in amplitude with depth is therefore equal to Z/h′ in the upper layer, and to −Z/h in the lower layer. The amplitude of the horizontal particle velocities can be derived from the vertical amplitudes because the relation existsThis numerical example shows that internal waves are characterized by large horizontal particle velocities. The corresponding velocity of progress of the internal wave is 78 cm/sec, whereas the ordinary long wave proceeds at a velocity of 4430 cm/sec.
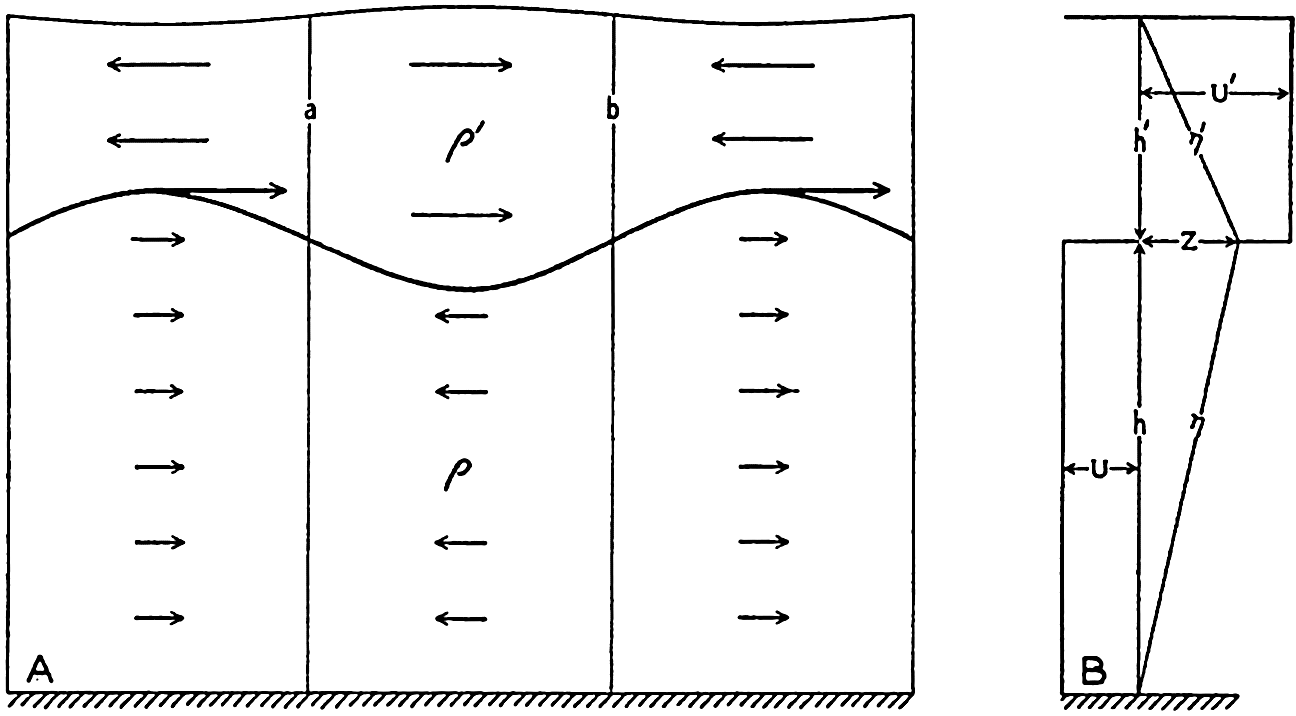
(A) Schematic representation of an internal wave at the boundary between two liquids of densities p and p′. (B) Schematic representation of the variation with depth of the amplitudes of the vertical displacements p and p′, and of the maximum horizontal velocities U′ and U.
[Full Size]
The character of the internal wave at the boundary between two liquids of different density is illustrated in fig. 152A, which shows the deformation of the boundary surface and the directions of the horizontal velocities within the two layers. The wave is supposed to progress from left to right. At the line marked a the horizontal currents in the upper layer are divergent, for which reason the lower boundary surface must rise, and the horizontal velocities in the lower layer are convergent, for which reason also the boundary surface must rise. At the line marked b the boundary surface must sink for similar reasons, and the wave must therefore progress from left to right, as stated. In the figure it is also indicated that the vertical displacement of the free surface is opposite in phase to that of the boundary surface, but the displacement of the free surface has been greatly exaggerated. The pressure at the bottom remains constant and equal to the hydrostatic pressure because the vertical accelerations are negligible. The amplitude of the deformation of the free surface can be computed from the hydrostatic equation and the result is as before, η0 = −Z(p − p′)/p.
If several boundary surfaces are present, several internal waves can occur simultaneously, and the greater the number of boundary surfaces, the greater the number of possible internal waves. On the basis of this reasoning, when the density varies continuously with depth one should expect an unlimited number of possible internal waves. That such is the case has been shown by Fjeldstad (1933), who has developed the theory of internal waves in water in which the density is a continuous function of depth. He deals with progressive waves only, and presents a complete
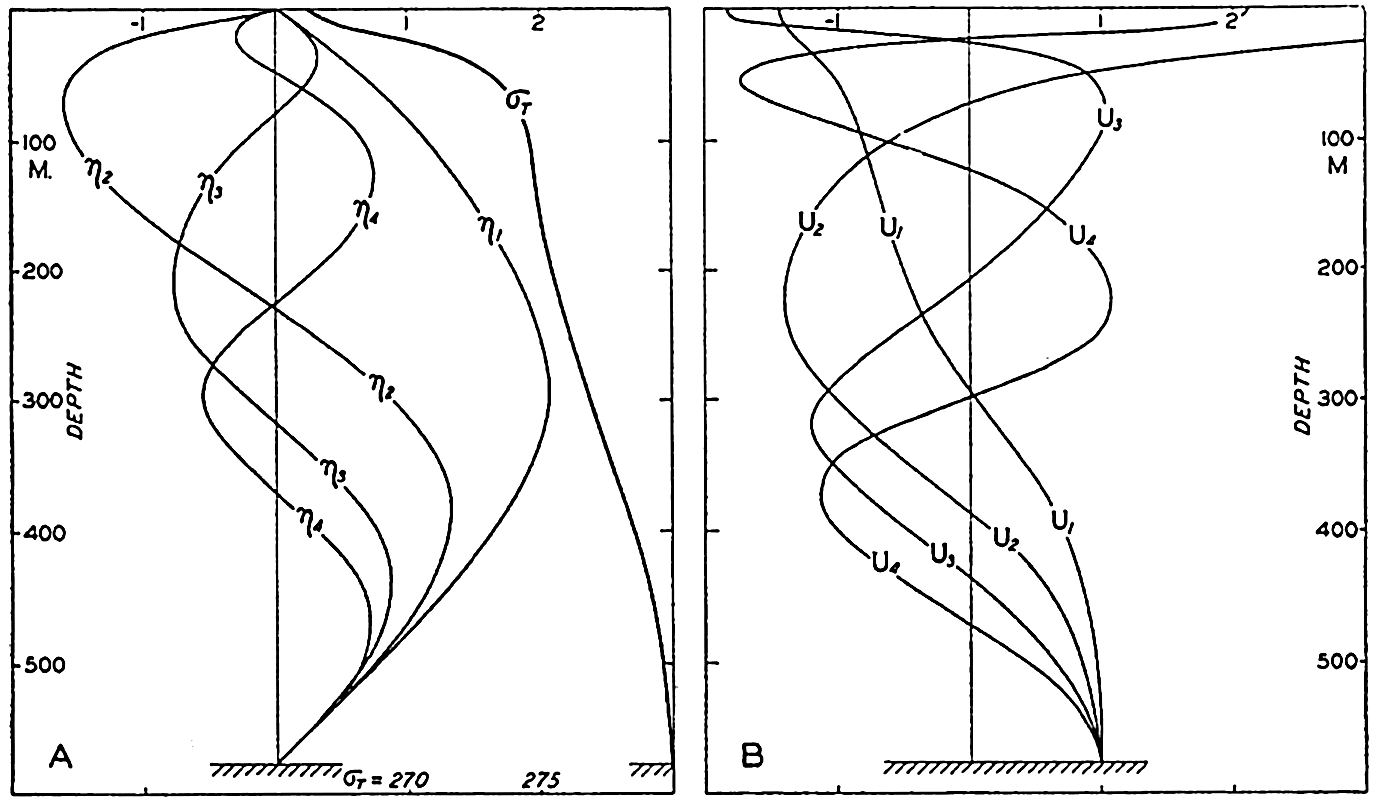
(A) Variation with depth of the vertical displacements corresponding to internal waves of first, second, third, and fourth order at Michael Sars Station 115 (according to Fjeldstad). The density distribution is shown by the curve marked σt. (B) Variation with depth of the amplitudes of the horizontal velocities corresponding to an internal wave of first, second, third, and fourth orders (according to Fjeldstad). Vertical displacements and amplitudes are plotted on an arbitrary scale.
[Full Size]
Figure 153A shows Fjeldstad's computed vertical displacements and horizontal velocities as functions of depth for the internal waves of first, second, third, and fourth orders, corresponding to the distribution of density as shown in the same figure, which was observed at Michael Sars station 115 (Helland-Hansen, 1930), where the depth to the bottom was 580 meters. The amplitudes of the accompanying horizontal velocities
Fjeldstad's method also leads to determination of the velocity of progress of waves of different orders, provided that the depth is constant and that the distribution of density remains unaltered in the direction of progress; but the periods of the waves cannot be determined theoretically and must be derived from observation. At Michael Sars station 115 the velocities of progress were c1 = 70 cm/sec, c2 = 39 cm/sec, c3 = 26 cm/sec, and c4 = 19.5 cm/sec; and for a wave of period 24 lunar hours the corresponding wave lengths are 62.5 km, 34.8 km, 23.2 km and 17.4 km, respectively. Evidently, the internal waves are short compared to tide waves. It should be observed that the velocity of progress increases when the difference in density between the upper and lower layers decreases, and also increases with increasing depth to the bottom. In low and middle latitudes the velocity of progress of the first-order wave will, however, rarely exceed 300 cm/sec. For diurnal or semidiurnal waves the corresponding wave lengths are 268 km or 134 km, respectively, and the waves of higher order are correspondingly shorter.
Observations indicating vertical displacements of water masses which may be related to internal waves have been made on numerous occasions when oceanographic observations have been repeated in the same locality at short time intervals. If observations of temperature at different depths are made at, say, hourly intervals, from an anchored vessel or from a vessel which maneuvers in such a manner that its position changes only one or two miles, it is often found that the temperature varies more or less periodically at all depths. Assuming that these variations are due to vertical displacements, one can find the vertical displacements at the different depths if the average temperature distribution is known. If, for instance, the average temperature at 200 m is 12.40° and at 220 m is 12.17°, it may be concluded when a temperature of 12.17° is observed at 200 m that water which under undisturbed conditions should be found at 220 m has been displaced 20 m upwards. If the temperature oscillation at a given depth d is periodic and has an amplitude of A°, the amplitude of the corresponding vertical oscillation is found by dividing the amplitude A° by the average temperature gradient at that depth, (dθ/dz)d. Similar conclusions may be based on observations of salinity and oxygen, and when all these elements have been observed good
If the observations have been carried out during a sufficiently long time, it is possible to find the period length of the oscillations. In a number of cases period lengths have corresponded to tidal period, and it has therefore been concluded that internal waves of tidal periods commonly occur in the ocean. It is not probable that such internal waves are caused directly by the tide-producing forces but it is more nearly probable, as suggested by Defant, that they are caused by the periodic variations of the actual tidal currents which may lead to periodic changes in the inclination of isosteric surfaces in the sea. Besides these internal waves of tidal periods, waves of other periods also exist.
The first observations of short-period variations which indicated the existence of internal waves were discussed by Helland-Hansen and Nansen (1909). On the Michael Sars Expedition to the North Atlantic in 1910, repeated serial observations were made at several stations, and on one occasion simultaneous observations in the Faeroe-Shetland Channel were conducted from the Michael Sars and the Scottish research vessel, the Goldseeker, the two vessels being about 106 km (57 mi) apart. The possible vertical displacements derived from the temperature observations can be well represented by two periodic oscillations of period length 12 and 24 lunar hours. The results of Helland-Hansen's harmonic analysis (1930) of these data are given in table 73. It appears that the oscillations at the two stations were different in respect to the vertical variations of amplitude and phase of the two waves, and in respect to the relative magnitude of the semidiurnal and diurnal oscillations. This might be expected if the oscillations were associated with progressive internal waves. If waves of different order are present, the combined result may be a complicated variation with depth of amplitudes and phase angles (fig. 156, p. 598), and the velocity of progress of such waves is so small, 0.7 to 2.5 km per hour, that different phases must be found at stations which are 106 km apart. Furthermore, the amplitudes may vary along a line at right angles to the direction of progress, owing to the earth's rotation, as in a Kelvin wave (p. 555).
In his discussion Helland-Hansen draws special attention to the fact that the observed variations of temperature may be caused by variations of horizontal currents and not by internal waves. In the Faeroe-Shetland Channel all isothermal surfaces slope considerably, and lateral displacement might therefore give rise to such variations as were recorded. The same reservation must always be made when interpreting oscillations of temperature in a region where a lateral temperature gradient exists.
Recent measurements by Seiwell (1937) have substantiated the view, however, that observed oscillations are due to vertical displacements and not to horizontal movement, because he selected a locality for repeated serial measurements in the region NNW of Bermuda within which, on several of the Atlantis cruises, very small horizontal gradients had been found. On July 12 and 13, 1936, Seiwell (1937) observed very large vertical displacements, reaching total ranges during 24 hours up to 80 m at depths of 500 to 600 m. As an example the observed temperatures at 500 m are shown in fig. 154 where the corresponding vertical displacements are also entered. The latter were computed by dividing the temperature
Variation of temperature (thin curve) at a depth of 500 meters on July 13, 1936, and corresponding vertical displacements (heavy curve). From Seiwell's observations (1937).
[Full Size]
| Depth (m) | Semidiurnal vertical displacements | Diurnal vertical displacements | ||||||
|---|---|---|---|---|---|---|---|---|
| Michael Sars 115 | Sc | Michael Sars 115 | Sc | |||||
| Amplitude (m) | Phase (lunar hours) | Amplitude (m) | Phase (lunar hours) | Amplitude (m) | Phase (lunar hours) | Amplitude (m) | Phase (lunar hours) | |
| 100 | 15 | 6.3 | 42 | 0.7 | 18 | 17.0 | 39 | 12.3 |
| 200 | 12 | 8.4 | 58 | 11.2 | 16 | 15.9 | 11 | 14.2 |
| 300 | 24 | 9.3 | 22 | 11.6 | 9 | 17.7 | 8 | 17.7 |
| 400 | 7 | 9.5 | 11 | 9.2 | 10 | 9.0 | 9 | 4.4 |
| 500 | 3 | 6.6 | 24 | 11.1 | 5 | 11.3 | 6 | 5.2 |
| 600 | 24 | 7.3 | 25 | 1.2 | ||||
Harmonic analysis showed that at all levels the major part of the observed oscillations could be represented as the sum of three oscillations of periods 24, 12, and 8 lunar hours. The amplitudes of the harmonic terms varied with depth, but the 24-hour term dominated at all levels and the 8-hour term was smallest at most levels. The facts that in this case horizontal motion cannot account for the observed variations of temperature and that the oscillations were periodic strongly suggest the presence of some kind of wave motion.
| Depth (m) | Semidiurnal waves | Diurnal waves | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Current | Vertical displacement | Current | Vertical displacement | |||||||
| Maximum current towards | Velocity (cm/sec) | Phase (lunar hours) | Amplitude (m) | Phase (lunar hours) | Maximum current towards | Velocity (cm/sec) | Phase (lunar hours) | Amplitude (cm) | Phase (lunar hours) | |
| 0 | N 41°W | 6.8 | 3.5 | |||||||
| 50 | N 30 W | 9.4 | 3.0 | N 12°W | 10.3 | 11.8 | ||||
| 100 | N 72 E | 5.4 | 1.9 | N 33 W | 4.8 | 15.9 | ||||
| 150 | N 67 E | 11.6 | 3.3 | 7 | 3.7 | N 84 W | 9.9 | 6.1 | 4 | 7.4 |
| 200 | N 61 W | 11.1 | 6.8 | 10 | 4.0 | N 63 W | 6.7 | 3.8 | 8 | 16.9 |
| 300 | N 42 W | 9.4 | 6.3 | 7 | 3.6 | N 49 W | 4.7 | 5.4 | 6 | 23.4 |
| 500 | N 51 W | 5.7 | 3.2 | 7 | 3.8 | N 14 W | 11.9 | 17.2 | 6 | 6.4 |
The existence of internal waves is also confirmed by the results of numerous current measurements from vessels anchored in deep water (Ekman and Helland-Hansen, 1931, Defant, 1932, Lek, 1938). Observations from different depths show that currents of tidal periods dominate; but, instead of being uniform from surface to bottom as would be expected if the currents were ordinary tidal currents, the amplitude and the time of maximum current (the phase) vary in a complicated manner with depth, and at some levels the semidiurnal currents are strongest, and at others, the diurnal. This is illustrated by the results of current measurements and repeated serial observations at Meteor anchor station 176 on the Mid-Atlantic Ridge in the South Atlantic Ocean, lat. 21°29.8′S, long. 11°41.5′W
It is evident that extremely complicated currents may be found if several internal waves of different orders, different phases, and different tidal periods are present, and if the currents associated with these waves are superimposed upon the ordinary tidal currents. At first glance it may appear hopeless to separate the latter from the currents of the internal waves of tidal periods, but fortunately these “internal tidal currents” can be eliminated if observations are available from a sufficient number of depths. Because (p. 588)
where vn is the horizontal particle velocity of the wave of nth order, and cn and ηn the corresponding velcoity of progress and vertical displacement; and because for all internal waves η is zero at the surface and at the bottom, one has generally When dealing with long internal waves at the boundary between two layers, the corresponding equation was V′h′ − Vh = 0.It follows from equation (XIV, 53) that currents associated with internal waves are eliminated by computing the average currents between the surface and the bottom, provided that observations from a sufficient number of depths are available. Such elimination was attempted by Defant when he derived the tidal currents from observations at anchor stations in the Atlantic Ocean (see p. 584), but the available data were mostly from the upper layers only, and this accounts perhaps for the fact that he found much greater velocities than those corresponding to the range of the tide.
So far, the effect of the earth's rotation and of friction have been neglected. It cannot be expected that Corioli's force alters the variation with depth of amplitude of the internal wave, and Fjeldstad's method should therefore in all cases give correct results as to the relative amplitudes. On the rotating earth the accompanying currents, however, will also be rotating if the period of the internal wave approaches the period of a pendulum day. Transverse currents will accordingly be present, but these must also satisfy equation (XIV, 53) and can therefore be eliminated if observations from many depths are available. The velocity
An internal wave in water consisting of two layers of different density can be considered as an oscillation of the boundary surface. Defant (1940) has shown that on the rotating earth the period of a free oscillation of a boundary surface in the sea approaches the period of the inertia oscillation when the dimensions of the oscillating system are great. In a basin of length l the longest period of the free oscillations is, with the previous notations and neglecting the earth's rotation,
The period of the inertia oscillation is Te = 2π/2ω sin ϕ. Defant obtains the result that on the rotating earth the period of the free oscillation is
provided that the width of the basin is at least as great as the length. It follows that if Tr is great compared to Te, which may happen if l is great, T approaches Te. Defant deals with a two-layer system only, but his general result is undoubtedly correct and is of the greatest importance to the interpretation of observed currents and vertical displacements associated with internal waves.As a numerical example values from the Baltic may be introduced, ρ − ρ′ = 2 × 10−3, h′ = 25 m, and h = 35 m. With these values one obtains Tr = 3.75 l (l in meters). If it is required that Te/Tr = 0.1, one obtains in latitude 57°49′, l = 136 km. In a basin of these dimensions, the difference between the periods of the free oscillations and the inertia oscillation would be only 1 per cent, and it seems therefore probable that a disturbance which would develop motion in the inertia circle would set up free oscillations of the boundary surface. A deeper basin or a basin in lower latitudes would have to be of greater dimensions; thus, with ρ − ρ′ = 2 × 10−3, h′ = 500 m, and h = 1500 m, one obtains Tr = 0.736 l, and with Te/Tr = 0.1, one finds that in the latitude 57°49′, l = 692 km, and in latitude 30°,l = 1170 km.
The friction will lead to a dissipation of the energy of the internal wave, and unless the wave is maintained by a periodic disturbance it will gradually die off. The current observations from the Baltic by Gustafson and Kullenberg, which were discussed on page 438 (fig. 104), can be interpreted as inertia oscillations that may be associated with an internal wave and as showing the gradual dissipation of the energy of the wave.
It is evident from this discussion that the internal waves greatly complicate the actual movement of the water masses and lead to the
Variation in depth of stated σt values on June 23 and 24, 1930, according to observations of the Snellius Expedition at Station 2534 in lat. 1°47.5′S, long. 126°59.4′E.
[Full Size]
An illustration of the application of Fjeldstad's theory is given by Lek (1938) in his discussion of results of current and serial measurements of the Snellius Expedition in the eastern part of the Netherlands East Indies, 1929–1930. On this expedition current measurements were made at a number of anchor stations and at one of these, station 253A, lat. 1°47.5′S, long. 126°59.4′E, very complete observations comprised hourly measurements during 26 hours of currents at 0, 50, 100, 200, 350, and 500 m, and hourly observations of temperature, salinity, and oxygen at seven depths between the surface and 800 m. The depth to the bottom was 1740 m. From the temperature and salinity data the density was computed. In fig. 155 is shown the variation in depth of different σt curves during the period of observation. From this graph one obtains immediately the impression that large vertical oscillations took place, some of which appear to have been of a diurnal, others of a semidiurnal, period. The phases of the oscillations appear to have varied with depth, the vertical oscillation at a depth of about 50 m being opposite in phase to the oscillation at a depth of about 230 m. Hence,
In order to examine the character of these waves, Lek, in cooperation with Fjeldstad, computed the relative amplitudes of the internal waves of first, second, third, and fourth orders by means of the average distribution of density between the surface and the bottom. Consider first the semidiurnal oscillations. It is evident that any observed variation with depth of amplitude and phase can be represented by a sufficiently large number of the theoretical internal waves of different orders, because the absolute values of the theoretical amplitudes and the phase angles of the theoretical displacements can be adjusted to fit the observed data. A certain check on the theory is, however, obtained if the number of the theoretical internal waves is smaller than the number of depths of observations.
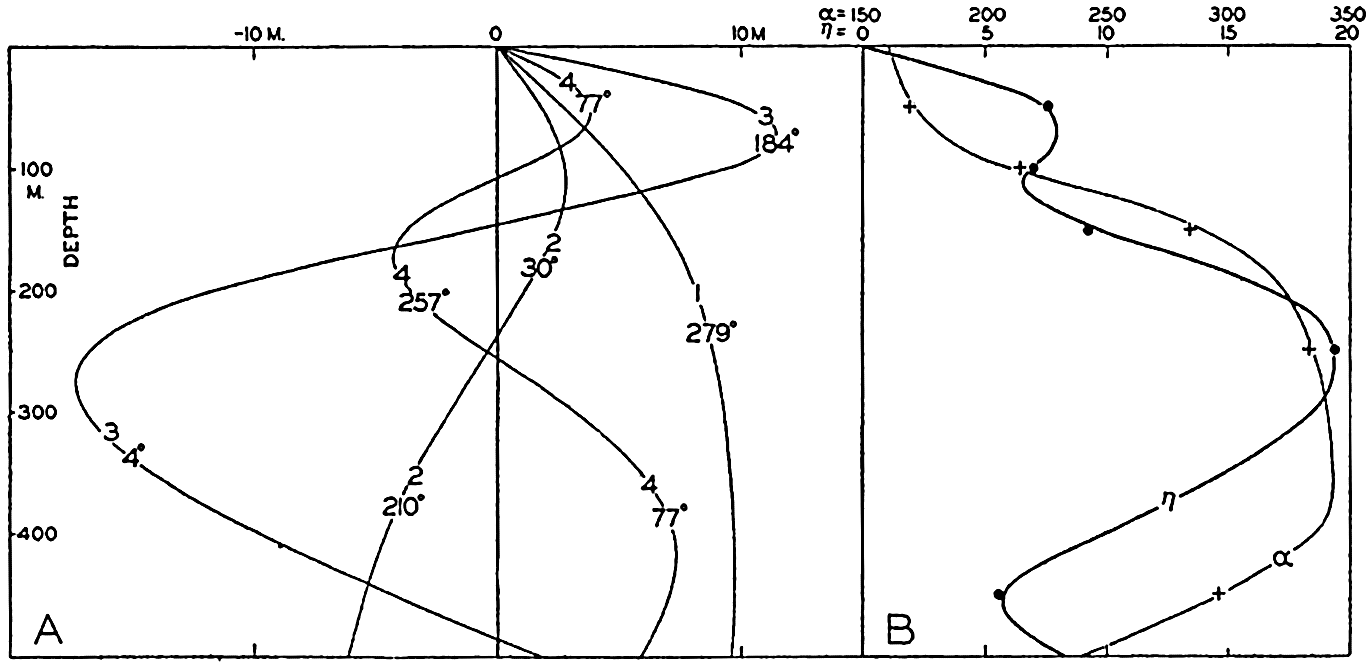
(A) Variation with depth of the amplitudes of internal waves of order 1 to 4 at Snellius Station 253A. The phases of the different waves are shown in the figure. (B) Curves show the variation with depth of amplitude η and phase α, as derived from the curves in (A). Crosses and dots indicate observed values (according to Lek and Fjeldstad).
[Full Size]
In the present case observations from five levels were used for determining the amplitudes and phases to be assigned to the internal waves or orders one to four, meaning that an adjustment was made, and that the validity of the theory could be checked to a certain extent by examining how closely the observed values would agree with the theoretical after making such adjustments. Figure 156A shows the adjusted amplitudes and phase angles of the internal waves of order one to four between the surface and 500 m. From this figure it is evident that the wave of third order is dominant. By combining these four waves one obtains
| Depth (m) | Amplitude (cm/sec) | Phase | ||
|---|---|---|---|---|
| Observed | Computed | Observed | Computed | |
| 0 | 21.8 | 31.4 | 144.9° | 126.8° |
| 50 | 21.6 | 15.1 | 120.3 | 139.0 |
| 100 | 13.7 | 15.6 | 247.8 | 247.5 |
| 150 | 14.0 | 19.5 | 237.7 | 247.6 |
| 200 | 14.9 | 13.0 | 228.8 | 225.6 |
| 350 | 9.0 | 0.5 | 260.9 | 202.5 |
| 500 | 7.8 | 6.1 | 2.9 | 352.7 |
These results cannot be considered as conclusive evidence as to the character of the observed displacements, because the numerical values of the theoretical terms have been adjusted to fit the data, but an entirely independent check can be obtained by computing the currents corresponding to the theoretical internal waves and comparing these computed values with the observed ones. When doing this, it should be borne in mind that the theory presupposes the existence of progressive waves, and agreement in phase of computed and observed currents would indicate that the internal waves actually were of the progressive type. It should also be borne in mind that the observed currents include ordinary tidal currents besides those associated with internal waves of tidal periods, and that for this reason certain discrepancies must be expected. The semidiurnal currents were not used as a check on the theory because there were reasons for believing that these were not of the simple progressive type, but the computed and observed diurnal currents which are shown in table 75 are in surprisingly good agreement, particularly when considering the reservations which were made. Lek points out that the greatest discrepancies between computed and observed values occur at a depth of 350 m, where according to the theory the current due to internal waves should nearly vanish, and that therefore the discrepancy may be due to the presence of actual tidal currents. It thus appears that in this case the complicated variations of the currents
Lek and Fjeldstad find the following velocities of progress: c1 = 234 cm/sec, c2 = 116 cm/sec, c3 = 77 cm/sec, c4 = 58 cm/sec. The corresponding lengths of the waves of period 24 lunar hours are 210 km, 104 km, 69 km, and 52 km, respectively.
This example illustrates the numerous complications which may be encountered anywhere in the ocean, and serves to emphasize the fact that many observations of currents over long periods of time are needed in order to obtain information as to the many types of motion present in the sea.
Standing internal waves may be present in bays or basins. The probability of such standing waves is great, because in heterogeneous water in a bay or a basin of a given form a large number of internal waves of different wave lengths are possible, corresponding to waves of different order and corresponding to different period lengths. An intermittent disturbance or a disturbance of tidal period may therefore bring about an oscillation which corresponds to one of the possible free oscillations of the system, particularly because a small amount of energy is needed for creating an internal wave.
In a bay of constant depth and width the periods of oscillation of free standing waves in the presence of two layers are
where n is a positive integer (p. 539). The periods of such standing waves may be very long. With l = 200 km = 2 × 10−7 cm, p − p′ = 2 × 10−3, h = 400 m = 4 × 104 cm, and h′ = 100 m = 104 cm, one obtains T1 = 3.25 days. When dealing with such long periods the effect of the earth's rotation must become conspicuous, and application of the formula is therefore restricted. This simple formula has nevertheless been used by Wedderburn in order to explain internal vertical oscillation of an amplitude of about 25 m and a period of about 14 days which O. Pettersson observed in Gulmarfjord on the southwest coast of Sweden during two months of 1909. With l = 200 km, p — p′ = 4 × 10−3, h = 100 or 200 m, and h′ = 20 m, corresponding approximately to the conditions at which the observations were made, and adding a correction for the width of the opening which was about 50 km (p. 541), one obtains T1 = 13.9 or 14.2 days.A computation of this nature may give approximately correct results if a distinct boundary surface is present and if the geometrical shape
In conclusion, two effects of internal waves should be emphasized because they have bearing on general oceanographic problems. In the first place the internal waves probably are of importance to the process of mixing. Where internal waves are present, large velocity gradients are often met with which lead to great values of the eddy viscosity. Furthermore, owing to the dissipation of energy by friction, a given water mass will never return exactly to the locality from which it started out, even in the absence of general currents, and consequently an exchange of water in horizontal direction must take place. The intensity of the mixing processes which are maintained by internal waves has not yet been examined, but it is probable that these processes are not negligible.
In the second place, it has been pointed out, particularly by Seiwell (1937), that owing to the existence of internal waves the distribution of mass along any vertical will be subject to periodic variations and, as a consequence, the geopotential height of the free surface relative to a given isobaric surface will vary periodically. This agrees with the statement (p. 588) that when dealing with internal waves on a boundary between two liquids the free surface will also show a wave motion of a small amplitude. The variations in height of the free surface are so small that when dealing with the internal wave they can be disregarded, but when examining results of dynamic computations they cannot be left out of account because these variations are of the same order of magnitude as the horizontal differences in geopotential height which may occur on distances up to 100 km or more. As an illustration, fig. 157 shows the variation of geopotential height of the free surface above the 800-decibar surface as derived from the serial observations at Snellius station 253A. It is seen that during 26 hours the height of the surface varies no less than 14.5 dyn cm. Seiwell has computed that, due to internal waves at Atlantis station 2639 (p. 453) the variations of the
Variation with time of the dynamic height of the surface over the 800-decibar surface at Snellius Station 253A.
[Full Size]
Bibliography
Cornish, Vaughan. 1912. Waves of the sea and other water waves. Chicago. Open Court Pub. Co.374 pp.1912. 
Cornish, Vaughan. 1934. Ocean waves and kindred geophysical phenomena. Cambridge University Press. 164 pp.1934. 
Darwin, G. H.1911. The tides and kindred phenomena in the solar system. 3rd ed.New York. Houghton, Mifflin.1911. 
Defant, A.1925.
“Gezeitenprobleme des Meeres in Landnähe”
. Probleme der kosmischen Physik, VI. Hamburg. 80 pp.1925. 
Defant, A.1929.
“Dynamische Ozeanographie”
. Einführing in der Geophysik. Berlin. III, 222 pp.1929. 
Defant, A.1932. Die Gezeiten und inneren Gezeitenwellen des Atlantischen Ozeans. Deutsche Atlantische Exped. Meteor1925–1927, Wiss. Erg., Bd. 7, Heft 1, 318 pp.1932. 
Defant, A.1940.
“Die ozeanographischen Verhältnisse während der Ankerstation des Altair am Nordrand des Hauptstromstriches des Golfstroms nördlich der Azoren”
. Ann. d. Hydrogr. u. Mar. Meteor., November-Beiheft, 4. Lief, 35 pp.1940. 
Ekman, V. W.1904.
“On dead water. Norwegian North Polar Exped.”
, 1893–1896, Sci. Results, v. 5, no. 15, 152 pp.1904. 
Ekman, V. W., and B. Helland-Hansen. 1931. Measurements of ocean currents (Experiments in the North Atlantic). Kungl. fysiografisca Sällskapet i Lund Förhandlingar, v. 1, no. 1. 1931. 
Fjeldstad, J. E.1929.
“Contribution to the dynamics of free progressive tidal waves”
. Norwegian North Polar Exped. with the Maud, 1918–1925, Sci. Results, v. 4, no. 3, 80 pp.1929. 
Fjeldstad, J. E.1933. Interne Wellen. Geofysiske Publikasjoner, v. 10, no 6, 53 pp.1933. Oslo. 
Fjeldstad, J. E.1936.
“Results of tidal observations. Norwegian North Polar Exped. with the Maud, 1918–1925”
, Sci. Results, v. 4, no. 4, 88 pp.1936. 
Fleming, Richard H.1938.
“Tides and tidal currents in the Gulf of Panama”
. Jour. Marine Research, v. 1, p. 192–206. 1938. 
Gaillard, D. D. W.1904.
“Wave action in relation to engineering structures”
. Prof. Pap. Corps. Engin., U. S. Army, no. 31, Washington, D. C. 1904. 
Gutenberg, B.1939.
“Tsunamis and earthquakes”
. Seismol. Soc. Amer., Bull., v. 29, p. 517–526. 1939. 
Harris, Rollin A.1894–1907.
“Manual of tides. Parts 1 to 5. Appendices to U. S. Coast and Geod”
. Surv., Reports. Washington, D. C. 
Helland-Hansen, B.1930.
“Physical oceanography and meteorology”
. Michael Sars North Atlantic Deep-Sea Exped., 1910, Rept. Sci. Results, v. 1, 115 + 102 pp.1930. 
Helland-Hansen, B., and F. Nansen. 1909.
“The Norwegian Sea”
. Norwegian Fishery and Marine Investigations, Report. v. 2, pt. 1, no. 2, 390 pp. + tables. 1909. 
Hidaka, K.1935.
“A theory of shelf seiches”
. Imperial Marine Observatory, Memoirs, v. 6, p. 9–11. 1935. Kobe, Japan. 
Hidaka, K.1939.
“Study of ocean waves by stereophotogrammetry (in Japanese)”
. Journal of Oceanography (Imperial Marine Observatory, Kobe, Japan), v. 11, no. 4, p. 693–703. 1939. 
Krümmel, O.1911. Handbuch der Ozeanographie, v. 2. Stuttgart. 764 pp.1911. 
Lamb, H.1932. Hydrodynamics. London. Cambridge University Press. 6th ed., 738 pp.1932. 
Lek, Lodewijk. 1938. Die Ergebnisse der Strom- und Serienmessungen. Snellius Exped. in the eastern part of the Netherlands East-Indies, 1929–1930, v. 2, pt. 3, 169 pp.1938. 
Marmer, H. A.1926. The tide. New York. D. Appleton. 282 pp.1926. 
Marmer, H. A.1926b.
“Coastal currents along the Pacific coast of the United States”
. U. S. Coast and Geod. Surv., Spec. Pub. 121, 77 pp.1926. 
Marmer, H. A.1927.
“Tidal datum planes. Washington, D. C. U. S”
. Coast and Geod. Surv., Spec. Pub. 135, 142 pp.1927. 
Marmer, H. A.1932. Tides and tidal currents. Physics of the earth, v. 5, Oceanography, p. 229–309. National Research Council, Bull. no. 85. Washington, D. C. 1932. 
Munk, W. H.1941.
“Internal waves in the Gulf of California”
. Jour. Marine Research, v. 4, p. 81–91. 1941. 
Patton, R. S., and H. A. Marmer. 1932. The waves of the sea. Physics of the earth, v. 5, Oceanography, p. 207–228. National Research Council, Bull. no. 85. Washington, D. C. 1932. 
Rossby, C.-G., and R. B. Montgomery. 1935.
“The layer of frictional influence in wind and ocean currents”
. Papers in Physical Oceanography, v. 3, no. 3, 101 pp.1935. 
Schumacher, A.1928.
“Die stereogrammetrische Wellenaufnahmen der deutschen Atlantischen Expedition”
. p. 105–120 in Ergänzungsheft 3, Zeitschr. f.d. Gesellschaft für Erdkunde zu Berlin. 1928. 
Schumacher, A.1939.
“Stereophotogrammetrische Wellenaufnahmen”
. Deutsche Atlantische Exped, Meteor, 1925–1927, Wiss. Erg., Bd. 7, H. 2, L. 1, 156 pp. and Atlas. Berlin. 1939. 
Schureman, P.1924.
“A manual of the harmonic analyses and prediction of tides”
. U. S. Coast and Geod. Surv., Spec. Pub. 98, 416 pp.1924. 
Seiwell, H. R.1937.
“Short-period vertical oscillations in the western basin of the North Atlantic”
. Papers in Physical Oceanography, v. 5, no. 2, 44 pp.1937. 
Shepard, F. P., and E. C. La Fond. 1939. Undertow. Science, v. 89, p. 78–79, 1939. 
Shepard, F. P., and E. C. La Fond. 1940.
“Sand movements along the Scripps Institution pier”
. Amer. Jour. Science, v. 238, p. 272–285. 1940. 
Shepard, F. P., K. O. Emery, and E. C. La Fond. 1941.
“Rip currents: A process of geological importance”
. Jour. Geology, v. 49, p. 337–369. 1941. 
Sverdrup, H. U.1927. Dynamic of tides on the North Siberian Shelf. Geofysiske Publikasjoner, v. 4, no. 5, 75 pp.1927. Oslo. 
Sverdrup, H. U.1940.
“The Gulf of California: Preliminary discussion of the cruise of the E. W. Scripps in February and March, 1939”
. Sixth Pacific Sci. Congr., California, 1939, Proc., v. 3, p. 161–166. 1940. 
Tannehill, I. R.1938.
“Hurricane of September 16 to 22, 1938”
. Monthly Weather Rev., v. 66, p. 268–288. 1938. 
Thorade, H.1928.
“Gezeitenuntersuchungen in der Deutschen Bucht der Nordsee”
. Deutsche Seewarte, Archiv. Bd. 46, Nr. 3, 85 pp., 1928. Hamburg. 
Thorade, H.1931. Probleme der Wasserwellen. Probleme der kosmischen Physik, XIII and XIV, 219 pp.1931. Hamburg. 
U. S. Beach Erosion Board. 1941.
“A study of progressive oscillatory waves in water”
. Tech. Series, Washington, Govt. Print. Off., no. 1, 39 pp.1941. 
van Veen, Joh. 1938.
“Water movements in the Straits of Dover”
. Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du. Conseil, v. 13, p. 7–36. 1938. 
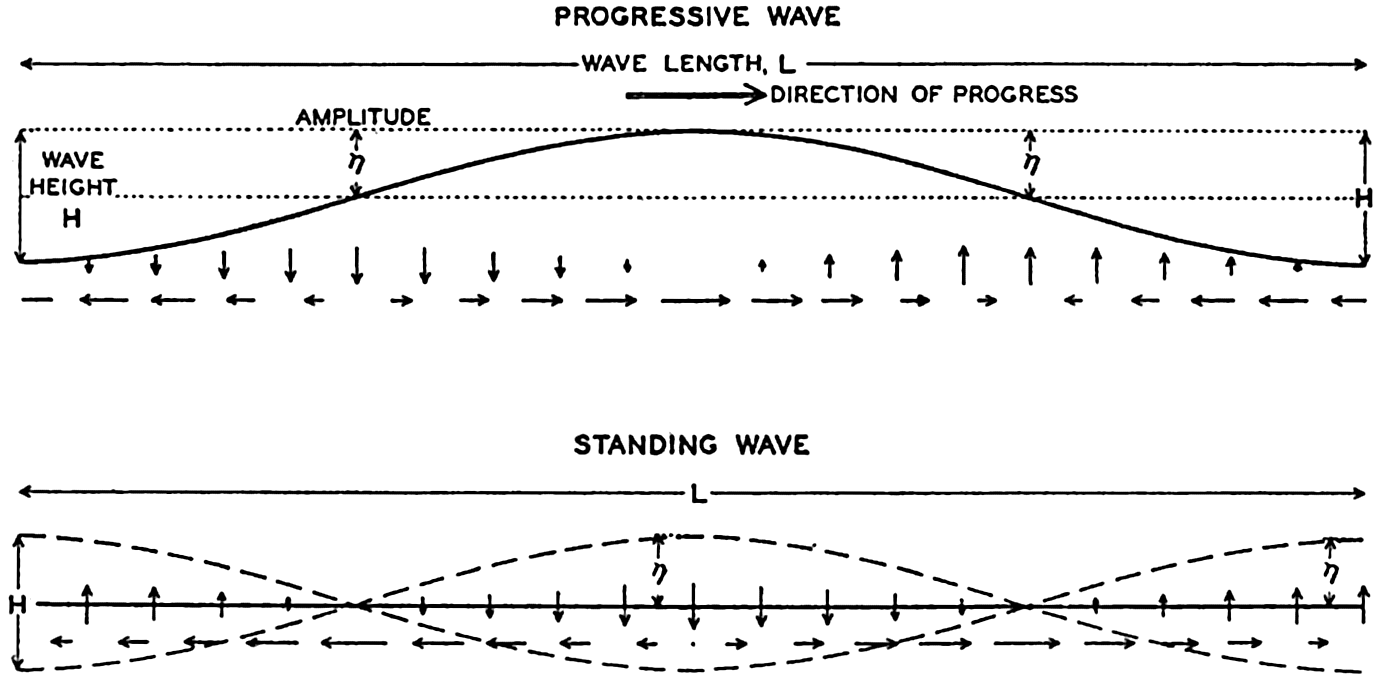
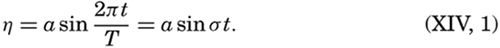
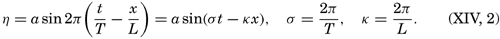


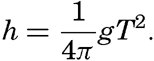
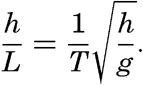
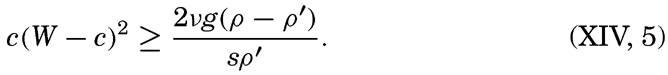

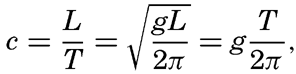
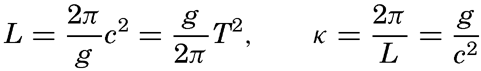
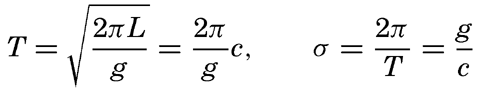
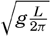 [
[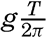 [
[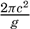 [
[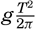 [
[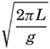 [
[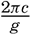 [
[