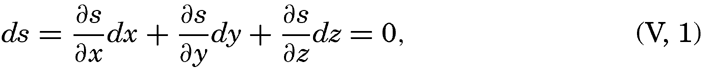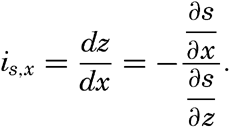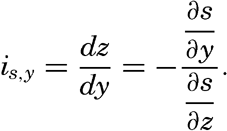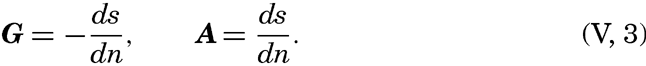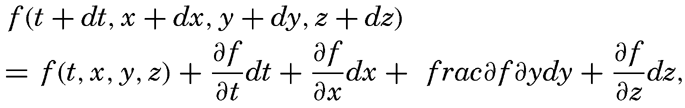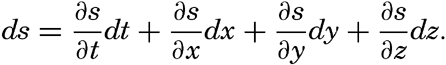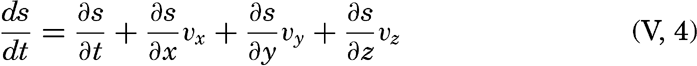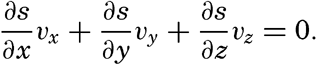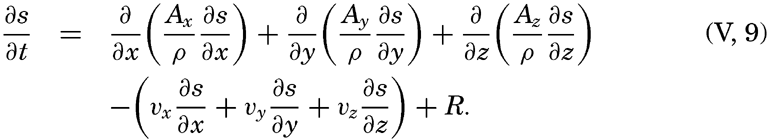V. Theory of Distribution of Variables in the Sea [PDF]
Scalar Fields
It cannot be too strongly emphasized that the ocean is three-dimensional and that the distribution of properties or the type of motion must be represented in space. For this purpose a convenient system of coordinates is needed. Any point in the ocean can be designated by means of its geographic latitude and longitude and its depth below sea level, but if one deals with a small area one may consider the surface of the earth within that area as flat, and can introduce ordinary rectangular coordinates with the horizontal axes at sea level and the vertical axis positive downward. By “sea level” is meant not the actual sea level but an ideal sea level, which is defined as a surface along which no component of gravity acts. The difference between the actual and the ideal sea level will be further explained when dealing with the distribution of pressure (p. 406).
The location in the ocean space of any given surface is completely determined if in every latitude and longitude one knows the depth of the surface below the ideal sea level. In a chart this surface can be represented by means of lines of equal depth below sea level (isobaths), which together render it picture of the topography of the surface. Thus, the topography of the sea bottom is shown by isobaths drawn at selected intervals of depth.
The quantities that must be considered when dealing with the sea are either scalars or vectors. A scalar quantity is a physical quantity whose measure is completely described by a number, that depends on the selected system of units. Pressure, temperature, salinity, density, and oxygen content can be mentioned as examples of scalar quantities. A vector is a physical quantity that is completely described by magnitude and direction. The velocity of a particle, the acceleration of a particle, and the forces acting on a particle are examples of vectors.
The magnitude of a vector, such as the numerical value of the velocity of a particle, is a scalar quantity. A vector can be represented by means of its components along the axes of a coordinate system, and these components are scalar quantities.
A continuous fluid is characterized, at every point in the space which it occupies, by a number of different properties. The space distribution of one particular property is called the field of that property. The field is called a scalar field if the property is a scalar quantity, and a vector field if the quantity is a vector. In the ocean there are scalar fields such as the pressure field, the temperature field, and the density field, and there are vector fields such as the velocity field, the acceleration field, and so on.
The term field was first applied to a vector field in order to describe the distribution of electromagnetic forces. Every student of physics has seen the magnetic field of force demonstrated by means of iron filings placed on a card above a magnet, but this experiment brings out only certain characteristics of the field. It shows the direction of the magnetic forces in one single plane, but it does not show the space distribution or the magnitude of the force of the field.
A scalar field is completely represented by means of equiscalar surfaces—that is, surfaces along which the scalar quantity has the same numerical value. The temperature field in the ocean, for instance, would be completely described if one knew exactly the form of the isothermal surfaces, and, similarly, the pressure field would be fully represented if one knew the form of the isobaric surfaces. However, it is impracticable to prepare space models that show the actual configuration of isothermal surfaces or other equiscalar surfaces in the ocean, and it would be impossible to publish such representations. For practical purposes one must select other forms of representation. One widely used method is to show the lines of intersection between equiscalar surfaces and the coordinate surfaces. A chart showing the distribution of temperature at sea level is an example of such representation. In this case the sea level represents one of the principal coordinate surfaces, and the isotherms represent the lines at which the surfaces of equal temperature in the sea intersect the sea surface. Similarly, a chart showing the distribution of temperature at a depth of 1000 m shows the lines along which the isothermal surfaces intersect the 1000-m surface, whereas the temperature distribution in a vertical section shows the lines along which the isothermal surfaces intersect the vertical plane that is under consideration.
A series of horizontal charts of isotherms in surfaces at different distances below sea level give a representation of the temperature field in the ocean, and a series of vertical sections showing isotherms give another representation of the same field.
On the other hand, one can make use of an entirely different method of representation. Instead of showing the lines along which the isothermal surfaces intersect a coordinate surface, one can represent the isothermal surface itself and can show the lines along which the coordinate surfaces at different distances below sea level intersect that surface. Such a
These topographic charts would represent charts of absolute topography, because it is assumed that the depths below the ideal sea level are known. This ideal sea level, however, is a fictitious level that cannot be determined by observations, and all measurements have to be made from the actual sea level. In practice, therefore, the topography of a surface in the ocean will not represent the absolute topography but a relative topography referred to the unknown shape of the actual sea surface. In many instances one need not take the difference between absolute and relative topography into account, because it generally amounts to less than 1 m. For instance, it can be neglected when one deals with isothermal surfaces, because the change in temperature on a fraction of a meter is generally negligible. When dealing with the isobaric surfaces, on the other hand, as will be explained in detail when discussing the field of pressure, one must discriminate sharply between absolute and relative topographies.
These matters have been set forth explicitly, because it is essential to bear in mind that one must always consider distribution in space, which can be fully described by means of equiscalar surfaces. These, however, may have highly complicated forms.
The mathematical definition of an equiscalar surface can be written
where s is the scalar quantity under consideration (temperature, pressure, density, and so forth), ∂ s/∂ x · dx is the change of the scalar on the distance dx, ∂ s/∂ y · dy is the change on the distance dy, and ∂ s/∂ z · dz is the change on the distance dz. Along the equiscalar surface the total change must be zero, as expressed by (V, 1).
In a vertical section in the x-z plane the equiscalar curves are similarly defined by
From the latter equation the slope of the equiscalar surfaces in the x-direction is obtained:
So far, the discussion has dealt with equiscalar surfaces in general. In practice, one may select these surfaces so that there is a constant difference between the value of the variable at any two surfaces. These surfaces are called standard equiscalar surfaces. In the case of temperature, the isothermal surfaces might be selected for every one degree of temperature; in the case of salinity, the isohaline surfaces might be selected for every 0.1 ‰, and so on. These surfaces would divide the space into thin layers characterized by a constant difference of the quantity at the two boundary surfaces of every layer. Such layers are called equiscalar sheets. It should be noted that the scalar is not constant within this sheet but has a constant average value. It is evident that the thickness of these sheets represents the rate at which the scalar varies in a direction at right angles to the equiscalar surfaces. Where the sheets are thin the variation is great, but where the sheets are thick the variation is small. The rate of variation can be represented by means of a vector whose direction is normal to the equiscalar surface and whose magnitude is inversely proportional to the thickness of the sheet. The vector representing the rate of decrease is generally called the gradient (temperature gradient, pressure gradient), and the vector representing the rate of increase is called the ascendant. If the scalar is called s, then the gradient, G, and the ascendant, A, are defined by the equations
Vectors are printed in bold-face type.
If the field is represented by means of a sufficient number of surfaces, these surfaces will completely define the gradients and ascendants that are characteristic of the distribution. Thus, the special vector fields of gradients and ascendants are entirely described by means of systems of equiscalar surfaces, but other vector fields cannot be described in that manner. Vector fields will be dealt with in chapter XII.
Relation between the Distribution of Properties and the Currents in the Sea
Consider any scalar quantity, s (temperature, salinity, pressure, oxygen content, and so on), the distribution of which is continuous in space and time, so that it can be represented as a function of time and the three space coordinates, s = f(t,x,y,z). Let us assume that this scalar quantity can be considered a property of the individual particles of the fluid. A particle in motion after a time dt will be in a new locality,
Dividing by dt and considering that dx/dt, dy/dt and dz/dt represent the components of the velocity, one obtains
The first term on the right-hand side represents the rate of change in a fixed locality—that is, the local change. The last three terms are together called the advection term, because they represent changes that take place in the presence of currents. This relationship is a purely formalistic one and gives no information as to the processes affecting the distribution; it merely states that within a field the individual time change can be considered as composed of two terms: the local time change and the advection.
A few important points can be brought out by means of the above equation: (1) the distribution of any scalar quantity is stationary—that is, independent of time if the local change is zero (∂s/∂ t = 0); (2) the advection terms disappear if there is no motion or if the field is uniform—that is, if either vx = vy = vz = 0 or ∂ s/∂ x = ∂ s/∂ y = ∂ s/∂ z = 0; (3) when the individual change is zero (ds/dt = 0), the local change is equal to the advection but is of opposite sign; (4) if the field of a property is stationary (∂ s/∂ t = 0) and if, further, the individual time change is zero (ds/dt = 0), equation (V, 4) is reduced to
This equation is fulfilled only if the flow is directed along the equiscalar surfaces of the property, as can be seen by comparison with equation (V, l), or by examination of the two-dimensional case.
Distribution of Conservative Concentrations in the Sea
The discussion has so far been of a purely formalistic nature. If one goes a step further and considers the processes that maintain or tend
The processes that tend to modify the concentrations can be divided into two groups: external processes, which are active only at the boundary surfaces of the fluid, and internal processes, which are active anywhere in the fluid. The external processes are of importance in determining the concentrations at the boundaries, and the internal processes, together with the boundary values, determine the distribution throughout the fluid.
By conservative concentrations are meant concentrations that are altered locally, except at the boundaries, by processes of diffusion and advection only. Heat content and salinity are two outstanding examples of conservative concentrations. Consider a cube the surfaces of which are of unit area and are normal to the coordinate axes. Through the two surfaces that are normal to the x axis, diffusion leads to a transport in unit time of (Ax/ρ)1(∂ s/∂ x)1 and (Ax/ρ)2(∂ s/∂ x)2, respectively, where both the coefficient, Ax, and the derivative, ∂ s/∂ x, may vary in the x direction. The coefficient of diffusion enters here in the “kinematic” form (p. 470) as A / ρ, where A is the eddy diffusivity, because concentrations have been defined as amounts per unit volume. The difference per unit length of these transports, ∂/∂ x[(Ax/ρ)(∂ s/∂ x)], represents the net change of concentration in the unit volume due to diffusion. In the presence of a current in the x direction, there will also be a net change of concentration due to advection. The concentration that a current of velocity, vx, transports through a unit surface in unit time is equal to svx, and, if this transport changes in the direction of flow, the concentration per unit volume is altered by —∂(svx)/∂ x. Similar considerations are applicable to transport through the other surfaces of the cube, and the combined local change of concentration, therefore, is the sum of terms representing diffusion and advection:
The last term can be written
Taking equation (V, 4) into consideration, one obtains
or, in words: Individual time change of concentration equals effect of diffusion.
In practice these equations must be greatly simplified. Consider, for example, a two-dimensional system in which the velocity is directed along the x axis, in which diffusion in the x direction can be neglected, and in which it can be assumed that the coefficient of vertical diffusion, A / ρ, is constant. For such a system the condition for a stationary distribution of s, (∂ s/∂ t = 0), is reduced to
This equation has been used by Defant (1929) and Thorade (1931) for studying the character of stationary distributions and by Defant (1936) for computing the ratio A / vx from observed distributions.
As another example, consider a uniform field for which ∂ s/∂ t=ds/dt and assume that Ax = Ay = 0. The above equations are then reduced to
which represents the equation of temperature conduction (p. 135). It may be observed that temperature is not a concentration according to the above definition, but since the temperature is proportional to the heat content, cpϑ, of a unit volume, s can mean temperature.
Other simplifications of the equations can be made, depending upon the nature of the problem under consideration (Montgomery, 1939, Sverdrup, 1939).
Distribution of Nonconservative Concentrations
By nonconservative concentrations are meant primarily concentrations whose distributions are influenced by biological processes besides
The local time change of concentration due to biological processes will be called R. Adding this quantity at the right-hand side of equation (V, 5) one can state
In words, local time change of concentration equals effects of diffusion minus advection plus biological processes. This equation can be simplified in the same manner as equations (V, 5) and (V, 6) (Seiwell, 1937, Sverdrup and Fleming, 1941).
The Principle of Dynamic Equilibrium
Experience shows that in a large body of water comparable, say, to the body of water in the Mediterranean Sea, the average conditions do not change from one year to another. The average distribution of temperature remains unaltered year after year, and the same is true as to the average salinity, oxygen content, and contents of minor constituents. If time intervals longer than a year are considered, say ten-year periods, it is probable that even the average number of different species of organisms remains unaltered, provided that the nonaquatic animal, man, does not upset conditions by exterminating certain species and depleting the stock of others. These unchanging conditions represent a state of delicate dynamic equilibrium between factors that always tend to alter the picture in different directions.
In dealing with conservative concentrations, diffusion and advection are at balance except at the sea surface, where external processes contribute toward maintaining the concentration at a certain level. This was illustrated when discussing the general distribution of surface salinity (p. 125), which was shown to depend on two terms, one that represents the external processes of evaporation and precipitation, and one that represents the internal processes of diffusion and advection. Similarly, the surface temperature depends upon heating and cooling by processes of radiation and by exchange with the atmosphere and upon conduction and advection of heat.
In a study of the subsurface distribution of temperature and salinity, it is not necessary to know the processes that maintain the surface values, but it is sufficient to determine these values empirically. If this could be done and if the processes of diffusion and the currents were known, the general distribution of temperature and salinity could be computed. Conversely, if these distributions were known, information as to diffusion and currents could be obtained. In oceanography only the latter method of approach has been employed.
When nonconservative concentrations are dealt with, the principle of a dynamic equilibrium implies that the effects of diffusion, advection, and biological processes cancel. Of the nonconservative concentrations, only the dissolved gases are greatly influenced by the contact with the atmosphere, and other nonconservative concentrations are practically unaltered by external processes.
Application of the principle of dynamic equilibrium can be illustrated by considering the distribution of oxygen. Below the euphotic zone, biological processes that influence the oxygen content always lead to a consumption of oxygen, and the processes of diffusion and advection therefore must lead to a replenishment that exactly balances the consumption. No further conclusions can be drawn. This obvious consideration has been overlooked, however, and some authors have interpreted a layer of minimum oxygen content as a layer of minimum replenishment (Wüst, 1935), while others have considered it a layer of maximum consumption (Wattenberg, 1938).
Conclusions as to the rapidity of consumption (and replenishment) could be drawn from the known distribution of oxygen only if the consumption depended upon the absolute content of oxygen, but the consumption appears to be independent of the oxygen content until this has been reduced to nearly nil (ZoBell, 1940). When all oxygen has been removed, consumption and replenishment must both be zero, and even this obvious conclusion should not be overlooked.
In certain instances a relation may exist between the oxygen distribution and the character of the current. Assume that a nearly horizontal internal boundary exists which separates currents flowing in opposite directions, that diffusion takes place in a vertical direction only, and that the coefficient of diffusion is independent of z. When dynamic equilibrium exists, equation (V, 9) is then reduced to
Since the consumption equals — R and is always positive, the curvature of s is positive when plotted against z. The curvature cannot remain positive at all depths, and therefore it is probable that s, the oxygen content, must be at a minimum near the boundary surface. Thus, a
Similar reasoning is valid when dealing with compounds that are removed from the water by organisms for building up their tissues and are returned to solution as metabolic products or by decomposition of organic tissues. A balance is maintained, but in many cases it is not correct to speak of “replenishment” by advection and diffusion, as in the case of oxygen, because the biological processes may lead to a net replenishment, in which case the physical processes must take care of a corresponding removal. Thus, in the deeper layers phosphates and nitrates are added to the water by decomposition of organic matter and removed by diffusion and advection.
When dealing with populations, similar considerations enter. It must be emphasized especially that the number of organisms present in unit volume of water gives no information as to the processes that operate toward changing the number. A small population of diatoms, say, may divide very rapidly without increasing in number, owing to the presence of grazers that consume diatoms. On the other hand, a large population of diatoms may not indicate a rapid production of organic matter, because further growth may be impossible owing to lack of nutrient salts in the water. The terms “population” and “production” have to be clearly defined and kept separate. (“Population” represents concentration, whereas “production” represents one of the processes that alter the concentration.
Another warning appears to be appropriate—namely, a warning against confusion between individual and local changes (p. 157). From the fact that a local population remains unaltered, it cannot be concluded that the population within the water which passes the locality of observation also remains constant—that is, that the individual time change is zero. Similarly, if a sudden change in population is observed in a given locality, it cannot be concluded that the processes which have been active in that locality have led to a rapid growth, because it is equally possible that a new water mass of other characteristics is passing the locality.
If the external influences were clear, if processes of diffusion and advection were known, and if biological and organic chemical processes were fully understood, the distribution of all concentrations could be accounted for. It would then be possible not only to explain the average distribution but also to account for all periodic and apparently random changes. This is the distant goal, but when working toward it one must be fully aware of the limitations of the different methods of approach.
Thus, complete description of the oxygen distribution below the euphotic zone is theoretically possible if the oxygen content in the surface
The dynamic equilibrium, the importance of which has been stressed, exists only insofar as average conditions within a large body of water and over a considerable length of time are concerned. During any part of the day or year the external or internal processes may be subject to periodic or random variation such that at a given moment no equilibrium exists (∂ s/∂ t ≢ 0). At the surface, heating periodically exceeds cooling, and cooling periodically exceeds heating, as a result of which the surface temperature is subjected to diurnal and annual variations that by processes of conduction are transmitted to greater depths. It is possible that longer periods exist which are related to periodic changes in the energy received from the sun, but these long-period variations are of small amplitudes. In many areas, shifts of currents lead to local changes of the temperature which are periodic in character if the shifts are associated with the seasons, or nonperiodic if they are related to apparently random events. In the discussion of the annual variation of temperature (p. 131) the effect of these different processes was illustrated. Similar reasoning is applicable to periodic and random variations of salinity and also to variations of nonconservative properties.
From what has been stated it is evident that in the discussion of the distribution of concentrations in the sea it is as yet impossible to apply a method of deduction based on knowledge of all processes involved in maintaining the distribution. Instead, one has to follow a winding course, discuss processes and their effects whenever possible, discuss actual distributions if such have been determined, and either interpret these distributions by means of knowledge gained from other sources as to acting processes or draw conclusions as to these processes from the distribution. In some instances the processes that maintain the boundary values can be dealt with at considerable length, but otherwise the observed boundary values have to be accepted without attempts at explanation. In all cases, however, it is essential to bear in mind that one is dealing with concentrations in a continuous medium and that general considerations as set forth here are always applicable.
Bibliography
Defant, Albert. 1929. Stabile Lagerung ozeanischer Wasserkörper und dazu gehörige Stromsysteme. Berlin Universität, Institut f. Meereskunde, Veröff., N.F., A. Geogr.-naturwiss, Reihe, Heft, 19, 33 pp., 1929.
Montgomery, R. B.1939.
“Ein Versuch, den vertikalen und seitlichen Austausch in der Tiefe der Sprungschicht im äquatorialen Atlantischen Ozean zu bestimmen”
. Ann. d. Hydrogr. u. Mar. Meteor., p. 242–46, 1939. Seiwell, H. R.1937.
“The minimum oxygen concentration in the western basin of the North Atlantic”
. Papers in Physical Oceanogr. and Meteorol., v. 5, 24 pp., 1937. Cambridge and Woods Hole, Mass. Sverdrup, H. U.1939.
“Lateral mixing in the deep water of the South Atlantic Ocean”
. Jour. Marine Research, v. 2, p. 195–207, 1939. Sverdrup, H. U., and R. H. Fleming. 1941.
“The waters off the coast of southern California, March to July, 1937”
. Scripps Inst. Oceanogr., Univ. Cralifornis, Bull., v. 4, no. 10, p. 261–378, 1941. Thorade, Hermann. 1931.
“Strömung und zungenförmige Ausbreitung des Wassers. Gerlands Beitr”
. z. Geophys., Bd. 34, Köppen-Bd. 3, p. 57–76, 1931. Wattenberg, Hermann. 1938.
“Die Verteilung des Sauerstoffs und des Phosphats im Atlantischen Ozean. Deutsche Atlantische Exped”
. Meteor 1925–1927, Wiss. Erg., Bd. 9, 1. Lief, 132 pp., 1938. Wüst, Georg. 1935.
“Die Stratosphäre. Deutsche Atlantische Exped”
. Meteor 1925–1927, Wiss. Erg., Bd. 6, 1 Teil, 2. Lief, 288 pp., 1935. ZoBell, C. E.1940.
“The effect of oxygen tension on the rate of oxidation of organic matter in sea water by bacteria”
. Jour. Marine Research, v. 3, no. 3, p. 211–223, 1940.