Chapter Eight—
Descartes in Relational Garb
"Why do we eat?" begins the popular French cookbook Je sais cuisiner (I know how to cook), by Ginette Mathiot. "Everyone has a pretty good idea. 'We need to eat in order to live.'" The question is how to do it. "In the present era, when the scientific spirit is increasingly asserting itself, nutrition often continues to be the victim of custom and prejudice and is governed by chance or caprice. But knowing how to nourish oneself is a science that one cannot scorn without detriment to one's health and to the family budget." Mme. Mathiot then goes on to explain that food responds to two "essential needs of our organism": the need for matter and the need for energy. Foods can thus be divided into two categories, depending on whether they provide energy or matter.[1] A few dozen pages later the reader has all the necessary information, together with the fundamental principles, to prepare a nutritious, economical, and tasty meal for any occasion that may arise.
A little less than three hundred years before the publication of Je sais cuisiner, René Descartes published his renowned Discourse on Method . In that work Descartes proposed a new "method" of thinking or problem solving. His method consisted of four rules, which Descartes writes in the informal, first-person style of the entire Discourse : (1) "to accept nothing as true that I did not know to be evidently so," (2) "to divide each of the difficulties I was examining into as many particles as I could," (3) "to conduct my thoughts in order, beginning with the simplest objects and those that are easiest to understand, and progressing, as if by degrees, to the understanding of the most compound," and (4)
"always to carry out enumerations so complete and reviews so general, that I would be certain of having omitted nothing."[2]
Let's see how Descartes's method applies to a given problem—eating. Why do I eat? That's easy: I need to eat in order to live ("to accept nothing as true that I did not know to be evidently so"). How do I determine what to eat? Subdivide: there are two different categories of food, and each of these may be divided into various actual species of edible things ("to divide each of the difficulties I was examining into as many particles as I could"). What to do with all these edible things to make them nutritious, economical, and tasty? Start with the basic principles of nutrition, move to the basic principles of cooking, and continue building from there ("to conduct my thoughts in order, beginning with the simplest objects and those that are easiest to understand, and progressing, as if by degrees, to the understanding of the most compound"). What do I do, now that I'm ready to head for the kitchen and prepare something to eat? Stock my kitchen with all the utensils necessary for successful cooking (Mathiot lists them on pages 51–52) and consult a list of thousands of recipes ("to carry out enumerations so complete and reviews so general, that I would be certain of having omitted nothing").
I don't know anything about Ginette Mathiot's upbringing and can't say whether or not she was a scholar of Descartes. But the method is unquestionably in her cookbook. How many American authors of cookbooks start out with the basic question and the most clearly evident truth about their subject and then reason in so systematic a fashion to the real substance of their books, namely the recipes?[3] The Cartesian method is pervasive in French thought. One sees again and again in writing of all sorts this urge always to start back at the beginning of a thing and then carry it through its steps to the general and abstract conclusions that follow from it. All American students of French know this style of thinking, just as French schoolchildren do, because when they learn to write those infuriating and tedious exercises in literary analysis called explications de texte, they are taught always to start with the facts, to reason from the concrete to the abstract, from the simple to the complex, from the specific to the general.
In his late work The Crisis of European Sciences and Transcendental Phenomenology Husserl made the claim that Descartes is the "original founding genius of all modern philosophy."[4] Descartes's contribution to the modern spirit was to expand Galileo's "mathematization of nature" into a global notion of philosophy as a "universal mathematics" (Universalmathematik ).[5] Descartes's entire method was based on mathe-
matical principles and designed to bring thought itself into accord with these principles. In the posthumously published "Rules for the Direction of the Mind" Descartes had written, several years before the Discourse, that to eliminate any obstacles in our efforts to discern the true from the false, we must follow an orderly method, like the one we see in the mathematical sciences. "Those who seek the straight path of truth must not concern themselves with any object about which they do not have certainty equal to [that afforded by] Arithmetic and Geometry."[6] In the Discourse and elsewhere Descartes talks repeatedly of the "certainty" and the "evidence" (that is, the state of being evident) of mathematical reasoning. I can't say for sure whether or not Descartes was the "original founding genius of all modern philosophy," but there is no mistaking the traces of his method in French thought.
Mallarmé and the Light of Reciprocal Reflections
In the first part of this book I suggested that Mallarmé was satirizing the Cartesian method in his introduction to English Words . If that is true, then it is no surprise to see the young Mallarmé in 1869 dreaming up a project for a book in which all the factors I've been talking about come together. It seems that in the late 1860s Mallarmé was considering taking a degree in linguistics, and in a fragmentary note somehow related to this plan he writes:
A strange little book, very mysterious, a bit in the manner of the Fathers, very distilled and concise—this in places that could give rise to enthusiasm (study Montesquieu).
In others, the great and long period of Descartes.
Then, in general, some La Bruyère and some Fénelon with a hint of Baudelaire.
Finally, some me [du moi ]—and some mathematical language.
(OC, , p. 851)
A paragraph or two farther on, he mentions the Discourse (misquoting the title) and then says, "We have not understood Descartes, foreigners have taken possession of him: but he did arouse French mathematicians" (OC, p. 851). Mallarmé never explains the intriguing little phrase about mathematical language. If by chance he meant something like the rigorous, methodical mode of exposition that Descartes's principles suggested, then we know that the closest he ever came to adopting the Cartesian method in his own writing was to parody it. And perhaps the
effort to parody that method was made only as the result of Mallarmé's having first internalized it.
The mathematical imagination had clearly seized hold of Mallarmé. But it is the "modern" kind of mathematics, the relational kind, that shows up time and again in his writings. Earlier I said that the theory Mallarmé appears to be proposing in "Crisis in Verse" led to a relational notion of language. In fact, if we look at that essay again, we can see that Mallarmé, without knowing it, is essentially giving us an illustration of Serres's argument about linear and tabular meanings. The "uniquestamp" view of meaning, where words turn out to be "materially truth itself," is really the linear view, or the symbolist view (in Serres's sense of symbolism). In this view one can draw a straight line from the signifying object to the thing it signifies. But in Mallarmé's enlightened view of language, meaning comes from the "reciprocal reflections" of words, and this sounds like Serres's notion of tabular meaning.
The idea of a group of relations appears several times in Mallarmé in one form or another. Later in "Crisis in Verse" he refers to music as "the set [ensemble ] of relations existing in everything" (OC, p. 368). Virtually the same phrase occurs in "The Book, Spiritual Instrument." Just after Mallarmé says, "Everything, in the world, exists to end up in a book," he lists the qualities that will be required in his book: "hymn, harmony and joy, like the pure set, grouped in some fulgurating circumstance, of relations between everything" (OC, p. 378). These phrases were composed later in Mallarmé's life. But even as early as 1866 he had adopted a relational view of poetic language. In a letter to François Coppée he says, "What we need to aim for above all in the poem is for words . . . to reflect on one another to the point where they appear no longer to have their own color but to be only the modulations of a scale ."[7] In a curious passage in a letter to another friend that same year, Mallarmé uses an image that suggests the same model. The young poet writes that he has just cast the plan for his entire oeuvre, after having discovered his own "center," "the center of myself, where I sit like a sacred spider, on the principal threads that have already come out of my mind and with whose help I will weave at the points of contact marvelous lacework."[8]
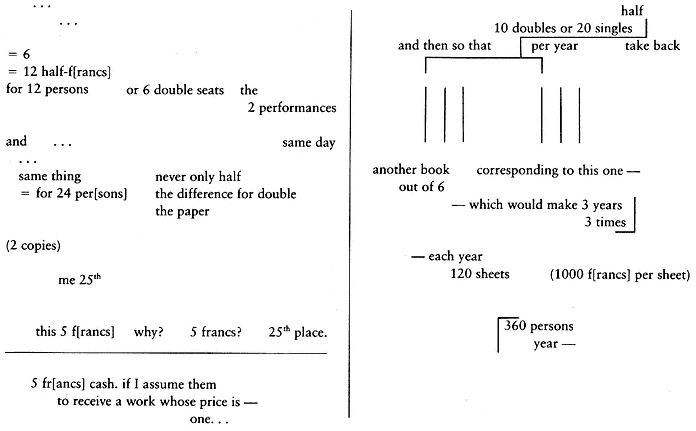
The place where we see Mallarmé's mathematical imagination at its best is his writings about the Book. In chapter 4 I described the manuscript notes that have been published under the title Le "Livre" de Mallarmé . It is full of numbers, calculations, and geometric designs. Some of the calculations appear to have to do with the number of spectators
at a performance of this mysterious work. Others have to do with the arrangement of pages in the work. Still others are about as apparently mundane a question as the amount of money the author will be able to collect from ticket sales at the performance. Sometimes all three appear together (see illustration).[9]
But even though it's hard to say what these manuscript notes are, we can see that the numbers are an essential part of the work that Mallarmé was contemplating. This is not just scratch paper on which the author figured his monthly budget. The recurrence of certain significant numbers, usually multiples of four, shows that all these details were integral to the work. Whatever this "work" was supposed to be, we can say with some confidence that its numerical properties were not going to be left to chance. In fact, one has the impression that the "content" could never be more precisely spelled out than it was because the essential nature of the work was not the content but exactly these numerical properties. Consider again the drawing on page 95. What is it? Not just doodling, because there are other designs in the manuscript that look similar and are accompanied by various terms that have occurred in lots of other places in the manuscript notes. It appears thus to have something important to do with what the work is. It's as if Mallarmé had set out to determine a set of geometric coordinates for his work and once that was done had decided nothing more was necessary.
How can a work have geometric coordinates? For one thing, it can be a performance in which the disposition of seats, spectators, and performers (the "operator") is an integral part of the work. In that case the work has coordinates in the literal sense, coordinates that belong to actual points in the space in which the performance takes place. Or it can be the sort of thing where there are mystical numerical correspondences between numbers of spectators and the amount of cash they pay for admission. Then the coordinates cannot be assigned to actual physical locations but exist instead as abstractions, and these abstractions are diagrammed in the manuscript notes. Or it can be a book whose pages may be shuffled and reshuffled in any number of combinations to generate as many different "works." In this "mobile-pages" conception the pages of the book are distributed in various determined locations of the space where the book is performed. In any of these cases the essential point about the work is that it is a relational structure.
One of the strangest things Mallarmé wrote is the text called Un coup de dés (A throw of the dice), published in 1897. There's no exact word for what this work is. In fact it's not even clear that Un coup de dés is
From Jacques Scherer, Le "Livre" de Matllarmé: Premières recherches sur des documents inédits
(Paris: Gallimard, 1957), pp. 37(A)–38(A).
the title. The text, twenty-one pages long, contains the sentence "Un coup de dés jamais n'abolira le hasard" ("A throw of the dice will never abolish chance") spread out in four pieces over seventeen pages ("Un coup de dés / jamais / n'abolira / le hasard"). This central sentence is printed in oversize type. In between its fragments are numerous phrases and sentences written in a variety of smaller types. The "poem," if that's what it is, is of course tricky to read. The main sentence gives it a kind of syntactic completeness and serves as a unifying device. The problem is what to do with all the other words. It is tempting to read them as a highly complex network of parenthetical and dependent clauses, where the clauses printed in smaller type depend on the ones printed in larger type. But even if you try to read it in this way, you get hopelessly bogged down in twenty-one pages of interlocking grammatical dependence and soon give up. Paul Valéry, who claims to be the first human being (other than the author) ever to see this work, says that Mallarmé first read it to him "in a low, even voice, without the slightest 'effect,' almost to himself."[10] The text actually may be read in many different ways: you may read one type size at a time, you may read through the text in the order in which the words are printed, or you may simply read in any order you choose. Once again we have a shuffling game, a relational scheme whose most prominent feature is precisely its refusal of linearity. This refusal is both syntactic and semantic—syntactic because a linear reading of the text is almost impossible, and semantic because this is one place where even the most old-fashioned thinker will see that meaning does not arise word by word in a linear fashion.
There is also no linear connection between the text and the person who wrote it. How do you establish an authorial voice for a thing that can't really be read in any of the traditional senses? no, there can be no sign of the author's presence, and strikingly enough, the disappearance of the author (a much-touted idea in Mallarmé's age) seems to be explained by the relational quality of the text. Think back to the passage in "Crisis in Verse" in which the notion of reciprocal reflections is introduced: "The pure work implies the elocutionary disappearance of the poet, who instead yields the initiative to words, mobilized by the clash of their inequality; they light up from their reciprocal reflections, like a trail of fire on gems, taking the place of that palpable breath in the lyric inspiration of yore or the enthusiastic personal direction of speech" (OC, 366). Once words start reflecting off each other, they can no longer reflect back to the author, or so the author appears to be suggesting. Right before the passage where Mallarmé talks about the "pure set . . .
of relations between everything" he says that the volume should "require no signatory" (OC, p. 378). In his autobiographical letter he speaks of a "text speaking of itself and without an author's voice" (OC, p. 663). And in Scherer's manuscript notes we read on the next-to-last page about a volume "for whose sense I am not responsible—not signed as such," this in the midst of a flurry of calculations determining the order and placement of pages (201 [A]).
"Things exist, we don't have to create them; all we have to do is grasp the relations between them; it is the threads of these relations that form verses and orchestras" (OC, p. 871). A sentence like this looks very structuralist avant la lettre . In fact, this and other passages convinced James Boon to write From Symbolism to Structuralism, in which he points out the affinities between the thought and poetics of French symbolist poets (Baudelaire, Mallarmé, Rimbaud, Verlaine, and, oddly, Rousseau and Proust) and the ethnology of structural anthropologist Claude Lévi-Strauss. For Boon, the passage I just quoted is emblematic of the whole worldview he sees in Mallarmé. Everything in Mallarmé's universe is relation, analogy, connection, and structure, just as it is in Levi-Strauss. The emphasis in both writers is always decisively shifted away from content. The one thing Boon doesn't discuss is the mathematical foundations of this type of thinking, but we know it's there for Mallarmé as it is for the entire structuralist movement.[11]
Valéry and the Discourse On His Method
Paul Valéry lived his life as though he had been put on earth to provide the rest of us with a caricature of the French mind. "Ce qui n'est pas clair n'est pas francais," goes the timeworn eighteenth-century expression that our French teachers taught us in high school. But clair in French means both "clear" in the sense of comprehensible and "light" in the sense of bright, and Valéry's poetry is filled with radiant Mediterranean sunshine. The mind strives for the clear and comprehensible because what is comprehensible is radiant. Valéry worshipped the human mind, especially his own. The "hero" of his prose work Monsieur Teste (Mister Head) says something that perfectly describes the author and his characteristic pose:"Je suis étant, et me voyant; me voyant me voir, et ainsi de suite . . ." ("I am [in the process of] being, and seeing myself; seeing myself see myself, and so on . . .").[12]
Valéry loved admiring the workings of his own mind. Wrapped up
with this fascination for the mind was a fascination for mathematics that went far beyond the numerical fantasies of Mallarmé. Unlike Mallarmé, Valéry actually fancied himself a mathematician, and he devoted an astounding amount of time and energy to studying contemporary mathematical theory and then trying to find applications for it in the most extraordinary fields. His friend Pierre Féline introduced him to a number of areas of mathematical study, among them group theory and transformation group theory. Valéry was apparently fond of using his knowledge of mathematics to dazzle his other friends, people like André Gide, who knew very little about such things.[13] The twenty-nine-volume set of Valéry's notebooks is a startling record of a mind obsessed with numbers, with itself, with its obsession with itself, with a mathematical expression of its own workings, and so on—a kind of monument to neo-Cartesian narcissism.[14]
Valéry's notebooks show a curious attitude toward "the original founding genius of all modern philosophy." To begin with, even though he devoted a substantial number of pages to ruminations on philosophers, Valéry was fond of playing the part of someone who is foreign to hard-core philosophy and doesn't quite understand it all. So when it comes to Descartes, he likes to talk about things that fussy, scholarly people would consider trivial. In one fairly long notebook entry he mentions the qualities that have struck him personally in various philosophers—this after saying that philosophers are boring to read and that their language is antipathetic to him. Of Descartes, Valéry can say only that it is the "individual" that "appears" to him, meaning, I assume, that he is attracted by the personal style of Descartes's writing.[15] He returns over and over again to the subject of Cartesian doubt and the most famous phrase from the Discourse on Method, "I think, therefore I am." And he speaks of the "insignificance" of the principles in the Discourse, saying that the charm of the work is "above its substance" (C, 16:728 [1:673]).
Like Descartes, Valéry sought clarity, certainty, evidence (again in the sense of "state of being evident"), and he sought it in mathematics. "Descartes. No occult qualities—made the greatest effort for Clarity, " Valéry muses at one moment in his notebooks (C, 10:103 [1:595]). "On Descartes: Clear and distinct ideas, " he writes a number of years later (C, 20:508 [1:700]). But the model he used was always the structural one, the one that placed the emphasis on the relation between elements rather than on the elements in and for themselves. Valéry saw the mind as essentially a relational system whose operation he attempted to de-
scribe in the language of group mathematics. "Every act of understanding is based on a group," he says (C, 1:331). "My specialty—reducing everything to the study of a system closed on itself and finite" (C, 19: 645). The transformation model came into play, too. At each moment of mental life the mind is like a group, or relational system, but since mental life is continuous over time, one "group" undergoes a "transformation" and becomes a different group in the next moment. If the mind is constantly being transformed, how do we account for the continuity of the self? Simple; by invoking the notion of the invariant. And so we find passages like this one: "The S[elf] is invariant, origin, locus or field, it's a functional property of consciousness" (C, 15:170 [2: 315]). Just as in transformational geometry, something remains fixed in all the projective transformations of the mind's momentary systems, and that something is the Self (le Moi, or just M, as Valéry notates it so that it will look like an algebraic variable). Transformation theory is all over the place. "Mathematical science . . . reduced to algebra, that is, to the analysis of the transformations of a purely differential being made up of homogeneous elements, is the most faithful document of the properties of grouping, disjunction, and variation in the mind" (O, 1:36). "Psychology is a theory of transformations, we just need to isolate the invariants and the groups" (C, 1:915). "Man is a system that transforms itself" (C, 2:896).
The Notebooks are not the only place where Valéry indulges in this kind of speculation. His mathematical theories turn up in his published writings, too. In an article in Mercure de France in 1899 he wrote about what he called the reversibility of states of consciousness. "The transformations that any given system undergoes are reversible when the system is able to return from a certain state to an earlier state, passing through the same states during the return as it had on its way here, only in reverse order. This definition, though its origin is in physics, is sufficiently general that one can attempt to apply it to the mind and view the mind as a system of transformations" (O, 2:1459). In a piece called "A Few Words about Myself," published in 1944, Valéry describes how he discovered at the age of twenty "that man is a closed system with respect to his cognition and his acts" (O, 2:1518). Later in the same essay he describes the entire credo of his youth:
There was a time when I saw.
I saw or wanted to see the figures of relations between things and not the things.
Things made me smile from pity. Those who paused to consider them were to me sheer idolaters. I knew that the essential thing was figure .
(O, 2:1532)
The term system has at least two important senses for Valéry, and several of his notebook entries show that the elaboration of the idea of systems was associated with Descartes. I mentioned earlier that Mallarmé had a metaphysical crisis in his twenties, which led him to some important philosophical discoveries that were to occupy his mind for the remainder of his life. In 1892 Valéry, who had just met Mallarmé the year before, had a "crisis" of his own. On the face of it, it was a rather trivial matter—a case of unrequited love. It did, however, lead him to a major turning point: he renounced the emotional life in favor of something that he would call the System (with a capital S ). The System was an ideal program of intellectual contemplation whose chief purpose was to submit all important phenomena of mental life to rigorous, dispassionate analysis, the sort of thing we see piecemeal in Valéry's notebooks, which in a significant sense are the result of this program.[16] But system (with a lowercase s ) also means relational system in the sense I've been using. When Valéry talks about the System he often feels the need to mention systems and to bring up Descartes:
Grosso modo the System has been the quest for a language or a notation that would make it possible to treat de omni re just as analyt[ic] geo [metry] allowed Des Cartes [sic ] to treat all figures.
The human body (viewed as a syst[em] of variables) must be able to reveal this secret.
(C, 9:82 [1:812])
In another long entry, written about fifteen years after this one, Valéry's subject is once again the System: "It used to be, would have been, is, was, and would be a kind of method à la Descartes—I mean Geometry—because it would have to do with a sort of systematic translation of the diversity of objects and the transformations of consciousness or the mind into elements and modes of functioning (observable or probable) of this mind." And a little later in the same entry he brings up once again the notion of system:"In short, it seemed ever more strongly to me that what appears almost always and necessarily, like things, world, ideas, cognition, was somewhere else, the product of a functioning—that is, a bounded, closed system, forced to return to itself" (C, 20:290–292 [1:846]).
Perhaps the most intriguing of the notebook statements on the System
and its Cartesian analogy is the one in which Valéry writes in adjacent columns about Descartes and himself. On the left side of the page are four brief phrases having to do with Descartes: "Discours de ma méthode" (instead of "Discours de la méthode"), "Story 1892" (the year of his crisis), "The finite—reduction to my system," and, in a reference to the Latin version of Descartes's famous sentence, "Instead of Cogito and Sum, my formula." On the right side of the page he writes this: "The System—is not a 'philosophical system'——instead, it's the system of me —my potential —my coming and going—my way of seeing and returning" (C, 18:55 [1:841]). As this entry and many others show, Valéry regarded Descartes's method not precisely as being similar to his own but as being a kind of analogical model, much as Kant invoked the name of Copernicus to call attention not to the content of his own new philosophy but to its revolutionary character.
The last entry I quoted is especially valuable because it hints at the reason for the difference between Descartes and Valéry. Descartes, too, founded a "system." In fact, his philosophy is often referred to as systemlike because of the coherence of its parts and its "closed" nature. But for Valéry, it is still just a philosophical system, that is, a corpus of writings on "philosophical" subjects. Valéry's System is different because its very logic is different. In Valéry we see the logic of relational systems, the "system of me." And what could be more systematic than a system of thought whose primary characteristic is that it is systemlike?
Valéry was consistent, and we find the system concept everywhere. In a world where the mind is a system, it is natural that the things the mind makes should look like systems, too. "I have eternally sought to define or construct a system of variables (that is, a systé[em] of notations)—and of the relations of the conditions among them that would make it possible to represent tangible life," reads an entry in the Notebooks (C, 18:608). One important category of things the mind makes is of course artworks, and not surprisingly, these behave like the systems (the minds) that created them. There's a reason for this, but it has to do with the subject of Part IV of this book, so I will put off talking about it until then. For now, let's just observe how the system concept works in Valéry's vision of artworks.
To a certain extent Valéry's remarks on artworks are historical. That is, he sees the relational quality of art partly as a phenomenon peculiar to the modern age. In an early article called "On Literary Technique" Valéry writes about the modern conception of the poet: "He's no longer the disheveled, delirious man, someone who writes an entire poem in a
night of fever; now he's a cold scientist [savant ], almost an algebraist, in the service of a refined dreamer" (O, 1:1809). Mallarmé is partly to be credited with the modern spirit in poetry, as Valéry says in another place: he was "the first writer who dared to envisage the literary problem in its full universality . . . He conceived as algebra what all the others have thought about only in the particularity of arithmetic."[17] But certain types of artwork for Valéry are intrinsically structural, regardless of the historical period during which they were created. Valéry was a firm believer in the poetry-prose distinction. In "Poetry and Abstract Thought" the emphasis is on the difference between poetic language and the language of prose. Valéry felt that the distinction extended to the entire work of an, which is to say that a poem as a whole is different from, say, a novel as a whole. The distinguishing factor is the relational quality of poems, as he explains in his "Homage to Marcel Proust": "And while the world of the poem is essentially closed and complete unto itself, being the pure system of the ornaments and possibilities [chances ] of language, the universe of the novel, even of the fantasy novel, is connected with the real world." (O, 1:770). One of Valéry's favorite art forms was dance, because it so clearly embodied the relational principles he wanted to see in everything. In an essay originally given as a lecture in 1936, "Philosophy of the Dance," he says: "No exteriority! The dancer has no outside . . . Nothing exists beyond the system that she forms through her acts" (O, 1:1398). And a paragraph later he describes dance as "a group of sensations that makes an abode for itself, . . . that emits from the depths of itself this beautiful series of transformations in space" (O, 1:1398). Valéry's personal dream was to create the perfect, mathematically determined work of art, something he mused about in his notebook the year before he died:
To arrive at the completion of a work by means of formal conditions accumulated like functional equations——
in such a way that the possible contents are more and more circumscribed —
Subject, characters, situations result from a structure of abstract restrictions—
(C, 28:468 [1:314–15])
If ever there was a prestructuralist thinker, it was Valéry. I say pre structuralist not only because Valéry's thought looks like structuralism even before there was any such field as structural linguistics, anthropology, or criticism but also because it shows the logical foundations of struc-
turalism in all their naked, unabashed glory. Few structuralists later in the twentieth century felt the need to expose the mathematical foundations of their thought or repeat the by then timeworn credo about how the importance is in the relations and not in the elements themselves. They had gone beyond this credo, had taken it all for granted as something that didn't need to be said in their elaborate discussions of structures and systems. But Valéry did feel the need to say it—over and over and over again. For him, the real truth—the real essence, to be more accurate—always had to be anchored firmly in the neo-Cartesian logic of relationalism. And the credo was always worth repeating, as if that would keep the relational essence from suddenly slipping away, leaving behind the most dreaded monster of all: things themselves .