PART I—
COMPUTATIONALISM AND ITS CRITICS

Chapter One—
The Computational Theory of Mind

The past thirty years have witnessed the rapid emergence and swift ascendency of a truly novel paradigm for understanding the mind. The paradigm is that of machine computation, and its influence upon the study of mind has already been both deep and far-reaching. A significant number of philosophers, psychologists, linguists, neuroscientists, and other professionals engaged in the study of cognition now proceed upon the assumption that cognitive processes are in some sense computational processes; and those philosophers, psychologists, and other researchers who do not proceed upon this assumption nonetheless acknowledge that computational theories are now in the mainstream of their disciplines.

But if there is general agreement that the paradigm of machine computation may have significant implications for both the philosopher of mind and the empirical researcher interested in cognition, there is no such agreement about what these implications are. There is, perhaps, little doubt that computer modeling can be a powerful tool for the psychologist, much as it is for the physicist and the meteorologist. But not all researchers are agreed that the cognitive processes they may model on a computer are themselves computations, any more than the storms that the meteorologist models are computations.

Similarly, there is significant disagreement among philosophers about whether the paradigm of machine computation provides a literal characterization of the mind or merely an alluring metaphor. Three alternative ways of assessing the importance of the computer paradigm stand out. The most modest possibility is that the computer metaphor will

prove an able catalyst for generating theories in psychology, in much the sort of way that numerous other metaphors have so often played a role in the development of other sciences, yet in such a fashion that little or nothing about computation per se will be of direct relevance to the explanatory value of the resulting theories. A second and slightly stronger possibility is that the conceptual machinery employed in computer science will provide the right sorts of tools for allowing psychology (or at least parts of psychology) to become a rigorous science, in much the fashion that conceptual tools such as Cartesian geometry and the calculus provided a basis for the emergence of Newtonian mechanics, and differential geometry made possible the relativistic physics which supplanted it. On this view, which will be discussed in the final chapter of this book, what the computer paradigm might contribute is the basis for the maturation of psychology by way of the mathematization of its explanations and the connections between intentional explanation and explanation cast at the level of some lower-order (e.g., neurological) processes through which intentional states and processes are realized. This view is committed to the thesis that the mind is a computer only in the very weak sense that the interrelations between mental states have formal properties for which the vocabulary associated with computation provides an apt characterization—that is, to the view that there is a description of the interrelations of mental states and processes that is isomorphic to a computer program. This thesis involves no commitment to the stronger view that terms like 'representation', 'symbol', and 'computation' play any stronger role in explaining why mental states and processes are mental states and processes, but only the weaker view that, given that we may posit such states and processes, their "form" may be described in computational terms. (You might say that, on this view, the mind is "computational" in the same sense that a relativistic universe is "differential.") The third and strongest view of the relevance of machine computation to psychology—one example of which will be the main focus of this book—is that notions such as "representation" and "computation" not only provide the psychologist with the formal tools she needs to do her science in a rigorous fashion, but also provide the philosopher with fundamental tools that allow for an analysis of the essential nature of cognition and for the solution of important and long-standing philosophical problems.

This book examines one particular application of the paradigm of machine computation to the study of mind: namely, the "Computational

Theory of Mind" (CTM) advocated in recent years by Jerry Fodor (1975, 1980a, 1981, 1987, 1990) and Zenon Pylyshyn (1980, 1984). Over the past two decades, CTM has emerged as the "mainstream" view of the significance of computation in philosophy. Its advocates have articulated a very strong position: namely, that cognition literally is computation and the mind literally is a digital computer. CTM is comprised of two theses. The first is a thesis about the nature of intentional states, such as individual beliefs and desires. According to CTM, intentional states are relational states involving an organism (or other cognizer) and mental representations. These mental representations, moreover, are to be understood on the model of representations in computer storage: in particular, they are symbol tokens that have both syntactic and semantic properties. These symbols include both semantic primitives and complex symbols whose semantic properties are a function of their syntactic structure and the semantic values of the primitives they contain. The second thesis comprising CTM is about the nature of cognitive processes—processes such as reasoning to a conclusion, or forming and testing a hypothesis, which involve chains of beliefs, desires, and other intentional states. According to CTM, cognitive processes are computations over mental representations. That is, they are causal sequences of tokenings of mental representations in which the relevant causal regularities are determined by the syntactic properties of the symbols and are describable in terms of formal (i.e., syntactic) rules. The remainder of this chapter will be devoted to clarifying the nature and status of these two claims.

As we shall see in chapter 2, CTM's advocates have also made a very persuasive case that viewing the mind as a computer allows for the solution of significant philosophical problems: notably, they have argued (1) that it provides an account of the intentionality of mental states, and (2) that it shows that psychology can employ explanations in the intentional idiom without involving itself in methodological or ontological difficulties. The claims made on behalf of CTM thus fall into the third and strongest category of attitudes towards the promise of the computer paradigm. The task undertaken in the subsequent chapters of this book is to evaluate these claims that have been made on behalf of CTM and to provide the beginnings of an alternative understanding of the importance of the computer paradigm for the study of cognition. In particular, we shall examine (1) whether CTM succeeds in solving these philosophical problems, and (2) whether the weaker possibility of its providing the basis for a rigorous psychology in any way depends upon either the

understanding of cognition and computation endorsed by CTM or its ability to explain intentionality and vindicate intentional psychology.

1.1—
Intentional States

CTM is a theory about the nature of intentional states and cognitive processes. To understand what this means, however, we must first become clear about the meanings of the expressions 'intentional state' and 'cognitive process'. The expression 'intentional state' is used as a generic term for mental states of a number of kinds recognized in ordinary language and commonsense psychology. Some paradigm examples of intentional states would be

—believing (judging, doubting) that such-and-such is the case,

—desiring that such-and-such should take place,

—hoping that such-and-such will take place,

—fearing that such-and-such will take place.

The characteristic feature of intentional states is that they are about something or directed towards something . This feature of directedness or intentionality distinguishes intentional states both from brute objects and from other mental phenomena such as qualia and feelings, none of which is about anything. The expressions 'intentional states' and 'cognitive states' denote the same class of mental states, but the two terms reflect different interests. The term 'intentionality' is employed primarily in philosophy, where it is used to denote specifically this directedness of certain mental states, a feature which is of importance in understanding several important philosophical problems, including opacity and transparency of reference and knowledge of extramental objects. The term 'cognition' is most commonly employed in psychology, where it is used to denote a domain for scientific investigation. As such, its scope and meaning are open to some degree of adjustment and change as the science of psychology progresses. A third term used to indicate this same domain is 'propositional attitude states'. This expression shows the influence of the widely accepted analysis of cognitive states as involving an attitude (such as believing or doubting) and a content that indicates the object or state of affairs to which the attitude is directed. Since the contents of mental states are often closely related to propositions, such attitudes are sometimes called propositional attitudes. These three ex-

pressions will be used interchangeably in the remainder of this book. In places where there is little danger of misunderstanding, the more general expression 'mental states' will also be used to refer specifically to intentional states.

1.2—
Mental State Ascriptions in Intentional Psychology and Folk Psychology

Attributions of intentional states such as beliefs and desires play an important role in our ordinary understanding of ourselves and other human beings. We describe much of our linguistic behavior in terms of the expression of our beliefs, desires, and other intentional states. We explain our own actions on the basis of the beliefs and intentions that guided them. We explain the actions of others on the basis of what we take to be their intentional states. Such explanations reflect a general framework for psychological explanation which is implicit in our ordinary understanding of human thought and action. A cardinal principle of this framework is that people's actions can often be explained by their intentional states. I shall use the term 'intentional psychology' to refer to any psychology that (a ) makes use of explanations involving ascriptions of intentional states, and (b ) is committed to a realistic interpretation of at least some such ascriptions.

This usage of the expression 'intentional psychology' should be distinguished from the common usage of the currently popular expression 'folk psychology'. The expression 'folk psychology' is used by many contemporary writers in cognitive science to refer to a culture's loosely knit body of commonsense beliefs about how people are likely to think and act in various situations. It is called "psychology" because it involves an implicit ontology of mental states and processes and a set of (largely implicit) assumptions about regularities of human thought and action which can be used to explain behavior. It is called "folk" psychology because it is not the result of rigorous scientific inquiry and does not involve any rigorous scientific research methodology. Folk psychology, thus understood, is a proper subset of what I am calling intentional psychology. It is a subset of intentional psychology because it employs intentional state ascriptions in its explanations. It is only a proper subset because one could have psychological explanations cast in the intentional idiom that were the result of rigorous inquiry and were not committed to the specific set of assumptions characteristic of any given culture's commonsense views about the mind. Many of Freud's theories, for example,

fall within the bounds of intentional psychology, since they involve appeals to beliefs and desires; yet they fall outside the bounds of folk psychology because Freud's theories are at least attempts at rigorous scientific explanation and not mere distillations of commonsense wisdom. Similarly, many contemporary theories in cognitive psychology employ explanations in the intentional idiom that fall outside the bounds of folk psychology, in this case because the states picked out by their ascriptions occur at an infraconscious level where mental states are not attributed by commonsense understandings of the mind.

In understanding the importance of CTM in contemporary psychology and philosophy of mind, it would be hard to overemphasize this distinction between the more inclusive notion of intentional psychology, which embraces any psychology that is committed to a realistic construal of intentional state ascriptions, and the narrower notion of folk psychology, which is by definition confined to prescientific commonsense understandings of the mental. For CTM's advocates wish to defend the integrity of intentional psychology, while admitting that there may be significant problems with the specific set of precritical assumptions that comprise a culture's folk psychology. On the one hand, Fodor and Pylyshyn argue that the intentionally laden explanations present in folk psychology are quite successful,^[1] that folk psychology is easily "the most successful predictive scheme available for human behavior" (Pylyshyn 1984: 2), and even that intentional explanation is indispensable in psychology.^[2] On the other hand, advocates of CTM are often more critical of the specific generalizations implicit in commonsense understandings of mind. Folk psychology may provide a good starting point for doing psychology, much as animal terms in ordinary language may provide a starting point for zoological taxonomy or billiard ball analogies may provide a starting point for mechanics; but more rigorous research is likely to prove commonsensical assumptions wrong in psychology, much as it has in biology and physics.^[3] Folk psychology is thus viewed by these writers as a protoscience out of which a scientific intentional psychology might emerge. One thing that would be needed for this transition to a scientific intentional psychology to take place is rigorous empirical research of the sort undertaken in the relatively new area called cognitive psychology.^[4] Such empirical research would be responsible, among other things, for correcting such assumptions of common sense as may prove to be mistaken. What is viewed as the most significant shortcoming of commonsense psychology, however, is not that it contains erroneous generalizations, but that its generalizations are not united by a single theo-

retical framework.^[5] CTM is an attempt to provide such a framework by supplying (a ) an account of the nature of intentional states, and (b ) an account of the nature of cognitive processes.

1.3—
CTM's Representational Account of Intentional States

The first thesis comprising CTM is a representational account of the nature of intentional states . Fodor provides a clear outline of the basic tenets of this account in the following five claims, offered in the introduction to RePresentations, published in 1981:

(a ) Propositional attitude states are relational.

(b ) Among the relata are mental representations (often called "Ideas" in the older literature).

(c ) Mental representation[s] are symbols: they have both formal and semantic properties.

(d ) Mental representations have their causal roles in virtue of their formal properties.

(e ) Propositional attitudes inherit their semantic properties from those of the mental representations that function as their objects. (Fodor 1981: 26)

Claims (a ) through (c ) provide Fodor's views upon the nature of intentional states, while claims (d ) and (e ) provide the means for connecting this representational account of intentional states with a computational account of cognitive processes and an account of the intentionality of the mental, respectively.

Fodor supplies a more formal account of the nature of intentional states in Psychosemantics, published in 1987. There he characterizes the nature of intentional states (propositional attitudes) as follows:

Claim 1 (the nature of propositional attitudes):

For any organism O , and any attitude A toward the proposition P , there is a ('computational'-'functional') relation R and a mental representation MP such that

MP means that P , and

O has A iff O bears R to MP . (Fodor 1987: 17)

On Fodor's account, Jones's believing that two is a prime number consists in Jones being in a particular kind of functional relationship R to a mental representation MP . This mental representation MP is a symbol token, presumably instantiated in some fashion in Jones's nervous system. MP has semantic properties: in particular, MP means that two is a

prime number. And Jones believes that two is a prime number when and only when he is relation R to MP .

There are some glaring unclarities about references to types and tokens of attitudes and representations in this formulation, but some of these are clarified when Fodor provides a "cruder but more intelligible" gloss upon his account of the nature of intentional states:

To believe that such and such is to have a mental symbol that means that such and such tokened in your head in a certain way; it's to have such a token 'in your belief box,' as I'll sometimes say. Correspondingly, to hope that such and such is to have a token of that same mental symbol tokened in your head, but in a rather different way; it's to have it tokened 'in your hope box.' . . . And so on for every attitude that you can bear toward a proposition; and so on for every proposition toward which you can bear an attitude. (Fodor 1987: 17)

On the basis of this gloss, it seems most reasonable to read Fodor's formulation as follows:

The Nature of Propositional Attitudes (Modified)

For any organism O , and any attitude-token a of type A toward the proposition P , there is a ('computational'-'functional') relation R and a mental representation token t of type MP such that

t means that P by virtue of being an MP -token, and

O has an attitude of type A iff O bears R to a token of type MP .^[6]

While there are arguably some significant residual unclarities about Fodor's formulation in spite of these clarifications,^[7] Fodor does make the main point adequately clear: namely, that it is the relationship between the organism and its mental representations that is to account for the fact that intentional states have the semantic properties and intentionality that they have. In the passage already quoted from RePresentations, for example, he writes that intentional states "inherit their semantic properties from those of the mental representations that function as their objects" (Fodor 1981: 26). And in that essay he also writes that "the objects of propositional attitudes are symbols (specifically, mental representations)" and that "this fact accounts for their intensionality and semanticity" (ibid., 25, emphasis added).^[8]

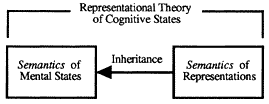
The first thesis comprising CTM is thus a representational account of the nature of intentional states . On this account, intentional states are relations to mental representations. These representations are symbol tokens having both syntactic and semantic properties, and intentional

[Full Size]

Figure 1

states "inherit" their semantic properties and their intentionality from the representations they involve (see fig. 1).

1.4—
Semantic Compositionality

An important feature of this account lies in the fact that the symbols involved in mental representation have both semantic and syntactic properties, and may be viewed as tokens in a "language of thought," sometimes called "mentalese." Viewing the system of mental representations as a language with both semantic and syntactic properties allows for the possibility of compositionality of meaning . That is, the symbols of mentalese are not all lexical primitives. Instead, there is a finite stock of lexical primitives which can be combined in various ways according to the syntactic rules of mentalese to form a potentially infinite variety of complex representations, just as in the case of natural languages it is possible to generate an infinite variety of meaningful utterances out of a finite stock of morphemes and compositional rules. Mentalese is thus viewed as having the same generative and creative aspects possessed by natural languages. So while the semantic properties of mental states are "inherited" from the representations they contain, those representations may themselves be either semantically primitive or composed out of semantic primitives by the application of syntactic rules.

1.5—
Cognitive Processes

If a representational account of the mind provides a way of interpreting the nature of individual thoughts, it does not itself provide any comparable account of the nature of mental processes such as reasoning to a conclusion or forming and testing a hypothesis, and hence does not provide the grounds for a psychology of cognition. For a psychology of cognition, something more is needed: a theory of mental processes that uses

the properties of mental representations as the basis of a causal account of how one mental state follows another in a train of reasoning. Suppose, for example, that one wishes to explain why Jones has closed the window. An explanation might well be given along the following lines:

(1) Jones felt a chill.

(2) Jones noticed that the window was open.

(3) Jones hypothesized that there was a cold draft blowing in through the window.

(4) Jones hypothesized that this cold draft was the cause of his chill.

(5) Jones wanted to stop feeling chilled.

(6) Jones hypothesized that cutting off the draft would stop the chill.

so, (7) Jones formed a desire to cut off the draft.

(8) Jones hypothesized that closing the window would cut off the draft.

so, (9) Jones formed a desire to close the window.

so, (10) Jones closed the window.

Here we have not a random train of thought, but a sequence of thoughts in which the latter thoughts are plausibly viewed as both (a ) rational in light of those that have gone before them, and (b ) consequences of those previous states—Jones formed a desire to close the window because he thought that doing so would cut off the draft. Moreover, a causal theory of inference would need to forge a close link between the semantic properties of individual states and their role in the production of subsequent states. It is changes in the content of Jones's beliefs and desires that we would expect to produce different trains of thought and different behaviors. If Jones had noticed the fan running instead of noticing an open window, we would expect him to entertain different hypotheses, form different desires, and act in a different way, all as a consequence of changing the content of his belief from "the window is open" to "the fan is running."

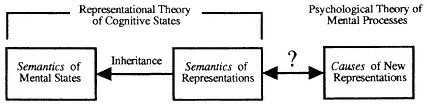
Now CTM's representational account of intentional states seems well suited to a discussion of the semantic relations between intentional states, since the semantic and intentional properties of intentional states are identified with those of the representations they involve. But when it

[Full Size]

Figure 2

comes to the question of how intentional states can play a causal role in the etiology of a process that involves the generation of new intentional states, the notion of representation, in and of itself, has little to offer. Viewing intentional states as relations to representations allows us to locate the semantic relationships between intentional states in relationships between the representations they involve, but it does little to show how Jones's standing in relation R to a representation MP at time t can play a causal role in Jones coming to stand in relation Q to a representation MP^* at t +  .

This seems to present a problem. In order for a sequence of representations to make up a rational, cogent train of thought, the question of which representations should occur in the sequence should be determined by the meanings of the earlier representations. In order for the sequence of representations to make sense, the later representations need to stand in appropriate semantic relationships to the earlier ones. But in order for a sequence of representations to be a causal sequence, the question of what representations will occur later in the sequence must be determined by the causal powers of the earlier representations. Now intentional explanations pick out representations by their content—that is, by their semantic properties. But if such explanations are to be causal explanations, they must pick out representations in a fashion that individuates them according to their causal powers. But this can be done only if the semantic values of representations can be linked to, or coordinated with, the causal roles they can play in the production of other representations and the etiology of behavior. This has been seen by some as a significant stumbling block to the possibility of a causal-nomological psychology, as it is notoriously problematic to view semantic relationships as causal relationships or to equate reasons with causes.^[9] The problem, then, for turning a representational theory of mental states into a psychological theory of mental processes is one of finding a way to link the semantic properties of mental representations to the causal powers of those representations (see fig. 2).

It is precisely at this point that the computer paradigm comes to be of interest. For computers are understood as devices that store and manipulate symbol tokens, and the manipulations that they perform are dependent upon what representations are already present, yet they are also completely mechanical and uncontroversially causal in nature. Machine computation provides a general paradigm for understanding symbol-manipulation processes in which the symbols already present play a causal role in determining what new symbols are to be generated. CTM seeks to provide an extension of this paradigm to mental representations, and thereby to supply an account of cognitive processes that can provide a way of discussing their etiology while also respecting the semantic relationships between the representations involved.

1.6—
Formalization and Computation

CTM's advocates believe that machine computation provides a paradigm for understanding how one can have a symbol-manipulating system that can cause derivations of symbolic representations in a fashion that "respects" their semantic properties. More specifically, machine computation is believed to provide answers to two questions: (1) How can semantic properties of symbols be linked to causal powers that allow the presence of one symbol token s₁ at time t to be a partial cause of the tokening of a second symbol s₂ at time t +   And (2) how can the laws governing the causal regularities also assure that the operations that generate new symbol tokens will "respect" the semantic relationships between the symbols, in the sense that the overall process will turn out to be, in a broad sense, rational?

The answers that CTM's advocates would like to provide for these questions can be developed in two stages. First, work in the formalization of symbol systems in nineteenth- and twentieth-century mathematics has shown that, for substantial (albeit limited) interpreted symbolic domains (such as geometry and algebra), one can find ways of carrying out valid derivations in a fashion that does not depend upon the mathematician's intuition of the meanings of the symbols, so long as (a ) the semantic distinctions between the symbols are reflected by syntactic distinctions, and (b ) one can develop a series of rules, dependent wholly upon the syntactic features of symbol structures, that will license those deductions and only those deductions that one would wish to have licensed on the basis of the meanings of the terms. Second, digital computers are devices that store and manipulate symbolic representations.

Their "manipulation" of symbolic representations, moreover, consists in creating new symbol tokens, and the regularities that govern what new tokens are to be generated may be cast in the form of derivation-licensing rules based upon the syntactic features of the symbols already tokened in computer storage. In a computer, symbols play causal roles in the generation of new symbols, and the causal role that a symbol can play is determined by its syntactic type. Formalization shows that (for limited domains) the semantic properties of a set of symbols can be "mirrored" by syntactic properties; digital computers offer proof that the syntactic properties of symbols can be causal determinants in the generation of new symbols. All in all, the computer paradigm shows that one can coordinate the semantic properties of representations with the causal roles they may play by encoding all semantic distinctions in syntax.

These crucial notions of formalization and computation will now be discussed in greater detail. These notions are, no doubt, already familiar to many readers. However, how one tells the story about these notions significantly influences the conclusions one is likely to draw about how they may be employed, and so it seems worthwhile to tell the story right from the start.

1.6.1—
Formalization

In the second half of the nineteenth century, one of the most important issues in mathematics was the formalization of mathematical systems. The formalization of a mathematical system consists in the elimination from the system's deduction rules of anything dependent upon the meanings of the terms. Formalization became an important issue in mathematics after Gauss, Bolyai, Lobachevski, and Riemann independently found consistent geometries that denied Euclid's parallel postulate. This led to a desire to relieve the procedures employed in mathematical deductions of all dependence upon the semantic intuitions of the mathematician (for example, her Euclidean spatial intuitions). The process of formalization found a definitive spokesman in David Hilbert, whose book on the foundations of geometry, published in 1899, employed an approach to axiomatization that involved a complete abstraction from the meanings of the symbols. The formalization of logic, meanwhile, had been undertaken by Boole and later by Frege, Whitehead, and Russell, and the formalization of arithmetic by Peano.

While there were several different approaches to formalization in nineteenth-century mathematics, Hilbert's "symbol-game" approach is of

special interest for our purposes. In this approach, the symbols used in proofs are treated as tokens or pieces in a game, the "rules" of which govern the formation of expressions and the validity of deductions in that system. The rules employed in the symbol game, however, apply to formulae only insofar as the formulae fall under particular syntactic types. This ideal of formalization in a mathematical domain requires the ability to characterize, entirely in notational (symbolic and syntactic) terms, (a ) the rules for well-formedness of symbols, (b ) the rules for well-formedness of formulas, (c ) the axioms, and (d ) the rules that license derivations.

What is of interest about formalizability for our purposes is that, for limited domains, one can find methods for producing derivations that respect the meanings of the terms but do not rely upon the mathematician's knowledge of those meanings, because the method is based solely upon their syntactic features. Thus, for example, a logician might know a derivation-licensing rule to the effect that, whenever formulas of the form p and pÉq have been derived, he may validly derive a formula of the form q . To apply this rule, he need not know the interpretations of any of the substitution instances of p and q , or even know what relation is expressed by É , but need only be able to recognize symbol structures as having the syntactic forms p and p Éq . As a consequence, one can carry out rational, sense- and truth-preserving inferences without attending to—or even knowing—the meanings of the terms, so long as one can devise a set of syntactic types and a set of formal rules that capture all of the semantic distinctions necessary to license deductions in a given domain.

1.6.2—
A Mathematical Notion of Computation

A second issue arising from turn-of-the-century mathematics was the question of what functions are "computable" in the sense of being subject to evaluation by the application of a rote procedure or algorithm. The procedures learned for evaluating integrals are good examples of computational algorithms. Learning integration is a matter of learning to identify expressions as members of particular syntactically characterized classes and learning how to produce the corresponding expressions that indicate the values of their integrals. One learns, for example, that integrals with the form   have solutions of the form  , and so on.

Such computational methods are formal, in the sense that a person's ability to apply the method does not require any understanding of the

meanings of the terms.^[10] To evaluate  , for example, one need not know what the expression indicates—the area under a curve—but only that it is of a particular syntactic type to which a particular rule for integration applies. Similarly, one might apply the techniques used in column addition (another algorithmic procedure) without knowing what numbers one was adding. For example, one might apply the method without looking to see what numbers were represented, or the numbers might be too long for anyone to recognize them. One might even learn the rules for manipulating digits without having been told that they are used in the representation of numbers. The method of column addition is so designed, in other words, that the results do not depend upon whether the person performing the computation knows the meanings of the terms. The procedure is so designed that applying it to representations of two numbers A and B will dependably result in the production of a representation of a number C such that A + B = C .

1.6.3—
The Scope of Formal Symbol-Manipulation Techniques

It turns out that formal inference techniques have a surprisingly wide scope. In the nineteenth and early twentieth century it was shown that large portions of logic and mathematics are subject to formalization. And this is true not only in logic and number theory, which some theorists hold to be devoid of semantic content, but also in such domains as geometry, where the terms clearly have considerable semantic content. Hilbert (1899), for example, demonstrated that it is possible to formulate a collection of syntactic types, axioms, and derivation-licensing rules that is rich enough to license as valid all of the geometric derivations one would wish for on semantic grounds while excluding as invalid any derivations that would be excluded on semantic grounds.

Similarly, many problems lying outside of mathematics that involve highly context-specific semantic information can be given a formal characterization. A game such as chess, for example, may be represented by (1) a set of symbols representing the pieces, (2) expressions representing possible states of the board, (3) an expression picking out the initial state of the board, and (4) a set of rules governing the legality of moves by mapping expressions representing legal states of the board after a move m to the set of expressions representing legal successor states after move m + 1. Some games, such as tic-tac-toe, also admit of algorithmic strategies that assure a winning or nonlosing game. In addition to games, it is

also possible to represent the essential features of many real-world processes in formal models of the sorts employed by physicists, engineers, and economists. In general, a process can be modeled if one can find an adequate way of representing the objects, relationships, and events that make up the process, and of devising a set of derivation rules that map a representation R of a state S of the process onto a successor representation R^* of a state S^* just in case the process is such that S^* would be the successor state to S . As a consequence, it is possible to devise representational systems in which large amounts of semantic information are encoded syntactically, with the effect that the application of purely syntactic derivation techniques can result in the production of sequences of representations that bear important semantic relationships: notably, sequences that could count as rational, cogent lines of reasoning.

1.6.4—
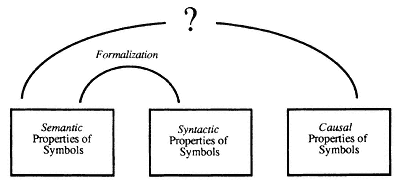
Computing Machines

The formalizability of limited symbolic domains shows that semantic distinctions can be preserved syntactically and that the application of syntactic derivation rules can result in a semantically cogent sequence of representations. In crude terms, formalization shows us how to link semantics to syntax. What is required, however, is a way of linking the semantic properties of representations with their ability to play a causal role in the generation of new representations to which they bear interesting semantic relationships (see fig. 3). In and of themselves, formal proof methods and formal algorithms do not provide such a link, since they depend upon the actions of the human computer who applies them. It is the paradigm of machine computation that provides a way of connecting the causal roles played by representations with their syntactic properties, and thus indirectly linking semantics with causal role.

The crucial transition from formal techniques dependent upon a human mathematician to mechanical computation came in Alan Turing's "On Computable Numbers" (1936). This paper was framed as an answer to the mathematical problem of finding a general characterization of the class of functions that admit of computational (i.e., algorithmic) solutions. Turing's approach to this problem was to describe a machine that was capable of scanning and printing symbols printed on a tape and governed in part by internal mechanisms and in part by the specific symbols found on the tape. Some of the details of this machine are described in chapter 5, but for present purposes it suffices to say that Turing

[Full Size]

Figure 3

showed that any computation that can be evaluated by application of a formal algorithm can be performed by a digital machine of the sort he specifies. The original intent of Turing's article was to provide a general description of all computable functions: a function is computable just in case it can be evaluated by a Turing machine. But in providing this answer to a problem in mathematics, Turing also showed something far more interesting for psychologists and philosophers: namely, that it is possible to design machines that not only passively store symbols for human use, but also actively distinguish symbols on the basis of their shape and their syntactic ordering, and indeed operate in a fashion that is partially determined by the syntactic properties of the symbols on which they operate. In short, Turing showed that it is possible to link syntax to causal powers in a computing machine.

A computing machine is a device that possesses several distinctive features. First, it contains media in which symbolic representations can be stored. These symbols, like written symbols, can be arranged into expressions having syntactic structures and may be assigned interpretations through an interpretation scheme. Second, a computer is capable of differentiating between representations in a fashion corresponding to distinctions in their syntactic "shape." Third, it can cause the tokening of new representations. Finally, the causal regularities that govern what new symbols the computer will cause to be tokened are dependent upon the syntactic form of the symbols already stored by the machine.

To take a simple example, suppose that a computer is programmed to sample two storage locations A and B where representations of integers are stored and to cause a tokening of a representation at a third

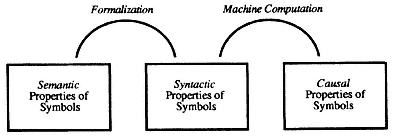
location C in such a fashion that the representation tokened at C will be a representation of the sum of the two numbers represented at A and B . The representations found at A , B , and C have syntactic structure: let us assume that each representation is a series of binary digits (1s and 0s). They also have semantic interpretations: namely, those assigned to them by the interpretation scheme employed by the designer of the program. Now when the computer executes the program, it will cause the tokening of a representation at C . Just what representation is tokened at C will depend upon what representations are found at A and B . More specifically, it will depend upon the syntactic type of the representations found at A and B —namely, upon what sequences of binary digits are present at those locations. What the computer does in executing this program is thus analogous to the application of a formal algorithm (such as that employed in column addition), which is sensitive to the syntactic forms of the representations at A and B . If the program has been properly designed, the overall process will accurately mimic addition as well, in the sense that what is tokened at C will always be a representation of the sum of the two numbers represented at A and B . That is, if the program is properly designed, the syntactically dependent operations performed by the machine will ensure the production of a representation at C that bears the desired semantic relations to the representations at A and B as well.^[11] The semantic properties of the representations play no causal role in the process—they are etiologically inert. But since all semantic distinctions are preserved syntactically, and syntactic type determines what a representation can contribute causally, there is a correspondence between a representation's semantic properties and the causal role it can play.

This example illustrates three salient points. The first is the insight borrowed from formal logic and mathematics that at least some semantic relations can be reflected or "tracked" by syntactic relations. The second is the insight borrowed from computer science that machines can be made to operate upon symbols in such a way that the syntactic properties of the symbols can be reflected in their causal roles. Indeed, for any problem that can be solved by the application of a formal algorithm A , it is possible to design a machine M that will generate a series of representations corresponding to those that would be produced by the application of algorithm A . These two points jointly yield a third: namely, that it is possible for machines to operate upon symbols in a way that is, in Fodor's words, "sensitive solely to syntactic properties" of the symbols and "entirely confined to altering their shapes," while at the same time

[Full Size]

Figure 4

the machine is so devised that it will transform one symbol into another if and only if the propositions
expressed by the symbols that are so transformed stand in certain semantic relations—e.g.,
the relation that the premises bear to the conclusion of a valid argument. (Fodor 1987: 19)

In brief, "computers show us how to connect semantical with causal properties for symbols " (ibid.). And this completes the desired linkage between semantics and causality: for domains that can be formalized, semantic properties can be linked to causal properties by encoding semantic differences in syntax and designing a machine that is driven by the syntactic features of the symbols (see fig. 4).

1.7—
The Computational Account of Cognitive Processes

We have seen that the first thesis comprising CTM was a representational account of the nature of intentional states: namely, that such states are relations to mental representations. The second thesis comprising CTM is a computational account of the nature of cognitive processes: namely, that cognitive processes are computations over mental representations, or "causal sequences of tokenings of mental representations" (Fodor 1987: 17). Fodor writes,

A train of thoughts, for example, is a causal sequence of tokenings of mental representations which express the propositions that are the objects of the thoughts. To a first approximation, to think 'It's going to rain; so I'll go indoors' is to have a tokening of a mental representation that means I'll go indoors caused, in a certain way, by a tokening of a mental representation that means It's going to rain . (ibid.)

This account may be broken down into several constituent claims. First, cognitive processes are sequences of intentional states. Now,

according to CTM, to be in a particular intentional state is just to be in a particular functional relation to a mental representation. So if an organism is undergoing a cognitive process, it is passing through a sequence of functional relations to mental representations. Second, there are causal relationships between the intentional states that make up a cognitive process. Being in relation R to a representation of type MP at time t (say, believing at 12:00 noon that it is going to rain) can be a partial cause of coming to be in relation R^* to a representation of type MP^* at time t +   (e.g., coming to a decision at 12:01 to go indoors). Third, the causal connection between the states picked out is not merely incidental, but depends in a regular way upon the syntactic properties of the mental representations. It is because the organism stands in relation R to a token of (syntactic) type MP at t that it comes to stand in relation R^* to a token of (syntactic) type MP^* at t +  , much as our adding program causes a particular representation to be tokened at C because representations with particular syntactic patterns are present at A and B . So just as the representations in computers can play a causal role in the generation of new representations, and do so by virtue of their syntactic form, so also "mental representations have their causal roles in virtue of their formal properties" (Fodor 1981: 26). Fourth, as in the case of a formal algorithm or a computer program, any semantic differences between mental representations are reflected by syntactic distinctions. So for any two mental representations MP and MP^* to which a single organism O is related, if MP and MP ^* differ with respect to semantic properties, they must be of different syntactic types as well.

To view mental processes in this way is to treat the mind as being quite literally a digital computer. A computer is a device that performs symbol manipulations on the basis of the syntactic features of the symbols, and it can do so in a fashion that respects such semantic features as are encoded in the syntax. According to CTM, mental states involve symbolic representations from which they inherit their semantic properties. All semantic differences between representations are syntactically encoded, and the mind is a device whose causal regularities are determined by the syntactic properties of its representations.

This account of the nature of cognitive processes allows intentional state ascriptions to pick out intentional states by way of properties that are correlated with their causal powers. Intentional state ascriptions pick out intentional states by the semantic values of the representations they involve. These semantic values are not themselves causally efficient. But, according to CTM, the semantic properties of representations are cor-

related with their syntactic types. So when representations are picked out by their semantic value, their syntactic type is uniquely picked out as well. But the syntactic type of a representation is a determinant of the causal role it can play in causing tokenings of other representations and in the etiology of behavior. And so intentional state ascriptions can pick out causes, and indeed the semantic properties by which intentional states are picked out are correlated with the causal roles that they can play, because semantic properties are correlated with syntactic properties, and syntactic properties determine causal powers. This provides for the possibility of accounting for mental causation in a way that does not require semantic properties to be causally active, and yet correlates semantic value with causal role.

1.8—
Summary: The Computational Theory of Mind

In summary, we have now seen that CTM consists in two main theses. The first thesis is a representational account of the nature of intentional states. On this view, intentional states are relations between an organism and mental representations. These representations are physically instantiated symbol tokens having both semantic and syntactic properties. The second thesis is a computational account of the nature of cognitive processes. Cognitive processes, according to CTM, are computations over mental representations. That is, they are sequences of tokenings of mental representations in which the presence of one representation can serve as a partial cause of the tokening of a second representation. Just what causal roles a representation may play in the generation of other representations and the etiology of behavior is determined by its syntactic properties, and not by its semantic value. But while a representation's semantic value does not influence what causal roles it can play, the semantic value is nonetheless coordinated with causal role, because all semantic differences between representations are preserved syntactically, and syntax determines causal role.

Chapter Two—
Computation, Intentionality, and the Vindication of Intentional Psychology

The Computational Theory of Mind has received a great deal of attention in recent years, both in philosophy and in the empirical disciplines whose focus is cognition. On the one hand, the computer paradigm has inspired an enormous volume of theoretical work in psychology, as well as related fields such as linguistics and ethology. On the other hand, philosophers such as Fodor have claimed that CTM provides a solution to certain long-lived philosophical problems as well. The primary focus of this book is upon CTM's claims to solve philosophical problems. Two of these are of primary importance. The first is the claim that CTM provides a philosophical account of the intentionality and semantics of intentional states —in particular, that it does so in a fashion that provides thought with the same generative and compositional properties possessed by natural languages. The second is the claim that CTM "vindicates" intentional psychology by providing a philosophical basis for an intentional psychology capable of satisfying several contemporary concerns—in particular, concerns for (1) the compatibility of intentional psychology with materialistic monism, (2) the compatibility of intentional psychology with the generality of physics, and (3) the ability to construe intentional explanations as causal explanations based on lawlike regularities. Together, these claims imply that viewing the mind as a computer allows us to "naturalize" the mind by bringing both individual thoughts and mental processes within an entirely physicalistic world view.

It is important to note that the status of these distinctively philosophical claims is largely independent of the claim that the computer paradigm

has been empirically fruitful in inspiring important theoretical work in psychology and other disciplines. On the one hand, the theory might ultimately prove to be philosophically interesting but empirically fallow. Such was arguably the case, for example, with representational theories of mind before CTM, and could turn out to be the case for computationalism as well if, in the long run, it goes the way of so many unsuccessful research programmes that initially showed such bright promise. On the other hand, it is possible to interpret psychological research inspired by the computer paradigm—"computational psychology" for short—in a fashion that is weaker than CTM. Fodor acknowledges this when he writes:

There are two, quite different, applications of the "computer metaphor" in cognitive theory: two quite different ways of understanding what the computer metaphor is . One is the idea of Turing reducibility of intelligent processes; the other (and, in my view, far more important) is the idea of mental processes as formal operations on symbols. (Fodor 1981: 23-24)

The first and weaker view here is a machine functionalism that treats the mind as a functionally describable system without explaining intentional states by appeal to representations. On this view,

Psychological theories in canonical form would then look rather like machine tables, but they would provide no answer to such questions as "Which of these machine states is (or corresponds to or simulates) the state of believing that P?" (ibid., 25)

The second and stronger application of the computer metaphor is Fodor's CTM, which adds the philosophically pregnant notion of mental representation to what is supplied by machine functionalism. As we shall see in the course of this chapter, Fodor's arguments for preferring CTM to functionalism turn largely upon its ability to "vindicate" intentional psychology and not merely upon factors internal to empirical research in psychology. And hence the strengths and weaknesses of the philosophical claims made on behalf of CTM are largely independent of the viability of computational psychology as an empirical research strategy.

2.1—
CTM's Account of Intentionality

The first philosophical claim made on behalf of CTM is that it provides an account of the intentionality of mental states. The basic form of this account was already introduced in chapter 1: namely, that mental states involve relationships to symbolic representations from which the states "inherit their semantic properties" (Fodor 1981: 26) and intentionality.

Or, in Fodor's words again, "Intentional properties of propositional attitudes are viewed as inherited from semantic properties of mental representations" (Fodor 1980b: 431). This claim that intentional states "inherit" their semantic properties, moreover, is intended to provide an explanation of the intentionality and semantics of intentional states. Beliefs and desires are about objects and states of affairs because they involve representations that are about those objects and states of affairs; intentional states are meaningful and referential because they involve representations that are meaningful and referential. In this chapter we will look at this account in greater detail, with particular attention towards (a ) locating it within the more general philosophical discussion of intentionality and (b ) highlighting what might be thought to be its strengths.

2.2—
Intentionality

Since the publication of Franz Brentano's Psychologie vom empirischen Standpunkt in 1874, intentionality has come to be a topic of increasing importance in philosophy of mind and philosophy of language. While Brentano's own views on intentionality have not proven to be of enduring interest in their own right, his reintroduction of the Scholastic notion of intentionality into philosophy has had far-reaching ramifications. Brentano's pupil Edmund Husserl ([1900] 1970, [1913] 1931, [1950] 1960, [1954] 1970) made intentionality the central theme of his transcendental phenomenology, and the work of subsequent European philosophers such as Martin Heidegger, Jean-Paul Sartre, Jacques Derrida, and Michel Foucault has been articulated in large measure against Husserl's views about the intentionality of mind and language. In the English-speaking world, problems about intentionality have been introduced into analytic philosophy by Roderick Chisholm (1957, 1968, 1983, 1984a, 1984b), who translated and commented upon much of Brentano's work, and Wilfred Sellars (1956), who studied under Husserl's pupil Martin Farber.^[1]

Several of the principal aspects of Brentano's problematic have been preserved in subsequent discussions of intentionality. Brentano's characterization of the directedness and content of some mental states has been adopted wholesale by later writers, as has his recognition that such states form a natural domain for psychological investigation and need to be distinguished both from qualia and from brute objects.^[2] Recently, moreover, there has been a strong resurgence of interest in the relationship between what Brentano called "descriptive" (i.e., intentional) and

"genetic" (i.e., causal, nomological) psychology. Brentano had originally thought that genetic psychology would eventually subsume and explain descriptive psychology, but subsequently concluded that intentionality was in fact an irreducible property of the mental and could not be accounted for in nonintentional and nonmental terms. This position is sometimes described as "Brentano's thesis." This discussion in Brentano is thus a direct forebear of current discussions of the possibility of naturalizing intentionality, with Brentano's mature position represented by writers such as Searle (1983, 1993).

On the other hand, later discussions have placed an increasing emphasis on several aspects of intentionality that are either given inadequate treatment in Brentano's account or missing from it altogether. Notable among these are a concern for relating intuitions about the intentional nature of mental states to other philosophical difficulties, such as psychophysical causation and the mind-body problem, and a conviction that intentionality is a property of language as well as of thought, accompanied by a corresponding interest in the relationship between the intentionality of language and the intentionality of mental states. This interest in the "intentionality of language" has taken two forms. On the one hand, writers such as Husserl (1900) and Searle (1983) have taken interest in how utterances and inscriptions come to be about things by virtue of being expressions of intentional states. On the other hand, Chisholm (1957) has coined a usage of the word 'intentional' that applies to linguistic tokens employed in ascriptions of intentional states.^[3] This widespread conviction that language as well as thought is in some sense intentional has been paralleled by a similar conviction that some mental states can be evaluated in the same semantic terms as some expressions in natural and technical languages. Notably, it is widely assumed that notions such as meaning, reference, and truth value can be applied both (a ) to occurrent states such as explicit judgments and (b ) to tacit states such as beliefs that are not consciously entertained, in much the fashion that these semantic notions are applied to linguistic entities such as words, sentences, assertions, and propositions. Providing some sort of account of the intentionality and semantics of mental states is thus widely viewed to be an important component of any purported "theory of mind."

2.3—
CTM, Intentionality, and Semantics

The motivation of CTM's account of intentionality found in Fodor (1981, 1987, 1990) plays upon several themes in the philosophical

discussion of intentionality. In particular, it is an attempt to exploit the relationship between the semantics of thought and language in a fashion that provides a thoroughly naturalistic account of the intentionality of mental states—in other words, an account that is compatible with token physicalism and with treating beliefs and desires as things that can take part in causal relations. Fodor writes,

It does seem relatively clear what we want from a philosophical account of the propositional attitudes. At a minimum, we want to explain how it is that propositional attitudes have semantic properties, and we want an explanation of the opacity of propositional attitudes; all this within a framework sufficiently Realistic to tolerate the ascription of causal roles to beliefs and desires. (Fodor 1981: 18)

Fodor begins his quest for such an account by making a case that intentional states are not unique in having semantic properties—symbols have them as well.

Mental states like believing and desiring aren't . . . the only things that represent. The other obvious candidates are symbols . So, I write (or utter): 'Greycat is prowling in the kitchen,' thereby producing a 'discursive symbol'; a token of a linguistic expression. What I've written (or uttered) represents the world as being a certain way—as being such that Greycat is prowling in the kitchen—just as my thought does when the thought that Greycat is prowling in the kitchen occurs to me. (Fodor 1987: xi)

It is worth noting that Fodor assumes here that words such as 'represent' can be predicated univocally of intentional states and symbols. But his example also involves an even stronger claim: namely, that symbolic representations such as written inscriptions "represent the world as being a certain way . . . just as [my] thought does." Here the implication would clearly seem to be that there is just one sort of "representation" present in the two cases—an assumption that will be shown to have significant consequences later in this book.

The succeeding paragraph in Psychosemantics begins to reveal what Fodor takes to be common to what initially appear to be separate cases (i.e., mental states and symbolic representation):

To a first approximation, symbols and mental states both have representational content . And nothing else does that belongs to the causal order: not rocks, or worms or trees or spiral nebulae. (Fodor 1987: xi)

It also reveals where his reasoning is headed:

It would, therefore, be no great surprise if the theory of mind and the theory of symbols were some day to converge . (ibid., emphasis added)

There are, however, at least two directions that a convergence of the philosophy of mind and semiotics might take. On the one hand, philosophers like Husserl (1900) and Searle (1983) have argued that the intentional and semantic properties of symbols are to be explained in terms of the intentional and semantic properties of mental states. As we have already seen, however, Fodor's view is quite the reverse: namely, that it is the semantic and intentional properties of mental states which are to be explained, and they are to be explained in terms of the intentional and semantic properties of symbols—specifically, the symbols that serve as the objects of the propositional attitudes. While Fodor does acknowledge that written and spoken symbols get their semantic properties from the states that they express, he nonetheless holds that

it is mental representations that have semantic properties in, one might say, the first instance; the semantic properties of propositional attitudes are inherited from those of mental representations and, presumably, the semantic properties of the formulae of natural languages are inherited from those of the propositional attitudes that they are used to express. (Fodor 1981: 31)

The resulting account of intentional states reduces the claim that a particular token intentional state has semantic or intentional properties to a conjunction of two claims to the effect that (a ) a mental symbol token has semantic or intentional properties, and (b ) an organism stands in a particular kind of functional relationship to that symbol token. As Fodor expresses it in the passage already cited from Psychosemantics,

Claim 1 (the nature of propositional attitudes):

For any organism O , and any attitude A toward the proposition P , there is a ('computational'-'functional') relation R and a mental representation MP such that

MP means that P , and

O has A iff O bears R to MP . (Fodor 1987: 17)

It seems clear that questions about the meaningfulness and (putative) reference of intentional states are to be construed as questions about the symbolic representations involved. The same may be said for truth value in those cases where the concept applies, though the applicability of truthfunctional evaluation to a given intentional state would seem to depend upon the attitude involved, since most kinds of cognitive attitudes (e.g., desire, dread, etc.) are not subject to truth-functional evaluation.

2.4—
The Virtues of the Account

There are several features of this account that render it attractive. First, the account locates the ultimate bearers of semantic properties in symbol tokens, and symbol tokens are among the sorts of things that everyone agrees can be physical objects. To the many who want intentionality and want materialism too, this is a substantial advance over previous theories that attributed intentionality either directly to minds (whose compatibility with materialism is in doubt) or directly to brain states (which are problematic as logical subjects of semantic predicates). The account also lends some clarity to the familiar analysis of intentional states in terms of intentional attitudes (such as belief and desire) and content. The attitude-content distinction is itself only a distinction of analysis. CTM fleshes this distinction out in a way that no previous theory had done. Attitudes are interpreted as functional relations between an organism and its representations, and content in terms of the semantic properties of the representations. CTM thus both retains and clarifies a central feature of the standard analysis of intentional states.

The account of intentionality and semantics offered by CTM also provides a way of understanding both narrow and broad notions of propositional content. According to CTM, what is necessary for an intentional state to have a particular content in the narrow sense—that is, what is necessary for it to be "about-X " construed opaquely, or in such a fashion as not to imply that there exists an X for the state to be about—is for it to involve a relationship between an organism and a symbol token of a particular formally delimited type. Whether the state is also contentful in the broad sense (i.e., "about X " under a transparent construal—one that does imply that there is an X to which the state is about) will depend upon how that symbol token is related to extramental reality: for example, whether it stands in the proper sort of causal relationships with X . While CTM does not provide an account of what relationships to extramental reality are relevant to the broad notion of content, the representational account of narrow content allows CTM to avoid several traditional pitfalls associated with the "hard cases" presented by illusions, hallucinations, false beliefs, and other deviant cases of perception and cognition. Notably, CTM escapes the Meinongian tendency to postulate nonexistent entities and the opposite inclination to identify the contents of intentional states with the extramental objects towards which they are directed.

Two features of CTM's account of intentionality, however, seem to

be of utmost importance: its relation to CTM's account of cognitive processes and its ability to endow thought with a compositional semantics. It is perhaps an understatement to say that CTM's representational account of intentionality would be of little interest outside of narrowly philosophical circles if it were not coupled with a causal theory of cognitive processes. Locating the arcane property of intentionality in the equally mysterious meanings of hypothetical mental representations would cut little ice were it not for the fact that treating thoughts as relations to symbols provides a way of explaining mental processes as computations. Indeed, as writers like Haugeland (1978, 1981) have noted, it is the discovery of machine computation that has revitalized representational theories of the mind.

The other signal virtue of viewing thoughts as relations to symbolic representations is that this allows us to endow the mind with the same generative and creative powers possessed by natural languages. We do not simply think isolated thoughts—"dog!" or "red!" Rather, we form judgments and desires that are directed towards states of affairs and represented in propositional form. And our ability to think "The dog knocked over the vase" is in part a consequence of our ability to think "dog" in isolation. We are, furthermore, able to think new thoughts and to combine the ideas we have in novel ways. If I can think "The dog knocked over the vase" and I can think "cat," I can also think "The cat knocked over the vase." Therefore there is more to be desired from a theory of intentional states than an account of the meanings of individual ideas: there is also the fact that thought seems to be generative and systematic.

Viewing the mind as employing representations in a language of thought gives us this for free. For we already have a way of answering the corresponding questions in linguistics by employing the principle of compositionality. If a language is compositional, then the semantic values of complex expression are a function of (a ) the semantic values of the lexical (or morphemic) atoms and (b ) the syntactic structure of the expression. The generative and systematic qualities of languages are explained by the use of iterative syntactic structures and the substitution of known lexical items into the slots of known syntactic structures. So if the semantic properties of our thoughts are directly inherited from those of the symbols they involve, and the symbols involved are part of a language employing compositional principles, then these explanations from linguistics can be incorporated wholesale into our psychology. The mind has generative and systematic qualities because it thinks in a language that has a compositional semantics.

This is an important result because it is virtually impossible to make sense of reasoning by way of a representational theory except on the assumption that complex thoughts, such as "The cat knocked over the vase," are composed out of simpler parts, corresponding to "cat" and "vase." For when one has a thought of a cat knocking over a vase, this thought is immediately linked to all kinds of other knowledge about cats and vases and causality. One may infer, for example, that an animal knocked over the vase, that something knocked over an artifact, or that the vase is no longer upright. If mental representations were all semantic primitives, the ability to make such inferences on the basis of completely novel representations would probably be inexplicable. The simplest explanation for our ability to combine our knowledge about cats with a representation meaning "The cat knocked over the vase" is that the representation has a discrete component meaning "cat," and that the overall meaning of the representation is determined by how the component representations are combined. This, however, points to the need for a representational system in which syntax and semantics are closely connected. For the only known way of endowing a system of representations with this kind of compositionality is by way of supplying the representational system with syntactic rules that govern how to form semantically complex representations out of semantic primitives. CTM provides for this compositionality, and it is not clear that any account not based on an underlying system of languagelike representations would be able to say the same.

2.5—
CTM as the Basis for an Intentional Psychology

The first important claim made on behalf of CTM is thus that it provides an account of the semantic and intentional properties of mental states. The second important claim made on behalf of CTM is that it provides a philosophical basis for intentional psychology. CTM's proponents believe that it provides a framework for psychological explanation that allows intentional state ascriptions to figure in such explanations, while also accommodating several contemporary concerns in philosophy of science. Three such concerns are of preeminent importance: (1) concerns that psychological explanations be causal explanations based on nomological regularities, (2) concerns that psychological explanations be compatible with the generality of physics (i.e., with the ability of an ideally completed physics to supply explanations for every token event), and (3)

concerns that the ontology implicit in psychology be compatible with materialistic monism. Proponents of CTM thus view their project as one of "vindicating commonsense psychology" or "showing how you could have . . . a respectable science whose ontology explicitly acknowledges states that exhibit the sorts of properties that common sense attributes to [propositional] attitudes" (Fodor 1987: 10).

The perceived need for such a "vindication" was occasioned by the disrepute into which intentional psychology—and indeed mentalism in general—had fallen in the first half of the twentieth century. By the time that the notion of computation was available as a paradigm for psychology, many philosophers and psychologists believed that there could not be a scientific psychology cast in mentalistic or intentional terms. The roots of this suspicion of mentalism and intentional psychology may be traced to the views about the nature of science in general, and psychology in particular, associated with two movements: methodological behaviorism in psychology and Vienna Circle positivism in philosophy. In order to understand fully the significant emphasis placed upon "vindicating intentional psychology" in articulations of CTM (particularly early articulations), it is necessary briefly to survey these other movements which were so influential in the earlier parts of this century.

2.6—
The Disrepute of Mentalism—a Brief History

The legitimacy of intentional psychology was seriously impugned in the first half of the twentieth century by ideas emerging from methodological behaviorists in psychology and from logical positivists in philosophy. Methodological behaviorism, as articulated by Watson (1913a, 1913b, 1914, 1924) and Skinner (1938, 1953), raised methodological concerns about explanations that referred to objects (mental states) that were not publicly observable and were not necessary (they argued) for the prediction and control of behavior.

Early logical positivism, as typified by Carnap's Aufbau (1928), adopted a "logical behaviorism" which Putnam describes as "the doctrine that, just as numbers are (allegedly) logical constructions out of sets, so mental events are logical constructions out of actual and possible behavior events " (Putnam [1961] 1980: 25). This interpretation of mental events is based upon a positivist account of the meanings of words, sometimes called the "verification theory of meaning." The criteria for verification of psychological attributes, the logical behaviorists argued,

consist in observations of (a ) the subject's overt behavior (gestures made, sounds emitted spontaneously or in response to questions) and (b ) the subject's physical states (blood pressure, central nervous system processes, etc.). Since motions and emissions of sounds are straightforwardly physical events, they argued, claims about psychological processes are reducible to statements in physical language.^[4] The conclusion, in Hempel's words, is that "all psychological statements which are meaningful, that is to say, which are in principle verifiable, are translatable into statements which do not involve psychological concepts, but only the concepts of physics. . . . Psychology is an integral part of physics" (Hempel [1949] 1980: 18).^[5]

Vienna Circle positivism was characterized by a tension between epistemological concerns (with a concomitant tendency towards phenomenalism) and a commitment to materialism . Logical behaviorism emerged in the context of the epistemological concerns and radically empiricist (and even phenomenalistic) assumptions of early Vienna Circle positivism. As a consequence, it involved the assumption that "observational terms refer to subjective impressions, sensations, and perceptions of some sentient being" (Feyerabend 1958: 35). Carnap's Aufbau was the most significant work advocating this kind of logical reduction, though the influence of phenomenalism may be seen clearly in the early works of Russell and in the nineteenth-century German positivism of Mach.

Yet Carnap soon rejected the Aufbau account of the relationship between physical and psychological terms and adopted a new understanding of science, emphasizing the materialist theme in positivism instead of the epistemological-phenomenalist theme. According to this view, observation sentences do not refer to the sense impressions involved in the actual observations, but to the (putative) objects observed, described in an intersubjective "thing-language."^[6] Thus in 1936 Carnap writes, "What we have called observable predicates are predicates of the thing-language (they have to be clearly distinguished from what we have called perception terms . . . whether these are now interpreted subjectivistically, or behavioristically)" (Carnap [1936-1937] 1953: 69). And similarly Popper writes that "every basic statement must either be itself a statement about relative positions of physical bodies . . . or it must be equivalent to some basic statement of this 'mechanistic' kind" (Popper 1959: 103).

Oppenheim and Putnam's "Unity of Science as a Working Hypothesis" (1958) has become a locus classicus for this newer view, commonly called reductive physicalism—the view that every mental type has a cor-

responding physical type and all psychological laws are thus translatable into laws in the vocabulary of physics.^[7] The ideal of science articulated by Oppenheim and Putnam shares with logical behaviorism and Skinnerian operationalism a commitment to a "reduction" of mentalistic terms, including intentional state ascriptions, but the "reductions" employed in the three projects differ both in nature and in motivation.^[8]

Now while these three scientific metatheories differ with respect to their motivations and their chief concerns, each contributed to a growing suspicion of intentional psychology. By the time the digital computer was available as a model for cognition, it was widely believed that one could not have a scientific psychology that employed intentional state ascriptions. This skepticism about intentional psychology reflected four principal concerns: (1) a concern about the nature of evidence for a scientific theory—particularly a concern that the evidence for psychological theories be publicly or intersubjectively observable; (2) a concern about the nature of scientific explanation —in particular, a concern that scientific explanations be causal and nomological; (3) an ontological concern about the problems inherent in dualism, and particularly a commitment to materialistic monism;^[9] and (4) a commitment to the generality of physics—that is, the availability of a physical explanation for every token event.

2.7—
Vindicating Intentional Psychology (1): Machine Functionalism

The proponents of CTM believe that it has supplied a way of preserving the integrity of explanations cast in the intentional idiom while also accommodating the concerns that had contributed to the ascendancy of reductive approaches to mind in the first half of the century. Historically, the attempt to vindicate intentional psychology involved two distinct elements: (1) the introduction of machine functionalism as a rigorous alternative to behaviorism of various sorts and to reductive physicalism, and (2) CTM's combination of machine functionalism with the additional notions of computation and representation .

In his 1936 description of computation, Alan Turing introduced the notion of a computing machine. The machine, which has come to be called a "Turing machine," has a tape running through it, divided into squares, each capable of bearing a "symbol."^[10] At any given time, the machine is in some particular internal condition, called its "m -configuration." The overall state of the Turing machine at a particular time is described by

"the number of the scanned square, the complete sequence of all symbols on the tape and the m -configuration" (Turing 1936: 232). A Turing machine is functionally specifiable: that is, the operations that it will perform and the state changes it will undergo can be captured by a "machine table" specifying, for each complete configuration of the machine, what operations it will then perform and the resulting m -configuration.

Machine functionalism is the thesis that intentional states and processes are likewise functionally specifiable—that is, that they may be characterized by something on the order of a machine table.^[11] The thesis requires some generalizations from the computing machine described by Turing. In Putnam's 1967 articulation, for example, the tape of the machine is replaced by "sensory inputs" and "motor outputs," and a corresponding adjustment is made to the notion of a machine table to accommodate these inputs and outputs. Putnam also generalizes from Turing's deterministic case, in which state transitions are completely determined by the complete configuration of the machine, to a more permissive notion of a "Probabilistic Automaton," in which "the transitions between 'states' are allowed to be with various probabilities rather than being 'deterministic"' (Putnam [1967] 1980: 226). Since a single physical system can simultaneously be the instantiation of any number of deterministic automata, Putnam also introduces "the notion of a Description of a system." Of this he writes,

A Description of S where S is a system, is any true statement to the effect that S possesses distinct states S₁ , S₂ , . . . , S _n which are related to one another and to the motor outputs and sensory inputs by the transition probabilities given in such-and-such a Machine Table. The Machine Table mentioned in the Description will then be called the Functional Organization of S relative to that Description, and the S_i such that S is in state S_i at a given time will be called the Total State of S (at that time) relative to that Description. (ibid., 226)

This provides a way of specifying conditions for the type identity of psychological states in functional terms. As Block and Fodor articulate it, "For any organism that satisfies psychological predicates at all, there exists a unique best description such that each psychological state of the organism is identical with one of its machine states relative to that description" (Block and Fodor [1972] 1980: 240).

A psychology cast in functional terms possesses the perceived merits of behaviorist and reductive physicalist accounts while avoiding some of their excesses. First, a functional psychology founded on the machine analogy seems to provide the right sorts of explanations for a rigorous

psychology. The machine table of a computer expresses relationships between types of complete configurations that are both regular and causal . If cognition is likewise functionally describable by something on the order of a machine table, psychology can make use of causal, nomological explanations.

Machine functionalism is also compatible with commitments to ontological materialism and to the generality of physics. A computing machine, after all, is unproblematically a physical object, all of its parts are physical objects, and all of its operations have explanations cast wholly in physical terms. If functional description is what is relevant to the individuation of psychological states and processes, the resulting functional psychology could be quite compatible with the assumptions that (a ) all of the (token) objects in the domain of psychology are physical objects, and that (b ) all of the token events explained in functional terms by psychology are susceptible to explanation in wholly physical terms as well.

While machine functionalism is compatible with materialism and token physicalism, it is incompatible with reductive or type physicalism, since functionally defined categories in a computer (e.g., AND-gates) are susceptible to indefinitely many physical implementations that are of distinct physical types. It is for this reason that much of the early computationalist literature focuses on comparing the merits of functionalism with those of reductive physicalism. For example, Fodor offers a general sketch of the case against reductive physicalism:

The reason it is unlikely that every kind corresponds to a physical kind is just that (a ) interesting generalizations . . . can often be made about events whose physical descriptions have nothing in common; (b ) it is often the case that whether the physical descriptions of the events subsumed by such generalizations have anything in common is, in an obvious sense, entirely irrelevant to the truth of the generalizations, or to their interestingness, or to their degree of confirmation, or, indeed, to any of their epistemologically important properties; and (c ) the special sciences are very much in the business of formulating generalizations of this kind. (Fodor 1974: 15)

Additional arguments for the benefits of functionalism over reductionism were marshaled on the basis of Lashley's thesis of equipotentiality, the convergence of morphological and behavioral features across phylogenetic boundaries, and the possibility of applying psychological predicates to aliens and artifacts (see Block and Fodor [1972] 1980). Advocates of functionalism thus see it as capturing the important insights of reductionists (compatibility with materialism and the generality of physics) while avoiding the problems of reductionism.

Advocates of machine functionalism view it as capturing the better side of behaviorism in similar fashion. Functional definition of psychological terms avoids appeals to introspection and private evidence, thereby satisfying one of the concerns of methodological behaviorists like Watson and Skinner. Any ontological suspicion of "the mental" is also avoided by machine functionalism, since computers are plainly objects that are subject to physical instantiation. Functionalism also permits the use of black-box models of psychological processes, much like behaviorism; and like the behaviorisms of Tolman and Hull (but unlike those of Watson and Skinner) it permits the models to include interactions between mental states and does not restrict itself to characterizations of states and processes in dispositional terms, thereby accounting for the intuition that psychological states can interact causally.

Machine functionalism is thus seen by its advocates as uniting the best features of behaviorism with those of physicalism. This, writes Fodor, allowed for the solution of

a nasty dilemma facing the materialist program in the philosophy of mind: What central state physicalists seemed to have got right—contra behaviorists—was the ontological autonomy of mental particulars and, of a piece with this, the causal character of mind-body interactions. Whereas, what the behaviorists seemed to have got right—contra the identity theory—was the relational character of mental properties. Functionalism, grounded in the machine analogy, seemed to be able to get both right at once . (Fodor 1981: 9, emphasis added)

2.8—
Vindicating Intentional Psychology (2): Symbols and Computation

Despite its significant virtues, machine functionalism alone is not sufficient for vindicating intentional psychology. What machine functionalism establishes is that there can be systems which are characterized by causal regularities not reducible to physical laws. What it does not establish is that physical objects picked out by a functional description of a physical system can also be mental states or that functionally describable processes can also be rational mental processes. First, there is an ontological problem: functionalism alone does not show that the physical objects picked out by functional descriptions can be the very same things as the mental tokens picked out in the intentional idiom. As a consequence, explanations in intentional terms are still ontologically suspect, even if there can be some functionally delimited kinds which are

unproblematic ontologically. The second problem is methodological: unless the kinds picked out by a psychology, even functional psychology, are the sorts of things susceptible to semantic relationships, the explanations given in that psychology do not have the characteristics that explanations in intentional psychology have.^[12]

CTM seeks to rescue intentional psychology from this impasse by uniting functional and intentional psychologies through the notion of symbol employed in the computer paradigm. Computers, according to the standard account, are not merely functionally describable physical objects—they are functionally describable symbol manipulators . Symbols, however, are among the sorts of things that can have semantic properties, and computer operations can involve transformations of symbol structures that preserve semantic relationships. This provides a strategy for uniting the functional-causal nature of symbols with their semantic nature, and suggests that a similar strategy might be possible for mental states. Thus Fodor writes,

Computation shows us how to connect semantical with causal properties for symbols . So, if having a propositional attitude involves tokening a symbol, then we can get some leverage on connecting semantical properties with causal ones for thoughts . (Fodor 1987: 18)

This, however, requires the postulation of mental symbols:

In computer design, causal role is brought into phase with content by exploiting parallelisms between the syntax of a symbol and its semantics. But that idea won't do the theory of mind any good unless there are mental symbols: mental particulars possessed of both semantical syntactic properties. There must be mental symbols because, in a nutshell, only symbols have syntax, and our best available theory of mental processes—indeed, the only available theory of mental processes that isn't known to be false—needs the picture of the mind as a syntax-driven machine. (ibid., 19-20)

It is this addition of the notion of symbol that makes CTM stronger than machine functionalism. And it is in virtue of this feature that CTM can lay some claim to solving problems that functionalism was unable to solve. First, it can lay claim to solving the ontological problem. The ontological problem was that functionalism provided no warrant for believing that the functionally individuated (physical) objects forming the domain of a functional psychology could also be mental states—in particular, it seemed doubtful that they could have semantic properties. But if some of those functionally delimited objects are physically instantiated symbols, the computationalist argues, this difficulty is solved. Symbols

can both be physical particulars and have semantic values. So if intentional states are relationships to physically instantiated symbol tokens, and the semantic and intentional properties of the symbol tokens account for the semantic and intentional properties of the mental states, then it would seem to be the case that mentalism is compatible with materialism.

The second problem for machine functionalism was that it was unclear how functionally delimited causal etiologies of physical events could also amount to rational explanations. But the computer paradigm also seems to provide an answer to this question. If we assume that (1) intentional states involve symbol tokens with semantic and syntactic properties, that (2) cognitive processes are functionally describable in a way that depends upon the syntactic but not the semantic properties of the symbols over which they are defined, and that (3) this functional description preserves semantic relationships, then (4) functional descriptions can pick out cognitive processes which are also typified by semantic relationships. Functional descriptions of computer systems are based in causal regularities, and so intentional explanations can pick out causal etiologies. And since the state changes picked out by the functional description are caused by the physical properties of the constituent parts of the system, intentional explanation is compatible with the generality of physics.

CTM thus purports to have accomplished a major tour de force. It claims to have vindicated intentional psychology by providing a model in which mentalism is compatible with materialism, and in which explanation in the intentional idiom picks out causal etiologies and is compatible with the generality of physics. The appeal of this achievement, moreover, has outlived the popularity of the movements in philosophy of psychology that originally motivated the desire for a "vindication" of intentional psychology. For while there are relatively few strict behaviorists or reductionists left on the scene in philosophy of science, it is still widely believed that a scientific psychology should employ causal-nomological explanations and be compatible with materialism and with the generality of physics. It is perhaps ironic that these desiderata emerged as consequences of particular short-lived theories in epistemology, philosophy of language, and the logic of science. The theories from which they emerged—the verification theory of meaning and the thesis that there are reductive translations between the languages of the various sciences—have largely been abandoned, but the suspicion of the mental they engendered has outlived them. And thus the "vindication" of intentional

psychology will likely continue to be perceived as a virtue so long as this suspicion remains.

2.9—
Summary

This chapter has examined two major claims made on behalf of CTM: that it offers an account of the intentionality and semantics of intentional states, and that it provides a vindication of intentional psychology. These results are largely independent of one another, but both depend heavily upon computationalists' largely uncritical use of the notion of symbol . Each of these two results is highly significant in its own right, and if CTM can make good on either claim, it will have made a significant contribution to philosophy of mind and psychology. The next chapter will discuss some problems that have been raised about CTM's account of intentionality and semantics, and will argue that a proper evaluation of the account will require an examination of the notions of symbol and symbolic representation .

Chapter Three—
"Derived Intentionality"

If the computational theory has excited a maelstrom of interest in recent years, it has received a generous share of criticism as well. One important line of criticism, developed most notably by John Searle (1980, 1983, 1984, 1990) and Kenneth Sayre (1986, 1987), has centered around the suitability of the notions of computation and symbolic representation for explaining the semantic properties of mental states. I shall argue that there are several distinct lines of argument to be had here, but they share in common an intuition that there is something, either about the notion of symbolic representation in general or about representation in computers in particular, that makes it impossible to account for the semantic properties of mental states in representational terms.

What I shall do in this chapter is examine the criticisms offered by Searle and Sayre, and develop out of them three distinct lines of argument against CTM. The first, the "Formal Symbols Objection," locates the problem in CTM's attempt to wed the notion of representation with that of computation. It does this by claiming that computation is defined as "formal symbol manipulation," and hence is defined only over meaningless "formal symbols," with the consequence that, if the mind is a computer, it cannot operate upon meaningful symbols as required by CTM. The remaining arguments locate the difficulty for CTM more generally in the nature of symbolic meaning. More specifically, they locate the problem in the claim that symbolic meaning is "derived," whereas the meaningfulness of mental states is not derived, but "intrinsic." There are, however, two kinds of "derivativeness" that need to be explored

here, as they provide the bases for two very different objections. The first, the "Causal Derivation Objection," agrees with CTM that there is a class of properties called "semantic properties" that can be predicated both of symbols and of mental states, but it claims that symbols must "derive" their semantic properties from preexisting meaningful mental states. The second, the "Conceptual Dependence Objection" makes a much more radical claim: namely, that the semantic vocabulary (i.e., the words used to express semantic properties) is systematically homonymous—or, more precisely, paronymous . On this view, words in the semantic vocabulary express different properties when applied (a ) to symbols and (b ) to mental states, and in such a fashion that an analysis of the meanings of these terms as applied to symbols will refer back to meaningful mental states. According to this objection, the "semantic properties" attributed to symbols are (a ) distinct from and (b ) conceptually dependent upon the "semantic properties" attributed to mental states.

The examination of these three lines of argument in this chapter will not itself yield a decisive verdict with respect to the viability of CTM. It will, however, make clear the questions that must be addressed in succeeding chapters in order to reach such a verdict. The main results of the chapter may be summarized as follows: CTM relies heavily upon the notion of symbolic representation as a notion that can be used to account for the meaningfulness of mental states. There is some question, however, about whether the notion of symbolic representation—and more precisely, symbolic meaning —may not itself be conceptually dependent upon the notion of meaningful mental states, and hence incapable of explaining them. In order to determine whether this is so, however, it will prove necessary to undertake a full-scale analysis of symbols and symbolic meaning (chapter 4) and apply the results of this to computers (chapter 5) and to CTM (chapter 7).

It will, moreover, prove necessary to examine an additional concern as well. This chapter and several of those that follow it will share in the assumption made by Searle and Sayre that when advocates of CTM speak of representations as "meaningful symbols," it is symbolic meaning that they have in mind—that is, the kind of semantic properties customarily attributed to symbols. It is this assumption that will undergird the examination of the nature of symbolic meaning and the attempt to apply this notion to an account of intentionality in chapter 6, and the thesis that will be advanced in this and the next three chapters—the paronymy of the semantic vocabulary—is somewhat radical. But in light of the suggestion that the semantic vocabulary might be systematically

paronymous, it will prove necessary to investigate a second reading of CTM as well: namely, that words in the semantic vocabulary, such as 'meaningful,' do not express the same properties when applied to mental representations that they express when applied to garden-variety symbols—that words in the semantic vocabulary have a special use when applied to mental representations, a use whose analysis will differ from that of the analysis of terms such as 'meaningful' as applied to gardenvariety symbols such as utterances and inscriptions. If this is the case, semiotics will prove irrelevant to the assessment of CTM, and the semantic properties of representations will have to be construed in some other way. In spite of the reasonableness of Searle's and Sayre's assumption that CTM attributes to mental representations the very same sorts of "semantic properties" that are attributed to inscriptions and utterances, this alternative reading must also be considered. Chapter 5 will develop an alternative interpretation of CTM's use of the words 'symbol' and 'syntax'. Chapters 7 and 8 will examine two distinct strategies for conceiving the semantic component of CTM in a way that does not depend on a semiotic analysis of representation.

3.1—
Searle's and Sayre's Criticisms

In light of the key role that the notion of symbol plays in CTM, it is quite natural that some of the more important criticisms of the computational theory have been based upon objections to computationalists' use of that notion. John Searle and Kenneth Sayre have both articulated objections to CTM that are directed against (supposed) problems with the use to which writers like Fodor and Pylyshyn put the notion of symbol, especially as it occurs within the context of discussions of machine computation.

Searle and Sayre have argued that, whatever the virtues of CTM may be, one thing that it cannot provide is a model for understanding the intentionality and semantics of mental states. This, they argue, is a straightforward consequence of defining the notion of computation in terms of formal symbol manipulation. Sayre sums up the problem in this way:

The heart of the problem is that computers do not operate on symbols with semantic content. Not even computers programmed to prove logical theorems do so. Hence pointing to symbolic operations performed by digital computers is no help in understanding how minds can operate on meaning-laden symbols, or can perform any sort of semantic information-processing whatever. (Sayre 1986: 123)

As Sayre sees it, the problem is that in order to provide a model for understanding cognitive (intentional) processes as manipulations of symbols, machine computation would have to provide a paradigm in which meaningful symbols were manipulated by a computer. But the very definition of computation as formal symbol manipulation, argues Sayre, prohibits this: "There is no purely formal system—automated or otherwise—that is endowed with semantic features independent of interpretation" (ibid.). And while the interpretation assigned by the programmer or user does, in some sense, lend semantic properties to symbols in computer memory, "whatever meaning, truth, or reference they have is derivative . . . tracing back to interpretations imposed by the programmers and users of the system" (ibid.).

The interpretations imposed by programmers and users are, in Sayre's view, quite irrelevant to the claims of CTM. For to say that a symbol in computer storage has some meaning (in virtue of an interpretation imposed by a programmer or user) is not to say something about what that symbol is , but rather to say something about how it is used . But computationalism attempts to explain human mental processes on the model of computation—that is, on the model of computers just as computers, not on the model of some use to which computers are or could be put. For Sayre, this seems to rule out the possibility of CTM providing a way of understanding the meaningfulness and intentionality of mental states: since computation is defined in formal terms, and claims about the meanings of computer symbols are claims about how computers are used, it seems to follow that "computers, just in and by themselves . . . do not exhibit intentionality at all" (Sayre 1986: 124). And hence, argues Sayre, thinking of mental activities as computations "is of no help in explaining the nature of the intentionality those activities exhibit" (ibid., 124-125).

A very similar case is made by John Searle in his 1984 book Minds, Brains and Science . Searle writes that "it is essential to our conception of a digital computer that its operations can be specified purely formally" (Searle 1984: 30). A consequence of this is that, in a computer, "the symbols have no meaning. . . . they have to be specified purely in terms of their formal or syntactic structure" (ibid., 31). Like Sayre, Searle deems this to be fatal to the ability to CTM to account for semantics and intentionality. He argues that "there is more to having a mind than having formal or syntactical processes. Our internal mental states, by definition, have certain sorts of contents. . . . That is, even if my thoughts occur to me in strings of symbols, there must be more to the thought than the

abstract strings, because strings by themselves can't have any meaning" (ibid.).

3.2—
Three Implicit Criticisms

The basic thread of criticism common to Searle and Sayre is clear enough: symbolic representation in computers does not provide a fit model for the intentionality of mental states. But if the general lines of the criticism are plain enough, the exact details are a bit more difficult. On the one hand, there seems to be some suggestion that the problem lies specifically with symbols in computers, to the effect that these symbols (unlike other symbols) are not meaningful at all, and hence are poor candidates for explaining the meaningfulness of mental states. On the other hand, other passages suggest a more general problem about the very nature of symbolic meaning—namely, that the semantic properties of symbols, even symbols in computers, are somehow "derived" from the meaningbestowing acts and conventions of symbol users, and that this somehow imperils the possibility of accounting for the meaningfulness of mental states in terms of the meaningfulness of symbols. I shall argue, moreover, that there are in fact two different senses in which symbolic meaning might be said to be "derivative," each of which can serve as the basis of an attack upon CTM. In the following sections, I shall discuss each of these variations upon Searle's and Sayre's texts in turn. My concern here will, moreover, be with analysis of the different lines of argument rather than with questions of exegesis.

3.3—
The Formal Symbols Objection

In some places, Searle and Sayre each seem to suggest that the problem for CTM lies specifically in the fact that it tries to wed the notion of computation to that of symbolic meaning . Sayre writes, for example, that "computers do not operate on symbols with semantic content," and he concludes from this that "pointing to symbolic operations performed by digital computers is no help in understanding how minds can operate on meaning-laden symbols" (Sayre 1986: 123). Similarly, Searle writes that the symbols in a computer "have no meaning. . . . they have to be specified purely in terms of their formal and syntactic structure" (Searle 1984: 31). This, according to Searle, is the crucial difference between mental states and symbols in computers:

The reason that no computer program can ever be a mind is simply that a computer program is only syntactical, and minds are more than syntactical. Minds are semantical, in the sense that they have more than a formal structure, they have a content. (ibid.)

A natural way of reading these passages would be that Searle and Sayre believe that computation is defined only over a special class of "formal symbols" that are, by definition, devoid of semantic content. Indeed, Searle writes that a computer "attaches no meaning, interpretation, or content to the formal symbols it manipulates." On this reading, the problem with the computer paradigm is that it cannot be applied to symbols that have semantic and intentional properties, and hence cannot be applied to the kinds of mental representations postulated by CTM. I shall call this objection the "Formal Symbols Objection."

It is easy to see how such a line of criticism might arise. If computers are defined as "formal symbol manipulators," it is tempting to conclude that this means that they are devices that manipulate some class of entities called "formal symbols"—that is, symbols devoid of semantic content. Moreover, this interpretation of CTM is not without textual support from important advocates of CTM. Pylyshyn, for example, speaks of computation as operation upon "meaningless symbol tokens," and goes so far as to bemoan the fact that (even) computationalists sometimes experience an "occasional lapse" in which "semantic properties are . . . attributed to representations" (Pylyshyn 1980: 114-115). It is, however, easy enough to find passages in expositions of CTM that are in contradiction with this interpretation as well. Fodor consistently insists that computers do operate upon symbols that have meanings, though he claims that computers have access only to the syntactic properties.^[1] And even Pylyshyn takes a line similar to Fodor's in his book Computation and Cognition .^[2] (There are some writers [e.g., Stich 1983] who have advocated a purely "syntactic" theory based on the computer metaphor, but their views are significantly at odds with CTM.)

Now if computation were restricted by definition to meaningless symbols, there would indeed be a problem with extending the computer paradigm to provide an account of the intentionality of mental states in the fashion indicated by CTM. For CTM requires that the mind be a system that performs computations over meaningful representations. As a consequence, if computation is defined as applying only to meaningless symbols, CTM demands the impossible, and the claims it makes are self-contradictory and hence false.

This criticism, however, seems based upon a dubious understanding of the notion of computation, and more particularly upon a dubious parsing of the expression 'formal symbol manipulator'. If the Formal Symbols Objection turns upon the claim that computers are, by definition, capable of manipulating only "meaningless formal symbols," the objection is deeply flawed and reflects a misunderstanding of the use of the word 'formal'. If this is Searle's and Sayre's point, they seem to have confused questions about the formal specifiability of symbol systems with questions about the meaningfulness of symbol tokens . Symbol tokens, strictly speaking, are neither formal nor informal. Derivation techniques are said to be formal if they do not depend upon the meanings of the symbols, and systems that employ symbol structures, such as logic or geometry, are said to be formal if they involve only formal derivation techniques. But formal logic and formal geometry generally do involve some degree of semantic interpretation. Indeed, it is only because the systems have interpretations that they can be regarded as logic and geometry . When one speaks of "formal symbol manipulations," the word 'formal' modifies the word 'manipulations', not the word 'symbol'; and when one speaks of computers as "formal symbol systems" one does not thereby imply that the symbols lack interpretations, but only that the symbol manipulations performed by the machine do not depend upon the interpretations of the symbols. There is thus no contradiction in saying that the mind is a computer that operates on meaningful symbols.

There is, of course, a much milder sort of objection that might be voiced about which symbols in computers do in fact have meanings, or indeed if any do. To the extent that symbols in computers might turn out to be meaningless, computers become less appealing as a model for the mind. But really this poses no significant threat to CTM. CTM's claim, after all, is not that production-model computers provide a good metaphor for the mind, but that the exact mathematical notion of computation provides the right sort of resources for supplementing a representational account of intentionality with a computational account of cognitive processes. And this claim requires only the possibility of consistently combining computation with representation in the case of mental states, regardless of whether it takes place in production-model computers. However, the persuasive force of the arguments marshaled in favor of CTM depend in large measure on the claim that the paradigm of machine computation shows that it is possible to combine symbolic meaning with syntactically driven computation in the desired fashion, and upon the assumption that this same union can be made to work in

the case of mental representations, and it remains to be seen whether an investigation of symbols and computation in computing machines will bear these assumptions out. An examination of symbolic representation in general, and representation in computers in particular, thus seems desirable.

3.4—
Derived Intentionality

If the Formal Symbols Objection does not seem to present serious problems for CTM, Searle's and Sayre's discussions raise what would seem to be a more serious objection as well. For while both writers sometimes speak as though the problem with CTM lies specifically with symbols in computers, each also says things that suggest that the problem is a problem concerning symbolic meaning generally. The nub of the problem is that symbolic meaning is "derived" from the meanings of mental states and from conventions governing the use of symbols, and thus CTM has the relationship between symbolic meaning and mental meaning precisely reversed.

Searle develops this view in his discussion of the relationship between intentional states and illocutionary acts. Searle holds that the sense in which intentional and semantic properties may be attributed to symbols in computers is precisely analogous to the sense in which they may be attributed to illocutionary acts such as assertions and promises. Illocutionary acts, according to Searle, have their intentional properties because they are expressions of intentional states: "In the performance of each illocutionary act with a propositional content, we express a certain Intentional state with that propositional content. . . . The performance of the speech act is eo ipso an expression of the corresponding Intentional state" (Searle 1983: 9). The intentionality of illocutionary acts (and other linguistic tokens) is derived from the intentionality of mental states. Indeed, illocutionary acts are said to be "intentional" in two ways, each of which depends upon the intentionality of a mental state. First, since a speech act derives its content from the intentional state of which it is the expression, it is intentional in the sense of having a content in virtue of its relationship to an intentional state with that same content. (An assertion is about Lincoln, for example, because it is an expression of a belief about Lincoln.) What unites the utterance with the intentional state it expresses, however, is a second intentional state—namely, the intention of the speaker that his utterance be an expression of a particular intentional state (see Searle 1983: 27).

The intentionality of symbols in computers, according to Searle, can be explained in just the same fashion. Symbols in a computer, like marks on paper or vocalized sounds, are not intrinsically meaningful. Meaning is imputed to symbols by some being who has intentional states. In the case of language, it is the speaker or writer. In the case of symbols in computers, it is the designer, programmer, or user. Intentional states have intentionality intrinsically; symbols have it only derivatively .

Sayre makes a case against the extendability of the computer paradigm in a similar fashion. Like Searle, he admits that symbols in computers may in some sense be said to have meanings and intentionality, but he maintains that "whatever meaning, truth, or reference they have is derivative . . . tracing back to interpretations imposed by the programmers and users of the system" (Sayre 1986: 123). Sayre argues that treating computers as dealing with meaningful symbols involves talking not just about the computer, but about the uses to which it is put and the interpretations imposed upon its symbols and its operations by the user. "Computers, just in and by themselves . . . do not exhibit intentionality at all" (ibid., 124). Since intentional states do have intentionality "in and by themselves"—that is, independently of impositions of interpretations from outside sources—the computer paradigm is ill suited to providing an understanding of the intentionality and semantics of mental states.

3.5—
The Ambiguity of "Derived Intentionality"

The notion of "derived intentionality" to which both Searle and Sayre appeal is of crucial importance in assessing CTM. Yet it is also ambiguous and admits of two significantly different interpretations. On one interpretation, the word 'derived' indicates something about how an object that has intentional or semantic properties got them. On this interpretation, words such as 'intentionality' and 'meaning' express the same properties when applied to symbols and mental states, and an object has derived intentionality just in case it received or inherited its intentional properties from another object having intentional properties by way of some causal connection. This will be called "causally derived intentionality." On the second interpretation, the "derivativeness" of the intentional properties of symbols is a logical feature of the way intentional properties can be ascribed to symbols . On this view, terms such as 'meaningful' and 'intentional' cannot be predicated univocally of sym-

bols and mental states, and hence any theory that depends upon the univocal application of such terms is conceptually confused. This will be called the "conceptually dependent intentionality" of symbols. These two notions have significantly different impacts upon CTM, and so will receive independent development. The Causal Derivation Objection assumes with CTM that there is one kind of property called "intentionality," and claims that there is a one-way inheritance relationship between mental states and symbols. The Conceptual Dependence Objection claims that what words in the semantic vocabulary signify when applied to symbols is (a ) distinct from and (b ) logically dependent upon what they signify when applied to mental states.

3.6—
Causally Derived Intentionality

The first way of interpreting the expressions 'intrinsic' and 'derived intentionality' is to construe them as pointing to differences in the sources of the intentional properties of mental states on the one hand, and symbols and illocutionary acts on the other. On this view, there is one property called intentionality which cognitive states, symbols, and illocutionary acts can each possess, but they come by it in different ways. Thus Searle writes,

An utterance can have Intentionality, just as a belief has Intentionality, but whereas the Intentionality of the belief is intrinsic, the Intentionality of the utterance is derived . The question then is: How does it derive its Intentionality? (Searle 1983: 27)

This way of phrasing the problem reflects Searle's views on the nature of the problem of linguistic or symbolic meaning:

Now the problem of meaning in its most general form is the problem of how do we get from the physics to the semantics; that is to say, how do we get (for example) from the sounds that come out of my mouth to the illocutionary act? (ibid.)

Searle's answer is that utterances come to have semantic properties because the person making the sounds intends "their production as the performance of a speech act" (ibid., 163). This is an instance of what Searle calls "Intentional causation": the speaker's "meaning intention" that the sounds express an intentional state is a cause of the fact that the utterance comes to have intentionality.^[3]

If the expression 'derived intentionality'—or more generally, 'derived

semantic properties '—is meant to signify this sort of causal dependence, we may clarify the usage of the expression in the following way:

Causally Derived Semantics

X has semantic property P derivatively iff

(1) X has semantic property P

(2) There is some Y such that

(a ) Y¹X ,

(b ) Y has semantic property P , and

(c ) Y 's having P is a (perhaps partial) cause of X 's having P .

X may be said to have semantic property P intrinsically just in case X has P and X does not have P derivatively.

Now I take it that both Searle and Sayre would wish to claim that symbolic meaning is causally derivative, whereas the intentionality of mental states is intrinsic. That is, they would claim that the semantic properties of symbols are causally derived from the semantic properties of the mental states of symbol users, while there is no Y such that a mental state M 's meaning P is causally dependent upon Y 's meaning P . If this is correct, then CTM errs in two respects: first, it assumes that the intentionality of mental states is derived (i.e., from mental representations) rather than intrinsic; second, it assumes that the intentionality of symbols can be accounted for without recourse to causal derivation from mental states.

3.7—
Assessing the Causal Derivation Objection

In order for the Causal Derivation Objection to prevail against CTM, it would be necessary to establish two claims:

(S1) The Derivative Character of Symbolic Meaning: Necessarily, all symbols with semantic properties have those properties by way of causal derivation.

(S2) The Intrinsic Character of Mental Semantics: All semantic properties of mental states are intrinsic (i.e., not causally derived).

It seems quite clear that, if these two claims are correct, CTM is fundamentally flawed. Unfortunately, the arguments provided by writers like

Searle and Sayre do not establish the derivative character of symbolic meaning, but merely the weaker claim that certain familiar kinds of symbols—inscriptions, utterances, symbols in computers—have their semantic properties by way of causal derivation. As for the claim that all semantic properties of mental states are intrinsic, no argument has been given for that claim at all.

Moreover, both of these claims have come under fire from proponents of CTM and other writers in cognitive science. I shall explore two lines of response, which I shall call the "Fodor move" and the "Dennett move."

3.7.1—
The "Fodor Move"

It is not too surprising to find that Fodor is a dissenter with respect to claim (S1). It is, however, illuminating to note how far he is willing to go along with Searle's analysis of symbolic meaning. Fodor largely agrees with the analysis Searle gives of the semantic properties of discursive symbols such as those involved in illocutionary acts, and he even seems to sympathize with the notion that one must give a similar sort of account of semantics for symbols in computers. But he also thinks that mental representations differ from discursive symbols precisely in this regard:

It is mental representations that have semantic properties in, one might say, the first instance; the semantic properties of propositional attitudes are inherited from those of mental representations and, presumably, the semantic properties of the formulae of natural languages are inherited from those of the propositional attitudes that they are used to express. (Fodor 1981: 31)

Thus Fodor agrees with Searle that there are certain properties called "semantic properties" that can be possessed by mental states and by discursive symbols. He agrees, additionally, that discursive symbols get their semantic properties from the intentional states they are used to express. He simply adds that there are these other, non discursive symbols in the mind that (a ) do not get their semantic properties the way discursive symbols do, but in some other fashion, and (b ) are the ultimate source of the semantic properties of intentional states. I shall call this reply to the Causal Derivation Objection the "Fodor move."

There seems to be little in Searle's texts to militate against the Fodor move. Searle agrees with Fodor that there is a class of properties such as "intentionality" that can be predicated indifferently of symbols and mental states. And, while he has argued convincingly that certain familiar

classes of symbols—perhaps all of the familiar classes—acquire their semantic properties by way of causal derivation, he has offered no reason to draw the stronger conclusion that there cannot be other classes of symbols that can acquire semantic properties by other means. There should, of course, be a burden of proof upon CTM's advocates to justify the claim that there is some other way for symbols to acquire meaning (and to do so without equivocating on the notion of "meaning"), but arguably this is precisely what they are doing when they seek to provide "theories of content" for representations.^[4]

3.7.2—
The "Dennett Move"

Claim (S2), which asserts the intrinsic character of the intentionality of mental states, has likewise met with disagreements. The very assertion of CTM involves its explicit denial, since CTM claims that mental states "inherit" their semantic properties from representations. Moreover, the claim of intrinsicality seems to swim against a strong current within cognitive science of attempts to explain high-order cognitive phenomena by breaking them down into (hypothetical) lower-order cognitive phenomena, sometimes explaining the semantic properties of the high-order phenomena by appeal to the semantic properties of their components. Dennett (1987) has perhaps taken this move as far as anyone, claiming that if sociobiology provides legitimate explanations, then the semantic properties of our mental states are ultimately traceable to the intentions of our genes. (Call this the "Dennett move.")

Now there are two ways of taking the Dennett move. On the strong reading, Dennett is really claiming that genes are in fact the ultimate source of intentionality—that they have intentionality intrinsically, and that everything else that has intentionality, including mental states and discursive symbols, has it derivatively. (On this view, many mental representations would not have intentionality intrinsically either, but the intentionality of intentional states could still be causally derived from that of mental representations.) This version of the Dennett move is only as plausible as (a ) the claims of sociobiology, and particularly (b ) the assumption that semantic properties can sensibly be ascribed to entities such as genes. I think that most readers find these claims, especially (b ), to be more than a little suspect. But there is also a weaker way of treating the Dennett move: namely, to take it as a kind of reductio of Searle's Causal Derivation Objection to theories like CTM. On this reading,

Dennett's real point is that once you let in the notion of causal derivation of intentionality, there is no reason to stop with intentional states, since cognitive scientists regularly explain beliefs and desires by appeal to infraconscious states to which they also impute semantic properties. Perhaps the chain does not go back so far as genes, but why assume that it stops with intentional states?

Now it may well be possible to muster an adequate reply to the Dennett move, but doing so would seem to require something beyond what is present in the Causal Derivation Objection. That objection already acknowledges that several diverse kinds of things (symbols and mental states) have semantic properties, and that the presence of semantic properties in one can cause semantic properties to be present in the other. What is to prevent the possibility of other kinds of entities having such properties as well, or to prevent them from causing the semantic properties of mental states? The answer one wants to give, perhaps, is that there is something simply outrageous about attributing semantic properties to genes or nerve firings—that these just are not among the sorts of things of which properties such as "meaning" and "intentionality" may sensibly be predicated. They are not proper logical subjects for belief attributions. To make a case for this, however, would require something more than the notion of causally derived intentionality provides—namely, an analysis of the nature of meaning and intentionality. It is here that the next line of criticism will find much of its appeal.

3.7.3—
Prospects of the Causal Derivation Objection

All in all, it seems that the notion of causally derived intentionality may serve to place a significant burden of proof upon would-be advocates of CTM, but it does not reveal any fundamental flaw with that theory. The burden of proof arises from the fact that mental representations would have to differ from all known kinds of symbols in a fundamental respect: namely, in how they come to have semantic properties. The only way we know of for symbols to acquire meaning is through interpretive acts. This does not preclude the possibility of symbols acquiring meaning in some other way, but it is likewise unclear that there is any other way for them to acquire meaning. Since CTM requires that there be another such way, its advocates had best show that there can be such a way. This, however, is arguably just what CTM's proponents are doing when they discuss "theories of content" for mental representations.

3.8—
The Conceptual Dependence Objection

While I rather expect that something on the order of causal dependence was what Searle and Sayre had in mind when they spoke of "derived intentionality," there is another way of interpreting the expression 'derived intentionality' which may damage CTM in a more fundamental manner. On the causal construal of Searle's expression 'derived intentionality', the term 'intentionality' could be predicated univocally of both mental states and symbols. The difference between cognitive states and symbols lay in how they came to have this one property. This is probably what Searle had in mind in his discussion of derived intentionality. But one might read the expression 'derived intentionality' in quite another way. One might read it as meaning "intentionality in a derivative sense ." On this reading, attributions of intentional and semantic properties to cognitive states and attributions of intentional and semantic properties to symbols are not attributions of the same properties .

3.8.1—
The Homonymy of 'Healthy': An Aristotelian Paradigm

In setting up the problem, it may be helpful briefly to recall Aristotle's discussion of homonymy. Aristotle points out that some words, such as 'healthy', are used in different ways when they are applied to different kinds of objects. We say that there are healthy people, healthy food, healthy exercise, healthy complexions, and so on. But when we say that some kind of food is healthy, we are not predicating the same thing of the food that we are predicating of a person when we say that he is healthy. If I say that fish is a healthy food, I mean that eating fish is conducive to health in humans. But if I say that Jones is healthy, I mean that he is in good health .^[5] (Individual fish can be healthy in the same sense that Jones is healthy, but they have ceased from being in good health by the time they are healthy food for Jones.) Yet words like 'healthy', according to Aristotle, are not merely homonymous. Rather, there is one meaning which is primary or focal, and the other meanings are all to be understood in terms of how they relate to the primary meaning. In the case of 'healthy', the primary meaning is the one that applies to people (or, more generally, to living bodies): to be healthy in the primary sense is to be in good health. Things other than living beings are said to be "healthy" in other senses because of the way that they relate to being in good health: for example, because of the way they contribute to being in good health (e.g., a healthy diet or

regimen), or because of the way they indicate good health (e.g., a healthy complexion). Aristotle calls this kind of homonymy paronymy or "homonymy pros hen ." The sense of 'healthy' that applies to food is dependent upon, and indeed points to the sense of 'health' that applies to bodies. "Healthy food" means "food that is conducive to bodily health." And similarly the senses of 'healthy' that apply to exercise, appearance, and so on point to the notion of bodily health. As a result, questions about the "healthiness" of a particular food amount to questions about how it contributes to bodily health . Someone who thought that bodily health was derived from the "health" contained in the food one ate would simply be mistaken about how the word 'health' is used. And it would betray conceptual confusion if one were to say, "I don't want to know how broccoli contributes to bodily health, I just want to know why it is healthy ."

Of course, someone could use the word 'healthy' in some new manner. For example, someone convinced that vitamins were the source of bodily health might start applying the word 'healthy' in a way that just meant "full of vitamins." This use of the word 'healthy' (to be indicated 'healthy_v ') would no longer be conceptually dependent upon the notion of bodily health. But 'healthy_v ' would not mean what 'healthy' is normally understood to mean either. In particular, one could not draw upon any implications of the normal use of the word 'healthy' in reasoning about things that are healthy_v . For example, presumably things are healthy_v in proportion to the number and quantity of vitamins present in them. A meal with ten thousand times the recommended daily allowance of all vitamins would be very healthy_v . But one cannot infer from this that such a meal would be healthy (conducive to health). First, since 'healthy_v ' no longer bears a semantic connection to the notion of bodily health, the analytically based inference does not go through. Second, the conclusion happens to be empirically false. Massive doses of some vitamins are not conducive to health, but toxic. Old words can be given completely new meanings, but then what you have is homonymy plain and simple. And not all of the things that may be said of things that can be said to be healthy can also be said of things that are healthy_v .

3.8.2—
"Derived Intentionality" as the Homonymy of 'Intentional'

Now one could interpret the expression 'derived intentionality' as pointing to a conceptual dependence between different uses of words such as 'intentional', 'intentionality', 'meaningful', 'referential'—in short, of all

words used in attributing intentional and semantic properties. And the nature of the dependence would be along the following lines: both symbols and mental states are said to be intentional, meaningful, referential, and so on. But words such as 'intentional' and 'meaningful' are not used in the same way when they are said of symbols as when they are said of mental states. Intentional and semantic terms are homonymous. But they are not merely homonymous. Rather, it is a case of paronymy, or homonymy pros hen, where there is a primary or focal sense of each term: specifically, the sense that is applied to cognitive states. The sense that is applied to symbols is "derivative" or conceptually dependent because it refers back to the sense that is applied to cognitive states. For example, when we say that a speech act is intentional, what we mean is that it is an expression olean intentional state . On this view, there would be no sense in which a speech act could be said to be intentional that did not point to an intentional state in similar fashion.

Now I believe that a view of this sort is implicit in some of the things written by Sayre and Searle, but I do not see that it is ever explicitly articulated in this form, or marshaled as an explicit objection to CTM.^[6] Searle's analysis, moreover, is confined almost exclusively to illocutionary acts, and is not developed more generally for symbols . Since CTM does not posit that mental representations are illocutionary acts, Searle's analysis would at very least have to be broadened if it is to provide a criticism of CTM. It is quite possible, however, that Searle has in mind something like this notion of conceptual dependency of symbolic intentionality and meaning when he blames the inadequacies of CTM upon the fact that the "meaningfulness" and "intentionality" of symbols in computers is "dependent" upon the intentions of users and programmers.

Sayre's analysis of the shortcomings of CTM might also be read as relying upon the premise that the kind of intentionality that symbols may be said to have is conceptually dependent upon the kind of intentionality that cognitive states may be said to have. Sayre places more stress than does Searle upon the role that computer users and programmers play in imbuing symbols in computers with meaning and intentionality. He writes, for example, that

none of the representations internal to the machine has meaning, or truth, or external reference, just in and by itself. Whatever meaning, truth, or reference they have is derivative . . . tracing back to interpretations imposed by programmers and users of the system. . . .

. . . My point is that computers, just in and by themselves, no matter how programmed, do not exhibit intentionality at all. (Sayre 1986: 123, 124)

If assertions which appear to be just about the meaningfulness of symbols in computers turn out to be (covert) assertions about the actions and intentions of computer users and programmers, then the computer paradigm does involve symbols with "intentional" and "semantic" properties, but only in the sense that it involves a  human-computer system in which the humans impute semantic and intentional properties to the symbols in the computer. If this be the case, there may well be problems about extending the model to account for intentionality in humans.

Unlike Searle, Sayre also touches more broadly upon the semantic features of symbols in general. In discussing the semantic properties of symbols in a natural language, he stresses the point that natural language symbols have semantic properties only because of interpretive conventions:

Inasmuch as the English word "cat" refers to cats, the word consists of more than can be uttered or written on paper. It consists of the symbolic form CAT (which can be instantiated in many ways in speech and writing) plus interpretive conventions by which instances of that form are to be taken as referring to cats . Similarly, the symbolic form Go means the opposite of STOP (or COME , etc.) by appropriate interpretive conventions of English, while by those of Japanese it means a board game played with black and white stones. But without interpretive conventions it means nothing at all . (Sayre 1986: 123, emphasis added)

If this passage is read with the notion of conceptual dependence in mind, it is extremely suggestive. If talk about the meaningfulness of symbols is necessarily (covertly) talk about linguistic conventions, then the meaningfulness of symbols is conceptually dependent upon conventions. And if this is the case, CTM may be in very serious trouble indeed.

3.8.3—
The Potential of a "Conceptual Dependence Objection"

While Searle's and Sayre's criticisms of CTM may well include the kernel of a "Conceptual Dependence Objection," no full-scale development of such an objection has yet been offered. Developing such an objection will, among other things, involve a careful examination of the notion of symbol and the ways that symbols of various sorts may be said to have semantic and intentional properties. Such an analysis will be undertaken in chapter 4.

But even prior to such an analysis, it is possible to see, in general terms, what force such an objection would have. CTM's representational

account of cognitive states consists primarily in the claim that these involve symbolic representations which have semantic properties. If the Conceptual Dependence Objection can be made to stick, however, all attributions of semantic and intentional properties to symbols refer to something more than the symbol: they refer to the beings who are responsible for the symbol's having an interpretation. This would present two kinds of problems for CTM. First, like the Causal Derivation Objection, it calls the credibility of the computer paradigm into question: it just seems incredible to postulate that there is some being (or beings) responsible for interpreting mental symbols. But there is also a more fundamental problem: if all attributions of symbolic meaning are (covertly) attributions of the imposition of meaning, then attributions of intentional and symbolic properties to any symbol would have to involve attributions of intentional states of some agent or agents responsible for the imposition of meaning upon that symbol. And this would seem to involve CTM in regress and circularity: CTM explains the intentionality and semantics of cognitive states in terms of the intentionality and semantics of symbols. But if the intentionality and semantics of symbols are, in turn, cashed out in terms of cognitive states, there is circularity in the interexplanation of cognitive states and symbols, and a regress of cognitive states responsible for the intentionality and semantics of other cognitive states. Such an objection would be far more damaging than the Causal Derivation Objection.

3.9—
The Need for Semiotics

This chapter has been devoted to a discussion of attacks marshaled against CTM that are directed specifically against its use of the notion of symbol . The upshot of the chapter is that the notion of symbol needs further elucidation. The first objection, the Formal Symbols Objection, turned upon claims about the symbols stored in and manipulated by computers—specifically, the claims that computers only could store or only do store meaningless "formal symbols." It was suggested that this objection rested upon a confusion about the meaning of expressions such as 'formal symbol manipulation'. The "formality" of formal systems and computers, it was argued, consists in the fact that the techniques through which derivations of symbols are effected are blind to the semantic properties of the symbols. A mathematical system or a computer can be formal in this sense and still operate upon meaningful symbols. Indeed both formalized mathematical systems (such as Hilbert's geometry) and dig-

ital computers often do involve meaningful symbols—that is, symbols that are assigned interpretations by the mathematician, the programmer, or the computer user. The Formal Symbols Objection is nonetheless very alluring, and the literature on computers and the mind is replete with suggestions that computers operate upon some special class of "meaningless formal symbols." The ambiguity of expressions such as 'formal symbol manipulation' and the difficulty of characterizing the semantic status of symbols in computers gives us reason to inquire more carefully into the nature of attributions of semantic properties to symbols in general and to symbols in computers in particular.

A general examination of the notion of symbol is also made necessary by our development of the notion of "derived intentionality." The Causal Derivation Objection consisted in the claim that the account one would give of the intentional and semantic properties of symbols cannot also be used as an account of the intentional and semantic properties of cognitive states, because symbols have their intentional and semantic properties only by virtue of causal derivation. But all that was really shown was that illocutionary acts and symbols in computers do not have intentionality intrinsically. Computationalists now generally agree that (a ) CTM does not provide a full-fledged semantic theory, and (b ) mental representations do not come by their intentionality the way symbols in computers do. The question of whether some other kinds of symbols might have intentionality and semantics intrinsically remains open.

Finally, the Conceptual Dependence Objection argues that the very notion of symbol makes essential reference to cognizers who are responsible for the imposition of meaning upon symbols, and upon the cognitive states which are involved in this imposition of meaning. This objection might well undercut CTM completely, but it has yet to be developed in detail and requires a careful examination of the nature of symbols as a prerequisite.

A further issue also arises here: if the semantic vocabulary does turn out to be systematically homonymous, it may turn out additionally that the kind of "meaning" that is to be attributed to mental representations is not the same kind of "meaning" that is attributed to symbols. So, in addition to assessing the question of whether symbolic meaning can explain mental meaning, it may prove necessary to examine whether there might be other kinds of "meaning" possessed by mental representations (i.e., other properties expressed by a distinct usage of the word 'meaning').

This sets some agenda for the remainder of this book. Chapter 4 will

undertake the task of clarifying the notion of symbol —specifically, it will examine what it is to be a symbol, what it is to have syntactic properties, and what it is to have semantic properties. This analysis will be applied to CTM in chapter 7 in order to assess the force of the objections marshaled by Sayre and Searle. Meanwhile, chapter 5 will explore an alternative way of interpreting the use of the words 'symbol' and 'syntax' by CTM's advocates, and chapters 8 and 9 will examine two ways of articulating a notion of "semantics" that is in important ways discontinuous with the usage of that word as applied to symbols.