Chapter II
Planck's Absolute Irreversibility

Against Atoms

Among the outspoken adversaries of Boltzmann's notion of irreversibility stood one of the most respected German thermodynamicists: Max Planck. In his dissertation work of 1879 this son of a law professor had raised the entropy law to the status of an absolute principle. Two years later he explicitly rejected the molecular hypothesis, precisely because it contradicted his conception of the second principle of thermodynamics:

When correctly used, the second principle of the mechanical theory of heat is incompatible with the hypothesis of finite atoms [here a footnote refers to Maxwell's demon argument]. One should therefore expect that in the course of the further development of the theory, there will be a fight between these two hypotheses that will cost the life of one of them. It would be premature to predict the outcome of this fight now; but for the moment it seems to me that, in spite of the great successes of the atomic theory in the past, we will finally have to give it up and to decide in favor of the assumption of continuous matter.^[31]

Planck's argument derived from Maxwell's earlier demon argument. The superhuman demon described in Maxwell's letter to Tait of December 1867 was able to discriminate between slow and fast molecules and, without expense of energy, to direct these two sorts of molecules toward different containers. The temperature gradient created in this way of course

[31] Planck 1882, 475; for Planck's background see, e.g., Heilbron 1986; for his antiatomistic positions see Kuhn 1978.

contradicted the second principle of thermodynamics. The conflict between the molecular hypothesis and the entropy law shown in this thought experiment convinced Maxwell that entropy was a subjective notion, namely, one depending on the physicist's incapability of controlling the motion of individual molecules. The same conflict led Planck to exclude the molecular hypothesis.^[32]

During the years following this first public condemnation of kinetic molecular theory, Planck successfully applied macroscopic thermodynamics to various systems (chemical equilibrium, solutions, thermocouples, etc.), which strengthened his opinion that atoms were superfluous. In 1891 he found in the meeting of German scientists at Halle a public occasion to denigrate Boltzmann's and Maxwell's kinetic theory. The results of this theory, he declared, were not in suitable proportion to the mathematical effort expended.^[33]

Boltzmann did not answer Planck's attack directly, but in 1894 he found a proper opportunity to confound his adversary. Planck had accepted the editorship of the posthumous fourth volume of Kirchhoff's lectures on physics. The last part was dedicated to a detailed exposition of Maxwell's kinetic theory, and it contained, among other things, a presentation of the proof of Maxwell's distribution based on collision numbers. In a paper published in Annalen der Physik , Boltzmann criticized the negligence of Kirchhoff's editor. Whereas Maxwell had equated the number dn of collisions with initial velocities belonging to two given elementary domains of velocity space to the number dn ' of collisions with final velocities in these domains, the proof by Kirchhoff-Planck equated two different expressions of the same dn : the one given by Maxwell, and another, dn^* , obtained by multiplying "the probability of collision of two molecules" sdW |v₁ - v₂ | by the population of the final state 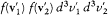. Boltzmann protested that the probability of collision of the two molecules equaled s dW |v₁ - v₂ | only if the past history of the molecules was unknown; a quite different expression had to be used when the molecules were known to have interacted in a given way.^[34]

Planck acknowledged this point but attributed responsibility for the mistake to Kirchhoff. He further claimed that the objection equally invalidated Maxwell's original reasoning (which reveals his ignorance of it). As a token of his good will, however, he offered an alternative deduction

[32] Maxwell to Tait, 11 Dec. 1867, Cambridge University Archive; Maxwell 1871, 308-309. See Klein 1970b.

[33] Planck 1891.

[34] Kirchhoff 1894, 134; Boltzmann 1894.

based on time reversal. When changing the direction of time, a stationary distribution of velocities is left unchanged and stationary; therefore, the number dn of collisions of a given kind must be equal to the number of collisions of the reverse kind, which is exactly Maxwell's dn '.^[35]

Boltzmann appreciated this argument, for it made the equality of dn and dn ' necessary and thus gave a new proof of the uniqueness of Maxwell's distribution without recourse to the H -theorem. In his published comments, Boltzmann emphasized the compatibility of the proof with the notion of molecular chaos. Indeed this concept, a fresh outcome of his discussions with British kinetic physicists, was precisely the one supposed to control the applicability of Maxwell's collision probabilities. On this occasion, in spite of his persisting dislike of atomism, Planck could gather that in kinetic theory irreversibility was intimately connected with some assumption of molecular chaos, whatever it meant. Besides, this incident may have convinced him that a new explanation of irreversibility was urgently needed to secure the foundations of thermodynamics.^[36]

Blackbody Radiation

Planck's belief in an absolute entropy principle excluded atomism but not Boltzmann's (and Clausius's) endeavor to give a mechanical explanation of entropy. With respect to mechanical reduction he believed entropy to be comparable to energy. Both quantities had to be determined not only by the thermodynamic state of the system but also by the underlying mechanical state. The problem was to find the proper mechanical basis. While in his opinion molecules would not do, the possibility of a continuum with well-chosen properties, the prime example being the electromagnetic ether, merited further exploration.

There was another reason to examine the relation between electrodynamics and thermodynamics: In the preceding years, several thermodynamic arguments had been successfully applied to the light emitted by heated bodies, and, since Maxwell's "dynamical theory of the electromagnetic field" (1864), the nature of light was often believed to be electromagnetic. Perhaps most important for someone in search of universal properties of nature, Kirchhoff had proved in 1859 an important theorem, a consequence of which was the universality of the spectrum of thermal radiation emitted by what he called a (perfect) blackbody.^[37]

[35] Planck 1895.

[36] Boltzmann 1895.

[37] Kirchhoff 1859. See Jungnickel and McCormmach 1986, 1:299-301; Jammer 1966, 2-6; and Kangro 1970.

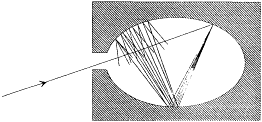
Figure 3.
Absorption of a radiation beam entering a pierced cavity.

By definition a blackbody absorbs any radiation falling upon it, which implies that it looks black in the common sense of the word as long as it is cold enough not to emit much thermal radiation. An excellent concrete realization of a blackbody is obtained by piercing a hole in a container whose walls are at least partially absorbing at all frequencies. Indeed, a light ray penetrating through the hole is both reflected and attenuated a great number of times by the inside walls, until it practically vanishes (see fig. 3). Let us now maintain the walls of this cavity at a constant high temperature. The radiation emitted by a portion of the walls interacts a great number of times with other portions of the walls, which leads to thermal equilibrium for the energy per unit volume u_vdv corresponding to a frequency interval dv .^[38] A simple proof of the universality of the spectral density u_v (not Kirchhoff's) goes as follows.

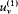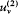Consider, ab absurdo , two cavities at the same temperature but with different spectral densities and . Connect them through a small tube in which is placed a filter F at the frequency v (fig. 4). If 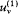is greater than 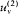, there must be a flow of radiation from 1 to 2; and this flow must be permanent since the excess of radiation energy in 2 must be re-absorbed in order to maintain the thermal equilibrium in 2. But a permanent energy flow between sources at equal temperature is incompatible with the second principle of thermodynamics. Therefore, it must be that

In 1884 Boltzmann assumed the electromagnetic nature of thermal radiation to prove Stefan's empirical law (1879): The total energy density u (given by 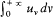u_vdv ) is proportional to the fourth power of the absolute

[38] The first definition of a blackbody is in Kirchhoff 1860. As Jammer explains, Kirchhoff's considerations originated in studies of solar radiation (Jammer 1966, 2-6). The use of a pierced cavity for the empirical study of blackbody radiation was first suggested by Christiansen 1884 and first realized by Lummer and Wien 1895.

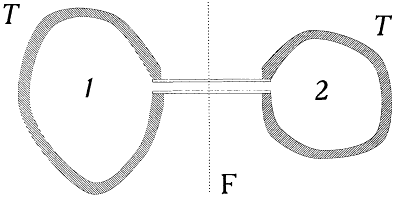
Figure 4.
Thought experiment leading to the universality of the blackbody spectrum. 
T  is the temperature of a thermal bath, and F a monochromatic filter.

temperature T . A slightly modernized version (in Planck's manner) follows.^[39]

According to Maxwell, an electromagnetic plane wave falling normally upon a perfectly reflecting surface exerts a mechanical pressure, the intensity of which is given by twice the energy density of the wave. Consider now the case of an isotropic radiation falling upon a reflecting plane P . The pressure exerted by the fraction of this radiation oriented in the direction z , within the solid angle dW , is given by p = 2u cos qdW /4p , where u is the total energy density, and q is the angle between the direction

and the normal to P . Since this pressure is directed along z , its component normal to P is p cos q , or 2u cos²qdW /4p . The average pressure, P , exerted on P is obtained by integrating the latter expression over all solid angles pointing toward P :

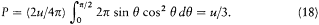
It should be further noted that in the case of blackbody radiation this pressure is independent of the reflecting quality of P . Indeed, if it were dependent, one could build a perpetual motion of the second kind by inserting in a blackbody cavity a plate silvered on one side and blackened on the other. One may therefore legitimately speak of a "radiation gas" with a definite pressure P , as Boltzmann did in his paper.

In this circumstance, the entropy variation

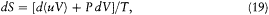
[39] Boltzmann 1884a, 1884b. For the context of this work see Carazza and Kragh 1989.

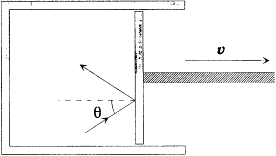
Figure 5.
Wien's perfectly reflecting piston, as used
 in the proof of the displacement law.

where V is the volume of the cavity, must be a differential. This implies (after subtraction of d(uV/T ) from dS )

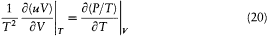
or, using (18) and Kirchhoff's law (which makes u a function of T only),

Integrating the latter equation gives

which is Stefan's law.

Boltzmann's original reasoning involved, for historical reasons not worth mentioning here, an adiabatic displacement of a reflecting piston inserted in a cylindrical blackbody cavity. During this displacement the spectrum of the reflected radiation differs slightly from that of the incident radiation, as a result of the Doppler effect. In 1894 Wilhelm Wien cleverly exploited this thought experiment to restrict the form of the function u_v (T ). ^[40]

Wien's argument, or more exactly Planck's version of it,^[41] starts with the consideration of a cavity with perfectly reflecting walls, one of which is part of a mobile piston (fig. 5). At the initial time this cavity contains isotropic electromagnetic radiation with the spectral density r_v . Under a slow displacement of the piston at a constant speed v , the light of frequency

[40] Boltzmann 1884b; Wien 1894.

[41] Planck 1906, 68-82.

v in an incident beam is Doppler-shifted by

where q is the angle of incidence, and c the velocity of light. In a time interval d t and for the same direction of incidence, the energy flux impinging upon the surface area S of the moving mirror is given by

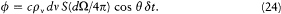
As a result of the Doppler shift of the reflected radiation, there is a variation d (p_v V) of the spectral energy at frequency v ; its value may be obtained by subtracting the flux at the frequency v , whose frequency will be increased above v , and adding the flux at the frequency v — d v, whose frequency will be increased just to v , by the reflection:

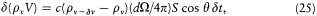
or, using (23) for d v,

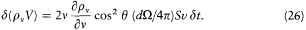
Noting that Svd t is equal to the variation in volume d V of the cavity, and integrating over q yields

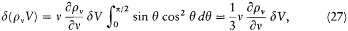
and

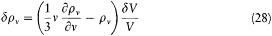
for the variation d r_v of the spectral density.

If the radiation initially contained in the cavity is blackbody radiation at a given temperature T (r_v = u_v (T )), then the radiation obtained after the adiabatic displacement of the piston must also be in thermal equilibrium (but at a different temperature). Indeed, if the opposite were true, one would have a state out of equilibrium connected to a state in equilibrium through an adiabatic reversible transformation, which is absurd.^[42] In this

[42] Planck (1906, 69-70) demonstrates the absurdity by considering the following cycle. The piston, initially containing blackbody radiation, is moved adiabatically to a different position (step 1); a little piece of a "black" substance is introduced inside the piston and removed (step 2); the piston is brought back adiabatically to its initial position (step 3); a little piece of "black" substance is introduced inside the piston (step 4). This is a cycle because both the total heat and the total work exchanged are zero; energy densities and temperatures are therefore equal m the initial and final states. If the radiation was not at equilibrium after step 1 or after step 3, entropy would be created during step 2 and step 4, without compensation during the adiabatic processes (1) and (3).

case the variation of the spectral density can be obtained in a second independent way, as the variation of the universal function u_v (T ) for the variation d T of temperature corresponding to the adiabatic transformation:

d T itself is readily obtained by equating the variation of the total radiation energy as given by the Stefan-Boltzmann law (equation 22) to the work performed by the piston against the radiation pressure (given by equation 18):

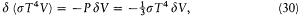
which implies

Equating the two expressions (28) and (29) for d u_v now gives

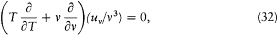
with the general integral:

where f is an arbitrary function. This is the so-called "displacement law" which allows the derivation of the blackbody spectrum at any temperature, once it is known at a given temperature.

Planck's Resonators

The empirical validity of Kirchhoff's law, Stefan's law, and Wien's displacement law left no doubt about the legitimacy of combining electrodynamic and thermodynamic laws; and Planck was well aware of these developments. In 1895 he decided to examine the electrodynamic mechanisms responsible for the thermalization of radiation, hoping to find in them the ultimate source of irreversibility and to perhaps determine the arbitrary function in Wien's displacement law. This grand program focused on a very simple system, a Hertz resonator: that is, a small, nonresistive, oscillating electric circuit interacting with electromagnetic waves, the characteristic wavelength of the oscillator being much larger than the oscillator. The simplest choice was considered the most adequate by Planck,

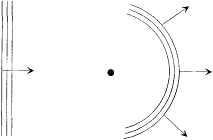
Figure 6.
Planck's intuition of the source of thermodynamic
 irreversibility: the diffusion of a plane electromagnetic 
wave by a resonator (at the frequency of the wave).

for in light of Kirchhoff's theorem, the properties of thermal radiation could not depend on the specific properties of the thermalizing system.^[43]

What first attracted Planck's attention was the apparent irreversibility of the interaction between radiation and resonator: a plane monochromatic wave falling upon a resonator forces vibrations of the resonator when the condition of resonance is approximately met; in turn these vibrations emit secondary waves over a wide angle (fig. 6). Also, an excited resonator left to itself emits radiation at its characteristic frequency and thereby gradually loses its energy. Such processes, resonant scattering or radiation damping, looked essentially irreversible, even though the total energy (that of the resonator plus that of radiation) was strictly conserved (in the absence of the Joule effect in the circuit). Planck concluded:

The study of conservative damping seems to me highly important, because it opens a new perspective on the possibility of a general explanation of irreversible processes through conservative interactions, a more and more pressing problem in contemporary theoretical physics.^[44]

These results of classical electrodynamics are now very well known; they are usually obtained through a specific model of the resonator, for instance an elastically bound electron. In 1895, however, the existence of the electron had not been proved; and Lorentz's formulation of electrodynamics, with its detailed analysis of microscopic sources, was not yet currently known (the famous Versuch was published in the same year).

[43] For earlier accounts of Planck's program, see Brush 1976, 628-640; Klein 1962, 1963a; Kuhn 1978; Needell 1980. A general survey of Planck's thermodynamic views is in Hiebert 1968.

[44] Planck 1896, 1897a, PAV 1:470.

Planck was therefore confined to a different method, first used by Hertz in 1889 for a calculation of the energy radiated by an oscillating dipole. In this method the detailed structure of the resonator was irrelevant .^[45]

As we shall observe in the following, Planck maintained this generality throughout his program and even gave it an essential role. It is therefore useful at this point to explain how the equation of a resonator in an electromagnetic field can be established with this method. Another reason for analyzing Planck's reasoning is that it is typical of a style of theoretical physics, namely, concentrating on the features of physical systems which can be determined on the basis of general principles only, without recourse to detailed microscopic assumptions. Nevertheless, hurried readers may be content with these general comments and may jump to the equation (62), p. 36, for the evolution of the dipolar moment f of a resonator.

The Resonator Equation

A variable distribution of charge and current is located around the origin O of coordinates, and its extension does not exceed the length d . According to Hertz, the simplest possible form of the electromagnetic field at a large distance r from O (r >> d ) derives from a vector potential directed along the z -axis

(here f ' denotes the derivative of the function f ) and from a scalar potential

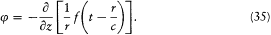
Indeed, A_z is isotropic, and the fields

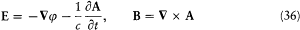
satisfy Maxwell's equations in an empty portion of space, as results from^[46]

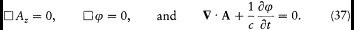
[45] Hertz 1889; Planck 1897a.

[46] Planck used Gaussian units (see Conventions and Notations at the front of this book). Hertz introduced the function f (which he denoted P ) but did without the potentials e and A.

A physical meaning is given to this solution by considering the particular case of a monochromatic source, for which 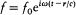. If the wavelength l exceeds the dimensions of the source d by a large amount, the scalar potential in the region defined by d << r << l is given by

This is precisely the form of the electric potential that would be created by a static dipole with an amplitude f (in Gaussian units). By a natural extrapolation, Hertz's solution should be regarded as the radiation created by an electric dipole with the varying amplitude f .

We now return to the general case, but with a limitation on the variations of the dipole f : these can be neither too fast nor too slow. More specifically, it will be necessary to assume that there exist two characteristic lengths 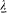and 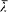such that 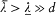and, at any time,

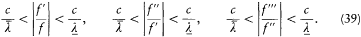
The energy dY/dt emitted in a time unit by the variable dipole can be derived by calculating the flux of the Poynting vector (c /4p ) E × B across a sphere centered in O with a radius 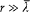. On this sphere the potentials (34) and (35) in spherical coordinates r , q , a (see fig. 7) are approximatively given by:

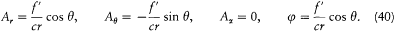
The resulting field strengths are (using (39))

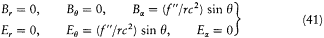
so that the Poynting vector is a radial vector with the amplitude (c /4p ) (f"/rc² )² sin²q . Its flux through the sphere is

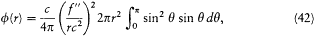
or

In a second step of his considerations, Planck superposed on Hertz's solution an external field E_e , B_e . This field must be a solution of Maxwell's

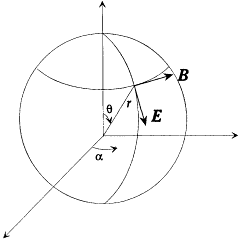
Figure 7.
The dipolar radiation field according to Hertz and Planck.

equations in empty space; and at any time the characteristic distance l _e over which it varies is assumed to greatly exceed the size d of the charge distribution. Then the energetic coupling between the variable charge distribution around O and the external field can be determined without knowing the internal structure of this distribution . To this end Planck cleverly considered the energy flux, F , through a sphere E centered on O, much larger than the charge distribution but small enough to make the variations of the enclosed fields negligible .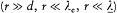

Assuming that the charge distribution exchanges energy only with the electromagnetic field (there is no Joule effect and no internal electromotive force), this flux must be equal to the diminution rate —dY/dt of the energy of the charge distribution plus the diminution rate —dW _e/dt of the energy of the external field enclosed by E in the absence of a charge distribution:

Another expression of this flux results from Poynting's formula:

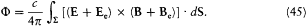
This integral may be split into four terms according to the development of the vector product. The one corresponding to E × B is the flux f₀ across E resulting from the field created by the charge distribution, and

it is simply obtained by noting that the flux f (r ) calculated above (formula 43) must be equal to its retarded value (the propagation time being r/c ):

The term corresponding to E_e × B_e exactly compensates —dW_e/dt . The coupling terms remain:

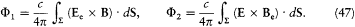
Since the radius r of S is much smaller than the length 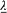, according to (34), (35), (36), and (39) the fields E and B on S are approximatively given by

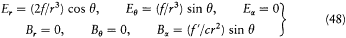
This leads to

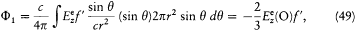
since the value of E_e at any point of the sphere may be replaced by its value in O.

One might easily believe that F₂ vanishes, because for a uniform B_e the corresponding integral vanishes: one has

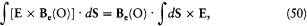
and the latter integral is a zero vector, since d S × E is always tangent to the parallels of S and has a constant modulus on a given parallel. Yet, F₂ is not zero, because the gradient of B_e contributes a term of the same order (in 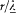) as F₁ . This term is

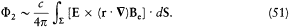
Because of the rotational invariance of d S × E, only the part 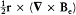of 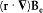contributes to this integral. Taking into account Maxwell's equation 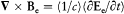, an elementary calculation then yields

Equating the two expressions (44) and (45) of F now gives

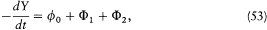
or

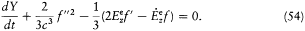
In the latter equation one can consider the time to be the only variable since, according to (39), f (t — r/c ) can be replaced with f (t ) whenever 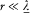. This gives

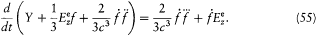
A further simplification of this equation is obtained by noticing that the terms accompanying Y in the parentheses are negligible, as results from the following remarks.

From the expressions (48) for E and B on S result the orders of magnitude f²/r ⁶ for the electric and f '²/c ²r⁴ for the magnetic energy density on S . Since r is much larger than the dimensions of the charge distribution, these densities must be very small compared with the contribution Y/(4/3)p r³ of the charge distribution to the average energy density inside S . This gives the inequalities

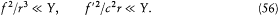
Besides, 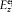must have the same order of magnitude as f"'/c³ in order that, in equation (55), the variations of f may be coupled to those of 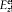. Finally, the inequalities (39) give, for ,

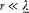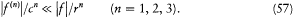
Taken together, these remarks allow us to write

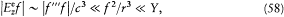
as previously asserted. Thanks to this property, one may, without any loss of information, redefine the energy of the charge distribution as the expression in the parentheses in equation (55), which gives the simpler equation

At this point Planck specified the form of Y in order to represent the case of a resonator, for which the variable distribution of charge and current is comparable to an oscillating circuit. From an analogy with the

theory of such circuits he set

wherein the two terms correspond to electric and magnetic energies that can be periodically transformed into each other. This hypothesis implies an equation for the evolution of f :

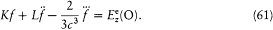
In the absence of an external excitation the term proportional to f produces a spontaneous (conservative) damping of the resonator oscillations as a result of the emission of radiation. In the presence of an external field, the electric field 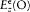at the resonator along the direction of its axis acts on its electric moment f if the Fourier spectrum of this field contains frequencies that are sufficiently close to the eigenfrequency 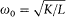of the resonator. If so, then the resulting field, which is the sum of the external field and the Hertz field produced by f , spreads out in every direction of space even if the external field propagates in a definite direction. This is the feature perceived as irreversible by Planck.

Since radiation damping is always very small (it takes a great number of periods), the previous equation is approximately equivalent to a simpler one:^[47]

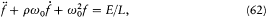
where E is an abbreviation for the exciting fiel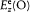d , and

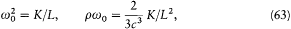
or

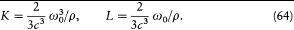
Planck's subsequent studies of radiation processes were based on these equations and on the energy formula (60).

Summary

Planck believed that the two principles of thermodynamics were absolutely valid. Just as certainly as the energy of a closed system remained constant,

so too for Planck its entropy could only increase in time. Every new theory had to be compatible with both principles—or it had to be rejected. As Planck repeatedly asserted in the years 1880-1895, kinetic molecular theories did not pass the test, for they implied the possibility of entropy-decreasing processes in closed systems. Such violations of the second principle had been shown to occur by Maxwell in his demon argument (1867), and again by Zermelo (1896) with the help of Poincaré's recurrence theorem.

Planck nevertheless studied Maxwell's kinetic theory, if only as a part of his duties as editor of Kirchhoff's lectures on thermodynamics, which included this topic. The resulting book, published in 1894, contained an unfortunate mistake in the proof of Maxwell's distribution law, which stirred a short but instructive polemic with Boltzmann. Planck proposed a better proof and in the process became acquainted with, though not convinced by, Boltzmann's idea of molecular chaos. On this occasion he might also have felt the need of an alternative microscopic foundation of thermodynamics. The following year he engaged upon a new program, the principal aim of which was to provide an electromagnetic explanation of the principles of thermodynamics.

Relations between electrodynamics and thermodynamics had already been found in the study of the so-called blackbody radiation, that is, radiation in thermal equilibrium with the walls of a cavity. That thermodynamics applied to this radiation was clear from the experimental verification of one of this theory's consequences: the universality of the blackbody spectrum (proved by Kirchhoff in 1859). That electromagnetic theory also applied was suggested by Boltzmann's proof (1884) of Stefan's law (1879), which rested upon the use of Maxwell's expression for radiation pressure. Finally, in 1894 Wien had shown that Boltzmann's latter argument could be extended to derive the so-called displacement law, which expresses the blackbody spectrum at an arbitrary temperature in terms of that for any given temperature. By then Hertzian waves had been discovered (1888), and most physicists believed in the electromagnetic nature of blackbody radiation.

Well aware of these developments, in 1895 Planck proposed that the electromagnetic interaction between matter and radiation could explain both thermodynamic irreversibility and the observed value of the blackbody spectrum. As the archetype of an energy-conserving, irreversible process, he imagined the scattering of a plane electromagnetic wave by a miniature version of a perfect Hertz resonator (small oscillating circuit with neither dissipation nor internal electromotive force). Planck then

proceeded to a quantitative evaluation of this effect. Unlike Lorentz, who had calculated electromagnetic scattering with the help of a specific model of elastically bound ions, Planck favored Hertz's phenomenological approach to electrodynamics and left the internal structure of the resonators undetermined. Just by balancing the energy flux through cleverly chosen surfaces enclosing the resonator, Planck deduced the mathematical form of the interaction between the electric moment of a resonator and the surrounding radiation. The resulting differential equation involved a damping term, which Planck interpreted as the sought-after source of irreversibility.