Chapter III
On Irreversible Radiation Processes
A Polemic with Boltzmann
In early 1897 Planck published the first of a series of five memoirs entitled "On irreversible radiation processes." His aim was to exploit the preceding equations in a systematic investigation of the uniformizing action of resonators on the radiation enclosed in a cavity with ideal (non-thermalizing) reflecting walls.[48]
In the first memoir he contented himself with some general considerations announcing the three main points to be proved:
1. the asymmetry of the system under time reversal
2. the absence of Poincaré recurrences
3. the evolution of the system toward a unique stationary final state, for which radiation would be homogeneous and isotropic and would have a definite spectrum.[49]
Boltzmann, as a specialist in both thermodynamics and electrodynamics, protested immediately and vigorously. Planck's objectives, he argued, could never be reached. Maxwell's equations—even in the presence of a resonator (without the Joule effect)—were just as reversible as
were the equations of mechanics. More generally, the analogy between electrodynamics and mechanics was sufficient to exclude Planck's objectives. For instance, Boltzmann explained, to the scattering of a wave by a resonator corresponded, in mechanics, the scattering of a parallel beam of particles by a fixed target. Nobody would have questioned the reversibility of the latter process; therefore the former also had to be reversible. In both cases the seeming irreversibility came from an arbitrary selection of a certain class from among the possible initial conditions, one excluding beams or waves converging toward the target.[50]
In his second memoir Planck replied to Boltzmann's criticism. From the beginning of his considerations, he stated, the external electromagnetic field was assumed to vary by a negligible amount over the dimensions of the resonator. This excluded singular fields converging toward the resonator. More generally, Planck denied physical character to solutions of this type, for they could not be realized except by extreme contortions.[51]
This answer failed to satisfy Boltzmann. The "anti-Planck" solutions (obtained from Planck's solutions by time reversal) were singular only in the physically inaccessible limit of an infinitely small resonator, so that the exclusion from nature of certain types of singularities could not affect the question of reversibility. In order to understand the thermodynamic irreversibility of radiation processes, Boltzmann suggested, one had to imitate the example of kinetic theory and introduce adequate concepts of probability and disorder:
"Just as in gas theory, in radiation theory one could define a state of maximal probability, more exactly a general formula that would include all states for which the waves are not ordered, but cross each other in the most diverse way."[52]
Planck could not easily adopt suggestions that reduced to naught his original project of deducing from radiation theory a strict, nonprobabilistic entropy law. In his third memoir, communicated in December 1897, he analyzed in some detail the case of a resonator placed at the center of a spherical (perfectly reflecting) cavity. On the basis of the exclusion of singular external fields he believed that he had proved an asymmetry of this system under time reversal. In order to reach his second objective, the exclusion of Poincaré's recurrences, he made a slight concession to
Boltzmann's viewpoint by introducing a notion of disordered radiation. But this notion was not statistical; it just meant the exclusion of some states of radiation "synchronized" with the resonator, on account of their being nonphysical.[53]
Boltzmann protested for a last time: Planck's expression for the time-reversed version of an equation used in his proof of irreversibility was simply wrong, for it "reversed" the external field without reversing the field of the resonator![54]
In his fourth memoir (1898) Planck humbly acknowledged his mistake and turned to a more systematic exploitation of the analogy between gas theory and radiation theory, as Boltzmann had earlier advised. Within the context of this program the central concept became that of "natural radiation"—the counterpart of molecular chaos; and the main theorem became a theorem of irreversibility, which was the counterpart of the H -theorem. In the fifth memoir Planck generalized his results to an arbitrarily shaped cavity, in the manner that will now be described in detail.[55]
Natural Radiation
The exciting field E (t ) and the electric moment f (t ) of the resonator are conveniently described by their Fourier transforms 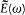 and
and 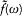 such that[56]
such that[56]
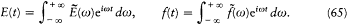
In these terms the resonator equation (62) becomes

where
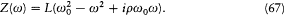
As a preparatory step, Planck characterized what he called the "directly measurable" quantities connected with the resonator and with its exciting field. There was first the secular average U (t ) of the energy Y (t ) of the resonator, which can be obtained by retaining only the slow frequencies
in the Fourier spectrum of the function Y (t ). More specifically, the Fourier transform 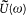 will be defined as the part of the Fourier transform
will be defined as the part of the Fourier transform  for which the frequency w is inferior to a cutoff
for which the frequency w is inferior to a cutoff 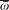 , with
, with 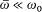 .[57] Then Planck defined the spectral (electric) intensity Jw 0(t ) of the exciting field as a quantity proportional to the secular average of the energy of a test-resonator with central frequency w0 , and a frequency width r w0 larger than
.[57] Then Planck defined the spectral (electric) intensity Jw 0(t ) of the exciting field as a quantity proportional to the secular average of the energy of a test-resonator with central frequency w0 , and a frequency width r w0 larger than  but much smaller than w0 . Physically, this means that the test-resonator must be damped in such a way that it can "follow" the secular variations of the field without, however, losing the quality of resonating at the frequency w0 . This can be achieved only by introducing a resistance r much larger than the one implied by pure radiation damping.
but much smaller than w0 . Physically, this means that the test-resonator must be damped in such a way that it can "follow" the secular variations of the field without, however, losing the quality of resonating at the frequency w0 . This can be achieved only by introducing a resistance r much larger than the one implied by pure radiation damping.
The secular energy U (t ) of the test-resonator is simply given by the secular average of Kf2 , for the two terms in the energy formula (60) have equal secular averages. Then, the form (66) of the resonator equation gives, for a frequency µ less than the cutoff  :
:
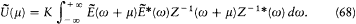
From the condition 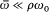 it can be inferred that Z-1 (w + µ ) ~ Z-1 (w ) (which means that the response of the resonator is not affected by a frequency shift of the excitation by an amount small compared with the width of the resonator). Consequently, the Fourier transform of the spectral intensity has the form
it can be inferred that Z-1 (w + µ ) ~ Z-1 (w ) (which means that the response of the resonator is not affected by a frequency shift of the excitation by an amount small compared with the width of the resonator). Consequently, the Fourier transform of the spectral intensity has the form
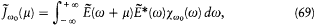
where c w 0(w ) is proportional to |Z-1 (w )|2 . The normalization of Jw 0(µ ) is obtained by requiring the integrated spectral intensity to be identical with the (secular)intensity 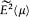 :
:
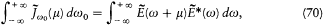
with the result

Consequently, equation (69) just means that 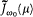 (µ) is an average of
(µ) is an average of 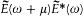 for frequencies w close to w0 , with the weight function c w 0.[58]
for frequencies w close to w0 , with the weight function c w 0.[58]
The Fundamental Equation
We now return to a genuine Planck resonator, that is, a resonator with purely radiative damping, and immerse it in cavity radiation, the walls of the cavity being perfectly reflecting (so that they have no thermalizing effect). Planck supposed the secular energy U (t ) of this resonator and the spectral electric intensity J w 0(t ) of the radiation to be the only directly measurable quantities at the place of the resonator. Accordingly, he looked for an equation directly relating these quantities, one that did not involve a more detailed mathematical description based on the functions f (t ) and E (t ). In this respect Planck's approach had an antecedent in Boltzmann's work: the Boltzmann equation directly rules the evolution of the velocity distribution of a gas, without requiring a detailed description of the configuration of individual molecules.[59]
The exact value of U (>t ) as a function of E (t ) results from the low-frequency part (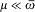 ) of equation (68):
) of equation (68):
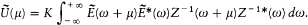
Unfortunately, this expression depends on the detailed form of the function 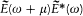 of the variable w . In order to counter this inconvenience, Planck introduced the hypothesis of "natural radiation," according to which the
of the variable w . In order to counter this inconvenience, Planck introduced the hypothesis of "natural radiation," according to which the 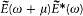 "perceived" by the resonator can be replaced by its measurable average
"perceived" by the resonator can be replaced by its measurable average 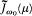 .
.
We remember that, in the absence of a better definition, Boltzmann had characterized molecular chaos as what legitimates Maxwell's collision formula; in a similar manner, Planck defined natural radiation as what legitimates the above mathematical prescription:
In the sequel I shall assume the validity of the following hypothesis, which is most natural and presumably unavoidable: In the calculation of U from equation [68], the quickly varying factor
in the integral can be replaced, without appreciable error, with its slowly varying average
. The problem of calculating U from
thus receives a perfectly determinate solution, to be verified by measurement.
On the qualitative side, Planck described natural radiation in a manner reminiscent of Boltzmann's reference to the irregularities of molecular motion: "We may grasp the concept of natural radiation in a less direct . . . but more intuitive manner: the deviations of the nonmeasurable, quickly
varying quantity 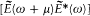 from its slowly varying average
from its slowly varying average 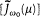 are small and irregular."[60]
are small and irregular."[60]
The corresponding formal substitution transforms equation (68) into
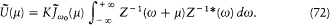
The resonance being very narrow, one can use an approximative expression for Z(w ):
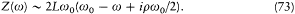
The integral in (72) becomes[61]
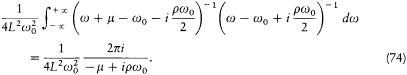
Using the relations (64), the following equation results:
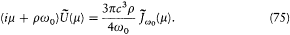
Planck's "fundamental equation" was just the Fourier transform of this equation:[62]
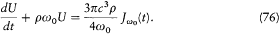
Accordingly, the energy of a resonator is increased at a rate given by the spectral electric intensity of the surrounding field at the frequency of the resonator, but also damped with a time constant (r w0 )-1 identical with that controlling the damping of the dipolar moment of the resonator.
The Electromagnetic H-Theorem
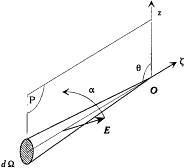
From this equation Planck could derive the measurable effects of a resonator on cavity radiation.[63] For this purpose he borrowed from optics the notion of a radiation beam, which he considered to provide the finest information about the radiation field that was accessible to measurement. An elementary conical beam is characterized by its direction z , by the solid angle dW in which it is confined, by its frequency, by its spectral
Figure 8.
Geometric parameters for a beam converging toward a resonator
(the electric field E must be orthogonal to the beam).
intensity (of energy flow) I v , and by its state of polarization. The latter property is given by the two principal directions (along which the intensity across a polarizer is extremal) and the corresponding principal intensities 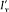 and
and 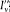 .
.
In this representation the radiation falling on a resonator at a time t from the direction z is characterized by two functions 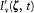 and
and 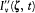 giving the principal intensities at the frequency v (with v = w /2p ), and by the angle a (t ) between one of the principal directions and the plane P defined by z and the electric moment of the resonator (see fig. 8). Since the part of the radiation with a frequency close to v0 (= w0 /2p ) is the only one affected by the resonator, we need only consider the intensities
giving the principal intensities at the frequency v (with v = w /2p ), and by the angle a (t ) between one of the principal directions and the plane P defined by z and the electric moment of the resonator (see fig. 8). Since the part of the radiation with a frequency close to v0 (= w0 /2p ) is the only one affected by the resonator, we need only consider the intensities 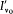 and
and 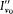 , and we can simplify the notation by dropping the index v 0 in the sequel. Then the intensity in the plane P is
, and we can simplify the notation by dropping the index v 0 in the sequel. Then the intensity in the plane P is
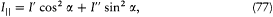
and the intensity in the direction normal to P is
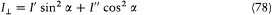
(one must have I|| + IS0094> + I ' + I " + I ).
The contribution of this beam to the electric intensity Jv0 (taking Jv0 = 2p Jw 0) is to the flux I||d W what the squared component 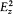 of the electric field of a plane wave traveling in the direction z and polarized in P is to the modulus of the Poynting vector, (c /4p ) |E × B|. Therefore,
of the electric field of a plane wave traveling in the direction z and polarized in P is to the modulus of the Poynting vector, (c /4p ) |E × B|. Therefore,
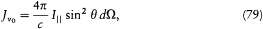
where q denotes the angle between z and the electric moment of the resonator. The corresponding energy absorbed by the resonator in a time unit,
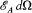 , is given by the right-hand side of the "fundamental equation" (76):
, is given by the right-hand side of the "fundamental equation" (76):
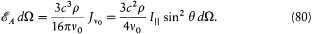
The total energy radiated by the resonator in a time unit is given by the damping term r w0U in the fundamental equation. As results from the expression (41) of dipolar radiation, the radiation emitted in the direction z is completely polarized in the plane defined by this direction and the electric moment, and its intensity varies with the azimuthal angle q like sin2q Consequently, the energy radiated in the solid angle dW around z amounts to
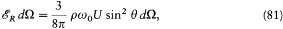
where the factor 3/8p gives the proper normalization, as results from
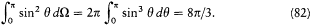
For the intensity of this emitted radiation to be defined, the finite breadth (Breite ) of the source, that is, its efficient cross section times its spectral width, must be taken into account. Planck identifies this breadth, s , with the ratio of the absorbed energy to the active part (the one contributing to Jv0 ) of the incoming flux:[64]
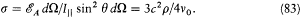
The intensity emitted in the direction z is therefore, using (81),
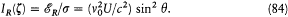
However, this radiation is only one part of the outgoing radiation (at a frequency v ~ y0 ) in the direction z . Another contribution comes from the part of the incoming radiation in the same direction z which is not absorbed by the resonator. The latter radiation is a mixture of a radiation polarized in the ^ direction with the intensity I^ , and of a radiation polarized in the || direction with the intensity I|| cos2q . Consequently, the principal directions of the total emerging radiation are these two directions, and its two principal intensities are
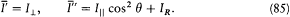
Calling 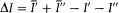 the intensity balance corresponding to a given direction z of absorption or emission, and using the identities (79),
the intensity balance corresponding to a given direction z of absorption or emission, and using the identities (79),
(84), and (85), the fundamental equation (76) can now be rewritten as
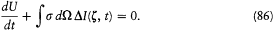
This equation means that the increase of the (secular) energy of the resonator is equal to the balance of the ingoing and outgoing fluxes of radiation energy.
Having expressed energy conservation in this form, Planck looked for a similar form for the total entropy variation of the system:
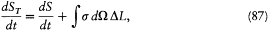
where S would represent the entropy of the resonator, and L an "intensity of entropy" corresponding to the intensity I of energy. Presumably guided by a formal analogy with Boltzmann's H -function, Planck posited (taking v = v0 , to simplify the notation)[65]
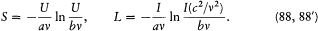
That S depended only on U/v was a consequence of Wien's displacement law, as will be seen later; and the factor c2 /v2 next to I was suggested by the relation IR (c2 /v 2 ) = U sin2q . For this choice Planck's "electromagnetic H -theorem" holds: the total entropy variation dST /dt is always positive, and it vanishes if and only if the distribution of intensities is isotropic and unpolarized. Planck's derivation of this result will now be given.
Using equation (86), one has
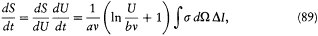
and, inserting this and (88') into (87),
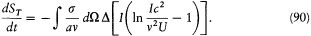
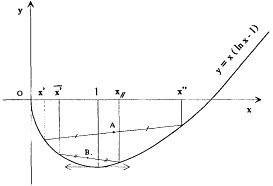
We are now left with the study of the sign of an expression of the form 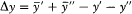 , where y = x (ln x - 1), and x = Ic2 /v2U . Writing the relations (77), (78), (84), and (85) in terms of the x variables gives
, where y = x (ln x - 1), and x = Ic2 /v2U . Writing the relations (77), (78), (84), and (85) in terms of the x variables gives
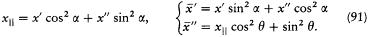
Figure 9.
Diagram for the proof of the electromagnetic H -theorem. The point A
has the ordinate (y ' + y ")/2, and the point B, ![]() . The concavity
. The concavity
of the curve implies that A is always "higher" than B, and therefore that
![]() .
.
As a first consequence, 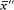 " lies between x || and 1. Since the function y = x (ln x - 1) is a concave function reaching its minimum for x = 1, this implies that y|| is larger than
" lies between x || and 1. Since the function y = x (ln x - 1) is a concave function reaching its minimum for x = 1, this implies that y|| is larger than 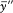 " and that
" and that
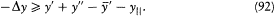
The positivity of the right-hand side results (fig. 9) from the concavity of the function x (ln x - 1) and from the fact that 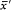 " and x|| always lie between x ' and x ", as can be seen from (91). Therefore, the total entropy variation is always positive.[66]
" and x|| always lie between x ' and x ", as can be seen from (91). Therefore, the total entropy variation is always positive.[66]
The total entropy variation vanishes only if Dy = 0 for any z , since Dy is always negative. In the above chain of reasoning, the inequalities can be replaced with equalities only if 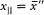 " and also x ' = x ', x " = x|| , up to a permutation of x ' and x ", which play symmetric roles. Once having eliminated the singular cases a = p /2, q = 0, these three equalities can be satisfied only if
" and also x ' = x ', x " = x|| , up to a permutation of x ' and x ", which play symmetric roles. Once having eliminated the singular cases a = p /2, q = 0, these three equalities can be satisfied only if 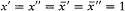 , which implies that incoming and outgoing radiations are isotropic and unpolarized. This concludes the proof of what might be regarded as Planck's greatest theorem.
, which implies that incoming and outgoing radiations are isotropic and unpolarized. This concludes the proof of what might be regarded as Planck's greatest theorem.
Once uniformity has been reached, the exciting intensity appearing in the fundamental equation (76) can be expressed in terms of the spectral density rv of the radiation field. Following Planck, rv is defined by applying to the energy density (E2 + B2 )/8p the same operations as those that
lead from 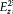 to Jv . Writing symbolically
to Jv . Writing symbolically 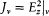 , the density may be written
, the density may be written

Isotropy implies
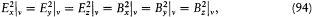
and

The fundamental equation (76) in the stationary case therefore reads:[67]

The Blackbody Law
None of the equations reached by Planck was yet able to determine the equilibrium spectrum of radiation; they just gave a relation between the average energy of a resonator and the density of the surrounding radiation. As noted in Planck's third memoir, a resonator acts only on radiation with frequencies close to its own resonance frequency and therefore cannot change the spectrum of cavity radiation, as long as its more detailed structure is not taken into account. Planck therefore gave up his original hope (see p. 39, point (3)) to describe with the help of his resonators the evolution of the radiation spectrum toward its equilibrium value. Nevertheless, he found another access to the equilibrium spectrum, by identifying the entropy function used in the electromagnetic H -theorem to the real thermodynamic entropy. This would be a legitimate procedure only if the form

of the resonator entropy was the sole form compatible with the irreversibility theorem. In his fifth memoir (1899) Planck asserted without proof this uniqueness of form and derived the equilibrium spectrum in the following manner.[68]
He first evoked Wien's displacement law to limit the choice of the arbitrary functions f and g in the above entropy formula. Thanks to the fundamental relation (96), this law can be expressed directly in terms of the resonator energy as

This implies dS = (v/T )j '(v/T )d (v/T ), which means that S must be a function of v/T , or another function of U/v , since U/v = j (v/T ). Consequently, the resonator entropy must have the form

The absolute temperature of a resonator in thermodynamic equilibrium is then given by the relation dS/dU = 1/T , with the result
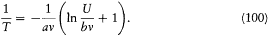
Inverting this equation provides[69]

Finally, the "fundamental equation" (96) gives for the spectral density uv of the blackbody spectrum

This law was not new. It had been proposed two years earlier by Wien on the basis of a fragile analogy with the exponential form of Maxwell's law. At the date of Planck's fifth memoir (early 1899) it was well confirmed by experimental measurements. At the price of incompletely justified assumptions about natural radiation and entropy, Planck therefore believed that he had reached the main objectives of his program: a deduction of irreversibility from electrodynamic processes, and a derivation of the universal law of blackbody radiation. As a clear manifestation of his trust in the fundamental character of his theory, he suggested that the constants a and b appearing in the resonator entropy be considered new fundamental constants and recommended natural units of length, time, mass, and temperature built from a, b, c , and the universal gravitation constant.[70]
Planck Versus Boltzmann
From a systematic comparison of Planck's reasonings with those which led Boltzmann to the H -theorem we may surmise that Planck benefited at various steps from suggestive analogies. Table 1 summarizes the correspondence between Planck's and Boltzmann's arguments. The first horizontal section refers to the most detailed, microscopic level of description, while the second refers to the "directly observable quantities." The third and fifth sections respectively give the equations ruling the microscopic evolution of the system and those ruling the directly observable quantities. The transition between these two types of equations is expressed in the fourth section, with the idea of disorder, and the corresponding simplification of the interaction within the system. The fifth section gives the functions of the directly observable quantities which always increase or decrease. The last section describes the final state of the system in terms of the directly observable quantities.
As appears from this table, the relevant analogies concerned general concepts or categories rather than specific mathematical expressions, except for that connecting the formulae for H and S . This should not
TABLE ONE | |
Boltzmann | Planck |
Molecular velocities: v1 , v2 , . . ., v:N | External fields: Ee (r, t ), Be (r, t ) Electric dipole: f(t ) |
Velocity distribution: f (v) | Secular resonator energy: U(t ) Beam intensities: I (z , t ) Electric intensity: J w (t ) |
Equations of molecular dynamics | Resonator equation (62) Maxwell's equations |
Maxwell's Ansatz (molecular chaos) | Planck's fundamental equation (natural radiation) |
Boltzmann's equation for f | Energy balancing (86) for U and beam intensities |
| |
Maxwell's distribution | Isotropic unpolarized radiation |
surprise us, because the original dynamic systems, the molecular gas on the one hand, the resonator in cavity radiation on the other, exhibited strong qualitative differences. As vague as it was, the idea of a selection of disordered states for which the evolution of all measurable quantities would not depend on finer uncontrollable details was all Planck needed to establish his "fundamental equation." The rest, as we saw, proceeded from the autonomous development of Planck's program, with the exception of the entropy formula.
Did such procedural parallelism imply that Planck would also accept Boltzmann's conception of irreversibility? Somewhat surprisingly, the answer is no. For about fifteen years Planck maintained his idea of an absolute entropy law. As we have seen, Boltzmann's notion of molecular chaos was intrinsically probabilistic: only with a certain probability did it grant a deterministic evolution of the velocity distribution. Moreover, an initially disordered state had to evolve toward ordered states after a sufficiently long time, as implied by Poincaré's recurrence theorem (since perpetual disorder would exclude recurrence). In contrast, Planck's natural radiation had to remain natural forever, and ordered states were absolutely (nonstatistically) excluded from his theory as being nonphysical. In his fourth memoir Planck made this point completely explicit:
If one wishes to apply to nature the preceding theory of irreversible radiation processes, one must admit that these processes, especially those which provide temperature equilibrium, have the properties of natural radiation in any circumstance and for an unlimited amount of time.[71]
Planck nevertheless observed that his differential equation of the dipole f (t ) combined with Maxwell's equations led to the Poincaré recurrence (at least in the case of a resonator placed at the center of a spherical mirror-cavity). This difficulty did not stop him: at the time scale at which Poincaré recurrences would occur, the deviations in the equation resulting from the detailed structure of the resonator had to play a role, and the dipolar differential equation would no longer be adequate for describing the evolution of the system. Planck commented:
This indetermination lies in the nature of things. Indeed, the physical problem has no definite solution as long as nothing is known about the resonator but its eigenfrequency w 0 and its damping constant r ; that our theory is able to determine the approximate course of phenomena while only these two constants
are given, must be regarded as a great advantage. For the same reason this theory cannot tell us more about the resonator than the determination of w0 and r . Precisely in this gap [Lücke ] does the hypothesis of natural radiation find its place; otherwise, this hypothesis would be either superfluous or impossible, for the processes would be completely determined without it.[72]
Thus Planck believed that the indetermination of the internal structure of his resonators made room for an everlasting disorder, which would make the evolution of the accessible properties of the system strictly irreversible. Not only did he not admit a probabilistic interpretation of natural radiation, but he reinterpreted Boltzmann's concept of molecular chaos in a way that would make kinetic theory acceptable to him. On this occasion he emphasized the analogy between gas theory and radiation theory:
Our electrodynamic interpretation of the second principle of thermodynamics suggests a brief comparison with the mechanical interpretation of the same principle, that is, with the corresponding questions in the kinetic gas theory. As is well known, here also we encounter the same, often-noted conflict between the fundamental equations of mechanics, which are perfectly reversible, and the second principle [of thermodynamics], which demands irreversibility for all real processes. But here also the conflict can be resolved in a very similar way by the introduction of a special hypothesis, which, as long as it remains valid, implies all consequences of the second principle. Boltzmann calls this "molecular disorder." This hypothesis is a necessary and sufficient condition for the existence of a definite function of the instantaneous state that perpetually increases in time and therefore shares the essential properties of entropy. However, the hypothesis of molecular disorder, once applied not only to the initial state but also to any subsequent time, has been shown to be incompatible with the assumption of a finite number of simple atoms confined within rigid walls; this circumstance impedes the introduction of the second principle, as a general principle, in [kinetic] gas theory. Some perceive here an objection to the legitimacy of [kinetic] gas theory, while others question the general validity of the second principle of thermodynamics. In reality one is not at all confined to these two alternatives. For whoever is willing to give up only one of the above assumptions, the existence of rigid walls—which, strictly taken, seems to be very improbable—there seems to be no obstacle whatsoever to a general application of the hypothesis of molecular disorder, and one is free to extend the second principle to arbitrarily long times even from the viewpoint of kinetic gas theory.[73]
As was the indefinite structure of resonators, the complexity of the walls of a container was supposed to maintain a perpetual chaos warranting
an absolute irreversibility of thermodynamic phenomena. In this way the assumption of disordered states, originally meant by Boltzmann as a marginal commentary on a certain collision formula, became central to Planck's conception of thermodynamics, which sought to maintain strict irreversibility.
Pursuing the comparison between natural radiation and molecular chaos, Planck gained some intuition about the nature of the disorder intervening in his radiation theory. He emphasized that his equations led to irreversible behavior for a single resonator, while Boltzmann's considerations required a very large number of molecules, and explained: "The principle of disorder on which every notion of irreversibility seems to rest steps in at very different moments [of the reasonings] in gas theory and thermal radiation theory" (emphasis added). Disorder in a gas consisted of the irregular multitude of molecular velocities and positions, while in the resonator case it had to do with the irregular multitude of Fourier components of the electric moment. There was spatial disorder in one case, temporal disorder in the other.[74]
Summary
In 1897 Planck defined the aim of his grand program in the first of a series of five memoirs "on irreversible radiation processes": to show that a system of ideal resonators acted irreversibly on radiation enclosed in a cavity with perfectly reflecting walls, leading eventually to a uniform, isotropic distribution of radiant energy. Moreover, he hoped that the spectrum of this radiation would evolve toward a well-defined final state, which, according to Kirchhoff's law, could only be the universal blackbody spectrum.
Planck's announcement of this project triggered a public polemic with Boltzmann. The latter argued that the laws of electrodynamics were just as reversible as the laws of molecular dynamics, so they could not be used to derive irreversible thermodynamic behavior. The only possible escape from this conclusion, Boltzmann suggested, would be—as he had done in gas theory—to shift to a statistical conception of irreversibility and to introduce a notion of "disordered" radiation that would be the counterpart of molecular chaos.
Eventually, after a few misconceived attempts to counter Boltzmann's objection, Planck did adopt a notion of disordered radiation, which he
called "natural radiation." As a first step toward defining this notion, he introduced the relevant "directly measurable quantities," that is, certain quadratic time-averages, one for the electric moment of the resonator and one for the electric field at the place of the resonator. These were indeed accessible to measurement, for instance, in the case of the field, through the resonance of a damped test-resonator. But the differential equation relating the resonator moment and the electric field did not imply a definite relation between these quadratic expressions, unless certain "cross-terms" were set to zero. The vanishing of cross-terms is precisely what defines Planck's natural radiation; it leads to an equation involving only the directly observable quantities, which Planck called the "fundamental equation." The analogy with molecular chaos was transparent enough. In both cases there were two levels of description: the detailed micro-level, which includes uncontrollable features of the model (dynamics of molecular collisions/electrodynamic interaction between resonator and radiation), and the "physical" level of description, which involves only physically meaningful quantities (Maxwell's collision formula/Planck's fundamental equation). In order to deduce the second level of description from the first a special assumption must be made, molecular chaos in one case, natural radiation in the other.
Planck then proceeded to derive a counterpart to Boltzmann's H -theorem. To this end he discussed the effect of a resonator on radiation beams and introduced expressions for the entropy of resonators and of beams in terms of the corresponding "measurable quantities." These expressions mirrored very closely Boltzmann's H -function, and, as in Boltzmann's case, they led to a perpetual increase of the total entropy. By this means Planck could prove that resonators made the surrounding radiation increasingly (spatially) uniform and unpolarized. However, the analogy with Boltzmann's H -theorem was imperfect in at least one respect: while the Boltzmann equation led to a definite final distribution of velocities, Planck's equations said nothing about the time evolution of the spectrum of radiation. In fact, contrary to his original hope, Planck gradually realized that his resonators were unable to redistribute radiation from one frequency to another.
Nevertheless, in his concluding memoir of 1899 (the fifth!) Planck managed to derive the blackbody spectrum. He just had to assume that his expression for the resonator entropy was the only one compatible with a global entropy increase and that it was identical with the thermodynamic entropy. Then standard thermodynamic reasoning, Wien's displacement law, and the "fundamental equation" led to a definite spectrum. To
Planck's satisfaction the resulting law was already well known (previously having been proposed by Wien on a frail theoretical basis) and fitted available observations excellently. Not doubting the fundamental character of this derivation, Planck extracted universal constants from his entropy formula (including h , under a different letter) and even combined them with the universal constant of gravitation to produce absolute units of length, time, and mass.
Apparently Planck had achieved his original aims: the demonstration that resonators could produce the irreversible change required by the second law, and a derivation of the blackbody spectrum. His introduction of "natural radiation" and the overall analogy of his irreversibility theorem with Boltzmann's H -theorem might suggest that he had in the process become a convert to the statistical conception of irreversibility and thus given up the motivating force behind his program, a nonstatistical foundation of the entropy law. This, however, was not the case. Planck maintained his absolute conception of irreversibility for fifteen more years. In his mind the "naturalness" of radiation was not a statistical property; instead, it applied to individual states of radiation. The internal structure of resonators, which Planck deliberately left undetermined in all his reasonings, was in charge of perpetually maintaining this naturalness. Similarly, in gas theory Planck imagined an indeterminate structure of the walls of containers that would maintain molecular chaos forever—and make kinetic theory acceptable to him. Planck's "elementary disorder" (a generic name for molecular chaos and natural radiation) was essential for strict irreversibility and thus became the central concept of his thermodynamics.