LAPACK
Our objective in developing LAPACK is to provide a package for the solution of systems of equations and the solution of eigenvalue problems. The software is intended to be efficient across a wide range of high-performance computers. It is based on algorithms that minimize memory access to achieve locality of reference and reuse of data, and it is built on top of the Levels 1, 2, and 3 BLAS—the de facto standard that the numerical linear algebra community has given us. LAPACK is a multi-institutional project, including people from the University of Tennessee, the University of California at Berkeley, New York University's Courant Institute, Rice University, Argonne National Laboratory, and Oak Ridge National Laboratory.
We are in a testing phase at the moment and just beginning to establish world speed records, if you will, for this kind of work. To give a hint of those records, we show in Table 5 some timing results for LAPACK routines on a CRAY Y-MP.
Let us look at the LU decomposition results. This is the routine that does that work. On one processor, for a matrix of order 32, it runs at four MFLOPS; for a matrix of order 1000, it runs at 300 MFLOPS. Now if we take our LAPACK routines (which are written in Fortran), called the Level 3 BLAS (which the people from Cray have provided), and go to eight processors, we get 32 MFLOPS—a speeddown . Obviously, if we wish to solve the matrix, we should not use this approach!
When we go to large-order matrices, however, the execution rate is close to two GFLOPS—for code that is very portable. And for LLT and QR factorization, we get the same effect.
Note that we are doing the same number of operations that we did when we worked with the unblocked version of the algorithms. We are not cheating in terms of the MFLOPS rate here.
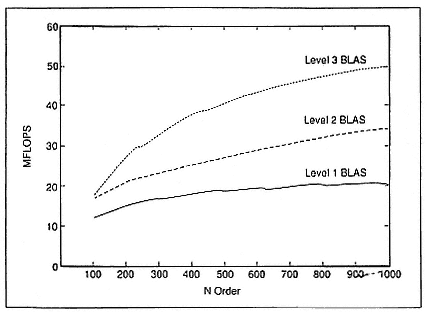
One other performance set, which might be of interest for comparison, is that of the IBM RISC machine RS/6000-550 (Dongarra, Mayer, et al. 1990). In Figure 3, we plot the speed of LU decomposition for the LAPACK routine, using a Fortran implementation of the Level 3 BLAS. For the one-processor workstation, we are getting around 45 MFLOPS on larger-order matrices.
Clearly, the BLAS help, not only on the high-performance machines at the upper end but also on these RISC machines, perhaps at the lower end—for exactly the same reason: data are being used or reused where the information is stored in its cache.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure 3.
Variants of LU factorization on the IBM RISC System RS/6000-550.