Parallel Algorithms and Implementation Strategies on Massively Parallel Supercomputers[*]
R. E. Benner
Robert E. Benner is a senior member of the Parallel Computing Technical Staff, Sandia National Laboratories. He has a bachelor's degree in chemical engineering (1978) from Purdue University and a doctorate in chemical engineering (1983) from the University of Minnesota. Since 1984, he has been pursuing research in parallel algorithms and applications on massively parallel hypercubes and various shared-memory machines. He was a member of a Sandia team that won the first Gordon Bell Award in 1987 and the Karp Challenge Award in 1988 and was cited in R&D Magazine's 1989 R&D 100 List for demonstrating parallel speedups of over 1000 for three applications on a 1024-processor nCUBE/ten Hypercube. Dr. Benner specializes in massively parallel supercomputing, with particular emphasis on parallel algorithms and parallel libraries for linear algebra, nonlinear problems, finite elements, dynamic load balancing, graphics, I/O, and the implications of parallelism for a wide range of science and engineering.
Introduction
This presentation is on parallel algorithms and implementation strategies for applications on massively parallel computers. We will consider examples of new parallel algorithms that have emerged since the 1983 Frontiers of Supercomputing conference and some developments in MIMD parallel algorithms and applications on first-and second-generation hypercubes. Finally, building upon what other presenters at this conference have said concerning supercomputing developments—or lack thereof—since 1983, I offer some thoughts on recent changes in the field.
We will draw primarily on our experience with a subset of the parallel architectures that are available as of 1990, those being nCUBE Corporation's nCUBE 2 and nCUBE/ten Hypercubes and Thinking Machines Corporation's CM-2 (one of the Connection Machine series). The nCUBE 2 at Sandia National Laboratories has 1024 processors with four megabytes of local memory per processor, whereas the nCUBE/ten has the same number of processors but only 0.5 megabytes of memory per processor. The CM-2 is presently configured with 16K single-bit processors, 128 kilobytes of memory per processor, and 512 64-bit floating-point coprocessors. This conference has already given considerable attention to the virtues and pitfalls of SIMD architecture, so I think it will be most profitable to focus this short presentation on the state of affairs in MIMD architectures.
An interdisciplinary research group of about 50 staff is active in parallel computing at Sandia on the systems described above. The group includes computational scientists and engineers in addition to applied mathematicians and computer scientists. Interdisciplinary teams that bring together parallel-algorithm and applications researchers are an essential element to advancing the state of the art in supercomputing.
Some Developments in Parallel Algorithms
In the area of parallel algorithms and methods, there have been several interesting developments in the last seven years. Some of the earliest excitement, particularly in the area of SIMD computing, was the emergence of cellular automata methods. In addition, some very interesting work has been done on adaptive-precision numerical methods, for which the CM-2 provides unique hardware and software support. In addition, there has been much theoretical and experimental research on various asynchronous methods, including proofs of convergence for some of the most interesting ones.
A more recent development, the work of Fredericksen and McBryan (1988) on the parallel superconvergent multigrid method, prompted a surge in research activity in parallel multigrid methods. For example, parallel implementations of classic multigrid have been demonstrated with parallel efficiencies of 85 per cent for two-dimensional problems on 1000 processors and about 70 per cent for three-dimensional problems on 1000 processors (Womble and Young 1990)—well in excess of our expectations for these methods, given their partially serial nature.
A new class of methods that emerged is parallel time stepping. C. William Gear (now with the Nippon Electric Corporation Research Institute, Princeton, New Jersey), in a presentation at the July 1989 SIAM meeting in San Diego, California, speculated on the possibility of developing such methods. Womble (1990) discusses a class of methods that typically extract a factor of 4- to 16-fold increase in parallelism over and above the spatial parallelism in a computation. This is not the dramatic increase in parallelism that Gear speculated might be achievable, but it's certainly a step in the right direction in that the time parallelism is multiplicative with spatial parallelism and therefore attractive for problems with limited spatial parallelism.
At the computer-science end of the algorithm spectrum, there have been notable developments in areas such as parallel load balance, mapping methods, parallel graphics and I/O, and so on. Rather than considering each of these areas in detail, the focus will now shift to the impact of parallel algorithms and programming strategies on applications.
Some Developments in Parallel Applications
The prospects for high-performance, massively parallel applications were raised in 1987 with the demonstration, using a first-generation nCUBE system, of 1000-fold speedups for some two-dimensional simulations based on partial differential equations (Gustafson et al. 1988). The Fortran codes involved consisted of a few thousand to less than 10,000 lines of code. Let's consider what might happen when a number of parallel algorithms are applied to a large-scale scientific computing problem; i.e., one consisting of tens of thousands to a million or more lines of code.
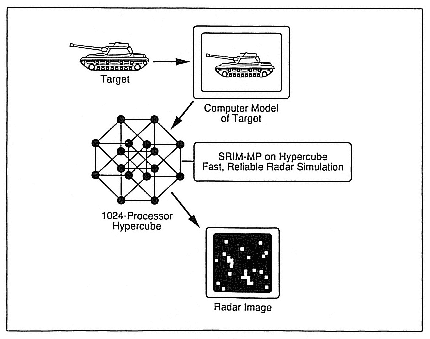
A case study is provided by parallel radar simulation (Gustafson et al. 1989). This is, in some sense, the inverse problem to the radar problem that immediately comes to mind—the real-time processing problem. In radar simulation one takes a target, such as a tank or aircraft, produces a geometry description, and then simulates the interaction of radar with
the geometry on a supercomputer (Figure 1). These simulations are generally based on multibounce radar ray tracing and do not vectorize well. On machines like the CRAY X-MP, a radar image simulator such as the Simulated Radar IMage (SRIM) code from ERIM Inc. typically achieves five or six million floating-point operations per second per processor. Codes such as SRIM have the potential for high performance on massively parallel supercomputers relative to vector supercomputers. However, although the novice might consider ray tracing to be embarrassingly parallel, in practice radar ray tracing is subject to severe load imbalances.
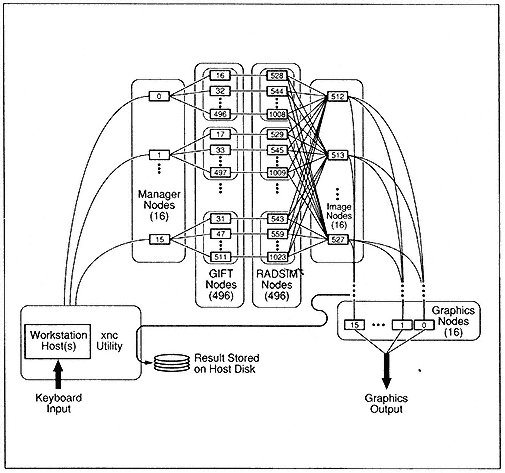
The SRIM code consists of about 30,000 lines of Fortran, an amalgamation of many different algorithms that have been collected over a period of 30 years and do not fit naturally into a half megabyte of memory. The implementation strategy was heterogeneous . That is, rather than combining all of the serial codes in the application package, the structure of the software package is preserved by executing the various codes simultaneously on different portions of the hypercube (Figure 2), with data pipelined from one code in the application package to the next.
Figure 1.
A parallel radar simulation as generated by the SRIM code.
Figure 2.
Heterogeneous image simulation using a MIMD computer.
The heterogeneous implementation uses a MIMD computer in a very general MIMD fashion for the first time. An observation made by one of our colleagues concerning the inaugural Gordon Bell Prize was that the parallel applications developed in that research effort were very SIMD-like and would have performed very well on the Connection Machine. In contrast, the parallel radar simulation features, at least at the high level, a true MIMD strategy with several cooperating processes: a load-balance process, a multibounce radar ray-tracing process, an imaging process, and a process that performs a global collection of the radar image, as well as a user-supplied graphic process and a host interface utility to handle the I/O.
The nCUBE/ten version of the radar simulation, for which one had to develop a host process, had six different cooperating programs. There are utilities on second-generation hypercubes that handle direct node I/O, so a host process is no longer needed. By keeping the application code on the nodes rather than splitting it into host and node code, the resulting parallel code is much closer to the original workstation codes of Cray Research, Inc., and Sun Microsystems, Inc. Over the long haul, I think that's going to be critical if we're going to get more people involved with using massively parallel computers. Furthermore, three of the remaining five processes—the load-balance, image-collection, and graphics processes—are essentially library software that has subsequently been used in other parallel applications.
Consider the religious issue of what qualifies as a massively parallel architecture and what doesn't. Massively parallel is used rather loosely here to refer to systems of 1000 or more floating-point processors or their equivalent in single-bit processors. However, Duncan Buell (also a presenter in this session) visited Sandia recently, and an interesting discussion ensued in which he asserted that massively parallel means that a collection of processors can be treated as an ensemble and that one is most concerned about the efficiency of the ensemble as opposed to the efficiencies of individual processors.
Heterogeneous MIMD simulations provide a nice fit to the above definition of massive parallelism. The various collections of processors are loosely synchronous, and to a large extent, the efficiencies of individual processors do not matter. In particular, one does not want the parallel efficiency of the dynamic load-balance process to be high, because that means the load-balance nodes are saturated and not keeping up with the work requests of the other processors. Processor efficiencies of 20, 30, or 50 per cent are perfectly acceptable for the load balancer, as long as only a few processors are used for load balancing and the bulk of the processors are keeping busy.
Some Developments in Parallel Applications II
Some additional observations concerning the development of massively parallel applications can be drawn from our research into Strategic Defense Initiative (SDI) tracking and correlation problems. This is a classic problem of tracking tens or hundreds of thousands of objects, which Sandia is investigating jointly with Los Alamos National Laboratory, the Naval Research Laboratory, and their contractors. Each member of the team is pursuing a different approach to parallelism, with Sandia's charter being to investigate massive parallelism on MIMD hypercubes.
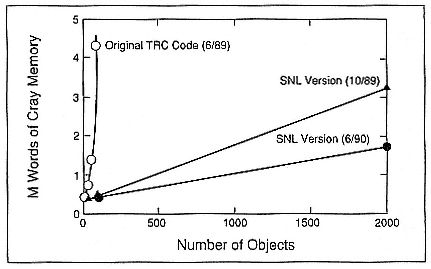
One of the central issues in parallel computing is that a major effort may be expended in overhauling the fundamental algorithms involved as part of the porting process, irrespective of the architecture involved. The course of the initial parallelization effort for the tracker-correlator was interesting: parallel code development began on the hypercube, followed by a quick retreat to restructuring the serial code on the Cray. The original tracking algorithms were extremely memory intensive, and data structures required extensive modification to improve the memory use of the code (Figure 3), but first-generation hypercube nodes with a mere half megabyte of memory were not well suited for the task.
Halbgewachs et al. (1990) developed a scheme for portability between the X-MP and the nCUBE/ten in which they used accesses to the solid-state device (SSD) to swap "hypercube processes" and to simulate the handling of the message-passing. In this scheme one process executes, sends its "messages" to the SSD, and is then swapped out for another "process." This strategy was a boon to the code-development effort. Key algorithms were quickly restructured to reduce the memory use from second order to first order. Further incremental improvements have been made to reduce the slope of the memory-use line. The original code could not track more than 160 objects. The first version with linear memory requirements was able to track 2000 objects on the Cray and the nCUBE/ten.
On the nCUBE/ten a heterogeneous implementation was created with a host process. (A standard host utility may be used in lieu of a host program on the second-generation hypercubes.) The tracking code that runs on the nodes has a natural division into two phases. A dynamic load balancer was implemented with the first phase of the tracking algorithm, which correlates new tracks to known clusters of objects. The second phase, in which tracks are correlated to known objects, is performed on the rest of the processors.
Figure 3.
Improved memory utilization: Phase 1, reduced quadratic dependence to linear;
Phase 2, reduced coefficient of linear dependence.
Given the demonstration of an effective heterogeneous implementation and the ability to solve large problems, suddenly there is user interest in real-time and disk I/O capabilities, visualization capabilities, etc. When only small problems could be solved, I/O and visualization were not serious issues.
Performance evaluation that leads to algorithm modifications is critical when large application codes are parallelized. For example, the focus of SDI tracking is on simulating much larger scenarios, i.e., 10,000 objects, as of September 1990, and interesting things happen when you break new ground in terms of problem size. The first 10,000-object run pinpointed serious bottlenecks in one of the tracking phases. The bottleneck was immediately removed, and run time for the 10,000-object problem was reduced from three hours to one hour. Such algorithmic improvements are just as important as improving the scalability of the parallel simulation because a simulation that required 3000 or 4000 processors to run in an hour now requires only 1000.
A heterogeneous software implementation, such as the one described above for the SDI tracking problem, suggests ways of producing heterogeneous hardware implementations for the application. For example, we can quantify the communication bandwidth needed between the different algorithms; i.e., the throughput rate needed in a distributed-computing
approach where one portion of the computation is done on a space platform, other portions on the ground, etc. In addition, MIMD processors might not be needed for all phases of the simulation. Heterogeneous implementations are MIMD at their highest level, but one might be able to take advantage of the power of SIMD computing in some of the phases. Furthermore, heterogeneous nodes are of interest in these massively parallel applications because, for example, using a few nodes with large memories in a critical phase of a heterogeneous application might reduce the total number of processors needed to run that phase in a cost-effective manner.
Given our experience with a heterogeneous implementation on homogeneous hardware, one can propose a heterogeneous hardware system to carry out the computation efficiently. We note, however, that it would be risky to build a system in advance of having the homogeneous hardware implementation. If you're going to do this sort of thing—and the vendors are gearing up and are certainly talking seriously about providing this capability—then I think we really want to start with an implementation on a homogeneous machine and do some very careful performance analyses.
Closing Remarks
What, besides those developments mentioned by other presenters, has or has not changed since 1983? In light of the discussion at this conference about risk taking, I think it is important to remember that there has been significant risk taking involved in supercomputing the last several years. The vendors have taken considerable risks in bringing massively parallel and related products to market. From the perspective of someone who buys 1000-processor systems before one is even built by the vendor, customers have also taken significant risks. Those who funded massively parallel acquisitions in the 1980s have taken risks.
I've seen a great improvement in terms of vendor interest in user input, including input into the design of future systems. This doesn't mean that vendor-user interaction is ideal, but both sides realize that interaction is essential to the viability of the supercomputing industry.
A more recent, encouraging development is the emerging commercial activity in portability. Commercial products like STRAND88 (from Strand Software Technologies Inc.) and Express (from Parasoft Corporation) have appeared. These provide a starting point for code portability, at least between different distributed-memory MIMD machines and perhaps also between distributed-memory and shared-memory machines.
We are much further from achieving portability of Fortran between MIMD and SIMD systems, in part due to the unavailability of Fortran 90 on the former.
Another philosophical point concerns which current systems are supercomputers and which are not. We believe that the era of a single, dominant supercomputer has ended, at least for the 1990s if not permanently. Without naming vendors, I believe that at least four of them have products that qualify as supercomputers in my book—that is, their current system provides the fastest available performance on some portion of the spectrum of computational science and engineering applications. Even given the inevitable industry shakeouts, that is likely to be the situation for the near future.
What hasn't happened in supercomputing since 1983? First, language standards are lagging. Fortran 8X has now become Fortran 90. There are no parallel constructs in it, although we at least get array syntax, which may make for better nonstandard parallel extensions. To some extent, the lack of a parallel standard is bad because it certainly hinders portability. In another sense the lack of a parallel standard is not bad because it's not clear that the Fortran community knows what all the parallel extensions should be and, therefore, what all the new standards should be. I would hate to see a new standard emerge that was focused primarily on SIMD, distributed-memory MIMD, or shared-memory MIMD computing, etc., to the detriment of the other programming models.
A major concern is that massive parallelism does not have buy-in from most computational scientists and engineers. There are at least three good reasons for this. First, recall the concern expressed by many presenters at this conference for education to get more people involved in supercomputing. This is especially true of parallel computing. A second issue is opportunity , i.e., having systems, documentation, experienced users, etc., available to newcomers to smooth their transition into supercomputing and parallel computing. The role of the NSF centers in making vector supercomputers accessible is noteworthy.
The third, and perhaps most critical, issue is interest . We are at a crossroads where a few significant applications on the Connection Machine, nCUBE 2, and Intel iPSC/860 achieve a factor of 10 or more better run-time performance than on vector supercomputers. On the other hand, there is a large body of applications, such as the typical mix of finite-element- and finite-difference-based applications, that typically achieve performance on a current massively parallel system that is comparable to that of a vector supercomputer, or at most three to five times the vector supercomputer. This level of performance is sufficient to
demonstrate a price/performance advantage for the massively parallel system but not a clear raw-performance advantage. In some cases, end users are willing to buy into the newer technology on the basis of the price/performance advantage. More often, there is a great deal of reluctance on the part of potential users.
User buy-in for massive parallelism is not a vector supercomputer versus massively parallel supercomputer issue. In 1983 we faced a similar situation in vector supercomputing: many users did not want to be concerned with vector processors and how one gets optimum performance out of them. In recent years the situation has gradually improved. The bottom line is that eventually most people who are computational scientists at heart come around, and a few get left behind. In summary, I hope that someday all computational scientists in the computational science and engineering community will consider advanced computing to be part of their career and part of their job.
References
P. O. Fredericksen and O. A. McBryan, "Parallel Superconvergent Multigrid," in Multigrid Methods , S. McCormick, Ed., Marcel Dekker, New York (1988).
J. L. Gustafson, R. E. Benner, M. P. Sears, and T. D. Sullivan, "A Radar Simulation Program for a 1024 Processor Hypercube," in Proceedings, Supercomputing '89 , ACM Press, New York, pp. 96-105 (1989).
J. L. Gustafson, G. R. Montry, and R. E. Benner, "Development of Parallel Methods for a 1024 Processor Hypercube," SIAM Journal on Scientific and Statistical Computing9 , 609-638 (1988).
R. D. Halbgewachs, J. L. Tomkins, and John P. VanDyke, "Implementation of Midcourse Tracking and Correlation on Massively Parallel Computers," Sandia National Laboratories report SAND89-2534 (1990).
D. E. Womble, "A Time Stepping Algorithm for Parallel Computers," SIAM Journal on Scientific and Statistical Computing11 , 824-837 (1990).
D. E. Womble and B. C. Young, "Multigrid on Massively Parallel Computers," in Proceedings of the Fifth Distributed Memory Computing Conference , D. W. Walker and Q. F. Stout, Eds., IEEE Computer Society Press, Los Alamitos, California, pp. 559-563 (1990).