7—
ALGORITHMS FOR HIGH-PERFORMANCE COMPUTING
This session focused on ways in which architectural features of high-performance computing systems can be used to design new algorithms to solve difficult problems. The panelists discussed the effect on algorithm design of large memories, the number of processors (both large and small), and special topologies. They also discussed scalable algorithms, algorithm selection, models of computation, and the relationship between algorithms and architectures.
Session Chair
Gian-Carlo Rota,
Massachusetts Institute of Technology
Parallel Algorithms and Implementation Strategies on Massively Parallel Supercomputers[*]
R. E. Benner
Robert E. Benner is a senior member of the Parallel Computing Technical Staff, Sandia National Laboratories. He has a bachelor's degree in chemical engineering (1978) from Purdue University and a doctorate in chemical engineering (1983) from the University of Minnesota. Since 1984, he has been pursuing research in parallel algorithms and applications on massively parallel hypercubes and various shared-memory machines. He was a member of a Sandia team that won the first Gordon Bell Award in 1987 and the Karp Challenge Award in 1988 and was cited in R&D Magazine's 1989 R&D 100 List for demonstrating parallel speedups of over 1000 for three applications on a 1024-processor nCUBE/ten Hypercube. Dr. Benner specializes in massively parallel supercomputing, with particular emphasis on parallel algorithms and parallel libraries for linear algebra, nonlinear problems, finite elements, dynamic load balancing, graphics, I/O, and the implications of parallelism for a wide range of science and engineering.
Introduction
This presentation is on parallel algorithms and implementation strategies for applications on massively parallel computers. We will consider examples of new parallel algorithms that have emerged since the 1983 Frontiers of Supercomputing conference and some developments in MIMD parallel algorithms and applications on first-and second-generation hypercubes. Finally, building upon what other presenters at this conference have said concerning supercomputing developments—or lack thereof—since 1983, I offer some thoughts on recent changes in the field.
We will draw primarily on our experience with a subset of the parallel architectures that are available as of 1990, those being nCUBE Corporation's nCUBE 2 and nCUBE/ten Hypercubes and Thinking Machines Corporation's CM-2 (one of the Connection Machine series). The nCUBE 2 at Sandia National Laboratories has 1024 processors with four megabytes of local memory per processor, whereas the nCUBE/ten has the same number of processors but only 0.5 megabytes of memory per processor. The CM-2 is presently configured with 16K single-bit processors, 128 kilobytes of memory per processor, and 512 64-bit floating-point coprocessors. This conference has already given considerable attention to the virtues and pitfalls of SIMD architecture, so I think it will be most profitable to focus this short presentation on the state of affairs in MIMD architectures.
An interdisciplinary research group of about 50 staff is active in parallel computing at Sandia on the systems described above. The group includes computational scientists and engineers in addition to applied mathematicians and computer scientists. Interdisciplinary teams that bring together parallel-algorithm and applications researchers are an essential element to advancing the state of the art in supercomputing.
Some Developments in Parallel Algorithms
In the area of parallel algorithms and methods, there have been several interesting developments in the last seven years. Some of the earliest excitement, particularly in the area of SIMD computing, was the emergence of cellular automata methods. In addition, some very interesting work has been done on adaptive-precision numerical methods, for which the CM-2 provides unique hardware and software support. In addition, there has been much theoretical and experimental research on various asynchronous methods, including proofs of convergence for some of the most interesting ones.
A more recent development, the work of Fredericksen and McBryan (1988) on the parallel superconvergent multigrid method, prompted a surge in research activity in parallel multigrid methods. For example, parallel implementations of classic multigrid have been demonstrated with parallel efficiencies of 85 per cent for two-dimensional problems on 1000 processors and about 70 per cent for three-dimensional problems on 1000 processors (Womble and Young 1990)—well in excess of our expectations for these methods, given their partially serial nature.
A new class of methods that emerged is parallel time stepping. C. William Gear (now with the Nippon Electric Corporation Research Institute, Princeton, New Jersey), in a presentation at the July 1989 SIAM meeting in San Diego, California, speculated on the possibility of developing such methods. Womble (1990) discusses a class of methods that typically extract a factor of 4- to 16-fold increase in parallelism over and above the spatial parallelism in a computation. This is not the dramatic increase in parallelism that Gear speculated might be achievable, but it's certainly a step in the right direction in that the time parallelism is multiplicative with spatial parallelism and therefore attractive for problems with limited spatial parallelism.
At the computer-science end of the algorithm spectrum, there have been notable developments in areas such as parallel load balance, mapping methods, parallel graphics and I/O, and so on. Rather than considering each of these areas in detail, the focus will now shift to the impact of parallel algorithms and programming strategies on applications.
Some Developments in Parallel Applications
The prospects for high-performance, massively parallel applications were raised in 1987 with the demonstration, using a first-generation nCUBE system, of 1000-fold speedups for some two-dimensional simulations based on partial differential equations (Gustafson et al. 1988). The Fortran codes involved consisted of a few thousand to less than 10,000 lines of code. Let's consider what might happen when a number of parallel algorithms are applied to a large-scale scientific computing problem; i.e., one consisting of tens of thousands to a million or more lines of code.
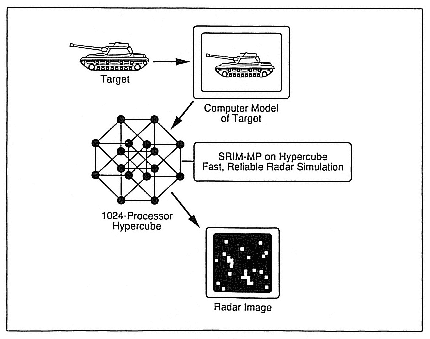
A case study is provided by parallel radar simulation (Gustafson et al. 1989). This is, in some sense, the inverse problem to the radar problem that immediately comes to mind—the real-time processing problem. In radar simulation one takes a target, such as a tank or aircraft, produces a geometry description, and then simulates the interaction of radar with
the geometry on a supercomputer (Figure 1). These simulations are generally based on multibounce radar ray tracing and do not vectorize well. On machines like the CRAY X-MP, a radar image simulator such as the Simulated Radar IMage (SRIM) code from ERIM Inc. typically achieves five or six million floating-point operations per second per processor. Codes such as SRIM have the potential for high performance on massively parallel supercomputers relative to vector supercomputers. However, although the novice might consider ray tracing to be embarrassingly parallel, in practice radar ray tracing is subject to severe load imbalances.
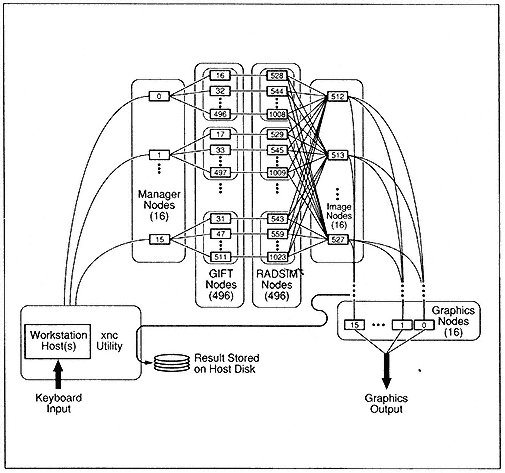
The SRIM code consists of about 30,000 lines of Fortran, an amalgamation of many different algorithms that have been collected over a period of 30 years and do not fit naturally into a half megabyte of memory. The implementation strategy was heterogeneous . That is, rather than combining all of the serial codes in the application package, the structure of the software package is preserved by executing the various codes simultaneously on different portions of the hypercube (Figure 2), with data pipelined from one code in the application package to the next.
Figure 1.
A parallel radar simulation as generated by the SRIM code.
Figure 2.
Heterogeneous image simulation using a MIMD computer.
The heterogeneous implementation uses a MIMD computer in a very general MIMD fashion for the first time. An observation made by one of our colleagues concerning the inaugural Gordon Bell Prize was that the parallel applications developed in that research effort were very SIMD-like and would have performed very well on the Connection Machine. In contrast, the parallel radar simulation features, at least at the high level, a true MIMD strategy with several cooperating processes: a load-balance process, a multibounce radar ray-tracing process, an imaging process, and a process that performs a global collection of the radar image, as well as a user-supplied graphic process and a host interface utility to handle the I/O.
The nCUBE/ten version of the radar simulation, for which one had to develop a host process, had six different cooperating programs. There are utilities on second-generation hypercubes that handle direct node I/O, so a host process is no longer needed. By keeping the application code on the nodes rather than splitting it into host and node code, the resulting parallel code is much closer to the original workstation codes of Cray Research, Inc., and Sun Microsystems, Inc. Over the long haul, I think that's going to be critical if we're going to get more people involved with using massively parallel computers. Furthermore, three of the remaining five processes—the load-balance, image-collection, and graphics processes—are essentially library software that has subsequently been used in other parallel applications.
Consider the religious issue of what qualifies as a massively parallel architecture and what doesn't. Massively parallel is used rather loosely here to refer to systems of 1000 or more floating-point processors or their equivalent in single-bit processors. However, Duncan Buell (also a presenter in this session) visited Sandia recently, and an interesting discussion ensued in which he asserted that massively parallel means that a collection of processors can be treated as an ensemble and that one is most concerned about the efficiency of the ensemble as opposed to the efficiencies of individual processors.
Heterogeneous MIMD simulations provide a nice fit to the above definition of massive parallelism. The various collections of processors are loosely synchronous, and to a large extent, the efficiencies of individual processors do not matter. In particular, one does not want the parallel efficiency of the dynamic load-balance process to be high, because that means the load-balance nodes are saturated and not keeping up with the work requests of the other processors. Processor efficiencies of 20, 30, or 50 per cent are perfectly acceptable for the load balancer, as long as only a few processors are used for load balancing and the bulk of the processors are keeping busy.
Some Developments in Parallel Applications II
Some additional observations concerning the development of massively parallel applications can be drawn from our research into Strategic Defense Initiative (SDI) tracking and correlation problems. This is a classic problem of tracking tens or hundreds of thousands of objects, which Sandia is investigating jointly with Los Alamos National Laboratory, the Naval Research Laboratory, and their contractors. Each member of the team is pursuing a different approach to parallelism, with Sandia's charter being to investigate massive parallelism on MIMD hypercubes.
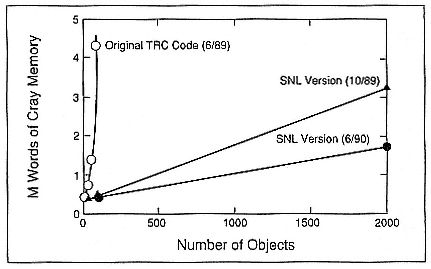
One of the central issues in parallel computing is that a major effort may be expended in overhauling the fundamental algorithms involved as part of the porting process, irrespective of the architecture involved. The course of the initial parallelization effort for the tracker-correlator was interesting: parallel code development began on the hypercube, followed by a quick retreat to restructuring the serial code on the Cray. The original tracking algorithms were extremely memory intensive, and data structures required extensive modification to improve the memory use of the code (Figure 3), but first-generation hypercube nodes with a mere half megabyte of memory were not well suited for the task.
Halbgewachs et al. (1990) developed a scheme for portability between the X-MP and the nCUBE/ten in which they used accesses to the solid-state device (SSD) to swap "hypercube processes" and to simulate the handling of the message-passing. In this scheme one process executes, sends its "messages" to the SSD, and is then swapped out for another "process." This strategy was a boon to the code-development effort. Key algorithms were quickly restructured to reduce the memory use from second order to first order. Further incremental improvements have been made to reduce the slope of the memory-use line. The original code could not track more than 160 objects. The first version with linear memory requirements was able to track 2000 objects on the Cray and the nCUBE/ten.
On the nCUBE/ten a heterogeneous implementation was created with a host process. (A standard host utility may be used in lieu of a host program on the second-generation hypercubes.) The tracking code that runs on the nodes has a natural division into two phases. A dynamic load balancer was implemented with the first phase of the tracking algorithm, which correlates new tracks to known clusters of objects. The second phase, in which tracks are correlated to known objects, is performed on the rest of the processors.
Figure 3.
Improved memory utilization: Phase 1, reduced quadratic dependence to linear;
Phase 2, reduced coefficient of linear dependence.
Given the demonstration of an effective heterogeneous implementation and the ability to solve large problems, suddenly there is user interest in real-time and disk I/O capabilities, visualization capabilities, etc. When only small problems could be solved, I/O and visualization were not serious issues.
Performance evaluation that leads to algorithm modifications is critical when large application codes are parallelized. For example, the focus of SDI tracking is on simulating much larger scenarios, i.e., 10,000 objects, as of September 1990, and interesting things happen when you break new ground in terms of problem size. The first 10,000-object run pinpointed serious bottlenecks in one of the tracking phases. The bottleneck was immediately removed, and run time for the 10,000-object problem was reduced from three hours to one hour. Such algorithmic improvements are just as important as improving the scalability of the parallel simulation because a simulation that required 3000 or 4000 processors to run in an hour now requires only 1000.
A heterogeneous software implementation, such as the one described above for the SDI tracking problem, suggests ways of producing heterogeneous hardware implementations for the application. For example, we can quantify the communication bandwidth needed between the different algorithms; i.e., the throughput rate needed in a distributed-computing
approach where one portion of the computation is done on a space platform, other portions on the ground, etc. In addition, MIMD processors might not be needed for all phases of the simulation. Heterogeneous implementations are MIMD at their highest level, but one might be able to take advantage of the power of SIMD computing in some of the phases. Furthermore, heterogeneous nodes are of interest in these massively parallel applications because, for example, using a few nodes with large memories in a critical phase of a heterogeneous application might reduce the total number of processors needed to run that phase in a cost-effective manner.
Given our experience with a heterogeneous implementation on homogeneous hardware, one can propose a heterogeneous hardware system to carry out the computation efficiently. We note, however, that it would be risky to build a system in advance of having the homogeneous hardware implementation. If you're going to do this sort of thing—and the vendors are gearing up and are certainly talking seriously about providing this capability—then I think we really want to start with an implementation on a homogeneous machine and do some very careful performance analyses.
Closing Remarks
What, besides those developments mentioned by other presenters, has or has not changed since 1983? In light of the discussion at this conference about risk taking, I think it is important to remember that there has been significant risk taking involved in supercomputing the last several years. The vendors have taken considerable risks in bringing massively parallel and related products to market. From the perspective of someone who buys 1000-processor systems before one is even built by the vendor, customers have also taken significant risks. Those who funded massively parallel acquisitions in the 1980s have taken risks.
I've seen a great improvement in terms of vendor interest in user input, including input into the design of future systems. This doesn't mean that vendor-user interaction is ideal, but both sides realize that interaction is essential to the viability of the supercomputing industry.
A more recent, encouraging development is the emerging commercial activity in portability. Commercial products like STRAND88 (from Strand Software Technologies Inc.) and Express (from Parasoft Corporation) have appeared. These provide a starting point for code portability, at least between different distributed-memory MIMD machines and perhaps also between distributed-memory and shared-memory machines.
We are much further from achieving portability of Fortran between MIMD and SIMD systems, in part due to the unavailability of Fortran 90 on the former.
Another philosophical point concerns which current systems are supercomputers and which are not. We believe that the era of a single, dominant supercomputer has ended, at least for the 1990s if not permanently. Without naming vendors, I believe that at least four of them have products that qualify as supercomputers in my book—that is, their current system provides the fastest available performance on some portion of the spectrum of computational science and engineering applications. Even given the inevitable industry shakeouts, that is likely to be the situation for the near future.
What hasn't happened in supercomputing since 1983? First, language standards are lagging. Fortran 8X has now become Fortran 90. There are no parallel constructs in it, although we at least get array syntax, which may make for better nonstandard parallel extensions. To some extent, the lack of a parallel standard is bad because it certainly hinders portability. In another sense the lack of a parallel standard is not bad because it's not clear that the Fortran community knows what all the parallel extensions should be and, therefore, what all the new standards should be. I would hate to see a new standard emerge that was focused primarily on SIMD, distributed-memory MIMD, or shared-memory MIMD computing, etc., to the detriment of the other programming models.
A major concern is that massive parallelism does not have buy-in from most computational scientists and engineers. There are at least three good reasons for this. First, recall the concern expressed by many presenters at this conference for education to get more people involved in supercomputing. This is especially true of parallel computing. A second issue is opportunity , i.e., having systems, documentation, experienced users, etc., available to newcomers to smooth their transition into supercomputing and parallel computing. The role of the NSF centers in making vector supercomputers accessible is noteworthy.
The third, and perhaps most critical, issue is interest . We are at a crossroads where a few significant applications on the Connection Machine, nCUBE 2, and Intel iPSC/860 achieve a factor of 10 or more better run-time performance than on vector supercomputers. On the other hand, there is a large body of applications, such as the typical mix of finite-element- and finite-difference-based applications, that typically achieve performance on a current massively parallel system that is comparable to that of a vector supercomputer, or at most three to five times the vector supercomputer. This level of performance is sufficient to
demonstrate a price/performance advantage for the massively parallel system but not a clear raw-performance advantage. In some cases, end users are willing to buy into the newer technology on the basis of the price/performance advantage. More often, there is a great deal of reluctance on the part of potential users.
User buy-in for massive parallelism is not a vector supercomputer versus massively parallel supercomputer issue. In 1983 we faced a similar situation in vector supercomputing: many users did not want to be concerned with vector processors and how one gets optimum performance out of them. In recent years the situation has gradually improved. The bottom line is that eventually most people who are computational scientists at heart come around, and a few get left behind. In summary, I hope that someday all computational scientists in the computational science and engineering community will consider advanced computing to be part of their career and part of their job.
References
P. O. Fredericksen and O. A. McBryan, "Parallel Superconvergent Multigrid," in Multigrid Methods , S. McCormick, Ed., Marcel Dekker, New York (1988).
J. L. Gustafson, R. E. Benner, M. P. Sears, and T. D. Sullivan, "A Radar Simulation Program for a 1024 Processor Hypercube," in Proceedings, Supercomputing '89 , ACM Press, New York, pp. 96-105 (1989).
J. L. Gustafson, G. R. Montry, and R. E. Benner, "Development of Parallel Methods for a 1024 Processor Hypercube," SIAM Journal on Scientific and Statistical Computing9 , 609-638 (1988).
R. D. Halbgewachs, J. L. Tomkins, and John P. VanDyke, "Implementation of Midcourse Tracking and Correlation on Massively Parallel Computers," Sandia National Laboratories report SAND89-2534 (1990).
D. E. Womble, "A Time Stepping Algorithm for Parallel Computers," SIAM Journal on Scientific and Statistical Computing11 , 824-837 (1990).
D. E. Womble and B. C. Young, "Multigrid on Massively Parallel Computers," in Proceedings of the Fifth Distributed Memory Computing Conference , D. W. Walker and Q. F. Stout, Eds., IEEE Computer Society Press, Los Alamitos, California, pp. 559-563 (1990).
The Interplay between Algorithms and Architectures:
Two Examples
Duncan Buell
Duncan A. Buell received his Ph.D. degree in mathematics from the University of Illinois at Chicago in 1976. He has held academic positions in mathematics at Carleton University in Canada and in computer science at Bowling Green State University in Ohio and at Louisiana State University (LSU). In 1985 he joined the Supercomputing Research Center in Bowie, Maryland, where he is presently a Senior Research Scientist. He has done research in number theory, information retrieval, and parallel algorithms and was part of a team at LSU that built a 256-bit-wide, reconfigurable parallel integer arithmetic processor, on which he holds a patent. He has written numerous journal articles and one book.
This presentation describes briefly, using two examples, the relevance of computer architecture to the performance achievable in running different algorithms.
This session is supposed to focus on architectural features of high-performance computing systems and how those features relate to the design and use of algorithms for solving hard problems.
Table 1 presents timings from a computation-bound program. This is a benchmark that I have created, which is the computational essence of the sort of computations I normally do. As with any benchmark, there are many caveats and qualifications, but you will have to trust me that this
| |||||||||||||||||||||||||||
table is generated honestly and that in my experience, performance on this benchmark is a reasonable predictor of performance I might personally expect from a computer. This is a program written in C; not being trained in archaeology, I tend to avoid antique languages like Fortran.
Table 2 displays counts of "cell updates per second." I will get to the details in a moment. This table has largely been prepared by Craig Reese of the Supercomputing Research Center (SRC). I apologize for the fact that the tables are in inverse scales, one measuring time and the other measuring a rate.
So what's the point? As mentioned in Session 3 by Harvey Cragon, there have been some things that have been left behind as we have developed vector computing, and one of those things left behind is integer arithmetic. This is a benchmark measuring integer arithmetic performance, and on the basis of this table, one could justifiably ask why one of the machines in Table 1 is called a supercomputer and the others are not.
As an additional comment, I point out that some of the newer RISC chips are intentionally leaving out the integer instructions—this is the reason for the poor performance of the Sun Microsystems, Inc., SUN 4 relative to the Digital Equipment Corporation DEC-5000. Those in the
| |||||||||||||||||||||
floating-point world will not notice the absence of those instructions because they will be able to obtain floating-point performance through coprocessor chips.
The second table is a DNA string-matching benchmark. This is a computation using a dynamic programming algorithm to compare a string of characters against a great many other strings of characters. The items marked with an asterisk come from published sources; the unmarked items come from computations at SRC. Some machines are included multiple times to indicate different implementations of the same algorithm.
As for precise machines, PNAC is Dan Lopresti's special-purpose DNA string-matching machine, and Splash is a board for insertion into a SUN computer that uses Xilinx chips arranged in a linear array. The timings of the Connection Machine CM-2 (from Thinking Machines Corporation) are largely C/Paris timings from the SRC Connection Machine.
And what is the message? The DNA problem and the dynamic programming edit distance algorithm are inherently highly parallel and dominated as a computation by the act of "pushing a lot of bits around." It should, therefore, not come as a surprise that the Connection Machine, with inherent parallelism and a bit orientation, outperforms all other machines. In Table 1, we see that the absence of integer hardware drags the Cray Research CRAY-2 down to the performance level of a workstation—not even the raw speed of the machine can overcome its inherent limitations. In Table 2, we see that the fit between the computation and the architecture allows for speedups substantially beyond what one might expect to get on the basis of mundane issues of price and basic machine speed.
Now, do we care—or should we—about the problems typified in these two tables? After all, neither of these fits the mode of "traditional" supercomputing. From K. Speierman's summary of the 1983 Frontiers of Supercomputing meeting, we have the assertion that potential supercomputer applications may be far greater than current usage indicates. Speierman had begun to make my case before I even took the floor. Yes, there are hard problems out there that require enormous computation resources and that are simply not supported by the architecture of traditional high-end computers.
Two other lessons emerge. One is that enormous effort has gone into vector computing, with great improvements made in performance. But one can then argue that in the world of nonvector computing, many of those initial great improvements are yet to be made, provided the machines exist to support their kind of computation.
The second lesson is a bitter pill for those who would argue to keep the 1050 lines of code already written. If we're going to come up with new architectures and use them efficiently, then necessarily, code will have to be rewritten because it will take new algorithms to use the machines well. Indeed, it will be a failure of ingenuity on the part of the algorithm designers if they are unable to come up with algorithms so much better for the new and different machines that, even with the cost of rewriting code, such rewrites are considered necessary.
Linear Algebra Library for High-Performance Computers[*]
Jack Dongarra
Jack Dongarra is a distinguished scientist specializing in numerical algorithms in linear algebra, parallel computing, advanced computer architectures, programming methodology, and tools for parallel computers at the University of Tennessee's Department of Computer Science and at Oak Ridge National Laboratory's Mathematical Sciences Section. Other current research involves the development, testing, and documentation of high-quality mathematical software. He was involved in the design and implementation of the EISPACK, LINPACK, and LAPACK packages and of the BLAS routines and is currently involved in the design of algorithms and techniques for high-performance computer architectures.
Dr. Dongarra's other experience includes work as a visiting scientist at IBM's T. J. Watson Research Center in 1981, a consultant to Los Alamos Scientific Laboratory in 1978, a research assistant with the University of New Mexico in 1978, a visiting scientist at Los Alamos Scientific Laboratory in 1977, and a Senior Scientist at Argonne National Laboratory until 1989.
Dr. Dongarra received a Ph.D. in applied mathematics from the University of New Mexico in 1980, an M.S. in computer science from the Illinois Institute of Technology in 1973, and a B.S. in mathematics from Chicago State University in 1972.
Introduction
For the past 15 years, my colleagues and I have been developing linear algebra software for high-performance computers. In this presentation, I focus on five basic issues: (1) the motivation for the work, (2) the development of standards for use in linear algebra, (3) a basic library for linear algebra, (4) aspects of algorithm design, and (5) future directions for research.
LINPACK
A good starting point is LINPACK (Dongarra et al. 1979). The LINPACK project began in the mid-1970s, with the goal of producing a package of mathematical software for solving systems of linear equations. The project developers took a careful look at how one puts together a package of mathematical software and attempted to design a package that would be effective on state-of-the-art computers at that time—the Control Data Corporation (scalar) CDC 7600 and the IBM System 370. Because vector machines were just beginning to emerge, we also provided some vector routines. Specifically, we structured the package around the basic linear algebra subprograms (BLAS) (Lawson et al. 1979) for doing vector operations.
The package incorporated other features, as well. Rather than simply collecting or translating existing algorithms, we reworked algorithms. Instead of the traditional row orientation, we used a column orientation that provided greater efficiency. Further, we published a user's guide with directions and examples for addressing different problems. The result was a carefully designed package of mathematical software, which we released to the public in 1979.
LINPACK Benchmark
Perhaps the best-known part of that package—indeed, some people think it is LINPACK—is the benchmark that grew out of the documentation. The so-called LINPACK Benchmark (Dongarra 1991) appears in the appendix to the user's guide. It was intended to give users an idea of how long it would take to solve certain problems. Originally, we measured
the time required to solve a system of equations of order 100. We listed those times and gave some guidelines for extrapolating execution times for about 20 machines.
The times were gathered for two routines from LINPACK, one (SGEFA) to factor a matrix, the other (SGESL) to solve a system of equations. These routines are called the BLAS, where most of the floating-point computation takes place. The routine that sits in the center of that computation is a SAXPY, taking a multiple of one vector and adding it to another vector:
![]()
Table 1 is a list of the timings of the LINPACK Benchmark on various high-performance computers.
The peak performance for these machines is listed here in millions of floating-point operations per second (MFLOPS), in ascending order from 16 to 3000. The question is, when we run this LINPACK Benchmark,
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
what do we actually get on these machines? The column labeled "Actual MFLOPS" gives the answer, and that answer is quite disappointing in spite of the fact that we are using an algorithm that is highly vectorized on machines that are vector architectures. The next question one might ask is, why are the results so bad? The answer has to do with the transfer rate of information from memory into the place where the computations are done. The operation—that is, a SAXPY—needs to reference three vectors and do essentially two operations on each of the elements in the vector. And the transfer rate—the maximum rate at which we are going to transfer information to or from the memory device—is the limiting factor here.
Thus, as we increase the computational power without a corresponding increase in memory, memory access can cause serious bottlenecks. The bottom line is MFLOPS are easy, but bandwidth is difficult .
Transfer Rate
Table 2 lists the peak MFLOPS rate for various machines, as well as the peak transfer rate (in megawords per second).
Recall that the operation we were doing requires three references and returns two operations. Hence, to run at good rates, we need a ratio of three to two. The CRAY Y-MP does not do badly in this respect. Each
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
processor can transfer 50 million (64-bit) words per second; and the complete system, from memory into the registers, runs at four gigawords per second. But for many of the machines in the table, there is an imbalance between those two. One of the particularly bad cases is the Alliant FX/80, which has a peak rate of 188 MFLOPS but can transfer only 22 megawords from memory. It is going to be very hard to get peak performance there.
Memory Latency
Another issue affecting performance is, of course, the latency: how long (in terms of cycles) does it actually take to transfer the information after we make a request? In Table 3, we list the memory latency for seven machines. We can see that the time ranges from 14 to 50 cycles. Obviously, a memory latency of 50 cycles is going to impact the algorithm's performance.
Development of Standards
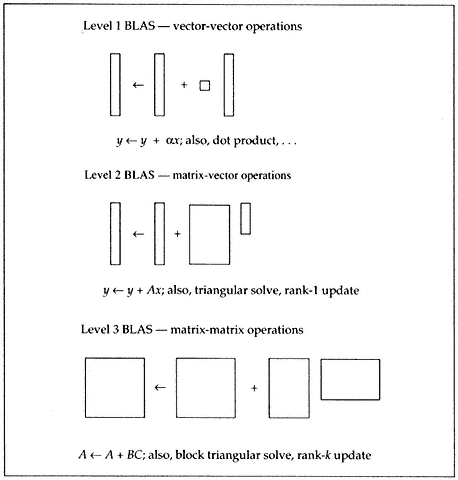
The linear algebra community has long recognized that we needed something to help us in developing our algorithms. Several years ago, as a community effort, we put together a de facto standard for identifying basic operations required in our algorithms and software. Our hope was that the standard would be implemented on the machines by many manufacturers and that we would then be able to draw on the power of having that implementation in a rather portable way.
We began with those BLAS designed for performing vector-vector operations. We now call them the Level 1 BLAS (Lawson et al. 1979). We later defined a standard for doing some rather simple matrix-vector calculations—the so-called Level 2 BLAS (Dongarra et al. 1988). Still
| ||||||||||||||||||||||||||||||||||||
later, the basic matrix-matrix operations were identified, and the Level 3 BLAS were defined (Dongarra, Du Croz, et al. 1990). In Figure 1, we show these three sets of BLAS.
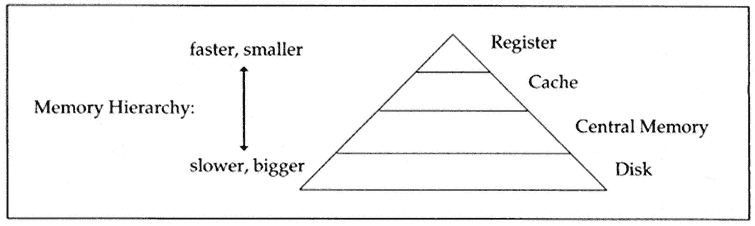
Why were we so concerned about getting a handle on those three different levels? The reason lies in the fact that machines have a memory hierarchy and that the faster memory is at the top of that hierarchy (see Figure 2).
Naturally, then, we would like to keep the information at the top part to get as much reuse or as much access of that data as possible. The higher-level BLAS let us do just that. As we can see from Table 4, the Level 2 BLAS offer the potential for two floating-point operations for every reference; and with the Level 3 BLAS, we would get essentially n operations for every two accesses, or the maximum possible.
Figure 1.
Levels 1, 2, and 3 BLAS.
Figure 2.
Memory hierarchy.
| ||||||||||||||||||||
These higher-level BLAS have another advantage. On some parallel machines, they give us increased granularity and the possibility for parallel operations, and they end up with lower synchronization costs.
Of course, nothing comes free. The BLAS require us to rewrite our algorithms so that we use these operations effectively. In particular, we need to develop blocked algorithms that can exploit the matrix-matrix operation.
The development of blocked algorithms is a fascinating example of history repeating itself. In the sixties, these algorithms were developed on machines having very small main memories, and so tapes of secondary storage were used as primary storage (Barron and Swinnerton-Dyer 1960, Chartres 1960, and McKellar and Coffman 1969). The programmer would reel in information from tapes, put it into memory, and get as much access as possible before sending that information out. Today people are reorganizing their algorithms with that same idea. But now instead of dealing with tapes and main memory, we are dealing with vector registers, cache, and so forth to get our access (Calahan 1979, Jordan and Fong 1977, Gallivan et al. 1990, Berry et al. 1986, Dongarra, Duff, et al. 1990, Schreiber 1988, and Bischof and Van Loan 1986). That is essentially what LAPACK is about: taking those ideas—locality of reference and data reuse—and embodying them in a new library for linear algebra.
LAPACK
Our objective in developing LAPACK is to provide a package for the solution of systems of equations and the solution of eigenvalue problems. The software is intended to be efficient across a wide range of high-performance computers. It is based on algorithms that minimize memory access to achieve locality of reference and reuse of data, and it is built on top of the Levels 1, 2, and 3 BLAS—the de facto standard that the numerical linear algebra community has given us. LAPACK is a multi-institutional project, including people from the University of Tennessee, the University of California at Berkeley, New York University's Courant Institute, Rice University, Argonne National Laboratory, and Oak Ridge National Laboratory.
We are in a testing phase at the moment and just beginning to establish world speed records, if you will, for this kind of work. To give a hint of those records, we show in Table 5 some timing results for LAPACK routines on a CRAY Y-MP.
Let us look at the LU decomposition results. This is the routine that does that work. On one processor, for a matrix of order 32, it runs at four MFLOPS; for a matrix of order 1000, it runs at 300 MFLOPS. Now if we take our LAPACK routines (which are written in Fortran), called the Level 3 BLAS (which the people from Cray have provided), and go to eight processors, we get 32 MFLOPS—a speeddown . Obviously, if we wish to solve the matrix, we should not use this approach!
When we go to large-order matrices, however, the execution rate is close to two GFLOPS—for code that is very portable. And for LLT and QR factorization, we get the same effect.
Note that we are doing the same number of operations that we did when we worked with the unblocked version of the algorithms. We are not cheating in terms of the MFLOPS rate here.
One other performance set, which might be of interest for comparison, is that of the IBM RISC machine RS/6000-550 (Dongarra, Mayer, et al. 1990). In Figure 3, we plot the speed of LU decomposition for the LAPACK routine, using a Fortran implementation of the Level 3 BLAS. For the one-processor workstation, we are getting around 45 MFLOPS on larger-order matrices.
Clearly, the BLAS help, not only on the high-performance machines at the upper end but also on these RISC machines, perhaps at the lower end—for exactly the same reason: data are being used or reused where the information is stored in its cache.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure 3.
Variants of LU factorization on the IBM RISC System RS/6000-550.
Algorithm Design
Up to now, we have talked about restructuring algorithms; that is essentially what we did when we changed them to block form. The basic algorithm itself remains the same; we are simply affecting the locality of how we reference data and the independence of operations that we are trying to focus on—the matrix-matrix operations.
Divide-and-Conquer Approach
Let us now talk about designing algorithms. In this case, the basic algorithm will change. In particular, let us consider a divide-and-conquer technique for finding the eigenvalues and eigenvectors of a symmetric tridiagonal matrix (Dongarra and Sorensen 1987). The technique is also used in other fields, where it is sometimes referred to as domain decomposition. It involves tearing, or partitioning, the problem to produce small, independent pieces. Then, the eigenvalue of each piece is found independently. Finally, we "put back" the eigenvalues of these pieces, and put back the eigenvalues of these others, and so on. We were successful. In redesigning this algorithm, we ended up with one that runs in parallel very efficiently. Table 6 gives ratios of performance on a CRAY-2 for up to four processors. As we can see from the table, we are getting four times the speed up, and sometimes even better. What's more, we have an example of serendipity: the same algorithm is actually more efficient than the "best" sequential algorithm, even in the sequential setting.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Accuracy
Working with LAPACK has given us an opportunity to go back and rethink some of the algorithms. How accurately can we solve NA problems (Demmel and Kahan 1988)? The answer depends on the accuracy of the input data and how much we are willing to spend:
• If the input data is exact, we can ask for a (nearly) correctly rounded answer—generally done only for +, *, /, , and cos.
• If the input H is uncertain in a normwise sense (true input = H + dH , where ||dH || / ||H || is small), the conventional backward stable algorithm is suitable; it is the usual approach to linear algebra, it does not respect sparsity structure, and it does not respect scaling.
• If the input H is uncertain in a component-wise relative sense (true input = H + dH , where maxi,j |dHij | / |Hij | is small), it does respect sparsity, it does respect scaling, but it does need new algorithms, perturbation theory, and error analysis.
In the end, we have new convergence criteria, better convergence criteria, and better error bounds. We also enhance performance because we now terminate the iteration in a much quicker way.
Tools
Our work in algorithm design has been supported by tool development projects throughout the country. Of particular note are the projects at Rice University and the University of Illinois. Other projects help in terms of what we might call logic or performance debugging of the algorithms—trying to understand what the algorithms are doing when they run on parallel machines. The objective here is to give the implementor a better feeling for where to focus attention and to show precisely what the algorithm is doing while it is executing on parallel machines (Dongarra, Brewer, et al. 1990).
Testing
Testing and timing have been an integral part of the LAPACK project. Software testing is required to verify new machine-specific versions. Software timing is needed to measure the efficiency of the LAPACK routines and to compare new algorithms and software. In both of these tasks, many vendors have helped us along the way by implementing basic routines on various machines and providing essential feedback (see Table 7).
The strategy we use may not be optimal for all machines. Our objective is to achieve a "best average" performance on the machines listed in Table 8. We are hoping, of course, that our strategy will also perform well
| ||||||||||||||||||||||||
| ||||||||||||||||||
on a wider range of machines, including the Intel iPSC, iWarp, MasPar, nCUBE, Thinking Machines, and Transputer-based computers.
Future Directions for Research
We have already started looking at how we can make "cosmetic changes" to the LAPACK software—adapt it in a semiautomatic fashion for distributed-memory architectures. In this effort, our current work on blocked operations will be appropriate because the operations minimize communication and provide a good surface-to-volume ratio. We also expect that this task will require defining yet another set of routines, this one based on the BLACS (basic linear algebra communication routines). Once again, we will draw on what has been done in the community for those operations.
As a preliminary piece of data, we show in Figure 4 an implementation of LU decomposition from LAPACK, run on a 64-processor Intel iPSC. Clearly, we are not yet achieving optimum performance, but the situation is improving daily.
Figure 4.
Pipelined LU factorization results for 64 and 128 nodes.
Some interest has also been expressed in developing a C implementation of the LAPACK library. And we continue to track what is happening with Fortran 90 and with the activities of the Parallel Computing Forum.
In the meantime, we are in our last round of testing of the shared-memory version of LAPACK. The package will be released to the public in 1992.
References
D. W. Barron and H. P. F. Swinnerton-Dyer, "Solution of Simultaneous Linear Equations Using a Magnetic-Tape Store," Computer Journal3 , 28-33 (1960).
M. Berry, K. Gallivan, W. Harrod, W. Jalby, S. Lo, U. Meier, B. Phillippe, and A. Sameh, "Parallel Algorithms on the Cedar System," Center for Supercomputing Research and Development technical report 581, University of Illinois-Urbana/Champaign (October 1986).
C. Bischof and C. Van Loan, "Computing the Singular Value Decomposition on a Ring of Array Processors," in Large Scale Eigenvalue Problems , J. Cullum and R. Willoughby, Eds., North-Holland, Amsterdam (1986).
D. Calahan, "A Block-Oriented Sparse Equation Solver for the CRAY-1," in Proceedings of the 1979 International Conference Parallel Processing , pp. 116-123 (1979).
B. Chartres, "Adoption of the Jacobi and Givens Methods for a Computer with Magnetic Tape Backup Store," technical report 8, University of Sydney, Australia (1960).
J. Demmel and W. Kahan, "Computing the Small Singular Values of Bidiagonal Matrices with Guaranteed High Relative Accuracy," Argonne National Laboratory Mathematics and Computer Science Division report ANL/MCS-TM-110 (LAPACK Working Note #3) (1988).
J. Dongarra, "Performance of Various Computers Using Standard Linear Equations Software in a Fortran Environment," technical report CS-89-85, University of Tennessee, Knoxville (1991).
J. Dongarra, O. Brewer, S. Fineberg, and J. Kohl, "A Tool to Aid in the Design, Implementation, and Understanding of Matrix Algorithms for Parallel Processors," Parallel and Distributed Computing9 , 185-202 (1990).
J. Dongarra, J. Bunch, C. Moler, and G. W. Stewart, LINPACK User's Guide , Society for Industrial and Applied Mathematics Publications, Philadelphia, Pennsylvania (1979).
J. Dongarra, J. Du Croz, I. Duff, and S. Hammarling, "A Set of Level 3 Basic Linear Algebra Subprograms," ACM Transactions on Mathematical Software16 , 1-17 (1990).
J. Dongarra, J. Du Croz, S. Hammarling, and R. Hanson, "An Extended Set of Fortran Basic Linear Algebra Subroutines," ACM Transactions on Mathematical Software 14 , 1-17 (1988).
J. Dongarra, I. S. Duff, D. C. Sorensen, and H. A. Van der Vorst, Solving Linear Systems on Vector and Shared Memory Computers , Society for Industrial and Applied Mathematics Publications, Philadelphia, Pennsylvania (1990).
J. Dongarra, P. Mayer, and G. Radicati, "The IBM RISC System 6000 and Linear Algebra Operations," Computer Science Department technical report CS-90-122, University of Tennessee, Knoxville (LAPACK Working Note #28) (December 1990).
J. Dongarra and D. Sorensen, "A Fully Parallel Algorithm for the Symmetric Eigenproblem," SIAM Journal on Scientific and Statistical Computing8 (2), 139-154 (1987).
K. Gallivan, R. Plemmons, and A. Sameh, "Parallel Algorithms for Dense Linear Algebra Computations," SIAM Review32 (1), 54-135 (1990).
T. Jordan and K. Fong, "Some Linear Algebraic Algorithms and Their Performance on the CRAY-1," in High Speed Computer and Algorithm Organization , D. Kuck, D. Lawrie, and A. Sameh, Eds., Academic Press, New York, pp. 313-316 (1977).
C. Lawson, R. Hanson, D. Kincaid, and F. Krogh, "Basic Linear Algebra Subprograms for Fortran Usage," ACM Transactions on Mathematical Software5 , 308-323 (1979).
A. C. McKellar and E. G. Coffman Jr., "Organizing Matrices and Matrix Operations for Paged Memory Systems," Communications of the ACM12 (3), 153-165 (1969).
R. Schreiber, "Block Algorithms for Parallel Machines," in Volumes in Mathematics and Its Applications, Vol. 13, Numerical Algorithms for Modern Parallel Computer Architectures , M. Schultz, Ed., Berlin, Germany, pp. 197-207 (1988).
Design of Algorithms
C. L. Liu
C. L. Liu obtained a bachelor of science degree in 1956 at Cheng Kung University in Tainan, Republic of China, Taiwan. In 1960 and 1962, respectively, he earned a master's degree and a doctorate in electrical engineering at MIT. Currently, he is Professor of Computer Science at the University of Illinois-Urbana/Champaign. Dr. Liu's principal research interests center on the design and analysis of algorithms, computer-aided design of integrated circuits, and combinatorial mathematics.
Let me begin by telling you a story I heard. There was an engineer, a physicist, and a mathematician. They all went to a conference together.
In the middle of the night, the engineer woke up in his room and discovered there was a fire. He rushed into the bathroom, got buckets and buckets of water, threw them over the fire, and the fire was extinguished. The engineer went back to sleep.
In the meantime, the physicist woke up and discovered there was a fire in his room. He jumped out of bed, opened his briefcase, took out paper, pencil, and slide rule, did some very careful computations, ran into the bathroom, measured exactly one-third of a cup of water, and poured it slowly over the fire. Of course, the fire was extinguished. And the physicist went back to sleep.
In the meantime, the mathematician woke up and also discovered there was a fire in his room. He jumped out of bed, rushed into the
bathroom, turned on the faucet—and he saw water come out. He said, "Yes, the problem has a solution." And he went back to sleep.
Today we are here to talk about design of algorithms. Indeed, we sometimes use the engineer's approach, and sometimes the physicist's approach, and occasionally the mathematician's approach.
Indeed, it is a fair question that many of you can stare into the eyes of the algorithmists and say that throughout the years we have given you faster and faster and cheaper and cheaper supercomputers, more and more flexible software. What have you done in terms of algorithmic research?
Unfortunately, we are not in a position to tell you that we now have a computer capable of 1012 floating-point operations per second (TFLOPS) and that, therefore, there's no need to do any more research in the algorithms area. On the other hand, we cannot tell you that our understanding of algorithms has reached such a point that a "uniFLOPS" computer will solve all the problems for us. What is the problem? The problem is indeed the curse of combinatorial explosion.
I remember it was almost 30 years ago when I took my first course in combinatorics from Professor Gian-Carlo Rota at MIT, and he threw out effortlessly formulas such as n5 , n log n, 2n , 3n , and nn . As it turns out, these innocent-looking formulas do have some significant differences. When we measure whether an algorithm is efficient or not, we draw a line. We say an algorithm is an efficient algorithm if its computational time as a function of the size of the problem is a polynomial function. On the other hand, we say that an algorithm is inefficient if its computational time as a function of the size of the problem is an exponential function. The reason is obvious. As n increases, a polynomial function does not grow very fast. Yet on the other hand, an exponential function grows extremely rapidly.
Let me just use one example to illustrate the point. Suppose I have five different algorithms with these different complexity measures, and suppose n is equal to 60. Even if I'm given a computer that can carry out 109 operations per second, if your algorithm has a complexity of n, there is no problem in terms of computation time (6 × 10-8 seconds). With a complexity of n2 or n5 , there is still no problem. There is a "small" problem with a complexity of 2n and a "big" problem with a complexity of 3n .
Now, of course, when the complexity is 3n , computation time will be measured in terms of centuries. And measured in terms of cents, that adds up to a lot of dollars you cannot afford. As Professor Rota once told us, when combinatorial explosion takes place, the units don't make any difference whatsoever.
So indeed, when we design algorithms it is clear that we should strive for efficient algorithms. Consequently, if we are given a problem, it would be nice if we can always come up with efficient algorithms.
On the other hand, that is not the case. A problem is said to be intractable if there is known to be no efficient algorithm for solving that problem.
From the algorithmic point of view, we have paid much less attention to problems that are really intractable. Rather, a great deal of research effort has gone into the study of a class of problems that are referred to as NP-complete problems. We have tackled them for 40 or 50 years, and we cannot confirm one way or the other that there are or are not efficient algorithms for solving these problems.
So therefore, although I begin by calling this the curse of combinatorial explosion, it really is the case, as researchers, that we should look at this as the blessing of combinatorial explosion. Otherwise, we will have no fun, and we will be out of business.
So now the question is, if that is the case, what have you been doing?
Well, for the past several years, people in the area of algorithmic design tried to understand some of the fundamental issues, tried to solve real-life problems whose sizes are not big enough to give us enough trouble, or, if everything failed, tried to use approximation algorithms that would give us good, but not necessarily the best possible, results.
Let me use just a few examples to illustrate these three points.
I believe the problem of linear programming is one of the most beautiful stories one can tell about the development of algorithms.
The problem of linear programming was recognized as an important problem back during the Second World War. It was in 1947 when George Dantzig invented the simplex method. Conceptually, it is a beautiful, beautiful algorithm. In practice, people have been using it to solve linear programming problems for a long, long time. And indeed, it can handle problems of fair size; problems with thousands of variables can be handled quite nicely by the simplex method.
Unfortunately, from a theoretical point of view, it is an exponential algorithm. In other words, although we can handle problems with thousands of variables, the chance of being able to solve problems with hundreds of thousands of variables or hundreds of millions of variables is very small.
In 1979, Khachin discovered a new algorithm, and that is known as the ellipsoid algorithm. The most important feature of the ellipsoid algorithm is that it is a polynomial algorithm. The algorithm by itself is
impractical because of the numerical accuracy it requires; the time it takes to run large problems will be longer than with the simplex method.
But on the other hand, because of such a discovery, other researchers got into the picture. Now they realize the ball game has moved from one arena to a different one, from the arena of looking for good exponential algorithms to the arena of looking for good polynomial algorithms.
And that, indeed, led to the birth of Karmarkar's algorithm, which he discovered in 1983. His algorithm is capable of solving hundreds of thousands of variables, and, moreover, his research has led to many other activities, such as how to design special-purpose processors, how to talk about new architectures, and how to talk about new numerical techniques. As I said, this is a good example illustrating algorithmic development. It demonstrates why it is important to have some basic understanding of various features of algorithms.
Let me talk about a second example, with which I will illustrate the following principle: when it becomes impossible to solve a problem precisely—to get the exact solution—then use a lot of FLOPS and try to get a good solution. And I want to use the example of simulated annealing to illustrate the point.
Back in 1955, Nick Metropolis, of Los Alamos National Laboratory, wrote a paper in which he proposed a mathematical formulation to model the annealing process of physical systems with a large number of particles. In other words, when you have a physical system with a large number of particles, you heat the system up to a high temperature and then slowly reduce the temperature of the system. That is referred to as annealing. Then, when the system freezes, the system will be in a state of minimum total energy. In Nick's paper he had a nice mathematical formulation describing the process.
That paper was rediscovered in 1983 by Scott Kirkpatrick, who is also a physicist. He observed that the process of annealing is very similar to the process of doing combinatorial minimization because, after all, you are given a solution space corresponding to all the possible configurations that the particles in the physical system can assume. If, somehow, you can move the configurations around so that you can reach the minimum energy state, you would have discovered the minimum point in your solution space. And that, indeed, is the global minimum of your combinatorial optimization problem.
The most important point of the annealing process is, when you reduce the temperature of your physical system, the energy of the system does not go down all the time. Rather, it goes down most of the time, but it goes up a little bit, and then it goes down, and it goes up a little bit again.
Now, in the terminology of searching a large solution space for a global minimum, that is a very reasonable strategy. In other words, most of the time you want to make a downhill move so that you can get closer and closer to the global minimum. But occasionally, to make sure that you will not get stuck in a local minimum, you need to go up a little bit so that you can jump out of this local minimum.
So therefore, as I said, to take what the physicists have developed and then use that to solve combinatorial optimization problems is conceptually extremely pleasing.
Moreover, from a mathematical point of view, Metropolis was able to prove that as T approaches infinity, the probability that the system will reach the ground state approaches 1 as a limit. For many practical problems that we want to solve, we cannot quite make that kind of assumption. But on the other hand, such a mathematical result does give us a lot of confidence in borrowing what the physicists have done and using that to solve optimization problems.
As I said, the formula I have here tells you the essence of the simulated-annealing approach to combinatorial optimization problems. If you are looking at a solution S and you look at a neighboring solution S', the question is, should you accept S' as your new solution?
This, indeed, is a step-by-step sequential search. And according to the theory of annealing, if the energy of the new state is less than the energy of the current state, the probability of going there is equal to one.
On the other hand, if the new state has an energy that is larger than the energy of the current state, then it depends on some probabilistic distribution. What I'm trying to say is, what I have here is nothing but some kind of probabilistic uphill/downhill search. And as it turns out, it will go quite well in many combinatorial-optimization problems.
And moreover, the development of such techniques will lead to a lot of interesting research questions. How about some theoretical understanding of the situation? How about possible implementation of all of these ideas? And moreover, simulated annealing basically is a very sequential search algorithm. You have to look at one solution, after that the next solution, after that the next solution. How do you parallelize these algorithms?
Let me quickly mention a rather successful experience in solving a problem from the computer-aided design of integrated circuits. That is the problem of placement of standard cells. What you are given is something very simple. You are given a large number, say about 20,000 cells. All these cells are the same height but variable widths. The problem is how to place them in rows. I do not know how many rows all together,
and I do not know the relationship among these cells except that eventually there will be connections among them. And if you do it by brute force, you are talking about 20,000! possibilities, which is a lot.
Yet, on the other hand, there is a software package running on Sun Microsystems, Inc., workstations for about 10 hours that produces solutions to this problem that are quite acceptable from a practical point of view. That is my second example.
Let me talk about a third example. As I said, since we do not have enough time, enough FLOPS, to get exact solutions of many of the important problems, how about accepting what we call approximate solutions? And that is the idea of approximation algorithms.
What is an approximation algorithm? The answer is, engineers wave their hands and yell, "Just do something!"
Here is an example illustrating that some basic understanding of some of the fundamental issues would help us go a long way. Let me talk about the job-scheduling problem, since everybody here who is interested in parallel computation would be curious about that. You are given a set of jobs, and these jobs are to be scheduled—in this example, using three identical processors. And of course, when you execute these jobs, you must follow the precedence constraints.
Question: how can one come up with a schedule so that the total execution time is minimum? As it turns out, that is a problem we do not know how to do in the sense that we do not know of any polynomial algorithm for solving the problem. Therefore, if that is the case, once you have proved that the problem is NP-complete, you are given a license to use hand-waving approximation solutions.
However, if you are given a particular heuristic, a particular hand-waving approach, the question is, what is the quality of the results produced by your particular heuristics? You can say, I will run 10,000 examples and see what the result looks like. Even if you run 10,000 examples, if you do not know the best possible solution for each of these examples, you're getting nowhere.
In practice, if I give you just one particular instance and I want you to run your heuristics and tell me how good is the result that your heuristic produces, how do you answer the question? As it turns out, for this particular example, there is a rather nice answer to that question. First of all, let me mention a very obvious, very trivial heuristic we all have been using before: whenever you have a processor that is free, you will assign to it a job that can be executed.
In this case, at the very beginning, I have three processors. They are all free. Since I have only one job that can be executed, I'll execute it. After
that, I have three processors that are free, but I have four jobs that can be executed. I close my eyes and make a choice; it's B, C, E. Do the rest, and so on and so forth.
In other words, the simple principle is, whenever you have jobs to be executed, execute them. Whenever your processors are free, try to do something on the processors. This is a heuristic that is not so good but not so bad, either. It can be proved that if you follow such a heuristic, then the total execution time you are going to have is never more than 1.66 times the optimal execution time. In the worst case, I will be off by 66 per cent. Now, of course, you told me in many cases 66 per cent is too much. But there's another way to make good use of this result.
Suppose you have another heuristic which is, indeed, a much better heuristic, and your total execution time is 'instead of . How good is'? Ah, I will compare it with my , since it is very easy for me to compute . If your ' is close to the value of , you might be off by 66 per cent.
On the other hand, if your ' is close to 3/5 of , you are in pretty good shape because you must be very close to 0 . This is an example to show you that although we do not know how to find 0 , although we do not know how to determine a schedule that will give me an optimal schedule, on the other hand, we will be capable of estimating how good or how bad a particular heuristic is, using it on a particular example.
To conclude, let me ask the question, what is the research agenda? What are we going to do?
First point: we should pay more attention to fundamental research. And it has been said over and over again, theoretical research has been underfunded. As a college professor, I feel it is alarming that our Ph.D. students who have studied theoretical computer science very hard and have done very well face very stiff competition in getting jobs in good places. There is a danger some of our brightest, most capable computer-science students would not want to go into more theoretical, more fundamental, research but would rather spend their time doing research that is just as exciting, just as important, but fosters better job opportunities.
I think we should look into possibilities such as arranging postdoctoral appointments so that some of the people who have a strong background in theory can move over to learn something about other areas in computer science while making use of what they learned before in theoretical computer science.
Second point: with the development of fast supercomputers, there are many, many opportunities for the theoreticians to make use of what they learn about algorithms, to solve some real live application problems.
Computer-aided design is an example; image-processing, graphics, and so on are all examples illustrating that theoreticians should be encouraged to make good use of the hardware and the software that are available so that they can try to help to solve some of the important problems in computer science.
Third point: when we compare combinatorial algorithms with numerical algorithms, combinatorial algorithms are way behind in terms of their relationship with supercomputing, and we should start building a tool library—an algorithm library—so that we can let people who do not know as much, who do not care to know as much, about algorithms make good use of what we have discovered and what we have developed.
And finally, I'm not saying that as theoreticians we necessarily need TFLOPS machines, but at least give us a lot more FLOPS. Not only will we make good use of the FLOPS you can provide, but you can be sure that we'll come back and beg you for more.
Computing for Correctness
Peter Weinberger
Peter J. Weinberger is Director of the Software and Systems Research Center at AT&T Bell Laboratories. He has a Ph.D. in mathematics from the University of California at Berkeley. After teaching mathematics at the University of Michigan, he moved to Bell Labs.
He has done research in various aspects of system software, including operating systems, network file systems, compilers, performance, and databases. In addition to publishing a number of technical articles, he has coauthored the book The AWK Programming Language.
At Computer Science Research at Bell Laboratories, a part of AT&T, I have a legitimate connection with supercomputers that I'm not going to talk about, and Bell Labs has a long-standing connection with supercomputers. Instead of going over a long list of things we've done for supercomputer users, let me advertise a new service. We have this swell Fortran-to-C converter that will take your old dusty decks—or indeed, your modern dusty decks, your fancy Fortran 77—and convert from an obsolete language to perhaps an obsolescent language named ANSI C. You can even do it by electronic mail.
I'm speaking here about what I feel is a badly underrepresented group at this meeting, namely, the supercomputer nonuser. Let me explain how I picked the topic I'm going to talk about, which is, of course, not quite the topic of this session.
When you walk through the Pentagon and ask personnel what their major problem is, they say it's that their projects are late and too expensive. And if you visit industry and talk to vice presidents and ask them what their major problem is, it's the same: their stuff is late and too expensive. If you ask them why, nine out of ten times in this informal survey they will say, "software." So there's a problem with software. I don't know whether it's writing it fast or getting it correct or both. My guess is that it's both.
So I'm going to talk about a kind of computation that's becoming—to be parochial about it—more important at AT&T, but it's intended to be an example of trying to use some semiformal methods to try to get your programs out faster and make them better.
The kind of calculation that I'm going to talk about is what's described as protocol analysis. Because that's perhaps not the most obvious supercomputer-ready problem, I'll describe it in a little bit of detail.
Protocol analysis of this sort has three properties. First, it's a combinatorially unsatisfactory problem, suffering from exponential explosion. Second, it doesn't use any floating-point operations at all, and so I would be delighted at the advent of very powerful zero-FLOPS machines (i.e., machines running at zero floating-point operations per second), just supposing they are sufficiently cheap, and possibly a slow floating-point operation, as well, so I can tell how fast my program is running.
Because these problems are so big, speed is important. But what's most important is the third property, memory. Because these problems are so big, we can't do them exactly; but because they are so important, we want to do them approximately—and the more memory, the better the approximation. So what I really want is big, cheap memory. Fast is important, but cheap is better.
So what are protocols? They are important in several areas. First, there's intercomputer communications, where computers talk through networks.
They are also important, or can be made important, in understanding the insides of multiprocessors. This is a problem that was solved 20 years ago, or maybe it was only 10, but it was before the Bell System was broken up. Thus, it was during the golden age instead of the modern benighted times. We each have our own interests, right? And my interest is in having large amounts of research money at AT&T.
The problem is that there are bunches of processors working simultaneously sharing a common memory, and you want to keep them from stomping all over each other. You can model the way to do that using
protocol analysis. As I said, this is a dead subject and well understood. Now let me try to tell this story without identifying the culprit.
Within the last five years, someone at Bell Labs bought a commercial multiprocessor, and this commercial multiprocessor had the unattractive feature of, every several days or so, dying. Careful study of the source, obtained with difficulty, revealed that the multiprocessor coordination was bogus. In fact, by running the protocol simulation stuff, you could see that not only was the code bogus, but the first proposed fix was bogus, too—although quite a lot less bogus in that you couldn't break it with only two processors. So that's actual protocols in multiprocessing.
There's another place where protocols are important, and that's in the phone system, which is increasingly important. Here's an intuitive idea why some sort of help with programs might be important in the phone system. You have just gone out and bought a fabulous new PBX or some other sort of electronic switchboard. It's got features: conferencing, call-waiting, all sorts of stuff. And here I am setting up a conference call, and just as I'm about to add you to the conference call, you are calling me, and we hit the last buttons at the same time. Now you're waiting for me and I'm waiting for you, and the question is, what state is the wretched switch in? Well, it doesn't much matter unless you have to reboot it to get it back.
What's interesting is that the international standards body, called the Consultative Committee in International Telegraphy and Telephony (CCITT), produces interoperability specifications for the telephone network in terms of protocol specifications. It's not exactly intuitive what the specification means, or if it's correct. In fact, there are two languages: one is a programming language, and the other is a graphical language, presumably for managers. You are supposed to use this language to do successive refinements to get a more and more detailed description of how your switch behaves. This example is in the CCITT standard language SDL (system definition language).
The trouble with international standards is that they are essentially a political process, and so you get the CCITT International Signaling System Seven Standard, and then you go around, if you happen to build switches for a living, and tell the customers that you're going to implement it. They say, "No, no, no, that's not what we use; we use CCITT Seven Standard except for all these different things."
So, what's a protocol, how are protocols modeled, and what's the point of modeling them? Take, for example, a typical computer-science pair of people. We have A, who is named Alice, and B, who is named Bob. Alice has a sequence of messages to send to Bob. The problem isn't with
Alice, Bob, or even the operating system. The problem is with the communications channel, which could have the usual bad properties—it loses messages. The whole system is correct if eventually Bob gets all the messages that Alice sends, in exactly the sequence Alice sends them.
Let me point out why this is not a trivial problem for those of you who don't believe it. The easiest thing is that Alice sends a message, and when Bob gets it, he sends an acknowledgment, and then Alice sends the next message, and so on. The problem is that the channel can lose the first message, and after a while Alice will get tired of waiting and send it again. Or the channel could lose the return message instead, in which case Alice will send the first message twice, and you will have paid your mortgage twice this month.
Now I'm going to describe what's called a sliding window, selective retransmission protocol. With each message there's a sequence number, which runs from 0 to M-1, and there can only be M/2 outstanding unacknowledged messages at once. Now you model these by what are called finite-state machines. For those of you who aren't into finite-state machines, a finite-state machine is just like a finite Markov chain without any probabilities, where you can take all the paths you're allowed to take, and on each path you might change some state variables or emit a message to one of your buddies.
The way we're going to prove this protocol correct is by modeling Alice by a finite-state machine and modeling Bob by a finite-state machine, and you can model each half of the protocol engine by a little finite-state machine. Then you just do all the transitions in the finite-state machines, and look at what happens. Now there's a sequence of three algorithms that have been used historically to study these problems.
I should point out that there's been a lot of talk here about natural parallelism, and the way you model natural parallelism in this example is by multiplying the state spaces together. You just treat the global state as the product of all the local states, and you get exponential complexity in no time at all. But that's the way it is in nature, too.
So you just build the transition graph for all these states, and you get this giant graph, and you can search around for all kinds of properties. In realistic examples you get numbers like 226 reachable states. These are not the biggest cases we want to do, they're just the biggest ones we can do. There are 230 edges in the graph. That's too big.
So you give up on that approach, and you look for properties that you can check on the basis of nothing other than the state you're in. And there are actually a lot of these properties.
Even in cases where we don't keep the whole graph, if each state is 64 or 128 bytes—which is not unreasonable in a big system—and if there are 226 reachable states, we're still losing because there is too much memory needed. So as you're computing along, when you get to a state that you have reached before, you don't have to continue. We also have to keep track of which states we've seen, and a good way to do that is a hash table—except that even in modest examples, we can't keep track of all the stuff about all the states we've seen.
The third step is that we use only one bit per state in the hash table. If the bit is already on, you say to yourself that you've already been here. You don't actually know that unless each state has its own hash code. All you know is that you've found a state that hashes to the same bit as some other state. That means there may be part of the state space you can't explore and problems you can't find. If you think two-dimensional calculations are good enough, why should this approximation bother you?
Now what do you want to get out of this analysis? What you want are little diagrams that give messages saying that you've found a deadlock, and it's caused by this sequence of messages, and you've blown it (again) in your protocol.
Now suppose I do the example I was doing before. With a two-bit sequence number and a channel that never loses anything, there are about 90,000 reachable states, and the longest sequence of actions before it repeats in this finite thing is about 3700 long. To see the exponential explosion, suppose you allow six sequence numbers instead of four. You get 700,000 reachable states, and the longest sequence is 15,000. In four sequence numbers with the message loss, the state space is huge, but the number of reachable states is (only) 400,000. Now if the channel could duplicate messages too, then we're up to 6 million reachable states, and we're beginning to have trouble with our computer.
Now if you do the one-bit thing and hash into a 229 table, you get very good coverage. Not perfect, but very good, and it runs a lot faster than with the full state storage, and it doesn't take a gigabyte to store it all.
If you break the protocol by allowing three outstanding messages, then the analyzer finds that immediately. If you change the channel so it doesn't make mistakes, then the protocol is correct, and there are 287,000 reachable states. That's three times bigger than the two-message version we started with.
There is some potential that formal methods will someday make programs a little bit better. Almost all of these methods are badly
exponential in behavior. So you'll never do the problems you really want to do, but we can do better and better with bigger and bigger memories and machines. Some of this can probably be parallelized, although it's not cycles but memory that is the bottleneck in this calculation.
So that's it from the world of commercial data processing.