Vectors Are Different
Steven J. Wallach
Steven J. Wallach, a founder of CONVEX Computer Corporation, is Senior Vice President of Technology and a member of the CONVEX Board of Directors. Before founding CONVEX, Mr. Wallach served as product manager at ROLM for the 32-bit mill-spec computer system. From 1975 to 1981, he worked at Data General, where he was the principal architect of the 32-bit Eclipse MV superminicomputer series. As an inventor, he holds 33 patents in various areas of computer design. He is featured prominently in Tracy Kidder's Pulitzer Prize-winning book , The Soul of a New Machine.
Mr. Wallach received a B.S. in electrical engineering from Polytechnic University, New York, an M.S. in electrical engineering from the University of Pennsylvania, and an M.B.A. from Boston University. He serves on the advisory council of the School of Engineering at Rice University, Houston, and on the external advisory council of the Center for Research on Parallel Computation, a joint effort of Rice/Caltech/Los Alamos National Laboratory. Mr. Wallach also serves on the Computer Systems Technical Advisory Committee of the U.S. Department of Commerce and is a member of the Board of Directors of Polytechnic University.
In the late 1970s, in the heyday of Digital Equipment Corporation (DEC), Data General, and Prime, people were producing what we called minicomputers, and analysts were asking how minicomputers were different
from an IBM mainframe, etc. We used to cavalierly say that if it was made east of the Hudson River, it was a minicomputer, and if was made west of the Hudson River, it was a mainframe.
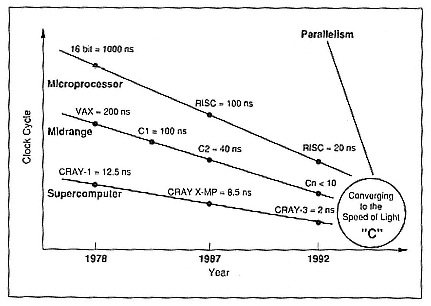
At the Department of Commerce, the Computer Systems Technical Advisory Committee is trying to define what a supercomputer is for export purposes. For those who know what that entails, you know it can be a "can of worms." In Figure 1, I give my view of what used to be the high-end supercomputer, which had clock cycle X. What was perceived as a microcomputer in the late 1970s was 20X, and perhaps if it came out of Massachusetts, it was 10- to 15X. Over time, we have had three different slopes, as shown in Figure 1. The top slope is a RISC chip, and that is perhaps where CONVEX is going, and maybe this is where Cray Research, Inc., and the Japanese are going. We are all converging on something called the speed of light. In the middle to late 1990s, the clock-cycle difference between all levels of computing will be, at best, four to one, not 20 to one.
The next question to consider is, how fast do things have to be to eliminate vectors and use scalar-only processors? That is why I titled my talk "Vectors are Different."
I think the approach to take is to look at both the hardware and the software. If you only look at the hardware, you will totally miss the point.
Figure 1.
Clock cycle over time since the late 1970s.
I used to design transistor amplifiers. However, today I tend to be more comfortable with compiler algorithms. So what I am going to do is talk about vectors, first with respect to software and then with respect to hardware, and see how that relates to scalar processing.
First, the reason we are even asking the question is because we have very highly pipelined machines. But, as Harvey Cragon pointed out earlier in this session, as have others, we have a history of vectorizing both compilers and coding styles. I would not say that it is "cookie-cutter" technology, but it is certainly based on the pioneering work of such people as Professors David Kuck and Ken Kennedy (presenters in Session 5).
I ran the program depicted in Figure 2 on a diskless SUN with one megabyte of storage. I kept wondering why, after half an hour, I wasn't getting the problem done. So I put a PRINT statement in and realized that about every 15 to 20 minutes I was getting another iteration. The problem was that it was page-faulting across the network. I then ran that benchmark on five different RISC machines or workstations, which are highly pipelined machines that are supposed to put vector processing out of business.
Examine Table 1 row by row, not column by column. What is important is the ratio of row entries for the same processor. The right way to view Table 1 means i is on the inner loop; the wrong way means j is on the inner loop. On the MIPS (millions of instructions per second), it was a
Figure 2.
Vectors—software.
| ||||||||||||||||||||||||||||||||||||||||||
difference of three to one. That is, if I programmed DO j, DO i versus DO i, DO j, it was three to one for single precision.
Double precision for the R6000 was approximately the same, which was the best of them because it had the biggest cache—a dual-level cache of R6000 (Table 1). Single precision for the R3000 was about 10 to one, and double precision was five to one. Now, that may sound counter-intuitive. Why should it be a smaller ratio with a bigger data type? The reason is that you start going nonlinear faster because it is bigger than the cache size. The Solbourne, which is the SPARC, is three to one.
We couldn't get the real *8 to run because it had a process size that was too big relative to physical memory, and we didn't know how to fix it. Then we ran it on RIOS (reduced instruction set computing), the hottest thing. The results were interesting—20 to one and 20 to one. Now you get the smaller cache, and in this case, you get almost 30 to one.
What does this all mean? What it really means to me is that to use these highly pipelined machines, especially if they all have caches, we're basically going to vectorize our code anyway. Whether we call it vectors or not, we're going to code DO j, DO i, just to get three or 10 times the performance. It also means that the compilers for these machines are
going to have to do dependency analysis and all these vector transformations to overcome this.
In our experience at CONVEX, we have taken code collectively and "vectorized" it, so that 99 times out of 100, you put it back on the scalar machine and it runs faster. The difference is, if it only runs 15 per cent faster, people say, "Who cares? It's only 15 per cent." Yet, if my mainline machine is going to be this class of scalar pipeline machines, 15 per cent actually is a big deal. As the problem size gets bigger, that increase in performance will get bigger also. By programming on any of those workstations, I got anywhere from three to 20 times faster.
No matter what we do, I believe our compiler is going forward, and soon these will be vectorizing compilers. We just won't say it, because it would do vector transformations anyway.
Now let's look at hardware. The goals of hardware design are to maximize operations on operands and use 100 per cent of available memory bandwidth. When I consider clock cycles and other things, I design computers by starting with the memory system, and I build the fastest possible memory system I can and make sure the memory is busy 100 per cent of the time, whether it's scalar or vector. It's very simple—you tell me a memory bandwidth, and I'll certainly tell you your peak performance. As we all know, you very rarely get the peak, but at least I know the peak.
The real issue as we go forward is, if we want to get performance, we have to design high-speed memory systems that effectively approach the point where we get an operand back every cycle. If we get an operand back at every cycle, we're effectively designing a vector memory system, whether we call it that or not. In short, memory bandwidth determines the dominant cost of a system.
Also, as we build machines in the future, we're beginning to find out that the cost of the CPU is becoming lower and lower. All the cost is in the memory system, the crossbar, the amount interleaving, and the mechanics. Consequently, again, we're paying for bandwidth. Figure 3 shows you some hard numbers on these costs, and these numbers are not just off the top of my head.
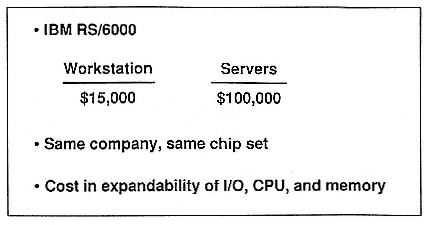
The other thing that we have to look at is expandability, which adds cost. If you have a machine that can go from baseline X to 4X, whatever that means, you have to design that expandability in from the start. Even if you buy the machine with the baseline configuration, there is overhead, and you're paying for the ability to go to 4X. For example, look at the IBM RS/6000, a workstation that IBM lists for $15,000. But it's not expandable in the scheme of things. It's a uniprocessor.
Figure 3.
Vectors—hardware.
Now let's examine the server version of the RS/6000. We are using price numbers from the same company and using the same chips. So the comparison in cost is apples to apples. When I run a single-user benchmark with little or no I/O (like the LINPACK), I probably get the same performance on the workstation as I do on the server, even though I pay six times more for the server. The difference in price is due to the server having expandability in I/O, CPU, and physical memory.
Workstations generally don't have this expandability. If they do, they start to be $50,000 single-seat workstations. There were two companies that used to make these kinds of workstations, which seems to prove that $50,000 single-user workstations don't sell well.
What is the future, then? For superscalar hardware, I think every one of these machines eventually will have to have vector-type memory systems to sustain CPU performance. If I can't deliver an operand every cycle, I can't operate it on every cycle. You don't need a Ph.D. in computer science to figure that out. If you have a five-inch pipe feeding water to a 10-inch pipe, you can expand the 10-inch pipe to 20 inches; but you're still going to have the same flow through the pipe. You have to have it balanced. Because all these machines so far have caches, you still need loop interchange or other vector transformations.
You're going to see needs for "blocking algorithms," that is, how to take matrices or vectors and make them submatrices to get the performance. I call it "strip mining." In reality, it's the same thing. That is, how do I take a data set and divide it into a smaller data set to fit into a register or memory to get high-speed performance? Fundamentally, it's the same type of algorithm.
So I believe that, again, we're all going to be building the memory systems, and we're going to be building the compilers. Superscalar hardware will become vector processors in practice, but some people won't acknowledge it.
Now, what will happen to true vector machines? As Les Davis pointed out in the first presentation in this session, they're still going to be around for a long time. I think more and more we're going to have specialized functional units. A functional unit is something like a multiplier or an adder or a logical unit. Very-large-scale integration will permit specialized functional units to be designed, for example, O(N2 ) operations for O(N) data. The type of thing that Ken Iobst was talking about with corner-turning (see the preceeding paper, this session) is an example of that. A matrix-multiply type of thing is another example, but in this case it uses N2 data for N3 operations. More and more you'll see more emphasis on parallelism (MIMD), which will evolve into massive parallelism.
The debate will continue on the utility of multiple memory paths. I view that debate as whether you should have one memory pipe, two memory pipes, or N memory pipes. I've taken a very straightforward position in the company: there's going to be one memory pipe. Not all agree with me.
I look at benchmarks, and I look at actual code, and I find that the clock cycle (the memory bandwidth of a single pipe) seems to be more of a determining factor. If I'm going to build a memory system to tolerate all the bandwidth of multiple pipes, because of parallelism, I believe, rather than having eight machines with three pipes, I'd rather have a 24-processor machine and utilize the bandwidth. I'd rather utilize the bandwidth that way because I get more scalar processing. Because of parallel compilers, I'll probably get more of that effective bandwidth than someone else will with eight machines using three memory pipes.
One other issue: there shall be no Cobol compiler. I have my lapel button that says, "Cobol can be eliminated in our lifetime if we have to." In reality, ever since we've been programming computers, we've had the following paradigm, although we just didn't realize it: we had that part of the code that was scalar and that part of the code that was vector. We go back and forth. You know, nothing is ever 100 per cent vectorizable, nothing is 100 per cent parallelizable, etc. So I think, going forward, we'll see machines with all these capabilities, and the key is getting the compilers to do the automatic decomposition for this.
If we're approaching the speed of light, then, yes, we're all going to go parallel—there's no argument, no disagreement there. But the real issue is, can we start beginning to do it automatically?
With gallium arsenide technology, maybe I can build an air-cooled, four-or five-nanosecond machine. It may not be as fast as a one-nanosecond machine, but if I can get it on one chip, maybe I can put four of them on one board. That may be a better way to go than a single, one-nanosecond chip because, ultimately, we're going to go to parallelism anyway.
The issue is that, since we have to have software to break this barrier, we have to factor that into how we look at future machines, and we can't just let clock cycle be the determining factor. I think if we do, we're "a goner." At least personally I think, as a designer, that's the wrong way to do it. It's too much of a closed-ended way of doing it.