Voting at the Political Fault Line "ss1.68"

TWO VIEWS OF PRIMARY ELECTION DYNAMICS

The two views of primary election dynamics agree on the basic structure of primary elections. Both sides see primary elections as the first phase in a multistage election process. Primary election laws define the rules of participation; that is, they define which voters are permitted to participate in candidate nominations. Both sides agree that under closed primaries, participation in the primary is limited to registered members of that party. Under blanket primaries, participation is extended to all registered voters, including partisans, independents, and members of other parties.^[2]

Where the two views differ is on their interpretation of the consequences of extending participation to all voters. Specifically, they differ in their expectations of how voters will behave in blanket primaries and how candidates will respond. As discussed in the introduction to this volume and the several chapters on voter behavior, voters in blanket primaries can engage in several forms of crossover voting—sincere crossover, hedging, and raiding. All three forms of crossover voting are difficult or impossible under closed primaries, since voters would need to anticipate their desire to cross over long before the election and re-register under a new party label. In some closed primary states, such as New York, voters must re-register a full year before the election. In California prior to 1998, the registration period was twenty-nine days—shorter but still potentially prohibitive for most voters (Bott 1991). Low rates of re-registration in closed primary states suggest that crossover voting in these systems rarely occurs. By contrast, voters in open primary systems (both traditional open and blanket) can decide to cross over at the polls, requiring no precommitment to one or the other party. Voters in blanket primaries are even less constrained by party and can cross over race by race.

The first view of primary election dynamics argues that of the three types of crossover behavior, sincere crossover and hedging will prevail. This is not to say that voters will never engage in raiding; rather, the argument is that most voters are not sufficiently informed to engage in such sophisticated behavior. Raiding requires voters to calculate (1) which candidate would pose the weakest challenge to their favored candidate; (2) whether that candidate can win the primary; and (3) whether that candidate will lose the general. Further, even if they are sufficiently informed to figure out how to raid the other party's primary, voters are likely to be risk-averse and may not vote for a candidate they dislike, even if it means increasing

― 194 ―

the possibility that the candidate they really like wins. Hence, under this first view, most crossover behavior is by centrist independents and moderates voting across party lines for their preferred candidates.

From the candidates' perspective, extending participation in the primary to centrist independent and moderate voters creates advantages for centrist and moderate candidates. Extending participation means shifting the primary electorate median voter toward the ideological center. In other words, the blanket primary median is closer to the ideological center than the closed primary median. Hence, moderate candidates with policy positions close to the median will prevail, resulting in the nomination of more conservative Democrats and more liberal Republicans compared to their closed primary counterparts.^[3] I refer to this prediction as the "moderation hypothesis."

The second view of primary election dynamics argues that of the three types of crossover behavior, the effects of raiding will prevail. This view recognizes the possibility that some voters, especially independents and moderates, may engage in sincere crossover voting and hedging, drawing candidates to the ideological center. However, they also argue that voters will sometimes face strong incentives to engage in raiding. The most favorable situation for raiding is when one party's primary is uncontested. Voters from that party waste their vote by casting it for their party's presumptive nominee. The question then becomes which candidate they should vote for from the other party. Voters ask if they are better off voting for the more preferred candidate in the other party (i.e., hedging), leading their top two candidates from the two parties to face off in the general election, or voting for the less preferred candidate in the other party (i.e., raiding), leading their most preferred candidate to face his or her weakest opponent. In the end, voters' choices will depend on their preferences relative to the candidates, their attitudes toward risk, and the several candidates' electoral prospects. As discussed above, critics of this view argue that voters are simply not well enough informed to behave in such a sophisticated manner. Defenders counter by pointing out the potential for candidates and campaign organizations to help voters coordinate their behavior.

From the candidates' perspective, the possibility of strategic crossover greatly complicates matters. On the one hand, extending participation to independents and members of other parties means shifting the primary electorate median voter toward the ideological center, as noted above. On the other hand, if some voters engage in raiding, it is no longer clear whose preferences become decisive. Hence, the question candidates must ask is: What types of voters are likely to cross over? To the extent that ideologically extreme voters cross over strategically, benefiting extremist candidates, this view results in what I refer to as the "polarization hypothesis."

To illustrate the logic of voter choice in blanket primaries, consider a

― 195 ―

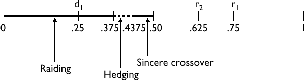
Figure 10.1. Example of crossover voting.

very simple example in which there are two parties, called D and R. Each party has a "front-runner" candidate designated as d₁ and r₁, respectively. For simplicity, I assume that only one party's primary (arbitrarily, the R party) is contested by candidate r₂. I simplify the example by assuming that all voters have single-peaked policy preferences (i.e., that they are riskneutral); that voters' ideal points are uniformly distributed over the unidimensional space [0,1] (hence the general election median voter's ideal point is located at .50); and that all voters with ideal points to the left of .50 are registered with the D party and all voters with ideal points to the right of .50 are registered with the R party. Voters are forward looking, in the sense that they seek to maximize the expected utility of their primary election vote by considering how it will impact their general election choices.^[4] To begin, I set d₁ = .25 and r₁ = .75 and assume that the R party's primary is contested by a moderate candidate whose ideal point is r₂ = .625. I illustrate the configuration of voter and candidate preferences in figure 10.1.^[5]

In figure 10.1, since the D party primary is uncontested, voters whose ideal points are closest to d₁ need not "waste" their votes in the uncontested D party primary, as they would under closed primaries. Rather, they can vote for one of the R party candidates. The question is, which one? Voters know that if r₁ wins the primary, d₁ and r₁ will meet in the general. Since d₁ and r₁ are equidistant from the general election median (at .5), r₁ will win the general election with prob=.50. If r₂ wins the primary, r₂ will beat d₁ with certainty. Therefore, all voters who prefer a lottery between d₁ and r₁ to a win by r₂ will vote for r₁. This will be the case for voters with ideal points from 0.00 up to .375. These voters have ideal points that are closer to d₁ than to r₂ and so prefer a primary outcome that gives d₁ some chance of victory in the general election. Voters to the right of .375 receive higher utility from r₂ than from the lottery, and so they vote for r₂. Since in this example the number of r₂ voters is greater than the number of r₁ voters, r₂ wins the primary and then the general.

This example is constructed to illustrate all three types of crossover voting. Voters with ideal points between .4375 and .5 engage in sincere crossover, voting for their most preferred candidate, r₂. Voters with ideal points between .375 and .4375 engage in hedging—they most prefer d₁, but prefer

― 196 ―

r₂ over the other R party candidate, r₁. Voters with ideal points between 0.00 and .375 engage in strategic crossover voting, voting for a weaker candidate in the other party's primary, r₁.

Note that a number of the example's assumptions, such as the frontrunner candidates' positions being equidistant from the general election median voter's ideal point, are critical to generate the precise predictions about r₂ winning the primary and the general. If we relax some of these highly restrictive assumptions—for example, if we allow candidates to take more extreme or more moderate positions, or for more than one challenger to enter, or for the number of D and R voters to be different, or for voters to be risk-averse, or for turnout to be probabilistic or uncertain—then optimal voter strategies and candidate responses become much more difficult to determine.^[6] The point of the example is not to make specific predictions about winning candidate positions, but rather to illustrate how all of these variables interact.