Tidal Currents
Tidal currents represent the motion of the water particles in the progressive or standing tide waves which on coasts and islands are recognized by the rise and fall of the tide. The tidal currents will therefore be of different character in different areas, depending upon the character
In order to discuss the general character of the tidal currents, it is necessary to repeat some of the equations that have been used previously. Disregarding friction and the rotation of the earth, placing the x-axis in the direction of progress of the tide wave, and assuming constant depth, one obtains the equations of motion and continuity in the form
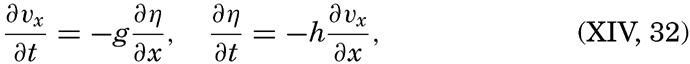
For a progressive wave,

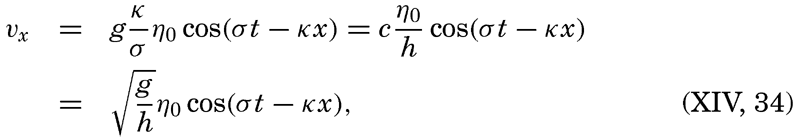
 is the velocity of progress of the wave.
is the velocity of progress of the wave.Thus, the velocity reaches its maximum in the direction of progress at high tide (η = η0) and its maximum in the opposite direction at low tide (η = −η0). The tidal current is alternating, changing its direction every half period.
For a standing wave

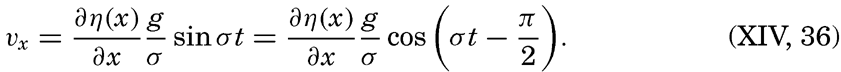
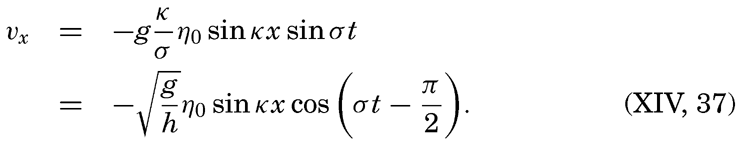
The total horizontal displacement during one half tidal period when the water flows in the same direction, if the maximum tidal current is called V, is
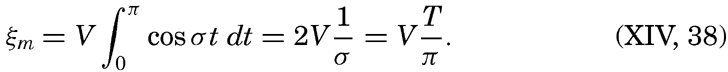
In order to get an idea of the corresponding velocities of the tidal currents and the maximum displacements, we shall consider the tide in a progressive wave of an amplitude (not range) of 100 cm. The corresponding maximum tidal currents in seas of different depths are shown in table 71.
| Semidiurnal tide | Depth (m) | ||||
|---|---|---|---|---|---|
| 100 | 500 | 1000 | 2000 | 4000 | |
| Maximum current {cm/sec | 31.3 | 14.0 | 9.9 | 7.0 | 4.9 |
| {knots | 0.61 | 0.27 | 0.19 | 0.14 | 0.10 |
| Maximum displacement {km | 4.4 | 2.0 | 1.4 | 1.0 | 0.7 |
| {nautical miles | 2.4 | 1.1 | 0.75 | 0.54 | 0.38 |
It appears from this table that in the open ocean the tidal currents cannot reach any appreciable velocities, but measurements demonstrate that the actual velocities are considerably higher than those tabulated, partly because the earth's rotation must be taken into account, and partly for reasons that as yet are unexplained. Before the effect of the earth's rotation is considered, tidal currents in waters of changing depth or changing width will be dealt with.
In a channel of rectangular cross section but variable depth, h, and width, b, the combination of the equations of motion and of continuity can be written (Lamb, 1932, p. 275)
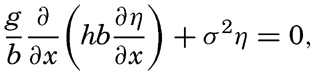
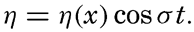
Fleming (1938) has used this equation for studying the tidal currents on a continental shelf related to a standing wave with a node line parallel to the coast. In this case, b is constant, and one obtains
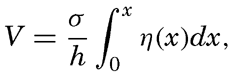
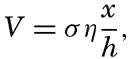
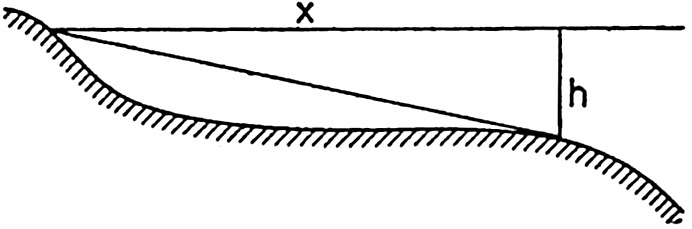
Schematic cross section of a continental shelf showing that the ratio x/h is at a maximum near the border of the shelf.
If the depth is constant, the velocity increases linearly with distance from the coast, but, if the slope of the bottom, x/h, is constant, the velocity is independent of the distance. Generally, the ratio x/h is not constant, and then the tidal currents reach a maximum at the distance x at which x/h is greatest. The profiles of many continental shelves are such that x/h is greatest near the border of the shelf (fig. 143), and the maximum tidal currents may therefore be expected near the border.
These considerations hold true not only in the case of a standing wave, but also, in general, if a transport of water toward the coast takes place during some part of the tidal period and away from the coast during some other part of the tidal period. Therefore they help to clarify some of the characteristics of tidal currents near coasts.
Another question of interest is that of tidal currents where the bottom topography is irregular, showing basins and submarine ridges and peaks. A basin is generally of small dimensions relative to the length of the tide wave (the semidiurnal tide wave is 4200 km long where the depth is 1000 m), and the tidal current, if existing, must therefore be in the same direction in the entire basin during one half tidal period, but such flow would necessitate the presence of ascending and descending motion of considerable velocity at the borders of the basin. If the depth of the basin below the general level of the sea bottom is 1 km and if the width of the area of ascending motion is 10 km, then the average ascending motion would have to be one tenth of the horizontal velocity. This type of flow would be possible in homogeneous
Variation in the width of bodies of water leads to other modifications of the tidal currents. Strong tidal currents through narrow sounds are readily accounted for by the fact that large amounts of water have to flow through these openings during each half tidal period. Consider a bay of surface area A square meters which is in communication with the open sea by an opening whose cross-section area is S square meters. Let the average range of the tide in the bay be 2η0 m. The total volume of water that flows into the bay in the time interval between low and high water is then A × 2η0 m3. The inflow, on the other hand, is equal to 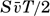 , where
, where 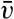 is the average velocity during the half tidal period (T/2) in which inflow takes place. The maximum velocity during that time is π/2 times the average velocity, but the flow is not uniform through the cross section. Observations have shown that in mid-channel the velocity is about one third larger than the average velocity. Therefore, the maximum velocity of the tidal currents in mid-channel is approximately
is the average velocity during the half tidal period (T/2) in which inflow takes place. The maximum velocity during that time is π/2 times the average velocity, but the flow is not uniform through the cross section. Observations have shown that in mid-channel the velocity is about one third larger than the average velocity. Therefore, the maximum velocity of the tidal currents in mid-channel is approximately
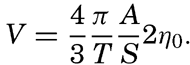
As a schematic example, let us consider a bay that has an area of 100 km2 and is in communication with the open sea through a channel that is only 200 m wide and 50 m deep. Let us assume that the range of the semidiurnal tide in the bay is 2 m. Then, in the time interval between high and low water (6.21 hours, or 22,356 seconds), 2 × 108 m3 of water must flow out through the channel, the cross section of which is 104 m2. The average current must therefore be
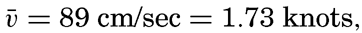
If, in the above example, the opening had been 1 km wide and 100 m deep, the maximum currents at the center of the channel would have been only 0.36 knots. This clearly demonstrates that exceptionally strong tidal currents can be expected only in narrow sounds or inlets. Marmer (1926) has computed the tidal currents at the opening of the Bay of Fundy and found no higher maximum velocities than 1.59 knots, in spite of the tremendous range of the tide at the head of the bay. This result, which is in agreement with observations, clearly shows that strong tidal currents are not encountered at the opening of such bays as the Bay of Fundy, where the cross-section area of the opening is great compared to the surface area of the bay.
The tidal energy can be well illustrated by considering the number of horsepower which can theoretically be developed by tidal currents flowing through a narrow sound connecting a basin with the open sea. The average number of horsepower during one half tidal period, ½T, is equal to gρA2η02/T. With A = 100 km2 and 2η0 = 2 m one obtains 360,000 h.p., but even under the best of conditions only a small fraction of this amount can be actually utilized. Owing to the depth and the width of the opening through which the tidal currents flow, the energy is not concentrated as in a waterfall, but is distributed over a large surface. Furthermore, the tidal power has an intermittent character varying from zero to its maximum value in one quarter tidal period and reaching much higher maximum values at spring tide than at neap tide. This makes utilization on a large scale extremely difficult, but on a small scale tidal power is being used in a few river estuaries. Marmer (1926) computes that theoretically the tides in the Bay of Fundy can produce no less on an average than 200,000,000 h.p., but he adds that by the time the scheme
Neglecting the earth's rotation, the tidal currents are alternating if they are associated with a single standing or progressive tide wave; but if several tide waves are present, interference takes place which may give rise to rotary tidal currents, meaning that the tidal currents regularly change direction and velocity during one tidal period. If the velocities are plotted as vectors from one central point, the end points of the vector will describe a closed curve during one tidal period (fig. 144), and in the absence of other currents the vector sum will be zero.
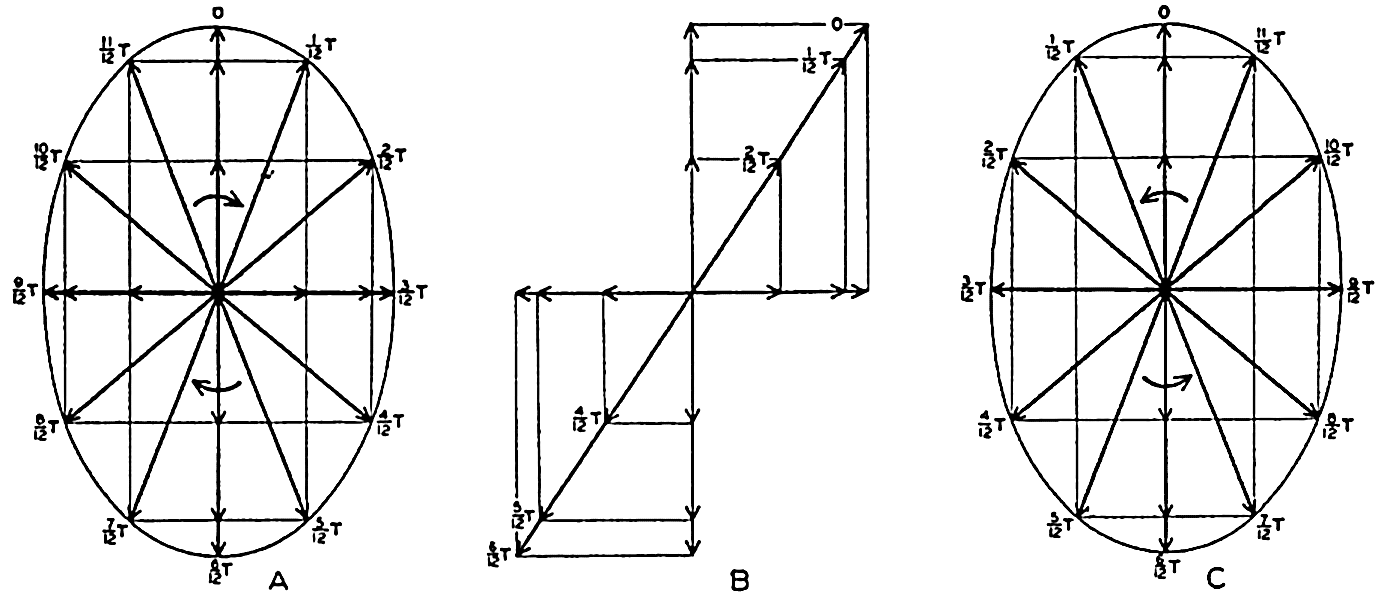
Examples of rotating currents produced by interference of tide waves progressing at right angles to each other and of different phases.
As a simple case, let us consider the interference between two tidal waves which progress along the positive x and y axes. If the depth is constant, the alternating tidal currents corresponding to the two waves are at the point x = y = 0
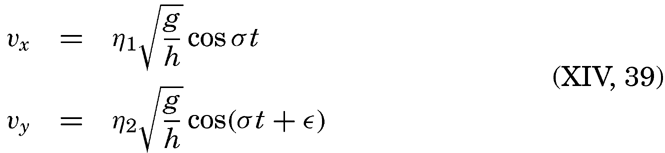
Assume next ∊ = π/2, meaning that the maximum velocity in the direction of the negative y axis is reached one quarter period after the maximum velocity in the positive x direction. The result will be a current which rotates clockwise, the end points of the vectors representing
If ∊ = −π/2, similar reasoning leads to the conclusion that the current will turn counterclockwise as shown in fig. 144C. In general, interference of tide waves leads to rotating currents, the direction of rotation being clockwise or counterclockwise, depending upon the phase difference between the two interfering waves, and the ratio between the axes of the resulting ellipse depending upon the phase difference and the amplitudes of the waves.
Except in narrow sounds the observed tidal currents are mostly rotating. If these currents resulted from interference, one should expect to find clockwise or counterclockwise rotation to be equally frequent, but in the Northern Hemisphere, from which most observations are available, clockwise rotation is by far the more common. This fact indicates that the rotary currents are as a rule not caused by interference but by the effect of the rotation of the earth.
On p. 555 are given the equations of motion and continuity which apply to long waves, taking the rotation of the earth into account. Two integrals of these equations have been given—one by Lord Kelvin, which is applicable to a tidal wave in an infinitely long canal of constant width and depth:
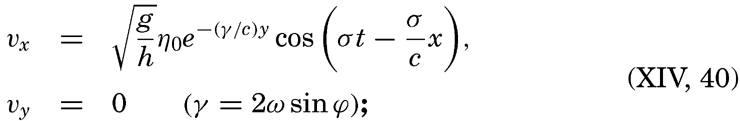
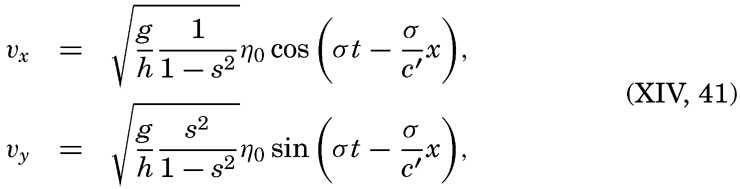
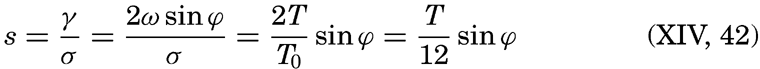
Measurements at lightships have shown that rotating currents occur at a short distance from the coasts, and measurements from vessels anchored in deep water have demonstrated that rotating currents are as a rule present in the open sea. Most of these observations have been made in the Northern Hemisphere where, in nearly all instances, clockwise rotation of the tidal currents has been encountered, whereas a few observations in the Southern Hemisphere have shown counterclockwise rotation. These facts present the best support of the concept that, in general, the rotating tidal currents are due to the effect of the earth's rotation and not to interference, but in some cases interference may complicate the picture. An exact mathematical treatment of the tidal currents of the ocean, however, encounters the same difficulties as the exact development of the dynamic theories of the tides.
As already stated, tidal currents and tides represent two different manifestations of the same phenomenon. When dealing with the tides it was shown that in any locality the tide can be represented by means of a series of harmonic terms having the same periods as the periods of the tide-producing forces. The tidal currents can be represented in a similar manner, but if one deals with rotating currents it is necessary to consider separately two components of the current, say, the N-S and the E-W components. Tidal currents are much more difficult to observe exactly, however, mainly because other types of currents are as a rule superimposed on them, and a great number of data are needed in order to eliminate the superimposed currents and obtain a clear picture of the periodic tidal motion. It can be shown, however, that the tidal currents are closely related to the character of the tide.
It was mentioned that on the Atlantic coast of the United States the tide is of the semidiurnal type, the diurnal components being small. In agreement with this feature it has been found that off the Atlantic coast the tidal currents are also of the semidiurnal type, meaning that during 24 lunar hours the end points of vectors representing the tidal
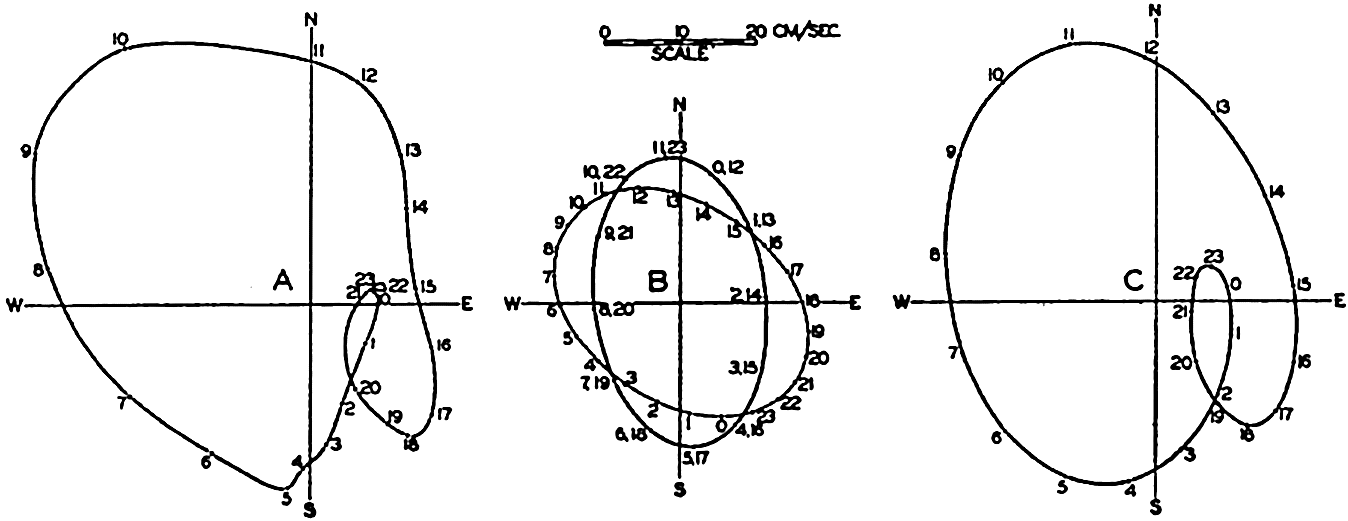
(A) Observed tidal currents at San Francisco light vessel. (B) Semidiurnal and diurnal tidal currents derived from the observations by harmonic analysis. (C) Tidal currents at the San Francisco light vessel computed from the semidiurnal and diurnal currents shown in B.
On the Pacific coast of the United States the tides are of the mixed type and are characterized by a considerable diurnal inequality. Off that coast, complicated tidal currents are present and in course of a lunar day the end points of the vector representing hourly velocities and directions of the tidal flow describe curves that have no similarity to ellipses but that nevertheless result from the combination of several current ellipses corresponding to tides of different periods. In most instances a good approximation to the observed conditions is obtained by combining the different semidiurnal periods to one single period of length 12 lunar hours and the diurnal periods to a single diurnal period of length 24 lunar hours. This is illustrated in fig. 145, in which the left-hand diagram represents the average tidal currents (Marmer, 1926b) during 24 lunar hours at San Francisco light vessel, which is anchored in 31 m of water at a distance of nine nautical miles from the nearest coast. The representation corresponds to those in fig. 144 except that the arrows have been omitted and only the curve joining their end points is shown. The hours marked along this curve represent the lunar hours after the highest high water at San Francisco, the time of that high water being marked 0h. Harmonic analyses of the semidiurnal and diurnal tidal currents leads to the results which are represented in the middle part of the figure. The semidiurnal and diurnal currents both reach about the same maximum velocities, but the semidiurnal rotates twice in 24 lunar hours, whereas the diurnal rotates once. The diagram to the right has been derived by combining the two, and this diagram is sufficiently like the one to the left to demonstrate that the complicated pattern is mainly a
The periods of the tidal currents are in agreement with the periods of the tide, but no general relationship has been established between the velocities of the tidal currents and the height of the tide. The reason is that the velocities of the tidal currents depend not only upon the height of the tide but also upon the depth to the bottom, the slope of the bottom, and the effect of the earth's rotation. Theoretical consideration of all these variables has not yet been possible and observations of currents are too few to permit the establishment of empirical laws.