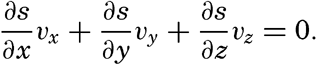The Oceans Their Physics, Chemistry, and General Biology "d3_2

Relation between the Distribution of Properties and the Currents in the Sea

Consider any scalar quantity, s (temperature, salinity, pressure, oxygen content, and so on), the distribution of which is continuous in space and time, so that it can be represented as a function of time and the three space coordinates, s = f(t,x,y,z). Let us assume that this scalar quantity can be considered a property of the individual particles of the fluid. A particle in motion after a time dt will be in a new locality,

― 157 ―

x + dx, y + dy, z + dz, where the scalar quantity under consideration has the value s + ds = f(t + dt, x + dx, y + dy, z + dz). The property, s, of the individual particle has therefore been changed by the amount ds in the time dt; that is, the time rate of change is ds/dt. This time rate can also be expressed by the characteristics of the field, because, by means of Taylor's expansion, one has

or, since s = f(t,x,y,z),

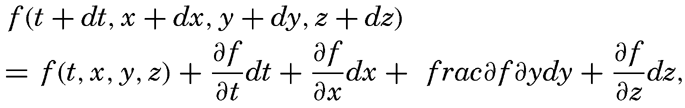
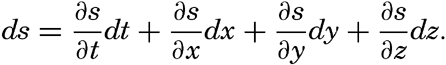
Dividing by dt and considering that dx/dt, dy/dt and dz/dt represent the components of the velocity, one obtains

The first term on the right-hand side represents the rate of change in a fixed locality—that is, the local change. The last three terms are together called the advection term, because they represent changes that take place in the presence of currents. This relationship is a purely formalistic one and gives no information as to the processes affecting the distribution; it merely states that within a field the individual time change can be considered as composed of two terms: the local time change and the advection.

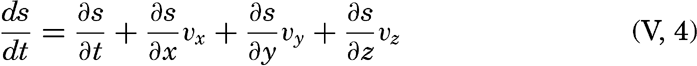
A few important points can be brought out by means of the above equation: (1) the distribution of any scalar quantity is stationary—that is, independent of time if the local change is zero (∂s/∂ t = 0); (2) the advection terms disappear if there is no motion or if the field is uniform—that is, if either v_x = v_y = v_z = 0 or ∂ s/∂ x = ∂ s/∂ y = ∂ s/∂ z = 0; (3) when the individual change is zero (ds/dt = 0), the local change is equal to the advection but is of opposite sign; (4) if the field of a property is stationary (∂ s/∂ t = 0) and if, further, the individual time change is zero (ds/dt = 0), equation (V, 4) is reduced to

This equation is fulfilled only if the flow is directed along the equiscalar surfaces of the property, as can be seen by comparison with equation (V, l), or by examination of the two-dimensional case.