Problem 2—
An Elliptical Orbit with the Center of Force at the Center of the Ellipse

As the second example of the application of the paradigm of Theorem 3 to direct problems, Newton determined the nature of the centripetal force required to maintain an elliptical orbit with the force center located at the center of the ellipse. Figure 5.6 is based on the diagram that Newton provided for this problem. As in the previous problem, the dynamic elements of Theorem 3 can be identified: the projected tangential path PR , the elliptical arc PQ , and the deviation QR , here constructed correctly as being parallel to the line of force PC . I break Newton's statement of the problem and its solution down into three steps as outlined earlier and provide a line-by-line commentary. I have not given a discussion of Problem 2 as detailed as that in the preceding problem or as detailed as that I shall give in the distinguished Kepler problem (Problem 3). Readers may

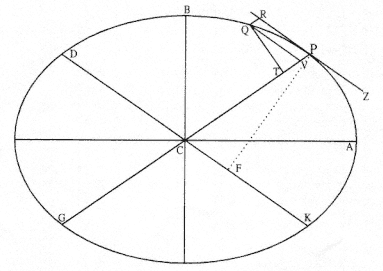
Figure 5.6
Based on Newton's diagram for Problem 2. A body  P  moves on an
elliptical orbit APQB  about a center of force C  located at the center of the
ellipse.

want simply to follow the flow of the solution to Problem 2 and reserve their energy for the solution to Problem 3.

Problem 2. A body orbits on a classical ellipse; there is required the law of centripetal force being directed to the center of the ellipse .

Step 1—
The Diagram

[Problem 2] Let CA and CB be the semi-axes of the ellipse; GP and DK conjugate diameters; PF and QT perpendiculars to these diameters; QV ordinate to the diameter GP; and QVPR a parallelogram .

[1-A] Let CA and CB be the semi-axes of the ellipse;

The semi-major axis CA and the semi-minor axis CB are constructed perpendicular to each other (see fig. 5.6). Note also that the conjugate diameters GP and DK (defined next) are not, in general, mutually perpendicular.

[1-B] GP and DK conjugate diameters;

The transverse diameter GP is constructed from the point P through the center C of the ellipse to the point G opposite point P (see fig. 5.6). The conjugate diameter DK is constructed parallel to the tangent PR , and it passes through the center C . The diameters GP and DK are said to be a

conjugal (united) pair. Many properties of the ellipse can be expressed in terms of these conjugate diameters.

[1-C] PF and QT perpendiculars to these diameters;

PF is normal to DK and will be used in the calculation of the circumscribed area to the ellipse given in Lemma 1. The line QT is constructed perpendicular to the diameter GP and will be used in the discriminate ratio QR / QT² (see fig. 5.7).

[1-D] QV ordinate to the diameter GP;

QV is constructed parallel to the tangent PR and hence is parallel to the conjugate diameter DK and furthermore is said to be ordinate to the transverse diameter GP (see fig. 5.7).

[1-E] and QVPR a parallelogram .

The deviation QR must be constructed parallel to the line of force PC , and is thus parallel to the conjugate diameter PV . The line segment QV is parallel to the tangent RP from [1-D]. Thus, QVPR is a parallelogram (see fig. 5.7).

Step 2—
The Analysis

In the analysis to follow, Newton expresses the discriminate ratio QR / QT² in terms of the given constant circumscribed area of the ellipse (BC × AC ) and the radius PC . Note that the particular radius PC from Problem 2 is equal to the general radius SP from Theorem 3. When the discriminate ratio was determined in terms of PC , then the linear dynamics ratio was also expressed in terms of PC . Thus, the proportional dependence of the force F on PC was known, and so the direct problem was solved (F µQR / (QT ² × PC² )).

[2-A] After these have been constructed, there will be [from the Conics] PV × VG to QV²as PC²to CD²andQV² / QT ² = PC² / PF² , and on combining these proportions PV × VG / QT² = PC² / (CD² × PF² )/PC² .

Find QT² : An expression for the line QT is obtained from the similarity of triangles QTV and PFC (i.e., QT / QV = PF / PC or QT² = QV² (PF² / PC ² )). Then, a relationship from Apollonius (i.e., PV × VG / QV² = PC² / CD² or QV² = (PV × VG ) (CD² / PC² )) is used to eliminate QV² from the expression for QT² (i.e., QT² = (PV × VG ) (PC² / CD² ) (PC² / PF ² )).

[2-B] Write QR in place of PV and BC × CA in place of CD × PF,

Find QR : The relationship PV = QR (from the parallelogram QRPV ) is used to introduce the deviation QR into the expression for QT ² and to obtain

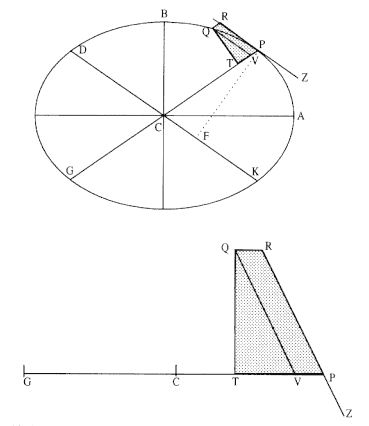
Figure 5.7
The bottom figure is abstracted from the full figure above. The line  QT
is constructed perpendicular to the conjugate diameter  GP , and the line
QV  is constructed parallel to the tangent  ZPR .

the following expression: QR / QT² = PC ⁴ / (VG ) (CD × PF )² , where (CD × PF ) is a constant equal to area (CA × CB ).

Step 3—
The Limit

[3-A] and in addition (with the points P and Q coalescing ) 2PC in place of VG, and, when the ends and middles are multiplied into each other, there will result QT² × PC² / QR = 2BC² × CA² / PC.

Find QR /(QT² × PC² ): Finally, when the point Q approached the point P , then the line VG approached the value 2PC , and the expression for the discriminate ratio becomes QR / QT² = PC ³ / 2(CA × CB )² .

[3-B] The centripetal force is therefore reciprocally as 2BC² × CA² / PC, that is (because 2BC² × CA²is given ), as 1/PC, that is, directly as the distance PC. Which was to be found .

Dividing both sides by PC ² gives the linear dynamics ratio QR / (QT² × PC² ) = PC / 2(CA × CB )² , which, because the area (CA × CB ) is a constant, gives the ratio as directly proportional to PC .

Conclusion

From Theorem 3, Fµ QR / (QT² × PC² ) µPC , or the centripetal force F required to maintain elliptical motion about a center of force located at the center C of the ellipse is directly proportional to the distance PC , which is the solution for Problem 2. Newton has thus demonstrated that the centripetal force required to maintain an elliptical orbit about a center of force located at the center of the ellipse is directly proportional to the first power of the distance PC . As noted earlier, such an orbit with such a center of force did not represent any particular physical situation. Newton intended this example purely as a demonstration of how the general paradigm in Theorem 3 was to be applied to yet another direct problem. The analysis for Problem 2 is more complicated than that for Problem 1, but it is relatively simpler than that for Problem 3. The particular example of Problem 2 is carried forward to the 1687 edition of the Principia in much the same form as given above for the tract On Motion .