The Focal Sphere

Independent of Byerly's work, studies of the mechanisms of earthquakes using first-motion data were pursued in Japan and Europe. In Japan, after the seminal work of Shida, a method was used that was based on the separa-

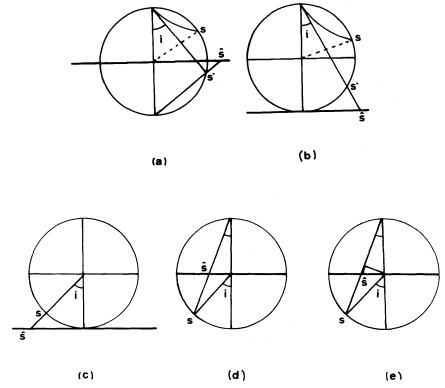
Figure 1
Projections of the Earth and the focal sphere: a) Extended positions and
Byerly's projection. b) Extended positions and central projection used by
Knopoff (1961a ). c) Central projection. d) Wulff-net stereographic
projection. e) Equal-area (Schmidt) stereographic projection.

tion of compressions and dilatations plotted on a geographical map and that took advantage of the dense network of seismographic stations. For simple source models, such as strike-slip faults, the pattern for near stations is four quadrants separated by straight lines, independent of the velocity distribution. Early Japanese work already used a variety of source models, in general, combinations of forces and couples with and without moments (Honda, 1962). The limitations of using the distribution of data on a geographical map, even for local earthquakes, was soon evident, and the method was not applicable to teleseismic distances. To obviate this problem, the concept of the focal sphere was developed, that is, a small sphere of homogeneous material and unit radius around the focus. Rays leaving the focus and arriving at a particular station intersect the surface of the sphere at points located by their azimuth and take-off angles i. Stations at any dis-

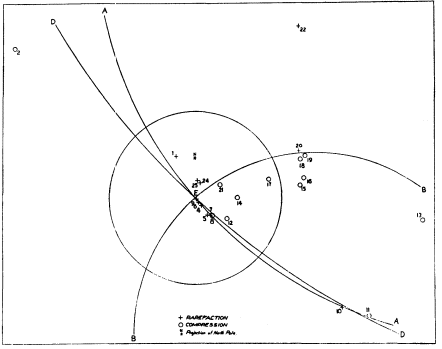
Figure 2
Fault-plane solution of the earthquake of July 6, 1934, off the
coast of northern California using Byerly's method (Byerly, 1938).

tance, D , can then be projected back, along the ray, to the surface of the focal sphere. The take-off angles for either local or teleseismic distances can be calculated if the distribution of velocity in the Earth is known.

Early work in Europe, such as that of Hiller in 1934, followed the same method as in Japan, using local stations. Koning (1942), in Holland, called attention to the use of the focal sphere; he was the first to use the Wulff stereographic projection, to project not the focal sphere but rather the surface of the Earth. This approach was fully developed by Ritsema (1952), who was the first to carry out the complete determination of the fault-plane solution using the Wulff-net projection of the focal sphere. The use of the Wulff net permits an easy separation of compressions and dilatations by two orthogonal planes (Ritsema, 1955). Ritsema (1958) calculated a useful set of (i , D ) curves for foci of different depth and applied this method to a number of earthquakes, mainly in southeast Asia and in Europe.

In Japan the focal sphere, called by Honda the "model sphere," was initially used to represent the results of the mechanism performed on geographical maps, in what was called the "mechanism diagram," by means of

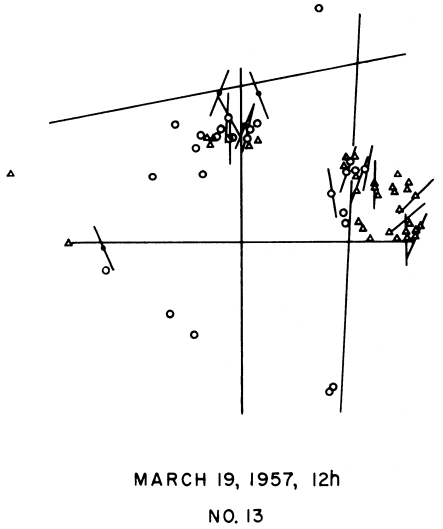
Figure 3
Fault-plane solution of the earthquake of March 11, 1957, in the
Aleutian islands based on the first motion polarities of P-waves
and S-wave polarization directions (Stauder and Udías, 1963).

an equal-area or Schmidt stereographic projection (fig.1e ). Honda's early work since 1931 followed this procedure. In 1958, Honda and Emura made the first use of this type of projection of the focal sphere to plot the data and separate compressions and dilatations by two orthogonal planes (Honda, 1962).

Focal-mechanism studies have been carried out in the Soviet Union since 1948. Russian seismologists used observations of first motions of P-, SV-, and SH-waves, plotting them on a Wulff-net projection of the focal sphere, which also represented the nodal lines for these waves (Keilis-Borok, 1956).

Another representation of the focal sphere on a plane is achieved by means of the central projection on which the nodal planes project as straight lines, but which inconveniently projects near stations at large distances from the center of the projection (fig. 1c ). This projection was used by Stauder to represent (fig. 3) P-wave first motions and S-wave polarization data (Stauder and Udías, 1963). The equivalence of the different representations and projections of the focal sphere was shown by Scheidegger (1957). The different projections of the focal sphere are shown in figure 1. Today, the equal-area projection is more generally used since it has a better definition near the center of the projection (fig. 4). For local earthquakes, ray-tracing techniques are applied with layered or variable velocity models of the Earth crust to project the observation points onto the focal sphere. In these cases values of the take-off angles depend strongly on the models used and the focal depth. For teleseismic distances the angles are derived from travel-time curves and depend on the assumed value of velocity at the focal depth.