Stravinsky and the Rite of Spring "d0e9213"

The Pitch-Class Set

Still, questions may linger about the completeness of the octatonic record in Part II, and in particular about the rapid collectional shifts and consequent "outside" pitch elements. Could the approach at this point benefit from, say, certain of Allen Forte's set-theoretic formulations? The answer here seems to be yes, but only up to a rather limited point. Readers familiar with Forte's analysis of Stravinsky's early works will have noted a number of correspondences. Forte frequently invokes the octatonic collection, the "superset" 8–28, and in connection with a passage from Zvezdoliki [The King of the Stars ] (1911–12) cites it as "one of Stravinsky's hallmarks."^[8] In Forte's The Harmonic Organization of "The Rite of Spring," the (0 2 3 5) tetrachord, pitch-class set 4–10, is encountered throughout, while its (0 2 5/0 3 5) incomplete form, 3–7, is identified as "a kind of motto trichord."^[9] In fact, most of the prominent sets in Forte's analysis are subsets of the octatonic collection. Of his two hundred and twenty pitch-class sets (sets of from three to nine elements, reduced to a "best normal order" by means of transposition or inversion followed by transposition), thirty-four are octatonic: seven from a possible twelve three-element sets, thirteen from the twenty-nine four-element sets, seven from thirty-eight five-element sets, six from fifty hexachords, and one from the thirty-eight seven-element sets, 7–31. These are easily spotted since the pitch numbering of these thirty-four "prime forms" will correspond to that either of the 1–2 half step-whole step ordering, (0 1 3 4 6 7 9 10 (0)), or the reverse 2-1 whole step-half step ordering, (0 2 3 5 6 8 9 11 (0)).

Beyond this point the two paths diverge as different objectives are brought into play. In particular, the segmentation, what Forte interprets as cohesive units in The

[8] Allen Forte, The Structure of Atonal Music (New Haven: Yale University Press, 1973), p. 118.

[9] Forte, The Harmonic Organization , p. 36.

― 208 ―

Rite , differs markedly from that proposed here. Reference is occasionally made to the dominant seventh, 4–27, but the triad, 3–11, is ignored altogether since, as Forte notes, trichords "are easily identifiable components of larger sets."^[10] In the view expressed here, however, the triad—not just the three-element trichord, but the triad —assumes, even under conditions of superimposition, a registral, instrumental, and notational reality—and to an extent that, on a strictly observational basis, many sections of The Rite seem more overtly triadic than many pieces of the later nineteenth-century tonal tradition (pieces on behalf of which the triad is nonetheless routinely invoked as a fundamental unit of musical structure).

Moreover, an emphasis is here placed on disposition, on the fixed, registral identities of recurring tetrachords, 0–5/6, 11 vertical spans, triads, and dominant sevenths. These matters are often obscured when, for purposes of comparison, of gauging the relatedness of sets and complexes of sets, such groupings are regularly reduced to their "prime forms" (by means, as indicated, of transposition or inversion followed by transposition.) Thus, a prime determinancy in Part II's Introduction at nos. 79–84 is not the triad tout court , 3–11, nor the tight disposition of the triad, but its persistent (0 3 7) minor articulation. But since the major and minor triads are inversionally equivalent and reduce to the single pitch-class set 3–11, the distinction is likely to be obscured. A similar case can be made for the dominant-seventh chord, whose special content and disposition are of such marked consequence to an octatonic reading of Part I and of the "Sacrificial Dance" in Part II. This determinacy is also obscured when it is subsumed under the broader implications of the set 4–27 and its (0, 2, 5, 8) "prime-form" numbering. (The strict inversion of this form yields The Rite 's familiar disposition; the "prime form" itself is not a dominant-seventh chord.)

Similarly, the two interval orderings of the octatonic collection, along with the three transpositions of distinguishable content, reduce to the single set 8–28. But the question of an octatonic presence in The Rite has not to do merely with the octatonic collection (that is to say, 8–28 tout court ) but equally with an octatonic collection. Contexts derive their octatonic character, their symmetrical cohesion, by virtue of their confinement to a single transpositional level for periods of significant duration. And this, too, points to a hearing and understanding of determinacy having as much to do with pitch and pitch-class identity as with interval-class identity.

This is not to suggest that these issues are ignored by Forte. Frequent reference is made to invariance in pitch-class content between transpositions or transformations of a given set, and then to the Rp relation, which has to do with pitch-class invariance among non-equivalent sets having the same number of elements. But here, too, Forte's conclusions are apt to vary from those reached from a predominantly octatonic or octatonic-diatonic perspective. Thus, Example 84 shows twelve single and "composite" sets invoked by Forte to identify the verticals and

[10] Ibid.

― 209 ―

Example 84

linear successions of Block C at no. 144 in the "Sacrificial Dance" and its subsequent near-repeat at no. 148.^[11] (Although in ascending "normal order," the pitch numbering of these sets has not been reduced to that of the "prime forms." Note that 0=C.)^[12] Only sets 5–10 and 6-Z23 are octatonic; the others are not subsets of the octatonic collection 8–28. But the fact that all ten non-octatonic sets miss the

[11] Forte, The Structure of Atonal Music , pp. 147–48. Forte uses the 1943 revision of the "Sacrificial Dance" for his analysis. The orchestration and barring of this passage are changed, but the chords themselves remain unaltered.

[12] With O = C (and with the sets not reduced to their "prime forms"), a (0 2 3 5 6 8 9 11) numbering will always—as is shown in Example 84—imply Collection II. A (0 1 3 4 6 7 9 10) numbering under these conditions will imply Collection III, while the numbering for Collection I (which lacks the C) will conform to neither of the two octatonic pitch-numberings.

― 210 ―

octatonic order by a single step (at pitch number 10 here), or, more importantly, that all sets, excluding the B

, refer to a single transpositional level, the octatonic Collection II, is of the highest importance for an octatonic hearing and understanding.^[13] The articulative makeup of the block is thus conditioned referentially by its confinement to Collection II, a confinement that in turn refers back to the initial, punctuating (D C A F

) dominant seventh of Block A. More specifically, too, the sets 6-Z19 and 6-Z45, which follow one another in Block C (see Example 79), are "maximally dissimilar" in interval content (the Ro relation: the interval vectors of the two sets have no common entries) and are said to be "completely detached."^[14] Yet from an octatonic standpoint the sets are close, the distinction having to do with Collection II's succession of triads in the lower parts: Collection II's (D F

A) triad is part of 6-Z19, while (A

C E

) is part of 6-Z45. Furthermore, in comparing versions of equivalent or Z-related sets, the invariants among the three occurrences of the complementary pair 6-Z23 and 6-Z45 are said to be "of little consequence," although all three refer, crucially, to Collection II.^[15] Invariance among the four occurrences of 6-Z43 is likewise deemed "not significant," although this non-invariance has crucially to do with the collectional shifts respecting Collections II and I, as was indicated in Example 83.^[16] In conclusion, Forte points to "the dearth of strongly represented Rp" in this music and to "the paucity of invariance among equivalent sets," noting that interval content, not pitch-class content, is of "prime importance."^[17]

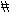
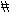
Incompatibility is not really the issue here. The notion of the pitch-class set and its attendant formulations ("similarity," "complementation," and so forth) can in no way be construed as "incompatible" with a more determined octatonic or octatonic-diatonic reading. At issue, rather, is the referential character of the octatonic and diatonic sets, the extent of their hegemony in The Rite and hence, ultimately, the degree of abstraction deemed necessary or desirable in formulating rules of equivalence and association that can account for the coherence or consistency of the harmonic and melodic materials.

Inevitably, a theorist's choices in this regard are to some extent guided by his preoccupations with other literatures and traditions. But this does not mean that the set-theoretic approach is awkwardly "neutral" or without an historical foundation. The Rite is unquestionably non-tonal, and frequently exhibits, as Forte has

[14] Forte, The Structure of Atonal Music , p. 154.

[15] Ibid., p. 159.

[16] Ibid.

[17] Ibid., p. 166.

― 211 ―

claimed, the kinds of harmonic structures prevalent in the "atonal" music of Schoenberg, Berg, and Webern.^[18] Nonetheless, as an attempt to cope with a large number of seemingly intractable works, pitch-class set analysis represents a retreat to more lenient and broadly defined terms of relatedness and association. The question, then, is whether, for its proper definition, the logic of The Rite requires the greater generality afforded by this retreat or whether, by means of an octatonic-diatonic determination, the piece remains susceptible to the more determinate rulings of a more familiar mode of reckoning, one characterized by scales, scalar orderings and numberings, triads, pitch-class priorities, and the like. The present discourse has of course opted for the second of these alternatives. Yet the underlying assumptions of set theory have by no means been ignored. While frequently in disagreement with the meaning and significance of many of Forte's set-theoretic conclusions, the present perspective may nonetheless be placed in sharper focus by a careful consideration of those results.