PART I—
INFERENCE AND METHOD
One—
Thoroughly Modern Meno
Clark Glymour and Kevin Kelly
1—
Introduction
The Meno presents, and then rejects, an argument against the possibility of knowledge. The argument is given by Meno in response to Socrates' proposal to search for what it is that is virtue:
Meno: How will you look for it, Socrates, when you do not know at all what it is? How will you aim to search for something you do not know at all? If you should meet with it, how will you know that this is the thing that you did not know?[1]
Many commentators, including Aristotle in the Posterior Analytics , take Meno's point to concern the recognition of an object , and if that is the point there is a direct response: one can recognize an object without knowing all about it. But the passage can also be understood straightforwardly as a request for a discernible mark of truth, and as a cryptic argument that without such a mark it is impossible to acquire knowledge from the instances that experience provides. We will try to show that the second reading is of particular interest.
If there is no mark of truth, nothing that can be generally discerned that true and only true propositions bear, Meno's remarks represent a cryptic argument that knowledge is impossible. We will give an interpretation that makes the argument valid; under that interpretation, Meno's argument demonstrates the impossibility of a certain kind of knowledge. In what follows we will consider Meno's argument in more detail, and we will try to show that similar arguments are available for many other conceptions of knowledge. The modern Meno arguments reveal a diverse and intricate structure in the theories of knowledge and of inquiry, a structure whose exploration has just begun. While we will attempt to show that our reading of the argument fits reasonably well
with Plato's text, we do not aim to argue about Plato's intent. It is enough that the traditional text can be elaborated into a systematic and challenging subject of contemporary interest.[2]
2—
The Meno
In one passage in the Meno , to acquire knowledge is to acquire a truth that can be given a special logical form . To acquire knowledge of virtue is to come to know an appropriate truth that states a condition, or conjunction of conditions, necessary and sufficient for any instance of virtue. Plato's Socrates will not accept lists, or disjunctive characterizations.
Socrates: I seem to be in great luck, Meno; while I am looking for one virtue, I have found you to have a whole swarm of them. But, Meno, to follow up the image of swarms, if I were asking you what is the nature of bees, and you said that they are many and of all kinds, what would you answer if I asked you: "Do you mean that they are many and varied and different from one another in so far as they are bees? Or are they no different in that regard, but in some other respect, in their beauty, for example, or their size or in some other such way?" Tell me, what would you answer if thus questioned?
Meno: I would say that they do not differ from one another in being bees.
Socrates: Suppose I went on to say: "Tell me, what is this very thing, Meno, in which they are all the same and do not differ from one another?" Would you be able to tell me?
Meno: I would.
Socrates: The same is true in the case of the virtues. Even if they are many and various, all of them have one and the same form which makes them virtues, and it is right to look to this when one is asked to make clear what virtue is. Or do you not understand what I mean?
There is something peculiarly modern about the Meno . The same rejection of disjunctive characterizations can be found in several contemporary accounts of explanation.[3] We might say that Socrates requires that Meno produce an appropriate and true universal biconditional sentence, in which a predicate signifying 'is virtuous' flanks one side of the biconditional, and a conjunction of appropriate predicates occurs on the other side of the biconditional. Let us so say. Nothing is lost by the anachronism and, as we shall see, much is gained.
Statements of evidence also have a logical form in the Meno . Whether the topic is bees, or virtue, or geometry, the evidence Socrates considers consists of instances and non-instances of virtue, of geometric properties, or whatever the topic may be. Evidence is stated in the singular.
The task of acquiring knowledge thus assumes the following form. One is presented with, or finds, in whatever way, a series of examples and non-examples of the feature about which one is inquiring, and from these examples a true, universal biconditional without disjunctions is to be produced. In the
Meno that is not enough for knowledge to have been acquired. To acquire knowledge it is insufficient to produce a truth of the required form; one must also know that one has produced a truth. What can this requirement mean?
Socrates and Meno agree in distinguishing knowledge from mere true opinion, and they agree that knowledge requires at least true opinion. Meno thinks the difference between knowledge and true opinion lies in the greater reliability of knowledge, but Socrates insists that true opinion could, by accident as it were, be as reliable as knowledge:
Meno: . . . But the man who has knowledge will always succeed, whereas he who has true opinion will only succeed at times.
Socrates: How do you mean? Will he who has the right opinion not always succeed, as long as his opinion is right?
Meno: That appears to be so of necessity, and it makes me wonder, Socrates, this being the case, why knowledge is prized far more highly than right opinion, and why they are different.
Socrates answers each question, after a fashion. The difference between knowledge and true opinion is in the special tie , the binding connection, between what the proposition is about and the fact of its belief. And opinions that are tied in this special way are not only reliable, they are liable to stay, and it is that which makes them especially prized:
Socrates: To acquire an untied work of Daedalus is not worth much, like acquiring a runaway slave, for it does not remain, but it is worth much if tied down, for his works are very beautiful. What am I thinking of when I say this? True opinions. For true opinions, as long as they remain, are a fine thing and all they do is good, but they are not willing to remain long, and they escape from a man's mind, so that they are not worth much until one ties them down by an account of the reason why. And that, Meno my friend, is recollection, as we previously agree. After they are tied down, in the first place they become knowledge, and then they remain in place. That is why knowledge is prized higher than correct opinion, and knowledge differs from correct opinion in being tied down.
Plato is chiefly concerned with the difference between knowledge and true opinion, and our contemporaries have followed this interest. The recent focus of epistemology has been the special intentional and causal structure required for knowing. But Meno's argument does not depend on the details of this analysis; it depends, instead, on the capacity for true opinion that the capacity to acquire knowledge implies. That is the capacity to find the truth of a question, to recognize it when found, to stick with it after it is found, and to do so whatever the truth may be.
Suppose that Socrates could meet Meno's rhetorical challenge and recognize the truth when he met it: what is it he would then be able to do? Something like the following. In each of many different imaginable (we do not say possible save in a logical sense) circumstances, in which distinct claims about
virtue (or whatever) are true, upon receiving enough evidence, and considering enough hypotheses, Socrates would hit upon the right hypothesis about virtue for that possible circumstance, and would then (and only then) announce that the correct hypothesis is indeed correct. Never mind just how Socrates would be able to do this, but agree that, if he is in the actual circumstance capable of coming to know, then that capacity implies the capacity just stated. Knowledge requires the ability to come to believe the truth, to recognize when one believes the truth (and so to be able to continue to believe the truth), and to do so whatever the true state of affairs may be.
So understood, Meno's argument is valid, or at least its premises can be plausibly extended to form a valid argument for the impossibility of knowledge. The language of possible worlds is convenient for stating the argument. Fix some list of predicates V, P1, . . . , Pn, and consider all possible worlds (with countable domains) that assign extensions to the predicates. In some of these worlds there will be true universal biconditional sentences with V on one side and conjunctions of some of the Pi or their negations on the other side. Take pieces of evidence available from any one of these structures to be increasing conjunctions atomic or negated atomic formulas simultaneously satisfiable in the structure. Let Socrates receive an unbounded sequence of singular sentences in this vocabulary, so that the sequence, if continued, will eventually include every atomic or negated atomic formula (in the vocabulary) that is satisfiable in the structure. Let w range over worlds. With Meno, as we have read him, say that Socrates can come to know a sentence, S, of the appropriate form, true in world w , only if
(i) for every possible sequence of presentation of evidence from world w Socrates eventually announces that S is true, and
(ii) in every world, and for every sequence from that world, if there is a sentence of the appropriate form true in that world, then Socrates can eventually consider some true sentence of the appropriate form in that world, can announce that it is true in that world (while never making such an announcement of a sentence that is not true in that world), and
(iii) in every world, and for every sequence from that world, if no sentence of the appropriate form is true in the world, then Socrates refrains from announcing of any sentence of that form that it is true.
Meno's argument is now a piece of mathematics, and it is straightforward to prove that he is correct: no matter what powers we imagine Socrates to have, he cannot acquire knowledge, provided "knowledge" is understood to entail these requirements. No hypotheses about the causal conditions for knowledge defeat the argument unless they defeat the premises. Skepticism need not rest on empirical reflections about the weaknesses of the human mind. The impossibility of knowledge can be demonstrated a priori. Whatever sequence of evi-
dence Socrates may receive that agrees with a hypothesis of the required form, there is some structure in which that evidence is true but the hypothesis is false; so that if at any point Socrates announces his conclusion, there is some imaginable circumstance in which he will be wrong.
We should note, however, that in those circumstances in which there is no truth of the required form, Socrates can eventually come to know that there is no such truth, provided he has an initial, finite list of all of the predicates that may occur in a definition. He can announce with perfect reliability the absence of any purely universal conjunctive characterizations of virtue if he has received a counterexample to every hypothesis—and if the number of predicates are finite, the number of hypotheses will be finite, and if no hypothesis of the required form is true, the counterexamples will eventually occur. If the relevant list of predicates or properties were not provided to Socrates initially, then he could not know that there is no knowledge of a subject to be had.
3—
Weakening Knowledge
Skepticism has an ellipsis. The content of the doubt that knowledge is possible depends on the requisites for knowledge, and that is a matter over which philosophers dispute. Rather than supposing there is one true account of knowledge to be given, if only philosophers could find it, our disposition is to inquire about the possibilities. Our notion of knowing is surely vague in ways, and there is room for more than one interesting doxastic state.
About the conception of knowledge we have extracted from Meno there is no doubt as to the rightness of skepticism. No one can have that sort of knowledge. Perhaps there are other sorts that can be had. We could restrict the set of possibilities that must be considered, eliminating most of the possible worlds, and make requirements (i), (ii), and (iii) apply only to the reduced set of possibilities. We would then have a revised conception of knowledge that requires only a reduced scope , as we shall call the range of structures over which Socrates, or you or we, must succeed in order to be counted as a knower. This is a recourse to which we will have eventually to come, but let us put it aside for now, and consider instead what might otherwise be done about weakening conditions (i), (ii), and (iii).
Plato's Socrates emphasizes this difference between knowledge and mere true opinion: knowledge stays with the knower, but mere opinion, even true opinion, may flee and be replaced by falsehood or want of opinion. The evident thing to consider is the requirement that for Socrates to come to know the truth in a certain world, Socrates be able to find the truth in each possible world, and never abandon it, but not be obliged to announce that the truth has been found when it is found. Whatever the relations of cause and intention that knowledge requires, surely Meno requires too much. He requires, as we have reconstructed his argument, that we come to believe through a reliable proce-
dure, a procedure or capacity that would, were the world different, lead to appropriately different conclusions in that circumstance. But Meno also requires that we know when the procedure has succeeded, and that seems much like demanding that we know that we know when we know. Knowing that we know is an attractive proposition, but it does not seem a prerequisite for knowledge, or if it is, then by the previous argument, knowledge is impossible. In either case, the properties of a weaker conception of knowledge deserve our study.
The idea is that Socrates comes eventually to embrace the truth and to stick with it in every case, although he does not know at what point he has succeeded: he is never sure that he will not, in the future, have to change his hypothesis. In this conception of knowledge, there is no mark of success. We must then think of Socrates as conjecturing the truth forever. Since Socrates did not live forever, nor shall we, it is better to think of Socrates as having a procedure that could be applied indefinitely, even without the living Socrates. The procedure has mathematical properties that Socrates does not.
For Socrates to know that S in world w in which S is true now implies that Socrates' behavior accords with a procedure with the following properties:
(i*) for every possible sequence of evidence from world w , after a finite segment is presented, the procedure conjectures S ever after, and
(ii*) for every possible sequence of evidence from any possible world, if a sentence of the appropriate form is true in that world, then after a finite segment of the evidence is presented the procedure conjectures a true sentence of the appropriate form ever after.
These conditions certainly are not sufficient for any doxastic state very close to our ordinary notion of knowledge, since Socrates' behavior may in the actual world accord with a procedure satisfying (i*) and (ii*) even while Socrates lacks the disposition to act in accord with the procedure in other circumstances. For knowledge, Socrates must have such a disposition. But he can only have such a disposition if there exists a procedure meeting conditions (i*) and (ii*). Is there? If the logical form of what is to be known is restricted to universal biconditionals of the sort Plato required, then there is indeed such a procedure. If Socrates is unable to acquire this sort of knowledge, then it is because of psychology or sociology or biology, not in virtue of mathematical impossibilities. Skepticism about this sort of knowledge cannot be a priori. There is no general argument of Meno's kind against the possibility of acquiring this sort of knowledge.
The weakening of knowledge may be un-Platonic, but it is not unphilosophical. Francis Bacon's Novum Organum describes a procedure that works for this case, and his conception of knowledge seems roughly to accord with it. John Stuart Mill's canons of method are, of course, simply pirated from Ba-
con's method. Hans Reichenbach used nearly the same conception of knowledge in his "pragmatic vindication" of induction, although he assumed a very different logical form for hypotheses, namely that they are conjectures about limits of relative frequencies of properties in infinite sequences.
So we have a conception of knowledge that, at least for some kinds of hypotheses, is not subject to Meno's paradox. But for which kinds of hypotheses is this so? We are not now captivated, if ever we were, by the notion that all knowledge is definitional in form. Perhaps even Plato himself was not, for the slave boy learns the theorem of Pythagoras, which has a more complicated logical form. We are interested in other forms of hypotheses: positive tests for diseases, and tests for their absence; collections of tests one of which will reveal a condition if it is present. Nor are our interests confined to single hypotheses considered individually. If the property of being a squamous cancer cell has some connections with other properties amenable to observation, we want to know all about those connections. We want to discover the whole theory about the subject matter, or as much as we can of it. What we may wish to determine, then, is what classes of theories can come to be known according to our weaker conception of knowledge. Here, as we use the notion of theory, it means the set of all true claims in some fragment of language. Wanting to know the truth about a particular question is then a special case, since the question can be formulated as a claim and its denial, and the pair form a fragment of language whose true claims are to be decided. What we wish to determine is whether all of what is true and can be stated in some fragment of language can be known.
Either the possibility of knowledge depends on the fragment of language considered or it does not. If it does, then many distinct fragments of language might be of the sort that permit knowledge of what can be said in them, and the classification of fragments that do, and that do not, permit such knowledge becomes an interesting task. For which fragments of language, if any, are there valid arguments of Meno's sort against the possibility of knowledge, and for which fragments are there not? These are straightforward mathematical questions, and their answers, or some of their answers, are as follows:
Consider any first-order language (without identity) in which all predicates are monadic, and there are no symbols taken to represent functions. Then any true theory in such a language can be learned, or at least there are no valid Menoan arguments against such knowledge.
If the language is monadic but with identity, or if the language contains a predicate that is not monadic, then neither the fragment that consists only of universally quantified formulas, nor the fragment that consists only of existentially quantified formulas, nor any part of the language containing either of these fragments, is such that every true theory in these fragments can be known.
In each of the latter cases an argument of Meno's kind can be constructed to show that knowledge is impossible.
4—
Times for All Things
The weakened conception of knowledge is still very strong in at least one respect. It requires for the possibility of knowledge of an infinite wealth of claims that there be a time at which all of them are known—that is, a single time after which all and only the truths in a fragment of language are conjectured. We might instead usefully consider the following circumstance: When investigating hypotheses in a fragment of language, Socrates is able, for each truth, eventually to conjecture it and never subsequently to give it up; and Socrates is also able, for each falsehood, eventually not to conjecture it and never after to put it forward. Plato's Socrates illustrates that the slave boy can "recollect" the Pythagorean theorem from examples and appropriate questions, and presumably in Plato's view the slave boy could be made to recollect any other truth of geometry by a similar process. But neither the illustration nor the view requires that the slave boy, or anyone else, eventually be able to recollect the whole of geometry. There may be no time at which Socrates knows all of what is true and can be stated in a given fragment of language. Yet the disposition to follow a procedure that will eventually find every truth and eventually avoid every falsehood is surely of fundamental interest to the theory of knowledge. Call a procedure that has the capacity to converge to the whole truth at some moment, as in the discussion of the previous section, an EA learning procedure, and call an AE learner a procedure that for each truth has the capacity to converge to that truth by some moment, and for each falsehood avoids it ever after some moment. Every EA learner is an AE learner, but is the converse true? Or more to the point, are there fragments of language for which there are AE procedures but no EA procedures?
There are indeed. Consider the set of all universal sentences, with identity, and with any number of predicates of any arity and any number of function symbols of any arity. By the negative result stated previously, there is no EA procedure for that fragment of language, no procedure that, for every (countable) structure, and every way of presenting the singular facts in the structure, will eventually conjecture the theory (in the language fragment) true in that structure. But there is an AE procedure for this fragment. If, for knowledge about a matter, Socrates is required only to have a disposition to follow an AE procedure for the language of the topic, then no Menoan argument shows that Socrates cannot acquire knowledge, even if Socrates does not know the relevant predicates or properties beforehand.
The improvement does not last. If we consider the fragment of language that allows up to one alternation of quantifiers, whether from universal to existential or from existential to universal, it again becomes impossible to acquire knowledge; there are no AE procedures for this fragment that are immune from arguments of Meno's kind.
5—
Discovery and Scope
Whether we consider EA discovery or AE discovery, we soon find that arguments of Meno's kind succeed. The same sort of results obtain if we further weaken the requirements for knowledge. We might, for example, abandon Plato's suggestion that when a truth is known it is not subsequently forgotten or rejected. We might then consider the requirement that Socrates be disposed to behave in accordance with a procedure that, as it considers more and more evidence about a question, is wrong in its conjectures only finitely often, is correct infinitely often, but may also suspend judgment infinitely often. Osherson and Weinstein have shown that even with this remarkably weak conception there are questions that cannot, in senses parallel to those above, be known. Or we might allow various sorts of approximate truth; for many of them, arguments parallel to Meno's are available.
The conceptions of knowledge we have discussed place great emphasis on reliability . They demand that we not come to our true beliefs by chance but in accordance with procedures that would find the truth no matter what it might be, so long as the procedures could be carried out. What the Meno arguments show is that in the various senses considered, for most of the issues that might invite discovery, procedures so reliable do not exist. The antiskeptical response ought to be principled retreat. In the face of valid arguments against the possibility of procedures so reliable, and hence against the possibility of corresponding sorts of knowledge, let us consider procedures that are not so reliable, and regard the doxastic state that is obtained by acting in accord with them as at least something better and more interesting than accidental true belief.
For each of the requirements on knowledge considered previously, and for others, we can ask the following kind of question: For each fragment of language, what are the classes of possible worlds for each of which there exists a procedure that will discover the truths of that fragment for any world in the class? The question may be too hard to parse. Let us define it in pieces. Let a discovery problem be any (recursive) fragment F of a formal language, together with a class K of countable relational structures for that fragment. One such class K is the class of all countable structures for the language fragment, but any subsets of this class may also be considered. A discovery procedure for the discovery problem is any procedure that, for every k in K and every presentation of evidence from k, "converges" to all of the sentences in F that are true in k. "Convergence" may be in the EA sense, the AE sense, or some other sense altogether (such as the weak convergence criterion considered two paragraphs previously).
What the results we have described tell us is that for many fragments F, if K is the set of all countable structures for F, then there are no discovery procedures for pairs <F, K>. That does not imply that there are no discovery proce-
dures for pairs <F, K'> where K' is some proper subset of K. Must it be that for knowledge, true belief has been acquired in accordance with a procedure that would lead to the truth in every imaginable sequence?
Suppose we think of inquiry as posing discovery problems, a question or questions, and a class of possible worlds or circumstances that determine various answers to the question. Depending on which world or circumstance is ours, different answers will be true. Successful inquiry, which leads to some kind of knowledge, accords with a procedure that will converge to the truth of the matter, whatever it may be, in each of these possible circumstances. It is possible for procedures to have the capacity to find the truth in each of a class of circumstances without having the capacity to find the truth in every imaginable circumstance.
When attention is restricted to a discovery problem that contains a restricted class of possible worlds of circumstances, that restriction constitutes a kind of background knowledge brought to inquiry. The background knowledge says that the actual circumstance is one of a restricted class of circumstances or possible worlds. The theory of recollection, Plato's solution to Meno's paradox, claims that inquiry is conducted with a special sort of background knowledge, stamped in the soul before birth. Two different reconstructions of Plato's solution fit the story, and we offer them both without choosing between them.
In the first account, the correct definitions are stored in the soul and need only be brought to mind. The presentation of examples and the process of recollection eventually brings forth the truth, and provides knowledge, not because the process using that same background knowledge would succeed no matter how the world (or rather the forms) might imaginably be, but because there is a guarantee that the world (or, rather again, the forms) accords with knowledge the soul possesses. The background knowledge is so complete that no inference from examples is required; examples only ease access to knowledge we already have.
In the second account a complete list of definientia , each characterizing a distinct form, is stored in the soul. An inquiry into the nature of virtue must then match instances of the usage of "virtue" with the appropriate definiens in the list. In this case the process of recollections involves an inductive inference from particular examples to a universal biconditional connecting a definiens in the list with a term denoting the subject of inquiry. On the assumptions that no two forms are such that the same individuals participate in both, and that there are only finitely many forms, Socrates can eventually conjecture the form of virtue, know that his conjecture is correct, and can do so no matter which definiens in the list happens to represent the form of virtue.
On either reconstruction, Plato's reply to Meno's paradox has two aspects, and the slave boy's rediscovery of the theorem of Pythagoras illustrates each of them. First, knowledge may be had by means other than the means of inquiry. It may be inherited, innate, stamped on the soul, and not acquired by general-
ization from examples given in this life. Second, given such prior knowledge the task of discovery or the acquisition of knowledge is reconceived and becomes feasible, for the inquirer need not be able to fix upon the truth in every imaginable circumstance, but only in those circumstances consistent with prior knowledge.[4]
Plato has little to say in the Meno about what souls do that gives them the knowledge we recollect in successful inquiry. We (or our souls) have background knowledge through a causal process that is not itself inquiry. We could instead entertain the thought that we acquire background knowledge through inquiry conducted in our past lives. The second alternative raises a number of interesting questions.
When we inquire into a question, the discovery problem we address depends upon our knowledge. The class of alternative circumstances, and thus alternative answers, that need be considered is bounded by our prior knowledge. If we know nothing, it is the class of all imaginable circumstances; if we know a great deal, the class of alternative circumstances may be quite small. Suppose as we go through life (or through a sequence of lives) we form conjectures about the answers to various questions, and while we reserve the right to change these conjectures upon further evidence, in the meanwhile we use them as though they were background knowledge for still other questions. Should evidence later arrive that causes us to abandon our conjectures, we will also have to reconceive the discovery problems in which we had taken those conjectures as background knowledge.[5]
Since we are not only uncertain what discovery problems we shall face, but more profoundly, we may be wrong in our construal of the discovery problems we presently face, it would seem only prudent to rely on learning procedures that have the widest possible scope. We know from what has gone before that Meno's argument, and derivatives of it, show that there is no procedure adequate for all discovery problems, but some procedures may do better than others. We can characterize a dominance relation between discovery procedures: Procedure A dominates procedure B provided A solves (in whatever sense may be specified) every discovery problem B solves, but not vice versa. A procedure is then maximal if no procedure dominates it. We might then take prudence to require that our manner of inquiry accord with a maximal procedure. Some second thoughts are called for. In the well-studied case in which what is to be learned is not a theory but a language, it is known that every maximal procedure solves the discovery problem that consists of learning any finite language on a fixed vocabulary, but no procedure solves any larger problem, posed by any larger class of languages on that same vocabulary. There is no maximal procedure that identifies even one infinite language. For problems that concern the learning of theories, one should expect something analogous: the maximal procedures will be very sparse and will fail to solve discovery problems that are readily solved by other methods.
Since, in all likelihood, we cannot fix beforehand on maximal methods, prudence can only recommend something more modest. When we recognize that one discovery procedure dominates another then, ceteris paribus , it is prudent to use the dominant procedure rather than the dominated procedure. Whether that is a sensible or feasible recommendation depends on the dominance structure of discovery procedures. If, for example, there is a readily described infinite chain of procedures, later members of the sequence dominating all earlier members, then the recommendation would give us a task worthy of Sisyphus. We would ever be changing one procedure for another, without rest and without end. Sometimes, much as the existentialists say, the best thing to do is to stop preparing to make inquiries and make them.
6—
Hypermodern Meno
Methodology amounts to recommendations restricting procedures of inquiry. Any such restriction can be thought of as determining a class of procedures, those that satisfy it. Besides methodology, psychology is another source of restrictions on procedures, and computation theory still another. For example, we might nowadays suppose that the discovery procedures available to us, even with the aid of machines, must be computable procedures, and invoking Church's thesis, restrict our attention to the class of Turing computable procedures for inquiry.
For any restriction on discovery procedures, the preceding discussion should suggest the following sort of question: What arguments of Meno's sort can be made against all procedures of this class? More exactly, for any restriction on discovery procedures, does the restriction also limit the class of discovery problems that can be solved? For both the EA and AE conceptions of successful inquiry, the requirement that procedures be computable limits the class of discovery problems that can be solved. There are discovery problems that can be solved by EA procedures but not by any computable EA procedures, and there are discovery problems that can be solved by AE procedures but not by any computable AE procedures. Methodological principles that are often regarded as benign also limit discovery when they are imposed in combination with the requirement of computability. A consistency principle applies to procedures that always conjecture theories consistent with the evidence; a conservative principle applies to procedures that never change a current conjecture until new evidence contradicts it. Either of these requirements, in combination with the requirement of computability, restricts the class of discovery problems that can be solved. It is easy to see that reverse is not true. That is, for every conservative, consistent, computable procedure, there is an inconsistent or unconservative (or both) procedure whose scope includes all discovery problems that can be solved by the first procedure.
When we investigate the restrictions on reliability that are implicit in meth-
odological restrictions, we are entertaining recommendations to hop from one procedure to another. The picture of inquiry sketched in the previous section suggests the same thing for different reasons: as we reconceive the discovery problems with which we are faced, we may change our minds about which methods are appropriate. In that spirit, some philosophers have recommended methodological principles on empirical grounds: procedures that accord with the principles have worked in the past.[6]
The effect of hopping from one procedure to another can only be itself some procedure for discovery that mimics other procedures when given various pieces of evidence. From the inside, a hopping procedure may feel different from a procedure that does not hop, but behaviorally, the disposition to hop from procedure to procedure as evidence accumulates simply is a procedure, located somewhere in the vast ordering of possible discovery procedures. Recommendations about when and how to change procedures as evidence accumulates thus amount to restrictions on acceptable procedures, and form part (thus far an uninvestigated part) of methodology as we have just construed that subject. Despite these caveats, if we are familiar with only a small set of methods, as seems to be the case, hopping among them can constitute a better procedure.
Recommendations about preferences among procedures may also come from the study of the scope of procedures, but that study cannot be algorithmic. There is no computable function that will tell us, for all ordered pairs of indices of discovery procedures, whether the first member of the pair dominates the second. We are instead landed somewhere within the analytical hierarchy of recursion theory, and just where it is that we have landed is an open question.
The general notion of hopping among procedures suggests an apparent paradox: Can an effective procedure that hops among procedures hop from itself to some other procedure? Can it hop back to itself? In a sense it can. If we think of a hopping procedure as a program that simulates other programs, then (by the recursion theorem) it can at various stages pursue a simulation of itself, or cease to simulate itself, and thus accept or reject itself as a method. Of course, no procedure can behave differently than it does.
7—
Real Learning
Some people may think that results and questions such as those we have derived from the Meno paradox are remote from real concerns about the acquisition of knowledge. One might complain that these are all formal results, and because of that, for some reason mysterious to us, of no bearing on real science and its philosophical study. The study of the connection between logical form and the possibility of successful inquiry, in various senses, strikes us as both theoretically interesting and profoundly practical. For every question that has
a logical form, or at least a tolerable variety of possible logical forms among which we may be undecided, these studies address the prospects for coming to know the answer.
Problems of a similar kind abound in the sciences, and questions (whose answers are in many cases unknown) about the existence of Menoan arguments against the acquisition of knowledge affect very practical issues about procedures of inquiry. We will give a few illustrations.
7.1—
Language Learning
Consider a child learning its first language. Somehow, within a few years, the child comes to be able to produce and to recognize grammatical sentences in the native language, and to distinguish such sentences from ungrammatical strings. Grammatical sentences of any possible language can be regarded as concatenations of symbols from some finite vocabulary. If we fix the finite vocabulary, then the number of distinct sets of strings built from that vocabulary is of course infinite, and in fact uncountably infinite. Suppose, however, we make the reasonable assumption that if a collection of strings is the collection of grammatical strings of some possible human language, then the collection is recursively enumerable. That is, for any set of strings of this kind there is a computable function such that, if a string is in the collection, the computable function will determine that it is. So, restricting attention to the languages that can be built on some particular vocabulary, the collection of possible natural languages is restricted to the recursively enumerable sets of strings made from that vocabulary. For each recursively enumerable set there is a program, actually an infinity of different programs, that when given an arbitrary string will compute "yes" if and only if the string is in the set (and will not return anything otherwise). The recursively enumerable sets can be effectively indexed in many different ways, so we can imagine each possible language to have a name that no other possible language has, and in fact we can imagine the name just to be a program of the kind just mentioned.
One way to think of the child's problem is this: on the basis of whatever evidence the environment provides, the child forms a sequence of programs that recognize a sequence of languages, until, eventually, the child settles on a program that recognizes the actual natural language in the child's environment. Psychological investigation suggests that children use positive evidence almost exclusively. That is, the evidence consists of strings from the language to be learned but does not include evidence as to which strings are not in the language.
With this setting, due essentially to E. Mark Gold,[7] an important aspect of human development is made formal enough to permit mathematical investigations to bear on issues such as the characterization of the collection of possible human languages. For a language to be possible for humans, humans must be
capable of learning it. Assuming that any possible human language could have been learned by any one human, it follows that the collection of possible human languages must be identifiable, or learnable, in the sense that for every language in the collection a human child, if given appropriate positive evidence, can form a program that recognizes that language. There are surprising results as to which collections of languages are, and are not, learnable. Gold himself proved that any collection containing all finite languages and at least one infinite language cannot be identified. Imposing psychologically motivated constraints on the learner, Osherson and Weinstein have argued that any learnable collection of languages is finite. A wealth of technical results is now available about language learning.
7.2—
Statistical Inference
One of the principal statistical tasks is to infer a feature of a population from features of samples drawn at random from that population. One can view an ideal statistician as drawing ever larger samples and using the statistical estimator to guess the value of the quantity of interest in the population. Some of the usual desiderata for statistical estimators are founded on this picture. For example, it is desired that an estimator be consistent , meaning that whatever value the quantity has in the population, for any positive epsilon the probability that the estimate of the quantity differs from the true value by more than epsilon approaches zero as the sample size increases without bound. This is clearly a convergence criterion; it implicitly considers a family of possible worlds, in each of which the quantity of interest has a distinct value. When the quantity is continuous, there will be a continuum of such possibilities. A consistent estimator must, given increasing samples from any one of these possible worlds, converge with probability one to a characterization of the value the quantity has in the world from which the data are obtained.
7.3—
Curve Fitting
Every quantitative empirical science is faced with tasks that require inferring a functional dependency from data points. Kepler's task was to determine from observations of planetary positions the function giving the orbits of planets. Boyle's task was to infer the functional dependency of pressure and volume from measures on gas samples. These sorts of challenges can usefully be viewed as discovery problems. Data are generated by a process that satisfies an unknown functional dependency, but the function is known (or assumed) to belong to some restricted class of functions. In principle, more data points can be obtained without bound or limit, although in practice we may lose interest after a while. In real cases, the data are subject to some error, but something may be known about the error—its bounds, for example, or its probability
distribution. The scientist's task is to guess the function from finite samples of data points. The conjecture can be revised as more evidence accumulates.
Many procedures have been proposed for this sort of discovery problem. Harold Jeffreys,[8] for example, proposed a procedure that uses Bayesian techniques together with an enumeration of the polynomial functions. Nineteenth-century computational designs, such as Babbage's, used differencing techniques for computing polynomials, techniques that could (in the absence of error) be turned round into discovery procedures. More recently Langley et al.[9] have tried doing exactly that, and have described a number of other procedures for inferring functional dependencies from sample data.
For any of these procedures, and for others, the foremost questions concern reliability. For any procedure we can and should ask under what conditions the conjectures will converge to an appropriate function. We can ask such questions for many different senses of convergence, and for many different accounts of what makes a function (other than the correct one) appropriate, but we should certainly try to formulate the issues and answer them. Very little work of this kind has been done; neither Jeffreys nor Langley and his collaborators characterize exactly when their procedures will succeed, although in both cases it is easy enough to find many classes of functions (e.g., classes including logarithmic, exponential, and similar transcendental functions) for which the procedure will fail in the long run. A more systematic study has been done for a related class of problems in which the data are finite pieces of the graph of a recursive function, and the discovery task is to identify the function by guessing a program that computes it.[10]
7.4—
Generating Functions
One of the characteristic kinds of discovery tasks, at least in the physical sciences, is the discovery of generating functions. The idea is easiest to understand through an example. When monatomic gases are heated they emit light, but only light of certain definite frequencies. For example, when atomic hydrogen emits light, the spectrum contains a series of lines following a line whose wavelength is 6563 angstroms. In addition, the spectrum of hydrogen contains a number of other series of lines. The spectral likes of other elements, notably the alkaline earth and alkali metal elements, can also be arranged in various series. Here is a kind of discovery problem: given that one can obtain the spectrum of such a gas, and can identify lines as lines of a common series, what is the function that determines the frequencies (or wavelengths) of the lines in the series? For the principal hydrogen series, Balmer solved this problem in 1885. Balmer's formula is
1/l = R (1/4 – 1/n2 )
where n is an integer greater than or equal to 3, l is the wavelength, and R is a
constant (the Rydberg constant). Balmer generalized his formula to give a parametric family
1/l = R (1/m2 – 1/n2 )
for which series for m = 1, 3, 4, and 5 have been found.
Balmer's formulas give a collection of discrete values for a continuous quantity, in this case the wave number, and they specify that collection by giving a (partial) function of the positive integers.
There are other famous discoveries in the natural sciences that seem to have an analogous structure. The central question in chemistry in the nineteenth century was the reliable determination of the relative weights of atoms. Alternative methods yielded conflicting results until in 1859 Cannizzaro noted that the relative vapor densities of compounds form series; for example, all compounds of hydrogen form a series, as do all compounds of oxygen, and so forth, for any element. Of the continuum of possible values for compounds of hydrogen, only a discrete set of values is founded, and Cannizzaro discovered that the vapor density of any hydrogen compound is divisible by half the vapor density of hydrogen gas. Analogous results held for compounds of other elements. Cannizzaro's discovery was of crucial importance in putting the atomic theory on a sound basis; Balmer's discovery formed the crucial evidence for the early quantum theory of matter.
We can imagine a scientist faced with the following kind of problem: an infinite but discrete series of values of a continuous quantity is given by some unknown function of a power of the integers, In , or of the positive integers, but the function may belong to a known class of functions of this kind. The scientist can observe more and more members of the series, without bound, and can form a series of conjectures about the unknown function as the evidence increases. The properties of discovery problems of this sort have not been investigated either in the scientific or in the philosophical literature; and aside from the obvious procedure of looking for common divisors of values of a quantity, we know of no discovery procedures that have been proposed.
7.5—
Theoretical Quantities and Functional Decompositions
If you have only a number of resistance-free batteries, wires of varying but unknown resistances, and a device for measuring current through a circuit, you can discover Ohm's law, that voltage in a circuit equals the current in the circuit multiplied by the resistance in the circuit, even though you have no device to measure voltage or resistance, and even though at the beginning of the inquiry you have no belief that there are properties such as voltage and resistance. Pick a wire to serve as standard, and let the current through each circuit with each battery serve to measure a property of each battery. Pick a
battery to serve as standard, and let the current through each circuit with each wire and that battery serve to measure a property of each wire. You will then find, by simple curve fitting, that the relations between these two properties and the current is described by Ohm's law. Langley et al. give a discovery procedure that solves this problem. But what is the general form of the problem?
Consider any real (or rational, or integer as the case may be) valued function of n-tuples of nominal variables. In the circuits considered previously, for example, current I is a function of each pair of values for the nominal pair (battery, wire). In general we have F (X1 , . . . , Xn ), Let F be equal to some composition of functions on subsets of the nominal variables. For example, I (battery, wire) = V (battery) * R (wire), where * is multiplication. A discovery problem consists of a set of functions on subsets of tuples of nominal variables, and for each tuple and set of functions, a function that is a composition of (i.e., some function of) that set. The learner's task is to infer the decomposition from values of the composite function.
Evidently a lot of clever science consists in solving instances of problems of functional decomposition, and thus discovering important but initially unmeasured properties. The properties of discovery problems of this kind, and of algorithms for solving them, are almost completely unstudied.
7.6—
"Underdetermination," or Answerable and Unanswerable Questions
A scientist often has in mind a particular question to which an answer is wanted. The aim is not to find the whole truth about the world, but to find the answer to one particular question. There is a tradition in philosophy, in physics, and even in statistics of considering contexts in which particular questions cannot be answered. Philosophers talk about "underdetermination" in such contexts, whereas physicists tend to talk about similar issues in terms of "physical meaningfulness" and statisticians in terms of "identifiability." The examination of such issues is in structure very much like Gold's consideration of classes of languages that cannot be identified. Arguments consider a collection of alternative structures of some kind, characterize the evidence generated from any structure, and establish that even "in the limit" some structures in the collection cannot be distinguished.
Consider a question about the shape of space: what is its global topology? In relativity, the evidence we can get at any time about that question is bounded by our past light cone; the discriminations we can make at any time are then determined by the data in that light cone and whatever general laws we possess. The general laws can be thought of as simply restricting the possible classes of space-time models. As time goes by, more and more of the actual universe is in the past of an imaginary, immortal observer. Are there collections of relativistic models for which such an observer can never determine the
global topology of space? It turns out that there are, and some of them are not too difficult to picture. Imagine that space is a three-dimensional sphere, and that space-time is an infinite sequence of three-dimensional spheres. Suppose the radius of the sphere expands as time goes on. At any moment the past light cone of an observer may include, at each past moment, some but not all of the sphere of space at that past moment. If the radius of space expands fast enough, then at no moment will the past light cone include all of space. Now consider another space-time made mathematically from the first by identifying the antipodal points on the sphere of space at each moment. The shape of space will be different in the two space-times. The sphere is simply connected: any closed curve on the surface of a sphere, even a three-dimensional sphere, can be contracted smoothly to a point. The projective space obtained by identifying antipodal points on the sphere is not simply connected. The two spaces have different topologies. Now imagine that space expands with sufficient rapidity that the past light cone of any point never reveals whether one is in the spherical space of the projective space. Many other classes of indistinguishable spacetimes have been described.[11]
7.7—
Indistinguishability by a Class of Procedures
Issues of distinguishability also arise in settings that are remote from cosmology. In the social sciences, engineering, and parts of biology and epidemiology, we often rely on statistical models of causal relations. Often an initial statistical model is thought to be in error, and a variety of algorithmic or quasialgorithmic techniques have been developed to find revisions. Factor analysis is one way; procedures that modify an initial model by means of "fitting statistics" are another; procedures that try to match the empirical constraints entailed by a model with those found in the data are still a third.
For each of these kinds of procedures the discovery framework poses a relevant question: For what classes of models can the procedure succeed in identifying in the limit? What are the collections of models such that, given data generated from any one model in the collection, as the size of the sample increases without bound the procedure will identify the model that actually generated the data?
Sometimes a variety of procedures share a feature; either they share a limit on the information they consider in forming a hypothesis, or they share a limit on the hypotheses they consider. In the latter case it is perfectly obvious that certain classes of models cannot be identified. In the former case, finding out what classes of models can and cannot be identified may take some work. The discovery paradigm emphasizes the importance of the work.
8—
Conclusion
There is a lot of structure behind the words that translators have given to Plato's Meno and to Plato's Socrates. The structure is, we hope, plausibly
attributed even though it is remarkably modern. That should be of no surprise to those who think philosophy really addresses enduring questions, and who think the questions of knowledge had the same force and urgency for the ancients as for ourselves.
Two—
The Concept of Induction in the Light of the Interrogative Approach to Inquiry
Jaakko Hintikka
1—
The Interrogative Model
This paper is a part of a larger enterprise. In the last few years I have developed an essentially new approach to inquiry, prominently including scientific inquiry.[1] This approach can be given the form of a model (or, more appropriately, a multidimensional spectrum of models) of inquiry, which I propose to call the interrogative model of inquiry . It can be used to understand a wide variety of phenomena and to solve a variety of problems. In this paper I will study one particular concept that can be put into an interesting systematic and historical perspective by means of the interrogative model, namely, the concept of induction .[2] In the study of this notion the interrogative model of inquiry turns out to be especially useful. Among other conclusions, we shall find interesting reasons for assigning induction in the accepted sense of the word a rather lowly place on the map of scientific methodology. At the same time, the interrogative model helps us to uncover a historically earlier sense of induction which in our days is virtually forgotten and to assign to it an important role in the scientific process.
I will assume familiarity with the main ideas of the interrogative model. There is in fact relatively little to be familiar with, as the main ideas on which this model is based are extremely simple. The model can be described in gametheoretical terms.[3] The model takes the form of a game which an idealized scientist, called the Inquirer , plays against Nature on a fixed model (universe of discourse). This model or "world" in practice is usually our actual world or some part of it. (Such parts as can serve as models of theories are often called in physics independent or isolated systems.) The game starts from a theoretical premise T. The Inquirer is trying to derive a preset conclusion C from T. At each stage, the Inquirer has a choice between a deductive move , in which a logical
conclusion is drawn from what the Inquirer has reached already, and an interrogative move , in which the Inquirer puts a question to Nature and registers the answer, when forthcoming, as an additional premise. Speaking of such questions is what presupposes that a model of the combined language of T and C is given to which the questions pertain. Nature's answers are assumed to be true in this model. In the applications contemplated here, "questions put to Nature" are typically intended to be observations and experiments.
In different varieties of the model, different assumptions are made as to what kinds of questions Nature can answer. One important dimension is represented by different restrictions on the logical complexity of the available answers, as measured by the number of quantifier kind changes (i.e., changes from an evidential to a universal quantifier or vice versa) in the quantifier prefix of the answer. Quantifier-free answers are called A0 = E0 answers. An+1 -answers have a prefix of the form (" x1 ) (" x2 ) . . . (" xk ) + an En -prefix, and En+1 -answers have a prefix of the form ($ x1 ) ($ x2 ) . . . ($ xk ) + an An -prefix. A2 -prefixes will also be called AE-prefixes.
Restricting Nature's answers to the A0 = E0 case is tantamount to restricting answerable questions to yes-or-no questions concerning the truth or falsity of atomic propositions in M. The restriction that limits Nature's answers to this case I have called the Atomistic Postulate . At first sight, it seems to characterize the logic of empirical sciences. For Nature will not tell us in one fell swoop what happens always and everywhere. All that she will directly inform the Inquirer of is what happens in particular cases—in particular observations or measurements. And this restriction is precisely what the Atomistic Postulate is calculated to capture.
It can in fact be argued that practically all recent philosophy of science has been based on the Atomistic Postulate, tacitly if not explicitly.[4] Yet this postulate is unacceptable, for when a controlled experiment is construed as Nature's answer to the Inquirer's question, the logical complexity of the answers is at least of the AE variety. Hence the logic of experimental sciences (as distinguished from purely observational sciences) is an AE logic rather than one characterized by the Atomistic Postulate.[5] This result prompts a major reevaluation of contemporary philosophy of science. The present paper is a part of that reevaluation.
2—
Conventional Induction Plays No Role in the Interrogative Model
The first observation that can be made here is that induction in our accustomed twentieth-century sense play absolutely no role in the original interrogative model. In this sense, induction means, in the first place, inference from particular cases to general truths and, secondarily, inference from particular cases to other particular cases. I shall here disregard the latter aspect, for the
following reason: If inferences from particulars to particulars satisfy certain conditions, the principles according to which they are made are logically equivalent to principles governing inferences from particulars to generalizations.[6] Hence it suffices for most purposes to consider only inferences from particular instances to general laws.
As the reader can ascertain, there is in the original interrogative model absolutely no slot for the kind of inference that induction is supposed to be. The only inferences that take place in an interrogative inquiry are deductive. The other moves (other than deductive ones) include in the first place interrogative ones. In them, no inferences are drawn. Instead, a question is addressed by the Inquirer to Nature and (depending on conditions that are defined when the interrogative model is further specified) answered by Nature. In some varieties of the model, the Inquirer can, instead of an interrogative or a deductive move, perform a definitory move (introduce a new concept by an explicit definition) or strengthen the conclusion to be proved (assertoric move). But in none of these extensions of the interrogative model is anything like an inductive move possible.
The original unreconstructed interrogative model of inquiry hence already leads to a remarkable result. It shows that it is possible to develop a rich and realistic model of at least some central aspects of the scientific enterprise without as much as mentioning induction. A fortiori , if the interrogative model should turn out to be, not only the truth and nothing but the truth, but the whole truth, Hume's problem would play no role whatsoever in a serious theory of the scientific method and of the scientific process.
What is especially interesting here is that the most important extensions of the original interrogative model also fail to vindicate the received concept of induction. I cannot examine these extensions in detail here. The main idea is nevertheless easy to appreciate.[7] Instead of assuming that the answers given by Nature are always true, it can be assumed that each such answer is true only with a certain probability. This does not yet specify a unique model, for it does not tell us how the probabilities of a true answer on different occasions depend on (or are independent of) one another. By choosing these probabilities in different ways we can adapt the interrogative model to different evidential situations. For instance, if Nature's answers to repetitions of one and the same question are independent of one another, the best way for the Inquirer to ascertain that Nature's answer is veridical may be to repeat the same question and hope for the same answer. This corresponds to a scientific situation in which an experiment or observation does not involve a systematic bias or other systematic mistakes.
It may happen, however, that an answer by Nature to a given question makes it likely that Nature should give the same answer to its repetitions. Then the best strategy for ascertaining Nature's veracity may very well be to try to derive the same conclusion by an altogether different line of reasoning. In this
way, the famous old idea of the consilience of scientific inference can be explained and vindicated.[8]
In all these different situations, however, we are still dealing with deductive rather than inductive reasoning. More accurately, we are dealing with strict inferences from merely probable premises. The is diametrically opposite to typical cases of inductive inference, which are nonbinding inferences from (typically indubitable) premises. It is seen, not only that inductive inferences are not incorporated in the extended interrogative model, but that there is no place for them in the interrogative model or in any of its most natural extensions.
3—
The Problem of Induction and the Atomistic Postulate
One can say much more here, however. Indeed, one can put the entire concept of induction in a sharper historical relief.
The concept of induction goes back to Aristotle's idea of epagoge .[9] Indeed, the Latin term inductio was first introduced as a translation of epagoge . It is far from clear, however, that epagoge really is the same idea as our received concept of induction, and it will be argued below that it is not. In any case, the "problem of induction," by which everybody means the problem of justifying induction, was only thrust to the forefront of philosophical discussion almost two thousand years after Aristotle by David Hume.[10] Why the time lag? Were pre-Humean philosophers too confused or too naive to appreciate the importance of the problem of induction? I don't think that they were. It can be shown, if I am right, that the ascendancy of "Hume's Problem" of induction is part and parcel of the same problem situation as contemporary philosophers' virtually unanimous assumption of the Atomistic Postulate. In fact, this is a natural occasion to put the entire concept of induction into an overall historical perspective.
First, it can be seen where the idea of inductive inference as an essential ingredient of the scientific process comes from. It is one possible reaction to the problem situation created by the assumption of the Atomistic Postulate. If this postulate is adopted, then a scientific theory (e.g., the initial theoretical premise T) cannot itself be derived by means of the interrogative procedure without an equally strong or stronger theoretical premise. For no nontrivial general laws can be deduced from particular propositions, for instance, from Nature's answers to questions concerning particular cases or particular situations. Hence, the suggestion goes, the two kinds of steps of the interrogative procedure, questions and deductive inferences, have to be supplemented by a third kind of step. This step is calculated to lead us from Nature's particular answers to general truths. And it is this role of generalizing steps that inductive inferences are supposed to play.
At the moment I am not discussing the intrinsic merits or demerits of this idea. What is relevant here is a simple historical prediction (or retrodiction) that can be based on my diagnosis of the rationale of the general idea of inductive inference. What follows from my analysis is that, for those philosophers and scientists who did not adopt that Atomistic Postulate, our received idea of induction was not likely to play the same role as it does for us. It was not needed as a supplement to deductive inference. There did not exist for such philosophers any Humean problem of justifying induction, for induction in our sense could largely be dispensed with. If such thinkers used the idea of induction, it was in some different kind of role altogether.
In particular, it can be expected that philosophers and methodologists who do not believe in the Atomistic Postulate will not abide by the current idea of induction as an inference from particular cases to a generalization. For, in the face of the Atomistic Postulate, it was precisely this kind of generalization that induction was supposed to mediate. If you don't accept the postulate, you don't need induction for this purpose.
Likewise, it is clear that the central role of "the problem of induction" is due to philosophers' adoption of the Atomistic Postulate.[11] Hence this problem of "justifying induction" can be expected to occupy only those philosophers who have tacitly accepted the postulate. This observation helps in fact to explain why "Hume's Problem" became a central problem in philosophy when it did—and also how, as I will show below.
Now, as a matter of historical fact, the Atomistic Postulate was not adopted in the earlier tradition of philosophy and science from Aristotle to Newton (inclusive), though for different reasons in the case of different historical figures. In the Aristotelian tradition, even perception can give us forms, which are already by themselves general concepts. Moreover, their presence in the soul ipso facto implied according to Aristotle awareness of certain general laws, namely, those laws that specify what forms necessarily accompany the given ones.[12] (Thinking of a certain form is for Aristotle to have it realized in one's soul. Hence what necessarily accompanies this form is also automatically present in the soul, that is, is also necessarily thought of.)
This rejection of the Atomistic Postulate by Aristotle is seen in other ways, too. Another indication is the fact, brought out by G. E. L. Owen and others, that the phainomena and endoxa which a theory was supposed to account for according to Aristotle, were not all particular facts but could include general laws.[13]
In Newton, his reason for dispensing with the Atomistic Postulate is different. It is Newton's firm belief in the experimental method as being able to give the Inquirer general laws as answers to experimental "questions put to nature."[14] Hence induction in our contemporary sense was not needed by Newton.
In either type of case, induction can therefore be expected to amount to
something essentially different from our post-Humean conception. A widespread failure to appreciate this historical fact has in my judgment seriously impaired philosophers' understanding of the early history of the concept of induction. I don't think that most philosophers or historians really have a realistic idea of what Aristotle or Newton meant by induction.
4—
Experimental Questions and Their Presuppositions
In spite of all this, the interrogative model nevertheless assigns to a somewhat different (but historically authentic) concept of induction an extremely interesting role. In order to see this, a starting point is offered by the logical situation outlined in my paper, "What Is the Logic of Experimental Inquiry?"[15] When carried further, this analysis naturally, not to say inevitably, leads to further insights. In the earlier discussion, the reader was probably bothered by the question as to how much new force answers to AE questions (and to more complicated questions) really give us—and what kind of information they do yield. For from the perspective used there it may legitimately look as if the presuppositions of the questions in question are so strong that they are unlikely even to have been established in a realistic situation of inquiry and so strong that answers to them will yield relatively little new information anyway. Witness, for example, the question whose presupposition is:

The logic of such sentences alone is almost tantamount to the entire second-order logic.[16] Hence the step from the presupposition (1) of a question put to Nature to its answer

or even to the desideratum
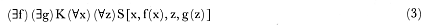
appears not to add terribly much new force to what the Inquirer already has.
Moreover, it is clear that the force of the presupposition (1) is largely due to the fact that it codifies certain independencies between different experimental variables. Now we normally think that such independencies can only be established experimentally. This expectation seems to me justified. But how can any experiment establish such independencies if they must have been found and incorporated into the presupposition of a question before the experimental question is put to Nature and answered by her?
These are genuine problems, and they force us to have another look at the most basic ideas on which the interrogative model is based. More specifically,
we must have some second thoughts about the role of presuppositions. Right from the beginning, I could have built the model in a slightly different way. I could have eliminated the role of the presupposition of a question altogether as a prerequisite to asking the questions. Of course, I must then allow the answerer to respond, even when the question does otherwise qualify as an answerable one, by rejecting its presupposition rather than by providing the Inquirer with an answer to it.[17]
This rule change seems to result in a better model of scientific inquiry than the previous one, at least in many applications. It goes some distance toward solving the problems just pointed out. However, a little bit more has to be said of the failures of the presupposition of a question in different cases. For a propositional question,

the failure of the presupposition

makes the question completely otiose, and likewise for simple wh-questions. But consider a question whose presupposition is:

Such a presupposition fails if for some values of x no y satisfies S[x, y]. Then the Inquirer ought not to ask which y does the job for those fruitless values of x. But there is no harm in asking the question for other values of x. And even more so if the presupposition (6) is true but has not been shown to be true for some values of x. This should not bar the Inquirer from raising the question.
In such cases, Nature's response to a question whose presupposition used to be (6) is naturally taken to be of the same form

as before, with f such as to sustain the existential generalization from

except that f can now be a partial function, that is, defined only for some values of x. This can be expressed in the usual notation by turning the reply (8) (minus "K") into a conditional one:

Instead of just one interval, we can of course in principle have in (10) several different nonoverlapping intervals. This, then, is what is natural to
think of as Nature's answer to an AE-type question. I shall assume in the following that this is what Nature's answers are like. Nature's reply may also include a rejection of the presupposition for certain values of x:
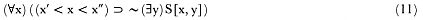
I shall ignore this possible component of Nature's response in what follows, however. It is the less important and less interesting part of the reply.
Thus it is seen that the natural way of defining the interrogative model is to allow the Inquirer to put AE questions to Nature even when the presupposition is not established. Nature's reply is not the negative of the (former) presupposition, even when it is false. Rather, it is a restricted functional dependence like (10).
5—
Induction as the Task of Extending Limited Generalizations
From what has been said, it is seen that there is an important dimension of the progress of scientific inquiry which we have not yet considered and which has not been considered very often in recent philosophy of science. It is not, strictly speaking, any longer an application of the interrogative model. However, its importance is in effect predicted by the interrogative model in the light of the remarks just made.
This dimension concerns the extension of a generalization like (10) to further values of x, that is, a step from (10) to

where x1 ' < x1 , x2 < x2 '.
More generally, the Inquirer has a number of partial generalizations

(i = 1, 2, . . . , k), where the intervals xi1 < x < xi2 are assumed not to overlap. These may have been established in part as (partial) answers to the same question, and in part as (partial) answers to different questions.
The dimension I have in mind is now twofold: (i) the Inquirer is trying to extend a generalization like (10) or (13) to longer intervals, perhaps to an unrestricted generalization; and (ii) the Inquirer is trying to unify the different partial dependences (laws, functions) fi (x) into one law, for example, into one and the same mathematical law.
This dual dimension is the focus of this paper. I have shown why it is important from the systematic viewpoint offered to us by the interrogative model. I will return to this systematic significance later in this paper. The main historical thesis I am proposing also concerns the same dimension. What
this thesis says is that the generalization and reconciliation task this dimension deals with is what was earlier meant by induction.
6—
Newtonian Induction
This historical thesis deserves a few comments and explanations. Indeed, Newton's idea of induction is seen from his famous methodological statement in the Opticks :
As in mathematics, so in natural philosophy, the investigation of difficult things by the method of analysis ought ever to precede the method of composition. This analysis consists in making experiments and observations, and in drawing general conclusions from them by induction, and admitting no objections against the conclusions but such as are taken from experiment, or other certain truths. For hypotheses are not to be regarded in experimental philosophy. And although the arguing from experiments and observations by induction be no demonstration of general conclusions, yet it is the best way of arguing which the nature of things admits of, and may be looked upon as so much the stronger by how much the induction is more general. And if no exception occur from phenomena, the conclusion may be pronounced generally. But if at any time afterward any exception shall occur from experiments, it may then begin to be pronounced with such exceptions as occur. By this way of analysis we may proceed from compounds to ingredients and from motions to the forces producing them, and in general from effects to their causes and from particular causes to more general ones, till the argument end in the most general. This is the method of analysis; and the synthesis consists in assuming the causes discovered and established as principles, and by them explaining the phenomena proceeding from them and proving the explanations.[18]
Here we can see the kind of concept of induction I propose to call the Newtonian one at work. Induction in this sense of the word occupies a niche in the scientific procedure indicated by the analysis carried out earlier in this paper. Induction is, in the simplest case, the step from a limited generalization of the form (10) to a less restricted generalization (12). In the extreme (ideal) case, the entire restriction (antecedent) in (10) is eliminated. This optimal case is what Newton describes as saying: "And if no exception occur from phenomena, the conclusion may be pronounced generally." What distinguishes a Newtonian inductive step from inductive inference in the twentieth-century sense is that its starting point is not a number of particular propositions but propositions which, logically speaking, normally possess already limited generality. For, as I have argued elsewhere, experiments could according to Newton yield as their result a general law.[19] (This is among other things seen from Newton's practice of resorting to results of experiments in proving general theorems and solving general problems in his Opticks .) Induction thus in-
creases the generality of the propositions the Inquirer has established, but in an entirely different sense from the twentieth-century idea of induction as an inference from the particular to the general. For in Newtonian induction, the increase in generality is one of degree, not of kind. Newton is in fact quite consistent in speaking of induction as a way of arguing from "observations and experiments." Given his conception of experiment, this means that the starting point of an inductive step can already possess (limited) generality.
It is not clear in what sense a Newtonian induction is an inference, either. In principle, the extension of the scope of a generalization can take place experimentally. This is not what Newton means, however. For he says that "although the arguing from experiments and observations by induction be no demonstration of general conclusions, yet it is the best way of arguing which the nature of things admits of." What Newton has in mind is a fact of scientific life familiar to all experimentalists. Even though a controlled experiment (or equivalent) can establish a generalization, the actual range over which the controlled variable can be varied is typically very narrow, indeed so narrow that the resulting restricted generalization is useless in studying other phenomena unless it can be further generalized by widening its scope (as is the step from (10) to (12) above), even before other experiments and observations have been made to help us extend it. This implies that induction in the sense of widening the scope of a generalization is a corrigible step of argument in a sense which, for example, Nature's limited-scope answer to an experimental question is not. I will return to this point later.
At the same time, the quotations from Newton show how tempting it might easily seem to be to assimilate Newtonian induction to our latter-day namesake conception. It is indeed possible that Newtonian induction was intended to comprise as a degenerate special case steps from particular measurement results to a generalization. But this temptation is nevertheless misleading. It has in some cases even misled translators. For instance, this is illustrated by the Motte-Cajori translation of Principia where one of the crucial sentences is made to disagree with our interpretation:
In this [experimental] philosophy particular propositions are inferred from the phenomena, and afterwards rendered general by induction.[20]
But there is no "particular" in the original, and the netural term "inferred" is a bad substitute for Newton's explicit word for deduction:
In hac philosophia propositiones deducuntur ex phaenomenis, & redduntur generales per inductionem.[21]
The correct translation thus goes somewhat as follows:
In this philosophy, propositions are deduced from phenomena and rendered general by induction.
If anything, Newton's terminology supports my interpretation, for a "proposition" normally meant in an axiomatic context of his day a general proposition.
Earlier in this paper, we saw that for Aristotle, phenomena could be the source of general truths (or general beliefs) and not just particular ones. The same is now seen to be true of Newton. For instance, in speaking of his laws of motion (which of course are supposed to be general truths par exellence ) Newton, on one occasion writes:
These Principles are deduced from Phaenomena and made general by Induction.[22] [emphasis added]
Since Newton uses "deduce" in a fairly strict sense, this makes sense only if Newton's "Phaenomena" are already general. Similar evidence is easily found elsewhere. (Cf. also what was established above.)
Thus those few hardy souls who have maintained that Newton's methodology was an "inductivist" one may after all have something going for them. But, of course, Newton was speaking of "induction" in a sense different from theirs.
7—
Newton and Mathematical Modeling
There is yet another similarity between Newton and Aristotle which has not been utilized in the literature on Newton. It is the role of induction in establishing the first principles of science in Aristotle. The way this oversight has pointed historians' and philosophers' attention in a wrong direction is seen in the views of those commentators who construe Newton's method as a construction of mathematical models.[23] This idea has been encouraged by Newton's relatively sparse mention of experiments and observations in the early books of the Principia . This seems to differentiate his procedure from that prescribed by the interrogative model, which apparently squares better with what Newton does in the Opticks .
The answer is that Newton assumes that most of the pertinent questions had been put to Nature before the definition and axioms (laws of motions) are formulated. We have in fact seen that Newton claimed in so many words that those laws (principles) were "deduced from Phaenomena & made general by Induction."[24] Hence the principles of the Principia do not just define a mathematical model. They are themselves not only somehow inspired by experience, as in any old mathematical model, but in fact derived from phenomena, Newton claims. This distinguishes Newton's procedure from typical hypothetico-deductive model construction, and it is well in keeping with the Aristotelian conception of a particular empirical science.
That Newton himself looked upon the Principia in this way is amply demonstrated by evidence. The following is a part of Newton's self-description of what he did in the Principia :
The Propositions in the following book were invented by Analysis. But considering that the Ancients (so far as I can find) admitted nothing into Geometry before it was demonstrated by Composition I composed what I invented by Analysis to make it Geometrically authentic & fit for the publick. And this is the reason why this Book was written in words at length after the manner of the Ancients without Analytical calculations. But if any man who understands Analysis will reduce the Demonstrations of the Propositions from their composition back into Analysis (which is very easy to be done,) he will see by [what] method of Analysis they were invented. [And] by this means the Marquess de l'Hospital was able to affirm that this this [sic] Book was [presque tout de ce Calcul.] almost wholly of the infinitesimal Analysis.[25]
And here is another Newtonian self-description, this time anonymous:
By the help of the new Analysis Mr. Newton found out most of the Propositions in his Principia Philosophiae : but because the Ancients for making things certain admitted nothing into Geometry before it was demonstrated synthetically, he demonstrated the Propositions synthetically, that the Systeme of the Heavens might be founded upon good Geometry. And this makes it now difficult for unskillful Men to see the Analysis by which those Propositions were found out.[26]
8—
Induction and Concept Formation
Already at the stage of analysis we have reached, a suggestive resemblance between Newtonian and Aristotelian induction is beginning to emerge. For Aristotle, the problem of induction was not first and foremost a problem of inference from particulars to a generalization. It was a problem of concept formation.[27] Particular cases were stepping-stones to the concepts or forms "induced" to be realized in the soul. Once they are formed, the laws governing them are obvious. (This is very closely related to Aristotle's rejection of the Atomistic Postulate.) Hence there is no such problem as the justification of induction for Aristotle. For Newton, too, the crucial step was the formation of the mathematical law on the basis of an experiment. The extension of this law to other cases is a lesser problem, and a problem that is at least partly mathematical (and hence conceptual) in nature, as we shall see later.
This similarity is not accidental, and it can be deepened by noting other points of contact between Newton and Aristotle.
9—
Hume Misinterpreted Newton
Some light on the history of the problem of induction in thrown by its origin. It was made a centerpiece of epistemology and philosophy of science by Hume. Now Hume's approach to methodological matters is characterized concisely as a misinterpretation of Newton's methodology. Hume wanted to introduce what he called the experimental method into philosophy.[28] For Hume, how-
ever, the term 'experimental' was merely a near-synonym of 'empirical', as one can easily show.[29] In general, the good David did not have any idea of a genuine controlled experiment. In particular, Hume totally failed to understand Newton's idea that an experiment can yield general laws (dependencies). Instead, he firmly assumed the Atomistic Postulate. Hence the logico-methodological reasons which I showed to underlie the modern (post-Humean) preoccupation of philosphers with "Hume's Problem" are exemplified in an actual historical setting by the originator of this alleged problem himself.
I will return later to the relation of Hume's problem to Newton's explicitly acknowledged admission of the corrigibility of induction.
10—
Reconciling Different Partial Generalizations
All this nevertheless amounts to treating only the simplest kind of inductive task, namely, the task of extending a generalization established for one interval of values of the controlled variable. (Cf. (1) above.) In the general case, the Inquirer faces the task of not only extending one interval but combining different kinds of functional dependence found to obtain over different (nonoverlapping) intervals. In this case, the problem is not simply extending a generalization but also reconciling with other partial generalizations. I will refer to this second aspect as the reconciliation problem.
This kind of reconciliation problem is not atypical in the history of science. A reader may in fact have here a déjà vu experience. For consider the problem situation which Planck faced and which I used as an example in the paper, "What Is the Logic of Experimental Inquiry?"[30] This problem situation is precisely one of reconciling partial generalizations with one another. Another important case in point is perhaps Einstein's discovery of the special theory of relativity, which may be considered a grand reconciliation of Newtonian mechanics and Maxwell's theory of electromagnetism. Other examples are easily found in the actual history of science.[31]
In Newton's own case, the combination and reconciliation problem is perhaps instantiated by his discovery of the law of gravitation. Newton had several ranges of two-body systems to generalize from, including those formed by falling terrestrial bodies and the earth; by the earth and the moon; and by the sun plus a planet obeying Kepler's laws. In this case, the reconciliation consisted mainly in ascertaining that the same gravitational constant was obtained in all the cases, for the laws themselves were of the same inverse-square form.
This kind of reconciliation task is an important variety of induction in the Newtonian sense of the word. It represents a problem situation which has played a major role in the development of science and which is therefore worth a study in its own right.
11—
The Reconciliation Problem and Aristotelian Induction
Before studying the structure of the reconciliation problem, it is in order to point out a remarkable similarity between an inductive reconciliation of different restricted mathematical laws and Aristotelian induction. I have analyzed in detail Aristotle's conception of epagoge in an earlier paper.[32] Since induction was calculated to establish at least some of the first premises of a science according to Aristotle, and since those first premises were identified by Aristotle with definitions, the process of induction in Aristotle must be the same as a search for a definition. Now Aristotle gives a vivid example of the search for a definition in Posterior Analytics B 13. The notion to be defined there is megalopsychia , an interesting notion that is likely to intrigue any student of Greek moral philosophy in its own right. Now how is it that Aristotle proposes to look for a definition of megalopsychia ? Here is his description:
I mean, e.g. if we were to seek what megalopsychia is we should inquire, in the case of some megalopsychia we know, what one thing they all have as such. For instance, if Alcibiades is megalopsychos , or Achilles and Ajax are megalopsychoi , what one thing do they all have? Intolerance of insults; for one made war, one waxed wroth, and the other killed himself [because of this intolerance]. Again in the case of others, e.g. Lysander and Socrates. Well, if here it [sc. the common characteristic that makes them megalopsychoi ] is being indifferent to good and bad fortune, I take these two things and inquire what both indifference to fortune and not brooking dishonour have that is the sam] . . . then we must again inquire if what we have now got have anything that is the same (with still other cases)—until we come to a single account; for this will be the definition of the object.[33]
The analogy with the reconciliation problem is striking. What Aristotle is in effect saying is that one first has to establish a number of restricted generalizations, each specifying the defining characteristic of megalopsychia in one type of case. The task of finding the definition of megalopsychia then consists in reconciling these partial generalizations, that is, in finding what (if anything) the different partial definitions have in common. In my paper "Aristotelian Induction" I showed that the structure of this kind of definition seeking is precisely the same as the so-called syllogistic induction Aristotle describes in Prior Analytics B 23.[34]
The differences between a typical Aristotelian induction and the inductive reconciliation problem are also clear. First, for Aristotle the partial generalizations to be integrated with one another are not established experimentally, but by examining our own reasons for calling a class of people megalopsychoi . Second, the partial generalizations in question are typically qualitative and not quantitative. However, neither of these differences affects essentially the similarity of the two reconciliation problems.
Here we have an interesting glimpse of what the cash value of the term 'induction' (or epagoge ) really was in pre-Humean philosophy of science.
It is especially interesting historically to see that the Aristotelians of the early modern period explicitly connected Aristotle's epagoge with his description of the search of a definition in Posterior Analytics B 13 and otherwise interpreted epagoge along the same lines I have done. It is also known that the young Newton read the Organon as well as the Aristotelian methodologists of his day. What historical insights a study of his notebooks might yield remains to be seen.
12—
The Structure of a Reconciliation Problem
It is now in order to discuss the reconciliation problem in its own right. What is the structure of induction in the sense of reconciliation of different partial generalizations? If a simple answer were forthcoming, we would understand the nature of scientific discovery much better than we actually do. Certain things can nevertheless be said. The task is to transform the different mathematical laws to a form where they can be seen to be special cases of a more general regularity. For instance, what Planck did was to argue that the Rayleigh-Jeans law amounts essentially to

where S is the entropy of an oscillator and U the energy.[35] In contrast, Wien's law goes together with the different law, namely:

Planck reconciled the laws (14) and (15) by regarding them as special cases of:

For small values of U this reduces to Wien's law and for large values of U essentially to the Rayleigh-Jeans law, which had been experimentally established by Rubens and Kurlbaum.
Once again, the final reconciliatory step appears both trivial and arbitrary. Jammer says that this step, "though mathematically a mere trifle, was one of the most significant and momentous contributions ever made in the history of physics."[36] The significance is of course not due to this one step but is in the line of thought that led Planck to a point where the competing partial general-
izations are directly comparable—or, rather, directly reconcilable. Such a line of thought normally takes the form of a mathematical manipulation of the laws in question. But such a manipulation of mathematical formulas must be guided by an insight into the actual physical situation. For instance, we can ask: How did Planck get from the original experimentally established radiation laws to the simple equations (14) and (15), which are not directly verifiable? In order to reach these equations, Planck has among other things to introduce a new concept, the concept of entropy, which he shunned earlier but which he now found himself forced to use. And this reliance on the concept of entropy is not just a facet of clever manipulation of mathematical expressions. It reflects Planck's newfound respect for statistical concepts in the analysis of physical situations. Unmistakably, such a combination of mathematical and physical considerations has something of the character of conceptual analysis. Small wonder, therefore, that Planck's line of thought led to a momentous new concept, namely, that of a quantum of energy.
Perhaps it is not too far-fetched to say that a physicist has to have some grasp of why each of the limited generalizations to be reconciled holds in its range, just as Aristotle assumed that in our search for a definition of megalopsychia we have to know, for each of the restricted ranges of cases we regard as stepping-stones toward a definition, why members of that class are called megalopsychoi : Socrates and Lysander because of their indifference to good and bad fortune, Alcibiades and Ajax and their ilk because of their intolerance to insult, and so on.
These observations also put in an interesting perspective the use of mathematics in an experimental science like physics. They show that the role of mathematics is far subtler than is usually spelled out. Mathematics is not just an aid in registering the outcomes of experiments. It is a tool, albeit not a mechanically applicable tool, that can be used to analyze a physical phenomenon. Mastering the mathematics used in a physical theory is very closely related to mastering the basic physical concepts of this theory. (Just think of what a crucial breakthrough von Neumann's work on the mathematical principles of quantum theory was for the actual development of this branch of physics.) In particular, the experimentation with mathematical equations which is calculated to bring the different mathematical laws (empirical generalizations) under the same roof inevitably takes on something of the character of conceptual analysis of the relevant physical situation.
The subtlety of the reconciliation problem shows how far a cry actual scientific argumentation is from the inductivist paradigm of making generalizations from particular cases. By the same token, it shows how much interesting argumentation is left untreated by the hypothetico-deductive conception of science.
Admittedly, there is a certain similarity between a reconciliation problem and the problem of establishing an inductive generalization in the twentieth-century sense of the term. In both uses, an inquirer moves from special cases to
a more general proposition. There nevertheless are important differences between the typical forms of modern induction and of the task of fitting several restricted laws under a more general one (in the sense of a law defined for a larger range of argument values). For one important thing, the restricted laws have to be reinterpreted in the reconciliation process. They cannot simply be considered instances of a generalization. For this reason, the reconciliation problem cannot, for example, be dealt with by means of existing inductive logics.
13—
The Uncertainties of Induction
Newton acknowledges that induction in his sense is not an incorrigible step:
And although the arguing from experiments and observations by induction be no demonstration, yet it is the best way of arguing which the nature of things admits of.[37]
It is of interest to ask, however, what in practice is the source of the uncertainty of a Newtonian (step of) induction. Does the source of trouble perhaps lie in unexpected discontinuities of nature? An experiment can establish a precise mathematical function. If this function is analytic, it has a Taylor expansion. That means that its behavior for the entire range of values for which it is defined by the same Taylor series is determined by its behavior in an arbitrarily small neighborhood of any point for which it is defined. Hence the kind of extension that is involved in "extrapolating" an analytic function seems to be a purely mathematical operation, and not conjectural at all. The only possible source of trouble seems to be hidden discontinuities of the function or of its derivatives outside the range of cases in which it has experimentally been found to hold.
It turns out, however, that this is not the only or even the main source of the uncertainty of Newtonian induction. Consider, for instance, Planck's problem situation. The two radiation laws he was trying to reconcile of course could not be considered precise special cases of a more general law. Rather, they were good approximations to the general law for different ranges of values, so good, indeed, that approximation fell within the range of observational error.
Hence the logic of Newtonian induction appears to be inextricably intertwined with the notions of approximation and of the margin of experimental or observational error. This is not the case logically speaking, however. Logically, the problem of inductive reconciliation of partial laws can arise and have the same logical properties also when the approximative character of the partial laws plays no role. For instance, Newton knew that Kepler's laws could not be completely accurate, because of the gravitational influence of different planets on one another's movements. Likewise, the orbit of the moon around the earth was known by him to be subject of the sun's perturbatory influence. But the
logical problem of reconciliation would have been the same even if he had in both cases been able to observe pure two-body systems.
In Planck's case, the two radiation laws are likewise approximations only. However, they would be precise laws if we could push the value of one of the variables to its limiting values (zero and infinity, respectively).
Hence what the crucial judgment-call typically is in a Newtonian induction is an independence or near-independence assumption. It has to be assumed either that the functional dependence that has been established is independent of further "hidden variables" or else that it is so nearly free from further factors that it can be considered the precise law for a suitable special case or range of values. Once again, the source of logical strength in scientific inference turns out to lie in establishing or assuming functional independence. This is in keeping with what was found in my paper "What Is the Logic of Experimental Inquiry?"[38]
Hence the logic of Newtonian induction is not essentially dependent on the quantitative character of the partial laws that have been established or on their character as approximations. In principle, a similar problem situation can arise in a theory expressible in a first-order language.
Notice also that this kind of uncertainty of Newtonian induction is rather different from the general uncertainty to which Hume called philosophers' attention.
Among other observations, we can now see that Popper's criticism of Newton's claim for having derived his law of gravitation from phenomena is without any force whatsoever.[39] Popper bases his criticism on the fact that Kepler's laws, which were the starting point of Newton's line of thought, cannot be strictly true if Newton's law of gravitation holds, for they do not allow for the gravitational interaction between different planets. How could Newton possibly have derived the true law of gravitation from false empirical generalizations, Popper asks? Yet we have seen that the merely approximate character of Kepler's laws is completely beside the point in evaluating the kind of "inductive" reasoning Newton used. It was perfectly possible for him to think of Kepler's laws as holding strictly for certain two-body systems. For those systems, the law of gravitation was, strictly speaking, implied by the laws of motion of a planet. The inductive step was then to note that the resulting law, established so far only for a certain range of two-body systems, agrees with other partial generalizations established for other ranges of cases. Popper's criticisms show merely that he has not begun to understand Newton's actual conception of scientific inference in general and of the role of induction in science in particular.
Three—
Aristotelian Natures and the Modern Experimental Method
Nancy Cartwright
1—
Historical Background
One of the great achievements of the scientific revolution, according to its adherents, was the banishment from modern science of the Aristotelian schemes of explanation which had dominated Scholastic studies. Aristotle was derided as a cuttlefish, a squid: the ink he discharged cast everything into obscurity. Consider one typical case, Pierre Gassendi in his Exercises against the Aristotelians (1624). Gassendi complains that Aristotelian explanations fail to explain. About the definition of motion as "the act of being in potentiality insofar as it is in potentiality," he remarks: "Great God! Is there any stomach strong enough to digest that? The explanation of a rather familiar thing was requested, but this is so complicated that nothing is clear anymore . . . The need for definitions of the words in the definitions will go on ad infinitum " (book 2, exercise 4, article 4).
The scientific revolutionaries favored the certainty of mathematics to the ambiguity of Scholastic accounts. Mathematics was "built on clear and settled signification of names, which admit of no ambiguity." This remark comes from Joseph Glanvill, whose defense of modern thought in Scepsis Scientifica earned him a place in the Royal Society in 1664. On Glanvill's account, Aristotle was exactly the opposite: "Peripatetic philosophy is litigious"; its accounts are "circular"; and its terms are "empty," "ambiguous," and lacking "settled, constant signification." The science of the Scholastics was involved in endless quarrels about words and very little actual investigation, in large part because it tried to explain the behavior of things by reference to their natures. But knowledge of natures, according to the new empiricists of the scientific revolution, is forever beyond our grasp; it is divine, not human. As Gassendi argues, it is not possible for mere humans to know "that something is by nature and in
itself, and as a result of basic, necessary infallible causes, constituted in a certain way" (book 6, article 1). Rather, "it can only be known how a thing appears to one or another" (book 6, article 6).
It is on account of this twofold fact that the Aristotelians got into useless debates over meanings: on the one hand, natures stood at the core of explanation for them; on the other, these natures were intrinsically unknowable. According to the empiricists, then, the Aristotelians inevitably resolved things into qualities that were occult; they could never be genuinely understood but only grasped by definition. Invariably this leads to a total circularity of explanation. The favored example is that of gravity. Glanvill tells us:
That heavy bodies descend by gravity is no better account than we would expect from a rustic; that gravity is a quality whereby a heavy body descends, is an impertinent circle, and teaches nothing. (Scepsis Scientifica , chap. 20)
For the empiricists, we must throw over this attempt to found science on occult natures and instead base everything on the kinds of qualities that appear to us in experience. Even here there is a danger that we may become too ambitious, and Glanvill warns: "If we follow manifest qualities beyond the empty signification of their names, we shall find them as occult as those which are professedly so" (Scepsis Scientifica , chap. 20).
Most modern accounts in the philosophy of science take it that the attempts of the scientific revolution to banish natures from science were successful. The idea of natures operating in things to determine their behaviors was replaced by the concept of a law of nature. Here is a short history, told by a modern-day empiricist, to illustrate:
Aquinas was at pains to contest a preceding scholastic view that everything which happens, does so because it is directly and individually willed by God. This would seem to make science a pointless enterprise; according to Aquinas it also denigrates creation. Yet theology points to God as ultimate cause. The reconciliation Aquinas offered was this: to explain why phenomena happen as they do, requires showing why they must; this necessity however derives from the natures of the individual substances involved—which themselves are as they are because of God's original design. Thus the necessity does derive ultimately from God's decrees for the world as a whole, made at the point of creation—but derives proximately from the local conditions and characters in the Aristotelian pattern . . .
. . . if we look more closely at the seventeenth century we see an insistence, even more adamant than Aquinas', upon the autonomy of physics from theology. Descartes insists on it most stringently . . .
The Drang nach Autonomie of physics, even as developed by such theological thinkers as Descartes, Newton, and Leibniz, needed an intermediate link between God's decree and nature. Aquinas had needed such a link to explain proximate causation, and found it in the Aristotelian substantial forms (individ-
ual natures). For the seventeenth century another kind was needed, one that could impose a global constraint on the world process. In general terms, this link was provided by the idea that nature has its inner necessities, which are not mere facts, but constrain all mere facts into a unified whole. The theological analogy and dying metaphor of law provided the language in which the idea could be couched. (Bas van Fraassen, Laws and Symmetry [Oxford: Clarendon Press, 1989], 4–6)
My thesis here is that this story is distorted (at least as it applies to modern experimental science). We have not replaced natures by laws of nature . For laws of nature are typically about natures, and what they produce. Rather, what we have done is to replace occult powers by powers that are visible, though it may take a very fancy experiment to see them. This is already apparent in Francis Bacon. Bacon still employs the Aristotelian idea of natures or essences, but for him these are not hidden. Bacon looks for the explanatory essences, but he looks for them among qualities that are observable. Consider his hunt for the essence of heat. He makes large tables of situations in which heat occurs, in which it is absent, and in which it varies by degrees. "Instances agreeing in the Form of Heat" (Novum Organum , 1620) include, for instance, rays of the sun; damp, hot weather; flames; horse dung; strong vinegar; and so forth. Then he looks to see what other quality is always present when heat is present, and always absent when heat is lacking. In this way, he finds the true, simple nature that consitutes heat: motion. The point is that Bacon still hopes to find the nature of heat, but among visible, not occult, qualities.
Modern explanation similarly relies on natures, I will argue; the modern natures are like Bacon's and unlike those of the Scholastics, in that they are attributed to observable structures and qualities. Generally they differ from Bacon's in that they do not lie on the surface and are not to be observed with the naked eye. Rather, we often need very subtle and elaborate experiments in order to see them. Modern science insists that we found explanation on experimentally identifiable and verifiable structures and qualities. But, I maintain, what we learn about these structures and qualities is what it is in their natures to do.
What we have done in modern science, as I see it, is to break the connection between what the explanatory nature is—what it is, in and of itself—and what it does. An atom in its excited state, when agitated, emits photons and produces light. It is, I say, in the nature of an excited atom to produce light. Here the explanatory feature—an atom's being in the excited state—is a structural feature of the atom, which is defined and experimentally identified independently of the particular nature that is attributed to it in this case.[1] It is in the nature of the excited atom to emit light, but that is not what it is to be an atom in an excited state. For modern science, what something really is—how it is defined and identified—and what it is in its nature to do are quite separate things. So even a perfect and complete modern theory would never have the
closed, deductive structure that the Aristotelians envisaged. Still, I maintain, the use of Aristotelian-style natures is central to the modern explanatory program. We, like Aristotle, are looking for "a cause and principle of change and stasis in the thing in which it primarily subsists" (Physics 2.1.192b22), and we, too, assume that this principle will be "in this thing of itself and not per accidens ."
Yet, even at this very cursory level of description, we differ from Aristotle in three important ways. First, as in my example of an atom in an excited state, we assign natures not to substances but rather to collections or configurations of properties, or to structures. Second, like the early empiricists and the mechanical philosophers of the scientific revolution, modern physics supposes that the "springs of motion" are hidden behind the phenomena and that what appears on the surface is a result of the complex interaction of natures. We no longer expect that the natures that are fundamental for physics will exhibit themselves directly in the regular or typical behavior of observable phenomena. It takes the highly controlled environment of an experiment to reveal them. Third, having made the empiricist turn, we no longer identify natures with essences. As I have described in this section, in modern science we separate our definition of a property from our characterization of what kind of change it naturally produces. Still, when we associate a particular principle of change with a given structure or characteristic, we expect that association to be permanent, to last so long as the structure is what it is. Indeed, it is this permanence of association that I will underline by claiming that modern science still studies Aristotelian-style natures. Of course, these are not really Aristotelian natures. For one thing, we seem to share none of the concerns about substance and individuation in which Aristotle's concept was embedded. There are a number of other differences as well. Nevertheless, I call them "Aristotelian" because of the inheritance through the Scholastics to the "New Philosophy" of Galileo, Bacon, and Descartes.
What I will do in the remainder of this paper is: first, explain in more detail what this claim amounts to by contrasting it with a more standard empiricist account of laws of nature; and second, provide one argument in favor of the thesis—an argument that says that one cannot make sense of modern experimental method unless one assumes that laws are basically about natures. The basic point of view I urge here is similar to that which I have written about at length in Nature's Capacities and Their Measurement (Oxford: Oxford University Press, 1989), but the fundamental argument is new.
2—
Natures and the Analytic Method
In defending natures, I take my principal antagonist to be the modern empiricist account of laws which rests on a distinction crucial to the thought of Locke, Berkeley, and Hume: the distinction between powers and sensible
qualities. According to Hume, powers are not accessible to us through our senses, and hence must be excluded from science. Nowadays, the distinction takes a slightly different form, between the power things have to behave in certain ways, on the one hand, and the actually exhibited behaviors, on the other. But modern empiricists in the Hume tradition remain just as eager as Hume himself to reject powers. Laws of nature, they insist, are about what things do . I want to maintain, by contrast, that fundamental laws are generally not about what things do but what it is in their nature to do. Consider Coulomb's law of electrostatic attraction and repulsion. Coulomb's law says that the force between two objects of charge q1 and q2 is equal to q1q 2 /r2 . Yet, this is not the force the bodies experience; they are also subject to the law of gravity. We say that Coulomb's law gives the force due to their charge. But this is no concept for an empiricist: Coulomb's is not the force that actually occurs; rather, it is a hypothetical power hidden away in the actual force.
I think the best account we can give is in terms of natures. Coulomb's law tells not what force charged particles experience but rather what it is in their nature, qua charged, to experience. Natures are something like powers. To say it is in their nature to experience a force of q1 q2 /r2 is to say at least that they can experience this force if only the right conditions occur for the power to exercise itself; for instance, if they have very small masses so that gravitational effects are negligible. It is also to say that their tendency to experience it persists, even when the conditions are not right; for instance, when gravity becomes important. Qua charged, they tend to experience a mutual force q1q2 /r 2 ; qua massive, they tend to experience a different force (Gm1m2 /r 2 ). What particles that are both massive and charged actually experience will be a function of what they experience qua charged and what they experience qua massive.
It is to mark this fact, the fact that charge always "contributes" the same force, that I use the Aristotelian notion of nature. But, as I remarked in referring to Bacon, these modern natures differ from Aristotle's in one very central respect. Although it is in the nature of charge to be subject to a force of q1q2 /r 2 , in the sense that this is what particles experience qua charged, this nature does not in any proper Aristotelian way reveal the essence of charge. What charge is depends on a lot of factors independent of Coulomb's law. As Gerd Buchdahl puts it, there is a mere "brute-fact connection" between what charge is and how charged particles behave qua charged (Metaphysics and the Philosophy of Science [Oxford: Blackwell, 1969]).
One customary response that Humeans make to the kinds of problems I am raising is to resort to counterfactuals. They talk not in terms of actually exhibited qualities and behavior but in terms of possible qualities and behaviors. Coulomb's law gives the force two bodies would experience if their masses were equal to zero. From an empiricist point of view this is a peculiar kind of counterfactual to find at the foundation of our study of motion, for it is one whose antecedent can never be instantiated. But that is not my principal concern.
Instead, I want to point out two other nonempiricist elements that are concealed in this account. The first comes to light when we ask, "Why do we want the masses to go to zero?" The answer: "Because we want to find out what the total force would be, were there no other forces at work." It is the "at work" that one should notice. Put in this blunt fashion, it suggests that the counterfactual account itself is grounded in ideas about powers and their operation, as no good Humean would allow. So the counterfactual antecedent "were the masses equal to zero" is used instead.
My second concern becomes apparent when one asks the obvious next question, "Why do we want to know what the force between charged bodies would be were no other forces at work?" This case is just one particular case among all conceivable ones, and a peculiarly inconvenient one at that. Why, then, are these circumstances so special? They are special because these are the circumstances in which all the hindrances are stripped away so that we can find out what charged particles do "on their own"—that is, what they do by virtue of being charged. This is how they would attract or repel one another were "only" charge at work; and it is how they try to behave even when other factors impede them.
We discover the nature of electrostatic interaction between charges by looking in some very special circumstances. But the charge interaction carries that nature with it, from one circumstance to another. That is why what we call the analytic method in physics works: to understand what happens in the world, we take things apart into their fundamental pieces; to control a situation we reassemble the pieces, we reorder them so they will work together to make things happen as we will. You carry the pieces from place to place, assembling them together in new ways and new contexts. But you always assume that they will try to behave in new arrangements as they have tried to behave in others. They will, in each case, act in accordance with their nature.[2]
The talk of pieces and assembly is a metaphor. How do the behaviors dictated by different natures combine when they are constrained to operate together? There is no general receipt; the answer is, at best, subject-specific. In mechanics, a total force is constructed by vectoral addition from the forces that each component tries separately to create. In the simultaneous-equation models of econometrics, the natural behavior of each independent mechanism is represented in a different equation; when a number of mechanisms work together, all the equations must be satisfied at once. The way in which literal mechanical pieces function together is different again. We employ the method of analysis and synthesis to make predictions and to shape behavior to our own wishes. In each case, we exploit the fact that the pieces when assembled together each continue to "contribute" in accord with their natures. What actually results in a specific case is fixed not only by the natures of the parts but also by the rules that dictate what happens in that domain when natures act together.
The analytic method is closely associated with what we often call Galilean idealization. Together idealization and abstraction form a familiar two-tiered process that lies at the heart of modern scientific inquiry. First, we try to find out by a combination of experimentation, calculation, and inference how the feature under study behaves, or would behave, in a particular, highly specific situation. By controlling for, or calculating away, the gravitational effects, we try to find out how two charged bodies would interact if their masses were zero. But this is just a stage; in itself this information is quite uninteresting. The ultimate aim is to find out how the charged bodies interact not when their masses are zero, nor under any other specific set of circumstances, but rather how they interact qua charged. That is the second stage of the inquiry: we abstract the nature of the charge interaction from how charges behave in these specially selected "ideal" circumstances.
The key here is the concept "ideal." On the one hand, we use this term to mark the fact that the circumstances in question are not real or, at least, that they seldom obtain naturally but require a great deal of contrivance even to approximate. On the other, the "ideal" circumstances are the "right" ones—right for inferring what the nature of the behavior is, in itself. Focusing on the first aspect by itself downplays our problems. We tend to think that the chief difficulties come from the small departures from the ideal that will always be involved in any real experiment: however small we choose the masses in tests of Coulomb's law, we never totally eliminate the gravitational interaction between them; in Galilean experiments on inertia, the plane is never perfectly smooth nor the air resistance equal to zero; we may send our experiments deep into space, but the effect of the large massive bodies in the universe can never be entirely eliminated; and we can perform them at cryogenic temperatures, but the conditions will never, in fact, reach the ideal.
The problem I am concerned with is not whether we can get the system into circumstances where it can operate on its own but rather: what does it mean when we say that the circumstances are ideal, or that the system is operating "on its own"? What is it that dictates which other effects are to be minimized, set equal to zero, or calculated away? This is the question, I maintain, that cannot be answered given the conventional empiricist account of laws. No doubt, in any particular experiment, the equipment we move about, the circumstances we contrive, and the properties we calculate away, are ones that can be described without mentioning natures. But in each case, what makes that arrangement of equipment in those particular circumstances "ideal" is the fact that these are the circumstances where the feature under study operates, as Galileo taught, without hindrance or impediment, so that its nature is revealed in its behavior. Until we are prepared to talk in this way about natures and their operations, to fix some circumstances as felicitous for a nature to express itself, and others as impediments, we will have no way of determining which
principle is tested by which experiment. It is this argument that I want to develop in the rest of this paper.
3—
How Do We Know What We Are Testing?
For anyone who believes that induction provides the primary building tool for empirical knowledge, the methods of modern experimental physics must seem unfathomable. Usually the inductive base for the principles under test is slim indeed, and in the best experimental designs, where we have sufficient control of the materials and our knowledge of the requisite background assumptions is secure, one single instance can be enough. The inference, of course, is never certain, nor irrevocable. Still, we proceed with a high degree of confidence, and indeed, a degree of confidence that is unmatched in large-scale studies in the social sciences, where we do set out from information about a very great number of instances. Clearly, in these physics experiments we are prepared to assume that the situation before us is of a very special kind: it is a situation in which the behavior that occurs is repeatable. Whatever happens in this situation can be generalized.
This peculiar kind of repeatability that we assume for physics experiments requires a kind of permanence of behavior across varying external conditions that is comparable to that of an essence, although not as strong. For example, we measure, successfully we think, the charge or mass of an electron in a given experiment. Now we think we know the charge or mass of all electrons; we need not go on, measuring hundreds of thousands. In so doing, we are making what looks to be a kind of essentialist assumption: the charge or mass of a fundamental particle is not a variable quantity but is characteristic of the particle so long as it continues to be the particle it is.
In most experiments we do not investigate just the basic properties of systems such as charge, but rather more complicated trains of behavior. Diagrammatically, we may think of Galileo's attempts to study the motions of balls rolling down inclined planes; or, entirely at the opposite end of the historical spectrum, the attempts in Stanford's Gravity-Probe-B experiment to trace the precession of four gyroscopes in space, to see how they are affected by the space-time curvature relativistically induced by the earth. Here, too, some very strong assumptions must back our willingness to draw a general conclusion from a very special case. On the surface, it may seem that the license to generalize in these cases can be put in very local terms that need no reference to natures. We require only the assumption that all systems so situated as the one in hand will behave identically. But I think on closer inspection we can see that this is not enough.
We may begin to see why by considering Hume himself. Hume maintained the principle "same cause, same effect." For him, every occurrence is an exem-
plar of a general principle. It is simply a general fact about the world, albeit one we can have no sure warrant for, that identically situated systems behave identically. Hence for Hume, the license to generalize was universal. But not for us. We cannot so easily subscribe to the idea that the same cause will always be succeeded by the same effect. Hume assumed the principle to be true, though not provable. He worried that principles like this one could only be circularly founded, because they could have no evidence that is not inductive. But nowadays we question not just whether our belief in them can be well-founded but whether they are true. Even if we were content with merely inductive warrant, in what direction does our evidence point? The planetary motions seem regular, as do the successions of the seasons, but in general, Nature in the mundane world seems obstinately chaotic. Outside the supervision of a laboratory or the closed casement of a factory-made module, what happens in one instance is rarely a guide to what will happen in others. Situations that lend themselves to generalization are very special, and it is these special kinds of situations that we aim to create, both in our experiments and in our technology. My central thesis here is that what makes these situations special is that they are situations that permit a stable display of the nature of the process under study, or the stable display of the interaction of several different natures.
The case is especially strong when we turn from fictional considerations of ideal reasoning to considerations of actual methodology. Here questions of true identity of circumstance drop away. We never treat complete descriptions; rather we deal with salient characteristics and relevant similarities . This is a familiar point. You do not have to specify everything. If the right combination of factors is fixed, you are in a position to generalize. Yet what makes a specific combination a right one? What is the criterion that makes one similarity relevant and another irrelevant? Case by case, after the fact, it seems we can avoid an answer. We need only say, "In this case, we have picked thus-and-so set of factors; and we assume that so long as this particular set of factors is fixed, the behavior that obtains will be general."
This is the position we arrived at a few paragraphs ago. It provides a defense, of kinds, one by one, of each generalization that we are willing to make on the basis of an experimental study. But it provides no account of what we do. Experiments are designed with intense care and precision. They take hard work, and hard thought, and enormous creative imagination. The Gravity-Probe experiment which I mentioned above is an exaggerated example. It will only be set running twenty years—twenty years of fairly continuous effort—after it was initiated, and it will have involved teams from thirty or forty different locations, each solving some separate problem of design and implementation.
What can account for our effort to make the experimental apparatus just so and no other way? Take the Gravity Probe as a case in point. Each effort is directed to solve a specific problem. One of the very first in the Gravity Probe
involved choosing the material for the gyroscopes. In the end, they are to be made of fused quartz, since fused quartz can be manufactured to be homogeneous to more than one part in 106 . The homogeneity is crucial. Any differences in density will introduce additional precessions, which can be neither precisely controlled nor reliably calculated, and these would obscure the nature of the general-relativistic precession that the experiment aims to learn about.
In this case, we can imagine that the physicists designing the experiment worked from the dictum, which can be formulated without explicit reference to natures, "If you want to see the relativistic precession, you had better make the gyroscope as homogeneous as possible," and they wanted to do that because they wanted to eliminate other sources of precession. But more than that is necessary. The total design of the experiment must take account not only of what else might cause precession but also of what kinds of features would interfere with the relativistic precession, what kinds of factors could inhibit it, and what is necessary to ensure that it will, in the end, exhibit itself in some systematic way. When all these factors are properly treated, we should have an experiment that shows what the nature of relativistic precession is. That is the form, I maintain, that the ultimate conclusion will take.
But that is not the immediate point I want to make. What I want to urge is that, by designing the experiment to ensure that the nature of relativistic precession can manifest itself in some clear sign, by blocking any interference and by opening a clear route for the relativistic coupling to operate unimpeded—according to its own nature—by doing just this, the Gravity-Probe team will create an experiment from which it is possible to infer a general law. At the moment, the form of this law is not my chief concern. Rather, what is at stake is the question, "What must be true of the experiment if a general law of any form is to be inferred from it?" I claim that the experiment must succeed at revealing the nature of the process (or some stable consequence of the interaction of natures) and that the design of the experiment requires a robust sense of what will impede and what will facilitate this. The facts about an experiment that make that experiment generalizable are not facts that exist in a purely Humean world.
It is, of course, not really true that my thesis about the correct form of natural laws is irrelevant to my argument. Put in the most simple-minded terms, what I point out is the apparent fact that we can generalize from a single observation in an experimental context just because that context is one in which all the relevant sources of variation have been taken into account. Then, after all, what I claim is that it is laws in the form I commend—that is, laws about natures—that determine what is and what is not relevant. This sets the obvious strategy for the Humean reply: laws, in the sense of universal or probabilistic generalizations, determine the relevant factors an experiment must control to ensure that it is repeatable. I will discuss this strategy briefly in
the next section. Before turning to it, though, I want to make some clarifications about the concept of generalizability.
I have been using the term 'generalizable' and the term 'repeatable'. Both can be taken in two senses in this discussion. I claim that the Gravity Probe aims to establish a general law about the nature of the coupling of a spinning gyroscope to curved space-time and thereby to learn something about the truth of the general theory of relativity. But along the way, as a by-product, the experiment will reveal, or instantiate, another considerably less abstract law, a law that can far more readily be cast into the conventional form of a universal generalization. This is a law to the effect that any fused-quartz gyroscope of just this kind—electromagnetically suspended, coated uniformly with a very, very thin layer of superfluid, read by a SQUID detector, housed in a cryogenic dewar, constructed just so . . . and spinning deep in space—will precess at the rate predicted. We expect a law like this to obtain because we expect the experiment to establish a stable environment in which whatever happens would happen regularly; that is, we expect the experimental results to be repeatable.
This is a sense of repeatability internal to the experiment itself: given that the experiment is a good one, if it were to be rerun in the same way with the same apparatus, it should teach the same lesson. We need not demand that the regularity instantiated be expressible in some particular language—or in any language, for that matter; nor, as Harry Collins stresses (Changing Order [London: Sage Publications, 1985]), need we insist that the knowledge of how to build the apparatus be explicit knowledge that could be read from the experimenter's notebooks or that could be written in a "how-to-build-it" manual.[3] Yet, if the experiment is to bear on the more general conclusion which we, in the end, want to establish, we do want to insist on the regularity. For part of what is meant by the hypothesis that the coupling between the gyroscope and the curvature has a special nature that bears on the truth of general relativity is that there is a proper, predictable way in which it will behave on its own, if only the circumstances are propitious. To the degree that we doubt that the experiment is repeatable, to that degree at least must we doubt that the behavior we see is a sign of the nature we want to discover.
Although the general (albeit low-level) law that expresses this first kind of repeatability is, it seems, a universal generalization of the conventional form, still the argument I want to make for the necessity of some nonstandard forms in the background bears on it just as forcefully as on the more abstract law that seems directly to describe natures. As with the higher-level law, so too, with the lower-level: if we want to understand why we are entitled to accept this law on such a thin inductive base as the Gravity Probe's four gyroscopes, and if we want to understand the painstaking details of design the experimenters labor over to produce the conditions of the law, we will have to use the idea of a nature, or some related non-Humean notion.
Indeed, I want to make a fairly strong claim here. In the order of generality, the low-level generalization about what happens in just this kind of experimental setup comes first, and the more abstract claim about the general nature of the coupling comes second. We tend to think that the order of warrant is parallel: the low-level generalization comes first and is most secure; the more abstract law derives what warrant it gets from the acceptance of the generalization. I want to urge that there is an aspect of warranting for which this picture is upside down. It is just to the extent that we acknowledge that the experiment is well designed to find out the natures of the interaction, described in the higher-level law, that we are entitled to accept the low-level generalization on the basis of the experimental results.[4]
This is the central argument with which this section began. But it bears repeating now that the distinction between low-level laws, in the form of generalizations, and high-level abstractions has been drawn. Most situations do not give rise to regular behavior. But we can make ones that do. To do so, we deploy facts about the stable natures of the processes we manipulate, and the circumstances that will allow these natures either to act unimpeded or to suffer only impediments that can have a stable and predictable effect. When we have such a situation, we are entitled to generalize from even a single case.[5]
The philosophical underpinning that supports these claims is a more radical shift from the picture in which the conventional view of laws is embedded than I have admitted so far. The conventional view sees laws as universal generalizations and thus takes regularities as given in Nature, as the things that Nature sets, by law. I want to urge that not only must we admit natures into our scientific world picture, contrary to Humean predilections, but in a sense we must eliminate regularities. These are, after all, very rare—at least when we focus on quantitatively exact behavior of the kind we study in physics[6] —and when they occur, either naturally or as a result of human contrivance, they can very plausibly be seen as the consequence of particularly fortunate arrangements that allow the processes involved to play out their stable natures in their occurrent behavior.
Return now to the two senses of repeatability. The first sense is internal to the specific experiment and bears on the low-level generalization that is instanced there. The second sense crosses experiments and bears on the high-level, abstract principle that is established: the results of an experiment should be repeatable in the sense that the high-level principles inferred from a particular experiment should be borne out in different experiments of different kinds. In Nature's Capacities and Their Measurement , this kind of repeatability played a central role in arguing for the abstract character of our high-level laws in physics and for the claim that these abstract laws describe what I here call "natures."[7] Low-level generalization is not enough. It is too tied to the specific details of the particular experiment; a generalization about what occurs there simply does not cover what occurs elsewhere.
We might think that the problem arises merely from the fact that the language of these low-level laws is not abstract enough: we should not be talking about what happens to a spherically homogeneous ball of fused quartz, coated with a superconductor and spinning, electromagnetically suspended, in midair. Rather, we should talk about a gyroscope, and how it precesses. Still the move to more abstract language will not permit us to retain the simple, unproblematic form of a universal generalization. For we do not want to record what all gyroscopes facing a significant space-time curvature do . Rather, we want to record what part the curvature-coupling contributes to how a gyroscope precesses, no matter what, in the end, various and differently situated gyroscopes do. As I described in section 2, that is the core of the analytic method. The point is that we want to learn something from an experiment that is transportable to entirely new situations where quite different circumstances obtain. We do that not by constructing super-abstract generalizations but rather by learning the nature of the pieces from which the new situations are built.
I will not dwell on this argument. More about it can be found in Nature's Capacities . The argument I have wanted to make here is different. In Nature's Capacities , I argue that we need something like natures if we are to generalize in the second sense—to infer from the results of one experiment some kind of law that can cover other situations as well. Here, I want to urge that we need the notion of natures to generalize in the first sense as well—to infer from the results of the experiment some general law that describes what happens, just in this experimental situation, whenever the experiment is run again. Returning to the remarks at the beginning of this section, I may put the point another way. How do we know which generalization, in this low-level sense, the experiment is testing? Not every feature of it is necessary to ensure its repeatability. The answer requires the notion of natures: the features that are necessary are exactly those which, in this very specific concrete situation, allow the nature of the process under study to express itself in some readable way. No weaker account will do. Without the concept of natures we have no way of knowing what it is that we are testing.
4—
Two Objections
I have been arguing that in order to understand what makes experiments special, what ensures that we can generalize from them, we must employ concepts repugnant to a Humean, such as nature, power, impediment, operation. The most obvious responses for a Humean to make would be either that the job can be equally well done by referring only to "occurrent properties" and their regular associations or else that this is a job that does not need to be done.
a . Consider the first objection. We want to figure out what factors are relevant—what factors need to be controlled in a given experiment if that ex-
periment is to be replicable. Imagine, for the sake of argument, that we have available an entire register of all lawlike regularities and that we are not going to quibble about the fact that most of these are as foreign to our world as unicorns. How are we to deploy them? What do we do to determine from this register whether a given factor in our experiment is relevant or not, and needs to be controlled? I suppose the procedure envisaged by the Humean is, very roughly, this: take all those laws whose consequents describe the same kind of behavior (for example, precessing in a gyroscope) as that of the law we wish to infer from our experiment; any factor that appears in the antecedents of one of these laws is a relevant factor—that is, a factor that must be controlled in any experiment to test the law at hand. But at which level of law are we to conduct our search?
At the lower level, there are a very great number of laws indeed. Gyroscopes of all shapes and materials and forms can precess, or fail to precess, in an inconceivable number of different determinate ways in a plentitude of different circumstances. The conditions are too numerous. They give us too many factors to control. Our experiments would be undoable, and the laws they entitle would be narrowed in scope beyond all recognition. But there is a deeper problem: how are these laws to be read? For the Humean, they must be the source of information about not only what factors are to be controlled but in exactly what way. Yet they cannot tell us that, for how a factor operates, at this very concrete level, is far too context-dependent. I give some examples of this kind of context dependence elsewhere.[8]
But I think the point is easy to see. To know exactly what to do with the superconducting coating in the Gravity Probe, one needs to know about the detailed construction of that particular experiment; and the laws one wants to look at are not more laws about precessions but rather laws about superconductors. The point is not whether these further laws are Humean in form or not but rather, how is the Humean to know to look at them? What is the prescription that sorts from among all the factors that appear in all the universal generalizations true in the world, which ones are to be fixed, and how, in this particular experiment?
Perhaps the answer comes one level up. Here I think is where we get the idea that there might be a relatively small number of fixed, probably articulable, factors that are relevant. We may think in terms of forces, how few in kind they are; or of long lists of causes and preventives. What is crucial is that at the abstract level, context seems irrelevant. Either it is or it is not the case that magnetic fields deflect charged particles; or that, as quantum mechanics teaches, an inversion in a population of molecules can cause lasing. Perhaps we can even find a sufficiently abstract law so that the problem seems to evaporate. For example, if we are thinking of an experiment where the effect we look for involves particle motions, we turn to the law F = ma, and that tells us that we must control all sources of force. In the gyroscope experiment, the law of
choice in this case would be
which gives the drift rate
The difficulty with this advice is that it does not justify the replicability we expect unless we join to it a commitment to stable powers of the kind I have been calling natures, or something very much like them. To see why, imagine a single successful run of the experiment, successful in the sense that first, we have indeed managed to set the total net torque, barring that due to relativistic coupling, equal to zero—or, as the Gravity Probe hopes to do, at least to an order of magnitude lower than that predicted for the relativistic effect; and second, it turns out that the observed precession is just that predicted. We seem to have succeeded in giving a purely Humean receipt for when to generalize, and this case fits. Roughly, we can generalize the quantitative relation we see between a designated input (here the relativistic coupling) and the precession actually observed in a given situation if that situation sets the remaining net torque equal to zero (or, more realistically, calculates it away), where the rationale for picking net torque = 0 as the relevant feature comes from the "Humean association" recorded in the functional law that describes the size of precessions.
The problem is that this does not get us the detailed generalization we expect (at the first, lower level). The Gravity-Probe team has worked hard to set the total net torque extremely low, by a large number of specific hard-won designs; and they are entitled to think that the results are replicable in that experimental design. What the Humean prescription entitles them to is weaker. It gives them the right to expect only that on any occasion when the net nonrelativistic torque is zero, the precession will be the value predicted from the general theory of relativity. But we expect the more concrete general claim to hold as well.
Consider the table of design requirements for the gyroscope experiment (diagram 1). The table tells how controlled each foreseeable source of torque must be in order for the total extraneous precession to be an order of magnitude smaller than that predicted from the relativistic coupling. Each such source—rotor homogeneity, rotor sphericity, housing sphericity, optimum preload, and so on—presents a special design problem; and for each, the experiment has a special solution. Using fused quartz to get maximum rotor homogeneity is, for example, the starting point for the solution of the first problem. What all this careful planning, honing, and calculation entitles us to is a far more concrete generalization than the one above about (near) zero

Diagram 3.1
Design Requirements for a Relativity Gyroscope with Limiting Accuracy of 0.5 × 10–16 rad/sec (0.3 milliarc-sec/year) (From C. W. F.
Everitt, coordinator, Report an a Program to Develop a Gyro Test of General Relativity [Stanford, Calif.: W. W. Hansen Laboratories,
Stanford University, 1980].)
external torque. We are entitled to infer from a successful run that in any experiment of this very specific design, the observed precession should be that predicted by the general theory of relativity.[9]
The table of requirements highlights the analytic nature of this kind of experiment, which I discussed in section 2. What happens if something goes wrong with the rotor housing as it was originally planned, and the fault cannot be repaired? With a lot of effort, the Probe team will make a new design and slot it into the old general scheme, making appropriate changes. Because we are working in a domain where we trust analytic methods, a peculiar kind of sideways induction is warranted: from the successful run with the original design plus our confidence in the new rotor housing and its placement, we are entitled to infer a second, highly specific "low-level" generalization to the effect that the precession in situations meeting the new design will be that predicted for relativistic coupling as well. Again, the new situation will indeed be one that falls under the "Humean" generalization involving zero torques. What is missing is the connection. The new situation is one of very small extraneous torque; but the expectation that it should be cannot be read from the regularities of nature.
The regularity theorist is thus faced with a dilemma. In low-level, highly concrete generalizations, the factors are too intertwined to teach us what will and what will not be relevant in a new design. That job is properly done in physics using far more abstract characterizations. The trouble is that once we have climbed up into this abstract level of law, we have no device within a pure regularity account to climb back down again.
b . The second argument is a more transcendental one. It does not attempt to show how it is possible to fix relevance in a world without natures but rather that it must be possible to do so. I borrow the form from arguments made by Bas van Fraassen and by Arthur Fine in debating more general questions of scientific realism. The argument presupposes that we can make available a pure data base, cleansed of natures and their non-Humean relatives. The objection goes like this: "You, Cartwright, will defend the design of a given experiment by talking about what impedes and what facilitates the expression of the nature in question. I take it this is not idle faith but that in each case you will have reasons for that judgment. These reasons must ultimately be based not in facts about natures, which you cannot observe, but in facts about actual behavior, which you can. Once you have told me these reasons, I should be able to avoid the digression through natures and move directly to the appropriate conclusions about relevance. Talk of natures may provide a convenient way to encode information about behaviors, but so long as we insist that scientific claims be grounded in what can be observed, this talk cannot contribute any new information."
But what about this decontaminated data base? Where is it in our experi-
ence? It is a philosophical construction, a piece of metaphysics, a way to interpret the world. Of course, we cannot do without interpretation. But this construction is far more removed from our everyday experience of the world as we interact with it and describe it to others than are homely truths about triggering mechanisms, precipitating factors, impediments, and the like which mark out the domain of natures. Consider an adaptation of van Fraassen's objection to causes, which is a version of essentially the same argument. The objection proceeds from the assumption that there is some defensible notion of a sensible property which is conceptually and logically distinct from any ideas connected with natures. We are then confronted with a challenge to explain what difference natures make: "Imagine a world identical with our own in all occurrences of its sensible qualities throughout its history. How would that world differ from our world?"
On one reading, this argument may be about sequences not of properties in the world but of our experiences of the world. These sequences are to remain the same, but we are to imagine that they are not caused in the usual way by what is going on in the world around us. This reading cannot be the one intended, though, since it does not cut in the right way, revealing special virtues for descriptions like 'is red' or 'is a jet-stream trail' in contrast with ones like 'has the power to relieve headaches' or 'attracts others, qua charged'.
I might further be invited to inspect my experiences and to notice that they are "really" experiences of successions of color patches, say, with powers nowhere to be found. The philosophical dialogue along this line is well rehearsed; I merely point in the familiar directions. My experiences are of people and houses and pinchings and aspirins, all things which I understand, in large part, in terms of their natures. I do not have any raw experience of a house as a patchwork of colors. Even with respect to colors, my experience is of properties like red, whose nature it is to look specific ways in specific circumstances. Sense data, or the given , are metaphysical constructs which, unlike natures, play no role in testable scientific claims. Once there was a hope to mark out among experience some raw pieces by using an epistemological yardstick: the "real" experiences were the infallible ones. After a great deal of debate it is not clear whether this criterion even lets in claims about felt pains; but it surely does not distinguish claims like 'The stripes are red' from 'Your pinching makes my arm hurt'.
The contemporary version of this argument tends, for these reasons, not to be in terms of sense experiences but in terms of sensible properties. But here there is a very simple reply. A world with all the same sensible properties as ours would already be a world with natures. As I remarked above, redness is the property whose nature, among other things, is to look just this way in normal circumstances, and to look systematically different when the circumstances are systematically varied.
Perhaps we are misled here by carrying over the conclusions of an earlier
metaphysics, conclusions for which the premises have been discarded. These premises involve the doctrine of impressions and ideas. In the immediately post-Cartesian philosophy of the British empiricists, sensible properties could be picked out because they looked like their impressions. Gaze at the first stripe on the American flag: redness is the property that looks like that . We do not have this copy theory; so we do not have properties that are identified like that. Correlatively, we can no longer make the same distinction separating powers and their properties as did these seventeenth-century empiricists. On their doctrine, the way things looked could get copied in the perceiver's impressions of them; but the various powers of a property could not. Since their ideas were copies of their impressions, necessarily their world, as imaged, had only inert properties. But we do not have the copy theory of impressions, nor do we adopt this simple theory of concept formation. For us, there are properties, and all properties have powers. (Perhaps, following Sydney Shoemaker, they are all just conglomerates of powers: cf. Identity, Cause, and Mind [Cambridge: Cambridge University Press, 1984], chap. 10.) What they are is given not by how they look but by what they do. When we use a particular power word to describe a property, we focus on one specific aspect of what it can accomplish. When we use an "occurrent" or "sensible" predicate, we refer to the property without highlighting any one thing it does, or any one particular way of identifying it. That is only a very rough characterization of the rules of use. But it points to the fact I want to stress: the distinction is one in language and in what we want to accomplish on specific occasions by using that language. Predicates can be roughly divided into types; but properties and powers are not separable in that way. The question of "How does the Hume world differ from ours?" may have made sense for Locke, Berkeley, and Hume; but without the copy theory of impressions and the related associationist theory of concept formation, nowadays it has an entirely trivial answer.
5—
A Historical Illustration
So far, I have couched the discussion in terms of making inductions from paltry samples, and that is because induction is the method that Humeans should favor for confirming laws. I think, though, that the process is far better understood as one of deduction; we accept laws on apparently slim experimental bases exactly when we can take for granted such strong background assumptions that (given these assumptions) the data plus the description of the experimental setup deductively imply the law to be established. Probably the most prominent advocate of a deductive method in reasoning from experiment to law is Isaac Newton. I think it will be helpful to look briefly at Newton's use of the "crucial experiment" in his theory of light and colors, and more particularly at Goethe's criticisms of it.
Newton's experimentum crucis is described in his first letter in 1671 to the
Royal Society in which he introduces his theory that white light consists of diverse rays of different refrangibility (that is, they are bent by different amounts when the light passes through a prism) and that color is a property of the ray which depends on its refrangibility. The work reported in the letter is generally taken as a model of scientific reasoning. Thomas Kuhn, for instance, claims that "Newton's experimental documentation of his theory is a classic in its simplicity." According to Kuhn, the opposition view might eventually have accounted for some of the data that appeared to refute it, "but how could they have evaded the implications of the experimentum crucis ? An innovator in the sciences has never stood on surer ground" ("Newton's Optical Papers," in Isaac Newton's Papers and Letters , ed. I. B. Cohen [Cambridge, Mass.: Harvard University Press, 1958], 36).
It is important to keep in mind that Newton believed that his claims were proved by his experiments. He claims "the Theory, which I propounded, was evinced by me, not inferring tis thus because not otherwise, that is, not by deducing it only from a confutation of contrary suppositions but by deriving it from experiments concluding positively and directly." Or, "If the Experiments, which I urge, be defective, it cannot be difficult to show the defects; but if valid, then by proving the theory they must render all objections invalid." One last remark to illustrate the steadfastness of Newton's views on the role of the experimentum crucis in proving this claim appears in Newton's letter of 1676, four years after his initial report to the Royal Society. This letter concerned the difficulties Anthony Lucas had reported in trying to duplicate Newton's experiments and also some of Lucas's own results that contradicted Newton's claims. Newton replies, "Yet it will conduce to his more speedy and full satisfaction if he a little change the method he has propounded, and instead of a multitude of things try only the Experimentum Crucis . For it is not number of experiments, but weight to be regarded; and where one will do, what need many?"
Goethe's point of view is entirely opposite to Newton's: "As worthwhile as each individual experiment may be, it receives its real value only when united or combined with other experiments . . . I would venture to say that we cannot prove anything by one experiment or even several experiments together" ("The Experiment as Mediator between Object and Subject," in Johann Wolfgang von Goethe, Scientific Studies , ed. and tr. Douglas Miller [New York: Suhrkamp, 1988]). For Goethe, all phenomena are connected together, and it is essential to follow through from each experiment to another that "lies next to it or derives directly from it." According to Goethe, "To follow every single experiment through its variations is the real task of the scientific researcher." This is illustrated in his own work in optics where he produces long series of "contiguous" experiments, each of which is suggested by the one before it. The point is not to find some single set of circumstances that are special but rather to lay out all the variations in the phenomena as the circumstances change in a
systematic way. Then one must come to see all the interrelated experiments together and understand them as a whole, "a single piece of experimental evidence explored in its manifold variations."
Goethe is sharp in his criticisms of Newton. Two different kinds of criticism are most relevant here. The first is that Newton's theory fails to account for all the phenomena it should, and that that is no surprise since Newton failed to look at the phenomena under a sufficient range of variation of circumstance. Second, Newton's inferences from the experiments he did make were not valid; the experimentum crucis is a case in point. The chief fault which Goethe finds with Newton's inferences is one that could not arise in Goethe's method. Newton selects a single revealing experiment to theorize from; since he does not see how the phenomena change through Goethe's long sequence of experiments, he does not recognize how variation in circumstance affects the outcome: "[Newton's] chief error consisted in too quickly and hastily setting aside and denying those questions that chiefly relate to whether external conditions cooperate in the appearance of color, without looking more exactly into the proximate circumstances" (Dennis L. Sepper, Goethe contra Newton [Cambridge: Cambridge University Press, 1988], 144).
The crucial experiment involves refracting a beam of light through a prism, which elongates the initial narrow beam and "breaks" it into a colored band—violet at the top, red at the bottom. Then differently colored portions of the elongated beam are refracted through a second prism. Consider diagram 2, which is taken from Dennis L. Sepper's study, Goethe contra Newton . In all cases, the color is preserved, but at one end of the elongated beam the second refracted beam is elongated more than it is at the other. In each case, there is no difference in the way in which the light falls on the prism for the second refraction. Newton immediately concludes, "And so the true cause of the length of the image was detected to be no other than that light consists of rays differently refrangible " (Newton's first letter to the Royal Society, 1671).
We should think about this inference in the context of my earlier cursory description of the modern version of the deductive method, called bootstrapping by Clark Glymour, who has been its champion in recent debates. In the bootstrapping account, we infer from an experimental outcome to a scientific law, as Newton does, but only against a backdrop of rather strong assumptions. Some of these assumptions will be factual ones about the specific arrangements made—for example, that the angle of the prism was 63°; some will be more general claims about how the experimental apparatus works—the theory of condensation in a cloud chamber, for instance; some will be more general claims still—for example, all motions are produced by forces; and some will be metaphysical, such as the "same cause, same effect" principle mentioned in section 3. The same is true of Newton's inference. It may be a perfectly valid inference, but there are repressed premises. It is the repressed premises that Goethe does not like. On Goethe's view of nature, they are not
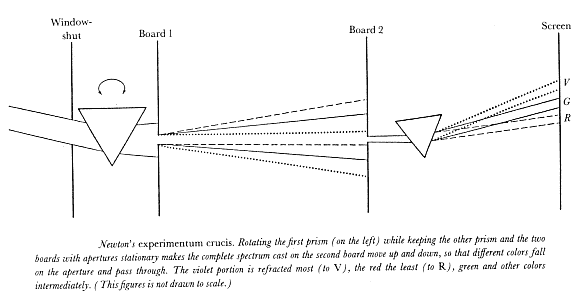
Diagram 3.2
(From Dennis L. Sepper Goethe contra Newton
[(Cambridge: Cambridge University Press, 1988].)
only badly supported by the evidence; they are false. Colors, like all else in Goethe's world,[10] are a consequence of the action of opposites, in this case light and darkness:
We see on the one side light, the bright; on the other darkness, the dark; we bring what is turbid between the two [such as a prism or a semitransparent sheet of paper], and out of these opposites, with the help of this mediation, there develop, likewise in an opposition, colors. (Theory of Colors , didactic part, paragraph 175)
Newton's argument requires, by contrast, the assumption that the tendency to produce colors is entirely in the nature of the light, and that is why this dispute is of relevance to my point here. As Sepper says, for Newton "the cause is to be sought only in the light itself."
Let us turn to Newton's reasoning. The argument is plausible, so long as one is not looking for deductive certainty. From Newton's point of view (though not from that of Goethe, who imagines a far richer set of possibilities), the two hypotheses to be decided between are: (a) something that happens involving white light in the prism produces colored light; or (b) colored light is already entering the prism in the first place. We can see the force of the argument by thinking in terms of inputs and outputs. Look at what happens to, say, the violet light in the second prism (diagram 3):
Diagram 3.3.
Compare this with the production of violet light in the first prism (diagram 4):
Diagram 3.4.
In both cases, the outputs are the same. The simplest account seems to be that the prism functions in the same way in both cases: it just transports the colored light through, bending it in accord with its fixed degree of refrangibility.
Consider an analogous case. You observe a large, low building. Colored cars drive through. Cars of different colors have different fixed turning radii. You observe for each color that there is a fixed and color-dependent angle between the trajectory on which the car enters the building, and the trajectory on which it exits; moreover, this is just the angle to be expected if the cars were driven through the building with steering wheels locked to the far left. Besides cars, other vehicles enter the building, covered; and each time a covered vehicle enters, a colored car exits shortly afterward. It exits at just that angle that would be appropriate had the original incoming vehicle been a car of the same color driven through with its steering wheel locked. Two hypotheses are offered about what goes on inside the building. Both hypotheses treat the incoming colored cars in the same way: on entering the building, their steering wheels get locked and then they are driven through. The two hypotheses differ, however, about the covered vehicles. The first hypothesis assumes that these, too, are colored cars. Inside the building they get unwrapped, and then they are treated just like all the other colored cars. The second hypothesis is more ambitious. It envisages that the low building contains an entire car factory. The covered vehicles contain raw material, and inside the building there are not only people who lock steering wheels, but a whole crew of Fiat workers and machinery turning raw materials into cars.
Obviously, the first hypothesis is simpler, but it has more in its favor than that. For so far, the second hypothesis has not explained why the manufactured cars exit at the angle they do, relative to their incoming raw materials; and there seems to be no immediate natural account to give on the second story. True, the cars are manufactured with fixed turning radii, but why should they leave the factory at just the same angle relative to the cart that carries in their raw materials as a drive-through does relative to its line of entry? After all, the manufactured car has come to exist only somewhere within the factory, and even if its steering wheel is locked, it seems a peculiar coincidence should that result in just the right exit point to yield the required angle vis-à-vis the raw materials. In this case, barring other information, the first, Newtonian, hypothesis seems the superior. The caveat, "barring other information," is central, of course, to Goethe's attack. For, as I have already remarked, Goethe was appalled at the small amount of information that Newton collected, and he argued that Newton's claim was in no way adequate to cover the totality of the phenomena. What looks to be the best hypothesis in a single case can certainly look very different when a whole array of different cases have to be considered.
The principal point to notice, for my purpose, is that the argument is not at all deductive. It can only become so if we already presuppose that we are looking for some fixed feature in light itself that will account for what comes
out of the prism—something, as I would say, in the nature of light. Any assumption like this is deeply contrary to Goethe's point of view. The first few paragraphs of Newton's letter, before the introduction of the crucial experiment, give some grounds for such an assumption on his part; Goethe makes fun of them:
It is a fact that under those circumstances that Newton exactly specifies, the image of the sun is five times as long as it is wide, and that this elongated image appears entirely in colors. Every observer can repeatedly witness this phenomenon without any great effort.
Newton himself tells us how he went to work in order to convince himself that no external cause can bring this elongation and coloration of the image. This treatment of his will, as already was mentioned above, be subjected to criticism for we can raise many questions and investigate with exactness, whether he went to work properly and to what extent his proof is in every sense complete.
If one analyzes his reasons, they have the following form:
When the ray is refracted the image is longer than it should be according to the laws of refraction.
Now I have tried everything and thereby convinced myself that no external cause is responsible for this elongation.
Therefore it is an inner cause, and this we find in the divisibility of light. For since it takes up a larger space than before, it must divided, thrown asunder; and since we see the sundered light in colors, the different parts of it must be colored.
How much there is to object to immediately in this rationale! [Goethe, 1793; quoted from Sepper, p. 101]
The contrast that I want to highlight is between Newton's postulation of an inner cause in light versus Goethe's long and many-faceted row of experiments. Goethe often remarks that he and Newton both claim to be concerned with colors ; Newton after all labels his account in the 1671 letter his "new theory of light and colors." But, in actuality, Goethe points out, Newton's work is almost entirely about the behavior of rays—that is, about the inner nature of light. Goethe's experiments often involve light, but it is not light that he studies. The experiments describe entire interacting complexes, such as evening light entering a room through a hole in a white blind on which a candle throws light ("snow seen through the opening will then appear perfectly blue, because the paper is tinged with warm yellow by the candlelight" [Theory of Colors , didactic part, paragraph 79]), or sunlight shining into a diving bell (in this case "everything is seen in a red light . . . while the shadows appear green" [Theory of Colors , didactic part, paragraph 78]), or a particularly exemplary case for the existence of colored shadows, a pencil placed on a sheet of white paper between a short, lighted candle and a window so that the twilight from the window illuminates the pencil's shadow from the candle ("the shadow will appear of the most beautiful blue" [Theory of Colors , didactic part, paragraph 65]). Even when described from the point of view of Goethe's final account of color forma-
tion, in the prism experiments Goethe is not looking at light but rather at light (or darkness) -in-interaction-with-a-turbid-medium.
Newton focuses on his one special experiment and maintains that the account of the phenomena in that experiment will pinpoint an explanation that is generalizable. The feature that explains the phenomena in that situation will explain phenomena in other situations; hence he looks to a feature that is part of the inner constitution of light itself. To place it in the inner constitution is to cast it not as an observable property characteristic of light but rather as a power that reveals itself, if at all, in appropriately structured circumstances. To describe it as part of light's constitution is to ascribe a kind of permanence to the association: light retains this power across a wide variation in circumstance—indeed, probably so long as it remains light. That is, I maintain, to treat it as an Aristotelian-style nature. This is why Newton, unlike Goethe, can downplay the experimental context. The context is there to elicit the nature of light; it is not an essential ingredient in the ultimate structure of the phenomenon.
6—
Conclusion
My argument in this paper hinges on a not surprising connection between methodology and ontology. If you want to find out how a scientific discipline pictures the world, you can study its laws, its theories, its models, and its claims—you can listen to what it says about the world. But you can also consider not just what is said but what is done. How we choose to look at the world is just as sure a clue to what we think the world is like as what we say about it. Modern experimental physics looks at the world under precisely controlled or highly contrived circumstances; and in the best of cases, one look is enough. That, I claim, is just how one looks for natures, and not how one looks for information about what things do.
Goethe criticizes Newton for this same kind of procedure that we use nowadays, and the dispute between them illustrates my point. Newton's conclusions in his letter of 1671, as well as throughout his later work in optics, are about the inner constitution of light. I claim that this study of the inner constitution is a study of an Aristotelian-style nature and that Newton's use of experiment is suited to just that kind of enterprise, where the experimentum crucis is an especially striking case. The colored rays, with their different degrees of refrangibility, cannot be immediately seen in white light. But through the experiment with the two prisms, the underlying nature expresses itself in a clearly visible behavior: the colors are there to be seen, and the purely dispositional property, degree-of-refrangibility , is manifested in the actual angle through which the light is bent. The experiment is brilliantly constructed: the connection between the natures and the behavior that is supposed to reveal them is so tight that Newton takes it to be deductive.
Goethe derides Newton for surveying so little evidence, and his worries are not merely questions of experimental design: perhaps Newton miscalculated, or mistakenly assumed that the second prism was identical in structure with the first, or Newton takes as simple what is not . . . Goethe's disagreement with Newton is not a matter of mere epistemological uncertainty. It is rather a reflection of deep ontological differences. For Goethe, all phenomena are the consequence of interaction between polar opposites. There is nothing in light to be isolated, no inner nature to be revealed. No experiment can show in a single behavior what light does qua light, for by itself there is nothing, no special single thing that it is in the nature of light to do. The empiricists of the scientific revolution wanted to oust Aristotle entirely from the new learning. I have argued that they did no such thing. Goethe, by contrast, did dispense with natures; there are none in his world picture. But there are, I maintain, in ours.
Four—
Genetic Inference:
A Reconsideration of David Hume's Empiricism
Barbara D. Massey and Gerald J. Massey
1—
Hume's Fork
What could be more banal than Hume's fork, the bifurcation of objects of inquiry (true propositions) into relations of ideas and matters of fact ? Surely historians have so thoroughly scrutinized this celebrated dichotomy that we can be confident of their deliverances on this topic. Let us review, then, the received view of Hume's fork.
True propositions like '3 times 5 equals one-half of 30' and the Pythagorean theorem express relations of ideas, while ones like 'Fire burns' and 'The sun will rise tomorrow' record matters of fact or real existence. What is distinctive about a relation of ideas is that its negation entails a contradiction. The negation of every matter-of-factual truth, in contrast, is conceivable and so does not entail a contradiction because whatever is conceivable is possible. Hume's taxonomy of true propositions (objects of inquiry) is clearly disjoint and exhaustive: each true proposition falls into one and only one of his two compartments. And that the classification is dichotomous, that is, necessarily disjoint and exhaustive, can be grasped a priori because it is based on the presence or absence of a single property, namely, conceivability of the proposition's negation.[1]
Against the received view we note that Hume regularly uses his fork as if it speared all propositions, the false ones no less than the true. For example, he often makes the prior assessment that a given proposition is matter-of-factual or a relation of ideas an important part of his determination of its truth value, as in this passage from the first Enquiry :
It is a question of fact, whether the perceptions of the senses be produced by external objects resembling them. How shall this question be determined? By experience surely, as all other questions of a like nature. But here experience is,
and must be entirely silent. The mind has never any thing present to it but the perceptions, and cannot possibly reach any experience of their connexion with objects. The supposition of such a connection is, therefore, without any foundation in reasoning.[2]
But this is to argue in a circle and bears witness to a fundamental incoherence in Hume's system of philosophy.
Nor is it clear that the classification is dichotomous even when limited to true propositions. Perhaps Hume did intend initially to make a true proposition's classification depend solely on the conceivability of its negation. If so, he soon forgot his resolve. For whether a proposition is matter-of-factual or a relation of ideas becomes for Hume as much a matter of how it can be known (via intuition and demonstration or via observation and causal inference) as a matter of how its negation can be conceived. For the most part this ambivalence causes Hume little discomfort, for the two ways of understanding the classificatory basis match up pretty well. But when they fail to line up, watch out! And, unluckily for Hume, they do indeed sometimes fail to line up—for example, in such important cases as the allegedly factual thesis of the double existence of objects and perceptions. Quine's doctrine that definitional status is a passing trait of the truths of science surely took its inspiration from verbal behavior like Hume's![3]
We are told that Hume's fork answers tolerably well to our necessary/contingent distinction and even to our a priori/a posteriori distinction. Furthermore, the story goes, Kant pretty much took over Hume's dichotomy while embellishing it in two significant ways. First, he promoted strict universality and necessity as the marks of the a priori, that is, of relations of ideas. Second, he subdivided the a priori itself into analytic and synthetic, thereby setting the stage for his famous interrogative "How are synthetic judgments a priori possible?"
But, as we shall shortly see, Kant fundamentally misunderstood Hume. Kant failed to see that Hume, the champion of modern empiricism, himself posited faculties of synthetic a priori cognition beyond anything that he, Kant, ever dreamed of. Kant should perhaps not be much faulted for this latter oversight, however. For, mirabile dictu , Hume himself failed to take much notice of the faculties of synthetic a priori cognition with which he liberally sprinkled his system of philosophy. So, anyway, we will argue.
2—
Hume's View of Animals
Let's begin our rethinking of Hume's fork by remarking upon a trait of David Hume that sets him apart from virtually all his contemporaries and predecessors and that has endeared him to animal lovers everywhere, namely, his resolute solidarity with "beasts." Never the species chauvinist, Hume saw human beings as animals among animals, distinguished in certain ways from beasts
but only extrinsically marked off from them by the greater power and subtlety of shared cognitive powers:
Next to the ridicule of denying an evident truth, is that of taking much pains to defend it; and no truth appears to me more evident, than that beasts are endow'd with thought and reason as well as men. The arguments are in this case so obvious, that they never escape the most stupid and ignorant.
We are conscious, that we ourselves, in adapting means to ends, are guided by reason and design, and that 'tis not ignorantly or casually we perform those actions, which tend to self-preservation, to the obtaining pleasure, and avoiding pain. When therefore we see other creatures, in millions of instances, perform like actions, and direct them to like ends, all of our principles of reason and probability carry us with an invincible force to believe the existence of a like cause.[4]
Further, Hume notes that the three primitive relations of his associationist psychology operate in animals no differently than in humans:
. . . there is evidently the same relation of ideas, and deriv'd from the same causes, in the minds of animals as in those of men. A dog, that has hid a bone, often forgets the place; but when brought to it, his thought passes easily to what he formerly conceal'd, by means of the contiguity, which produces a relation among his ideas. In like manner, when he has been heartily beat in any place, he will tremble on his approach to it, even tho' he discover no signs of any present danger. The effects of resemblance are not so remarkable; but as that relation makes a considerable ingredient in causation, of which all animals shew so evident a judgement, we may conclude that the three relations of resemblance, contiguity and causation operate in the same manner upon beasts as upon human creatures.[5]
The fact that human and animal behavior closely resemble each other, and hence that the animal mind is like the human mind,
furnishes us with a kind of touchstone, by which we may try every system in this species of philosophy. 'Tis from the resemblance of the external actions of animals to those we ourselves perform, that we judge their internal likewise to resemble ours. . . . When any hypothesis, therefore, is advanc'd to explain a mental operation, which is common to men and beasts, we must apply the same hypothesis to both; and as every true hypothesis will abide this trial, so I may venture to affirm, that no false one will ever be able to endure it.[6]
Here, then, is a philosopher who knows animals and takes them seriously. He prides himself on the alleged fact that his own philosophical system deals evenhandedly with humans and animals. He justifies this pride by a theory of evidence that characterizes as better supported those systems that are evenhanded in the aforementioned respect. It may come as a shock, therefore, when we demonstrate shortly that Hume's treatment of the cognitive powers of humans and animals is decidedly asymmetrical. Even more surprisingly, we will
show that the imbalance favors beasts. More surprising still will be the consequences of this psychological asymmetry for Hume's system, and for Kant's as well.[7]
Hume observes in the Section "Of the reason of animals" in Book I of the Treatise that:
men are not astonish'd at the operations of their own reason, at the same time, that they admire the instinct of animals, and find a difficulty in explaining it, merely because it cannot be reduc'd to the very same principles. To consider the matter aright, reason is nothing but a wonderful and unintelligible instinct in our souls, which carries us along a certain train of ideas. . . . This instinct, 'tis true, arises from past observation and experience; but can any one give the ultimate reason, why past experience and observation produces such an effect, any more than why nature alone shou'd produce it? Nature may certainly produce whatever can arise from habit: Nay, habit is nothing but one of the principles of nature, and derives all its force from that origin.[8]
Hume's writings are replete with talk of cognitive instincts , cognitive propensities , cognitive inclinations , and the like. These instincts or propensities seem to come in two quite different varieties which we will call generalized and specialized . A good illustration of a generalized cognitive instinct is the inductive propensity, the cognitive instinct that Hume has in mind in the passage just cited. The inductive instinct determines us to pass to the idea of B when presented with the idea of A, and to transfer vivacity from the idea of A to that of B, when we have experienced a number of cases where an A is followed by a B and no cases where a B has failed to follow an A. It is a propensity shared by humans and animals alike. Other generalized cognitive instincts will be enumerated presently and will be found also to be common to humans and animals.
By specialized cognitive instincts we mean what people commonly refer to as instincts , that is, those cognitive endowments responsible for complex behavior that is adaptive but unlearned. Hume describes the affinity of "experimental reasoning," notably the inductive propensity, to the specialized cognitive instincts with an eloquence unsurpassed anywhere in his writings:
But though animals learn many parts of their knowledge from observation, there are also many parts of it, which they derive from the original hand of nature; which much exceed the share of capacity they possess on ordinary occasions; and in which they improve, little or nothing, by the longest practice and experience. These we denominate INSTINCTS, and are so apt to admire, as something very extraordinary, and inexplicable by all the disquisitions of human understanding. But our wonder will, perhaps, cease or diminish; when we consider, that the experimental reasoning itself, which we possess in common with beasts, and on which the whole conduct of life depends, is nothing but a species of instinct or mechanical power, that acts in us unknown to ourselves; and in its chief operations, is not directed by any such relations or comparisons of ideas, as are the
proper objects of our intellectual faculties. Though the instinct be different, yet still it is an instinct, which teaches a man to avoid the fire; as much as that, which teaches a bird, with such exactness, the art of incubation, and the whole economy and order of its nursery.[9]
For Hume, much and perhaps even most animal knowledge is instinctive. Such knowledge is not learned or acquired through experience. On the contrary, it is directly implanted in the animal by a providential Nature independently of experience. Modern ethology and contemporary cognitive science support Hume's contention. The newborn wildebeest (gnu) does not have to learn that the lioness bearing down on it is dangerous, or that this circumstance calls for rapid locomotion in an opposite direction; it comes into the world ready-equipped with such vital information. Even more to our point, the neonatal wildebeest, unlike the human infant, is not condemned to acquire knowledge of its visual space experimentally; it derives from the original hand of Nature the spatial knowledge that the human baby must learn slowly and painfully. That is to say, much that in humans is or would have to be learned experimentally by means of the inductive instinct is possessed innately by beasts. A generous Mother Nature lavishes true matter-of-factual beliefs on animals, but she only begrudgingly grants humans a generalized cognitive endowment by means of which they can wrest from her those facts of life they must know to survive. In short, Hume's Nature functions not as a solicitous Mother to the human species but as a cold Stepmother who sends her charges into the world impoverished and uninstructed to survive on their wits alone.
These decidedly Humean doctrines explode the myth of evenhandedness in Hume's psychological treatment of animals and humans. True, both humans and animals possess generalized cognitive endowments like the inductive propensity, but only animals possess specialized cognitive endowments that afford them a priori knowledge of countless matters of fact or real existence.
3—
A Second Look at Hume's Fork
According to the received view, Hume championed empiricism by demonstrating that no matter of fact or real existence can be known a priori; experience alone makes such knowledge possible. Certainly, Hume himself claims to have done just this. But we have seen that Hume attributes to animals a priori knowledge of matters of fact with a liberality that would astonish even the most rabid rationalist. Had Kant rightly understood Hume, he would have rephrased his famous query thus: "How is a priori knowledge of matters of fact possible for animals when it is not possible for human beings ?"
To ask this question is almost to answer it. For we cannot then help but notice that it is clearly an empirical matter whether human beings or any other organisms possess a priori knowledge of matters of fact. No one should have appreciated this circumstance better than Hume. In the already cited passage
from the Treatise about reason's status as instinct, Hume expressly remarks that "Nature may certainly produce whatever can arise from habit: Nay, habit is nothing but one of the principles of nature, and derives all its force from that origin." He surely intends that any matter-of-factual belief acquired by an organism by means of its inductive instinct could have been planted directly in the organism by Nature; that is, it could have been part of the organism's native endowment.
What, then, of Hume's celebrated demonstration that knowledge of matters of fact or real existence is impossible a priori, that all such knowledge is and must be predicated on experience? Hume's argument turns crucially on the conceivability of alternatives to every matter of fact. Even to Adam's reason in the fullness of its paradisiacal powers, the proposition that fire burns would have recommended itself no more and no less than the proposition that fire freezes; only repeated experience of fire enabled poor Adam, no doubt suffering acutely from second-degree burns, to infer that fire does indeed consume:
And as the power, by which one object produces another, is never discoverable merely from their idea, 'tis evident cause and effect are relations, of which we receive information from experience, and not from any abstract reasoning or reflexion. There is no single phaenomenon, even the most simple, which can be accounted for from the qualities of the objects, as they appear to us; or which we cou'd foresee without the help of our memory and experience.[10]
If you understand "reason" narrowly enough, you will find that Hume's argument is sound but irrelevant to the issue whether matters of fact can be known a priori. But if you take "reason" broadly enough to make the argument relevant , you will discover it to be unsound . Here's why.
Let narrow reason be a faculty limited to concepts, that is, a faculty of forming concepts and of analyzing and comparing them. Hume's argument does indeed show that narrow reason cannot discriminate among matter-of-factual propositions in a nonarbitrary way. But of course there is much more to mind than narrow reason. In particular, mind may encompass other cognitive faculties that exhibit partiality to certain matter-of-factual propositions, perhaps even to many of the true propositions belief in which is requisite to survival and well-being. This is no mere speculative hypothesis. We know from our experience of animals that their minds must include some such faculties of a priori factual cognition.
Let broad reason be a faculty coextensive with mind. To show that all factual propositions fare alike at the tribunal of broad reason would indeed be to show that "our reason, unassisted by experience, [can never] draw any inference concerning real existence and matter of fact."[11] But Hume's appeal to the conceivability of the negation of every matter-of-factual proposition reveals nothing about the capacity of broad reason innately to seize upon certain factual propositions while rejecting others.
We did not ourselves conjure up the distinction between narrow reason and broad reason, handy though it is for making our point. The honor of authorship is dubiously Hume's. You will find an ambiguity corresponding to the distinction traded on in all his arguments against the a priori knowability of causal connections. It is unfortunate that this ambiguity blinded him and a legion of later philosophers to the fallaciousness of his favorite demonstration.
Let us look again at the two bases for classifying propositions as relations of ideas or matters of fact, namely, whether their negations are conceivable and whether they are knowable through mental activity independently of experience. Whether or not a proposition like 'Fire burns' or 'The sun will rise tomorrow' is matter-of-factual will itself be an empirical matter, a matter of fact, if we adopt the second basis, that is, if we make the proposition's status a matter of the manner in which it can be known. When we give Hume's fork this basis, we discover that his celebrated empiricist thesis —no factual proposition can be known a priori—becomes itself empirical , a genuinely Humean line but perhaps not genuinely Hume's. By contrast, to choose the first basis for Hume's fork saves more of the letter of Hume's philosophy but only by cutting against its grain.
Hume was a supremely sharp and meticulous thinker. How, then, could he have been blind to the glaring defects in his empiricist doctrines that we have pointed out? We hinted at an answer earlier. So long as he ignored the a priori cognition of animals while denying to humans any specialized cognitive instincts or endowments, the two bases for his fork matched up pretty well, close enough anyway for philosophical work!
Can we defend Hume against the charge of invidious anomaly which we have leveled at his philosophical psychology, namely, that it credits animals with both generalized and specialized cognitive instincts but credits humans only with generalized ones? One tack might be to argue that specialized cognitive instincts like those found in animals are incompatible with highly developed generalized cognitive instincts of the sort found in humans, that is, that the highly developed generalized cognitive instincts would cancel or so completely dominate the specialized ones that the latter would have no cognitive role to play.
But this is not a tack on which Hume can easily sail. He delights in asserting that nature so ruthlessly dominates reason that competition between them is no contest at all. At best, reason will enjoy the upper hand only briefly, because
there is a great difference betwixt such opinions as we form after a calm and profound reflection, and such as we embrace by a kind of instinct or natural impulse, on account of their suitableness and conformity to the mind. If these opinions become contrary, 'tis not difficult to foresee which of them will have the advantage. As long as our attention is bent upon the subject, the philosophical and study'd principle may prevail; but the moment we relax our thoughts, nature will display herself, and draw us back to our former opinion. Nay she has
sometimes such an influence, that she can stop our progress, even in the midst of our most profound reflections, and keep us from running on with all the consequences of any philosophical opinion.[12]
For Hume, therefore, if either is to annihilate the other, the specialized cognitive instincts will cancel the generalized ones.
Here is a more promising tack. Perhaps the "anomaly," as we call it, is no embarrassment to Hume at all. Perhaps it registers a plain matter of fact recognized by Hume and taken account of in his philosophical psychology. After all, contemporary scientists and philosophers agree that human beings innately possess various generalized cognitive endowments, but they heatedly debate whether humans innately possess specialized cognitive endowments. Consider, for example, the Skinner-Chomsky-Quine controversy over innate linguistic endowments. Chomsky pleads that specialized cognitive endowments are needed to explain certain features of linguistic behavior; Quine and Skinner insist that we can explain all aspects of verbal behavior by means of the experience and generalized cognitive endowments of language-users; anything more is unneeded and undesirable.[13]
4—
Hume:
Empiricist or Rationalist?
Hume is liberal, almost profligate, in endowing human beings with cognitive instincts. For example, in addition to the inductive instinct already encountered, there is what we will call the externalizing propensity , the instinct that determines rustics to attribute unbroken duration to certain of their intermittent perceptions and that determines the learned to posit a universe of enduring, mind-independent objects. It is not peculiar to humans; animals too possess the externalizing propensity. Then there is the egoizing propensity , the instinct that determines human beings to take themselves to be substantial selves, that is, to personify certain bundles of perceptions. Animals, too, seem to possess the egoizing propensity. There may also be a causal propensity that determines both humans and animals to expect a cause of every event they meet with, but this conjecture is more controversial and we will not insist upon it. One stumbles upon many other cognitive propensities or instincts in Hume's philosophy, but this is not the place to enumerate them.[14]
Notice that all these cognitive instincts are generalized endowments. The beliefs that the externalizing propensity and the egoizing propensity occasion, Hume's so-called natural beliefs , are themselves quite general: belief in bodies, belief in external objects, belief in personal selves. Experience is required to trigger them, but no particular experiences. Whatever be the experience of a human or animal, it will come to have these natural beliefs, at least so long as its experience or train of impressions exhibits a modicum of coherency. Inductive beliefs, that is, the beliefs produced by the inductive propensity, are different. They are particular beliefs such as 'Fire burns' or 'The sun will rise
tomorrow'. Not any old experiences trigger them. Unless Adam consorts frequently enough with fire, he will never acquire the belief that it burns. (At least he will not acquire this belief directly through the inductive propensity. He may come to hold this belief because of something Eve told him, thereby acquiring it indirectly through the inductive propensity, or madness or disease contracted after their expulsion from Paradise might perhaps produce it in him.)
We have already seen that Hume took Nature to implant many particular beliefs of the 'Fire burns' variety directly into animals, beliefs determined by specialized cognitive endowments or instincts. What experiences trigger these beliefs, if indeed they are triggered by experience? It would seem that no special experiences are required to trigger them; if they are triggered at all, they are triggered by any experiences whatsoever. But this cannot be the whole story. Surely the neonatal wildebeest contentedly sucking its mother's teat is not thinking about lions until sight of the charging lioness triggers its belief that lions are dangerous. Shall we say that the terrified wildebeest had the dispositional belief that lions are dangerous all along but that the awesome spectacle presented by the charging lioness triggered its occurrent belief that lions are dangerous? That is, shall we say that the beliefs produced by specialized cognitive instincts are dispositional, that they are present in the animal apart from and prior to any experience, and that relevantly appropriate particular experiences are requisite only to trigger the corresponding occurrent beliefs?
We might as well say so, for Hume's writings offer no help. You will search them in vain for the distinction between dispositional and occurrent belief, partly because eighteenth-century philosophers did not make much of it and partly because the distinction ill comports with his theory of belief as a certain feeling connected to a proposition.
Let us take stock of where we have arrived in our attempt to defend Hume. We have seen that Hume posited a number of generalized cognitive instincts common to humans and animals, that some of these generalized instincts engender very general beliefs (the so-called natural beliefs ) in both humans and animals, that these generalized instincts generate these general beliefs independently of particular experiences, that the inductive instinct (itself a generalized instinct) gives rise to particular beliefs in both humans and animals but only when triggered by particular experiences of a relevant kind, and that animals are innately endowed with specialized cognitive instincts that engender many particular dispositional beliefs independently of experience although appropriate experiences are needed to trigger the corresponding occurrent beliefs. To save Hume, we need add only one more item to this litany, namely, that our experience of human beings gives us no reason to suppose that they are innately endowed with any specialized cognitive instincts, the ones that generate particular beliefs independently of particular experiences.
There still remains an anomaly in Hume's philosophical psychology, that is, a respect in which humans and animals do not fare alike, but it is an anomaly
that does Hume's reputation more credit than injury. According to Hume, only animals possess specialized cognitive instincts, not because some unbridgeable spiritual divide separates humans from animals, nor because of any philosophical preconceptions or biases about the human or the animal mind, but because of the brute fact that only brutes have instincts keyed to brute facts . It might well have been different. If newborn humans behaved more like neonatal wildebeests, then we would credit ourselves, too, with specialized cognitive instincts, with a generous portion of instinctive knowledge of matters of fact served up by a benevolent Mother Nature.
So, if we understand by empiricism the doctrine that no organism can have a priori knowledge of particular matters of fact, Hume turns out to be an antiempiricist, indeed an unbridled rationalist. But if we take empiricism to be the thesis that human beings do not have a priori knowledge of particular matters of fact but must acquire such knowledge on the basis of appropriate particular experiences, Hume was an empiricist for pretty convincing empirical reasons. And, for an empiricist, could there be a better kind of reason for being an empiricist?
Does Hume then deserve to be canonized as the patron saint of modern empiricism? It all depends on whom you survey. What one might call dogmatic empiricism refuses a priori knowledge of any fact, general as well as particular, to every organism. Dogmatic empiricists will find Hume's attribution to both animals and humans of generalized cognitive instincts, cognitive endowments productive of such general knowledge as the natural beliefs in an external world and a substantial self, altogether as noxious as the specialized cognitive instincts which he attributed to beasts alone. These dogmatists might well upbraid Hume for failing to recognize that his fork has no tine for the natural beliefs. (The negations of these propositions are conceivable and so they are factual, yet they can be known more or less independently of experience.) So, even if he had not professed to find specialized cognitive endowments in animals, Hume's treatment of the natural beliefs itself and alone constitutes a betrayal of empiricism in the eyes of these zealots. Hence, dogmatic empiricists will not hesitate to deliver their verdict loud and clear: David Hume sold out to rationalism.
But neither in philosophy nor in ordinary life should we permit fanatics to decide what is virtuous. In its widest signification, empiricism denominates those varieties of philosophy that take observation and experience seriously, especially scientific observation and scientific experimentation. Nothing we have said about Hume detracts from his reputation in this regard. True, his system of philosophy recognizes a great deal of a priori knowledge of matters of fact, both general and particular. But from an empiricist point of view, the saving grace is that this recognition is itself based on observation and experience of a fairly compelling sort. By grounding his innatist views about cognitive endowments thoroughly in observation and experience, that is, by making a priori
knowledge an a posteriori matter, Hume earned forever the respect and admiration of nondogmatic empiricists.
A close examination of Hume's philosophy shows that the choice between empiricism and rationalism, as philosophical doctrines rather than philosophical attitudes or approaches, is not the binary a priori matter that many philosophers seem to take it to be. Hardheaded empiricists may countenance numerous faculties of a priori factual cognition without forfeiting membership in Hume's Club. Other empiricists may be more restrained in their postulation of such faculties. Still others may eschew them altogether. Nevertheless, their respective memberships in Hume's Club are secure so long as observation and experience furnish the reasons why they hold these views. However, some philosophers might, for essentially a priori reasons, repudiate all faculties of a priori factual cognition and yet suffer the humiliation of having their membership applications rejected by Hume's legatees. For it is not one's views about a priori factual cognition but one's reasons for them that make an empiricist or a rationalist out of a philosopher!
Five—
Philosophy and the Exact Sciences:
Logical Positivism as a Case Study
Michael Friedman
Much of modern philosophy developed in close association with the development of the exact sciences: the sciences of mathematics, optics, astronomy, and physics. Many modern philosophers—Descartes, Leibniz, and Kant, for example—took these exact sciences as paradigmatic of objective and rational knowledge and, moreover, took this conception of objectivity and rationality as the starting point of their philosophizing. In the present century this kind of conception has been championed by the logical positivists, who took mathematics and mathematical physics as paradigmatic not only of objective and rational knowledge but of objective or "cognitive" meaningfulness as well. Accordingly, they spoke disparagingly of the "cognitive meaninglessness" of ethical discourse, religious discourse, poetic discourse, and of course traditional philosophical ("metaphysical") discourse.
With the demise of logical positivism it has become fashionable to attack the ideal of scientific objectivity and rationality which they championed as well. Taking the exact sciences of mathematics, optics, astronomy, and physics as paradigmatic of objective and rational knowledge is now dismissed as vulgar "scientism," and we are now told that the world of modern mathematical physics, for example, is just one world picture among others—with no special claim to objective validity. In particular, the systems of representation embodied in the disciplines of art, literature, social science, or religion are equally legitimate and equally "objective." When such "relativistic" sentiments are expressed even by eminent philosophers of science, they become especially compelling and must certainly give one pause.
Nevertheless, I want here to oppose this new "relativism." I agree, of course, that logical positivism is a failed philosophical movement; but I think that the reasons for this failure have been very badly misunderstood. Indeed,
contemporary critics of logical positivism operate with an extremely superficial and stereotypical characterization of that movement which misses entirely both its most distinctive aims and its real intellectual problems. As a result, the true nature of our current "relativistic" predicament remains hidden from us. I hope here to shed light on this predicament through closer attention to the actual history of logical positivism and, in particular, through closer attention to the intimate relationship between that history and the parallel developments taking place in the exact sciences themselves. My story will, I hope, lead to a renewed appreciation for the philosophical importance and centrality of the exact sciences.
I
Let me begin by briefly indicating the extent to which logical positivism has been seriously misrepresented and badly misunderstood. Recent critics—such as Kuhn, Hanson, Toulmin, and Feyerabend[1] —portray the logical positivists as both naively empiricist and naively ahistorical. Science is seen as the continuous accumulation of more and more accepted facts, facts that either record direct observations or generalize from such observations by a straightforward process of induction. It follows, then, that the logical positivists must have been inspired only by what Kuhn calls "normal science" and that they must have neglected entirely the fundamentally discontinuous transitions that occur during so-called "scientific revolutions"—where the most important example of the latter, for Kuhn, is the replacement of Newtonian physics by Einstein's theory of relativity.[2] Yet a brief examination of the actual history of logical positivism reveals that one of its most fundamental inspirations is precisely this Einsteinian revolution. The early writings of the logical positivists—of Schlick, Reichenbach, and Carnap, in particular—all focus on the theory of relativity, a theory whose revolutionary impact is explicitly recognized in the course of a polemic against their philosophical predecessors.[3] Specifically, the development of non-Euclidean geometry and Einstein's theory of relativity is taken by these writers to undercut decisively the conception of space and time bequeathed to them by the Kantian philosophy; and this, in fact, is the starting point of their philosophizing. So whatever else may be true, these philosophers can certainly not be accused of an ahistorical neglect of scientific revolutions.
What about the charge of naive empiricism? The logical positivists are supposed to have a crudely "atomistic" conception of scientific observation and experiment: observation is nothing but immediate contact with "the given" which, as such, can take place outside the context of any scientific theory whatsoever. Yet this naively empiricist conception of observation is, on the whole, explicitly rejected by the positivists. Thus, Reichenbach, in the introduction to his 1924 book on relativity theory, writes:
Every factual statement, even the simplest one, contains more than an immediate perceptual experience; it is already an interpretation and therefore itself a theory. . . . We shall have to make use of the scientific theory itself in order to interpret the indications of our measuring instruments. Thus we shall not say, "a pointer is moving," but "the electric current is increasing." The most elementary factual statement, therefore, contains some measure of theory.[4]
This clear statement of what is now called the "theory-ladenness" of observation is virtually indistinguishable from any randomly selected statement of the doctrine from Kuhn or Hanson. Carnap, in his 1928 classic of positivist thought, The Logical Structure of the World —a work that is often taken as paradigmatic of the logical positivists' alleged naive empiricism—explicitly opposes an "atomistic" conception of experience or "the given" and instead endorses a "holistic" conception derived from Gestalt psychology.[5] Finally, the issue is subject to a spirited debate in the pages of the positivists' official journal Erkenntnis in the years 1932–1935.[6] The participants in this debate are Carnap, Schlick, Neurath, and Hempel: all but Schlick agree that there are no such things as pure or theory-independent observation-sentences ("protocol-sentences"); all but Schlick explicitly renounce the project of looking for an empiricist foundation of knowledge on the immediately "given" data of experience. Once again, the "naive empiricist" label simply does not fit.
II
As indicated above, the logical positivists begin their philosophizing by reacting against the Kantian system. But what in particular are they reacting against? Kant, like the positivists, views the exact sciences of mathematics and physics—and, specifically, the application of the former to the latter embodied in the brilliantly successful mathematical physics initiated by Newton—as paradigmatic of objective and rational knowledge. His fundamental problem is to explain how such knowledge is possible: How is it possible that mathematics, in its full precision, applies to the chaotic and apparently imprecise world of sense? Kant's solution to this problem is based on his theory of space and time: specifically, on his doctrine that space and time are "pure forms of our sensible intuition." It is this Kantian doctrine, above all, that the positivists are concerned to reject; and so, to understand their position, we have to say a few words about the meaning and significance of the doctrine.
First, Kant conceives pure mathematics as itself making essential reference to space and time. Geometry involves the construction or generation of figures in space—on the "blackboard of the imagination," as it were; arithmetic involves the successive addition of unit to unit in time. This conception, which is liable to seem either quaint or ridiculous to a sophisticated modern mathematician, actually makes extremely good sense in the context of the mathematics of Kant's day. For the proof structure of Euclid's Elements —unlike that of
modern formulations of Euclidean geometry such as Hilbert's, for example[7] —does essentially involve a definite process of spatial construction: the procedure of construction with straightedge and compass. Moreover, the new calculus that is just being developed at the time, especially in the form of Newton's so-called theory of fluxions, makes an even more essential appeal to spatio-temporal intuition—in particular, to the intuitive idea of motion. As Newton himself puts it in a well-known passage from "The Quadrature of Curves":
Mathematical Quantities [are] generated by a continual motion . Lines are described, and by describing are generated . . . by a continual motion of Points. Surfaces are generated by the motion of Lines, Solids by the motion of Surfaces, Angles by a rotation of their Legs, Time by a continual flux, and so in the rest.[8]
In other words, for Kant, as for Newton, the only way even to conceive or represent mathematical quantities is by an intuitive process of spatiotemporal construction.
Lying behind this Kantian conception of pure mathematics is a fundamental difference between the Aristotelian subject-predicate logic that dominated Western thought until the latter part of the nineteenth century and the modern "symbolic" or "mathematical" logic developed by Frege and Russell. For within Aristotelian subject-predicate logic it is impossible adequately to represent the idea of an infinite aggregate or structure—for example, the idea of the infinity of the points on a line or the idea of the infinite extendibility of the series of natural numbers. Since for Kant logic is subject-predicate logic, these ideas—which are of course essential to all mathematical thinking—cannot be captured or represented in an axiomatic or deductive system in the manner of modern mathematics. On the contrary, the only way even to think such ideas is via the indefinite extendibility of our spatiotemporal intuition: by the fact that there is always "room"—that is, space and time—for "one more" number in the series of natural numbers, "one more" extension of a given finite line segment, and so on. This is why, for example, Kant says in the Critique of Pure Reason that "I cannot represent to myself a line, however small, without drawing it in thought, that is gradually generating all its parts from a point" (B203).
In any case, it is this conception of the necessarily intuitive character of pure mathematics that enables Kant to explain how mathematics is applicable to the chaotic world of sense, to explain how mathematical physics is possible. For Kant argues that the space and time of pure intuition—the space and time underlying the constructive procedures of pure mathematics—is the very same space and time within which we perceive or experience nature through the senses. The idea is that, in the absence of a rigorous mathematical framework within which to order and interpret our sense perceptions, they would not amount to experience or knowledge in the full-blooded sense. Instead of objective experience and rational knowledge, we would be left with merely subjective
association of representations. As Kant puts it in a well-known passage from the Prolegomena to Any Future Metaphysics , it is only the rigorous framework of mathematical physics that allows us "to spell out sensible appearances in order to read them as experience" (§30).
This Kantian explanation of the applicability of mathematics to sensible nature has one crucially important consequence. For Kant, there is only one spatiotemporal framework that can possibly play such an experience-constituting role: the spatiotemporal framework of our pure intuition. Indeed, as we have seen, in abstraction from our spatiotemporal intuition it is quite impossible even to think or represent spatiotemporal ideas. But our spatiotemporal intuition, for Kant, has a fixed and determinate structure: space is necessarily Euclidean, time is necessarily Newtonian (more precisely, space-time is necessarily Newtonian). As a result, the spatiotemporal framework underlying (Newtonian) mathematical physics is a priori fixed or determined independently of all empirical data. There can be no question of subjecting this framework to confirmation, refutation, or revision in the face of experience; on the contrary, it alone makes objective experience first possible.
Now it is precisely here, of course, that the Kantian system comes to grief. For the development of nineteenth- and twentieth-century mathematics and mathematical physics is notable for the creation of a wide variety of alternatives to the Euclidean-Newtonian framework. I need here only mention the development of non-Euclidean geometries by Gauss, Bolyai, and Lobachevsky in the first third of the nineteenth century and the very general frameworks for both Euclidean and non-Euclidean geometries later devised by Riemann and Klein. These developments culminate in Einstein's work on relativity theory in the early years of the present century, wherein the new non-Euclidean and non-Newtonian frameworks are actually applied to nature. In particular, Einstein's special theory of relativity (1905) makes use of Klein's ideas in articulating a non-Newtonian theory of time (more precisely, of space-time); Einstein's general theory of relativity (1915) draws heavily on Riemann's work in developing a very strongly non-Euclidean conception of both space and time (more precisely, of space-time).
In the face of these new developments, the Kantian conception of pure intuition can no longer be sustained. Indeed, during this same period, mathematicians are developing techniques that free pure mathematics from any dependence whatsoever on spatiotemporal intuition. Here I am referring to the so-called "rigorization" of the calculus initiated by Bolzano and Cauchy in the early eighteenth century that culminates in the "arithmetization" of analysis by Weierstrass. As a result of this work, the calculus is purged of all reference to intuitive ideas of motion and change and is instead given a purely "formal" foundation on the modern ideas of function, convergence, and limit. Moreover, what makes this "formal" conception of mathematics itself possible is the
new perspective on logic and mathematical reasoning first adequately formulated by Frege. For, as suggested above, it is only this new logic that allows us to represent ideas involving infinity (which of course are especially basic to the calculus) in a "formal" or nonintuitive manner. In other words, it is the development of the new mathematical logic, above all, that makes possible the modern picture of mathematics as based on deductive systems involving strict logical inference from explicitly stated axioms—axioms which therefore stand in no need whatever of an intuitive interpretation.
III
But what about the development of logical positivism? As I have said, the logical positivists are in clear agreement with Kant about the paradigmatic status of mathematics and mathematical physics as exemplars of objective and rational knowledge. Further, the positivists also agree with Kant on the underlying reason for this privileged status. Mathematics and mathematical physics are paradigmatic of objectivity and rationaliaty because it is only by ordering, interpreting, and structuring our sensory perceptions within a rigorous mathematical framework that we can first "objectify" them—that is, transform them from mere appearance into objective experience . In other words, it is mathematical physics alone that makes possible a full-blooded notion of objective knowledge in the first place. Thus, for example, Schlick in his General Theory of Knowledge draws a sharp distinction between knowledge or cognition (erkennen ) and acquaintance with (kennen ) or experience of (erleben ) the immediately given. The latter, since it is momentary or "atomistic," cannot possibly yield knowledge. On the contrary, knowledge is possible only when we embed such momentary perceptions within a rigorous system of interconnected judgments of which the systems developed by mathematical physics are paradigmatic.[9] Similar themes are dominant in the early writings of the other logical positivists.[10]
It should be clear, on the one hand, how far we are from a naively empiricist conception of knowledge and experience. In particular, the "theory-ladenness" of observation is rigorously articulated and explicitly defended—and defended for fundamentally Kantian reasons. Yet, on the other hand, it is also clear that the Kantian system as a whole is no longer tenable. In particular, Kant's doctrine of pure intuition has collapsed completely. Pure mathematics no longer requires a basis in spatiotemporal construction but can instead proceed purely "formally" via strict logical deduction within an axiomatic system. As a result, pure mathematics has no intrinsic connection whatever with either spatiotemporal intuition or sense experience, and it is no longer possible to maintain that any mathematical theory has a necessary relation to our experience of nature. Similarly, there is no longer a single, privileged spatiotemporal framework—the Euclidean-Newtonian framework—lying at the basis of
mathematical physics. Many such frameworks are now possible, and some of them have been already successfully applied to nature in Einstein's theory of relativity.
This situation constitutes the philosophical context within which logical positivism develops. The attempt to preserve a basically Kantian conception of knowledge and experience in the face of the collapse of Kant's doctrine of pure intuition creates fundamental, and ultimately unresolved, intellectual tensions. The underlying problem can perhaps be expressed as follows. We wish to follow Kant in insisting upon the need for a general theoretical framework in order to confer objectivity and rationality on our sense experience. We also wish to follow Kant in maintaining the privileged position of mathematics and mathematical physics. Yet there is no longer a single spatiotemporal framework that alone can perform this "objectifying" function. On the contrary, each of the many possible frameworks appears to exemplify its own particular standards of objectivity and rationality. Are we not forced, therefore, into a position of epistemic and conceptual "relativism" which undermines the very notions of objectivity and rationality that we are trying so hard to preserve?
This problem can be best appreciated, I think, if we juxtapose the philosophical efforts of the logical positivists with the so-called Marburg Neo-Kantianism of Cohen, Natorp, and especially Cassirer. These thinkers agree with the logical positivists in their assessment of the significance of Kant's philosophical achievement: Kant's achievement consists precisely in clearly recognizing and articulating the "objectifying" function of mathematics and mathematical physics. These thinkers—especially Cassirer—also agree with the logical positivists that Kant's doctrine of pure spatiotemporal intuition can no longer be maintained in the context of modern mathematics and mathematical physics.[11] But from these two ideas Cassirer draws explicitly "relativistic" conclusions: a doctrine which he calls "logical idealism." Since there is no longer a single, privileged framework for objective and rational thought, mathematical-physical thinking as such provides only one such framework among others. Thus, art, religion, myth, and metaphysics provide equally good rational frameworks—or what Cassirer calls "symbolic forms"—for each supplies its own characteristic standards of truth and hence objectivity.
The logical positivists refer to this "relativistic" doctrine as the Coherence Theory of Truth, for it views coherence and consistency within a particular symbolic framework as sufficient for objective truth—truth relative to that framework , of course—and supplies no means whatever for adjudicating disputes between such frameworks. Since the positivists wish to follow Kant in maintaining the privileged status of mathematics and mathematical physics, this doctrine is anathema to them; and they therefore do everything they can to distance themselves from it. Yet, at the same time, this proves to be no easy task; for, as we have seen, the positivists agree completely with the Marburg School on their underlying premises. This is the basis for the ensuing dialectic.
The problem of adjudicating between competing theoretical frameworks arises for the logical positivists in their earliest writings on relativity theory—most clearly, perhaps, in Schlick's 1915 paper on relativity theory. The trouble begins when Schlick explicitly acknowledges that there are alternative theories equally capable of accounting for the data that are explained by Einstein's new theory (e.g., and especially, the famous Michelson-Morley experiment of 1887). There is Einstein's theory itself, of course, which explains the anomalous data by radically revising the classical conceptions of space and time. But there is also the so-called "aether" theory of Lorentz, Fitzgerald, and Poincaré, which explains the very same data by retaining the classical conceptions of space and time and invoking compensatory disturbances—contractions and retardations—in the rods and clocks we use to measure space and time. The two theories lead to all the same empirical predictions—they are "empirically equivalent"; and so the choice between them is radically underdetermined by all the empirical facts. This kind of "theoretical underdetermination" is a dramatically new phenomenon in the history of science which, for example, is simply not possible in the context of the Newtonian physics of Kant's day.[12]
How, then, can we adjudicate the dispute between the two theories? How, in particular, can we rationalize our preference for the Einsteinian framework? In 1915 Schlick frankly admits that he has no satisfactory answer. It appears, to be sure, that Einstein's theory is "simpler" and less "ad hoc" than the competing "aether" theory. Yet we have no clear account of what such "simplicity" really comes to nor, more importantly, any assurance that "simplicity"—whatever it may be—is a reliable guide to truth. Why in the world should nature respect our —merely subjective—preference for "simplicity"? Once again, therefore, the objectivity of physical theory is subject to doubt.
Throughout the 1920s Schlick and the other logical positivists—Reichenbach, in particular—attempt to solve this epistemological problem by means of the doctrine of "conventionalism" which they derive from Poincaré.[13] The idea here is that two theories agreeing on all empirical data—two theories such as relativity theory and the "aether" theory that truly are "empirically equivalent"—are not really two conflicting theories at all. Their disagreement is only apparent, and so there is no need rationally to adjudicate the choice between them. The situation is precisely analogous, in fact, to two different coordinate systems or two different systems of units (the metric system and the English system, say). Rather than a substantive disagreement over objective truth, we are faced with a merely pragmatic question of convenience. In this sense, the choice is a purely conventional one.
Now this doctine, when consistently thought through, does in fact lead to a kind of radical empiricism. Since we wish to hold that two "empirically equivalent" theories are therefore completely equivalent descriptions of the same objective facts, we are committed to the view that the empirical facts—that is,
the observable facts—are all the objective facts there are. We are committed to the view that the entire content or meaning of a scientific theory is lodged in its consequences for actual and possible observations. And, in fact, around 1930 this view hardens into a kind of dogma for the logical positivists in the form of the notorious Verifiability Principle.[14] The "cognitive meaning" of all discourse is declared to consist in its implications for actual and possible observations; and this principle is ruthlessly wielded both to solve the problem of underdetermined theory choice and to question the "cognitive meaningfulness" of all nonscientific discourse—of art, religion, myth, and metaphysics in particular. In this way, the positivists hope to divorce themselves from the "relativistic" and "idealistic" doctrines of the Marburg School once and for all.
Yet this kind of radical empiricism could not be consistently sustained. In the first place, it proves to be impossible to articulate a conception of "cognitive meaning" that can support the Verifiability Principle. In particular, it proves to be impossible to view advanced theories such as Einstein's theory of relativity as mere summaries of actual and possible observations; and this fact is explicitly acknowledged, with characteristic honesty and rigor, by the positivists themselves.[15] Second, and perhaps even more fundamentally, the notions of observation and empirical fact are subject to more weight than they can possibly bear. For, given the Neo-Kantian context of positivist thought, theory is supposed to give meaning to observation rather than the other way around, and an empiricist foundation for objective knowledge on supposedly pure or "theory-neutral" observation reports is quite impossible. As I indicated above, this fact is also explicitly acknowledged in the pages of the positivists' official journal Erkenntnis in the years 1932–1935,[16] wherein all parties except Schlick explicitly reject an empiricist foundation for knowledge—and reject such a foundation precisely on the grounds of the "theory-ladenness" of all observation. (Schlick, by contrast, perceptively but vainly warns that such a conception leads inevitably to the Coherence Theory of Truth.)
At this juncture, Carnap, who is clearly the deepest and most rigorous of the logical positivists, writes perhaps his greatest work: The Logical Syntax of Language . In this book the empiricist tendencies of logical positivism shrink to the point of vanishing, and Carnap instead rigorously articulates an explicitly "relativistic" viewpoint that is very close indeed to the Marburg School, on the one hand, and to much contemporary "relativism," on the other. Carnap's "relativistic" attitude is encapsulated in his famous Principle of Tolerance:
In logic, there are no morals . Everyone is at liberty to build up his own logic, i.e., his own form of language, as he wishes. All that is required of him is that, if he wishes to discuss it, he must state his methods clearly, and give syntactical rules instead of philosophical arguments.[17]
But what does this principle really say?
First, Carnap views rules of logic—and hence criteria for meaningfulness and truth—as embodied in one or another language system or linguistic framework. Moreover, many such systems—many such linguistic frameworks—are possible, and all are equally legitimate. Indeed, since criteria for meaningfulness and truth—and hence criteria for objective knowledge—are internal to particular linguistic frameworks, there can be no question whatever of rationally adjudicating disputes between such frameworks. The only substantive questions are those that can be formulated within a given framework, and the choice of one framework rather than another—as a choice external to the frameworks under consideration—can only be made on the basis of pragmatic criteria of convenience. In other words, disputes within a single framework (internal questions) can be adjudicated by rational and objective criteria relative to that framework; disputes between different frameworks (external questions) cannot be so adjudicated.[18]
Second, however, Carnap sees the articulation and elaboration of the logical rules definitive of this or that linguistic framework as taking place within a definite and precise metadiscipline—a discipline he calls logical syntax.[19] Building on earlier logical-mathematical work of Hilbert and Gödel, Carnap views this discipline as itself a branch of pure mathematics. Indeed, in light of Gödel's so-called "arithmetization of syntax," this discipline can be viewed as a particularly neutral and uncontroversial branch of mathematics—a fragment of elementary arithmetic. Yet within this neutral and uncontroversial metadiscipline we can still describe the linguistic rules or logical syntax of much stronger and more controversial frameworks. In particular, given any such linguistic framework, we can, from the standpoint of our syntactic metadiscipline, draw a clear and precise distinction between those sentences definitive of the rules of that framework—the so-called logical or analytic sentences—and those sentences expressing substantive truths formulated within that framework—the so-called factual or synthetic sentences. We thereby give clear and precise content to the distinction between external and internal questions. Moreover, although the notion of truth simpliciter has indeed been relativized, the resulting notion of true-in-a-given-framework is "absolute." For this latter notion can itself be precisely and rigorously characterized within the framework-neutral metadiscipline of logical syntax. In this way, Carnap hopes to avoid the tendency toward vicious circularity inherent in the Coherence Theory of Truth; and it is here, rather than in any radical empiricism, that Carnap makes his last stand against the Marburg School.
More specifically, Carnap sets himself apart from the Marburg School in continuing to give pride of place to the exact sciences; and he does this, in fact, in two distinct yet interrelated ways. On the one hand, Carnap is able to show that, in an appropriately designed linguistic framework, the sentences of classical mathematics—and even some of the basic principles of classical physics such as physical geometry—turn out to be analytic truths in the above sense.
These sentences and principles are therefore constitutive of objectivity and rationality relative to this given framework, and Carnap has thus captured an important part of the traditional Kantian conception of the sciences. On the other hand, Carnap's metadiscipline of logical syntax itself takes place within the most exact of the exact sciences—namely, elementary arithmetic. This gives Carnap a fixed and exact place to stand from which he can articulate his thoroughgoing "relativism"—that is, his distinction between sentences that are analytic relative to a given framework and those that are synthetic, and thus his relativized notion of true-in-a-given-framework.
Alas, however, it was not meant to be. For it turns out to be impossible, in most cases of interest, to characterize even this relativized notion of true-in-a-given-framework in such an "absolute" or framework-neutral way. In particular, it is a consequence of Gödel's celebrated Incompleteness Theorem (1931) that, for any linguistic framework embodying a significant portion of classical mathematics, such a characterization can only be drawn within a still richer and more controversial framework.[20] The metadiscipline of logical syntax is in no way framework-neutral, and Carnap's dream of a truly objective and impartial notion of rationality—albeit one that is considerably weakened and explicitly relativized—is not to be had. As a result, we must question the objectivity and meaningfulness of the very distinction that motivates Carnap's program in the first place: the distinction between change of framework (or external questions), on the one hand, and change of substantive theory within a framework (or internal questions), on the other. In other words, the general notion of linguistic or theoretical framework is itself thrown into doubt.
IV
My story has been a story of failure. In particular, the positivists have failed to develop an adequate alternative to the Coherence Theory of Truth: the explicitly "relativistic" doctrines of the Marburg School. Does it follow that this Marburg "relativism" survives intact and, accordingly, that our contemporary "relativist" tendencies are on the right track after all? I think not. The underlying idea of such "relativism," I take it, is that our ordinary notion of truth simpliciter is to be replaced with a relativized notion of true-in-a-given-framework or true-in-a-given-symbolic-form. But if this move is to have any point, the notion of true-in-a-given-framework should have a different status from our old "naive" notion of truth simpliciter . Specifically, this new notion should not require further relativization; it should itself be "absolute." Compare the situation in relativity theory—which, for Cassirer at any rate, was always the model for his relativizing move. Relativity theory, as is well known, replaces the Newtonian notion of absolute simultaneity with a relativized notion of simultaneous-relative-to-a-given-inertial-frame. But this latter notion is itself absolute—once we specify the relevant frame.
Carnap's Logical Syntax , as I understand it, is an attempt to make clear sense of just this kind of relativizing move. In particular, it is an attempt to articulate a neutral metaperspective—logical syntax—from which we can survey all possible linguistic frameworks and within which we can develop a precise notion of true-relative-to-a-framework. This notion, since it is defined within our framework-neutral metaperspective, will itself have the desired "absolute" status. (This is what I had in mind when I said that Carnap hopes to avoid the tendency toward vicious circularity inherent in the Coherence Theory of Truth.) Gödel's Theorem then undermines this Carnapian project by showing that there is no such framework-neutral metaperspective. Yet it certainly does not follow that "relativism" emerges triumphant. On the contrary, the one possible standpoint from which we could hope coherently to articulate such a thoroughgoing "relativism" has been pulled out from beneath our feet.
Nor does it follow that the exact sciences have been in any way diminished in philosophical importance or centrality. Here we should remember that Gödel's Theorem is itself a theorem of elementary arithmetic. Under the Gödel numbering the theorem says that a certain number—the Gödel number of Gödel's unprovable sentence—is not in a certain set of numbers—the set of Gödel numbers of provable formulas. Moreover, this latter set of numbers can itself be defined in the language of elementary arithmetic—that is, in terms, ultimately, of addition and multiplication. In these terms, Gödel's Theorem merely expresses a rather arcane fact of elementary arithmetic: if you subject numbers with certain properties to certain arithmetical operations (a sequence of additions and multiplications in a definite order), you do not get a certain other number. The point is that Gödel's Theorem is itself as exact as exact can be: in principle, it is a proposition of the same kind as 2 + 2 = 4.
Now this last result of the exact sciences has, I have argued, the most profound consequences for our philosophical understanding of the exact sciences. In particular, it shows that the logical positivists' attempt to give a Neo-Kantian explanation for the special status of the exact sciences cannot succeed; for it shows that the neutral metaperspective that alone could support their attempted explanation does not exist. As a result, we cannot, from a peculiarly philosophical vantage point—from a transcendental vantage point, as it were—explain the special status of the exact sciences at all. Yet it does not follow that the exact sciences do not have this special status. On the contrary, in precisely this failure of the positivist program the exact sciences have shown their special status in a completely unexpected and unprecedented way. We—as philosophers—cannot answer a question we have long desired to answer. But we now know exactly why we cannot answer it, and we know this on the basis of the most exact truths of elementary arithmetic. In other words, the exact sciences have themselves shown, and have shown exactly, the limits of our philosophical knowledge.[21] Such precise knowledge of the limits of our knowledge must inevitably strike a philosopher with Kantian sympathies as just the
kind of defense of objectivity and rationality toward which the modern philosophical tradition has been aiming all along.
Six—
Language and Interpretation:
Philosophical Reflections and Empirical Inquiry
Noam Chomsky
In the philosophical literature of the past forty years, there have been several influential currents that seem to me problematic in important, even essential, respects. I have in mind, in the first place, approaches that take as their point of departure certain conceptions of how language is studied, or should be studied, by the empirical scientist—or the "field linguist," to use the terms of Quine's familiar paradigm. One can include here Quine,[*] Donald Davidson, and others who have moved toward a form of pragmatism and "naturalized epistemology," incorporating questions thought to be of philosophical significance within their conception of empirical science, but also others who adopt a different starting point: Michael Dummett, and many of those influenced by Wittgenstein and ordinary language philosophy, for example.
To illustrate the flavor of these ideas, take some comments of Richard Rorty in his article in the Davidson volume.[1] He writes that "Davidson is surely right that Quine 'saved philosophy of language as a serious subject' by getting rid of the analytic-synthetic distinction. Quine's best argument for doing so was that the distinction is of no use to the field linguist."
As for the "field linguist," all that he "has to go on is his observation of the way in which linguistic is aligned with non-linguistic behavior in the course of the native's interaction with his environment, an interaction which [the linguist] takes to be guided by rules of action," specifically, the "regulative principle" that "most of the native's rules are the same as ours, which is to say that most of them are true" ("rules" here apparently referring to beliefs). We need not be concerned about "a conceptual scheme, a way of viewing things, a perspective (or . . . a language, or a cultural tradition)," because "the field linguist does not need them," so "therefore philosophy does not need them either." Quine and Davidson agree that "a theory of meaning for a language is
what comes out of empirical research into linguistic behavior," when this is properly pursued, in accord with the doctrines of "holism and behaviorism."
This line of thought, Rorty continues, leads to a form of pragmatism that he espouses and attributes to James and Davidson, including crucially the denial of any relations of "'being made true' which hold between beliefs and the world." Rather, "We understand all there is to know about the relation of beliefs to the world when we understand their causal relations with the world."
Putting aside the conclusions that Rorty reaches,[2] consider his assumptions. If the best argument for dispensing with the analytic-synthetic distinction is that it is of no use to the field linguist, then virtually everyone who actually works in descriptive semantics, or ever has, must be seriously in error, since such work is shot through with assumptions about connections of meaning, which will (in particular) induce examples of the analytic-synthetic distinction. One would be hard put to find studies of language that do not assign structures and describe the meaning of 'kill', 'so', and so on, in such a way that there is a qualitative distinction, determined by the language itself, between the sentences 'John killed Bill, so Bill is dead' and 'John killed Bill, so John is dead'. Or to take another case, it would be difficult to find a study of referential dependence in natural language that does not conclude that the language itself determines that the relation holds between 'Mary' and 'herself' in
(1) Mary expects to feed herself
but not when the same expression is embedded in the context 'I wonder who—,' yielding
(2) I wonder who Mary expects to feed herself
Such syntactic-semantic properties will induce cases of the analytic-synthetic distinction; thus they will yield a distinction between 'Mary expects to feed herself, so Mary expects to feed Mary ' (analytic, with the three occurrences of 'Mary' taken to be coreferential) and 'I wonder who Mary expects to feed herself, so I wonder who Mary expects to feed Mary ' (not analytic, under the same interpretation). But what Quine is alleged to have demonstrated goes beyond the matter of analyticity, reaching to the conclusion that there are no semantic connections that can be attributed to the language faculty itself as distinct from our general systems of belief; elsewhere, Rorty takes this to be one of the two fundamental discoveries that undermine a traditional world picture.
As is well known, Quine and others have offered their own account of these distinctions. I will return to these proposals and how they might be evaluated in accordance with the canons of inquiry of the natural sciences, but will merely note here that reference to "the field linguist" can surely not be understood as reference to those who actually do linguistic work. Rather, it has a normative character, referring to the way such work ought to be done, keep-
ing to the conditions of "holism and behaviorism" legislated by the philosopher but not followed in practice by the errant scientist. While it might turn out on investigation that this stance is justifiable, those with an appreciation of the history of the discipline might be pardoned some initial skepticism.
To select another example to illustrate the flavor of these discussions, consider Dummett's argument in the same volume that the "fundamental sense" in which we must understand the concept of language is the sense in which Dutch and German are different languages (he gives a different example, but the point is the same), each of them a particular social practice "in which people engage," a practice that "is learned from others and is constituted by rules which it is part of social custom to follow." Thus Dutch and German exist in this "fundamental sense," "independently of any particular speakers"; every individual speaker "has" such a language, but typically has only a "partial, and partially erroneous, grasp of the language." The intended import of Dummett's proposal is far-reaching. He is telling us what notion of "language" is essential for philosophical purposes, for the theory of meaning in particular; and also, as he makes clear, it is this concept of language that is in his view required for explaining the use of language, specifically, for understanding "what long-range theory someone brings to a first linguistic encounter with another." It is, therefore, a proposal that bears on the empirical study of language, of people, of what they know and what they do. Perhaps he means to allow that linguists may follow some different course for their special concerns, but clearly these proposals bear on the proper practice in empirical inquiry into language and its use.
Here the paradoxical flavor is of a somewhat different order. It lies in the conflict between Dummett's proposal and the commonplace assumption in empirical practice that there is no useful general sense in which we can characterize "language" so that Dutch and German are two distinct "languages," which people know only "partially" and "erroneously." This is so whether we are studying language structure, psycholinguistics, language change, typology, problems of communication, or whatever. People who live near the Dutch border can communicate quite well with those living on the German side, but they speak different languages in accordance with the sense of the term that Dummett argues is "fundamental"; and those on the German side of the border, with their "partial knowledge" of the language German, may understand nothing spoken by people living in some other region, who "have" a different "partial knowledge" of the language German in Dummett's sense. It is for such reasons as these that no such concept plays any role in empirical inquiry into language or psychology. Such terms as 'English' and 'Japanese' are used for general expository discourse, but with the understanding that their commonsense usage, which Dummett rather uncritically adopts, is to be abandoned when we turn to actual study of language, behavior, and communication.[3] If Dummett's concept is indeed fundamental for empirical inquiry and for philo-
sophical purposes, then either philosophy, or the empirical study of language and behavior, or both, are in deep trouble, for reasons that should be familiar. The concept of language that Dummett takes to be essential involves complex and obscure sociopolitical, historical, cultural, and normative-teleological elements, which may be of some interest for the sociology of identification within various social and political communities and the study of authority structure, but which plainly lie far beyond any useful inquiry into the nature of language or the psychology of users of language.
To take one example, consider the study of language acquisition. In ordinary usage, we say that a child of five and a foreign adult are on their way toward acquiring English, but we have no way to designate whatever it is that they "have." The child, in the normal course of events, will come to "have" English (at least partially and erroneously), though the foreigner probably will not. But if all adults were suddenly to die and children were somehow to survive, then whatever it is they are speaking would be a human language, though one that does not now exist. Ordinary usage provides no useful way to describe any of this, since it involves too many disparate and obscure concerns and interests. This is one reason why the concept of language that Dummett adopts is useless for actual inquiry. This matter is of some importance when we consider the reliance on notions of "misuse of language," "community norms," "social practice," and "rule following" that are often adopted as if they are sufficiently clear; they are not.[4]
In this connection, it is perhaps worthwhile to recall some further truisms; in rational inquiry, in the natural sciences or elsewhere, there is no such subject as "the study of everything." Thus it is no part of physics to determine exactly how a particular body moves under the influence of every particle or force in the universe, with possible human intervention, and so on. This is not a topic. Rather, in rational inquiry we idealize to selected domains in such a way (we hope) as to permit us to discover crucial features of the world. Data and observations, in the sciences, have an instrumental character; they are of no particular interest in themselves, but only insofar as they constitute evidence that permits one to determine fundamental features of the real world, within a course of inquiry that is invariably undertaken under sharp idealizations, often implicit and based on common understanding, but always present. The study of "language" in Dummett's sense verges on "the study of everything" and is therefore not a useful topic of inquiry, though one might hope, perhaps, to build up to a study of aspects of such questions in terms of what comes to be understood about particular components of this hopeless amalgam.
The conception of language as a "social practice" that Dummett and others propose raises further questions, as becomes clear when it is applied to concrete examples. Consider again the examples (1) and (2):
(1) Mary expects to feed herself
(2) I wonder who Mary expects to feed herself
In (1), 'feed herself' is taken to be predicated of Mary, but in (2) it is predicated of some (female) person distinct from Mary; thus from (2) it follows that I wonder which female person Mary expects to feed that very person, but not that I wonder which person Mary expects to feed Mary herself. The example raises many pertinent questions, among them, how we know these facts. The answer seems to be that the initial state of the shared language faculty incorporates certain principles concerning referential dependence (Binding Theory), and when certain options left undetermined in the initial state are fixed by elementary experience, then we have no more choice as to how to interpret (1) and (2) than we have about whether to perceive something as a red triangle or as a person. Social custom appears to have nothing to do with the matter in such cases, though early experience helps set certain details of the invariant, biologically determined mechanisms of the mind/brain. The same seems to be true rather generally. Taken literally at least, the proposals of Dummett and others concerning "social practice" appear to be false, as a matter of empirical fact. At the very least, some argument would be required to show why they should be considered seriously.
If language is construed as a social practice in the manner of these discussions, then it is tempting to understand knowledge of language as the learned ability to engage in such practices, as Dummett suggests, or more generally, as an ability that can be exercised by speaking, understanding, reading, talking to oneself, and so on: "to know a language just is to have the ability to do these and similar things" (Anthony Kenny).[5] The temptation is reinforced by a common construal of knowledge more generally as a kind of ability. This view contrasts with the conception of a language as a generative procedure that assigns structural descriptions to linguistic expressions, knowledge of language being the internal representation of such a procedure in the brain (in the mind, as we may say when speaking about the brain at a certain level of abstraction). From this point of view, ability to use one's language (to put one's knowledge to use) is sharply distinguished from having such knowledge. The latter conception has two primary virtues: (1) it seems to be the right way to approach the study of human knowledge, knowledge of language in particular, within the general framework of the natural sciences, and it has proven a highly productive approach; (2) it is in accord with normal preanalytic usage, a secondary but not entirely insignificant matter. In contrast, the approach in terms of practical ability has proven entirely unproductive and can be sustained only by understanding "ability" in a way that departs radically from ordinary usage.
To see why this is so, suppose that Jones, a speaker of some variety of what we call "English" in informal usage, improves his ability to speak his language by taking a public-speaking course, or loses this ability because of an injury or disease, then recovering that ability, say, with a drug. Note that a speaker of Japanese, under the same circumstances, would recover Japanese , not English, with the same drug, and plainly recovery in such cases differs
radically from acquisition; a child could not acquire English or Japanese without any evidence. In all such cases, something remains constant, some property K, while ability to speak, understand, and so on, varies. In ordinary usage, we say that K is knowledge of language; thus Jones's knowledge remained constant while his ability to put his knowledge to use improved, declined, recovered, and so on. The account in terms of internal representation of a generative procedure accords with informal usage in this case. Note further that other evidence (say, from autopsy, were enough known about the brain sciences) might lead us to conclude that Smith, who never recovered English, not having taken the drug, nevertheless retained his knowledge of English intact after having completely lost his ability to speak and understand.[6]
If knowledge is ability, then the property K must be a kind of ability, though plainly not ability in the quite useful normal sense of the word, since ability varied while K remained constant. We must therefore contrive a new technical sense of the term 'ability': call it K-ability . Then K-ability remained constant while ability varied.[7] K-ability is completely divorced from ability, has the properties of the old concept of knowledge, and might as well be called 'knowledge', doctrinal matters aside.
It is rather ironic that these moves should be presented as in the spirit of the later Wittgenstein, who constantly argued against the practice of constructing artificial concepts, divorced from ordinary usage, in defense of certain philosophical doctrines. In fact, the Wittgensteinian construal of knowledge as a species of ability seems to be a paradigmatic example of the practice that Wittgenstein held to be a fundamental source of philosophical error.
Notice that similar considerations show that knowing-how —for example, knowing how to ride a bicycle—cannot be analyzed in terms of abilities, dispositions, and so on; rather, there appears to be an irreducible cognitive element. Notice finally that an account of knowledge in terms of ability, taken in anything like its normal sense, has proved utterly unproductive. One might try accounting for the simple examples (1) and (2) in terms of Jones's abilities, for example. No such endeavor has ever been undertaken, and a close look at the problems makes it reasonably clear why it would have no hope of success.
The paradoxical flavor of ideas in the range I have been sampling becomes clearer when we look more closely at some of the specific injunctions. Take again Rorty's observation, taken as obvious without discussion, that "all the linguist has to go on is his observation of the way in which linguistic is aligned with non-linguistic behavior in the course of the native's interaction with the environment," apart from the "regulative principle" that the native informant is generally speaking truly. This conception, he notes, is drawn from Quine and Davidson. Thus in Quine's familiar paradigm of "radical translation," "field linguists" observing Jones must support their hypotheses entirely in terms of observation of Jones's behavior (or that of members of the "Jungle community," taken to be homogeneous; if it is not homogeneous, none of the
arguments will go through, and if it is homogeneous, we may dismiss the community in favor of Jones without loss for these purposes, as I will do). I should note that in referring to Quine, textual questions arise, since in response to queries and criticism he has given many different versions of his paradigm, and these are not consistent;[8] but it is the one just cited, which Davidson and Rorty adopt, that is necessary if we are to be able to draw from Quine's paradigm any of the conclusions that are held to be important.
Before proceeding, let us note again that these prescriptions are radically different from the actual practice of the "field linguist." They are also completely foreign to the standard methods of the natural sciences. In the philosophical literature, the issues are generally discussed with regard to the theory of meaning, and in particular, with regard to aspects of the theory of meaning about which little is known (not, say, in connection with such matters as referential dependence, about which a good deal is understood). This is dubious practice, because it means that controls on speculation by empirical knowledge and theoretical understanding are very slight. But if the doctrine has any validity, it should hold with regard to all of our attributions of linguistic competence, and Quine, at least, has sometimes held that this is so. Thus he has argued that the same considerations hold when his "field linguist" alleges that in the sentence 'John contemplated the problem' there are two phrases, the noun phrase 'John' and the verb phrase 'contemplated the problem,' not, say, the two phrases 'John contemplated' and 'the problem' or 'John contemp' and 'lated the problem'. According to Quine, at least when he is keeping to the assumptions required for his well-known conclusions to follow, this attribution of some property (knowledge, or whatever we choose to call it) to the informant Jones must be based exclusively on evidence about Jones's behavior —in fact, evidence used in accord with highly restrictive canons that he outlines. And the same would be true in the study of sound structure, the relation of a reflexive to its antecedent, or whatever.[9]
It is worth noting that no linguist, or empirical scientist generally, would ever agree to be bound by such strictures. A comparable assumption in biology would be that in testing hypotheses about embryological development of humans, we cannot consider evidence obtained from the study of E. coli, or fruit flies, or apes, or physics. To mention one crucial case, in actual practice, every linguist approaches the study of a particular language on the basis of assumptions drawn from the study of other languages. Thus any linguist operating by the norms of the sciences would readily use evidence derived from the study of Japanese to help ground assumptions about Jones's knowledge of English. The logic is straightforward, and quite correct. There is overwhelming empirical evidence that people are not genetically "tuned" to acquire one rather than another language; rather, the "initial state" of their language faculty may be assumed to be uniform to a very good approximation. Presented with an array of evidence, the child acquires a specific language, making
use of the resources of the initial state that determine a substantial part of the knowledge (competence) acquired; the initial state can be regarded as a fixed, biologically determined function that maps evidence available into acquired knowledge, uniformly for all languages.[10] Study of Japanese may, of course, provide us with evidence, perhaps compelling evidence, about the initial state, namely, by means of a comparison between what comes to be known and what is presented, the two being mediated by the resources of the initial state. If speakers of Japanese employ some formal property of language structure (say, c-command ) in interpreting referential dependence, and the evidence available to the Japanese child does not somehow "compel" or is not even conducive to this uniform result, we are entitled to attribute to the initial state a version of Binding Theory, incorporating this property and relevant principles involving it, and thus to explain the facts observed. But the initial state is shared by the English speaker Jones, and hypotheses about his initial state will of course have consequences as to the proper description of the cognitive state he attains. The conclusions derived from Japanese concerning Jones's knowledge of English might be far-reaching. Thus evidence about referential dependence in Japanese might prove relevant for determining the position of phrase boundaries in English.[11]
All of this is just standard scientific practice, never questioned—or even discussed, because it is so uncontroversial—in the natural sciences. But Quine and those influenced by his paradigm are enjoining the "field linguist" to depart radically from the procedures of the sciences, limiting themselves to a small part of the relevant evidence, selected in accordance with behaviorist dogma; and also to reject the standard procedures used in theory construction in the sciences. The point is not academic; the normal practice of descriptive linguists crucially exploits these assumptions, which again should be the merest truisms.
We may put the point differently. The linguist and the child face radically different tasks. The child, endowed with certain innate capacities, acquires knowledge of a language—automatically, and with little if any choice in the matter. The linguist is trying to find out what knowledge the child acquires, and what innate properties of the mind/brain are responsible for this process of growth of knowledge (trying to find out what the child knows in advance of experience, to use a locution that seems to be quite appropriate). The linguist will quite properly use conclusions about innate properties, however derived, for the description of the knowledge attained—in particular, for the study of meaning, this domain having the same status as any other.
In fact, Quine's injunctions, consistently applied, would be still more extreme than this example indicates. Thus evidence from language pathology, or genetic variation, or neural structure, or biochemistry, or in fact evidence from any source, would be regarded by any scientist as potentially relevant in principle to determining the nature of the initial state or the state of knowledge
attained, since these are simply elements of the natural biological world; Quine too insists on this point with regard to study of the natural world, apart from the study of humans above the neck when undertaken by "linguists," in his sense of this term. If it could be shown that some facts about the neural structure of the brain provide a natural realization of rule systems of one kind (say, with the breakdown of 'John contemplated the problem' into the two phrases 'John' and 'contemplated the problem'), but not other kinds, then this line of argument would be acceptable in the sciences to help settle the question of what is the correct description of Jones's knowledge—the cognitive state attained by John (the question of the choice of constituent structure, in the case in question). The same is true with regard to the theory of meaning, or any empirical inquiry. But all of these paths, familiar in the natural sciences, are excluded by fiat under the Quinean conditions on the work of the "linguist" in accord with the paradigm that is widely adopted in the philosophical literature.
Quine has qualified these doctrines in interesting ways. A closer look at these qualifications reveals more clearly the arbitrary character of the stipulations imposed and the persistent misunderstanding of the empirical issues. As an example of arbitrary stipulation, consider Quine's discussion of the evidence that might lead us to assign one or another constituent structure to the sentences of Jones's English.[12] If this evidence derives from psycholinguistic experiments on perceived displacement of clicks,[13] then it counts; if the evidence derives from conditions on referential dependence in Japanese or on the formation of causative constructions in numerous languages, then it does not count—though this is evidence interpreted in the normal manner of the natural sciences, along the lines discussed a moment ago. Perhaps Quine might be interpreted as holding that evidence of the former type (so-called "psychological evidence") is in fact more powerful and persuasive than the so-called "linguistic evidence"; if so, this would simply be another error, since the opposite is the case, for the present at least. In fact, Quine appears to hold that the evidence differs in its epistemological character, a notion that is completely untenable. Evidence does not come labeled "for confirming theories" ("psychological evidence") or "for purposes of 'simplicity and general translatability' " ("linguistic evidence"). It is just evidence, good or bad, compelling or noncompelling, given the theoretical frameworks in which it can be interpreted for the purposes of sharpening or confirming hypotheses.
As an example of misunderstanding of empirical issues, consider Quine's discussion of the so-called "coordinate structure constraint," a descriptive generalization that covers, for example, the radical difference in status between the interrogative expressions derived by questioning "Mary" in the sentences 'John saw Bill and Mary' and 'John saw Bill with Mary': that is, the difference between 'who did John see Bill and?', 'who did John see Bill with?'. Quine concludes that the "striking uniformity" exhibited in this constraint is not "a
hint of a trait of all language" but "a hint of genetic kinship of the languages that seem most readily grammatized in these terms."[14] This conclusion, however, is based on a serious misunderstanding of the empirical issues at stake. The problem is to explain how each child knows the relevant difference between 'who did John see Bill and?' and 'who did John see Bill with?' It cannot be that the child relies on evidence from the history of language, and the child typically has no relevant experience to determine (by "induction," or whatever) that the simple rule "Front wh -phrase" is somehow blocked in the expression 'John saw Bill and who' but not in 'John saw Bill with who' (in colloquial English). Children do not, for example, produce 'who did John see Bill and?', then to be informed by their parents that this is not the way it is done; and languages have not "drifted" to incorporate this "simplification" of the rule of question formation over many millennia.[15] The problem, in short, is one of poverty of stimulus, and speculations about genetic kinship of languages have nothing whatsoever to do with it, in this and innumerable other similar cases.[16]
A similar refusal to permit the study of language to be pursued in the manner of the natural sciences is illustrated in other connections. Consider Donald Davidson's article "A Nice Derangement of Epitaphs" in the volume cited earlier.[17] Davidson considers the thesis that the goal of the descriptive study of meaning is to construct "an explicit theory" that "is a model of the interpreter's linguistic competence," a "recursive theory of a certain sort," and that we can "describe what an interpreter can do" only by appeal to such a theory. He then proceeds: "It does not add anything to this thesis to say that if the theory does correctly describe the competence of an interpreter, some mechanisms in the interpreter must correspond to the theory." Similar points have been made by Dummett and others.[18]
For anyone approaching these problems from the standpoint of the natural sciences, the final comment quoted is utterly wrongheaded. If it had any validity, the analogous comment would apply in the study of visual perception, or chemistry. As elsewhere, it adds a great deal to the thesis to say that "some mechanisms in the interpreter . . . correspond to the theory." That is, natural scientists who construct a theory that "describes what an interpreter can do" will proceed to attribute to the subject certain fixed and explicit mechanisms that would have the properties assumed in this descriptive account, not others. The attribution might be at an abstract level, in terms of mentally represented rule-systems, or in terms of other abstract entities such as neural nets, or in terms of cellular structure, or whatever; all of this is just standard natural science. Having proceeded to attribute specific structure and mechanisms to the person's mind/brain—often at some remove from unknown "more elementary" physical mechanisms—the natural scientist is then in a position to test the theory in terms of a wide array of evidence, for example, evidence drawn from other languages in the manner just illustrated, or evidence from pathol-
ogy or the brain sciences or biochemistry. Davidson's injunction blocks these efforts to employ the methods of rational inquiry in the sciences to determine whether the postulated account of the interpreter is indeed true, and to modify it if (as is likely) it is not.
The same problem arises when Quine, David Lewis, Dummett, and many others object that some philosophical problem arises when linguists attribute to a speaker-hearer a specific internalized rule-system, and then seek to determine whether this theory of the person is true by the standard methods of the sciences. Perhaps this is even pure "folly," as Quine has argued, to be overcome by proper reflection on methodology. The perceived problem is that for a fixed array of observed behavior, or a fixed infinite set of utterances selected on some obscure basis and taken by the philosopher to be "the language," it is of course possible to construct infinitely many different theories that are consistent with this evidence ("grammars," as they are sometimes called); it is therefore held to be an unwarranted move to postulate that one of them is "true" and others "false"—unless, Quine sometimes holds, there is "psychological evidence," with its mysterious properties that "linguistic evidence" lacks, to support one or another hypothesis. The argument is often buttressed by an analogy to the study of formal languages, which are completely irrelevant and highly misleading in this connection. If valid, the argument would hold throughout the sciences; in fact, it is nothing more than a form of skepticism that no one takes seriously in the study of the natural world for reasons that were clear by the seventeenth century, as Richard Popkin observes.[19] The natural scientist will attribute to the subject a specific system, not some other one (a "grammar," to use a misleading term), and will then proceed to determine whether this assumption is correct by seeking evidence of as wide a variety as possible, including crucial evidence from other languages, along the lines just discussed. Of course, there will always remain empirical indeterminacy, since this is empirical science, not mathematics, but that is all there is to say about the matter. A considerable literature exists arguing the contrary, but it is based on fundamental fallacies of reasoning.[20] Among these fallacies are the mistaken assumptions just discussed: that evidence about Jones's competence can only be drawn from Jones's behavior (interpreted in terms of the regulative principle about truth) and that it adds nothing to a description of Jones's behavior to attribute to Jones a specific internal mechanism, perhaps a particular system of rules or some form of neural organization that realizes them.
The point can be illustrated, again, with the matter of phrase-structure boundaries. Suppose we have two kinds of evidence for the placement of the major boundary after the subject in 'John—contemplated the problem', evidence from referential dependence in Japanese ("linguistic evidence") and evidence from perceptual displacement of clicks ("psychological evidence"). The first kind of evidence is subject to the familiar sort of indeterminacy.
So is the second. Suppose that under experimental conditions established to yield the right results (typically, after many attempts that go wrong), clicks will be perceptually displaced to the subject-predicate boundary, not the verb-object boundary. These results can be interpreted as supporting the conclusion that the structure is [NP—V NP], not [NP V—NP] or [NP—V—NP]. But it is easy to apply Quine's argument to show that there is "no fact of the matter" in this case. Plainly, there are many other interpretations of the experimental results. Perhaps clicks are perceptually displaced to the middle of a constituent, not its boundary; or perhaps the subject is responding by identifying the phrase-structure boundary directly below the major one. All other relevant experiments could be reinterpreted along similar lines, as can certainly be done in principle—though it is not so simple in practice, in the case of either the "psychological" or the "linguistic" evidence. The issues are the same throughout; or rather, there are no issues relevant here, since they hold of empirical inquiry generally.
When conclusions are drawn about phrase boundaries or other aspects of language on the basis of "linguistic evidence," Quine is reluctant to accept them "without further light on the nature of the supposed equipment,"[21] but when the same conclusions are based on "psychological evidence," these qualms do not arise. This epistemological dualism makes no sense whatsoever; it is a long step backward from traditional metaphysical dualism, which was a rational reaction, on assumptions now known to be faulty,[22] to perceived empirical problems. The qualms, such as they are, are in principle the same, whatever the evidence on which conclusions are based, and are simply features of empirical inquiry. As for the "supposed equipment," it raises no problems of principle that differ from those characteristic of all theory construction in the empirical sciences.
Yet another paradox arises within this framework. Linguists, it is argued, are not permitted to attribute one particular language system rather than others to the individual or idealized community that they are studying;[23] they are not permitted to explore what is true of the brain, described at the level at which we construct rule systems and the like. But something is true of the brain; there is something about my brain that is more or less like yours and crucially different from the brain of a speaker of Swahili. Therefore someone should be permitted to study these aspects of the real world, but not linguists, who are restricted to inquiry into Jones's behavior and may not proceed to attribute specific mechanisms to Jones's mind/brain and to use evidence from other languages (or from any domain, in principle) to verify the accuracy of their conclusions about these mechanisms. Accepting these terminological strictures about what the linguist must do, the rational step is to abandon linguistics (including the study of meaning in accord with the conditions stipulated in the Quinean paradigm). Having abandoned these pointless pursuits, we may now turn to this other subject, where we are permitted to attribute
specific mechanisms to Jones's mind/brain and to investigate these hypotheses by the methods of the sciences, using whatever evidence is at hand—in fact, the actual practice of linguists that is condemned in this curious, though extremely influential tradition in modern philosophy, which, in a final irony, prides itself on its "naturalism" and adherence to the methods of the sciences.
In his most recent effort to justify the strictures he imposes, in the January 1987 issue of the Journal of Philosophy , Quine offers the following argument.[24] For the linguist, he argues, "the behaviorist approach is mandatory." The reason is that in acquiring language, "we depend strictly on overt behavior in observable situations . . . There is nothing in linguistic meaning, then, beyond what is to be gleaned from overt behavior in observable circumstances," and the same holds true, by parity of argument, for the study of pronunciation, phrase structure, or whatever aspect of language we choose. Furthermore, as he makes explicit once again, the relevant behavior for the linguist is that of the natives to whom he/she is imputing knowledge of language: "If translators disagree on the translation of a Jungle sentence but no behavior on the part of the Jungle people [tacitly assumed to be homogeneous] could bear on the disagreement, then there is simply no fact of the matter," and the linguist who holds that there are facts to be discovered, and that some theories (grammars) are correct and others not, is guilty of serious methodological error or pure "folly" (recall that the "translator" stands for the language learner as well[25] and that the same argument holds for pronunciation, phrase structure, etc.).
Consider now the following analogous argument. In reaching its final physical structure in the passage from embryo to mature state, the organism depends strictly on nutrition provided from outside (including oxygen, etc.). There is nothing in the physical structure of the mature organism, then, beyond what is to be gleaned from the nutritional inputs. The student of human development and its outcome, then, must limit attention to these inputs; for the biologist, "the nutritionist approach is mandatory." The argument is the same as Quine's, and we see at once why it is untenable. True, the embryo "depends" on the nutritional environment just as the language learner "depends" on overt behavior. But what does the term "depends" include? Here we turn to the structure of the organism, which we may think of abstractly as a mapping M of external inputs into mature state. In the absence of such structure, observed behavior will lead to no knowledge of language and nutrition will lead to no growth. Quine of course recognizes this. Thus Quine's field linguist, pursuing the path of the language learner, "tentatively associates a native's utterance with the observed concurrent situation" and is permitted to make use of other hypotheses that allegedly correspond to capacities with which the language learner is endowed. If clarified, these hypotheses would constitute a theory of the innate structure of the organism and the mapping M.
As is agreed on all sides, without innate structure there is no effect of the
external environment in language (or other) growth; in particular, without innate structure Jones could not have developed in a specific way from embryo to person, and his language faculty could not have assumed the state of mature competence that underlies and accounts for Jones's behavior. The child is endowed with this innate structure and therefore grows to maturity along a course that is largely inner-directed; the task of the scientist is to discover what the innate endowment is and what is the nature of the state attained. Currently, the best theory is that the initial state of the language faculty incorporates certain general principles of language structure, including phonetic and semantic principles, and that the mature state of competence is a generative procedure that assigns structural descriptions to expressions and interacts with the motor and perceptual system and other cognitive systems of the mind/brain to yield semantic and phonetic interpretations of utterances. A vast range of empirical evidence is relevant in principle to determining just how this proposal should be spelled out in detail. Again, all of this is normal science, yielding theories that are true or false[26] regarding Jones's competence and his initial state, part of the human biological endowment. Perhaps this approach should be abandoned in terms of some other conception, now unavailable, but to establish this conclusion it does not suffice to demand that the linguist abandon the methods of the sciences.
As in his earlier formulations of these ideas, Quine's specific stipulations about the innate structure (hence the mapping M) are completely arbitrary, apart from their historical antecedents, here irrelevant. There is no reason to accept them in the case of language, just as comparable dogmatism about "dependence" would be rejected out of hand in the study of other aspects of the growth of organisms. Furthermore, there is compelling evidence that they are false, insofar as they are explicit. As in the study of physical development generally, the rational investigator will dismiss these dogmatic assumptions about the nature of "dependence" (i.e., about innate structure) along with other doctrines such as those just sketched, and will use whatever evidence can be found concerning the structure of the organism, the mapping M, and the nature of the states attained in particular cases. The conclusions that Quine, Davidson, Rorty and many others draw remain unargued. Nothing can be resurrected from the Quinean picture with regard to these matters, so far as I can see, though some of his conclusions, in particular, with regard to "meaning holism," may well turn out to be correct, at least in large part.
Let us return now to the "analytic-synthetic" distinction, and the Davidsonian argument that by "getting rid of it," Quine "saved philosophy of language as a serious subject." Recall that what is at issue here is not simply this distinction but the question of language-determined semantic connections generally. As I mentioned, we cannot appeal to Rorty's argument, attributed to Quine, that the "field linguist" finds the distinction "of no use." In practice, semantic structure is regularly attributed to lexical items in descriptive work
and theoretical studies on the semantics of natural language, and from these and other structural properties, semantic connections of various kinds are derivable, including analytic connections. There are good reasons for these standard assumptions about lexical structure. Acquisition of lexical items poses what is sometimes called "Plato's problem" in a very sharp form. As anyone who has tried to construct a dictionary or to work in descriptive semantics is aware, it is a very difficult matter to describe the meaning of a word, and such meanings have great intricacy and involve the most remarkable assumptions, even in the case of very simple concepts, such as what counts as a nameable thing. At peak periods of language acquisition, children are acquiring ("learning") many words a day, perhaps a dozen or more, meaning that they are acquiring words on very few exposures, even just one. This would appear to indicate that the concepts are already available, with much or all of their intricacy and structure predetermined, and that the child's task is to assign labels to concepts, as might be done with limited evidence given sufficiently rich innate structure. And these conceptual structures appear to yield semantic connections of a kind that will, in particular, induce an analytic-synthetic distinction, as a matter of empirical fact.
To the extent that anything is understood about lexical items and their nature, it seems that they are based on conceptual structures of a specific and closely integrated type. It has been argued plausibly that concepts of a locational nature, including goal and source of action, object moved, and so on, enter widely into lexical structure, often in quite abstract ways. In addition, notions like actor, recipient of action, instrument, event, intention, causation, and others are pervasive elements of lexical structure, with their specific properties and interrelations. Consider, say, the words 'chase' or 'persuade'. They clearly involve a reference to human intention. To chase Jones is not only to follow him but to follow him with the intent of staying on his path, perhaps to catch him. To persuade Smith to do something is to cause him to decide or intend to do it; if he never decides or intends to do it, we have not succeeded in persuading him. Furthermore, he must decide or intend by his own volition, not under duress; if we say that the police persuaded Smith to confess by torture, we are using the term ironically. Since these facts are known essentially without evidence, it must be that the child approaches language with an intuitive understanding of concepts involving intending, causation, goal of action, event, and so on, and places the words that are heard in a nexus that is permitted by the principles of universal grammar, which provide the framework for thought and language, and are common to human languages as systems that enter into various aspects of human life. These elements also appear to enter into an integrated "conceptual scheme," a component of the initial state of the language faculty that is fleshed out in specific ways, with predetermined scope and limits, in the course of language growth, one aspect of cognitive development. There may be revision and restructuring of such conceptual
schemes,[27] but care must be taken to separate out the various factors that enter into the course of development, including, quite possibly, genetically determined maturation that yields effects perceived only in late stages of cognitive growth.
Notice again that we appear to have connections of meaning in such cases as these; we have a rather clear distinction between truths of meaning and truths of fact. Thus, if John persuaded Bill to go to college, then Bill at some point decided or intended to go to college and did so without duress; otherwise, John did not persuade Bill to go to college. Similarly if John killed Bill, then Bill is dead (though John may or may not be, depending on the facts). These are truths of meaning, not of fact. The a priori framework of human thought, within which language is acquired, provides necessary connections among concepts, reflected in connections of meaning among words, and more broadly, among expressions involving these words, as in the example of referential dependence mentioned earlier. Syntactic relations provide a rich array of further examples. For example, there seems to be a clear distinction between the sentence 'everyone who lives upstairs lives upstairs' and 'everyone who lives upstairs is happy.' Quine appears to believe that this distinction is more problematic and obscure than his distinction between "grammatical" and "ungrammatical," which he regards as somehow crucial for the linguist's investigations.[28] The opposite is the case. In fact, an absolute distinction between "grammatical" and "ungrammatical" appears to have little if any significance. It can be established one way or another, or perhaps better, not at all, since it is doubtful that the concept, in Quine's sense, plays any role in the theory of language. The reasons were discussed in the earliest work in generative grammar, actually the only work in which an effort was made to develop such a concept in some manner that might be relevant to linguistic theory, but in terms that were long ago understood to be inappropriate.[29]
It appears, then, that one of the central conclusions of modern philosophy is rather dubious: namely, the contention, often held to have been established by work of Quine and others, that one can make no principled distinction between questions of fact and questions of meaning, that it is a matter of more or less deeply held belief. This conclusion has been supported by reflection on an artificially narrow class of examples, among them, concepts that have little or no relational structure. In the case of such sentences as 'cats are animals', for example, it is not easy to find evidence to decide whether the sentence is true as a matter of meaning or fact, or whether there is an answer to the question in this case, and there has been much inconclusive controversy about the matter. When we turn to concepts with an inherent relational structure such as 'persuade' or 'chase', or to more complex syntactic constructions such as those exhibiting referential dependence or causative and relative constructions, then it seems that semantic connections are readily discerned. Contrary to what
Rorty and others assert, this is the common assumption of empirical work in the study of linguistic meaning, and, furthermore, it seems to be a reasonable assumption.
The status of a statement as a truth of meaning or of empirical fact can only be established by empirical inquiry, and considerations of many sorts may well be relevant; for example, inquiry into language acquisition and variation among languages. The question of the existence of analytic truths and semantic connections more generally is an empirical one, to be settled by inquiry that goes well beyond the range of evidence ordinarily brought to bear in the literature on these topics. Suppose that two people differ in their intuitive judgments as to whether I can persuade John to go to college without his deciding or intending to do so.[30] We are by no means at an impasse. Rather, we can construct conflicting theories and proceed to test them. One who holds that the connection between 'persuade' and 'decide' or 'intend' is conceptual will proceed to elaborate the structure of the concepts, their primitive elements, the principles by which they are integrated and related to other cognitive systems, and so on, and will seek to show that other properties of language and other aspects of the acquisition and use of language can be explained in terms of the very same assumptions about the innate structure of the language faculty, in the same language and others, and that the same concepts play a role in other aspects of thought and understanding. One who holds that the connection is one of deeply held belief, not connection of meaning, has the task of developing a general theory of belief fixation that will yield the right conclusions in these and numerous other cases. Suppose one holds, with Paul Churchland for example, that the connection is based on the "semantic importance" of sentences relating 'persuade' and 'decide' or 'intend' (i.e., that these sentences play a prominent role in inference, or serve to introduce the term 'persuade' to the child's vocabulary, and thus are more important than others for communication).[31] One then faces the task of showing that these empirical claims are in fact true. The first tack, in terms of innate conceptual structure, seems far more promising to me, and is the only approach that has any results or even proposals to its credit, but it is a matter of empirical inquiry, not pronouncements on the basis of virtually no evidence. Specifically, arguments against the first (conceptual) approach in terms of indeterminacy, unclarity, open issues, and so on, establish nothing unless it is shown that alternative approaches in terms of some (now unavailable) theories of belief fixation or semantic importance are not subject to these problems.
The whole matter requires extensive rethinking, and much of what has been generally assumed for the past several decades about these questions appears to be dubious at best. There is, it seems rather clear, a rich conceptual structure determined by the initial state of the language faculty (perhaps drawing from the resources of other genetically determined faculties of mind), waiting
to be awakened by experience. All of this is much in accord with traditional rationalist conceptions and even, in some respects, the so-called "empiricist" thought of James Harris, David Hume, and others.
Many have found such conclusions completely unacceptable, even absurd; the idea that there is something like an array of innate concepts and that these are to a large degree merely "labeled" in language acquisition, as the empirical evidence suggests, certainly departs radically from many common assumptions. Some, for example Hilary Putnam, have argued that it is entirely implausible to suppose that we have "an innate stock of notions" including carburetor and bureaucrat .[32] If he were correct about this, it would not be particularly to the point, since the problem arises in a most serious way in connection with simple words such as 'table', 'person', 'chase', 'persuade', 'kill', and so on. But his argument for the examples he cites is not compelling. It is that to have given us this innate stock of notions, "evolution would have had to be able to anticipate all the contingencies of future physical and cultural environments. Obviously it didn't and couldn't do this."
Notice that the argument is invalid from the start. To suppose that in the course of evolution, humans come to have an innate stock of notions including carburetor and bureaucrat does not entail that evolution was able to anticipate every future physical and cultural contingency—only these contingencies. But that aside, notice that a very similar argument had long been accepted in immunology: namely, the number of antigens is so immense, including even artifically synthesized substances that had never existed in the world, that it was considered absurd to suppose that evolution had provided "an innate stock of antibodies"; rather, formation of antibodies must be a kind of "learning process" in which the antigens played an "instructive role." But this assumption may well be false. Niels Kaj Jerne won the Nobel Prize for his work challenging this idea, and upholding his own conception that an animal "cannot be stimulated to make specific antibodies, unless it has already made antibodies of this specificity before the antigen arrives," so that antibody formation is a selective process in which the antigen plays a selective and amplifying role.[33] Whether or not Jerne is correct, he certainly could be, and the same could be true in the case of word meanings, the argument being quite analogous.
Furthermore, there is good reason to suppose that the argument is at least in substantial measure correct even for such words as 'carburetor' and 'bureaucrat', which, in fact, pose the familiar problem of poverty of stimulus if we attend carefully to the enormous gap between what we know and the evidence on the basis of which we know it. The same is often true of technical terms of science and mathematics, and it surely appears to be the case for the terms of ordinary discourse. However surprising the conclusion may be that nature has provided us with an innate stock of concepts, and that the child's task is to discover their labels, the empirical facts appear to leave open few other possi-
bilities. Other possibilities (say, in terms of "generalized learning mechanisms") have yet to be coherently formulated, and if some day they are, it may well be that the apparent issue will dissolve.
In fact, it is not clear what thesis is being proposed by Putnam and others who reject what they call "the innateness hypothesis"; I should add that though I am alleged to be one of the exponents of this hypothesis, perhaps even the arch-criminal, I have never defended it and have no idea what it is supposed to be. Whatever the truth may be about antibody formation, it is based on the innate resources of the body and its immune system, and the task of the scientist is to find out what these resources are. Exactly the same is true of concept formation and language acquisition. For this reason, people who are supposed to be defenders of "the innateness hypothesis" do not defend the hypothesis or even use the phrase, because there is no such general hypothesis; rather, only specific hypotheses about the innate resources of the mind, in particular, its language faculty. General arguments against some unformulated "innateness hypothesis" have no bearing on actual hypotheses about innateness, in the case of growth of language and conceptual systems or other forms of physical growth.
Putnam offers a counterargument to the one just sketched on analogy to the immune system. He points out that concepts "often arise from theories ," and the number of possible theories (or perhaps even "theory types ") is so immense, even for "short" theories, as to make "the idea that evolution exhausted all the possibilities in advance wildly implausible." The argument is correct, but again irrelevant. In the first place, we are considering what humans are capable of acquiring, and there is no reason to believe that "all theories" can be learned or constructed by humans, nor is it even clear what sense this thesis has.[34] Furthermore, Putnam's original argument was supposed to bear on the specific words 'bureaucrat' and 'carburetor', and no cardinality argument is relevant to these cases, or to any substantive empirical hypothesis about innate structure. In other words, his argument that "evolution couldn't have done that" simply does not hold in the cases for which it is offered. The argument that evolution couldn't have done "everything"—even what is beyond human capacity—might hold if one could make some sense of it, but such an argument would not be relevant here, even if it could be given in a coherent form.
In the same connection, Putnam argues that the thesis of "meaning holism," with the Quinean principle that "revision can strike anywhere," contributes to undermining certain conclusions concerning the innate structure of conceptual systems and language generally. But this line of argument is questionable. Suppose that the thesis of "meaning holism" is correct in the sense that, as Putnam puts it, there are no "'psychologically real' entities which have enough of the properties we preanalytically assign to 'meanings' to warrant an identification," and reference is fully determined only on holistic
grounds. Nevertheless, it does not follow that semantic connections cannot be completely fixed and stable as a matter of biological endowment. Thus certain relations may remain stable as other considerations lead to various choices about fixing of reference. Furthermore, empirical considerations of the kind discussed earlier bear on the question of whether it is indeed true that "revision can strike anywhere." The point cannot be established for natural language by reference to the practice of the natural sciences from which Putnam draws many of his examples; these arguments, assuming them to be correct, do not suffice to show the absence of intrinsic semantic and conceptual structure based on fixed properties of the human mind. The thesis of "holism" may be correct in some measure or form, but the questions of semantic connections in natural language remain to be settled by empirical study, and for the present at least, the evidence appears to support their existence—rather strongly, it seems to me.
Let us pursue further Davidson's argument in his paper "A Nice Derangement of Epitaphs," in which he purports to show that the study of actual communication undermines a "commonly accepted account of linguistic competence and communication" and shows that "there is no such thing as a language, not if a language is anything like what many philosophers and linguists have supposed. There is therefore no such thing to be learned, mastered, or born with." This conception of language, which Davidson believes to be refuted, is founded on three basic assumptions concerning what he calls "first language" or "prior theory," a "complex system or theory" shared more or less by speaker and hearer. The assumptions are (1) that the prior theory is "systematic" in the sense that the interpreter who has this theory is able to interpret utterances on the basis of properties of their parts and the structure of the utterance; (2) that this method of interpretation is shared; and (3) that the component elements of the system are governed by learned conventions or regularities. The third of these assumptions is untenable for other reasons, but instead of delaying on this matter, let us present it in the form required for Davidson's argument: the component elements of the system are available, as he puts it, "in advance of occasions of interpretation"; it is a fixed element in communication situations, for interpreters at a fixed state of language knowledge.
To refute this conception, Davidson observes that in ordinary communication situations the interpreter makes use of all sorts of conjectures and assumptions about what the speaker may have in mind, relying on properties of the situation, the speaker's presumed intentions, and so on. The interpreter thus "adjusts his theory," modifying the "prior theory" to a "passing theory" that is "geared to the occasion." But this "passing theory cannot in general correspond to an interpreter's linguistic competence." This "passing theory is not a theory of what anyone (except perhaps a philosopher) would call an actual natural language," Davidson continues, and "'Mastery' of such a language
would be useless, since knowing a passing theory is only knowing how to interpret a particular utterance on a particular occasion." Furthermore, communication can proceed quite well when the prior theory is not shared by speaker and hearer, and the prior theory too is not what "we would normally call a language" since it is a psychological particular, specific to the speaker-hearer with features that are not shared through the "community." The interpreter has some kind of "strategy," a "mysterious process by which a speaker or hearer uses what he knows in advance plus present data to produce a passing theory," and for communication, what two people need "is the ability to converge on passing theories from utterance to utterance." Given these facts, there is no longer any use for "the concept of a language," for "shared grammar or rules," for a "portable interpreting machine set to grind out the meaning of an arbitrary utterance"; rather, we need something more evanescent, mysterious and "holistic," "the ability to converge on a passing theory from time to time." We thus are led to "abandon . . . not only the ordinary notion of a language, but we have erased the boundary between knowing a language and knowing our way around in the world generally." "In linguistic communication nothing corresponds to a linguistic competence" based on the three principles just mentioned, because "there are no rules for arriving at passing theories." At the conclusion of the discussion, however, Davidson asserts that a passing theory is derived somehow "from a private vocabulary and grammar," that is, from a "prior theory" meeting the first and perhaps a version of the third condition, but possibly not shared in the "community"; there is then a "prior theory" and there are surely certain methods, not others, "for arriving at passing theories," whether or not one wants to call these methods "rules."
The various parts of the argument are largely correct, but they do not seem to show very much. In particular, no reason has been offered to doubt that there is a "prior theory" in the usual sense of the study of language and knowledge of language—that is, a specific generative procedure incorporated in a specific mature state of the language faculty. Of course, this "prior theory" will be quite different from what is called "a language" in ordinary usage, but this is because no such concept plays a role in empirical inquiry into language and mind, as already noted.
In the face of Davidson's arguments, we may continue to suppose that there is, to very good first approximation, a fixed and invariant language faculty that maps presented evidence onto a system of rules and principles (or whatever turns out to be correct with regard to the cognitive state attained) that assign interpretations to utterances. Call this acquired system a "generative procedure." To know a language is to have an internal representation of this generative procedure, which we will express at various levels of abstraction from "more elementary" mechanisms and will seek to relate to such mechanisms, in the normal manner of the natural sciences.[35] Proceeding in accord with normal practice, we may also seek to construct a "parser," a device, also
attributed to the mind/brain, which incorporates the generative procedure attained along with other specified structures and properties,[36] and maps presented utterances into structural descriptions that are interpreted by other components of mind. So far, we are dealing with feasible questions of empirical inquiry.
There is also a further problem, which we can formulate in vague terms but which cannot be studied in practice: namely, to construct an "interpreter" that includes the parser as a component along with all other capacities of the mind, whatever they may be, and accepts nonlinguistic as well as linguistic inputs. This interpreter, presented with an utterance and a situation, assigns some interpretation to what is being said by a person in this situation. The study of communication in the actual world of experience is the study of the interpreter, but this is not a topic for empirical inquiry, for the usual reasons: there is no such topic as the study of everything. Similarly, science does not investigate other phenomena of the world as presented to us in everyday experience. The interpreter, as Davidson correctly observes, includes everything that people are capable of doing, which is why it is not an object of empirical inquiry, and why nothing sensible can be said about it. We might hope to learn something about various elements of the interpreter, proceeding by the normal methods of the sciences, beginning with the "private vocabulary and grammar" that constitute the language attained, proceeding to the parser, then perhaps, to the extent feasible, turning to other elements of the mind and of situations that enter into normal human life. But if we begin with the demand for a theory of everything, we will find nothing; it is unnecessary to construct elaborate arguments to establish this point.[37] The situation is no different in the far more advanced sciences. The proper conclusion is not that we must abandon concepts of language that can be productively studied, but that the topic of successful communication in the actual world of experience is far too complex and obscure to merit attention in empirical inquiry, except as a guide to intuitions as we pursue research designed to lead to some understanding of the real world, communication included. These observations have no bearing on whether or not there is a "prior theory," an internalized generative procedure, in the normal sense of empirical practice.
Davidson's "passing theory" is not a useful notion; about this, he is surely correct. The interpreter will construct all sorts of "passing theories" (though, crucially, not any sort), changing moment to moment, because the interpreter as Davidson conceives it includes everything available to human intelligence; but it makes no sense to call its transient states "theories" or to consider them a subject of direct inquiry. Crucially, nothing in Davidson's argument bears on the assumption that the "prior theory" (though not understood quite in his terms) remains a fixed and invariant element of the "interpreter" (as of the narrower idealized parser) and that it enters into the functioning of the interpreter.
In this discussion, Davidson focuses attention on malapropisms and so-called "misuse of language" more generally. Here some care is necessary. Let's again take Jones, a speaker of a variety of what we informally call "English." Jones has mastered a generative procedure that associates with utterances structural descriptions, including semantic properties, and has other capacities of mind that allow him to produce and interpret linguistic expressions making use of these structural descriptions. Let us call this generative procedure his "I-language," where I is to suggest "internalized" (in the mind/brain) and "intensional" (in that the procedure is a function enumerating structural descriptions, considered in intension with a particular description);[38] here we are referring to specific postulated mechanisms of the mind/brain, considered abstractly.
Jones may speak in a way that is not in accord with his I-language, or may offer judgments inconsistent with his I-language; judgments about ourselves, like others, can be mistaken, and much more than I-language is involved in behavior. This is an uninteresting case of misuse of language; call it the "individual sense."
Suppose that Jones, like most of us, normally says such things as 'hopefully, we'll be able to solve that problem', or uses the word 'disinterested' to mean uninterested Various authority figures tell us that this is "wrong," a "mistake," not in accord with the "rules of English." Jones is "misusing his language," namely, English, a language of which he has only a partial and perhaps distorted knowledge, as in Dummett's "fundamental sense" of language. Even if 95 percent of the population, or for that matter everyone but William Safire and a few others, were to behave in the manner of Jones, these cases would still constitute "misuse of language." Or Jones may try to adapt to the practice of some community for some reason, or perhaps for no reason at all, and may fail to do so, in which case people observing Jones may speak informally of a misuse of the language of this community. These concepts of "misuse of language," which we may call "the community sense," may be of interest for the study of the sociology of group identification, authority structure, and the like, but they have little bearing on the study of language, so far as we know. We understand this perfectly well in the case of pronunciation. Thus to say that one variety of English is "right" and another "wrong" makes as much sense as saying that Spanish is right and English wrong; and the same is true, though for some reason the point seems more obscure, with regard to other aspects of language.
Another possible sense of the concept "misuse of language" derives from Hilary Putnam's notion of "the division of linguistic labor." Thus in the lexicon represented in my mind/brain, the entry for 'elm' and 'beech', or 'mass' and 'kinetic energy', may include an indication that the reference for these terms is to be determined by experts to whom I defer. Then I might apply the terms inaccurately, in the sense that the reference is not in accord with the
determinations of these experts. In this case, I might be said to be "misusing my own language."[39] Let us call this the "expert sense" of misuse of language. Again, nothing of great moment appears to follow, surely nothing relating to the approach to language within the framework of individual psychology sketched earlier, and typically followed in practice.[40] Notice that no useful concept of "language" or "community" emerges from these considerations. Thus my expert for 'elm' and 'beech' may be an Italian gardener who speaks not a word of English, and who corrects my usage through reference to the technical Latin names that we share; and my expert for 'mass' and 'kinetic energy' may be a monolingual German physicist. But we would not conclude that German and Italian are included in English, or that all of us form a "community" in any useful sense of the term.
Is there any other concept of "misuse of language"? I am aware of none. If so, the concept plays no important role in the study of language, meaning, communication, or whatever. To take some examples of the kind that Tyler Burge has discussed, suppose that Jones uses the term 'arthritis' to refer to a pain in the thigh. Suppose this is the usage of his village, but not the usage of the outside community. Jones is not misusing his language in the individual sense; his usage is true to his I-language. In his village, he is not misusing his language in the community sense, but outside its borders, he is. Depending on how 'arthritis' is represented in Jones's mental lexicon, he may or may not be misusing his language in the "expert sense." How should we attribute beliefs about arthritis to Jones? Here intuitions differ, and it may be that evidence is too slim, for the moment, to settle the point satisfactorily. Putting aside the "expert sense," suppose we use the term 'I-belief' to refer to the concept that is like belief, except that Jones has the same belief within his village and in the wider community, namely, the belief that we would express, in our I-language, by saying that he has some kind of body pain.[41] This may or may not be the same as the concept of belief in our ordinary language, but it is the concept that seems to be required for the study of what is misleadingly called "the causation of behavior"—misleadingly, because it is unclear that behavior is "caused" in any useful sense of the term. Clearly, there is no reason to suppose that the concepts of general psychology will be those of ordinary usage, just as the concepts of physics, or of the subbranch of psychology called "linguistics," typically are not. Nor is it at all obvious to me that there is a reasonable branch of science (or to be more accurate, human science, meaning the kind of scientific inquiry that humans, with their particular cognitive capacities, are capable of undertaking) that deals with questions of this nature.
It has not, I think, been established that there is anything more to say about the matter. In particular, reference to "misuse of language," to "norms," to "communities," and so on, seems to me to require much more care than is often taken. These concepts are obscure, and it is not clear that they are of any use for inquiry into language and human behavior. Any argument that
relies on these notions merits careful scrutiny, and I doubt that familiar arguments can withstand it. Communities are formed in all sorts of overlapping ways, and the study of communities and their norms quickly degenerates into the study of everything. The fact remains that Jones speaks and understands the way he does on the basis of the I-language he has acquired in the course of language growth; and if Jones does or does not follow what we choose, for some transient purpose, to call "community norms" or "social practice," it is on the basis of this internalized I-language (along with much else). Boris, a monolingual speaker of some variety of Russian, has a different I-language, and follows different "norms." I can understand Jones, within limits, because my I-language is not too different from his, and because he and I more or less share other unknown properties that enter into the full interpreter; this is not a topic of empirical inquiry as it stands, in its unanalyzed complexity. That seems to me the way we should approach these questions.
In these terms, we can develop a concept of "knowledge of language" that is appropriate for the inquiry into language and mind; namely, mastery and internal representation of a specific I-language. The linguist's grammar is a theory of the I-language, and universal grammar is the theory of the initial state of the language faculty. Jones's I-language is one particular mature state—or output, regarding the language faculty as a function that maps evidence into I-language. What about the concept language? We might simply understand languages as I-languages, thus taking a language to be something like "a way of speaking," the "finite means" that provide for "infinite use" in the terms of Wilhelm von Humboldt's characterization of language, also an effort to capture his concept of language as a "process of generation" rather than a set of "generated objects." We thus take language to be, in effect, a "notion of structure" that guides the speaker in forming "free expressions," in Otto Jespersen's terms. For empirical inquiry, I think that is an appropriate decision, though obviously not for ordinary discourse. Or we might want to construct a concept of language divorced from cognitive states, perhaps along lines suggested by James Higginbotham. Taking knowledge of language to be a cognitive state, we might construe the "language" as an abstract object, the "object of knowledge," an abstract system of rules and principles (or whatever turns out to be correct) that is an image of the generative procedure, the I-language, represented in the mind and ultimately in the brain in now-unknown "more elementary" mechanisms. Since the language in this sense is completely determined by the I-language, though abstracted from it, it is not entirely clear that this further step is motivated, but perhaps it is.
In these terms, it seems to me that the questions about language and its use that can be subjected to empirical inquiry can readily be formulated and, as far as we now know, best addressed. There may well be many other questions that are not subject to empirical inquiry in the manner of the sciences, and perhaps never will be, if humans are themselves part of the natural world
and thus have specific biological capacities with their scope and limits, like every other organism. We must be careful not to succumb to illusions about evolution and its adaptive miracles. There is nothing in the theory of evolution that suggests that we should be able to answer questions that we can pose, even in principle, even if they have answers, or that we should be able to pose the right questions. To the extent that we can, we have empirical science, a kind of chance convergence of properties of the mind and properties of the extramental world. There is nothing surprising about this; we take for granted that something similar is true of rats and bees, and should not be surprised to learn that humans are biological organisms, not angels. But within the limits of human science, it seems to me that the best guess as of the present is that the framework I have just briefly outlined is a proper one for inquiry into the empirical questions about language and mind; and within it, there are some notable successes and many intriguing prospects.