Plato and Aristotle
We may begin with two central issues in the philosophies of science of Plato and Aristotle. When Plato comes to discuss the generation of the physical world, in the Timaeus , he refers to this repeatedly as a "likely story,"
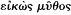
[114] Cf. De arte 3, CMG 1.1.10.19ff. (accepting Heiberg's text).
[115] Among more recent discussions of the Timaeus in particular should be noted those of Witte 1964, Schulz 1966, Gadamer 1974/1980, Zeyl 1975, Vlastos 1975a, Scheffel 1976. On the general issue of the imperfection of per-ceptible phenomena, the contributions of Cooper 1970, Nehamas 1972–73, 1975, 1982–83, and Burnyeat 1976 are fundamental. Cf. Irwin 1977. For what follows see also G. E. R. Lloyd 1968a and 1983b.
need not detain us long. The alternative expression,
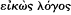
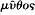
Both the nature of the reservations Plato expresses and their scope need to be considered carefully. The fundamental ontological distinction that dictates the status of any account of the physical world is, of course, that between being and becoming. What comes to be, insofar as it comes to be, cannot be the object of certain knowledge. That is stressed at Ti. 27d5ff. and repeatedly in what follows. Yet in respect of
[117] A. E. Taylor 1928, e.g., pp. 59ff.; criticised by Cornford 1937, pp. 29f.
[118] Comparisons with the hypotheses of modern science are, then, liable to be misleading, at least insofar as they had better not be, in principle, beyond the reach of empirical support or refutation.
[119] Friedländer 1958–69, vol. 1, p. 251. Heisenberg himself occasionally referred in admiring terms to Plato's atomic theory, e.g., 1945/1952, p. 57, 1955/1958, pp. 59f.; cf. also Feyerabend 1981b, p. 84.
being itself no such reservation applies; on the contrary, concerning what is stable Timaeus makes the considerable demand that the accounts should "so far as possible" be irrefutable and unchangeable (or invincible) ones.[120] Whenever the cosmologist or the natural philosopher has to do with the intelligible model—the Forms—after which the visible cosmos is constructed, there should, in principle, be no falling short.[121]
Moreover, the claim in respect to the particular cosmological account set out in the Timaeus is that it is "inferior to none in likelihood."[122] The visible cosmos is not of course identical with the intelligible model. In the work of creation the Craftsman has to bring order into what is already in chaotic motion.[123] He has to contend with the factor Plato calls necessity or the wandering cause.[124] Yet he made the cosmos as like the model as he could. Four points are worth emphasising. First, the model the Craftsman uses is itself eternal and unchanging; the importance of this is spelled out at Ti. 28a ff., where the inferiority of any production based on a created model is stressed. Secondly, the product of his workmanship is good . The theme is a recurrent one and is given a triumphant climax in the final sentence of the Timaeus , where the likeness of the intelligible model is described as a perceptible god, greatest and best and fairest and most perfect.[125]
[123] Ti. 30a, 52d ff.
[124] Ti. 47e ff. Broadly, reason "persuades" necessity in the sense that the best ends are secured within the framework of the possibilities set by the inherent properties and characteristics of the material available.
Thirdly, what the Craftsman does is to bring order into precosmic chaos or disorder, an order that the natural philosopher, for his part, can and should study and discover.[126] Fourthly, the Craftsman's own work is indissoluble, even if that of the lesser divine Craftsmen does not share that characteristic.[127]
While the whole account of becoming is undercut as no more than a likely story, the particular grounds for hesitation expressed concerning particular items in the exposition vary. Timaeus baulks at a detailed discussion of planetary motion, for instance, in part for fear of making his account disproportionately long.[128] Length is again a factor mentioned when he draws back on the question of why the half-equilateral is the fairest of scalene triangles.[129] Here we are told that if someone is able to give a better account of the construction of the elementary bodies, his is the victory of a friend, not an enemy.[130] The longer account that Timaeus refers to, but does not give, would not necessarily be an end of the matter: "should anyone refute this and discover that it is not so, we do not grudge him the prize."[131] But that is certainly not to deny, but, rather, to assert, that the problem might be advanced.
To be sure, elsewhere the deflation of the value and importance of parts, at least, of the exercise is underlined, as, for example, at Ti. 59c–d when Timaeus speaks of probable accounts of becoming as a "moderate and intelligent pastime" undertaken "for the sake of recreation,"[132] where the particular problems he is about to tackle concern the varieties and compounds of the simple bodies. Again at 68b–d we are told that to try to state the different proportions of the constituents that go to make up particular colours would be to betray an ignorance
[127] Ti. 41a–b.
[128] See Ti. 38d–e, and cf. 40c–d, which refers to the pointlessness of a discussion of planetary motion without visible models to consult.
[129] Ti. 54a–b.
[130] Ti. 54a.
of the difference between God's nature and man's, for on that question not even a probable account is possible.[133]
To take stock on the chief issues that concern us here, the first and most obvious contrast between Plato and most of his predecessors relates to the explicitness with which he confronts the question of the status of any account of the natural world. Secondly, on many topics on which both the pre-Socratic natural philosophers and many medical theorists had tended to express themselves dogmatically, implicitly making unqualified claims for the correctness of their assertions, Plato states his reservations, both general and particular, about the possibility of attaining certainty. But if in principle and in practice he is undeniably an anti-dogmatist on many questions in physics and cosmology, we should not underestimate the dogmatic elements that remain. If certainty is not possible concerning becoming, it is demanded "so far as possible" for being, including the intelligible order the divine Craftsman uses as his model. Above all, the issue of the goodness of the created world and of its creator is not a matter of doubt. In the Timaeus we are merely told that it would be impious to deny this,[134] but in the Laws Plato was to treat those who denied that the world is the product of benevolent, rational order as a threat to the state he there describes and, as such, subject to sanctions of formidable severity, including death, if they do not modify their views.[135] Teleology especially is not negotiable.
By insisting that physics deals with what is true "for the most part"[136] as well as with what is true "always" Aristotle drew a distinc-
[133] Ti. 68b and 68d. When, in the latter text, Timaeus says that no test is possible for us, since god alone is able to mix the many into one and again to dissolve the one into the many, whereas no man is or ever will be capable of doing either of these, the blending in question appears to be not a matter of mixing pigments, but one of combining fundamental atomic particles. Yet the expression is unclear, and Plato certainly does not distinguish as carefully as he might between the two types of blending, leaving it possible to read Timaeus' remarks as suggesting that one cannot even hope to discover which pigments added to which give which compound colours.
[134] Ti. 29a.
[135] See Lg. 889a ff., 896d, 897b–c, 907d ff., and cf. also Phlb. 28d–e.
tion that marks his distance from Plato. Yet that very distinction points to a well-known crux in his thought, one that relates, broadly, to the tension between the demand for scientific theories to be certain and an appreciation that not everything in science is or can be. On the one hand Aristotle insists, in the Posterior Analytics , that
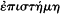
Yet—an obvious question—how can a study that deals with what is true only "for the most part" conceivably be a science or yield episteme as Aristotle defines it? At least, if "for the most part" is interpreted in a statistical sense (more than half, but not all), then syllogisms that have both premises true "for the most part" will not yield conclusions that hold "for the most part," let alone universally. If most B's are A, and most C's are B, it will not follow that most C's are A; it will not follow that any are. Moreover, when only one premise is true for the most part, the other universally, they will not necessarily combine to give a conclusion that is true "for the most part." "Most B's are A" and "all C's are B" together do not yield "most C's are A." And when the
[138] See APo. 1.2.71b20ff., and 1.4.73a21ff.
[139] The most famous examples of this come in his discussion of the reproduction of bees, where he states, among other things, that the facts, or what occurs, have not been sufficiently ascertained (De Generatione Animalium, GA , 760b27ff.), and on the question of the number of celestial spheres needed to account for the motions of the sun, moon, and planets (Metaph. 1073b10ff., 13ff.; cf. 1074a14ff.). Cf., e.g., Somn. Vig. 454b21ff., Resp. 476a5ff., GA 721a1f., 14ff., 741a34ff., 746b4ff., 757b22f., 762a33ff.
major premise is universal, the conclusion is again not "for the most part" if that is taken to exclude "universally": "all B's are A" and "most C's are B" together do not rule out "all C's are A."
In the light of the difficulties in Aristotle's opaque and elliptical discussions[140] it has been suggested that "for the most part" is not purely statistical but is used, rather, as a temporal operator (i.e., "not always") or as a quasi-modal operator ("not necessarily") or corresponds to some admittedly unanalysed notion of what holds "by nature."[141] Yet Aristotle himself, it must be said, nowhere elucidates the concept, nor does he explain how syllogisms incorporating propositions true "for the most part" meet the requirements laid down for understanding in the opening chapters of the Posterior Analytics , notably the requirement that it is of what cannot be otherwise than it is.
Some alleviation of the general problem is possible. The Posterior Analytics , it has been argued,[142] has primarily a pedagogic aim: it presents certain recommendations about how a mature science is to be taught, or at least about how to set out a body of theorems in good deductive order so that their connections are revealed and the explanations they incorporate are grasped as the explanations they are. Manifestly, Aristotle has very little to say, in this work, on the problems of discovery, about how scientific understanding is acquired in the first
[140] The chief texts in the Organon are in APr. 1.27, APo. 1.30 and 2.12. In APo. 1.30.87b19ff., Aristotle remarks that when, in syllogisms, the propositions are necessary, the conclusion is also necessary; when for the most part, the conclusion is also likewise—where "for the most part" is clearly contrasted with "necessary," 87b22–23—but the main aim of the chapter is to refute the notion that there is demonstrative knowledge of what happens by chance. At APo. 2.12.96a8–19, he stipulates that for the conclusion to be true "for the most part," as opposed to universally, the middle term must also hold "for the most part"—where this is contrasted with what holds universally, for all and always (96a15–16). However, the greatest difficulty for the statistical view is in APr. 1.27.43b33ff. There when the "problems" are "for the most part," the syllogisms consist of propositions that are—either all or some of them—"for the most part," and this appears to envisage the possibility of syllogisms with both premises true "for the most part."
[141] Apart from the perceptive remarks in J. Barnes' commentary on APo. , 1975 ad loc., see the full discussion in the elegant paper devoted to the topic by Mignucci 1981.
[142] Most forcefully, in recent times, by J. Barnes 1969/1975.
place.[143] At the same time, the examples he gives show that his discussion is not restricted to the already well-established disciplines such as mathematics and the exact sciences. Although most of his illustrations are drawn from such fields, a fair number, particularly in the second book, relate to zoological or botanical questions.[144] Presumably he has in mind an ideal that these studies can eventually attain, for certainly they had not done so in his day.[145] Yet for that ideal to be realised, either we have to imagine that the studies as set out will deal solely with universal and necessary propositions, or the difficulties in extending the schema to cover propositions true only "for the most part" have to be resolved—with corresponding modifications, no doubt, to the ideal itself.[146]
The value of the model in the Posterior Analytics as a model of demonstration, however, remains. If we recall the complex and confused uses of the terms for necessity and demonstration in the Hippocratic writers, we can see the advances made.[147] Aristotle stipulates precisely
[144] See, for example, APo. 98a35ff., 99a23ff., b4ff.; cf. J. Barnes 1969/1975, pp. 70ff.
[145] This is not to deny that connections can be found between the recommendations of the Posterior Analytics and the actual practice of the zoological treatises. Lennox 1987, for instance, has recently drawn attention to the concern, in the latter, to establish the widest class of which a character is true (cf. APo. 1.4.73b26ff. and 5.74a4ff.): cf. also Pellegrin 1986. But neither of these studies tackles the problems raised by physics dealing with what is true "for the most part."
[146] At APo. 94a36ff., in his discussion of the different types of causes that may serve as middle terms, Aristotle even gives an example of a historical explanation to illustrate the efficient cause. Moreover, this is one that involves reference to a singular term (the Athenians' raid on Sardis, cited as provoking the Persian war) and so falls outside the scope of the theory of the syllogism set out in the Prior Analytics .
[147] See above at nn. 47–66. Aristotle himself notes at PA 639b21ff., cf. Metaph. 1015a20ff., both that many of his predecessors reduced their expla-nations to the necessary (by which he means that they took no account of the final cause) and that they failed to distinguish the senses of necessity. This is not to deny, of course, that certain distinctions continue to be ignored by Aristotle himself, as is clearly shown by Sorabji, 1980a, and cf. Waterlow 1982b.
what conditions have to be met to justify the claim that conclusions have been demonstrated. True premises and valid inference are not enough: the premises must be prior to and explanatory of the conclusions. In a sequence of demonstrations the ultimate starting-points (they comprise definitions, axioms, and hypotheses) must themselves be indemonstrable (on pain of an infinite regress) but known to be true.[148] Whatever other obscurities remain, necessity as logical consequence is now deployed with confidence, and we have a whole subtle discussion of necessity as a modal operator, even though, again, the precise interpretation of many points in Aristotle's treatment remains controversial.[149]
But the clarity of the model has been bought at a price in terms of the range of its applicability. In mathematics and the exact sciences there is little difficulty in fulfilling Aristotle's criteria: a body of theorems can be presented in systematic order and their derivation from a set of axioms and definitions made clear. Yet the situation is very different in the natural sciences, and not just for the reason already mentioned, that these deal with propositions some of which are true only "for the most part." For the model to be applicable here we have also to be able to answer the thorny question of the nature of the indemonstrable starting-points. Over and above the general regulative principles that govern all discourse—the laws of contradiction and of excluded middle—what will count as axioms in zoology and botany, in meteorology or geology?[150] Can we envisage the definitions in such fields having the status of such starting-points?
[148] See APo. 72a5ff., cf. b18ff., 76a31ff.
[149] See especially Sorabji 1980a, and cf. Lear 1980, chap. 1.
[150] The dictum that "nature does nothing in vain" is often appealed to, in the zoological treatises especially, as the grounds for particular explanations, and it may be said to act as some kind of general regulative principle governing the zoologist's inquiry, one which must be accepted for that inquiry to be fruitful and one that is chiefly to be justified by the results obtained by its use. On the other hand, it is unlike both the laws of excluded middle and contradic-tion, and the particular mathematical axioms that Aristotle mentions (such as the equality axiom that if equals are taken from equals, equals remain: e.g., APo. 76a41). No attempt is or can be made to prove the latter, while the former are to be supported by what he calls an "elenctic demonstration" (Metaph. 1006a11ff., 15ff.), which proceeds by pressing any opponent who would deny them to signify something, to himself or to another (cf. Lear 1980, pp. 98ff.). Clearly, opposition to the dictum that nature does nothing in vain cannot be dealt with in that way. Rather, we have several serious attempts to discuss the consequences of its denial, notably in Ph. 2.8.198b10ff. and PA 1.1, especially 640a18ff., even if in the body of the physical treatises it is thereafter generally assumed—as Aristotle may hold it has to be, for progress to be made in scientific inquiry.
Definitions and demonstrations are, as Aristotle points out in his acute if often problematic discussions of their interrelations in the Posterior Analytics ,[151] crucially interdependent. Take first one of his astronomical examples. Lunar eclipse is not just any loss of light that the moon suffers (a cloud obscuring it will not count), but loss of light due to the interposition of the earth. But if you ask for the explanation, you will receive the information packed into the full definition. Why does it suffer eclipse? Because the earth intervenes.[152] Similarly, in one of the botanical examples alluded to:[153] deciduousness is not just any
[151] See APo. 75b30ff., 2.8, 93a14ff., 10, 93b29ff., 94a11ff. Aristotle recognises that before we are in a position to give a definitive definition we sometimes have some grasp of the subject inquired into (93a21ff., 29ff.), as well as some understanding of the meaning of the term (93b29ff.), though these points do not receive much elaboration in his discussion. See R. Bolton 1976, Ackrill 1981.
loss of leaf that a tree suffers (if it is diseased and drops its leaves, that will not count), but loss of leaf from the coagulation of the fluid or sap at the junction of the leaf-stalk. The fully fledged syllogism that sets out why broad-leaved trees are deciduous might run: all trees that have sap that coagulates are deciduous; all broad-leaved trees have sap that coagulates; so all broad-leaved trees are deciduous. This syllogism meets the criterion for a demonstration, for the conclusion is drawn through a middle term that is explanatory. But everything depends, evidently, on the truth of the definition.
From this point of view, all that the theory of demonstration does is to provide a set of rules for the proper articulation of propositions in such a way as to reveal the explanations as the explanations they are. But for the botanist in the field, obviously the chief task is the acquisition of the knowledge, not its articulation. As Aristotle's own practice in, for example, the zoological treatises shows, he is generally far short of being able to resolve the main problems he raises by demonstrations containing explanations proceeding from incontrovertible starting-points.
But whatever tensions remain between his theory and his practice, Aristotle did, as we said, transform the understanding of demonstration, and whatever the limitations of his model in other fields, the possibility of its application to mathematics and the exact sciences was clear. His formal logic differs in several fundamental respects from Euclid's practice in the systematic presentation of a body of geometrical theorems in the Elements.[154] In particular, Euclid's arguments are not syllogistic, and attempts to recast them in syllogistic form reveal the artificiality of that exercise.[155] Yet what Aristotle's theory and Euclid's practice have in common is the conception of demonstration proceeding by rigorous deductive argument from indemonstrable
[154] The problem of the relationship between Euclid's postulates and Aristotle's axioms has been much discussed, e.g., by Scholz 1930/1975, H. D. P. Lee 1935, Einarson 1936, von Fritz 1955/1971, Berka 1963, I. Mueller 1969, Gómez-Lobo 1976–77, Hintikka 1981, Leszl 1981.
[155] See, for example, Corcoran 1973, R. Smith 1978, Novak 1978, and especially I. Mueller 1969, 1974, and 1981.
axiomatic starting-points. Here, one may say, was a new style of wisdom indeed. Moreover, the ideal thus jointly derived (very roughly speaking) from Aristotle and Euclid was to prove enormously influential[156] and well beyond the exact sciences.[157] Physical scientists and medical writers too often advocated demonstration more geometrico and in some unlikely contexts. Just what will count as the indemonstrable premises in element theory and meteorology, in physiology, embryology, and pathology, a difficulty already in Aristotle, does not become much clearer later in those such as Galen who also hankered after deductive certainty.[158]
[156] Although the incontrovertibility of mathematical arguments was their pride, the insistence on rigorous deductive proof had certain inhibiting consequences within Greek mathematics itself. The best-known and most obvious illustration of this comes with Archimedes' comments on his own mechanical method, based on a notion of indivisibles, in his Method , (HS) 2.428.18ff., 438.16ff. In this a plane figure whose area is to be determined is thought of as composed of a set of parallel lines indefinitely close together, balanced against corresponding lines of the same length in a figure of known area: thus the desired area can be found in terms of the known one. Archimedes remarks explicitly that this is not a method of proof, only one of discovery: its results have thereafter to be proved strictly, using reductio and the method of exhaustion. The method remained unexploited by later Greek mathematicians, in part, no doubt, because this treatise itself was not generally known. Yet that is not the whole story, since some of the theorems in On the Quadrature of the Parabola implicitly depend on a similar method. An additional, more substantial factor may lie in the reluctance on the part of Greek mathematicians of any period to rely on informal methods. It is in this respect that the contrast between Greek mathematics and the mathematics of Cavalieri and others in the seventeenth century is most marked. On the Archimedean method, see, for example, Knorr 1981 and 1982a, who argues that the difficulty lay with its application of mechanical ideas rather than with its use of indivisibles, and who remarks, 1981, pp. 174ff., on the inhibiting influence of the insistence on formal procedures.
[157] Even in the exact sciences in antiquity, however, axiomatisation is generally incomplete judged by modern standards: cf. further below, Chap. 5 n. 111.
[158] Galen's own treatise On Demonstration , in fifteen books, is not extant, but even while he recognises the stochastic elements in medicine, references to the ideal of geometrical method and attempts to deploy it recur throughout his work. There is now a very full discussion of this aspect of Galen's methodology in J. Barnes (forthcoming). For the fragments of the work On Demonstration see I. von Müller 1897.
Nevertheless, one strand of a dogmatic tradition thereby attained a measure of philosophical respectability in the wake of the development of the theory of demonstration and of its practice in the mathematical sciences, and one clear benefit from this was a greater awareness of the questions of the formal analysis and validity of arguments—though Stoic logic takes as much of the credit for this as Aristotle's.[159] Yet over against that tradition, the recognition of the dangers of dogmatism, and a certain tentativeness and open-mindedness, can also be amply exemplified in some of Aristotle's successors, as they can in Aristotle himself. We may turn first to Theophrastus and to two works in the Aristotelian Corpus that are in the main the products of the Lyceum—the Problemata and the Mechanics —for excellent illustrations of the continuing tension between the dogmatic and the tentative.