Theorem 3—
The Linear Dynamics Ratio
Theorem 3 is Newton's crowning achievement in dynamics. It sets forth the combination of geometric elements that provide the basic paradigm for his primary solution of direct problems. Figure 4.13 makes visual these basic geometric elements: the displacement QR is the deviation from the linear path PR produced by the centripetal force directed toward the center of force S , and the triangular area PSQ is given by one-half of the product QT × SP . In the limit as the point Q approaches the point P , the force is assumed to be constant and its magnitude is proportional to the displacement QR divided by the square of the time (i.e., the parabolic approximation). From Theorem 1, the time is proportional to the area PSQ . Thus, combining the parabolic approximation and the area law, the force is shown to be proportional to the linear dynamics ratio QR / (QT2 × SP2 ), or as Newton preferred, "the centripetal force would be reciprocally as the solid (SP2 × QT2 ) / QR ."
The results of Theorem 3 are valid for any general curve and are not restricted to circles or ellipses (for example, Newton employed it to calculate the force necessary to produce a spiral motion). Nevertheless, New-
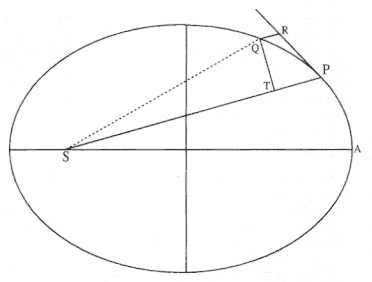
Figure 4.13
Based on Newton's diagram for Theorem 3.
ton's thoughts must have been on the distinguished Kepler problem when he drew the diagram for this theorem, because the general curve in figure 4.13 looks very much like an ellipse (in fact, it is an ellipse). He does not employ any of the specific properties of an ellipse, however, in obtaining the general relationship between the force and the dynamic elements of the general curve. In the following, the theorem is divided into a number of separate lines and detailed commentaries are given for each line.
Demonstration
[A] Theorem 3. In the indefinitely small figure QRPT the line segment QR is, with the time given, as the centripetal force ,
Or, QRµF for a given time. The applied force is assumed to be approximately constant in magnitude and direction in the limit as the point Q approaches the point P , or as Newton puts it, "in the indefinitely small figure QRPT ." Thus, the elemental arc of the general curve can be approximated by an elemental arc of a parabola. The tangential displacement PR is the inertial displacement the body would have made in a given time in the absence of a centripetal force under the sole action of the velocity it had at point P . The deviation QR is the linear displacement the body would have made in the same given time under the sole action of a constant applied force directed along the line SP from the initial point P to the center of
force S . The resultant displacement PQ is given from the parallelogram rule by the sum of the tangential displacement PR due to the initial "innate force" at point P and the linear displacement QR due to the continuous applied force. [In terms of modern notation, the displacement QR = (1/2) (F / m ) (t2 ) for a constant force F and mass m , where F / m is the acceleration. Thus, for a given time, QR = (t2 / 2m ) F = k1F , (where k1 is a constant equal to t2 / 2m ) or the displacement QR is directly proportional to the force F .]
[B] and, with the force given, as the square of the time ,
Or, QRµt2 for a given force. This condition follows from Hypothesis 4 (or in the revised Lemma 2: "The space with which a body, with some centripetal force impelling it, describes at the very beginning of its motion, is in the doubled ratio of the time"). [In modern notation, from section [A], QR = (1/2) (F /m )(t2 ) = (F /2m ) (t2 ) = k2t 2 , where k2 is a constant equal to F /2m . Thus, for a given force F the displacement QR is directly proportional to the square of the time t .]
[C] and hence, when neither is given, as the centripetal force and the square of the time conjointly ;
Or, QRµ (F ) (t2 ). From the expressions [A] and [B], when neither the time nor the force is given, the line segment QR depends directly upon both the force and the square of the time. [In modern notation, QR = (1/2m ) (F ) (t 2 ) = k3 (F ) (t2 ), where k3 is a constant equal to 1/2m . Thus, QR is directly proportional to the product of the force and the square of the time.]
[D] that is, as the centripetal force taken once and the area SQP proportional to the time (or its double , SP × QT) taken twice .
Or, QRµ (F ) (t2 ) µ (F ) (SP × QT )2 . From [C], the displacement is proportional to the first power of the force ("taken once") and the second power of the time ("taken twice"). From Theorem 1, the time is proportional to the triangular area SQP , which is equal to one-half the base SP times the height QT (see fig. 4.14), or the product SP × QT is the double of the area where ultimately the arc QP will approach the chord QP .
[E] Let each part of this proportionality be divided by the line segment QR and there will result unity as the centripetal force and SP2 × QT2 / QR conjointly, that is the centripetal force reciprocally as SP2 × QT2 / QR. Which was to be proven .
Or, 1/Fµ (SP2 × QT2 ) / (QR ). Thus, "the centripetal force would be reciprocally as the solid SP2 × QT2 / QR ." [Divide QR = k3 (F ) (SP2 × QT2 ) by QR , and one has 1 = k3 (F ) (SP2 ) × QT2 ) / QR = k3 (F ) / (QR ) / (SP2 × QT2 ), or 1/F = k3 (SP 2 × QT2 ) / (QR ).]
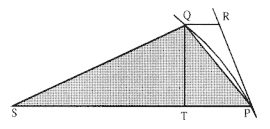
Figure 4.14
The shaded triangular area is equal to one-half of the
product of the base SP and the height QT . As the
point Q approaches the point P , the arc QP
approaches the chord QP .
Corollary. Hence if any figure is given, and on it a point toward which the centripetal force is directed , [then ] it is possible for a law of centripetal force to be found which will make a body orbit on the perimeter of that figure .
The result above represents a general theorem to be employed in obtaining solutions to direct problems: Given the orbit of the particle and given the center of force relative to that path, one seeks to find the law of force that will maintain the given orbit in terms of the distance SP from the particle P to the force center S .
[Corollary] Specifically, the solid SP2 × QT2 / QR reciprocally proportional to this force must be computed. We shall give examples of this point in the following problems .
Specifically, from the geometry of the given orbit and force center, one must express the discriminate ratio QR /QT2 in terms of SP and constants of the orbits. The force will then be expressed in terms of the distance SP alone.