Stravinsky and the Rite of Spring "d0e6972"

The Octatonic Pitch Collection

Listed above are thus the principal articulative units, the common denominators, so to speak, often with dispositions of marked character. What may in turn be judged the referential glue of this vocabulary, what binds within and between blocks and sections, is very often the octatonic pitch collection. More precisely, the referential character of this vocabulary is very often determined by its confinement, for periods of significant duration, to one of the three octatonic collections of distinguishable content.

As was defined in Chapter 5, the octatonic collection is a set of eight distinct pitch classes that, arranged in scale formation, yields the interval ordering of alternating 1s and 2s (half and whole steps). Such an arrangement obviously yields only two possible interval orderings or scales, the first of these with its second scale degree at the interval of 1 from its first (a 1-2, half step-whole step ordering), the second with its second scale degree at the interval of 2 from its first (a 2-1, whole step-half step ordering). These are shown in Example 62, with the 1-2 ordering and consequent (0 1 3 4 6 7 9 10 (0)) pitch numbering on the left side, the reverse 2-1 ordering and (0 2 3 5 6 8 9 11 (0)) numbering on the right. And the issue as to which of these orderings might pertain to a given context naturally hinges on questions of priority, vocabulary, and articulation. Thus the (0 2 3 5) tetrachord with its 2-1-2 ordering suggests the 2-1 ordering as cited on the right side in Example 62. And octatonic contexts which are (0 2 3 5) tetrachordally oriented will tend therefore to

Example 62

― 144 ―

suggest this 2-1 ordering as the most favorable approach in scale formation. Similarly, when octatonically conceived, the 0–11 vertical interval span invariably suggests the 2-1 ordering and its consequent (0 2 3 5 6 8 9 11 (0)) numbering on the right side in Example 62; the latter is in fact closely linked to The Rite's (0 2 3 5) tetrachordal articulation. (Note, in other words, the 0–11 span of this numbering.) On the other hand, the (0 1 3 4) tetrachord, of only slight consequence in The Rite , and the root-positioned (0 4 7/0 3 7) major and minor triads tend more readily to suggest the 1-2 ordering on the left side of Example 62.

The collection is limited to three transpositions; there are only three octatonic collections of distinguishable pitch content. These are also shown in Example 62, labeled I, II, and III. Thus, respecting Collection I with the 1-2 ordering on the left side in Example 62: had we, following the initial C

, transposed beyond D (Collection II) and E

(Collection III) to E, this final transposition would merely have yielded the initial collection (Collection I), starting only with the E rather than the C

. Moreover, since this transposition to E defines the interval of 3 (the minor third) with the initial C

(as pitch number 0), transpositions at 6 and 9 will entail similar duplications. And it follows that this minor-third (0, 3, 6, 9) symmetrically defined partitioning is fundamental to the integrity of the single octatonic collection: given an octatonic fragment, transpositions at 3, 6, and 9 will remain confined to that collection.

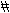
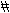
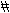
Finally, note that the 1-2 ordering on the left side in Example 62 ascends, while the reverse 2-1 ordering on the right descends. This is in principle in order to allow representation of longer spans of material, spans that, confined to a single collection, may nonetheless in vocabulary and articulation implicate both orderings. In other words, respecting Collection I again, with the ascending 1-2 ordering at C

on the left side: were we to switch to the 2-1 ordering and yet remain committed to the customary ascending approach in scale representation, the resultant scale would no longer represent Collection I but, rather, Collection III. However, by descending with the 2-1 ordering from C

, not only do we remain confined to Collection I but the (0, 3, 6, 9) symmetrically defined partitioning elements in terms of (C

, E, G, B

) remain the same.

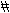
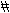
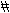
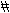
Still, the descending formula, the reading-down situation on the right side of Example 62, is not wholly a question of analytical convenience. In many "Russian" pieces it is often an "upper" (0 2 3 5) tetrachord, along with an "upper" pitch number 0, that assumes priority by means of doubling, metric accentuation, and persistence in moving from one block or section to the next. And if the scalar ordering and pitch numbering are to reflect these conditions, the descending formula is the logical course. Throughout large sections of the "Augurs of Spring," the "Ritual of Abduction" and "Spring Rounds" in Part I, a punctuating E

, along with an (E

C B

) tetrachord with which this E

identifies articulatively, assume priority. And it is by descending from the E

, with the (0 2 3 5) tetrachordal numbering synchronized with the principal (E

C B

) unit, that the priority of these units is properly represented: (0 2 3 5 6 8 9 11) in terms of (E

C B

A G F

E), Collection III. (Again, to ascend from the E

with the 2-1 ordering would have yielded a

― 145 ―

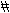
different octatonic collection, in this case Collection II.) Moreover, the symmetrical discipline conveniently allows for options of this kind. The 2-1–2 ordering and consequent (0 2 3 5) pitch numbering of this present tetrachord remain the same whether ascending or descending.

In general summation, Examples 63 and 64 partition the octatonic collection by means of the various articulative groupings cited above.^[15] In Example 63 the 2-1 ordering is shown on the left side, where brackets outline the four overlapping (0 2 3 5) tetrachords at 0, 3, 6, and 9. Notice the two non-overlapping (0, 6) tritone-related tetrachords, which together yield the all-important 0–11 vertical span. Separate realizations are given below for each of the three content-distinguishable collections.

On the right side in Example 63 the familiar disposition of the dominant-seventh chord is applied in similar fashion. Here, too, superimposed over its (0, 3) minor-third-related major triad, the compound configuration, encountered already in terms of (E

G) (C E G) in the "Augurs of Spring," likewise encompasses the 0–11 span. More essential, however, is the exposed, upper interval of 5, or the fourth of the dominant seventh's closed, first-inversion articulation. Thus the E

-B

fourth or incomplete (E

) tetrachord of Collection III's (E

G) dominant seventh connects with the (E

C B

) tetrachord on the left side of Example 63. Associations of this type are crucial to the special registral and articulative layout of The Rite . Indeed, as will be noted, the descending scale is applied to both the triadic and the tetrachordal side of Example 63, and in recognition not only of the "upper" conditions of priority noted already but of this essential link between the typically closed, first-inversion articulation of the dominant seventh and the (0 2 3 5) tetrachord.

Example 64 offers a different view of these formulae. The three collections are partitioned at four successive levels, by their (0, 3, 6, 9) partitioning elements at the first level and by their (0 2 3 5) tetrachords at the second. At the third level the 0–11 vertical span encompasses the upper 0–5 fourth of the (0 2 3 5) tetrachord, while brackets encircle the lower of the two tritone-related fourths to cover those fewer instances where the lower or both of the collection's (0 2 3 5) (6 8 9 11) tetrachords prevail. Hence the 0–11 designation becomes 0–5, 11, or, more comprehensively still, 0–5/6, 11.^[16] Indeed, in light of its comprehensive application, 0–5/6, 11 may

[15] See Pieter C. van den Toorn, The Music of Igor Stravinsky (New Haven: Yale University Press, 1983), pp. 48–60. In this earlier volume, the triadic and (0 2 3 5) tetrachordal groupings, yielding the ascending and the descending forms of the scale, respectively, are represented by two separate schemes labeled Model A and Model B. This strict separation was maintained in order to pinpoint critical distinctions involving the whole of Stravinsky's music, from the early "Russian" period to neoclassicism and early serialism. Here, however, with the analysis confined to the articulative routine of The Rite , these models are easily condensed to a single descending mode of representation.

[16] In connection with Béla Bartók's music, this 0–5/6, 11 vertical span was identified as "cell z" by Leo Treitler in his "Harmonic Procedure in the Fourth Quartet of Béla Bartók," Journal of Music Theory 3, 2 (1959): 292–98. Treitler's designation came in partial response to an earlier study by George Perle, where two other "cells" were labeled "x" and "y"; see George Perle, "Symmetrical Formations in the StringQuartets of Béla Bartók," Music Review 16 (1955): 300–312. The role of "cell z" in Bartók's music generally—its relationship to other symmetrical cells, interval cycles, and various octatonic and diatonic orderings—is discussed at length in Elliott Antokoletz, The Music of Béla Bartók (Berkeley: University of California Press, 1984), pp. 67–137.

― 146 ―

Example 63

be envisioned as a kind of basic sonority in The Rite , the shell of its octatonic content. As was noted in Chapter 5, it accounts in large measure for the static "vertical chromaticism" that may be inferred: the upper (0 2 3 5) tetrachord or 0–5 fourth is made to stand in a fixed, polarized opposition to the lower pitch number 11.^[17] At the final level in Example 64 the (0, 3, 6, 9) partitioning elements of each of the three scales are represented by round notes.

― 147 ―

Example 64

― 148 ―

Example 64
(continued)