Eight—
Array Seismology—Past, Present and Future Developments
E. S. Husebye and B. O. Ruud
Introduction
Array seismology was born on September 19, 1957. On that day a nuclear explosion, code-named Rainier, was detonated under the Nevada desert principally to explore the ability of an underground test, unhampered by weather and concerns over radioactive fallout, to fulfill all the needs of a nuclear weapons test program. Rainier demonstrated this ability. The resulting seismological data were studied intensely in both scientific and political circles, setting a pattern that still prevails. Rainier and subsequent underground tests also demonstrated that the only effective way to detect such explosions was by seismic means. Thus, the science of seismology was given a rather prominent role in a political question: arms control. A specific aspect of the arms control issues was tied to banning all nuclear weapons testing. Such a ban was (and is) presumed to prevent (or at least severely curtail) the development of new, advanced nuclear weapons systems and also to prevent nuclear weapons proliferation. Note that first-generation bombs of the Nagasaki and Hiroshima types hardly require testing, while those of the third and fourth generation require twenty to thirty tests. In this case, successful evasion schemes would be exceedingly difficult (Massé, 1987).
The introduction of seismology to the political arena had, thus, already occurred by August 1958 when scientific experts from the United States, the Union of Soviet Socialist Republics, and the United Kingdom met in Geneva to design a seismic verification system as part of a Comprehensive Nuclear Test Ban Treaty. The outcome of this and subsequent Geneva Conferences was important to seismology on two accounts. First, they resulted in the recommendation of a global seismic monitoring system comprising 180 small array stations often SPZ (short-period vertical) seismographs complemented with three-component SP (short-period) and LP (long-period) instrumenta-
tion; ten of these arrays were for sea-floor deployment. Second, it was recognized that seismology per se was unable to meet political requirements for creating a reliable and acceptable vertification system. Already at that time magnitude and yield estimates were the subject of expert controversy, adding to the political problems.
The outcome of the Geneva Conferences proved very beneficial for seismology. As a result of these conferences, several countries, notably the United States and the United Kingdom, launched large-scale research programs to modernize seismology and provide the technical means for monitoring compliance with treaties limiting or banning underground nuclear weapons tests (for example, see Kerr, 1985). The first concrete step toward establishing array seismology stemmed from the U.S. Berkner Panel's recommendation, in 1959, to construct large arrays with hundreds of sensors as a cost-efficient alternative to the "Geneva" concept of numerous small arrays of a few kilometers' aperture (see Bolt, 1976, chapter 6). This recommendation led to the only two large arrays ever built, namely, LASA (Montana) in 1964 (operational in 1971, closed down in 1978) and NORSAR (Norway) in 1971 (still in operation but with its size reduced). The United Kingdom's seismic monitoring program led to the construction in the 1960s of four medium-sized arrays at Eskdalemuir (Scotland), Yellowknife (Canada), Garibidinaur (India), and Warramunga (Australia), all of which are still in operation. Other major national array programs are those tied to the Gräfenberg array (West Germany) and the Hagfors array (Sweden). Array designs, developments, and deployments have now come almost full circle, as exemplified by the third-generation NORESS array (Norway) with an aperture of 3 km and twenty-five SPZ instruments, reasonably close to the original Geneva concept of 1958.
In this article, we address array development and operation over their current life span of nearly three decades. Particular emphasis is on operational principles and array performance in the context of earthquake surveillance and seismological research. We also consider future prospects of array operations in view of inexpensive mobile array deployments and innovative analysis techniques for three-component station records.
Above, we very briefly mentioned major political events and arms control issues leading to "forensic" (Thirlaway, 1985) and array seismology. These topics are adequately detailed in many books and will not be discussed further here. However, recommended references are Bolt (1976), Dahlman and Israelson (1977), Husebye and Mykkeltveit (1981), Press (1985), Kerr (1985), and Tsipis et al. (1986).
The Array Concept
There is no strict definition of an array, although seismological arrays generally have three or more identical instruments properly spaced (spacing being
governed by characteristic noise and signal correlation distances, which are naturally frequency dependent), centralized data acquisition, and integrated real-time processing. In this paper we will generally consider an array to have these properties.
An essential array capability is the locating of incoming signals in f-k (frequency–wave number) space, which in turn signifies a certain ray path in the Earth and/or the source location. Using the polarization characteristics of seismic waves, f-k locations of incoming signals can also be achieved on the basis of a single-site, three-component station (Christoffersson et al., 1988). In the extreme, such stations may be considered an array, albeit the requirement of a two-dimensional sensor layout is not met. Likewise, we may consider a small network used for monitoring local earthquake activities as an array, conditioned on real-time integrated signal processing, which is technically and economically feasible today. A remaining flaw would be poor to nonexistent signal correlation, which can be overcome by replacing individual signals by their envelopes (Hilbert transform), thus constituting the basis for so-called incoherent beamforming (Ringdal el al., 1975).
The major arrays noted above (like NORSAR, Yellowknife, Gräfenberg, and Hagfors) all comply with our definition of an array. Centralized data acquisition and integrated real-time processing are most important, if seismological networks are to be considered arrays, and are of economic interest as well. For example, if integrated signal processing is not feasible, why have real-time transfer of waveform data, which is rather costly? Alternatively, the relatively modest signal parameter data (like arrival time, amplitude, and slowness) from a single three-component station are extracted in situ or at a local center. Thus, off-line centralized processing of parametric data is feasible, and is essentially the way organizations like the National Earthquake Information Center (NEIC), the International Seismological Centre (ISC), and the European-Mediterranean Seismological Center (EMSC) operate.
Array Developments, Design Criteria, and Data-Processing Schemes
The concept of seismic arrays was first introduced to the seismological community by the conference of scientific experts convening in Geneva in 1958 as a principal means for monitoring compliance with a potential test-ban treaty barring or limiting yields of underground nuclear weapons tests. The scientific rationale for these recommendations was that properly summing the outputs from clusters of sensors would result in significant signal enhancement and at the same time provide estimates of signal direction. Although the array concept at that time was novel to seismologists, geophone clustering was widely used in seismic exploration. Furthermore, array usage was well established in other fields like radar, sonar, and radio astronomy, and the theoretical framework for associated signal processing or so-called anten-
na theory had been formulated. Ignoring the historical perspectives of the theoretical developments, we proceed to give a brief presentation of common array data-processing techniques as used in both operational and research contexts. Simple schemes like delay-and-sum processing (beamforming) and semblance are very popular, not only because they are easy to use but also due to their robustness in a complex signal environment. A few article and book references here are Capon (1969), Ingate et al. (1985), Aki and Richards (1980), Haykin (1985), and Kanasewich (1981).
Phased-Array Beamforming
Real-time array data processing is usually based on this method. Denoting the i th sensor output as yi (t) and its position vector ri , the signal estimate or beam
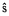
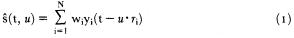
where u is the horizontal (back azimuth) slowness vector, and wi are weights. An unbiased estimate of
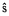
A simple power estimate for the beam signal in the time window [T1 , T2 ] for slowness u is:
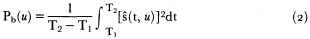
A more compact form is obtainable by introducing the data covariance matrix, namely:
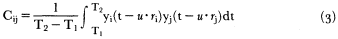
Equation (2) can be now written in matrix form as:

where the asterisk denotes transpose.
The so-called N th root beamforming (Muirhead and Datt, 1976) is known to have better directivity than conventional methods. Thus, it would be an advantage to use the Nth root beam in equation (2) for slowness estimation.
f-k Power Spectrum
The conventional frequency-wavenumber power estimate, also called classical beamforming, is defined as:
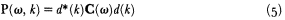
where C (w ) is the spectra covariance matrix. d is a complex vector of phase delays and sensor weights defined as

The relative advantage of the f-k signal power estimate, equation (5), is that the spectral covariance matrix is calculated just once for each frequency because the wavenumber dependence rests with the d -vector in equation (6). The disadvantage is that narrow-frequency-band estimates easily become unstable. Also, to ensure computational efficiency, the C (w ) matrix is often estimated for a fixed time window, while time domain beamforming always accounts for move-out time across the array.
Broadband f-k Power Spectrum
The instability of conventional f-k analysis can be overcome by introducing its broadband variant. Using the relation k =wu and integrating the f-k spectrum over the band [W1 , W2 ] we get:
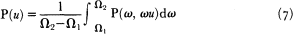
Note that this scheme is not computationally efficient as the spectral covariance matrix must be estimated for many frequencies. Also, time domain beamforming is broadband, in view of the prefiltering passband commonly used.
High-Resolution Beamforming Methods
The best known of these methods is the maximum likelihood (ML) f-k estimator given by Capon (1969):
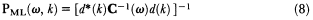
A similar approach is applicable in the time domain using the so-called maximum-likelihood (ML) weights,
Formally, the ML estimates are derived on the assumption that wavelets with different slownesses are statistically independent. For real signals this is seldom the case, hence the inability of high-resolution estimators to resolve correlating signals (for example, see Duckworth, 1983; Hsu and Baggeroer, 1986).
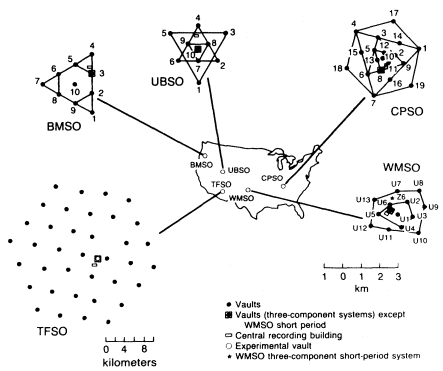
Figure 1
Configurations of various seismometer arrays at observatories constructed
to evaluate detection capabilities of stations similar to those recommended
by the Conference of Experts, Geneva (after Romney, 1985).
Semblance Methods
Semblance is a simple coherency measure defined as S = Pb /Pav . Here Pb and Pav are, respectively, beam power and average single-channel power, which implies that semblance is in the interval (0, 1). Because semblance is independent of signal power, it provides a convenient confidence measure in displays of wave-train time-varying properties like velocity spectra (see fig. 8 below).
The time-domain semblance estimate is defined as:

where r is the correlation matrix [rij = Cij /(Cii · Cjj )1/2 ]. An ML variant of semblance is obtained using the ML weights discussed above, namely:

The semblance estimator is robust and thus works relatively well even for complex signals.
To summarize, most array data processing schemes were developed in the 1960s, so progress has been modest in this field in recent years. A potentially beneficial research avenue may be in adaptive signal processing, as used in radar and sonar for separately estimating interfering signals (see Bøhme, 1987; Monzingo and Miller, 1980; and Urban, 1985).
Array Deployment in the 1960s
The Geneva recommendations for small arrays as the principal seismological tool for comprehensive test ban (CTB) verification dominated the United States array research program in the ensuing years, although the Berkner Panel also recommended the use of large arrays (for a detailed account of these scientific-political discussions, see Bolt, 1976, chaps. 5 and 6). The first arrays to be deployed were the Wichita Mountain Observatory (WMSO), Unita Basin Observatory (UBSO), Blue Mountain Observatory (BMSO), and Cumberland Plateau Observatory (CPSO), while the Tonto Forest Observatory (TFSO) was significantly larger, as illustrated in figure 1. These arrays were operational for about ten years. Although having excellent site locations, with low noise and high signal sensitivity, these arrays seemingly did not contribute much toward array research. A major drawback was analog recording, which prevented integrated, real-time operation except for vertical stacking (no delay times used). In 1963 the first of the UK-type arrays was completed in Scotland which also used analog recording. The L-shaped configuration of these arrays (fig. 2) gave a rather skewed response pattern but did minimize costly ditching for cables.
The quantum leap in array development came with the construction of the LASA (Montana) array in 1964, achieved in the incredibly short time of just nine months (Anonymous, 1965). The LASA array remained unique on several accounts: its aperture of 200 km (fig. 2), its deployment of 630 shortand long-period seismometers, and, most important, its use of digital signal recording. The second large-aperture array to be constructed was NORSAR, a joint U.S.-Norway venture completed in 1970, with an aperture of 100 km and 196 seismometers (fig. 3). At about the same time, the Gräfenberg array was completed, unique in its use of broadband instruments (Buttkus, 1986).
In summary, the 1960s saw tremendous development in array technologies in terms of new, compact, and high-sensitivity seismometers, data transfer via links and cables over large distances, and ingenious recording systems including digital tapes. However, most of the array recordings were in analog form, thus limiting their use in broader seismological research. An integral part of array deployment was the development of schemes for handling the
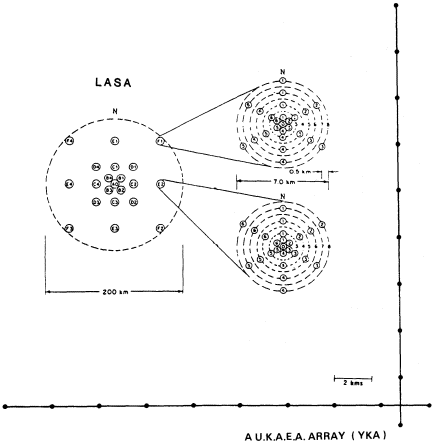
Figure 2
The L-shaped Yellowknife, Canada, array and the 200-km aperture LASA,
Montana, array. Each of the twenty-one LASA subarrays initially comprised
twenty-five short-period instruments (later reduced to sixteen) plus one three-
component long-period seismometer.
multichannel data generated, and the theoretical foundation for array data processing as it is known today was laid in the 1960s.
Seismic Array Operation in the 1970s
The 1960s were the decade of array deployment, while the 1970S were the decade of continuous real-time operation. For example, although LASA was completed in 1964, it did not become fully operational until 1971, coincident in time with NORSAR. The reason for this was simply that field instrumentation was commercially available, but an integrated computer
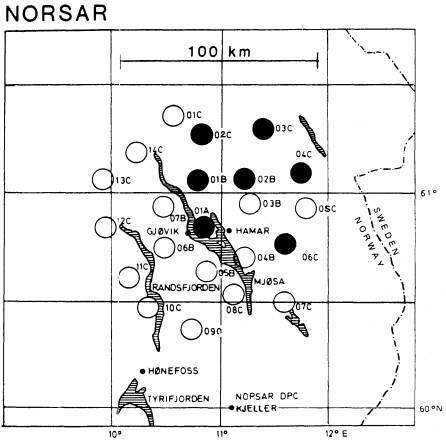
Figure 3
NORSAR. Each circle represents one subarray consisting of six short-period
and one three-component long-period instruments. All twenty-two subarrays
were in operation from 1971 to October 1, 1976, whereas only a subset of
seven subarrays (filled circles) have been in operation since then.
hardware-software system had to be developed specifically for array operation. For example, IBM (Federal Systems Division) spent more than four years on this task before completing the LASA and NORSAR data-processing systems (see Bungum et al., 1971). After these arrays became operational, it took a year before the software was reasonably bug-free and, equally important, before the staffs at the respective array data centers in Alexandria, Virginia, and Kjeller, Norway, had mastered the automated array operations. For example, multiple-phase recordings like P and PP were initially featured as separate events simply because the analyst did not have a display of the complete wave record. Shortcomings of this kind were easy to
detect because otherwise there would have been a marked increase of earthquake activity in the North Atlantic well off the midoceanic ridges.
More subtle problems were tied to the apparently larger number of earthquakes detected during local nighttime than during the day. With no scientific rationale for such a phenomenon, the alternative was that this was an artifact of array operation. The explanation turned out to be a diurnal change in noise characteristics, which were relatively broadband during the daytime, due to high-frequency cultural noise, and thus corresponded to a marked difference in detector false alarm rates for a fixed threshold. A few of the many nightly false alarms would inevitably be classed as "true" events, thus explaining the apparently higher earthquake activity. The solution to the problem was to keep the false-alarm rate flat by making the detector threshold a function of diurnal time (see Steinert et al., 1976). Also worth mentioning is that a "high-level" constraint was imposed on LASA not to report core phases, yet such events inevitably were recorded. In the array bulletin, such events were located at 105° distances. In due time, these artifactual epicenter solutions "filtered" into NEIC and ISC files and, not too surprisingly, have been the subject of a few tectonic studies and modeling.
The LASA and NORSAR arrays were termed teleseismic arrays, stemming from the fact that their large apertures, and hence large station separations, permitted operation only in essentially the 1.0–2.5-Hz band. This meant that local and regional event signals could not be handled properly due to poor signal correlation at higher frequencies (Ingate et al., 1985). This problem was further aggravated by the limited number of beams to be deployed due to limited computer capacity (IBM 360/40 computers of 1964). Poor detectability of regional events was to a large extent overcome by introducing so-called incoherent or envelope beamforming. The signal envelopes were highly correlated—even though the "originals" were not—and were of relatively low frequency (see Ringdal et al., 1975). Although envelope beamforming suppressed only the noise level variance (not the noise level per se) by a factor of
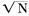
An interesting feature of array recordings is that sensor amplitudes for an individual event vary considerably and can be approximated by a log-normal probability distribution function (Husebye et al., 1974). Furthermore, any of the twenty-two NORSAR subarrays would, for one or more earthquake source regions within the teleseismic distance window, exhibit the largest signal amplitude. In other words, the amplitude "response" of the NORSAR siting structure is highly selective in terms of angle of incidence of the incoming wavefront (see figure 4).
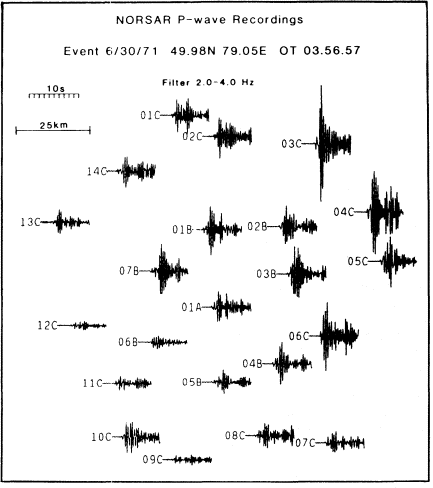
Figure 4
NORSAR. P-wave recordings from the center instruments of each subarray
for an explosion in eastern Kazakhstan ( mb = 5.4, distance 38°). Note the
large variations in signal amplitude and waveform complexity across the
array. The signal frequency contents are similar for all instruments with
the best signal-to-noise ratio in the band 2.0 to 4.0 Hz.
A practical aspect of the skewness in P-amplitude distributions across large arrays like LASA and NORSAR is that using only the four to six "best" subarrays for a given event results in signal-to-noise ratio enhancement, which is only marginally improved by including the remaining sixteen to eighteen subarrays in the beamforming process (Berteussen and Husebye, 1974). In the extreme, a single sensor may exhibit a signal-to-noise ratio roughly similar to that obtainable using the whole array. This, in turn, reflects a common observational fact regarding array monitoring of earthquake occurrence—almost all events (signals) detected by an array are visible on a subarray beam or single-channel record trace. This knowledge was once applied, but without much success, as an additional constraint to discriminate (nonparametric tests) between signal and noise wavelets for triggering close to the detector threshold (Fyen et al., 1975). The fundamental problem was that lowering detector threshold values causes the number of false alarms to increase more rapidly than the number of events expected from the log N recurrence relation (see fig. 5). In other words, even with elaborate processing schemes, there is little point in analyzing detections at and below thresholds at which the false alarm rate starts increasing rapidly. Besides, information extractable from small detections is not particularly useful in any context except generating "nocturnal" seismicity.
After a few years of practical experience in real-time operations of the LASA and NORSAR arrays, the work became rather routine and, moreover, expertly handled by analysts. At this time (around 1975) the more fundamental issue of large-array operation came into focus: could a limited number of large arrays manage the required seismic-event surveillance functions for monitoring compliance with a potential CTB? The performance of these arrays was relatively impressive; uptime on a monthly/yearly basis was 90–95 percent, and daily detections amounted to about twenty to twenty-five events, subject to seasonal variations and uncertainty in event locations of 50–200 km. However, the detection capability of these arrays, at body wave magnitude (mb ) ~ 4.0 at the 90 percent confidence level for favorable regions (see Ringdal et al. 1977), was not entirely superior to that of some ordinary stations at excellent quiet sites. In short, the problem of detecting weak signals is tied not only to suppressing ambient noise, but the site amplification factor also is important. In the extreme, a single instrument at NORSAR exhibited signal-to-noise ratios comparable to those of the best array beam, as hinted at above.
In the midseventies, after about five years of automated large-array operation, it became clear that even several large arrays of the LASA-NORSAR type would not be adequate for test-ban monitoring of nuclear weapons of yields down to 1 kiloton (mb~ 4.0 in granite). In particular, P-signals recorded in the teleseismic window would not provide a credible diagnostic
Figure 5
Number of detections by the automatic NORSAR
detector as a function of STA/LTA (signal-to-noise) ratio
for the period July to December 1972. The number of
detections increases sharply below a signal-to-noise ratio
of 12 dB where false alarms generated by noise fluctuation
dominate detections triggered by real events.
for source identification. This realization, in combination with funding problems, regrettably resulted in curtailing the NORSAR operation to seven operative subarrays, while LASA was closed down in 1978.
In summary, it was demonstrated during the 1970S that automated array operation was technically feasible, but large arrays were not sufficient for test-ban monitoring. Furthermore, P-signals in the teleseismic window were adequately understood in terms of generation mechanisms and propagation path effects, while their diagnostic power for source identification remained doubtful.
Array Operation in the 1980s
The hallmark of array seismology is the intimate link between research progress and easy access to data of superior quality. In the 1980s, with research emphasis on observations in the local (0–10°) and regional (10–30°) distance ranges, array observations from the 1960s and 1970s were not adequate in bandwidth or dynamic range. The very first step was, naturally, to reexamine the array concept vis-à-vis high-frequency seismic signals at relatively short distances. Basic data for this problem were easy to obtain, at least in the case of NORSAR, by using the existing cable infrastructure. That is, a subarray could easily be reconfigured to sensor spacings ranging from 100 to 1,200 m without costly field work. The analysis of these and similar observations focused upon parameters critical for array design, namely, noise and signal levels and spatial noise and signal correlations as functions of frequency. The most significant results were that the noise level outside the microseismic band of 0.5–2.5 Hz decreased at a rate of about f–4 up to about 10 Hz, and that the noise correlation function exhibited negative values of around 0.05 to 0.15 at certain station separations. Furthermore, for local and regional phases, the signal-to-noise ratios peaked in the 3–8 Hz band, while signal correlation decreased rapidly beyond 6–8 Hz. These noise and signal characteristics were built into the design of the new regional array NORESS (fig. 6) in that not all array elements were used because the close spacing of A- and B-ring elements would otherwise have entailed partly positive, that is, constructive, noise interference. For details see Mykkeltveit et al. (1983), Ingate et al. (1985), Bungum et al. (1985), and the NORSAR Semiannual Technical Summaries (editor L. B. Loughran, NORSAR).
As mentioned above, the NORESS design is aimed at optimizing signal-detection capabilities, but the penalty is a certain lack of spatial resolution, which naturally affects the array's event location capabilities (see Harris, 1982; Ruud et al., 1988). Even the much larger NORSAR and LASA arrays were not well suited for precise locations using standard epicenter estimation techniques. Using two arrays jointly for event locations would, of course, improve performance (Jordan and Sverdrup, 1981), but significant progress here would depend on the ability to extract more information from the array records. An interesting development in this context is the deployment of an additional regional array, ARCESS, in northern Norway (Karasjok, operational in October 1987), planned to be operated in tandem with NORESS for exploring expert system techniques to realize these goals.
The success of NORESS and the general availability of relatively cheap digital data technology have led to a revival of array research programs in several countries, notably Australia, Canada, Germany, UK, and Sweden. Such arrays, with apertures mostly 10 to 30 km, are somewhat larger than NORESS, but the research problems are much the same, with an emphasis on automated operation and interactive analysis workstation design.
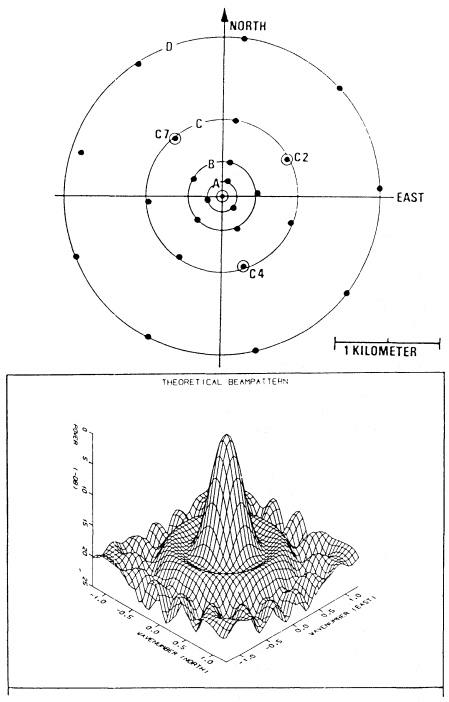
Figure 6
The NORESS array located near NORSAR site 06C (fig. 3). Three-component
stations are marked by small circles. The center vault also contains a Geotech
KS-36000-04 broadband bore-hole seismometer and a high-gain high-frequency
(125-Hz) three-component seismometer. The array response in the f -k domain
is also shown; contour levels are in dB down from the maximum.
Not only classical array seismology has benefited from recent advances in the fields of microcomputers and telecommunications. The same technology can easily be adapted to single-site three-component station operations, and of particular interest here is the development of flexible analysis techniques for handling this kind of data. For example, Christoffersson et al. (1988) have demonstrated a novel approach to decomposing three-component wavefield records using their phase information. A practical application of this technique to event location has been demonstrated by Ruud et al. (1988). In terms of performance, a single three-component station does not compare unfavorably with a small-aperture array, at least at local distances.
Detectors for picking P and S (Lg) phases at local distances have also been designed (see Magotra et al., 1987), thus supporting the feasibility of operating single-site three-component stations in ways similar to those of an array. Note that networks of such three-component stations with a centralized hub for joint analysis of data from many stations would indeed be a most powerful tool for monitoring compliance with a potential CTB.
To summarize, the 1980s have seen a revival of array seismology, particularly in developing new, small arrays and "digitally" upgrading previously deployed arrays. Most work has been aimed at automating array operation and designing interactive workstations for analyst screening of final results, tied mainly to bulletin preparation. Regarding data analysis, hardly any progress has taken place in the field of array processing and signal estimation techniques. Of some importance in this context is the novel analyzing technique of three-component recordings (Christoffersson et al., 1988; Magotra et al., 1987), which is likely to strongly upgrade the signal information retrievable from individual stations. Interestingly, the current U.S. Geological Survey (USGS) deployment of a national 150-station three-component broadband seismograph network, with near-real-time parameter and waveform event data transmitted by satellite to NEIC/USGS headquarters in Golden, Colorado, is providing a practical test of these developments (R. Massé, personal communication).
Arrays—Future Developments
Array deployments in the past decades demonstrated that the integrated operation of hundreds of seismometers is technically feasible in a real-time environment, but the potential monitoring performance in a CTB context has been less convincing. The main reason for this is a signal-amplitude decay in the 100-to-3,000-km range of between 1 and 2 magnitude units, which means that array surveillance performance in the teleseismic window is relatively inefficient. Another crucial factor is the significant decrease in noise level at frequencies above 2.5 Hz, thus giving an additional edge to surveillance at
local and regional distances. With this realization, large array operations were regrettably curtailed at the end of the 1970s, and in the 1980s array seismology research interests have focused on monitoring at local and regional distances. Related problems are a need for improved physical understanding of wave propagation in the crustal waveguide, notably that of Lg waves. So far, most efforts have been in the design, deployment, and operation of small aperture arrays. NORESS may be considered a prototype of the joining of developments and operational experience over the past decades with general technological advances. Small-array event detection is relatively very good because of good signal-to-noise ratios above 2.5 Hz and the use of a sensor configuration that takes advantage of destructive noise interference during beamforming. Despite this, array seismology is at a crossroads. Considering the costs of array construction (about four million dollars for NORESS) and operation and demonstrated monitoring/surveillance performance, are arrays competitive with relatively dense networks of high-quality three-component stations that can be placed and run for a fraction of the cost? The problem is that arrays are still operated as superstations. The essential wave-field parameters extracted are onset time, amplitude, period, and the P-slowness vector. These are sufficient for producing fast bulletins but not much more. They are insufficient to identify source type at regional distances, which remains an unsolved problem despite much effort.
A single three-component station can now easily provide the same signal parameters, and a combination of several such observations yields a relatively comprehensive spatial view of the signal source. We implicitly refer to the way past and present earthquake surveillance has been performed, namely, by extracting few signal parameters from many stations. For an array, essentially one point of observation, to overcome this disadvantage it has to extract more information from the entire wave-field record. In other words, techniques for more extensive seismogram parameterization are required. Several approaches are feasible and will be briefly discussed below.
The Expert System Analog
This approach is currently exploited to ensure automated array operation in combination with interactive workstations for refinements of analysis results. A basic ingredient is an advanced data-management system that would have a "memory" of previous events in a given area, which in turn would ensure the "learning" aspect of operation. At the present stage of development, more extensive seismogram parameterization techniques have been given low priority. This system is not, strictly speaking, "expert," since there is no attempt to incorporate subtle analyst knowledge. The system is data driven, and refinements would be tied to identifying patterns in the records on the presumption that earthquake occurrence is somewhat stationary. This
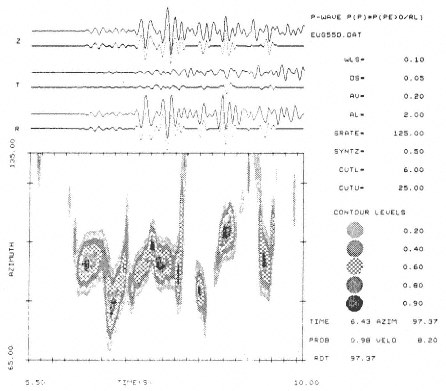
Figure 7
Three-component analysis of Shot 7, EUGENO-S Refraction Profile 4 in
southern Sweden, distance 205 km. Signal processing parameters: SRATE
= sample rate; WLS = window length; DS and AV = updating intervals
for time and azimuth, respectively; AL = a smoothing parameter (see
Christoffersson et al., 1988, for details on the method).
7a ) c2 probabilities of P-wave particle motions. Original (solid) and filtered
(dotted) records: lower probability (SYNTZ) for filtering/weighting = 0.50;
lower (CUTL) and upper (CUTU) velocity passband of 6.5 km s–1 and 25.0
km s–1 . Lower right: cursor reading (+) off the screen.
7b ) P-wave velocities instead of c 2 probabilities. Original (solid) and filtered
(dotted) records: lower probability (PROBLIM) for computing contours =
0.50; lower (CUTL) and upper (CUTU) velocities for filtering/weighting
6.0 km s–1 and 15.0 km s–1 .Lower right: cursor reading (+) off the screen.
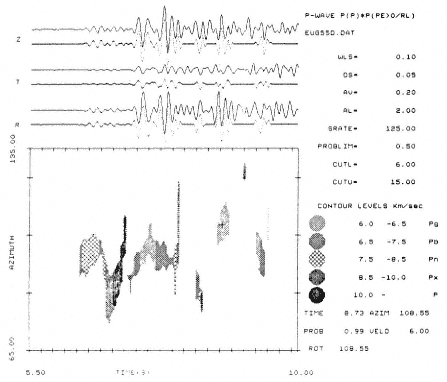
is the way a trained analyst works, recognizing characteristic waveforms of signals from specific areas; the tricky problem here is, naturally, to quantify the extent of similarity (T. Bache, personal communication).
Wave-Field Parameterization
This novel approach by Christoffersson et al. (1988) to three-component wave-field decomposition analysis is convenient for illustrating the problem involved (see fig. 7). The slowness vector variation along the P-wave train exhibits a distinct pattern that, at least, is stationary for NORESS three-component stations and repeated Semipalatinsk underground nuclear tests. More interesting here is that signal similarities are almost identical for one station and many explosions but disparate between two three-component NORESS stations For the same explosion (see Ruud et al., 1988). In other words, very localized siting structures appear to have a profound effect on the recorded wave field, hence the "correlation distance" of pattern similarities in the receiver area appears to be very small, of the order of 0.5–1.0 km. However, on the source side the corresponding correlation distance is of the order of tens of kilometers, at least as regards Semipalatinsk explosions.
These preliminary results from extensive wave-field parameterization may have important ramifications regarding vastly improved event location and source classification capabilities of small arrays and/or single three-component stations. Research in this field is well worth pursuing, including attribute processing as used in seismic prospecting (for example, see Vidale, 1986) and its recently introduced "ARMAG-Markov" variants (Tjøstheim, 1981; Karlsen and Tjøstheim, 1988).
Array Signal Processing
The theoretical groundwork of present-day array data processing schemes was formulated in the 1960s, and in this respect it suffices to refer to the many contributions from scientists at the Massachusetts Institute of Technology's (MIT) Lincoln Laboratory and Texas Instruments and Teledyne groups located at that time in Alexandria, Virginia. The analytic techniques developed were tied to processing P-waves in the teleseismic window, for which the implicit modeling of the P-signal as a single wavelet was quite adequate (Christoffersson and Husebye, 1974). For events at local and regional distances this assumption is less valid, in view of the more complex wave train of even the first-arriving P-wave. For example, narrow band f-k analysis may occasionally produce gross errors in slowness estimates due to either a corresponding weak signal coherency or interference. Broadband estimation techniques produce far more stable results, but the problem remains in the sense that slowness is a function of the frequency band used and of the window positioning in the signal (see fig. 8). This example illustrates both the strength and weakness of arrays. Even a small-aperture array like NORESS illuminates the complexities of the Earth, particularly the lithosphere, while our ability to quantify the structural heterogeneities as manifested in the seismogram remain relatively primitive. Not much progress in solving these kinds of problems has been made in the last decades. We consider such progress essential to justify operation and deployment of arrays in the next decade. Again, the reason is that networks of high-quality three-component stations will easily outperform array surveillance of global seismicity and CTB monitoring unless more precise signal and source information is extracted from the records.
Seismological Research Using Array Data
The characteristic feature of an array is its ability to provide a two-dimensional, high-quality sampling of the wave field in a digital form. The sensor spacing is such that P-signal coherency is preserved while noise coherency is zero or slightly negative, as in the case of NORESS. Research applications of array data are in general aimed at exploiting the above characteristic features, and some major achievements, briefly presented in this section, have been accomplished.
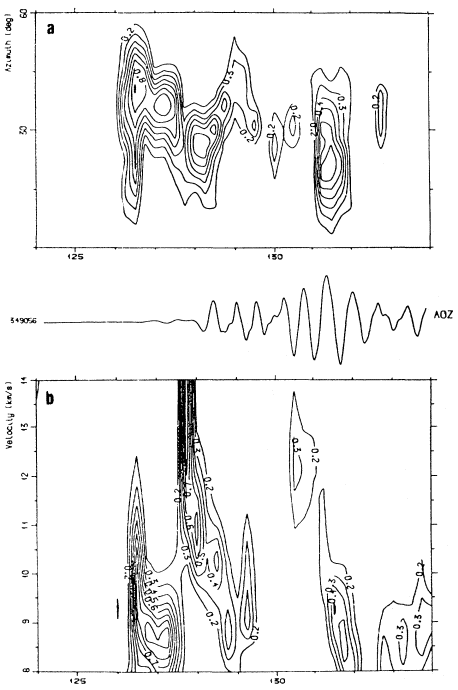
Figure 8
ML-Semblance analysis of NORESS recordings from an underground
Novaya Zemlya explosion. Traces: that of AOZ displayed. Just as in
case of three-component analysis, the slowness vector estimate varies
considerably with window positioning in the P-wave train.
Microseisms and Cultural Noise Studies
Some thirty years ago, microseismic studies were popular among seismologists, with a focus on generation mechanisms (coastal surf and low-pressure passage) and propagation efficiencies. Data from LASA and NORSAR in combination with the f-k analysis technique proved effective tools for demonstrating the relationship between low-pressure movements in, say, the North Atlantic and Norwegian seas and associated coastal surfs on the one hand, and the corresponding noise field variability at the array on the other (Bungum et al., 1971; Korhonen and Pirhonen, 1976).
Also, specific cultural noise studies have been undertaken, notably to explain a noise power spectra peak at 2.067 Hz, reflecting "energy" leakage from imperfectly balanced turbines at hydroelectric power plants (Hjortenberg and Risbo, 1975). The energy leakage may be considered a steady-state signal source and has been exploited as a means for monitoring tiny P- and S-velocity changes as a function of tidal crustal loads (Bungum et al., 1977). In the 1980s noise research has been tied to noise correlation as a function of sensor separation and its practical use for signal enhancement. New arrays like NORESS are equipped with instruments of high dynamic range (120 dB), which testifies to the relative importance of localized noise sources. For example, dam overflow in connection with spring flooding in the nearby Glomma River generated Rayleigh-type noise wavelets easily picked up by the NORESS detector. Incidently, this effect was first seen in the analysis of three-component records, as associated detections were initially attributed to instability in the analysis technique itself.
To summarize, noise-field analysis is important for optimizing array configuration and operation, while microseismic studies are definitely passé. However, an interesting avenue for future research may be the use of steadystate noise sources and even microseisms for imaging/tomographic mapping of structural heterogeneities. A work of interest on this topic is that of Troitskiy et al. (1981).
Gross Earth Structures—p-[tau]Gross Earth Structures—p-t Inversion
The first use of array data for structural mapping was tied to "inverting" P-arrival times and associated dT/dD (or slowness) observations (see Chinnery and Toksöz, 1967; King and Calcagnile, 1976). The techniques used to analyze these data were initially Monte Carlo simulations and/or Abel's integral equation. The latter technique was later refined and is now generally known as p-t inversion. It has found widespread application in refraction and wide-angle reflection data analysis (Stoffa et al., 1981). Due to the stationarity of both arrays and earthquake activities, only average information about earth structures can be provided in this way. However, due to the exceptionally good signal-to-noise ratios provided by array records, such data have provided detailed information on major secondary discontinuities
like those at 400 and 650 km (see Husebye et al., 1977). Travel-time triplications associated with these discontinuities are particularly visible in NORSAR records of many western Russian underground explosions (King and Calcagnile, 1976). Likewise, mapping and identifying various core phases and associated travel-time branches have been demonstrated (Doornbos and Husebye, 1972). Today, this kind of research is mainly history, in view of the limited Earth sampling offered by an array. The trend is toward using the comprehensive ISC data files and other seismological observations for generating laterally varying and partly anisotropic Earth models (see Anderson, 1985).
To summarize, array data analysis in the 1960–1970S provided relatively detailed mapping of major discontinuities in the upper mantle and resolved controversies regarding the generation mechanisms of so-called PKP precursor waves. There are still research avenues of interest in this context, such as dynamic modeling of travel-time branches for the 400- and 650-km discontinuities. At NORSAR such recordings exhibit consistent and profound changes in amplitude and frequency content between different phases, which must reflect strong lateral variations across these boundaries.
Chernov Media, Three-Dimensional Mapping, and Tomography
Perhaps the largest contribution of arrays to the science of seismology was an early realization that the earth was distinctly inhomogeneous. This was rather obvious from visual inspections of multisensor panels of P-wave array records, since both time and amplitude anomalies were of nearly the same order as those usually attributed to major regional structural differences (see fig. 4). With the recognition of pronounced heterogeneities in the array (LASA and NORSAR) siting areas and in the lithosphere, the next problem was to develop tools for modeling this phenomenon. The first significant step was by Aki (1973) who used the Chernov random-medium theory to model P-wave time and amplitude variations. A variant of this same theory was used by Clearly and Haddon (1972) to explain the scattering origin in the lowermost mantle of the so-called PKP precursor waves. Studies similar to those of Aki and others were undertaken at NORSAR, which also in this case resulted in a reasonable fit to the observational data (Berteussen et al., 1975). In another study, Husebye et al. (1974) demonstrated that P-wave amplitudes exhibit an approximately log-normal distribution, which subsequently led to the development of maximum-likelihood magnitude estimation procedures (Ringdal, 1975; Christoffersson, 1980). The common denominator for these studies was the use of an essentially statistical description of earth heterogeneities. In particular, the random-medium concept used for modeling Earth structures caused conceptual problems with many of our colleagues, and indeed we felt a bit uneasy ourselves. The lithosphere is definitely solid, hence deterministic approaches should be used for its mapping
and modeling. The solution to this fundamental seismological problem, a scientific breakthrough, came with a visit of Aki to NORSAR during the summer of 1974. The concept of block-inversion (the ACH-method), or three-dimensional imaging, was formulated after only a month, and this particular project was finalized at the Massachusetts Institute of Technology in 1975. The data first to be used in mapping lithosphere heterogeneities were P-travel-time anomalies from NORSAR, LASA, and the southern California network (Aki et al., 1976, 1977; Husebye et al., 1976). Dziewonski et al. (1977) extended the method to global mantle mapping, and others like Spencer and Gubbins (1980) introduced smart inversion schemes for joint estimation of source and structural parameters. The latter concept is particularly important in regional studies. The inversion technique initially offered by Aki, Christoffersson, and Husebye has now been extended to other seismological observations, including full waveform inversion, and is generally labeled Earth tomography. Instead of going into details here, we refer to recent major contributions on this topic by Carrion (1987), Goldin (1987), Nolet (1987), and Tarantola (1987).
As a curiosity, we should like to mention here that the development appears to have come full circle, as Flatté and Wu (1988) recently used scattering theory to provide a "scattering" three-dimensional image of the lithosphere beneath NORSAR based on essentially the same data as Aki et al. (1977) and Haddon and Husebye (1978), but using the correlation functions of these observations.
To summarize, the largest and most lasting contribution to seismology from arrays is that their observed puzzling P-wave time and amplitude anomalies led to the concept of Earth tomography, a major activity in Earth sciences today. However, the modeling of short-period P-amplitude anomalies remains problematic, although some success has been documented in this field as well (for example, see Haddon and Husebye, 1978; Thomson and Gubbins, 1982; Nowack and Aki, 1986).
Coda Waves and Associated Scattering Phenomena
In array seismology, wave-scattering phenomena have been, and still are, a major research topic. As mentioned previously, initial interests were focused on explaining and modeling precursory waves for PKP, PP, and other phases. A related, and by far more severe, problem is that of explaining and modeling the so-called coda waves (see Aki, 1969). Although many theoretical studies on this problem have been undertaken (see Wu and Aki, 1988), a remaining basic problem is that of decomposing the coda wave train. What we need to know, partly as a prerequisite for further theoretical investigations, is what wave types constitute the coda, say P and Lg waves. For such purposes, small-aperture arrays and single three-component stations are both eminently suited. Using maximum-likelihood variants of
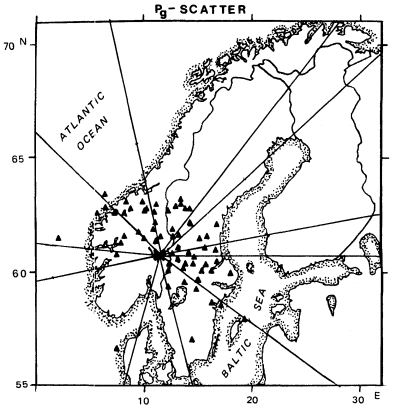
Figure 9
Locations of secondary "sources" for coda phases of Pg wave type
subject to scattering at the receiver site. Thin lines represent azimuth
of the events used in analysis. Note that scattering efficiency
appears to be relatively weak to the south and west. The location
of the scattering sources is based on three-component analysis.
broadband f-k analysis, Dainty (1988) has segmented the coda (usually within the 40–120-s window relative to the P-wave arrival) into scattering contributions from source and receiver sites. The outcome depends on source type, that is, earthquake or explosion, and focal depth. Since coherency is low in the coda, seldom exceeding 0.4 units for 3-s windows, relatively long windows of 10–20-s have to be used to ensure stable results. On the other hand, three-component records are less subject to severe interference, compared to a two-dimensional sensor deployment and permit time windows of one second in coda analysis. In other words, scattered P-wavelets are easy to identify and locate (see fig. 9) using the techniques mentioned in Christoffersson et al. (1988) and Ruud et al. (1988).
To summarize, small-aperture arrays have proved an important tool for
decomposing the coda and hence providing an improved insight into the extent of mode-conversion and wave-propagation efficiencies in the heterogeneous lithosphere. Such problems are important in the context of extensive wavefield parameterization. Likewise, path-dependent coda excitation may provide a clue to earthquake prediction (Aki, 1988) and thus provide an additional rationale for coda-wave research. In parallel to the Chernov media-to-tomography development mentioned above, a statistical modeling approach may also be most fruitful here in the initial stages (see Karlsen and Tjøstheim, 1988).
Discussions and Conclusions
In this article we have presented an overview of array seismology as it has evolved over the past decades. Our viewpoints are to some extent colored by intimate familiarity with NORSAR, LASA, and NORESS design and operation. However, the operation and research tied to these arrays are representative of array seismology per se, although activities of other arrays are not so well cited in the scientific literature. Anyway, array seismology has contributed significantly to the development of our science, both on observational and theoretical bases, which reflects the two unique features of an array, namely, superior data quality paired with dense two-dimensional wave-field sampling. Today, the technical edge of arrays is mainly lost as networks of high-gain, digital, three-component stations, affordable even for academic institutions and consortia, can be operated in much the same way as an array. Naturally, conventional beamforming is not feasible, but incoherent (envelope) beamforming is (Ringdal et al., 1975); alternatively, individual station detectors may be used (Magotra et al., 1987). Added flexibility here would come from developments of mobile arrays which, within a few years, are likely to comprise many hundreds of high-quality field instruments.
So, what will likely be the future role of the mentioned stationary arrays now in operation and similar ones possibly yet to be deployed? First of all, their contribution to general seismological research will be modest in view of their small aperture, with the notable exception of coda studies. However, past NORSAR and LASA records remain unique and thus will still be of importance in research if they are generally available.
Arrays in future CTB monitoring roles are a "touchy" political/seismological problem. For example, comprehensive simulation studies of seismic surveillance of both Russia and the United States have been undertaken by Evernden et al. (1986), while the same topic was covered in U.S. Congress hearings as part of the formulation of monitoring policies. In a technical note here by Bache, one conclusion was that a network of about
forty three-component stations would have roughly the same capability for monitoring Russia as a net of twenty NORESS-type arrays. Such a conclusion is not entirely surprising, in view of the amplitude-distance dependence and the obvious need to view a seismic source from different angles to properly identify its mechanism. We do not consider this to be a "black/white" problem, but believe that a blend of small arrays and three-component stations will offer the best tool for CTB monitoring. This being said, the relative importance of arrays in this context will depend on our ability to extract far more information from the array records; the above-mentioned expert-system approach, in combination with ingenious coda-processing schemes, is a promising avenue.
Our concluding remark is that arrays, although conceived and deployed mainly for political purposes, have proved extremely beneficial for seismology. In the future, new breeds of arrays will be even more important as mobile arrays, now technically feasible, will permit scientific experiments aimed at the detailed mapping of specific parts of the lithosphere or the Earth's deep interior. Perhaps most important are recent advances in computing and data-storage technology that permit any seismologist to participate in these efforts (see Berry chap. 3 in this volume.) In short, today we have a global seismological community, while tomorrow we will have a global research brotherhood as well.
Acknowledgments
With two decades of involvement in array seismology, we have had the opportunity and pleasure to meet many prominent scientists from many countries. I should like to mention specifically an acquaintance with K. Aki, who sees exciting research problems where others just see recordings, and A. Christoffersson, who has a knack for modeling both signal parameters and wave forms. Extensive monitoring discussions with GSE (Group of Scientific Experts) friends in Geneva, like R. Alewine, III, K. Muirhead, M. Henger, S. Lundbo, and others, are also much appreciated. Finally, the invitation to attend the Berkeley Seismograph Stations Centennial Symposia is acknowledged, and special thanks go to Prof. B. A. Bolt.
References
Aki, K. (1969). Analysis of the seismic coda of local earthquakes: Source, attenuation and scattering effect. J. Geophys. Res., 74: 615–631.
——— (1973). Scattering of P-waves under the Montana LASA.J. Geophys. Res., 78: 1334–1346.
——— (1988). The impact of earthquake seismology to the geological community since the Benioff Zone Centennial. Bull. Geol. Soc. Am., (submitted).
Aki, K., A. Christoffersson, and E. S. Husebye (1976). Three-dimensional structure of the lithosphere under Montana LASA. Bull. Seism. Soc. Am., 66: 501–524.
——— (1977). Determination of the three-dimensional seismic structure of the lithosphere. J. Geophys. Res., 82: 277–296.
Aki, K., and P. G. Richards (1980). Quantitative Seismology: Theory and Methods. Freeman, San Francisco, vols. I and II.
Anderson, D. L. (1985). Evolution of Earth structure and future directions of 3D modeling. In A. U. Kerr, ed., The VELA Program; Twenty-five Years of Basic Research. Executive Graphics Services, Defense Advanced Research Projects Agency, Rosslyn, Va., 399–418.
Anonymous (1965). Large Aperture Seismic Array. Advanced Research Projects Agency Technical Report, Washington, D.C.
Berteussen, K.-A., A. Christoffersson, E. S. Husebye, and A. Dahle (1975). Wave scattering theory in analysis of P-wave anomalies at NORSAR and LASA. Geophys. J., 42: 403–417.
Berteussen, K.-A., and E. S. Husebye (1974). Amplitude pattern effects on NORSAR P-wave detectability. Sci. Rep. 2-74/75, NTNF/NORSAR, Kjeller, Norway.
Böhme, J. F. (1987). Array processing. In J. L. Lacoume et al., eds., Signal Processing. North Holland, Publ. 4, Amsterdam, 437–482.
Bolt, B. A. (1976). Nuclear Explosions and Earthquakes: The Parted Veil. W. H. Freeman, San Francisco, 309 pp.
Bungum, H., E. S. Husebye, and F. Ringdal (1971). The NORSAR array and preliminary results of data analysis. Geophys. J., 25: 115–126.
Bungum, H., S. Mykkeltveit, and T. Kværna (1985). Seismic noise in Fennoscandia, with emphasis on high frequencies. Bull. Seism. Soc. Am., 75: 1489–1514.
Bungum, H., T. Risbo, and E. Hjortenberg (1977). Precise continuous monitoring of seismic velocity variations and their possible connection to solid earth tides. J. Geophys. Res., 82: 5365–5373.
Bungum, H., E. Rygg, and L. Bruland (1971). Short-period seismic noise structure at the Norwegian Seismic Array. Bull. Seism. Soc. Am., 61: 357–373.
Buttkus, B. (1986). Ten years of the Gräfenberg array. Geol. Jahrbuch Reihe E, Heft 35, Hannover.
Capon, J. (1969). High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE, 57: 1408–1418.
Carrion, P. (1987). Inverse Problems and Tomography in Acoustics and Seismology. Penn Publishing Co., Atlanta, Ga.
Chinnery, M. A., and M. N. Toksöz (1967). P-wave velocities in the mantle below 700 km. Bull. Seism. Soc. Am., 57: 199–226.
Christoffersson, A. (1980). Statistical models for seismic magnitude. Phys. Earth Planet. Inter., 21: 237–260.
Christoffersson, A., and E. S. Husebye (1974). Least square signal estimation techniques in analysis of seismic array recorded P-waves. Geophys. J. R. Astr. Soc., 38: 525–552.
Christoffersson, A., E. S. Husebye, and S. F. Ingate (1988). Wavefield decomposition using ML-probabilities in modeling single-site three-component records. Geophys. J. 93: 197–213.
Cleary, J. R., and R. A. W. Haddon (1972). Seismic wave scattering near the
core-mantle boundary: A new interpretation of precursors to PKP. Nature, 240: 549–51.
Dahlman, O., and H. Israelson (1977). Monitoring Underground Nuclear Explosions. Elsevier, Amsterdam, The Netherlands, 440 pp.
Dainty, A. M. (1988) Studies of coda using array and three-component processing. In R. S. Wu and K. Aki, eds., PAGEOPH Special Issue on Scattering and Attenuation of Seismic Waves.
Doornbos, D.J., and E. S. Husebye (1972). Array analysis of PKP phases and their precursors. Phys. Earth Planet. Inter., 5: 387–399.
Duckworth, G. L. (1983). Processing and Inversion of Arctic Ocean Refraction Data. Sc.D. thesis, Massachusetts Institude of Technology and Woods Hole Oceanographic Institude, Cambridge, Mass.
Dziewonski, A. M., B. N. Hager, and R. J. O'Connell (1977). Large-scale heterogeneities in the lower mantle. J. Geophys. Res., 82: 239–255.
Evernden, J. F., C. B. Archambeau, and E. Cranswick (1986). An evaluation of seismic decoupling and underground nuclear test monitoring using high-frequency seismic data. Rev. Geophys., 24: 143–215.
Flatté, S. M., and R. S. Wu (1988). Small-scale structure in the lithosphere and asthenosphere deduced from arrival-time and amplitude fluctuations at NORSAR. In R. S. Wu and K. Aki, eds., PAGEOPH Special Issue on Scattering and Attenuation of Seismic Waves.
Fyen, J., E. S. Husebye, and A. Christoffersson (1975). Statistical classification of weak seismic signals and noise at the NORSAR array. Geophys. J. R. Astr. Soc., 42: 529–546.
Goldin, S. V. (1987). Seismic Travel Time Inversion. SEG Bookmart, Tulsa, Okla.
Haddon, R. A. W., and E. S. Husebye (1978). Joint interpretation of P-wave travel time and amplitude anomalies in terms of lithospheric heterogeneities. Geophys. J., 55: 263–288.
Harris, D. B. (1982). Uncertainty in direction estimation: A comparison of small arrays and three-component stations. Lawrence Livermore National Lab., Tech. Rep. UCID-19589, Livermore, Calif.
Haykin, S., ed. (1985). Array Signal Processing. Prentice-Hall, Englewood Cliffs, N.J., 433 PP.
Hjortenberg, E., and T. Risbo (1975). Monochromatic components of the seismic noise in the NORSAR area. Geophys. J. R. Astr. Soc., 42: 547–554.
Hsu, K., and A. B. Baggeroer (1986). Application of the maximum likelihood method (MLM) for sonic velocity logging. Geophys., 51: 780–787.
Husebye, E. S., A. Christoffersson, K. Aki, and C. Powell (1976). Preliminary results on the 3-dimensional seismic structure under the USGS Central California Seismic Array. Geophys. J. R. Astr. Soc., 46: 319–340.
Husebye, E. S., A. Dahle, and K.-A. Berteussen (1974). Bias analysis of NORSAR and ISC reported seismic event mb magnitudes. J. Geophys. Res., 79: 2967–2978.
Husebye, E. S., R. A. W. Haddon, and D. W. King (1977). Precursors to ṔṔ and upper mantle discontinuities. J. Geophys., 43: 535–543.
Husebye, E. S., and S. Mykkeltveit, eds. (1981). Identification of Seismic Sources—Earthquakes or Underground Explosions. NATO ASI Series, D. Reidel Publishing Co., Dordrecht, The Netherlands, 876 pp.
Ingate, S. F., E. S. Husebye, and A. Christoffersson (1985). Regional arrays and optimum data processing schemes. Bull. Seism. Soc. Am., 75: 1155–1177.
Jordan, T. H., and K. A. Sverdrup (1981). Teleseismic location techniques and their application to earthquake clusters in the south-central Pacific. Bull. Seism. Soc. Am., 71: 1105–1130.
Kanasewich, E. R. (1981). Time Sequence Analysis in Geophysics. University of Alberta Press, Alberta, Canada, 480 pp.
Karlsen, H., and D. Tjøstheim (1988). Autoregressive segmentation of signal traces with applications to geological dipmeter measurements. Dept. of Mathematics, Bergen University, Norway.
Kerr, A. U., ed. (1985). The VELA Program. Twenty-five Years of Basic Research. Executive Graphic Services, Defense Advanced Research Projects Agency (DARPA), Rosslyn, Va., 964 pp.
King, D. W., and G. Calcagnile (1976). P-wave velocities in the upper mantle beneath Fennoscandia and western Russia. Geophys. J., 46: 407–432.
Korhonen, H., and S. Pirhonen (1976). Spectral properties and source areas of storm microseisms at NORSAR. Sci. Rep. 2-75/76, NTNF/NORSAR, Kjeller, Norway.
Magotra, N., N. Ahmed, and E. Chael (1987). Seismic event detection and source location. Bull. Seism. Soc. Am., 77: 958–971.
Massé, R. P. (1987). Seismic Verification of Nuclear Test Limitation Treaties: Workshop 2. Identification. Office of Technical Assessment, Congress of the United States, Washington, D. C.
Monzingo, R. A., and T. W. Miller (1980). Introduction to Adaptive Arrays. Wiley, New York.
Muirhead, K.J., and R. Datt (1976). The N -th root process applied to seismic array data. Geophys. J. R. Astr. Soc., 47: 197–210.
Mykkeltveit, S., K. Åstebøl, D. J. Doornbos, and E. S. Husebye (1983). Seismic array configuration optimization. Bull. Seism. Soc. Am., 73: 173–186.
Nolet, G., ed. (1987). Seismic Tomography, with Applications in Global Seismology and Exploration Geophysics. D. Reidel, Dordrecht, The Netherlands.
Nowack, R. L., and K. Aki (1986). Iterative inversion for velocity using waveform data. Geophys. J. R. Astr. Soc., 87: 701–730.
Press, F., ed. (1985). Nuclear Arms Control: Background and Issues. National Academy Press, Washington, D.C., 378 pp.
Ringdal, F. (1975). On the estimation of seismic detection thresholds. Bull. Seism. Soc. Am., 65: 1631–1642.
Ringdal, F., E. S. Husebye, and A. Dahle (1975). P-wave envelope representation in event detection using array data. In K. G. Beauchamp, ed., Exploitation of Seismograph Networks. Nordhoff-Leiden, The Netherlands, 353–372.
Ringdal, F., E. S. Husebye, and J. Fyen (1977). Earthquake detectability estimates for 478 globally distributed seismograph stations. Phys. Earth Planet. Inter., 15: 24–32.
Romney, C. F. (1985). VELA Overview: The early years of the seismic research program. In A. U. Kerr, ed., The VELA Program. Twenty-five years of Basic Research. Executive Graphics Services, Defense Advanced Research Projects Agency, Rosslyn, Va., 38–65.
Ruud, B. O., E. S. Husebye, S. F. Ingate, and A. Christoffersson (1988). Event loca-
tion at any distance using seismic data from a single, three-component station. Bull. Seism. Soc. Am., 78: 308–325.
Spencer, C., and D. Gubbins (1980). Travel-time inversion for simultaneous earthquake location and velocity structure determination in laterally varying media. Geophys. J. R. Astr. Soc., 63: 95–116.
Steinert, O., E. S. Husebye, and H. Gjøystdal (1976). Noise variance fluctuations and earthquake detectability. J. Geophys., 41: 289–302.
Stoffa, P. L., P. Buhl, J. B. Diebold, and F. Wentzel (1981). Direct mapping of seismic data to the domain of intercept time and ray parameter—A plane wave decomposition. Geophys., 46: 255–267.
Tarantola, A. (1987). Inverse Problem Theory. Elsevier, Amsterdam, The Netherlands, 613 pp.
Thirlaway, H. I. S. (1985). Forensic seismology. In A. U. Kerr, ed., The VELA Program. Twenty-five years of Basic Research. Executive Graphics Services. Defense Advanced Research Projects Agency, Rosslyn, Va., 17–25.
Thomson, C.J., and D. Gubbins (1982). Three-dimensional lithospheric modeling at NORSAR: Linearity of the method and amplitude variations from the anomalies. Geophys. J. R. Astr. Soc., 71: 1–36.
Tjøstheim, D. (1981). Multidimensional discrimination techniques—Theory and applications. In E. S. Husebye and S. Mykkeltveit, eds., Identification of Seismic Sources—Earthquakes or Underground Explosions. D. Reidel, Dordrecht, The Netherlands, 663–694.
Troitskiy, P., E. S. Husebye, and A. Nikolaev (1981). Lithospheric studies based on holographic principles. Nature, 294: 618–623.
Tsipis, K., D. W. Hafemeister, and P. Janeway (1986). Arms Control Verification: The Technologies That Make It Possible. Pergamon Brasey's International Defense Publications, Washington, D.C., 419 pp.
Urban, H. G., ed. (1985). Adaptive Methods in Underwater Acoustics, NATO ASI Series C. D. Reidel, Dordrecht, The Netherlands.
Vidale, J. F. (1986). Complex polarization analysis of particle motion. Bull. Seism. Soc. Am., 76: 1393–1405.
Wu, R. S., and K. Aki, eds. (1988). Scattering and attenuation of seismic waves. PAGEOPH Special Issue. Vol. 128; no. 1/2.