Chapter V
The Bohr Atom (1913-1916)

Horrid Assumptions

Bohr's leading role in the development of atomic theory began in 1913 with a fundamental memoir "On the constitution of atoms and molecules," published in three parts in the Philosophical Magazine . The first part of this trilogy introduced the concept of "stationary states" in atoms, the stability of which transcended mechanical explanation. As Heilbron and Kuhn have shown, the essential motivation for the introduction of this bold hypothesis was the impossibility of adapting the mechanical stability arguments of the Thomson atom to the new planetary models.^[1]

In Thomson's model of 1904, electrons rotated within a sphere of uniformly distributed positive electricity, and they were arranged symmetrically on densely populated rings (their number being much higher than the atomic number). The first feature provided mechanical stability for certain types of electronic configurations, the second one approximate radiative stability, at least until b and a scattering experiments required a reduction of the total electron number down to the atomic number. Most interestingly, the criterion of mechanical stability limited the relative numbers of electrons on the rings in a way which seemed to duplicate the periodic structure of Mendeleev's table, if only the electron numbers of successive chemical elements were assumed to differ by one unit.^[2]

[1] Bohr 1913; Heilbron and Kuhn 1969.

[2] See Heilbron 1964, 1968.

In Rutherford's nuclear atom, mechanical and radiative stability were both lacking, so that it was only by Bohr's fiat that electrons remained on stationary orbits. Also, new clues for the electronic configuration of atoms were needed, and a new explanation of chemical periodicity would have to be found. Having been proposed in this context, Bohr's original notion of stationary state included only the "normal" (unexcited) state of atoms. However, in order to exploit spectral data, particularly the Balmer formula, Bohr introduced excited stationary states, with higher energies but similar indifference to mechanical and electrodynamic perturbations. Changes in atoms could occur only as sudden jumps between two such supposedly stable states, and electromagnetic radiation could be emitted only during these jumps.^[3]

As a first step toward the determination of the stationary states and the emitted radiation, Bohr introduced two "principal assumptions":

I. "that the dynamic equilibrium [i.e., the motion] of the systems in the stationary states can be discussed by help of the ordinary mechanics, while the passing of systems between different stationary states cannot be treated on that basis," and

II. "that the latter process is followed by the emission of a homogeneous [i.e., monochromatic] radiation, for which the relation between the frequency and the amount of energy emitted is the one given by Planck's theory [of blackbody radiation]."

This second assumption was the boldest of all, for it generally gave for the frequency of the emitted radiation a frequency different from that of the motion in the original state of the emitting atom. Einstein had well anticipated, for instance in his theory of specific heats (1906), the idea of a discrete selection of mechanical states implied in the notion of stationary state; but he was "astonished" by Bohr's further departure from ordinary conceptions and judged it to be an "enormous achievement."^[4]

In their first rough formulation, the "principal assumptions" were not sufficient to determine the stationary states, even in the simplest case of the hydrogen atom. Some other hypothesis was needed to select a discrete subset of motions among all those permitted by ordinary mechanics. I will not explain here how Bohr reached this hypothesis, the so-called quantum rule; rather, I will discuss the various formulations found in the 1913

[3] See Heilbron and Kuhn 1969.

[4] Bohr 1913, 7; Einstein's reaction (at the Vienna congress) is taken from Hevesy to Bohr, 23 Sept. 1913, BCW 2: [532].

trilogy. In the first formulation the quantum rule takes the form of a simple relation between the orbital frequency v in a given stationary state and the frequency v of the monochromatic radiation emitted by an electron making a transition from rest at infinity to this stationary state.

Bohr's focus on the latter type of transition deserves a comment: his main interest was not in the theory of spectra but in the building of atoms, which could be imagined as being synthesized from originally separated electric charges. As we shall later see, in the early twenties Bohr based the construction of his second atomic theory on this idea of a correspondence between the properties of stationary states and the characteristics of the radiation emitted during their formation.

For the hydrogen atom, Bohr simply assumed 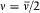, without any solid justification but success. This made, somewhat naturally, the frequency of the radiation emitted during the formation of a given stationary state the average of the initial (zero) and final (v) orbital frequencies. He then applied assumption (II) to this process, giving to the energy emitted during the above process one of the values permitted by Planck's theory of radiation, that is to say, an integral multiple of the quantum hv . This yields the relation

where E_x is the energy in the original, unbound state, and E _n the energy in the final stationary state. In purely orbital terms, one has the formal quantum rule

Assumption (I) includes the validity of ordinary mechanics for the motion of the charged particles in a given stationary state. In Rutherford's nuclear model (the one adopted by Bohr) this gives, for the hydrogen atom, a Keplerian elliptic motion of the electron around the nucleus. For an infinitely heavy nucleus, the total mechanical energy E (taking 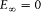) is related to the orbital frequency through

where m is the mass of the electron and e its charge. Combined with the rule (2), this relation gives^[5]

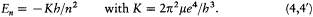
[5] Bohr 1913, 4-5. The system of units (Gaussian) is such that the Coulomb energy is given by -e /r .

The stationary states being now completely determined, the energy spectrum of the hydrogen atom can be calculated by a direct application of assumption (II). For a transition from n ' to n ", the frequency v _n'n' ' of the emitted radiation satisfies

if one-quantum processes are the only ones permitted. This gives

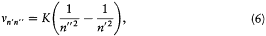
in conformity with Balmer's empirical formula.

Altogether, the above reasoning hardly provided a deduction of the hydrogen spectrum, since it relied on a loose, even inconsistent, analogy with Planck's radiation theory. For instance, the process of formation of the stationary state n was taken to be a n -quantum radiation process, whereas in the derivation of the series spectrum the quantum transitions were taken to induce a one-quantum radiation process. Bohr, always excellent at self-criticism, immediately perceived the fault and mended it in the last part of the same paper. There he abandoned his tentative conception of the formation of atoms and introduced instead the idea of an asymptotic agreement between quantum theory and classical electrodynamics. With this new constraint he was able to re-derive the value of K (Rydberg's constant) and also to discover the correct correspondence between orbital frequencies and radiation frequencies.

In general, the frequency of the radiation emitted in a transition between two successive stationary states is different from its orbital frequency in the original state (and from any harmonic of it), in sharp contrast with classical electrodynamics, as Bohr put it. However, in the limit of high quantum numbers, for which the orbital motion is very slow, one should expect an approximate equivalence between these two frequencies. In conjunction with relation (5), this implies

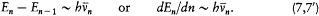
Assuming the form E_n = - Kb/n² (now taken from the empirical series), one has^[6]

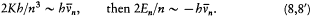
The latter relation, being identical with Bohr's original quantum rule (2), leads to the same expression (4') of the Rydberg constant as before. More

[6] Ibid., 8-9. As he later realized (Bohr 1914), Bohr could have derived the asymptotic form of E_n by integrating the differential equation resulting from (3) and (7').

generally, for transitions in which n decreases by a relatively small amount t , the following asymptotic relation holds:

that is to say, the frequency of the emitted radiation nearly equals the harmonic t of the orbital frequency. Bohr commented:

The possibility of an emission of a radiation of such a frequency may also be interpreted from analogy with the ordinary electrodynamics, as [read "since" instead of "as"] an electron rotating round a nucleus in an elliptical orbit [the circular orbit would give only harmonic oscillations] will emit a radiation which according to Fourier's theorem can be resolved into homogeneous components, the frequencies of which are [], if is the frequency of revolution of the electron.^[7]

This was the first germ of the analogy later extended under the name of the correspondence principle. In 1913, however, the theory was still at an exploratory stage. The basic assumptions were too unsettled to allow for fruitful exploitation of formal analogies. A little after the publication of his trilogy, Bohr expressed in private great doubts about the "horrid assumptions" of his new theory and about the possibility of a generalization to systems more complex than the hydrogen atom or the harmonic oscillator:

I tend to believe that in this problem there are buried very considerable difficulties, which can be avoided only by departing from the usual considerations to an even greater extent than has been necessary up to now, and that the preliminary success is due only to the simplicity of the systems considered.

This kind of utterance, a Kierkegaardian readiness to forecast great conceptual leaps, would recur whenever Bohr perceived a state of crisis—for instance in 1922-23, when the Bohr-Sommerfeld theory underwent difficulties, and in the late twenties, when the atomic nucleus seemed to disobey quantum-mechanical laws.^[8]

Confirmations and Perturbations

Although not mentioned in the above account of the basic assumptions of Bohr's new atomic theory, the main object of the 1913 trilogy was to

[7] Bohr 1913, 14.

[8] Bohr to McLaren, 1 Sept. 1913, BCW 5:[91]; Bohr to Oseen, 28 Sept. 1914, BCW 2: [557]-[560].

develop a new ring model, a substitute for Thomson's models of atoms and molecules (to which I will later return), in an endeavor to recover the properties of Mendeleev's table of elements. This part of Bohr's work was too speculative to receive unambiguous empirical confirmation. Nevertheless, in the years 1913-1914, various events improved Bohr's confidence in the basic truth of at least part of his "horrid assumptions." These assumptions appeared to give the first germs of a successful theory of atomic spectra when applied to the spectra of one-electron systems (H, He⁺ ) and to the new field of X-ray spectra.^[9]

Furthermore, Franck and Hertz unwittingly provided an independent confirmation of the concept of stationary state. In 1914 they observed an energy threshold in the electron-stopping power of mercury vapor. This threshold, Bohr explained the following year, corresponded to a transition between the normal state and another (first excited) stationary state of the mercury atom (and not, as Franck and Hertz had originally thought, to the ionization of the atom). The supramechanical stability implied by the assumption of stationary states was now empirically proved to comprehend stability with regard to electron impacts.^[10]

In a paper published in 1914 Bohr examined the effect of electric and magnetic fields on the spectrum of the hydrogen atom. According to Stark's observations in the electric case, every spectral line split into a number of components; the separation between the components was proportional to the intensity of the applied field, with a proportionality coefficient depending on the line. The available method of quantization was too restricted to permit a complete explanation of this effect. Bohr therefore limited his investigation to large values of the quantum number n and to strictly periodic motions. In this case he could derive the quantized energy levels E_n from the relation (7'):

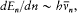
which he named "correspondence principle" in one of his manuscripts. This is, as far as I know, the earliest occurrence of this expression in Bohr's writings; at this early stage it only meant the asymptotic agreement between the quantum-theoretical and the classical values of the frequency of the emitted radiation.^[11]

[9] See Heilbron and Kuhn 1969.

[11] Bohr 1914. For Stark's empirical discovery see Jammer 1966, 106-107. The mentioned manuscript is m BCW 2: [382].

For the hydrogen atom in an electric field X, there are only two periodic motions of a given amplitude 2a . The corresponding orbits are rectilinear and parallel to the field; the total energy E and the frequency are given by the formulae

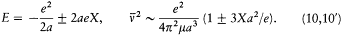
The elimination of a and the "correspondence principle" (7') give doubled energy levels:

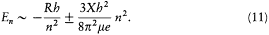
According to the relation D E = hv , a double level-splitting should imply a quadruple line-splitting. However, Bohr retained only the doublet

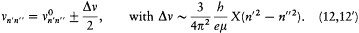
His justification deserves special attention: "In order to obtain the continuity necessary for a connection with ordinary electrodynamics, we have assumed that the system can pass only between the different states in each series." Bohr meant that a transition between a level with the + sign and a level with the — sign would have corresponded to a discontinuous change in the orbit, even in the limit of high quantum numbers for which the classical principle of continuity ought to hold approximately. This is the first historical example of a derivation of a selection rule on the basis of an assumed correspondence between properties of the classical motion and quantum-theoretical radiation. Interestingly, the precise form taken here by this correspondence requirement, an identification of the connectivity (in the sense of the possibility of quantum transitions) of stationary states with the connectedness (in the topological sense) of classical motions in these states, was the one later used by Bohr in his application of the correspondence principle to the helium atom.^[12]

Within the explicit high-n limit, Bohr's theory of the Stark effect of hydrogen was a successful one; it gave the observed proportionality of the splitting to the field intensity, the approximative position of the two extreme components (the dominant ones) of the multiplets observed in the case of the lines Hb and Hg , for which the quantum numbers are not too

[12] Bohr 1914, 515.

small (n ' = 4, 5; n " = 2), and the correct polarization of these two components (the latter again being determined by analogy with the classical motion).^[13]

To Bohr the Zeeman effect was a different matter. In the case of hydrogen, Lorentz's classical model of an elastically bound electron or Rutherford's classical model led to the observed triple splitting with a linearly polarized unshifted central line and two circularly polarized lines shifted by

where B is the intensity of the magnetic field. This frequency shift was independent of the quantum number n , and the resulting spectrum violated Ritz's combination principle, according to which spectral lines are generated by taking all possible differences of series of spectral "terms" (as implied by Bohr's relation v = DE/h ). Furthermore, Bohr mistakenly believed that classically, the total energy of the atom remained unchanged during the application of a magnetic field. All these circumstances seemed to exclude an explanation of the Zeeman effect of the same nature as that given for the Stark effect.^[14]

Consequently, Bohr interpreted the Zeeman effect as a violation of assumption (II), the rule DE = hv . "In order to obtain the connection with the ordinary mechanics" this rule had to be modified into

More generally, until Sommerfeld inaugurated the quantum theory of multiperiodic systems, Bohr believed that the relation DE = hv applied only to strictly periodic motions. In other cases, he wrote in 1916, "we cannot, even in the limit [of large quantum numbers] obtain a relation between

the frequency of the radiation and the motion of the system if we assume that the radiation is monochromatic."^[15]

Periodic Systems

In 1915 Bohr undertook to consolidate the general foundations of the quantum theory. The proliferation of careless calculations and speculations based on Bohr's model had made such a task necessary. For instance, in early 1915 Debye and Sommerfeld had published calculations of the dispersion of light by the Bohr atom, in which they assumed classical electrodynamics to apply to the perturbation of stationary orbits. The results contradicted empirical data. Bohr and his friend Oseen were not at all surprised by this failure: classical electrodynamics, since it failed to explain the stability of stationary states, could a fortiori not be expected to represent correctly their reaction to external radiation. Observing that a theorist of Sommerfeld's stature could overlook such a central point, Bohr was compelled to clarify his positions.^[16]

The results of this general clarification were ready for publication in early 1916, under the title "On the application of the quantum theory to periodic systems." On this occasion Bohr first isolated the "fundamental assumption" of his quantum theory, namely,

that an atomic system can exist permanently only in a certain series of states corresponding with a discontinuous series of values of its energy, and that any change of the energy of the system including absorption and emission of electromagnetic radiation must take place by a transition between two such states. These states are termed "the stationary states" of the system.

From then on this would be the first, most unshaken postulate of Bohr's atomic theory, in spite of (or because of) its "entirely negative character." The other assumptions, those necessary to positively determine stationary states, emitted radiation, and statistical properties, could be specified only in particular cases, and were not well ascertained. In 1915-16, in conformity with his previous investigation of the Zeeman effect, Bohr did not even believe in the generality of the relation DE = hv (which would nevertheless become his second postulate a year later).^[17]

When he wrote this essay, Bohr could formulate positive assumptions only for the quantization of strictly periodic systems. In this case he could

[15] Bohr 1914, 520; Bohr [1916], [445].

[16] Debye 1915; Sommerfeld 1915a; Oseen 1915; Bohr to Oseen, 20 Dec. 1915, BCW 2: [564]-[566]. See Hoyer's comments in BCW 2 : [336]-[339].

[17] Bohr [1916], [434], [445].

rely on Ehrenfest's adiabatic hypothesis (1913) for deriving a general quantum rule, that is, a prescription to derive the energy of the stationary states of the system. Granted that stationary states are obtained through a discrete selection among the classically possible motions of the system, Ehrenfest's hypothesis further required "permitted" motions to transform into other permitted motions during infinitely slow ("adiabatic") changes of the forces acting in and on the system. Bohr found the assumption most natural. Indeed, part of it, the continuous transformability of stationary states during slow variations of external conditions, could be viewed as a "direct consequence of the necessary stability of these states," while the rest of it, the applicability of ordinary mechanics to the slowly transforming system, was hardly less plausible than the similar assumption for the electronic motion of a given system in a stationary state. Bohr once justified the latter point:

If . . . the variation [of the external conditions] is performed at a constant or very slow changing rate, the forces to which the particles of the system will be exposed will not differ at any moment from those to which they would be exposed if we imagine that the external forces arise from a number of slowly moving additional particles which together with the original system form a system in a stationary state.^[18]

Take the simplest possible case, a quantized harmonic oscillator. As results from an old theorem of Boltzmann (to be later stated in detail), an adiabatic change of the parameters (mass or elastic constant) does not alter the ratio 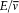, so that the oscillator remains in a stationary state. According to Ehrenfest's adiabatic hypothesis, this property admits a wide generalization: under any (nonsingular) adiabatic deformation of the original oscillator—including ones that destroy the harmonicity—the system remains in a stationary state.^[19]

Consider now an arbitrary mechanical system with one degree of freedom allowing finite motions. Then any finite motion (which does not converge toward a fixed point) is periodic (as is shown on p. 107) and is adiabatically connected to the motion of a harmonic oscillator. Consequently, the stationary states of the system are completely determined by

[18] Ehrenfest 1914a. See Klein 1964b, 1970c, and Ehrenfest 1923b. Ehrenfest used the word "adiabatic" because the theorem by Boltzmann on which his consideration was based had been established m the context of formal mechanical analogies for the relation dS =d Q/T. In these analogies a slow variation of a parameter of a simple periodic mechanical system represented an adiabatic transformation of a thermodynamic system. Quotations from Bohr to Ehrenfest, 5 May 1918 (AHQP), and Bohr 1918a, 8, also in BCW 3:[74].

[19] Ehrenfest 1914a; Boltzmann's theorem is in Boltzmann 1904, 2:182.

the quantization of the latter oscillator. Even better, the quantum rule for the original system can be explicitly written as

where is the frequency of the motion and 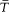is the average of the kinetic energy over one period. Indeed, 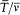is adiabatically invariant according to the above-mentioned theorem of Boltzmann, and in the case of a harmonic oscillator it is identical with 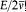. Since this invariance also holds for any number of degrees of freedom, Bohr assumed the same form of the quantum rule to apply to any periodic system (i.e., systems for which all bounded motions are periodic).^[20]

A simple proof of Boltzmann's theorem given by Bohr goes as follows.^[21] The system is described by the canonical coordinates q = (q _l , . . .q_i , . . .q_s ) and p = (p_l , . . . p_i ,. . .p _s ), which satisfy Hamilton's equations

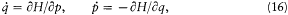
where H(q, p ) is the Hamiltonian function, and the collective derivatives are defined as

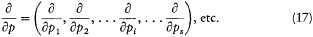
The kinetic energy T being a quadratic function of p ,

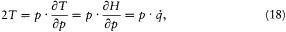
where the dot products are defined according to

This implies

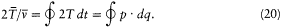
I call the latter integral I . Its adiabatic invariance is proved as follows:

Consider periodic functions q (t ) + d q(t ) and p (t ) + d p(t ), which are infinitely close to solutions q (t ) and p (t ) of Hamilton's equations for H ; these functions do not have to be solutions of the original equations of motion, and their common period does not have to be identical with the original period. Since the integral I is independent of the choice of the

[20] Bohr [1916], [435].

[21] Ibid., [435]-[436]. A more explicit version of the same proof is in Bohr 1918a, 10-12, also in BCW 3: [76]-[78].

integration parameter, let us temporarily choose this parameter with a range independent of the period of q (t ) (for instance, 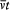would do). Then the variation of I during the infinitesimal variation of q and p is simply given by

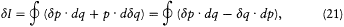
where the last expression has been obtained by partial integration of the second term. We now switch to the integration parameter t (the time), in order to get

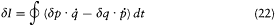
and, with the help of Hamilton's equations,

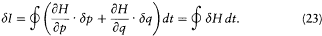
We now further assume that q + d q and p + d p have been obtained from q and p through a Hamiltonian evolution from t = -q to t = 0, with the Hamiltonian function

wherein l is a parameter varying slowly and smoothly from 0 to 1:

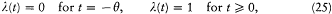
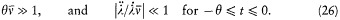
During this evolution the original Hamiltonian H varies according to

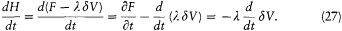
Integration with respect to t gives

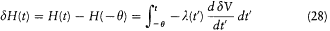
or, after partial integration, and for ,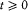

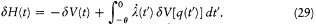
In the latter integral, q (t ') may be replaced by its nonperturbed value (obtained by putting F = H ), if only first-order contributions to d H are retained. Then d V[q (t' )] is a periodic function of t ' with the period 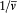; since the variation of 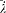is negligible during such a period, d V can be re-

placed in the integral by its average value 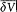over a period. This gives

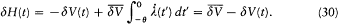
The adiabatic invariance of I results from combining (23) and (30):

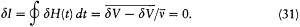
In the above proof of the adiabatic theorem, Bohr accorded a special importance to the identity (23):

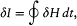
for it granted in the following way coherence between the quantum rule I = nh and the postulate of stationary states. Consider two neighboring periodic motions of the same periodic system. Then H is a constant for both motions, and the identity (23) reduces to

which implies that H depends only on I (as long as the space of periodic motions of the system is connected in the topological sense). In this way the quantum rule completely determines the energy of the system. Bohr emphasized the importance of this result in the following terms:

It will be seen that [the dependence of the energy on I only] constitutes a necessary condition for the application of ordinary mechanics to the stationary states of periodic systems. Otherwise, we could by suitable variations of the external conditions make the systems emit or absorb energy, without a transition between stationary states corresponding to different values of n .^[22]

This remark is very typical of Bohr's striving for mutual compatibility among his assumptions. Quantum theory, as based on the postulate of stationary states, was utterly anticlassical. Therefore, the importation of a whole piece of classical theory (for the determination of the motion in stationary states) could only be allowed insofar as the involved classical concepts did not conflict with the concept of stationary states. In judging this condition the adiabatic principle played an essential role, and so would, some time later, the correspondence principle. It was indeed part of Bohr's greatness to realize that successful heuristic principles also had something to say about the inner consistency of new theoretical schemes.

In the same text of 1916, Bohr generalized the idea of asymptotic correspondence, introduced in 1913, to any strictly periodic system. Here

[22] Bohr [1916], [437].

again the identity (23) provided the necessary connection, when applied to two neighboring stationary states of a given system, I = nh and I = (n - t )h . In this case too the relation (32) holds, for both motions derive from the same Hamiltonian H . This gives

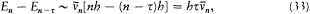
which means again an asymptotic agreement between the frequencies of the light emitted in the quantum transitions from a given stationary state, and the harmonics of the corresponding orbital frequency.^[23]

The above essay never reached publication, because while he was holding proofs from the Philosophical Magazine Bohr became aware of two spectacular developments of his quantum theory: Sommerfeld and his followers had found quantum rules for nonperiodic systems, and Einstein had furthered the conceptualization of quantum radiation processes. Bohr immediately realized the possibility and necessity of extending the foundations of quantum theory.

Summary

Bohr's first atomic theory emerged in 1913 from an endeavor to explain the properties of chemical elements on the basis of Rutherford's new planetary model of atoms. While the most obvious property expected from real atoms was their stability with respect to external perturbations, Bohr found that Rutherford's model was unstable, both mechanically and electrodynamically. Not discouraged by this conflict, he proposed a supramechanical notion of stability that was embodied in his concept of "stationary state." By definition the stationary states were subjected to the following assumptions, which were mostly suggested by the quantum theory of Planck and Einstein, and the simple regularities of the hydrogen spectrum:

1. an atom can exist permanently only in a discontinuous series of stationary states.

1'. transitions between stationary states occur very suddenly, and therefore elude description in terms of ordinary mechanics and electrodynamics.

2. the motion of electrons in a stationary state is determined by applying ordinary mechanics to Rutherford's model.

3. the frequency of the radiation emitted or absorbed during a transition between two stationary states is given by the difference in energy

[23] Ibid., [443]-[444].

between these states divided by Planck's constant (this is the frequency rule: DE = hv ').

Assumption (1) was obviously anticlassical but could be regarded as an extension of Einstein's ideas on quantization. Assumption (3) was more revolutionary, for it contradicted the hitherto unquestioned identity between the frequency of the motion in a source and the frequency of the radiation emitted by the source.

Assumptions (1) and (2) were not sufficient to determine the energy of stationary states. Bohr therefore introduced a "quantum rule" in order to select stationary motions from among the continuous manifold of classically possible ones. For the simple case of the hydrogen atom Bohr's 1913 memoir contained two conceptions of the quantum rule, both of which involved some analogy with classical electrodynamics. In the first, Bohr considered the spontaneous synthesis of the n^th stationary state from an electron at rest at infinity and a hydrogen nucleus. Assuming (2) and an n -quantum version of (3) (namely, DE = nhv ), the energy of the n^th stationary state of the hydrogen atom was obtained by setting the (homogeneous) frequency of the emitted radiation equal to half the final orbital frequency. In doing this Bohr renounced the exact classical relation between motion and emitted radiation but required an analogous relation to subsist at the quantum level. Such a requirement was the vaguest meaning of what Bohr would later call "correspondence principle."

A more precise anticipation of the correspondence idea appeared in Bohr's other conception of the quantum rule. Using his frequency rule, Bohr inferred from the empirically known properties of the hydrogen spectrum that the energy of the n^th stationary state was proportional to 1/n² ; and he derived the proportionality factor from the following condition: in the limit of high quantum numbers, for which stationary states are very close to one another, the frequency spectrum given by quantum theory must be almost identical with the spectrum which classical electrodynamics would yield (when applied to the motion in the initial state). More precisely, Bohr found that the transition between the stationary states n and n — t corresponded to the t^th harmonic of the motion in the n^th stationary state (in the following I will use quotation marks to imply this precise meaning of the verb "correspond"). This remark was essential to the later formulation of the correspondence principle.

Bohr's ambition was not limited to the hydrogen atom. His memoir of 1913 also pretended to give clues about more complex atoms, and even molecules. However, early confirmations of Bohr's ideas occurred only for

one-electron systems, hydrogen and ionized helium, and for the general idea of stationary state, with Bohr's interpretation of collision experiments (Franck and Hertz). This was enough to persuade Bohr, if not all theorists, that his theory contained a kernel of truth.

In 1914 he achieved another success in explaining the Stark effect of the hydrogen atom (the splitting of spectral lines induced by an external electric field). His theory, albeit partial and approximate (limited to high quantum numbers and to periodic motions), is of special historical interest, for it provided a first glimpse of a very important aspect of the correspondence principle, the derivation of selection rules for quantum transitions. For each value of the quantum number n of an unperturbed stationary state, Bohr's calculation gave two different orbits, say + and -. The frequency rule should, therefore, have given a quadruple splitting of every line. But this was at variance with the observed dominance of doublets (only the most intense lines were retained). Bohr resolved the contradiction by noting that transitions between + and - orbits had no classical counterpart, because the + orbits were qualitatively very different from the — orbits, even in the limit of high quantum numbers. Asymptotic agreement with the classical spectrum could only be obtained by "selecting" transitions between orbits of the same kind.

Bohr was less successful with the Zeeman effect (the line-splitting induced by a magnetic field). Zeeman spectra did not seem to be compatible with the frequency rule (because of what would later turn out to be the selection rule Am = 0, ±1); further, Bohr (wrongly) believed that the energy of the classical orbital motion was not affected by the magnetic field. Consequently, he excluded an explanation of the type employed in the Stark case and instead replaced the rule DE = hv with a modified rule DE = h (v + d v); then he had no better way to determine the frequency shift d v than taking it from Lorentz's theory of the (normal) Zeeman effect.

In 1916 Bohr judged the time to be ripe for a clarification of the foundations of his theory. The only fundamental assumption of atomic theory, he now believed, was that of the (supramechanical) stability of stationary states (1 and 1'). All other assumptions, including the frequency rule, he thought, could hold only in the case of periodic systems. For the sake of definiteness, however, Bohr limited his considerations to this special case and applied ordinary mechanics to the motion in stationary states. For periodic systems (like a harmonic oscillator or the hydrogen atom), ordinary mechanics, together with Ehrenfest's adiabatic hypothesis, led to an explicit quantum rule.

According to Bohr's adaptation of Ehrenfest's hypothesis (1913), slow continuous ("adiabatic") deformations of an atomic system kept the system in a stationary state, and they were governed by ordinary mechanics. As a corollary, in order to determine the stationary states of a given system one just had to imagine a continuous deformation leading from the original system to a simpler system. If the quantum rule was already known for the simpler one, one had the rule for the original.

Bohr adopted the adiabatic principle not only on account of its calculational benefits but also because it blended harmoniously with his concept of stationary state. Since atomic systems could rest only in stationary states, it followed that slow deformations of them had to proceed along stationary states. Moreover, if ordinary mechanics applied to the motion in stationary states, it also had to apply to the slow deformations, because the system responsible for the forces inducing the deformation could be associated with the atomic system to form a larger, closed system in a strictly stationary state. Last but not least, the quantum rule deduced from the adiabatic principle automatically provided the necessary asymptotic agreement between quantum and classical spectrum. These very Bohrian comments tended to show a subtle harmony between two antagonistic aspects of the new atomic theory: the anticlassical notion of stationary state, and the limited recourse to ordinary mechanics.

Bohr had just finished writing down the above considerations when he learned of important developments of his theory that had taken place abroad. For this reason he decided not to publish anything until he could reach a, now necessary, synthesis.