5.2—
Symbols in Computers

At this point, I wish to shift attention to a second application of the Semiotic Analysis. In the remainder of this chapter, I shall consider the applications of the Semiotic Analysis to symbols in computers . There are really two parts to this exercise. First, I shall argue (against the Formal Symbols Objection articulated in chapter 3) that it is quite unproblematic to say that computers do, in fact, both store and operate upon objects that may be said to be symbols, and do have syntactic and semantic properties in precisely the senses delineated by the Semiotic Analysis. To be sure, the story about how signifiers are tokened in microchips is a bit more complicated than the story about how they are tokened in speech or on paper, but it is in essence the same kind of story and employs the same resources (namely, the resources outlined in the Semiotic Analysis). Second, I shall address claims on the opposite front to the effect that there is something special about symbols in computers, and that computer science has in fact revealed either a new kind of symbol or revealed something new and fundamental about symbols in general. I shall argue that this sort of claim, as advanced by Newell and Simon (1975), is a result of an illegitimate conflation of the functional analysis of computers with their semiotic properties. Or, to put it another way, Newell and Simon are really using the word 'symbol' in two different ways: one that picks out semiotic properties and another that picks out functionally defined types. Neither of these usages explains the other, but both are important and useful in understanding computers.

5.2.1—
Computers Store Objects That Are Symbols

In light of the centrality of the claim that computers are symbol manipulators, it is curious that virtually nothing has been written about how computers may be said to store and manipulate symbols. It is not a trivial problem from the standpoint of semiotics. Unlike utterances and inscriptions (and the letters and numerals on the tape of Turing's computing machine), most symbols employed in real production-model computers are never directly encountered by anyone, and most users and even programmers are blissfully unaware of the conventions that underlie the possibility of representation in computers. Spelling out the whole story in an exact way turns out to be cumbersome, but the basic conceptual resources needed are simply those already familiar from the Semiotic Analysis. I have divided my discussion of symbols in computers

into two parts. I shall give a general sketch of the analysis here and provide the more cumbersome technical details in an appendix for those interested in the topic, since the details do not contribute to the main line of argumentation in the book.

The really crucial thing in getting the story right is to make a firm distinction between two questions. The first is a question about semiotics: In virtue of what do things in computers count as markers, signifiers, and counters? The second is a question about the design of the machine: What is it about computers that allows them to manipulate symbols in ways that "respect" or "track" their syntax and semantics? Once we have made this distinction, the basic form of the argument that computers do indeed operate upon meaningful symbols is quite straightforward:

(1) Computers can store and operate upon things such as numerals, binary strings representing numbers, and so on.

(2) Things like numbers and binary strings representing numbers are symbols.

\ (3) Computers can store and operate upon symbols.

Of course, while one could design computers that operate (as Turing's fictional device did) upon things that are already symbols by independent conventions (i.e., letters and numerals), most of the "symbols" in production-model computers are not of this type, and so we need to tell a story about how we get from circuit states to markers, signifiers, and counters. I shall draw upon two examples here:

Example 1: The Adder Circuit

In most computers there is a circuit called an adder . Its function is to take representations of two addends and produce a representation of their sum. In most computers today, each of these representations is stored in a series of circuits called a register . Think of a register as a storage medium for a single representation. The register is made up of a series of "bistable circuits"—circuits with two stable states, which we may conventionally label 0 and 1, being careful to remember that the numerals are simply being used as the labels of states, and are not the states themselves. (Nor do they represent the numbers zero and one.) The states themselves are generally voltage levels across output leads, but any physical implementation that has the same on-off properties would function equivalently. The adder circuit is so designed that the pattern that is formed in the output register is a func-

tion of the patterns found in the two input registers. More specifically, the circuit is designed so that, under the right interpretive conventions, the pattern formed in the output register has an interpretation that corresponds to the sum of the numbers you get by interpreting the patterns in the input registers.

Example 2: Text in Computers

Most of us are by now familiar with word processors, and are used to thinking of our articles and other text as being "in the computer," whether "in memory" or "on the disk." But of course if you open up the machine you won't see little letters in there. What you will have are large numbers of bistable circuits (in memory) or magnetic flux density patterns (on a disk). But there are conventions for encoding graphemic characters as patterns of activity in circuits or on a disk. The most widely used such convention is the ASCII convention. By way of the ASCII convention, a series of voltage patterns or flux density patterns gets mapped onto a corresponding series of characters. And if that series of characters also happens to count as words and sentences and larger blocks of text in some language, it turns out that that text is "stored" in an encoded form in the computer.

Now to flesh these stories out, it is necessary to say a little bit about the various levels of analysis we need to employ in looking at the problem of symbols in computers and also say a bit about the connections between levels. At a very basic level, computers can be described in terms of a mixed bag of physical properties such as voltage levels at the output leads of particular circuits. Not all of these properties are related to the description of the machine as a computer. For example, bistable circuits are built in such a way that small transient variations in voltage level do not affect performance, as the circuit will gravitate towards one of its stable states very rapidly and its relations to other circuits are not affected by small differences in voltage. So we can idealize away from the properties that don't matter for the behavior of the machine and treat its components as digital —namely, as having an integral and finite number of possible states.^[3] It so happens that most production-model computers have many components that are binary —they have two possible states—but digital circuits can, in principle, have any (finite, integral) number of possible states. Treating a machine that is in fact capable of some continuous variations as a digital machine involves some idealization, but then so do most descriptions relevant for science. The digital description of the machine picks out properties that are real (albeit idealized),

physical (in the strong sense of being properties of the sort studied in physics, like charge and flux density), and nonconventional .

Next, we may note that a series of digital circuits will display some pattern of digital states. For example, if we take a binary circuit for simplicity and call its states 0 and 1, a series of such circuits will display some pattern of 0-states and 1-states. Call this a digital pattern . The important thing about a digital pattern is that it occupies a level of abstraction sufficiently removed from purely physical properties that the same digital pattern can be present in any suitable series of digital circuits independent of their physical nature. (Here "suitable series" means any series that has the right length and members that have the right number of possible states.) For example, the same binary pattern (i.e., digital pattern with two possible values at each place) is present in each of the following sequences:

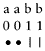
It is also present in the music produced by playing either of the following:

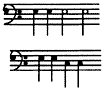
And it is present in the series of movements produced by following these instructions:

(1) Jump to the left, then

(2) jump to the left again, then

(3) pat your head, then

(4) pat your head again.

Or, in the case of storage media in computers, the same pattern can be present in any series of binary devices if the first two are in whatever counts as their 0-state and the second two are in whatever counts as their 1-state. (Indeed, there is no reason that the system instantiating a binary pattern need be physical in nature at all.)

Digital patterns are real . They are abstract as opposed to physical in

character, although they are literally present in physical objects. And, more importantly, they are nonconventional . It is, to some extent, our conventions that will determine which abstract patterns are important for our purposes of description; but the abstract patterns themselves are all really there independent of the existence of any convention and independently of whether anyone notices them.

It is digital patterns that form the (real, nonconventional) basis for the tokening of symbols in computers. Since individual binary circuits have too few possible states to encode many interesting things such as characters and numbers, it is series of such circuits that are generally employed as units (sometimes called "bytes") and used as symbols and representations. The ASCII convention, for example, maps a set of graphemic characters to the set of seven-digit binary patterns. Integer conventions map binary patterns onto a subset of the integers, usually in a fashion closely related to the representation of those integers in base-2 notation.

Here we clearly have conventions for both markers and signifiers. The marker conventions establish kinds whose physical criterion is a binary pattern. The signifier conventions are of two types (see fig. 7). In cases like that of integer representation, we find what I shall call a representation scheme, which directly associates the marker type (typified by its binary pattern) with an interpretation (say, a number or a boolean value). In the case of ASCII characters, however, marker types typified by binary patterns are not given semantic interpretations. Rather, they encode graphemic characters that are employed in a preexisting language game that has conventions for signification; they no more have meanings individually than do the graphemes they encode. A string of binary digits in a computer is said to "store a sentence" because (a ) it encodes a string of characters (by way of the ASCII convention), and (b ) that string of characters is used in a natural language to express or represent a sentence. I call this kind of convention a coding scheme . Because binary strings in the computer encode characters and characters are used in text, the representations in the computer inherit the (natural-language) semantic and syntactic properties of the text they encode.

It is thus clear that computers can and do store things that are intepretable as markers, signifiers, and counters. On at least some occasions, things in computers are intended and interpreted to be of such types, though this is more likely to happen on the engineer's bench than on the end-user's desktop. It is worth noting, however, that in none of this does the computer's nature as a computer play any role in the story.

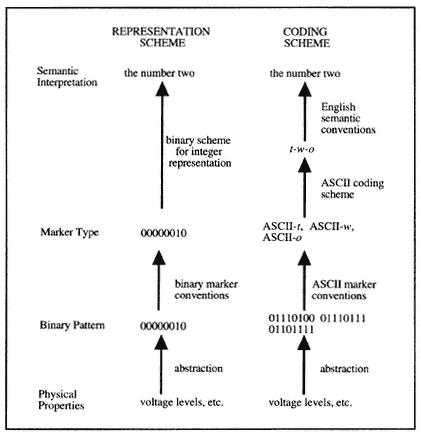
Figure 7

The architecture of the computer plays a role, of course, in determining what kinds of resources are available as storage locations (bistable circuits, disk locations, magnetic cores, etc.). But what makes something in a computer a symbol (i.e., a marker) and what makes it meaningful are precisely the same for symbols in computers as for symbols on paper: namely, the conventions and intentions of symbol users.

Now of course the difference between computers and paper is that computers can do things with the symbols they store and paper cannot. More precisely, computers can produce new symbol strings on the basis of existing ones, and they can do so in ways that are useful for enterprises like reasoning and mathematical calculation. The common story

about this is that computers do so by being sensitive to the syntactic properties of the symbols. But strictly speaking this is false. Syntax, as we have seen and will argue further in the next chapter, involves more than functional description. It involves convention as well. And computers are no more privy to syntactic conventions than to semantic ones. For that matter, computers are not even sensitive to marker conventions. That is, while computers operate upon entities that happen to be symbols, the computer does not relate to them as symbols (i.e., as markers, signifiers, and counters). To do so, it would need to be privy to conventions.

There are really two quite separate descriptions of the computer. On the one hand, there is a functional-causal story; on the other a semiotic story. The art of the programmer is to find a way to make the functionalcausal properties do what you want in transforming the symbols. The more interesting symbolic transformations you can get the functional properties of the computer to do for you, the more money you can make as a computer programmer. So for a computer to be useful, the symbolic features need to line up with the functional-causal properties. But they need not in fact line up, and when they do it is due to an excellence in design and not to any a priori relationship between functional description and semiotics.

5.2.2—
A Rival View Refuted

Now while I think this last point is true, I can hardly pretend that it is uncontroversial . There is a rival view to the one that I have just presented, and this rival view has enjoyed quite a bit of popularity over the years. On this view, there is something about the functional nature of the computer that contributes to, and even explains, the symbolic character of what it operates upon. Due to the prevalence of this alternative theory, I think it is worth presenting it with some care and venturing a diagnosis of what has gone wrong in it.

Some writers claim that computer science has revealed important truths about the nature of symbols. Newell and Simon (1975), for example, claim that computer science has discovered (discovered! ) that 'symbol' is an important natural kind, whose nature has been revealed through research in computer science and artificial intelligence. Their central concern is with what they call the "physical symbol system hypothesis." Newell and Simon describe a "physical symbol system" in the following way:

A physical symbol system consists of a set of entities, called symbols, which are physical patterns that can occur as components of another type of entity called an expression (or symbol structure). . . . Besides these structures, the system also contains a collection of processes that operate on expressions to produce other expressions. . . . A physical symbol system is a machine that produces through time an evolving collection of symbol structures. (Newell and Simon [1975] 1981: 40)

Their general thesis is that "a physical symbol system has the necessary and sufficient means for intelligent action" (ibid., 41). They define a physical symbol system as "an instance of a universal machine" (ibid., 42), but seem to regard this as a purely natural category defined in functional terms, not as a category involving the conventional component involved in markers, signifiers, and counters. Indeed, they claim that computer science has made an empirical discovery to the effect that symbol systems are an important natural kind, defined in physical, functional, and causal terms. It looks as though their "symbols" are supposed to be characterized precisely by "physical patterns" (ibid., 40), although perhaps the functional organization of the system plays some role in their individuation. Their characterizations of how symbols in such systems can "designate" objects and how the system can "interpret" the symbols are also quite peculiar:

Designation . An expression designates an object if, given the expression, the system can either affect the object itself or behave in ways depending on the object.

Interpretation . The system can interpret an expression if the expression designates a process and if, given the expression, the system can carry out the process. (ibid., 40)^[4]

Newell and Simon regard the physical symbol system hypothesis as a "law of qualitative structure," comparable to the cell doctrine in biology, plate tectonics in geology, the germ theory of disease, and the doctrine of atomism (ibid., 38-39).

It is this kind of claim that has aroused the ire of critics such as Sayre (1986), Searle (1990), and Horst (1990), for whom such claims seem to involve gross liberties with the usage of words such as 'symbol' and 'interpretation'. In the eyes of these critics, Newell and Simon have in fact coined a new usage of words such as 'symbol' and 'interpretation' to suit their own purposes—a usage that arguably has a different extension from the ordinary usage and undoubtedly expresses different properties.

In one sense, I think this criticism still holds good. Here, however, I should like to draw a more constructive conclusion. For Newell and Simon are also in a sense correct, even if they might have been more circumspect about their use of language: computer science does indeed deal with an important class of systems, describable in functional terms, that form an empirically interesting domain. Their usage of the expressions 'symbol system' and 'symbol' do pick out important kinds relevant to the description of such systems. And the historical pathway to understanding such systems does in fact turn upon Turing's discussion of machines that do, in a perfectly uncontroversial sense, manipulate symbols (i.e., letters and numerals). But while it has proven convenient within the theory of computation to speak of functionally describable transformations as "symbol manipulations," this involves a subtle shift in the usage of the word 'symbol', and the ordinary notion of symbol is not a natural kind, nor are systems that manipulate symbols per se an empirically interesting class.

In order to illustrate this claim, it will prove convenient to tell a story about the history of the use of the semiotic vocabulary in connection with computers and computation. The story begins with Turing's article "On Computable Numbers" (1936)—the article in which he introduces the notion of a computing machine. The purpose of this article is to provide a general characterization of the class of computable functions, where 'computable' means "susceptible to evaluation by the application of a rote procedure or algorithm." Turing's strategy for doing this is first to describe the operations performed by a "human computer"—namely, a human mathematician implementing an algorithmic procedure (Turing always uses the word 'computer' to refer to a human in this article); second, to develop the notion of a machine that performs "computations" by executing steps described by Turing as being analogous to those performed by the human mathematician; and third, to characterize a general or "universal" machine that can perform any computations that can be performed by such a machine, or by anything that can perform the kinds of operations that are involved in computation.

It is worth looking at a few of the details of Turing's exposition. Turing likens

a man in the process of computing a real number to a machine which is only capable of a finite number of conditions, q₁ , q₂ , . . . , q_R , which will be called "m -configurations". The machine is supplied with a "tape" (the analogue of paper) running through it, and divided into sections (called "squares") each capable of bearing a "symbol". (Turing 1936: 231)

(Note the scare quotes around 'symbol' here. One plausible interpretation is that Turing is employing this word in a technical usage, not necessarily continuous with ordinary and existing usage.)

To continue the description: the machine has a head capable of scanning one square at a time, and is capable of performing operations that move the head one square to the right or left along the tape and that create or erase a symbol in a square. Among machines meeting this description, Turing is concerned only with those for which "at each stage the motion of the machine . . . is completely determined by the configuration" (Turing 1936: 232). The "complete configuration" of the machine, moreover, is described by "the number of the scanned square, the complete sequence of all symbols on the tape, and the m -configuration" (ibid.). Changes between complete configurations are called "moves" of the machine. What the machine will do in any complete configuration can be described by a table specifying each complete configuration (as a combination of m -configuration and symbol scanned) and the resulting "behaviour" of the machine: that is, the operations it performs (e.g., movement from square to square, printing or erasing a symbol) and the resulting m -configuration.

The symbols are of two types. Those of the first type are numerals: 0s and 1s. These are used in printing the binary decimal representations of numbers being computed.^[5] Those of the second type are used to represent m -configurations and operations; for these Turing employs Roman letters, with the semicolon used to indicate breaks between sequences. The symbols are typified by visible patterns,^[6] and are meant to be precisely the letters and numerals actually employed by humans. Indeed, the operations of the computing machine are intended to correspond to those of a human computer (i.e., a human doing computation), whose behavior "at any moment is determined by the symbols which he is observing, and his 'state of mind' at that moment" (Turing 1936: 250). Again, Turing first describes the behavior of a human computer (ibid., 249-251), and then proceeds to describe a machine equivalent of what the computer (i.e., the human) does:

We may now construct a machine to do the work of this [human/SH] computer. To each state of mind of the [human] computer corresponds an "m -configuration" of the machine. The machine scans B squares corresponding to the B squares observed by the [human] computer. (ibid., 251)^[7]

To summarize, Turing's description of a computing machine is offered as a model on which to understand the kind of computation done by

mathematicians, a model on which "a number is computable if its decimal can be written down by a machine" (ibid., 230).

Now there are two things worth noting here. First, if there is a similarity between what the machine does and what a human performing a computation does, this is entirely by design: the operations performed by the machine are envisioned quite explicitly as corresponding to the operations performed by the human computer (though Turing is not careful to say whether "correspondence" here is intended to mean "type identity" or "analogous role"). Second, while this machine is unproblematically susceptible to analysis both (a ) in terms of symbols and (b ) in the functional terms captured by the machine table, it is important to see that the factors that render it susceptible to these two forms of analysis are quite distinct .

On the one hand, it is perfectly correct to say that this machine is susceptible to a functional analysis in the sense of being characterizable in terms of a function (in the mathematical sense) from complete configurations to complete configurations. Indeed, that is what the machine table is all about. What renders the machine appropriate for such an analysis is simply that it behaves in a fashion whose regularities can be described by such a table, and any object whose regularities can be described by such a table is susceptible to the same sort of analysis, whether it deals with decimal numbers or not.

On the other hand, it is perfectly natural to say that Turing's machine operates upon symbols. By stipulation, it operates upon numerals and letters. Numerals and letters are symbols. Therefore it operates upon symbols. Plausibly, this may be construed as a fact quite distinct from the fact that it is functionally describable. Some functionally describable objects (e.g., calculators) operate on numbers and letters, while others (e.g., soda machines) do not. Likewise, some things that operate upon numbers and letters (e.g., calculators) are functionally describable, while others (e.g., erasers) are not (see fig. 8). Moreover, what makes something a numeral or a letter is not what the machine does with it, but the conventions and intentions of the symbol-using community. (Whatever one thinks about the typing of symbols generally, this is surely true for numerals and letters.)

Now how does one get from Turing's article to Newell and Simon's, forty years later? I suspect the process is something like the following. For the purposes of the theory of computation (as opposed to semiotics), the natural division to make is between the semantics of the symbols (say, the fact that one is evaluating a decimal series or an integral) and the formal

Figure 8

techniques employed for manipulating the symbols in the particular algorithmic strategy.^[8] And from this standpoint, it does not matter a whit what we use as symbols—numerals, letters, beads on an abacus, or colored stones. And more to the point, it does not matter for the functional properties of the operations performed by the machine whether it operates on numerals and letters (as Turing's machine was supposed to) or upon equivalent sets of activation patterns across flip-flops or magnetic cores or flux densities on a disk. As far as the theory of computation goes, these can be treated as "notational variants," and from an engineering standpoint, the latter are far faster and easier to use than letters and numerals. And of course these circuit states (or whatever mode of representation one chooses) are at least sometimes "symbols" in the senses of being markers, signifiers, and counters: there are conventions like the ASCII convention and the decimal convention that group n -bit addresses as markers and map them onto a conventional interpretation, and there are straightforward mappings of text files in a computer onto ordinary text.

The occupants of computer memory thus live a kind of double life. On the one hand, they fall into one set of types by virtue of playing a certain kind of role in the operation of the machine—a role defined in functional-causal terms and described by the machine table. On the other hand, they fall into an independent set of types by dint of (possible) subsumption under conventionally based semiotic conventions. Both of these roles are necessary in order for the machine to plausibly be said to be "computing a function"—for example, evaluating a differential equation—but they are separate roles . If we have functional organization

without the semiotics, what the machine does cannot count as being, say, the solution of a differential equation. This is the difference between calculators and soda machines. More radically, however, addresses in computer memory only count as storing markers ("symbols" in the most basic sense) by virtue of how they are interpreted and used. (We could interpret inner states of soda machines as symbols—that is, invoke conventions analogous to the ASCII convention for thus construing them—but why bother?) On the other hand, we also do not get computation if we have semiotics without any functional-causal organization (writing on paper) or the wrong functional-causal organization (a broken calculator).

Now I think that what Newell and Simon have done is this: they have recognized that computer science has uncovered an important domain of objects, objects defined by a particular kind of functional organization that operates on things that correspond to symbols. And because they are interested more in the theory of computation than in semiotics (or the description of natural language), they have taken it that the important usage of the word 'symbol' is to designate things picked out by a certain kind of functional-causal role in systems that are describable by a machine table. What they have not realized is that this usage is critically different from an equally important, but distinct, usage necessary for talking about semiotics. Nor, as Searle and Sayre have noted, do writers who make this move seem adequately sensitive to the dangers of paralogistic argument that emerge from this oversight.