Chemical Processes

During the past decade, volcanic petrologists have made great strides in understanding the complex origins of magma chemistry as revealed by analyses of phenocryst and glassy components of volcanic products. Because these analyses provide abundant quantitative data, mathematical approaches are particularly suited for modeling the origins of chemical signatures.

Magma composition generally evolves with time as a result of (a) initial melting from source rocks, (b) fractional crystallization caused by cooling and the loss of volatile constituents, and (c) comingling with magmas of different composition (Carmichael et al ., 1974). The behavior of chemical species during these three important differentiation processes can be quantitatively modeled by using chemical data provided through bulk and modal analyses in which trace-element behavior is most indicative of the differentiation mechanism (Arth, 1976; Allegre and Minster, 1978).

The Rayleigh equation (Rayleigh, 1896; Gast, 1968; Greenland, 1970) applies to fractional crystallization and predicts the concentration of a particular chemical species remaining in the liquid (c₁ ) after crystallization of a specific fraction of crystalline phase when the original species concentration is c_o :

k_d = the Nernst distribution coefficient, which expresses the fraction of the chemical species in the liquid that enters the crystalline phase. F = the fraction of original melt remaining. For cases in which the chemical species enters two or more phases, k_d is replaced by D_o , the weighted average of solid-liquid partition coefficients of all the phases. If crystallization is incomplete at some value of F, then c₁ given by Eq. (1-7) must be multiplied by k_d or D_o , depending upon the number of phases involved.

For conditions of partial melting, in which the liquid phase remains in equilibrium with the residual solid phases until it is removed (Shaw, 1970), the Berthelot-Nernst equation predicts c₁ by

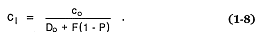
Here P = the bulk partition coefficient for the phases that melt, and F = the fraction of melted material. When only one phase is melted, P = D_o .

Fractional crystallization and partial melting result in a logarithmic relationship between species concentration in the solid/liquid phases and the degree of melting or crystallization. When both fractional crystallization and partial melting occur and D_o approaches zero, Eqs. (1-7) and (1-8) reduce to c₁ = c_o /F. If one assumes that fractional crystallization occurs when there is equilibrium between the total crystallizing solid and melt, its description takes a form analogous to that of partial melting [Eq. (1-8)].

For situations in which chemical trends are the result of mixing two magmas of different compositions, a mass balance equation (Gast, 1968) predicts the resulting concentration in the magma (c_x ) of some species; m_m1 , c₁ , m_m2 , and c₂ are the magma mass and species concentration of magma 1 and magma 2, respectively:

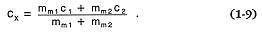
In contrast to fractional crystallization and partial melting, the concentration of a chemical species in a mixed magma is linearly dependent on the degree of mixing.

Isotopic tracers are also very useful for determining the origin and evolution of magmas (Taylor, 1971; Friedman and O'Niel, 1977; DePaolo, 1985). As in the case of stable isotopes such as oxygen, the isotopic composition is related to a standard. For oxygen, the heavy-isotope ¹⁸ O abundance is expressed

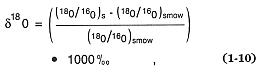
where the subscripts s and smow denote the sample and standard mean ocean water isotopic ratios, respectively. Whereas stable isotopes are considered excellent chemical tracers, radiogenic isotopes are employed in dating techniques and are widely used in geochemistry (Faure, 1977).