V
Navigation and Astronomy in the Voyages

Derek Howse

In this study I shall first deal with the state of navigation at the beginning of the eighteenth century and the state at the end. This period saw many advances in navigation, particularly in the field of finding longitude, advances which, though they were used by explorers of all nations at the end of the eighteenth century, did not become normal practice at sea until the nineteenth. After navigation I shall deal with astronomy—astronomy as practiced by explorers —as well as what was done in meteorology, geomagnetism, tides, and the measurement of gravity.

Navigation: The Early Years

At the beginning of the eighteenth century, navigation was dominated by what the navigators themselves called "the three L's"—the lead , for measuring the depth of water; latitude , which was comparatively easy to find by measuring the sun's height above the horizon or that of the Pole Star;

and lookout , the need for which is self-evident. To these ought, perhaps, to be added one more L and two C's—the log , for measuring the ship's speed through the water; the compass to steer by and to take bearings with; and the chart to show where one has come from and where one is going, as well as the dangers on the way.

The state of the art at that time is conveniently summarized on the title page of John Seller's Practical Navigation of 1669 (Figure 5.1), which shows two navigators of the time with the tools of their trade—a cross staff to find latitude by observations of Polaris; two versions of the back-staff to find latitude by observations of the sun at noon; an azimuth compass for finding magnetic variation, generally by bearings of the sun near sunrise or sunset; a steering compass ; a nocturnal for finding the time by night; a portable universal equinoctial sundial for finding the time by day; a simple wooden quadrant for measuring altitudes; and, of course, a book of charts . There is no lead or log here, but Figure 5.2 shows a navigator of about eighty years later with a Hadley quadrant for latitude—of which more anon—and an English log and a compass at his feet. It shows also his logboard, the second and third columns giving the hourly log reading in knots and fathoms.

We have mentioned finding latitude, time, and magnetic variation, but not, you will notice, finding longitude—be-cause at that time it could not be done at sea. From the time he saw his last land—his departure fix—until he made a landfall, the navigator had to keep track of his progress by "dead reckoning," that is, by making the best estimate of his course and speed made good over the ground, hour by hour, watch by watch, day by day. He would take into account the courses steered by compass, the speeds measured by log, the magnetic variation, the leeway, the currents (tidal and otherwise), and add to these his own experience as to how the ship's course and speed were affected by wind and sea. At noon every day, he would work out his "day's run" from these data, resolve that into its north-south and east-west components, and

Figure 5.1.
Title page of John Seller's Practical Navigation [1669]. The navigator 
on the left is holding a cross staff, the navigator on the right a backstaff,
 with another version on the table beside him. Azimuth compasses
 are on the table left center and center, steering compass right; nocturnal
 hanging left, portable equinoctial sundial hanging right with quadrant
 above; atlas of sea charts (Seller's own English Pilot) on table center 
bottom. (Reproduced courtesy of National Maritime Museum, London.)

Figure 5.2.
A master's mate observing with a Hadley quadrant. On the ground,
 left to right, lead and line, log reel with line leading to log ship, and
 azimuth compass. The log board has the standard headings: 
H[our]; K[nots]; F[athoms]; Course; Wind; Remark[s]. From the title
 page of the manuscript "A book of Drafts and Remarks . . . by 
Archibald Hamilton, late master's mate, of his majesty's ship St Ann. 
1763" (NMM Ms NVP/11). (Reproduced courtesy of the National 
Maritime Museum, London.)

compute his daily noon position in latitude and longitude. If the weather was clear at the critical moment of noon, he could check his dead-reckoning latitude—his "latitude by account"—against his latitude by meridian altitude. But it was not possible to check the longitude in the same way and, as such errors are cumulative, after a long ocean voyage the dead-reckoning longitude might be many hundreds of miles in error, sometimes with disastrous results.

These restrictions imposed a navigating strategy known as "running down the latitude" which can best be explained by taking a real-life example. On 5 November 1681, the buccaneer ship Trinity sailed for the West Indies from southern Chile, missed the entrance of the Strait of Magellan, rounded Cape Horn at a distance of some 250 miles (reaching a latitude of 58°23' south), and sailed up the center of the South Atlantic until the latitude of Barbados (13°10' north) was reached on 18 January 1682. Then she turned west, keeping in the same latitude. Ten days later, an hour before daybreak on the morning of 28 January—nearly three months and 9,000 miles after leaving Chile—they sighted the island of Barbados on the port bow at a distance of two and a half leagues.^[1] A quite remarkable feat of navigation which proved that the strategy really worked!

The Longitude

The theory of finding longitude astronomically has been well known since classical times. This concept is inexorably bound up with the rotation of the earth on its axis—one complete revolution (360 degrees) in a day, 15 degrees in an hour. To find the difference of longitude between the meridian of the place you are and some reference or "prime meridian"—shall we call that Greenwich from now on, though it was not so used until the 1770s?—all you need to know is your own local time (which could be symbolized by a sundial) and the local time on the prime meridian at that very same moment (which could be symbolized

Figure 5.3.
How the angular distance from sun to moon changes in six hours. Quantities 
are for 1 October 1772 (rounded off) from the Nautical Almanac table reproduced
 in Figure 5.6.

by a chronometer showing Greenwich time). The difference between these two times—say one hour or 15 degrees—is the difference of longitude.

This sounds easy. Certainly finding one's own local time astronomically is not difficult, though something a bit more refined than a sundial is needed. The difficult part is knowing Greenwich time at that same instant. The simplest method is for the ship to have some kind of timekeeper which always keeps Greenwich time—that was in fact the ultimate solution, as we shall see—but producing such a machine, capable of keeping accurate time for months, even years, in every climate and in a ship which rolls, heaves, and pitches, was no easy task.

In the seventeenth and early eighteenth centuries, the astronomical longitude-finding method which seemed to have the most promise depended upon the fact that the moon moves comparatively fast against the background of the stars—approximately its own diameter (1 degree) in one hour (Figure 5.3). Think of the moon as the hand of a clock and the sun and stars as time markers on the clock dial. Johann Werner had suggested as long ago as 1514 that angular distances between the moon and these time markers—the sun and the brighter stars in the zodiac—could be used to give Greenwich time. But this would only

be useful if these lunar distances, as they came to be called, could be predicted accurately several months—even years—ahead, so that the navigator could have them before he started his voyage.

The snag was that the going of that moon clock is highly irregular and, in the seventeenth century, neither the laws governing the moon's apparent motion nor the relative positions of the star time markers one with another were known to the required accuracy. It was to provide these very data that Charles II specifically founded his Royal Observatory at Greenwich in 1675, directing his 27-year-old royal astronomer John Flamsteed "forthwith to apply himself with the most exact care and diligence to the rectifying the tables of the motions of the heavens, and the places of the fixed stars, so as to find the so-much-desired longitude of places for perfecting the art of navigation."^[2]

After forty years' labor, Flamsteed's star catalog was published posthumously in 1725, providing one ingredient of the lunar-distance package at sea—a frame of reference against which to measure the moon's position (in King Charles's words, "the places of the fixed stars"). The second ingredient, the king's "rectifying the tables of the motions of the heavens," was not yet complete though well on the way. There was a third ingredient—an angle-measuring instrument of the required accuracy—but that was not available either.

It is worth noting that Edmond Halley—who was to continue Flamsteed's work at Greenwich—made two Atlantic voyages in a naval vessel called the Paramore between 1698 and 1700 "to improve the knowledge of the Longitude and variations of the Compass."^[3] These are said to be the first sea voyages undertaken with a purely scientific object.

The Longitude Act, 1714

In 1707, Admiral Sir Clowdisley Shovel, with twenty-one ships of the Royal Navy, was returning from Gibraltar to England. On 22 October, having had observations for lati-

tude the previous day—here is one of the L's—and satisfied by soundings—here is the lead, another L—that they were at the mouth of the English Channel and clear of all danger, the fleet ran to the eastward in thick weather. At 7:30 that evening, five ships struck the rocks of the Gilstone Ledges in the Scilly Isles. This disaster—four ships were lost with nearly two thousand men—was a profound shock to the British public. And there had been several other maritime disasters recently, though none of the same magnitude.

In fact, the Shovel disaster was caused as much by bad charts as by bad navigation. Even if there had been a method of finding longitude, the shipwrecks would probably still have occurred. Nevertheless, the disaster's very magnitude made such an impression on the British public that they became more than ever receptive to any measure which might make navigation safer—and in the 1710s, "discovering the longitude" seemed to hold the key.

In 1714, a book called A New Method of Discovering the Longitude both at Sea and Land was published. In it the mathematicians William Whiston and Humphrey Ditton made a proposal that vessels should be moored in known positions at intervals along the trade routes, each fitted with a mortar which would, every midnight by Peak of Tenerife time, fire a projectile vertically which would burst at precisely 6,440 feet. Though the subject of great mirth among members of Swift and Pope's Scriblerus Club, this proposal was nevertheless taken seriously by some people and Whiston and Ditton presented a petition to Parliament asking for a reward. This was followed a month later by another petition, this time by sea captains and merchants, asking Parliament to give serious attention to the longitude problem.

Taking only a month to pass through all its parliamentary stages, "An Act for Providing a Publick Reward for such Persons or Persons as shall Discover the Longitude at Sea" was given the Royal Assent by Queen Anne on 20 July 1714, only twelve days before her death. Rewards of unprecedented magnitude were offered: £10,000 to the

discoverer of a method which determined the longitude to 60 geographical miles (96 kilometers), £15,000 if accurate to 40 miles (64 kilometers), £20,000 if accurate to 30 miles (48 kilometers). The method had to be proved to be "practicable and useful at sea" on a voyage to the West Indies. Commissioners—later to be called the Board of Longitude-were appointed to administer these provisions. The Astronomer Royal was ex officio a member of the board. The provisions were to apply to all who qualified, regardless of nationality.

Twenty thousand pounds of the 1720s is probably equivalent to a million pounds or more today—a prize indeed, which was to stimulate many advances in astronomy, navigation, mathematics, and horology over the next hundred years, just as Parliament hoped. The immediate effect was the publication of a welter of pamphlets by hopeful inventors, none of whom was successful and many of whom were cranks. Indeed, "finding the longitude," coupled with "squaring the circle" (for which the board received many suggestions quite unconnected with longitude), passed into the English language as expressing something which, if not downright impossible, was at least extremely difficult to achieve.

The Invention of the Reflecting Quadrant

The next development was a fundamental one, though not stimulated directly by the Longitude Act. This was the invention of the double-reflection quadrant which, when developed into the sextant twenty-five years later, was to make possible the measurement of lunar distances to the required precision at sea. (With a quadrant measuring to 90 degrees, lunar observations with the sun are possible only on eight days each lunar month; with a sextant measuring to 120 degrees, sun-moon observations are possible on fifteen or sixteen days out of the twenty-nine each

month.) Surprisingly, in 1731 the basic idea came to two people quite independently on either side of the Atlantic: In England, the inventor was John Hadley, vice-president of the Royal Society; in America, it was Thomas Godfrey, glazier, self-taught astronomer, and friend of Benjamin Franklin, from Philadelphia. The Royal Society investigated the claims of both parties and came to the conclusion that this was indeed a near-simultaneous invention by both Hadley and Godfrey. Nevertheless, to many generations of seamen the instrument came to be known as Hadley's quadrant—or just plain "Hadley." Poor Godfrey!

The Nautical Almanac

Two of the three ingredients of the lunar-distance solution were now available to the required accuracy: Flamsteed had provided the star catalog, Hadley and Godfrey the measuring instrument. All that the navigator now needed were predictions of the moon's position in lunar-distance form. This required an accurate knowledge of the laws governing the moon's motion and, throughout the early eighteenth century, the world's best mathematicians turned their minds to the problem, using observational data provided by the world's best astronomers—men such as Newton, Halley, Lemonnier, Bradley, Cassini de Thury, D'Alembert, and Clairaut.

The person who finally produced lunar tables of the required accuracy was the German astronomer Tobias Mayer, using equations produced by the Swiss mathematician Leonhard Euler. Both men subsequently received awards, though not of the highest amounts. In 1755, the Astronomer Royal James Bradley compared Mayer's tables with his own observations at Greenwich and found them sufficiently accurate to determine the moon's place to 75 arc-seconds and consequently the longitude to about half a degree. Due to the constraints imposed by the Seven Years' War, the sea trials carried out by Captain Campbell in

1757-1758 were inconclusive so far as the tables were concerned, though they did lead to the invention of the nautical sextant we know today.

It was not until 1761 that Mayer's tables were properly tested at sea—by Nevil Maskelyne, the future Astronomer Royal, on voyages to and from Saint Helena where the Royal Society had sent him to observe the transit of Venus that year. He took some very successful lunar-distance observations, generally to a positional accuracy of better than one degree. Immediately after his return, he published his British Mariner's Guide , explaining lunar-distance observations to seamen in simple terms, using a method devised by the French astronomer Abbé Nicolas-Louis Lacaille. In his voyage to Barbados in 1763 to try out Harrison's watch (of which more anon), Maskelyne once again proved the worth of Mayer's tables.

In January 1765, only a month or so after returning from Barbados, Maskelyne was appointed Astronomer Royal at the age of thirty-three. His first act was to persuade the Board of Longitude that a nautical ephemeris must be published soon. Planned and executed by Maskelyne with characteristic energy, The Nautical Almanac and Astronomical Ephemeris for the Year 1767 was published in November 1766 and this remarkable publication has continued annually until the present day.

Any navigator using Maskelyne's nautical almanac to find longitude—and a very high proportion of deep-sea navigators of all nations did so—must end up with an answer based on the meridian of Greenwich. Indeed, from 1774 to 1788 this applied even to those using the official French almanac Connaissance des temps where, with Maskelyne's agreement and assistance, the British lunar-distance tables were reprinted verbatim—but with a note that the idea had come from a Frenchman, Lacaille. The other tables in the French almanac were based on the meridian of Paris.

The navigator, having obtained a Greenwich-based longitude, needed to plot his position on a chart. So map and

chart publishers the world over began to provide longitude graduations based on the meridian of Greenwich. When in 1884, at the International Meridian Conference in Washington, D.C., the need came to agree internationally upon a prime meridian for longitude and time, it was Greenwich that was chosen—rather than, say, Paris—be-cause by that time nearly three-quarters of all the world's shipping tonnage was using charts based on Greenwich. And this chain of events started in 1766 with Maskelyne's first Nautical Almanac .

The Marine Chronometer

The ultimate solution of the longitude problem (before the electronic age, that is) proved not to be lunar observations but the marine chronometer. Providing its error is known or can be estimated, this device will provide Greenwich time with no computation. All that one then requires in order to discover the longitude is an altitude observation of the sun or a star at least two hours before or after meridian passage in order to find local time. The difference between the local time just found and Greenwich time indicated by the chronometer (corrected for its known or estimated error) then gives the longitude—the whole operation is known as "longitude by chronometer."

As this volume is primarily about exploration, I shall not recount the long story of how the highest award was made—eventually—to John Harrison for his fourth timekeeper, a large silver watch. Suffice it to say that it was on Cook's second voyage (1772-1775) that it was eventually proved that a longitude timekeeper was a practical possibility. In Cook's two ships were four longitude watches—Larcum Kendall's copy of the prizewinner, made to the Board of Longitude's order in case the latter's success had been a fluke, and three submitted by John Arnold.^[4] Near the end of his three-year voyage, Cook wrote to the Secretary of the Admiralty as follows: "Mr Kendals Watch has

Figure 5.4.
Performance of timekeepers on Cook's second voyage. The rectangles
 represent the periods when the rates of the timekeepers were checked
 ashore, the width indicating the number of days' readings, the height
 the range of values obtained. The curve is drawn through the mean
 of the rates found at each place. The temperatures are the mean of 
those recorded.

exceeded the expectations of its most zealous Advocate and by being now and then corrected by lunar observations [Cook had the new nautical almanac] has been our faithfull guide through all the vicissitudes of climates."^[5] Its performance can be judged from the graphs in Figures 5.4 and 5.5, which show its rate of going on every occasion the astronomers landed their instruments during Cook's second and third voyages.

Explorers' Observations at Sea

Let us now leave the general history of navigation and consider some examples specifically connected with exploration. The importance of Captain Cook's three voyages in

Figure 5.5.
Performance of timekeepers on Cook's third voyage.

the history of science was largely the result of scientific bodies such as the Royal Society and the Board of Longitude being allowed to take an active part in the planning, execution, and analysis of the voyages, giving a model on which to base the scientific organization of so many future voyages, both British and foreign. These were the first British voyages to carry trained astronomers, naturalists, and artists to observe and record what they saw. The astronomers were provided with the best instruments that money could buy, many of which, being public property, were used again in subsequent voyages by Vancouver, Flinders, and others. A few still survive.

The scientific results of these voyages were published by the Board of Longitude, and it is from these that I shall take most of my examples.^[6] Let us first look at the observations made at sea. Every day at noon, weather permitting, meridian altitudes of the sun would be observed with the sextant to find latitude. We know that in Cook's ships several officers would do this together, both as training for the officers and to increase precision. A similar ritual has survived in many ships to modern times. Among the secondary aims of Cook's last two voyages was to try out the newfangled longitude timekeepers. At sea, a longitude-by-watch observation would be taken morning and afternoon if there were no clouds.

Now let us turn to lunar-distance observations—or "lunars" as they were familiarly called. One of the most practical features of the new almanac was a table giving predicted lunar distances from the sun and zodiacal stars every three hours throughout the year, a feature suggested by Lacaille to cut down the arithmetical work done by navigators (Figure 5.6). And so it proved: the time taken to work out a sight and obtain a longitude was cut from over four hours to an hour or so.

Now to the navigator's procedure. Essentially he needed to measure the angular distance between the moon and (in the case of Figure 5.7) a star. But it is also necessary to

Figure 5.6.
Lunar-distance tables from The Nautical Almanac and Astronomical 
Ephemeris for the year 1772. Published by order of the Commissioners
 of Longitude (London, 1770). The quantities in Figure 5.3 come from
 this table. (Reproduced courtesy of the National Maritime Museum, London.)

Figure 5.7.
Lunar-distance observations showing the three near-simultaneous
 observations required to find longitude by lunar distance: (1) the 
angular distance between the moon and a selected star (or the sun); 
(2) the altitude of the moon above the horizon; and (3) the altitude 
of the star or sun above the horizon.

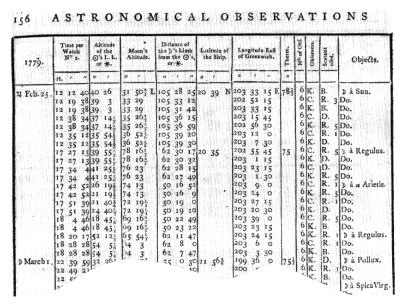
Figure 5.8.
Lunar-distance observations taken on board the Resolution off the 
Hawaiian Islands a week or so after the death of Cook. The penultimate
 columns indicate the observers (C = Clerke, who took command of the 
Resolution after Cook's death; K = Lieutenant James King, who ultimately
 took command of the expedition after Clerke's death some months later)
 and the sextants used (the makers being B = John Bird, D = Peter Dollond,
 R = Jesse Ramsden). From the published astronomical observations,
 Cooke, King, and Bayly, Original Astronomical Observations,
 p. 156. (Reproduced courtesy of the Bancroft Library.)

measure the altitudes of the two bodies as nearly simultaneously as possible in order to correct for parallax and refraction. The lunar distances predicted in the almanac assume the observer is at the center of the earth. In fact the observer is some feet above the earth's surface, and, furthermore, both bodies appear too high because of atmospheric refraction, the amounts depending upon their respective altitudes—the lower the altitude, the more the refraction. Both these effects had to be allowed for; indeed, "clearing the distance," as it was called, was the most

Figure 5.9.
Meteorological observations in the Discovery. Cook was murdered 
on 14 February 1779. From Cooke, King, and Bayly, Original Astronomical 
Observations, p. 332. (Reproduced courtesy of the Bancroft Library.)

laborious part of the whole computation.^[7] If the sun or star was more than two hours from the meridian, then the altitude found at the same time as the lunar distance could be used to obtain local time—our symbolic sundial time. Otherwise, it was necessary to wait for the body to be on a suitable bearing, the time difference from the lunar observation being noted from a watch with a second hand. Figure 5.8 shows the results of a series of lunar observations on Cook's third voyage.

Other observations taken at sea included those for magnetic variation with an azimuth compass; meteorological observations with barometers and thermometers (Figure 5.9)—a primitive form of anemometer or wind gauge was taken but was not a great success; and the salinity of seawater with water sampler bottles and a hydrostatic balance (Figure 5.10).

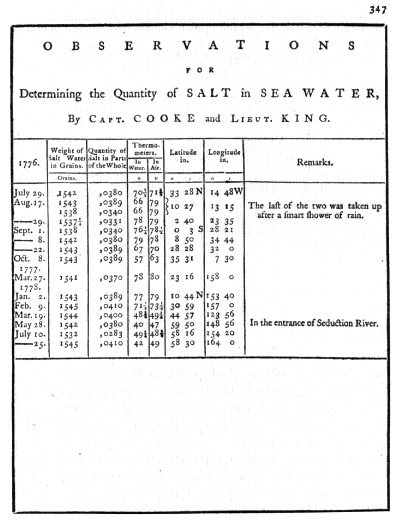
Figure 5.10.
Salinity observations on board the Resolution. Those
 in 1776 were made in the Atlantic when on passage from
 Plymouth to the Cape of Good Hope, that in 1777 in the South
 Pacific, those in 1778 in the North Pacific. From Cooke, King,
 and Bayly, Original Astronomical Observations, p. 347. (Reproduced
 courtesy of the Bancroft Library.)

Figure 5.11.
Diagram of the transit of Venus.

Observations Ashore

Now let us see what was done ashore in the physical sciences. Overtly at least, the prime purpose of Cook's first voyage was itself astronomical—participation in that vast international project, the observation of the transit of Venus on 3 June 1769, when astronomers from eight different nations traveled all over the globe, an operation as important and complex in the eighteenth century as was the International Geophysical Year in the twentieth.

Twice every 113 years, Venus passes directly between the earth and the sun and appears for a few hours silhouetted against the bright solar disk. Edmond Halley, of comet fame, pointed out in 1716 that observing such a transit could provide a method of measuring one of the fundamental units of astronomy, the distance of the earth from the sun.^[8] As shown in Figure 5.11, an observer at A in the Northern Hemisphere would see Venus crossing the sun along track a to a '. An observer at B in the Southern Hemisphere would see Venus crossing the sun along track b to b '. If the angular distance PQ can be found, this will give a measure of the sun's distance, provided the geographical positions of A and B are accurately known.

Though Halley knew that he himself would not live to see the next pair of transits (in 1761 and 1769), he urged that every advantage should be taken of these opportunities and that observations should be planned for as many

different places as possible in order to mitigate against the effects of bad weather at any one place:

Therefore, I strongly urge diligent searchers of the Heavens (for whom, when I shall have ended my days, these sights are being kept in store) to bear in mind this injunction of mine and to apply themselves actively and with all their might to making the necessary observations. And I wish them luck and pray above all that they are not robbed of the hoped-for spectacle by the untimely gloom of a cloudy sky; but that at last they may gain undying glory and fame by confining the dimensions of the celestial orbits within the narrower limits.^[9]

Halley's pleas did not fall on deaf ears. Many scientific expeditions were dispatched to remote parts of the world for the transits of 1761 and 1769, particularly by the British and French. Thus it was that, in 1768, Cook sailed on his first voyage to the South Sea as one of three British transit-of-Venus expeditions—the other two went to the North Cape of Norway (William Bayly and Jeremiah Dixon) and to Hudson's Bay, Canada (William Wales). In addition, the Royal Society sent Charles Mason to Northern Ireland and the Board of Longitude sent John Bradley to the Lizard in Cornwall, while the transit was observed in all European observatories (and a few in North America) where the sky was clear, including Greenwich. All were supplied with the same type of instruments, wherever possible by the same makers.

For the transit, Cook and his astronomer Charles Green set up an observatory on Point Venus at Matavai Bay on the north coast of Tahiti. The transit itself was observed—the thermometer was showing 119°F at the time—with a two-foot Gregorian reflecting telescope by James Short fitted with a micrometer for measuring small angles within the field of the telescope.

The local times of the various events during the observation—the first and last contacts of Venus with the sun's disk, for example—had to be known to the greatest possible accuracy, and all expeditions were supplied with astronomical regulator clocks by John Shelton. The clock

used by Cook in Tahiti had been used by Maskelyne in the 1761 transit of Venus in Saint Helena, had been to Barbados with him for the trials of the Harrison watch in 1763-1764, and had gone to Pennsylvania for determining the Mason-Dixon line in 1765-1767. After Cook returned, the same clock was used again by Maskelyne for his experiment for "weighing the earth" in Scotland in 1774; it went to New South Wales with Sir Thomas Brisbane in 1822-1823, to South Shields for pendulum experiments in 1854, to the top of Ben Nevis in Scotland in 1888-1904; today it is in the Royal Scottish Museum in Edinburgh. Other Shelton clocks went on Cook's last two voyages, to the Arctic with Parry and others (1818-1825), to the Antarctic with James Clark Ross (1839-1842), and to India for the Trigonometrical Survey (1865-1873); one went to its second transit of Venus with the U.S. expedition to New Zealand in 1882.^[10]

The going of the clock (and of the watches on the second and third voyages) had to be checked every clear day by equal altitude observations of the sun morning and afternoon, the mean of which gave the moment of noon. This was done with an astronomical quadrant of one foot radius by John Bird. This—and I quote Cook's own words—"stood upon the head of a large cask fixed firm in the ground, and well filled with wet heavy sand" (Figure 5.12).^[11]

The last requirement for the transit itself was an accurate geographical position. For latitude, the same astronomical quadrant was used to measure meridian zenith distances of the sun and stars. For longitude, lunar distances were observed with a Hadley sextant, using altitudes measured with the astronomical quadrant. And all these instruments had to be protected from the elements and the natives by one or more wood-and-canvas tent observatories and day-and-night sentries.

Cook and his astronomers used these same instruments to make other observations ashore on all the voyages, the precise times of which, when compared with the times of

Figure 5.12.
An astronomical quadrant in use (1777). The astronomer William 
Bayly can be seen taking an observation of the sun with his 
quadrant, which is placed on a cask filled with wet sand. Detail from 
a view at Anamooka, Friendly Islands, engraved by W. Byrne after
 John Webber. (Reproduced courtesy of the National Maritime
 Museum, London.)

those same phenomena at Greenwich, gave longitude determinations. These were observations of the eclipses of Jupiter's satellites, of solar and lunar eclipses, of occultations of stars passing behind the moon, and of the transit of Mercury—none of which occur very often but the Greenwich times of which were predicted in the almanac. And, of course, there might be comets; although they could not be predicted, the measurement of their position was important to astronomy.

Finally, Cook and his officers made many nonastronomical observations ashore. First there were the meteorological and magnetic observations as at sea but with the addition of observations for magnetic dip with a dip circle. Incidentally, it is an early example of international scientific cooperation that, in 1785 in an interval between wars, the British Board of Longitude lent two of the dip circles used on Cook's third voyage to La Pérouse. (These were never seen again.) Then there were the observations of the tides—how long before or after the moon crossed the meridian did high water occur, what was the magnitude of the rise and fall, and how did that magnitude vary between spring and neap tides? From the amount of clock gained or lost at Tahiti compared with its performance at Greenwich, Maskelyne found that the force of gravity at Tahiti was 99.7 percent of its amount at Greenwich. Incidentally, it was principally these ongoing gravity measurements which caused these transit-of-Venus clocks to travel the world so extensively during the next hundred years or so, all with the object of determining precisely the "figure of the earth"—the amount it is flattened at the poles.^[12]

Conclusion

I have used Cook's voyages to provide my examples largely because they are the best documented. But other explorers, British, French, and Spanish, used the same methods and instruments. Charles Darwin said of Cook's surveying and mapping that "he added a hemisphere to the civilized world." No less important was the wealth of other scientific data and specimens—on a scale never before equaled, particularly in natural history—that he and his shipmates brought back. The careful planning, execution, and subsequent publication of this vast volume of data did an enormous amount for the advancement of science generally and was as important in its own way as were the geographical discoveries.