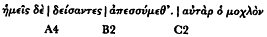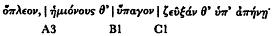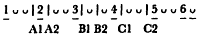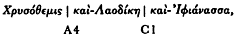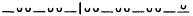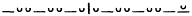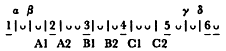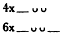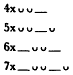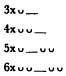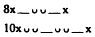The Homeric Hexameter
Outer Metric
Let us turn first to a consideration of what O'Neill (1942) has conveniently designated the "outer metric," that is, the foot-based or podic structure of
[33] The emphasis is Nagy's own—see 1974, 140-49; 1976, 251-57.
[34] A second perspective on the diachronic process should also be briefly mentioned. If Nagy's formulation is correct, and if we someday have enough hard proof of the earliest stage in the process to deem a significant part of Homeric formulaic diction pre- or proto-metrical, then we will still have to deal with the metrical dimension of formulas. For in this case the metrical aspect will become even more important to an understanding of traditional structure than it is now: the foregrounding of certain patterns as proto-metrical will indicate, at least crudely, the relative age of various elements in the diction and the calibration of the hexameter over time. Compare the linguistic archaeology practiced by Hoekstra (1964) and Janko (1982).
the hexameter.[35] After this standard description, we shall address the more complex questions involved with the "inner metric," the internal structure of the line.
The hexameter may be schematized as follows:
 | |
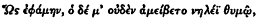 | (Od. 9.287) |
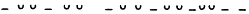 | |
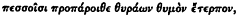 | (Od. 1.107) |
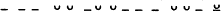 | |
According to conventional notation, the line is here shown to be composed of six "feet," or metra, numbered 1 through 6. Each of the first five metra may be eider dactylic (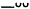 ) or spondaic (
) or spondaic (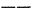 ), although a spondee in position 5 is rare. The sixth metron is always disyllabic, its second element being regarded as long by position if not by nature (brevis in logo ). The last two metra, the fifth almost always dactylic and the sixth disyllabic and spondaic by necessity, thus sound the closing cadence to the line, a cadence that, as explained above, some metrists have found echoed in other Indo-European meters. From this perspective the hexameter is a so-called quantitative meter, depending for its shape on the distribution of relatively long and short syllables over six podic units. In this seine it is not primarily stress-emphasis but rather phonologically determined quantity that yields the metron structure of the hexameter.[36]
), although a spondee in position 5 is rare. The sixth metron is always disyllabic, its second element being regarded as long by position if not by nature (brevis in logo ). The last two metra, the fifth almost always dactylic and the sixth disyllabic and spondaic by necessity, thus sound the closing cadence to the line, a cadence that, as explained above, some metrists have found echoed in other Indo-European meters. From this perspective the hexameter is a so-called quantitative meter, depending for its shape on the distribution of relatively long and short syllables over six podic units. In this seine it is not primarily stress-emphasis but rather phonologically determined quantity that yields the metron structure of the hexameter.[36]
[35] For a survey of modern metricians to 1905, see Porter 1951, 3-8; on colometry per se, see Barnes 1987.
Quantities are distributed in a number of ways, the variability represented by the thirty-two possible types arising (from the point of view of outer metric only) from dactylic-spondaic substitution in the five substitutable metra:[37]
(1) Wholly dactylic | 1 | D D D D D | |
(2) Wholly spondaic | 1 | S S S S S | |
(3) 4D, 1S | 5 | S D D D D | |
D S D D D | |||
D D S D D | |||
D D D S D | |||
D D D D S | |||
(4) 1D, 4S | 5 | D S S S S | |
S DS S S | |||
S S DS S | |||
S S S DS | |||
S S S S U | |||
(5) 3D, 2S | 10 | D D D S S | S D D S D |
D D S D S | S D S D D | ||
D S D D S | D S D S D | ||
S D D D S | D S S D D | ||
S S D D D | D D S S D | ||
(6) 2D, 3S | 10 | S S S D D | D S S D S |
S S D S D | D S D S S | ||
S D S S D | S D S D S | ||
D S S S D | S D D S S | ||
D D S S S | S S D D S | ||
Total = 32 types | |||
Theoretically, then, the number of syllables in a Homeric line can vary from twelve (wholly spondaic) to seventeen (five dactyls plus the brevis in longo or "final anceps"). Table 3 documents the syllabic distribution in the nearly twenty-eight thousand lines of the Iliad and Odyssey .[38] As these figures make evident, while all six possible syllabic categories are occupied,[39] the great majority of lines are either fifteen or sixteen syllables in length (over 72 percent for both poems)—that is, almost three-quarters of the Iliad and Odyssey is composed of lines consisting of either three or four dactyls and, correspondingly, either three or two spondees, counting metron 6 as spondaic. This favored con-
[37] As noted above, the sixth and final metron is invariably disyllabic, with the last syllable understood as long by convention.
[38] I derive statistics on outer metric from LaRoche 1898 and from Jones and Gray 1972.
[39] Examples of all six possible patterns exist, but the only statistically important types are those with two to five dactyls, or fourteen to seventeen syllables.
TABLE 3. | ||||||
No. of dactyls/ | 5/17 | 4/16 | 3/15 | 2/14 | 1/13 | 0/12 |
Iliad | ||||||
Number | 3,011 | 6,680 | 4,661 | 1,248 | 91 | 2 |
Percent | 19.2 | 42.6 | 29.7 | 8.0 | 0.6 | negl. |
Odyssey | ||||||
Number | 2,255 | 4,918 | 3,860 | 1,011 | 62 | 4 |
Percent | 18.6 | 40.6 | 31.9 | 8.3 | 0.5 | negl. |
figuration is quantitatively the longum-breve rhythm of the hexameter, an illustration of what I call the "syllabicity" of the line. From this point of view, the hexameter, while not absolutely syllabic (as are for example many Latin and Romance meters), demonstrates a relatively focused syllabicity, taking a fifteen-or sixteen-syllable shape 72 percent of the time. If we add in the wholly dactylic seventeen-syllable possibility, the total comes to over 91 percent and the syllabic focus becomes even more apparent.
This statistical profile may be more finely articulated by determining how the dactyls are distributed. In other words, in those hexameter combinations of dactyls and spondees which can take more than a single form, we may profitably inquire about the absolute position of each metron-type. Within the fourteen-, fifteen-, and sixteen-syllable lines, the placement of metra is as shown in table 4.[40] Avoidance of the fifth-metron spondee—very probably the tradition's effort to preserve the Indo-European closing rhythm and, synchronically, the line-ending cadence for the hexameter—may be seen at the root of many of these statistical phenomena. In the sixteen-syllable line, for example, the spondee is conspicuously unusual in metron 5, and this pattern continues through the fifteen- and fourteen-syllable lines. The chart of metron configurations in the hexameter above also shows the spondee to be relatively rare in metron 3, the predominant locus of the mid-line break; again the pattern extends through the shorter lines. Exactly what the significance might be of the third and fifth metrons' strong tendency toward dactylic shape will be developed in the section below on inner metric. For the moment, let us simply notice that this tendency occurs at points of structural closure, marking half- and whole-line segmentation.
[40] On the comparison of the Iliad and the Odyssey , Jones and Gray (1972, 208) remark: "As far, then, as the outer metric is concerned the similarities far outweigh the differences." The Iliadic Catalog of Ships, filled with proper names and other spondaic forms, is apparently an exception to this general rule; see Rudberg 1972, 20-21.
TABLE 4. | ||||||||||
Sixteen Syllables | ||||||||||
Spondee in metron | Number | Percent | ||||||||
1 | 3,669 | 31.6 | ||||||||
2 | 4,116 | 35.5 | ||||||||
3 | 1,154 | 9.9 | ||||||||
4 | 2,374 | 20.5 | ||||||||
5 | 285 | 2.5 | ||||||||
Fifteen Syllables (descending order of frequency) | ||||||||||
Spondees in metra | Number | Percent | ||||||||
1 + 2 | 2,256 | 26.9 | ||||||||
2 + 4 | 1,795 | 21.1 | ||||||||
1 + 4 | 1,756 | 20.7 | ||||||||
(other categories less populated) | ||||||||||
Fourteen Syllables (descending order of frequency) | ||||||||||
Dactyls in metra | Number | Percent | ||||||||
3 + 5 | 1,061 | 46.5 | ||||||||
4 + 5 | 369 | 16.2 | ||||||||
1 + 5 | 230 | 10.1 | ||||||||
TABLE 5. | ||||||||||
Pattern | Iliad | Odyssey | ||||||||
Number | Percent | Number | Percent | |||||||
D | D | D | D | D | S | 3,034 | 19.3 | 2,256 | 18.6 | |
D | S | D | D | D | S | 2,292 | 14.6 | 1,820 | 15.0 | |
S | D | D | D | D | S | 2,207 | 14.1 | 1,457 | 12.0 | |
D | D | D | S | D | S | 1,346 | 8.6 | 1,023 | 8.4 | |
S | S | D | D | D | S | 1,261 | 8.0 | 996 | 8.2 | |
D | S | D | S | D | S | 968 | 6.2 | 829 | 6.8 | |
S | D | D | S | D | S | 967 | 6.2 | 791 | 6.5 | |
D | D | S | D | D | S | 648 | 4.1 | 503 | 4.2 | |
S | S | D | S | D | S | 584 | 3.7 | 478 | 3.9 | |
D | S | S | D | D | S | 461 | 2.9 | 457 | 3.8 | |
Another perspective on the dactylic-spondaic texture of the hexameter may be gained by noting the frequency of occurrence of various metron configurations. Table 5 documents the ten most common patterns. It is worthy of mention that these configurations, the ten most frequently occurring of the
thirty-two possibilities, account for a full 87 to 88 percent of the Iliad and Odyssey . In fact, the first three alone make up almost half of all lines in the two epics.
These observations on the podic rhythm of the metra provide an initial characterization of structure in the hexameter. It is clear even from these few remarks that the line is not merely a six-part symmetrical unit that repeats over and over again; it should be equally evident that conceiving of a simplistic verse form cannot help but obscure any conceptions of formulaic structure based on it. The possibilities inherent in the hexameter are many, and all are at one time or another realized; from a statistical standpoint, however, relatively few of these multiple possibilities account for most of the actual lines in the Homeric corpus. Speaking generally and from the perspective of outer metric only, we can make the following points about the hexameter: (1) over 90 percent of all lines arc composed of between fifteen and seventeen syllables, over 70 percent of either fifteen or sixteen syllables; (2) spondaic substitution is common in metra 1, 2, and (somewhat less frequently) 4, but much rarer in metron 3 and positively avoided in metron 5; (3) the line ends typically with a "quantitative close," consisting of a dactylic fifth metron and the spondaic anceps. A preliminary view of the hexameter must, in short, emphasize its focused syllabicity and tendency toward certain patterns of dactylic-spondaic alternation. These patterns, with the exception of metron 6, favor spondaic substitution in the opening rather than the closure of half-lines or hemistichs. This tendency is an aspect of right justification, in this case of dactylic feet within half-lines. As we move on to a discussion of inner metric, we would do well to bear in mind these features of the hexameter's outer metric: focused syllabicity, favored patterns of dactylic-spondaic substitution, and right justification.
Inner Metric
In this section I shall treat the internal structure of the line, for it is the rhythm of the inner versus the outer metric that gives the hexameter its characteristic texture. Indeed, as Milman Parry discovered, the internal structure is that dimension of the line which bounds or encapsulates the formula and which constitutes the "same metrical conditions" that Parry cited as a necessary condition for formulaic diction.
The first step in this description is to identify the three principal caesuras,[41] or prosodic breaks, in the hexameter. The diagram below, showing the inner metric of the hexameter, indicates these breaks in terms of multiples of three basic positions, A (1-4), B (1 and 2, the masculine [or penthemimeral] and feminine [or trochaic] caesuras), and C (1 and 2, the hepthemimeral caesura and bucolic diaeresis).
[41] The term caesura is employed here in a strictly metrical sense without any implication of a pause between elements. On ancient theories of the metrical caesura, see esp. Bassett 1919.
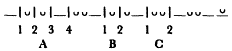
| (Od. 9.396) |
| (Od. 6.73) |
I take this diagram and the theory it summarizes from Hermann Fränkel's "Der homerische und der kallimachische Hexameter,"[42] in which the author goes on to posit cola , those sections of the line delimited by the caesura system, as the basic constituents of the hexameter. He concentrates not on word-breaks per se, that is, but rather on the material that they enclose—the colon-words in the line.[43]
As one might expect, total agreement does not exist among all scholars about the location or meaning of caesura boundaries. Howard Porter (1951) would limit the A break to Fränkel's A3 and A4 and move the C1 to a position after the opening longum of the fifth metron:
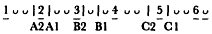
While this formulation reduces the number of caesuras from eight to a seemingly more workable six, it sacrifices: a full coverage of colon-types, especially in respect to the A and C boundaries; in the case of Porter's reassignment of C1, concurrence with actual observed data and comparative evidence;[44] and a more general descriptive and analytical adequacy, as will be seen below. But if we cannot entirely harmonize Porter's system with observed fact, some of his generalizations about the nature of cola are apposite. For example, he comments (p. 17):
Positively the colon is an exacted sequence of syllables produced by a brief rhythmic impulse. Four, rarely three, such sequences of syllables constitute the complex unit of the line. They vary in length from 4 to 8 morae. Each colon is usually marked off by word-ends. Any word-end can sere this function. In the hexameter a colon is frequently a short unit of meaning but need not be.
[42] In H. Fränkel 1955, 100-156. Fränkel's original exposition of this material was in "Der kallimachische und der homerische Hexameter" (1926). For more recent remarks, including comments on G. S. Kirk's criticisms of his original proposals, see Fränkel 1968, 6-19.
[43] As a more recent investigator, Berkley Peabody, has put it (1975, 68), "cola properly should be labeled, not caesuras; for, to take a Parmenidean position, caesuras are without substance or meaning in themselves."
[44] As Peabody (1975, 348 n .4) points out; see also Ingalls 1970, 5.
These remarks help to clarify the definition of the colon, with the only qualification being adjustment of the morae, or counts, per colon, depending on the placement and number of caesura-positions.
Another scholar who disagrees with Fränkel's system of breaks, and even with the four-colon structure that they segment, is Geoffrey S. Kirk (1966).[45] To begin with, he seconds Porter's exclusion of Fränkel's A1 and A2 positions but not his relocation of C1. In fact, Kirk (p. 82) rejects the underlying principle behind binary positions: "Alternatively, of course, we can say that there is no 'alternate' to the bucolic caesura, and that in the nearly 40% of Homeric verses which do not have that caesura the latter part of the verse does not in practice normally fall into two word-groups." He then proceeds to consideration of Porter's data, attempting to demonstrate that the four-colon theory is statistically inadequate, and later to his own analysis of a sample passage from the Iliad for the same purpose. Kirk argues further that the apparent A and C caesuras are the result of "word-length availability" in the Greek language rather than metrical or sense grouping. To summarize, he would explain the hexameter as
a complex of causes, some obvious and others less so: the B caesura is a structural division of the verse primarily designed to integrate it and prevent it from falling into two equal parts; the C caesura tends to introduce a distinct verse-end sequence; the tendency to caesura around the middle of the first 'half' of the verse is due primarily to the average lengths of Greek words available in the poetical vocabulary.... The inhibitions on word-end at 31/2 and 71/2 and [Meyer's and Hermann's Bridges, respectively] arc caused by the desire to avoid any strong possibility of three successive trochaic cuts, that on 4 [between the second and third metra] being due to the desire to avoid a monosyllabic ending, especially after a heavy word, to a major part of the verse. (p. 103)
In addition to the problems of invoking modern criteria and tautologically assuming that Homeric words—which are, after all, embedded in Homeric meter—should serve as unambiguous evidence for available word-length (both of which problems Kirk admits, pp. 103-4), there arc other logical flaws in his formulation. The first and most basic is his tacit contention that the half-line break, or B caesura, should be the standard against which we measure the "inadequacies" of the A and C breaks. But if all breaks were of the same frequency and occurred without variation in the same positions, the hexameter would be a much less fluid and subtle instrument than it most obviously is. To deny a four-colon structure on the basis of Kirk's disclaimer is to require a meter to become a pattern without flexibility, a hardened and stylized set of stringencies which could never accommodate the "mighty line" of Homeric epic.
To carry this idea a bit further, the greater stability of the C (as compared
[45] See also Kirk's later remarks (1985, 18-24).
to the A) caesura need not be only a function of the line-ending closure identified by Kirk and described earlier, though it most certainly is in part due to that closing cadence. Instead, we may understand the 60 percent occurrence of the bucolic diaeresis as in part the opening boundary of the fourth colon in the form of the typical adonean rhythm, which is also the familiar final cadence in the line. Indeed, the two concepts seem to be complementary rather than mutually exclusive. Finally, Kirk's notion of "word-length availability" as determining colon extent does not prove out when applied to the line as a whole. If all caesuras are to be held up to the standard of the B break and therefore taken as equal, the assortment of word-lengths that open the line should multiply variabilities at mid-line and further multiply possibilities at the C caesura. At the very least, the A and C breaks should occur in approximately corresponding variability, with the two-position B boundary making the C perhaps more flexible than the A, which takes its departure from the one-position line-beginning. But although Kirk's model would predict these phenomena, they do not occur. Apparently the A and C caesuras must be explained in another way.
The most recent extensive study of the colometric structure of the hexameter is that of Berkley Peabody (1975), who would assign line-breaks in the following positions:
His schema thus differs from Fränkel's in the deletion of the first two of the A positions. Peabody's placement of the three breaks covers most of the lines in his object text, Hesiod's Works and Days (A1 or A2, 90 percent; B1 or B2, 99 percent; and C1 or C2, 90 percent), and he founds his theory of cola on comparative diachronic studies of Greek, Indic, and Iranian meters. From this caesura-system he derives twelve principal colonic forms that populate the four-part structure (p. 68; some examples with spondaic substitution):
1 | 2 | 3 | 4 |
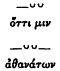 | 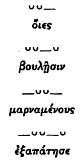 | 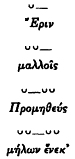 | 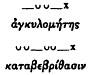 |
I find this recension of colometric theory far the most satisfying of the modifications of Fränkel's original proposals, both because of the comparative diachronic evidence on which it stands and also because it best acknowledges the complexity and flexibility of the hexameter. While one cannot expect absolute congruity of every Homeric or Hesiodic line with any abstraction (for as one moves toward that pattern-example congruity, one also moves toward a schema at the expense of a meter), a theory that accounts for variability and subtlety is inherently more useful and appealing than one that does not. Before going any further with Peabody's modifications, however, let us return to Fränkel's original ideas to clarify some issues.
Fränkel's exposition of cola, based ultimately on an earlier study by Eduard Fränkel (1932), was the first to posit the four-part structure of the Homeric lines. Contrary to Porter's and Kirk's later claims, he does not demand an absolute and firm sense-break (Sinneseinschnitt ) at every point of caesura, but admits throughout that some caesuras are stronger demarcations than others.[46] Rather, he places the colon boundaries at the positions most commonly marked by editors' punctuation. To be fair, this method is not unambiguous, since it tends to isolate an editor's idea of syntactic boundaries over a sample of lines and then to apply that information back to metrical structure.[47] Still, his results do partition the Homeric line effectively and give an excellent first approximation of the dynamics of the inner metric.
Fränkel explains the exceptions to his rules in terms of an occasional "heavy word" (schweres Wort ), which, because of its length of six morae or more, bridges a colon boundary and makes the given colon overlong.[48] As one of many examples, he offers Iliad 9.145, which contains a bridged B caesura (verschobene B-Zäsur ):
| [no B] |
Without a mid-line break, the result of the eight-morae schweres Wortbild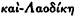 ,[49] the line seems to be divided into three rather than four cola. Of course, the bridging of the hemistich boundary occurs, as we know, only
,[49] the line seems to be divided into three rather than four cola. Of course, the bridging of the hemistich boundary occurs, as we know, only
[46] E.g., H. Fränkel 1955, 104: "Zwischen beiden Extremen, Satzgrenze und Wortgrenze, gibt es Einschnitte jeden Grades. Ein Mass für die absolute Stärke eines Einschnittes gibt es nicht, abet die relative Stärke der Sinneseinschnitte in einer Wortfolge ist oft unmittelbar ersichtlich."
[47] Fränkel's statistics are taken from a table compiled by A. Ludwich in Rossbach and Westphal 1867-68.
[48] He remarks (1955, 107): "Dem verspäteten Einschnitt geht ein Wort oder Wortbild...von mindestens 6 Moren voraus . Unter dem Gewicht eines solchen 'Schweren Wortes' (SW), wie wir es nennen wollen, kann ein Einschnitt um eine oder mehr Stellen zurückgedrückt werden."
[49] The idea of Wortbild includes both compounds and words combined with enclitics or proclitics. Cf. the "accentual groupings" in the Serbo-Groatian deseterac as described by Maretic[*] (below).
about once in a hundred Homeric lines. Somewhat more frequent is the bridging of A and C: caesuras, as in the following examples:
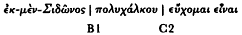 | (Od. 15.425 [No A]) |
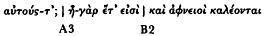 | (Od. 15.433 [No C]) |
In these two lines the A and C breaks are, respectively, verschobene , and the hexameters again appear to divide into three rather than four cola. However, through Fränkel's combination of multiple possibilities for caesura placement with "heavy word" bridges, he is able to account for all the complexities in these and other particular actualizations—including even those places in the line at which word-break is seldom tolerated, Meyer's and Hermann's Bridges. Both of these zeugmata, the former after a second-metron trochee and the latter after a fourth-metron trochee, are explained as interruptions of the colon system and for that reason are avoided.[50]
In sum, Fränkel's original system well suits the protean flexibility of the hexameter, a flexibility which fosters a correspondingly supple formulaic diction, as the author himself recognizes (1955, 116): "Den Sängern war es darum möglich die Inhalts- und Kolongliederung ohne harten Zwang so weitgehend zusammenfallen zu lassen, well ihnen das Zäsurensystem eine grosse Zahl von legitimen Varianten zur Auswahl stellte—vier für A, und je zwei für B und C."
In a series of articles dating from 1970, Wayne B. Ingalls has championed Fränkel's system and argued against its critics. Using Porter's own data on the Iliad and Odyssey , he points out (1970, 6) that Porter's displacement of the C caesura is not statistically justified and shows that "even Fräkel's additional alternative A-caesuras at 1 and 11/2 [after the longum in metron 1 and after the first trochee, respectively], rare as they are, are more common than Porter's C2, at 9 [after the longum in metron 5]."[51] In dealing with
[50] I mint in part agree with Kirk, especially in the case of Hermann's Bridge, that these zeugmata are avoided on the basis of a general prohibition against "trochaic cuts." The trochee will falsely signal line-end by imitating, in combination with a previous dactyl, the "quantitative close" or final adonean, that portion of the hexameter from the bucolic diaeresis on. But again I see no reason why these aspects of Fränkel's and Kirk's explanations must be viewed as mutually exclusive.
[51] O'Neill and Porter refer to various line-positions by means of a schema that counts every two morae as a whole integer and every mora as a half integer:
[]1, : Fränkel's additional A caesuras (A1, A2); 2, 3: Common A caesuras (A3, A4); 5: B151/2; : B2; 7: C1; 8: C2.
Kirk's objections, Ingalls demonstrates the essential subjectivity of arguments that depend on assertion and are not buttressed at all points with statistics. He then turns to a re-evaluation of Kirk's colonic analysis, which is shown to derive from eliminating two of Fränkel's A caesuras and all C breaks except the bucolic diaeresis. As Ingalls reveals, Kirk's methodology is flawed, for one cannot use one set of rules to determine breaks and another set to define cola: "In so doing [Kirk] naturally precludes the possibility of much concurrence between colometric and semantic units" (p. 11). On the basis of this re-analysis, then, Ingalls is able to dismiss Kirk's objections to the original colon-system and argue that, in the meaning Fränkel had intended, each colon is indeed a sense-unit.
In two later studies (1972, 1976) Ingalls widened his perspective to take in the relationship between metrical cola and formulas. Though this relationship is more properly the subject of later chapters, we may look briefly at some of his more important conclusions which have to do with our present concerns about metrical structure. First, he feels that Parry's original definition of the formula is tied too closely to its syntactic identity as noun plus epithet, and that this first approximation cannot be generalized to other kinds of formulas without becoming misleading. This argument bears directly on our understanding of the link between meter and formula and, if accepted, seems to indicate the need for a finer articulation of the blanket phrase "under the same metrical conditions." Second, he prescribes the colon as a metrical rationalization (Ingalls 1972, 122):
The formulae from Parry's analysis, then, confirm the intimate connection between formular usage and the colometric structure of the hexameter. Just as the formulae are the linguistic building blocks of the verse, so the cola are the metrical blocks. In other words, the metrical shapes of the formulas tend to coincide with those of the cola with which the verse is composed.[52]
As we shall see in chapter 4, the formulaic process is more complicated than a simple one-to-one relationship between formula and colon, but Ingalls's suggestions, based on Fränkel's colometry, are an important step toward a deeper understanding of that process.
As mentioned above, Peabody's discussion of inner metric in the hexameter is in many ways the most productive approach so far advanced. I shall follow the main descriptive outlines of his presentation both in this chapter and later on, but first let us make clear that the difference between the Fränkel-Ingalls and Peabody theories is basically one of statistical and diagrammatic convenience.[53] From a statistical point of view, Peabody's elimination of the
[52] Since Parry was of course working with caesura-bound phraseology, this approach h perhaps not as novel as it might seem. What makes it convincing is the impressive colonic analysis of Nagler's traditional phrases (see esp. Ingalls 1972, 115-18).
[53] For figures on relative percentage occurrence of the original Sinneseinschnitte , see Fränkel 1955, 104-5.
A1 and A2 caesuras, the only difference between the two systems of colon-structure, equalizes the variance among A, B, and C breaks at two apiece and affects only 4 percent of the sample. Further, even the 4 percent affected is not lost entirely, but simply reassigned to the "all others" category. The number of possible cola is greatly reduced by this simplification, since the possibilities for the beginning point of colon 2 and the ending point of colon 1 are cut in half, from four to two each. From a statistical and presentational perspective, then, more is gained than lost by Peabody's simplified view of the A caesura.[54]
Summary of Inner Metric
What is needed at this point is a standard for ranking, a quantitative measure of the importance of each word-break. As Kirk and others have stressed, the B caesura is the most regular, with the B1 and B2 positions providing a mid-line break in 99 percent of Homeric lines. There simply are no other points in the hexameter where word-break is so regularly observed. If Peabody (1975, 45-65) is right about the prehistory of the Homeric line as two shorter verses joined in a single hybrid (cf. G. Nagy 1974, 49-102), then we have a diachronic explanation of why this hemistich boundary should be so prominent in the synchronic sample of Homeric hexameters. But however we conceive of that prehistory, the shape of the hexameter as we know it indicates that the first and primary segmentation of the line is into two parts—two unequal hemistichs or half-lines:
Possibility 1 (B1 caesura):
Possibility 2 (B2 caesura):
Or, in mora-count:
Possibility 1: 10x | 12x + 1
Possibility 2: 11x | 11x + 1
In either case a slightly longer colon follows a shorter one. This is the most consistently observed dimension of the inner metric: a segmentation at the half-line level.
The A and C: boundaries operate on another level of segmentation, as their
[54] While any descriptive model can be more or less useful according to its innate complexity and ability to represent faithfully the empirical facts, any concept of inner metric will remain an abstraction that names and explains rather than is that inner metric. Our task in all areas of this comparative prosody chapter is to choose the abstraction that communicates the most valuable data in the most convenient manner. If by admitting two positions per caesura we can control 96 percent of the sample, then we have, formally speaking, a very workable model.
lower frequency figures make apparent. While this does not mean that they are to be discounted or questioned as caesuras, it does indicate that the cola which they form will have one boundary less consistently marked than the other. The colon system as a whole thus depends on Schnitte of at least three different types: (1) the absolutely regular line-beginning and line-end, always separated by twenty-three counts or morae and ending with the typical closing rhythm; (2) the B caesura, or hemistich boundary, which may take one of two positions and thus form two possible pairs of half-line segments; and (3) the A and C caesuras, whose two positions (four in all) account for a somewhat smaller percentage of all Homeric lines, about 90 percent. To look at the same situation in another way, we could say that Fränkel's "heavy words" bridge breaks according to the following schedule: (1) line-beginning and line-end can never be bridged; (2) the two-position B caesura can be bridged only 1 percent of the time; and (3) the two-position A and C caesuras can be bridged about 10 percent of the time. These are three distinct levels of segmentation in the hexameter, coordinated to be sure, but distinct from one another in frequency and variability of position.
Yet there seems also to be a fourth level of segmentation: Fränkel's A1 and A2 and the two word-breaks commonly found within colon 4. These four structure points occur decidedly less regularly than the main caesuras, but they appear often enough to beg the question of whether any or all of them should be classed as caesuras. Because they seem to function at another level of segmentation, I prefer to distinguish these four positions by labeling them juncture points , thus preserving the integrity of the colon structure and avoiding ambiguity in terminology. I believe, however, that they must be considered along with the more regular aspects of inner metric if we are to obtain a full description of the hexameter. By recognizing these juncture points as structural markers but not as caesuras, we can, first, encode in our model for the Homeric line important structural details beyond the hemistich and colon which may lead to a better understanding of phraseology and, second, preserve a relatively simple assortment of what I shall call, with Peabody, "principal colonic types." We can, in other words, limit the A, B, and C caesuras to two possibilities each and thereby limit the number of cola that they can bound to twelve. The levels of segmentation can be seen in table 6.[55] The principal colonic types, after Peabody (1975, 68) are as shown in figure 1. If we thus dispense with Fränkel's A1 and A2 caesuras, preferring to interpret these two breaks and the breaks at and 10 as juncture points within the first and final cola, and adopt with modifications Peabody's statistically more presentable model,
[55] The percentage occurrences cited for juncture points consist of ranges based on the following individual percentages: a (at 11/2), Il = 39 percent and Od = 38 percent; b (at91/2 ), Il = 30 percent and Od = 34 percent; g (at 91/2 ), Il = 44 percent and Od = 51 percent; and d (at 10), Il = 35 percent and Od = 32 percent. Note that these are simply word-end percentages and are not meant to indicate a metrical boundary.
TABLE 6. | |||
Level | Percent Occurrence | Increment Bound | Position(s) |
1. Line-beginning and Line-end | 100 | 23x | 1 each |
2. Hemistich boundary (B) | 99 | 10x | 2x + 1 or 11x | 11x + 1 | 2 |
3. Colon boundaries | 90 | 12 principal colonic forms | 2 each |
4. Juncture points | 30-51 | colon segmentation in cola 1 and 4 | 2 each in cola 1 and 4 |
Figure 1. Principal Colonic Types in the Hexameter | |||
1 | 2 | 3 | 4 |
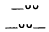 | 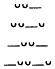 | 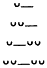 | 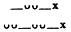 |
we shall have at once a more detailed and a more flexible descriptive instrument. The resulting schema for the hexameter is thus as follows:
The six main caesuras (A1, A2, B1, B2, C1, C2) and the juncture points (a , b , g , d ) determine the inner metric of the line. In the next chapter I shall study the relationship of this colonic structure to the verbal data of the Homeric epos, stressing Peabody's insight (1975, 74) that "the remarkable statistical coincidence of the forms of the elements used in the epos with the forms of the principal cola is significant. This coincidence goes far toward proving the essential unity of the metrical and linguistic traditions in the epos. It also shows that the colon, both in origin and function, is a linguistic period, a 'word form.'"[56]
For the moment, however, let us conclude this description of inner metric in the hexameter with a consideration of "right justification," the metrical phenomenon mentioned above in relation to Indo-European meter and the outer metric of the Greek epic line. In the case of the podic structure of the hexameter, the evidence of the tendency toward right justification was the relative
[56] See Russom 1987 on the coincidence of metrical units and word-forms in the Old English alliterative meter.
frequency in various positions of the dactylic metron, Which occurred more regularly toward the end than toward the beginning of each hemistich and most regularly as part of the closing cadence, or adonean clausula, of the line as a whole. Diagrammatically we may represent this two-level function as follows:
Level | Manifestation |
Whole line | Line closure and dactylic metron 5 |
Hemistich | Preference for dactylic metra 3 and 5 |
This characteristic texture means that the syllabically more extensive metra, those which have either a greater number of syllables (or, to put it another way, more short syllables) tend toward the right or end of metrical units within the hexameter. Still from the perspective of outer metric, then, syllabic extent and short syllables tend statistically to migrate toward the end of these units. Conversely, the left-hand or beginning portions of line and half-line will lean statistically in the opposite direction, that is, toward a shorter syllabic extent and the long syllables of spondaic substitution. This characteristic distribution is, of course, a tendency rather than a rule, but it will prove significant for our discussion of formulaic diction, since the texture of metrical units will be affected by right justification. In other words, lexical elements will typically arrange themselves, both over time and synchronically, in a right-justified order, a relative placement which is to a discernible degree overseen by the ending dactylic cadence of line and hemistich. Since the quantitative close or final cadence is more frequently observed than the preference for a dactyl in metron 3, the second hemistich and whole line will, in general, show the effect of right justification more regularly than will the first hemistich. The basic inclination, however, affects all parts of the line.
The same tendency toward situating longer metrical elements with more short syllables toward the end of metrical units in the hexameter is also apparent in the inner metric, although here it is of course the measure of mora-count which determines the "length" of increments. The hemistich patterns of 10x | 12x + 1 and 11x | 11x + 1, determined as they are by the B1 and B2 caesuras in the third metron, divide the hexameter into two unequal parts: in both cases a shorter first half is followed by a longer second half. By using Peabody's method for schematizing cola, we can analyze these hemistichs for the same tendency toward right justification at the level of the colon (1975, 69):[57]
[57] But at this point the tendency ends; right justification seems not to enter into the internal texture of the first and fourth cola, specifically that texture created by the juncture points examined above. In colon 1, where these points occur at 1 and 11/2 , two of the four possible segmentations can yield relatively longer colon-parts in the latter section of the unit, measuring by syllables. Measuring by morae, however, the situation is more balanced, with one possibility being right-justified, a second left-justified, and the remaining two symmetrical. The fourth colon operates in a similar manner; in fact, the segments in this last colon tend, if anything, toward left rather than right justification.
1 | 2 | 3 | 4 |
|
|
|
|
Computing by morae (symbolized as x )—that is, by assigning a count of 2 to each longum and 1 to each breve—one arrives at the table above. We can point out a number of instances of right justification in this diagram. First, cola 2 and 4 are on the average considerably longer than their half-line partners, cola 1 and 3, respectively. Second, the most spacious colon of the four is the last one, which, it will be recalled, involves the closing cadence to the line. At the levels of both whole line and hemistich, then, the hexameter forms itself in larger metrical units as one moves from left to fight, from beginning to end. What is more, this tendency is apparent from the perspective of both inner and outer metric. But the pattern does not extend to segments formed by juncture points; apparently the influence of this Indo-European characteristic ends at the hemistich level.
To summarize these remarks on fight justification, then, I would stress its prominent motive force in the formation of both inner and outer metric in the hexameter. To take the latter first, dactyls migrate toward the ends of both lines and half-lines, making these terminal sections more expansive by both syllable- and mora-count and more densely populated by short syllables. For its part, the inner metric manifests fight justification in a longer second hemistich and relatively more expansive second and fourth as compared to first and third cola. Although the principle does not extend to the inner texture of cola, it does figure in all units of the line that recur with regularity. In general, the Homeric hexameter locates the more extensive elements to the right, or toward the end, of a given metrical unit.
We recall that the features ascribed by most scholars to the reconstructed Indo-European ancestor of the hexameter and other poetic lines are four: (1) a quantitative basis, (2) consistent syllabic extent, (3) a regularly placed caesura within the line, and (4) right justification. Because all these features are to varying degrees reflected in both the inner and the outer metric of the Homeric line, we may envision a diachronic history underlying the synchronic patterns of the extant texts. Homeric phraseology takes its shape from these prosodic patterns, ancient Greek reflexes of Indo-European compositional habits culminating over time in the hexameter diction we find in the Iliad and Odyssey . For the moment, however, the important point is that, notwithstanding a seminal ancestry with many interrelated progeny, Homeric prosody is itself a singular prosody, with rules and tendencies very much its own. To put the matter succinctly—however much it may genetically owe to earlier forms, the Homeric hexameter is tradition-dependent.