2. The Heracleitean-Protagorean Problematic (151e-160e)
That Plato should assign to a mathematician the role of defining knowledge as sense perception is not surprising when we consider that for the Greeks mathematics centered on geometry, whose proofs were illustrated by diagrams. The Meno , however, reminded us that what one learns only by looking at the diagrams is not knowledge at all. Socrates says there about the slave: "At present these opinions, having just been stirred up in him, are like a dream. If, however, one were to ask him the same things many times and in many ways, you know that finally he would have knowledge of them that is no less accurate than anyone's" (85c-d). The slave's opinions will not be transformed into knowledge until he frees himself from dependence on particular diagrams or formulations.
In the Theaetetus Socrates pursues the opposite path, moving within the realm of sense perception rather than abstracting from it. To begin with, Theaetetus's model of surds and roots bears only a superficial resemblance to the diagram of the Meno . Whereas Socrates used that diagram as a means of discovery, Theaetetus uses his model only as a means of classifying what is already known. It is a preliminary application of the method of collection and division ("we tried to collect them [the roots] into a unity," 147d; "we divided all number into two," 147e). Moreover, when Theaetetus uses this mathematical example as
an instance of knowledge, Socrates does not proceed to make a connection between the nature of mathematics and the nature of knowledge generally, and to use this as an impetus to lead his partner in the direction of the intelligible, as in previous dialogues. Socrates instead pushes him in the contrary direction, to the most phenomenalistic way of conceiving knowledge. The world is just as it seems to each observer. Plato begins the dialogue with the most elementary conception of knowledge, that is, the lowest grade of information, mere sense experience. From this he will generate under the pressure of criticism progressively more complete models, in accordance with the method of hypothesis.[9]
By beginning in this way Plato is able to respond to the attack on stability launched by Heracleitus, who insisted that conceptual distinctions are always arbitrary, regardless of whether they refer to values such as beauty, or factual demarcations such as up and down, day and night, or alive and dead. The world of thought, like the world of beings, is pure becoming or flux, and conceptual knowledge is therefore delusory. The next generation took the next step and wondered how, if Heracleitus is right, it is possible for him to say so without inconsistency. Accordingly, his disciple Cratylus rejected his teacher's claim that we cannot step into the same river twice, for we cannot step into it even once. And to make his point with greater consistency Cratylus abandoned speech altogether and limited himself to pointing with his finger.[10]
It is against this background that the Theaetetus takes place, a dialogue explicitly concerned with the Heracleitean foundations of fifth-century sophistry. Today's "postmodernists" have advanced worldviews that are parallel in some ways to that of the Ephesians. Like their Presocratic counterparts, they attempt to break down the perceived structures of experience into negativity and flow—the problematic of the Theaetetus is of interest today not only for historical reasons. It is no accident that the reaction of the analytic-minded mathematician Theodorus to the school of Heracleitus is evocative of the reaction of contemporary analysts and traditionalists to Deconstructionists:
It is no more possible, Socrates, to discuss these doctrines [with their adherents] . . . than with maniacs. For they are, in accordance with their trea-
[9] For this interpretation of the method of hypothesis, see my PP 127-38. Kenneth Sayre points out that "the Theaetetus unquestionably is Plato's most ambitious and sustained attempt to apply the method of hypothesis in matters of philosophic argumentation" (Plato's Analytic Method [Chicago: University of Chicago Press, 1969] 232).
[10] Aristotle, MetaphysicsG .5.1010 11-13.
tises, completely in motion; and as for keeping to an argument or a question and calmly answering and asking in turn, there is less than nothing of that in them . . . . If you ask one of them something, he pulls an enigmatic little phrase out of his quiver and shoots it off. And if you try to get an account of what be said, you will be hit anew by another turn of phrase. You will never reach any conclusion with any of them; nor, indeed, do they themselves with one another; but they take very good care to let nothing be stable, either in an argument or in their own souls.
(179e-180b)
Socrates' rejoinder, that the Heracleiteans probably exaggerate these qualifies to Theodorus because of his hostility, reminds us that Plato himself shows considerable respect for Heracleitus's doctrines, and in the Timaeus describes the cosmos as partly grounded in chaos. The degree of his endorsement of Heracleitean destructuring is obscured by his concern about the propriety of disseminating such views even if they are true. Half a page after Theodorus's remarks, Socrates says,
Have we not heard from the ancients, who concealed it from the many by means of poetry, that the origin of all things, Oceanus and Tethys, are flowing streams, and that nothing stands still? And also from the modems who, because they are wiser, reveal these things openly so that even the cobblers may hear them and learn their wisdom and cease from their foolish belief that some things stand still while others are in motion, and, once they have learned that all things are in motion, may honor these teachers?
(180c-d)
In view of his belief that we do ordinary people no favor by convincing them that stability is an illusion, we must expect that whatever affinity Plato has for the views of Heracleitus will not be straightforwardly acknowledged. Nevertheless, these doctrines are taken very seriously in the Theaetetus . We need to consider how receptive Plato is to the objections against natural stability and to what extent his own philosophy of form justifies itself against the considerations that lead to the destabilizing of what appears to be stable. In the Parmenides Plato threw the theory of forms into uncertainty. And even though Parmenides reaffirmed the need for forms if thinking and discourse are to be possible, the forms are missing from the Theaetetus , at least on the surface. We would expect them to make an appearance when Socrates discusses the problem of quantitative relativity: it seems unproblematic to assert that six dice are more than four by a half and less than twelve by a half (154c), but, he says (in a dear echo of the method of hypothesis), we need "to observe our thoughts in relation to themselves, whichever ones we think, to see whether for us they are consonant with one another or
not at all" (154e; cf. Phaedo 100a, 101d). In the present case, three such beliefs produce tension with the statement about the relative size of numbers:
Nothing can ever become more or less, either in size or number, as long as it is equal to itself.
And second, that to which nothing is added and from which nothing is subtracted, is neither increased nor decreased, but is always equal.
Third, that something previously was not, but later is, without becoming, is impossible.
(155a-b)
"These three admissions fight with themselves in our minds when we talk about the dice," or when we say that if Theaetetus grows taller, then Socrates goes from being taller to being shorter without changing size (155b-c). Their "fight with themselves" presumably consists of the fact that each of them seems clearly true when taken just by itself, but clearly false when applied to the relative largeness and smallness Of numbers (the dice) and sizes (Socrates and Theaetetus).[11] It is important to keep in mind that the fight must be a tension within each statement, rather than a tension among them, for the examples of the dice and Theaetetus falsify either all three of the admissions together or none at all. (It is misleading therefore to translate
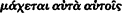
In the Phaedo (100e-103a) such problems are resolved by means of the theory of forms: relations like larger and smaller are not corporeal properties of individuals. They are therefore not subject to the three admissions mentioned above, which apply only to nonrelational subjects. They are conceived instead as relational essences, which are distinct from any corporeal individual, but which may be participated in by individuals in certain circumstances. Accordingly, we would not say, in violation of the first principle ("admission"), that Socrates, while remaining equal to himself, has gone from being taller to being shorter, but only that in one comparison he participates in the relation "taller" and in another "shorter." Nor would we say, in violation of the second principle, that Socrates has decreased without anything having been
[11] Polansky 94 puts it somewhat differently, by describing the tension as resulting from the possibility of interpreting each statement either as referring to something in itself, or as referring to it relative to something rise. Thus in each case the subject is unchanged in itself but may be different relative to something else.
subtracted from him, but only that he participates in a different relation because the size of the other referent (Theaetetus) has changed. Nor again, in violation of the third principle, that Socrates has gone from not-short to short without a process of becoming, but only that he participates in one relational form rather than the other because of a becoming that attached to the other referent.
Unlike the Phaedo , the Theaetetus makes no mention of the theory of forms and offers no solution. Theaetetus himself is left in a state of perplexity by the puzzles, and Socrates remarks, "This feeling—wonder—very much pertains to philosophy. For there is no other beginning of philosophy than this, and it seems that the one who said that Iris is the child of Wonder did not genealogize badly" (155d). This metaphor of "parent and child" pervades the Theaetetus . It was implicit at the beginning of this passage as well. If Socrates only wanted to illustrate the simple "paradox" that six dice could be both more (than a smaller quantity) and less (than a greater one) without changing, why did he needlessly complicate the example by making the larger and smaller quantities, not five and seven as we would expect, but four and twelve—the extremes of which six is the harmonic mean? He even goes to the trouble of pointing out, for no apparent reason, that six is not only more than four and less than twelve, but more than four by a half and less than twelve by a half (154c). The only purpose this would seem to serve is to make us think of six as a kind of product or "offspring" of four and twelve, as the mean that unifies them.[12] The parent-child relation is in fact the dominant leitmotiv of the dialogue. The Theaetetus contains at least six explicit references to parentage, and at least seven references to the relation for which parental procreation is a metaphor, that is, the explanation of something as a product of the intercourse of two prior elements.
The explicit references begin (1) when Socrates, after being told about Theaetetus by Theodorus, immediately asks who Theaetetus's father is (144c). (2) Later he speaks of his own mother, Phaenarete (149a)—the only time in any dialogue that he does so.[13] (3) He then goes on to compare the formulating of opinions to giving birth (151, 157c-d), and (4) subsequently refers to the deceased Protagoras's theory as an orphan (164e). In between were (5) the reference to Wonder as
[12] Cf. Rosemary Desjardins, The Rational Enterprise: Logos in Plato's Theaetetus (Albany: SUNY Press, 1990) 186.
[13] Thomas Chance reminds me that Socrates mentions his father, Sophroniscus, at Euthydemus 297e.
the father of philosophy (155d), and (6) the forthcoming discussion of perception as the "twin offspring" of objective and subjective becoming (136a-157c).
The same phenomenon—the explanation of an existent as the product of two progenitors—is operative without the parentage metaphor in (1) Socrates' definition of day as the mixture of earth and water (147c), which is to serve as a model for Theaetetus in his search for a definition of knowledge. (2) In response to Socrates' example of clay, Theaetetus recounts his and his young friend Socrates' idea of classifying all numbers into those that are the product of two equal roots (squares) and those that are the product of two unequal roots (oblongs). (3) Socrates himself is presented as a mixture of Theaetetus's looks (143e) and young Socrates' name (147d; cf. Statesman 257d). (4) In the present passage we have seen that relations like bigger and smaller can be explained only as the product of two referents, not as the property of one. (5)The analysis of syllables at 203 shows that they are normally the product of mixing vowels and consonants. (6) At 209d Socrates refers to the skytalê "a staff about which a strip of leather was rolled, on which dispatches were so written that when unrolled they were illegible until rolled again upon another staff of the same size and shape" (Fowler). It too is therefore a model of intelligibility based on the intercourse between two elements. (7) The dialogue as a whole, that is, the account of the conversation between Socrates and Theaetetus, is a product of the joint efforts of Eucleides and Socrates (143a).
The significance of all this emphasis on parentage will be considered later on. At this point, after the implicit demonstration that relations must be a product of (at least) two terms, and the reference to Wonder and Iris as father and child, we are given a biparental model of sense perception. If none of the uninitiated is listening—by whom Socrates means coarse materialists who deny the existence of anything nonperceptible, including change—Socrates will introduce Theaetetus to the mysteries of much cleverer people. These are evidently the Heracleiteans. No criticism is offered of this doctrine, and the presumption seems to be that it is a view that Plato accepts,[14] but Socrates is noncommittal when Theaetetus tries to find out whether he subscribes to this theory (157c).
[14] Not all scholars would agree. See, for example, Terence Irwin, "Plato's Heracleiteanism" (Philosophical Quarterly 27 [1977] 1-13); David Bostock, Plato's Theaetetus (Oxford: Clarendon Press, 1988) 153. The question remains continuously in view during Burnyeat's discussion of the first part of the dialogue (TP 7-65).
Within Heracleitean flux changing things may be described as gradual processes or "slow motions," some of which are capable of acting upon or being acted upon by others, in such a way that perception results (156a). Perception is accordingly like the offspring of two parents. The progeny is always twins. When the slow motion that is a gradually changing object comes within range of the slow motion that is a gradually changing eye, they produce the twins, perception and the perceived thing—for example, the perception of whiteness and the representation of a white object (156d). These progeny of the slow motions—that is, of the gradual motions of changing things—are quicker because they move from place to place: from their mutual birthplace between the eye and the object, the perception moves to the eye, and the perceived object moves to its perceived location. Accordingly, "nothing is one , itself by itself, but it always comes to be for someone" (157a). Any perceived thing is only phenomenal, in something like Kant's sense: it is the product of the intercourse between a thing in itself and our organs of perception. The physical world is therefore only a construction; the world in itself is pure flux or motion. The world of discrete and self-identical things is "objective" only in the sense that the phenomenal world is so for Kant: it is the world that is "given" in normal experience. The doctrine applies not only to individual things but also to "universals." "It is necessary to speak in this way both with regard to individuals and about multitudes collected together [
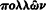
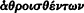
One of the reasons that Plato is usually held to subscribe to the flux theory of perception is that it fits in with his view of the physical world as "becoming" rather than "being." But all the evidence of the previous dialogues indicates that this further extension of the theory, by which "multitudes collected together," or universals, are relativized in the same way as sensibles, is one to which he does not subscribe. On the Heracleitean hypothesis, however—which is being explored here—the natural interpretation of universals is that they are artificial constructs abstracted (not "recollected") from particular experiences.
It might seem, Socrates points out, that we can dispute this doctrine by pointing to the fact that in dreams, madness, and other illnesses, perceptions of reality contradict those of normal, waking perceivers, and are objectively false (157e-158a). If we recognize that some opinions are false, then we must be able to recognize a standard of correct-
ness, in which case, pace Protagoras, not everyone is the measure of truth. This objection proves to be without substance, for according to the theory our judgments do not have the same referents as those of anyone else—sick people and dreamers included—and therefore do not contradict one another and cannot be considered false. If wine that everyone judges to be sweet is judged by me to be bitter because I am sick, there is no contradiction. When I say "this wine" I am referring not to the "wine in itself" but to one of the twin offsprings of both the wine and my organs of perception. This offspring is numerically different from the offspring that anyone else intends by the phrase "this wine," and that is the partial offspring of their organs of perception. The doctrine is thus compatible with the principle of noncontradiction[15] and not falsifiable on any obvious grounds. Accordingly, Socrates proceeds to explore more subtle problems to which the hypothesis leads.