The Electrical Vortex
The beam of charged particles undergoing acceleration constitutes a current that can be considered the secondary ciruit of a transformer. Recall the watchword of the faith of the electrodynamicist: F = evH / c , where F signifies the force exerted on a particle carrying a charge e and moving with velocity v by a
[39] Allibone in Hendry, Cambridge physics , 154, 165, 172; McKerrud to Cockcroft, 5 June and 14 Jul 1930, and Hopwood to N.R. Davis, 11 Jul 1930 (CKFT, 20/59). For European forerunners of Cockcroft's multiplier, see Ising, Kosmos, 11 (1933), 155–7.
magnetic field of strength H , and c stands for the speed of light.[40] For the formula to hold, H must be perpendicular to the plane defined by v and r . Since F stands at right angles to v , it can neither speed up nor retard the motion of the particle; instead it pushes it constantly toward a fixed point, forcing the particle to describe the arc of a circle. The situation appears in figure 2.12. The greater the velocity v , the larger the radius r of the circle must be so that the tendency of the particle to fly off at a tangent can be countered by an inward magnetic push. The balance of tendency (mv2/r ) and push (evH / c ) gives the most important relation we shall have to consider, the "cyclotron equation,"

where m is the mass of the particle.
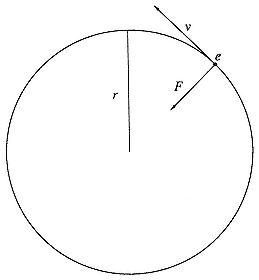
Fig. 2.12
The force on an electron circulating in a
magnetic field. The field H is perpendicular to
the plane of the paper; the force ( ev / c )H is
perpendicular to the velocity v and directed
toward the orbit's center.
[40] The factor c is required to write the watchword in electrostatic units, which we use exclusively throughout; H is then in gauss.
In October 1927, an electrical engineer named Rolf Wideröe presented his doctoral dissertation at the Technische Hochschule, Aachen. In it he described experiments based on the cyclotron equation and the transformer principle. By increasing H in time, Wideröe developed an electric force in the direction of v (the transformer principle); and by constructing specially shaped poles for the electromagnet producing H , he made it possible for particles to remain in circular orbit with constant radius (the cyclotron equation). As he observed, to obtain the necessary centripetal and tangential forces from the same electromagnet, its poles must provide a field that is half as strong at the electrons' orbit as within it—a condition easier to state than to realize.[41] Wideröe called this device a beam transformer; it can be applied practically only to electrons , which, because of their small mass, can attain useful energies under the electric force produced by the time change in H. Evidently the entire acceleration must be accomplished during that part of the cycle of the alternating current energizing the electromagnet in which the electromagnetic force acts in the desired sense.
That is the theory. In practice even the partial cycle was more than Wideröe could use, since he did not succeed in holding his electrons to circular orbits within the evacuated glass doughnut in which he tried to accelerate them. The best he could do, even with several extra coils arranged to compensate for unevenness in the H field, was to guide the electrons around a circuit and a half before they ran into the walls of their doughnut.[42] He thus confirmed the prediction of his former professor, Wolfgang Gaede, an expert in vacuum technology, who had refused to allow the project in his institute at the Technische Hochschule in Karlsruhe on the ground that it was sure to fail. That had driven Wideröe to Aachen, to the more optimistic Walter Rogowski, an expert on cathode-ray tubes and oscilloscopes. As Wideröe later explained
[41] Wideröe, 1928, in Livingston, Development , 107. A magnetic field H perpendicular to a circle of radius r and changing at the rate of dH/dt within the circle gives rise to a tangential electric force (er /2c ) (dH/dt ) and hence to a tangential acceleration dv/dt = (er /2mc ) dH/dt . To balance the resultant increase in "centrifugal force," a changing field H' at the orbit of magnitude (er/mc ) dH'/dt is required by the cyclotron equation. Hence H' = H /2.
[42] Livingston, Development , 113; Wideröe, Europhysics news, 15:2 (1984), 9.
his failure to implement his idea, which had come to him as early as 1922, "The theory of the stabilizing forces acting on the orbit had not yet been developed sufficiently."[43]
No more did the electrical vortex succeed in Cambridge, where Walton tried to implement Rutherford's suggestion of acceleration in the "electrodeless discharge." Here electrons in an evacuated tube without electrodes serve as carriers of the secondary current, the primary being generated in a coil wrapped around it. A supplementary magnet supplied the additional H field, which, according to Walton's detailed and correct calculations, would hold the electrons to a tight circular path within the tube. Walton charged a condenser to 40 kV and discharged it through the coil, setting up oscillations that produced the required varying magnetic field. If all went as calculated, the electrons would attain an energy of 536 keV in a quarter of a cycle. They declined to be regulated, ran into gas molecules, and scattered into the tube wall. Walton gave them up and joined Cockroft in multiplying voltages.[44]
The idea was so good and so obvious that several other physicists flirted with it before Cockcroft and Walton's success with straight tubes and high voltages in 1932. The friendly rivals from South Dakota each tried his hand. Working with Breit, Tuve set up an apparatus similar to Wideröe's, but independently of Wideröe. Tuve and Breit made an important improvement by injecting the electrons into their accelerator at high speeds via an electron gun and claimed to have obtained an acceleration to 1.5 MeV, but they nevertheless ended no more successfully than Wideröe; "No provision has been made [they wrote] to repeat the process very often." Lawrence thought that he could correct the fault of Walton's design, which did not make sufficient provision for axial focusing, with extra coils to create a field that would drive errant electrons back to their orbital plane. He had his assistants realize his design. On June 10, 1931, he tried it, with no better luck than his predecessors. The same success would have attended the efforts of Leo Szilard, had he attempted to make flesh the transformer-accelerator for which he applied for a
[43] Wideröe, Zs. angew. Phys., 5 (1953), 187.
[44] Walton, Cambr. Phil. Soc., Proc., 25 (1929), 469-81. Cf. Kerst, Nature, 157 (1946), 90–3, and Walton in Hendry, Cambridge physics , 51.
German patent in January 1929.[45] There were other patents as well. One of them, secured by Max Steenbeck, a physicist at the laboratories of the Siemens electrical company in Berlin, perhaps referred to a machine that worked.[46]
The method can be made to work. After a decade's experience in focusing beams of fast particles in other sorts of accelerators and in electron microscopes, physicists managed to construct a magnetic system capable of steering and speeding electrons on circular orbits within evacuated tubes. Szilard proposed to have a try in 1938, in collaboration with a physicist at the Clarendon Laboratory at Oxford, James Tuck; their unimplemented design was perhaps the most promising put forward before the first conspicuous success. That was achieved in 1939 and, on a larger scale, in 1940 by Donald Kerst at the University of Illinois.[47] He had the assistance of a former student of Oppenheimer's, Robert Serber, in computing the motions of the electrons. The business continued at General Electric's research laboratory, where a machine for 22 MeV and then for 100 MeV came into existence during the war. Just after the war, Kerst's "betatron" had an important influence on machines built in Berkeley.[48]