THREE
Ingenium and Figuration The Mathematics of the Regulae

Having discovered the importance of imagination in works from the years 1618-1621, we can now begin to ascertain what they contribute to an interpretation of the Regulae ad directionem ingenii.

The Regulae is unfinished. According to Rule 12, it was to have consisted of three parts with twelve rules each. The first, which is complete in the sense that there are twelve rules (rule headings) with discussion (rule commentary), lays down the basic principles of the method of properly ordering knowledge. The second, for which there are only six rules with commentary (13-18) and another three with just rule headings (19-21), was to have discussed problems that could be understood perfectly, even if the solution was not yet known (AT X 429). The third, sketchily planned but not executed, was to have treated problems not perfectly understood.

Interpretations of the Regulae usually emphasize several things: method, intuition and deduction, the unity of knowledge, simple natures, and the mathematization of thought. Very few emphasize the question of psychology,^[1] that is, the question of the powers of the soul that make intuitus and deductio possible and that allow the development of a method. From our earlier examination of Rule 12's account of the internal senses and its definition of ingenium as the power of treating images whether newly made or remembered, we recognize that the traditional rifle, which speaks of rules for the direction of the ingenium, is intimately tied to psychological matters.^[2] 'Ingenium' has, in English, typically been translated as 'mind', but

[1] Jean Laporte, Le Rationalisme de Descartes (Paris: Presses Universitaires de France, 1945), esp. 43-76, is an important exception, as is also Ferdinand Alquié, La Découverte métaphysique de l'homme chez Descartes, 2d ed. (Paris: Presses Universitaires de France, 1966).

[2] Of course, we cannot be certain what title, if any, the treatise bore in manuscript. In the French inventory of the posthumous papers of Descartes, the Regulae is given under item F: "Neuf cahiers, reliez ensemble, contenant partie d'un Traité des Regles utiles & claires pour la direction de l'esprit en la recherche de la verité." After examining the extant testimonies about the title, Marion argues that the first Latin edition of 1701, version A (Regulae ad directionem ingenii ), ought not to be completely authoritative. Just as crucial as the themes of rules and the direction of the spirit is the theme of the search for truth. He contends that the title of the French inventory is best; in the Latin of Pierre Borel, author of the Vitae Renati Cartesii (1656), it would read Regulae utiles et clarae ad ingenii directionem in veritatis inquisitione.

this is far too generic a concept to render even what Descartes expressly says about it. We might then well begin by asking, What is ingenium?

A. THE NATURE OF INGENIUM AND THE CONTEXT OF PHILOSOPHICAL PSYCHOLOGY

In English, the term is usually rendered as 'mind'; a revised version of a recent translation uses 'native intelligence'.^[3] The standard, hardly controversial, but also not very illuminating French rendering is esprit.^[4] In the few extant French letters before 1630, Descartes used 'esprit' in French wherever 'ingenium' might be expected in Latin. But Rule 12 makes it sufficiently clear that Descartes had in mind something rather more determinate than any of these terms conveys, Ingenium, as we have seen, is defined there as the action of the knowing power "when it at one moment forms new ideas in phantasia, at another applies itself to [or bears down on, concentrates on] those already made" (AT X 416). The formation of new ideas in phantasia, however, was defined a few lines earlier as imaginatio proper, and concentration on those already formed amounts to what was defined as remembering (reminisci ).^[5] Ingenium is therefore the general faculty of forming and acting upon images, which, because of the syn-

[3] Haldane and Ross typically use 'mind', and for the plural, 'mental powers'. CSM uses 'mind'; in Selected Philosophical Writings (1988), a one-volume selection of CSM, 'mind' has been changed to 'native intelligence', which, as we shall see, more accurately conveys an essential aspect of ingenium. In the present work, ingenium and ingenia will be left untranslated.

[4] The 1644 Latin translation of the Discourse on the Method authorized by Descartes renders esprit as ingenium, and the 1647 Frenching of the Meditations renders the few occurrences of ingenium as esprit.

[5] The Latin reads: "proprie autem ingenium appellatur, cum modo ideas in phantasia novas format, modo jam factis incumbit." The definitions of reminiscence and imagination/conception read: "si ad imaginationem solam ut diversis figuris indutam, dicitur reminisci; si ad eamdem ut novas fingat, dicitur imaginari vel concipere." The activity of imagining per se, that is, the application of the knowing power to the imaginative organ in order to shape or contrive new ideas, would seem to be exactly what the first modo clause of the ingenium definition describes. Similarly, the second modo clause appears to describe the application of the knowing power to imagination, insofar as it is already arrayed with various figures (with a strong sense of bearing down on the figures or ideas suggested by incumbit ).

onymy between 'imaginari' and 'concipere', would also mean the faculty of forming and acting upon what is conceived. It can be considered autonomous in that it does not directly depend for its contents on the external world but on the operations of the cognitive or knowing power in the organ phantasia. The very next paragraph of Rule 12 further emphasizes the unity of the power in question by arguing that memory, at least insofar as it is of corporeal things, is a power of imagination ("but the memory, at least that which is corporeal and similar to the recordation of beasts, is not at all distinct from imagination"); moreover, the same passage assigns to imagination the powers of moving (in addition to being moved by) intellect and of acting upon (in addition to being acted upon by) the senses.

The power of imagination/ingenium undergoes a rapid expansion of its psychophysiological competencies in these passages from Rule 12. In light of this and the definition of ingenium proper as imagination plus reminiscence, the Regulae ad directionem ingenii appears to be rules for the direction of the faculty of conceiving images, understood as a single, unified power.^[6]

Pressing too hard on synonymy and the exact wording of a text can lead to distortions in interpretation, of course. One could point out, for instance, that the language of the Regulae, even that of Rule 12 taken by itself, is not always consistent; at the very least there seems to be frequent terminological vacillation. For example, 'deductio', 'inductio', and 'enumeratio' are all used for what is arguably the same mental process.^[7] In Rule 12, 'intellectus' is sometimes used as an equivalent for 'vis cognoscens', the knowing power howsoever it manifests itself, but at other times in a strict sense of the knowing power acting on its own, apart from imagination. Again in Rule 12, the opposition of 'body' and 'spirit' is sometimes formulated alternatively as that of 'matter' and 'intellect'.

These terminological tensions, as we might call them, have not gone unnoticed individually, but their systematicity has been largely hidden from view by an almost total unawareness of the relevance of traditional philosophical psychology and the degree to which Descartes initially worked within its presuppositions. In the later works there are only hints and traces of this earlier concern. It is not so much that Descartes deliberately hid this from view, for instance by "sanitizing" the autobiographical account of his intellectual career in the Discourse. Descartes was under no obligation to describe every twist and turn of his philosophical education, especially not

[6] Wolfson remarks a tendency in early modern Scholasticism to reduce the number of internal senses, even to a single one. The example he gives is Eustace of St. Paul, an early seventeenth-century writer known to Descartes. Wolfson, 'Internal Senses in Latin, Arabic, and Hebrew Philosophic Texts,' 126; see also Etienne Gilson, Index scolastico-cartßsien (Paris: Alcan, 1913). S.V. 'imagination', pp. 137-139.

[7] But see chap. 4, Secs. D and E, below, for possible distinctions.

those paths that he had decided were impassable. (Moreover, the part of his philosophical apprenticeship that I am reconstructing here turns out to be at least consistent with most of what he says in the Discourse and elsewhere.) Nor is it the case that he ultimately rejected imagination as cognitively unimportant. Rather, after the Regulae he found it necessary to delimit its domain more carefully; yet what remained to it included nothing less than the whole of geometry and therefore also the substance of the physical world. But in comparison with the imagination of his earliest philosophical speculation, this was a very considerable restriction, for through principles of analogy its scope had formerly extended into the highest realms of spiritual truth.

It is a measure of the degree to which Descartes's writings shifted the philosophical horizon that we are scarcely aware of this development of his thought. That is, Descartes changed the terms and framework within which physiological, philosophical psychology was conceived and set an agenda radically different from the preceding tradition, which had drawn not just on Aristotle but on Plato and the Stoics as well. As a result it is easy to be insensible to the rich vocabulary and careful distinctions to be found in that tradition, a vocabulary and distinctions that are almost inevitably obscured in modern translations and interpretations.^[8] One need only compare English-language translations of Descartes's psychological terminology in the Regulae to the original Latin to recognize a conceptual flattening. 'Ingenium' is the outstanding example of this flattening. To render it as 'mind' or 'spirit' is to miss its specific character. Even the French 'esprit', which would seem to have Descartes's implicit authority, is far too approximate to come to terms with it.^[9]

The evidence of Rule 12 presented so far should make it compulsory that we look more deeply into the possibility that the universe of the Regulae is different from what we have thought. In beginning this investigation it is important to realize that although imagination and ingenium are points of focus, they lead into a different world of philosophical discourse. Moreover, what is at issue is not simply the Regulae or the early Descartes, so that those whose major concern is the "mature" philosophy might safely ignore these matters. Earlier we noted that Descartes justifies his use of

[8] As Descartes found it the vocabulary was almost exclusively Latin. By 1600, the traditional psychology had already been simplified and even vulgarized, and it did not survive long enough to be carried over fully into philosophy written in the vernacular languages. Indications of the remnants of this psychology in the seventeenth and the first half of the eighteenth century can be gleaned from John W. Yolton, Perceptual Acquaintance from Descartes to Reid (Minneapolis: University of Minnesota Press/Oxford: Basil Blackwell, 1984).

[9] The significance of ingenium has escaped even the philosophical subtlety and historical learning of Marion, who in his French translation and commentary uses esprit without cavil; nor is ingenium included in the index or in the list of Latin-French correspondences.

'idea', a term central to his later thought, by noting that philosophers use it "for signifying the forms of perceptions of the divine mind, although we recognize no phantasia in God" (AT VII 181; the French has "for signifying the forms of the conceptions of the divine understanding, although we do not recognize in God any fantasy or corporeal imagination" [AT IX 141]). If this is not enough to convince us of the relevance of these investigations of imagination for understanding Descartes as a whole, we need only remind ourselves once more that Descartes made the cogito , rendered into French as je pense and into English as 'I think', a vital part of the subsequent history of philosophy. By following the course of the Meditations, a thinker can presumably recognize her essence as res cogitans, the thing that engages in cogitatio—which in the Regulae is assimilated to imaginatio.^[10] We already recognize that in Scholastic psychology cogitatio is the activity of the vis cogitativa, which, along with imaginatio, is one of the internal senses, and that there was already in Avicenna and Averroês a tendency to assimilate the active functions of imagination to cogitativa. Is it not possible that if we do not take this into account, if we do not search out the ways in which a tradition may have shaped or at least affected Descartes's understanding of these matters, we run the risk of missing dimensions that are essential to the entire philosophy of Descartes?

B. THE MEANING OF 'INGENIUM'

In his commentary on the Discourse on the Method, Etienne Gilson distinguishes three senses of 'esprit' (having noted that the Latin equivalent is 'ingenium'): first, thought as substantial and personal—and, taken in its most general acceptation, as opposed to extension; second, memory and imagination, as distinct from reason in its proper sense (here Gilson refers to Rule 12); third, spirit as distinct from 'soul' (the latter term tends to include vegetative and motive powers and therefore might encourage the confusion of body and soul),^[11] But, as the definition of Rule 12 already suggests and as I hope will become clear from the remainder of this chapter, ingenium as used by Descartes in the period before 1630, though most closely resembling the second of the senses identified by Gilson, not only encompasses aspects of the others but also goes beyond them. Descartes's notion of 'ingenium' clearly takes on the personal and substantial aspect

[10] Cf. AT X 387 1. 12 with 388 1. 3. Giovanni Crapulli believes on the basis of the 1684 Dutch version N (which has "beweeging van denking" throughout) that "motion of imaginatio " should be emended to "motion of cogitatio. " See René Descartes, Regulae ad directionem ingenii, ed. Giovanni Crapulli, International Archives of the History of Ideas, no. 12 (The Hague: Martinus Nijhoff, 1966), 22. A, H, and AT all have imaginatio, however.

[11] René Descartes, Discours de la méthode, 5th ed., ed. Etienne Gilson (Paris: J. Vrin, 1976), 86.

indicated in Gilson's first sense of 'esprit', and if it does not really include the vegetative, it certainly includes the motive powers by virtue of phantasia's central control of the nerve and motor systems. This personal substantiality is understood as corporeal (and thus extended) as well as intellectual and spiritual: ingenium emphasizes the human person's endowment as a particular, corporeal-spiritual being, who because of those particularities has a somewhat greater or lesser aptitude for realizing the potentialities, especially cognitive ones, that are common to all human beings qua human. The notion therefore does not presume the radical dichotomy of thought and corporeality to be found in the later Descartes. Moreover, Descartes's ingenium is a cognitive power that is able to recognize the forms and relations of images and to manipulate them accordingly, so that it exercises functions of the Avicennan vis cogitativa and the Thomist particular reason.

In classical Latin, 'ingenium', a commonly used word derived from in -and gignere (to bear, produce, beget) and thus suggesting something inborn or innate, indicated in its most basic sense the sum of inborn faculties or powers. Of human beings it indicated the original power of inborn disposition, with also the more specific sense of a strong and firm soul. With regard to the intellect, it could be used generally of the powers of the mind and extended metonymically to the whole human being; used particularly, it could be synonymous with prudence, ingenuity, and the like, indicate single faculties of mind, or refer specifically to the faculties of invention or phantasia. It could be used of deficient or bad parts or characteristics of mind or soul; and, finally, it could occasionally be used of beasts and other natural things in the sense of their nature or faculties.^[12]

'Ingenium' is not uncommon in medieval Scholastics. For the most part it is not singled out for technical or specialized use (unlike 'ratio' or 'phantasia') but continues to convey the chief meanings of classical Latin usage. In Thomas Aquinas, for example, it can indicate ingenuity or cleverness, but also the sum of human powers or human intellectual powers; and in some formulations it suggests the properly human powers of knowing that therefore fall short of reaching the things of revelation.^[13]

The term does have a more systematic use in the works of Hugh of St. Victor (d. 1141), including the Didascalicon and his writings on meditation. In these works ingenium is paired with memoria as the two natural powers (naturae ; they are contrasted by Hugh to practice and discipline) that are necessary to prolonged study or meditation. Memoria enables human beings to retain what they have experienced and read, whereas inge-

[12] S.v. 'ingenium', Thesaurus linguae latinae, 25 vols. (Leipzig: B. G. Teubner, 1900-), vol. 7, pt. l, 1522-1535.

[13] See Petrus De Bergomo, ed., In opera Sancti Thomae Aquinatis Index seu Tabula Aurea (Paris: 1880; phototype ed. Alba-Rome: Editiones Paulinae, n.d.), 505.

nium is the natural aptitude for grasping or conceiving those things properly in the first place.^[14]

The word had a programmatic importance for Italian Renaissance humanists, as the human power of understanding and invention that in its flexibility and adaptability underlies the effective use of words and that contrasts with a reason (ratio) that deals with the eternal and thus transcends ail things specifically human.^[15] In the late sixteenth-century commentary on Aristotle's dialectics by the Jesuit cardinal Francisco de Toledo, a work that was certainly available to Descartes at the Collège Henri IV at La Flèche, 'ingenium' is used to indicate the highest rational powers of recognition (the fundamental modes of the syllogism, he says, depend on principles revealed by natural light from which the human ingenium is unable to dissent). The word is also not infrequent in the commentaries on Aristotle produced at the Jesuit University of Coimbra toward the end of the sixteenth century, and it even takes on a quasi-technical meaning in the one devoted to On Generation and Corruption. There 'ingenium' is equivalent to the embodied human spirit, the individual human being as a particularized corporeal manifestation of the species. Thus the term is broad enough to cover the peculiarities induced by individualization as well as the general nature and powers due to the species.^[16]

Ingeniurn takes up slightly more than a full two-column page in Rudolphus Goclenius's early seventeenth-century Lexicon philosophicum, which concisely summarizes the variety of learned acceptations of Latin and Greek philosophical terms.^[17] Goclenius starts with the key general and specific

[14] See book 3 of Hugh of St. Victor, The Didascalicon of Hugh of St. Victor: A Medieval Guide to the Arts, trans. Jerome Taylor (New York: Columbia University Press, 1961), esp. chaps. 7 and 8. The Didascalicon is perhaps the premier medieval treatise on the nature of science and method. Ingenium is prominent also in Hugh's "De modo dicendi et meditandi," in J.-P. Migne, ed., Patrologiae Cursus Completus, 2d ser. (Paris, 1854; known as Patrologiae Latinae ), 176: 875-880, esp. 877. The relationship of Hugh's work to Descartes and possible influences of this constellation of topics on Descartes's thinking deserve further investigation.

[15] See Ernesto Grassi, Heidegger and the Question of Renaissance Humanism: Four Studies, Medieval and Renaissance Texts and Studies, vol. 24 (Binghamton, N.Y: Center for Medieval and Early Renaissance Studies, 1983), 20, 73-76; and Hanna-Barbara Gerl, Einführung in die Philosophic der Renaissance (Darmstadt: Wissenschaftliche Buchgesellschaft, 1989), 154—163. Ingenium was fundamental to the invention of concetti or conceits in baroque aesthetics; see Joseph A. Mazzeo, Renaissance and Seventeenth-Century Studies (New York: Columbia University Press/London: Routledge & Kegan Paul, 1964), 29-43, and M. Fumaroli, ed., Critique et créa tion littéraires en France au xvii' siècle, Colloque International du Centre National de la Recherche Scientifique, no. 557, Paris, 4-6June 1974 (Paris: Editions du Centre National de la Recherche Scientifique, 1977).

[16] See Franciscus Toletus, Introductio in dialecticam Aristotelis (Venice, 1588), 163; Coimbran College of the Society of Jesus, In duos libros de Generatione et Corruptione Aristotelis, 2d ed. (Lyon, 1606), 485-489.

[17] S.v. 'ingenium' in Rudolphus Goclenius, Lexicon philosophicum quo tanquarn clave philosophiae fores aperiuntur (Frankfurt: M. Becker, 1613; photographic reprint Hildesheim: Georg Olms, 1964), 241-242.

uses: the most general is for the "inborn power and nature of any thing whatever"; the specific proper meaning indicates "the power of successfully and easily discovering and contriving in human beings, and the power of memory"; and the specific improper refers in analogical use to animals and in metonymic use to arts discovered through ingenium. His discussion makes several points important for our purposes. He remarks that

ingenium spoken most properly is the constitution of the rational faculty of the rational soul for understanding something or discovering or teaching. Or ingenium is the natural aptitude or faculty by which we teach, and through [which] we ourselves think, or discover something. The genus of ingenium is euphuia,^[18] more broadly indeed the latter is open to the former, since (generally it is the native goodness of soul or body) specifically it is the good constitution by nature of the rational soul now with respect to the true, now with respect to the good, nor is euphuia only of ingenium but also of natural judgment. Scheckius, Topic. at 39, agrees: "This in fact is euphuia, to be able to rightly elect the true and flee the false." But for Aristotle the part of ingenium is the natural facility for judging something.

Goclenius remarks further that a function of ingenium is eumatheia, "the right constitution for learning disciplines" and the habit of swiftly discovering middle terms, and he distinguishes it from sunesis, which is nevertheless affine to ingenium. After noting political, pneumatic (spiritual), and theological senses of an ingenium apart from judgment, he points out that Scaliger differs from those who subordinate judgment to ingenium and quotes the Jesuit Peter Molina, who said that "philosophy is the file of judgment, and the whetstone of ingenium," to show that memory is not necessary for good judgment. He concludes,

The variety of ingenium depends sometimes on the temperament of the body, sometimes on the various disposition of the mind, and the constitution of the organs, and of the auxiliary faculties, as of the phantasia (imaginatricis).
The distinctions of ingenium are various. For the ingenium is subtle, or thick, acute or obtuse. Perspicacious or less perspicacious, quick or slow, sharp or less sharp (because of which also sharpness [acrimonia] is attributed to judgment).

Thus ingenium has chiefly to do with the natural powers of things and, in human beings, with the natural powers associated with the rationality that differentiates them from animals, but that also includes the corporeal basis attendant on their being rational animals. It is associated with quickness of judgment and learning and the right constitution for learning in a

[18] This term and also the eumatheia and sunesis that Goclenius subsequently mentions appear in Aristotle's Nicomachean Ethics. Euphuia is 'natural gift', 'good natural parts', or 'cleverness' (e.g., at 1114b3-10); eumatheia is 'readiness in learning'; sunesis 'intelligence in practical judging'.

disciplined or scientific way; it is closely dependent on the disposition of the physical organs that aid the mind, especially the imagination.

The advantage of referring to Goclenius is that he reflects learned usage contemporary with Descartes's youth. 'Ingenium' was not just a word for philosophers' and theologians' treatises, however. We must recall that Latin was the language of instruction and communication at La Flèche, both inside and outside the classroom, and so Descartes would surely have picked up any colloquial meanings that the word had. It is interesting to note, then, that in assessing the performance of their pupils, the Jesuits used 'ingenium' as one of their categories, more or less synonymous with what we would today call "natural ability," "talent," or "aptitude." Thus René the schoolboy would have heard himself and his mates evaluated with respect to their ingenia in the following terms: mediocre, sufficiently acute, optimum, dull, very sharp, deficient in ingenium, does not lack ingenium, of moderate ingenium, somewhat acute, most perspicacious, lit-de apt for logic, of at most mediocre ingenium, minimally sharp, obtuse, not well constituted by ingenium, ingenious boy, has a good memory, less prompt ingenium, of sharpest ingenium and outstanding in memory, various and mutable ingenium, acute and subtle, stupid.^[19] The ingenium the instructors were assessing was an individuated capacity for learning, particular to each student.^[20] in which the premium was placed on quickness, penetration, and good memory.

C. DESCARTES AND INGENIUM

It is reasonable to think that the young Descartes would have been affected by, or at least aware of, the standard technical acceptations of philosophical terms common in his day, as well as the meanings of everyday language, even when he ultimately chose (as in the case of intuitus ; see AT X 369) to adapt terms to his own purposes. I wish to suggest, then, that 'ingenium' as used by Descartes, at least before 1630, lies on the semantic axis laid out by usage common in the late sixteenth and early seventeenth century, a usage that is in fact not far removed from that of classical times but that underwent developments in accord with the prevalent psycho-physiology. This axis would of course not necessitate that every occurrence of the term in Descartes bear the same meaning. But each occurrence

[19] All of these are taken from "report cards" kept at La Flèche; see Rochemonteix, Un Collège deJésuites aux XVII et XVIII siè, 4;205-206, 348-350.

[20] Given that the grade list Rochemonteix published evaluates 27 boys and considering that marks for ingenium were usually given in just one or two words, there is relatively little duplication from student to student. This would indicate that the instructor took some care to differentiate each case and thus confirms the essentially personal and individual character of ingenium.

should typically refer to inborn powers that are proper to human beings as such. More likely than not, the term will indicate intellectual or cognitive powers, often with at least some suggestion of the individualization or personalization of them due to the corporealization of spirit. 'Ingenium' therefore would be best understood in the first instance as particular corporealized spirit, that is, spirit that includes some of the peculiarities arising from this corporeal particularity.^[21] Putting aside for the most part the so-called vegetative powers (nutrition, reproduction, and the like), ingenium would be the native human endowment that gives rise to a human essence exhibiting personality and character. With emphasis placed on the cognitive side, it would be the embodied mind that has access to the fundamental principles of knowing (the natural light), and therefore the corresponding cognitive activity or knowing power would reflect both corporeality and spirituality. By virtue of ingenium, each human being would have all the peculiarities of his or her personal existence, but that personal existence would also include the powers and functions that are common to all human beings per se.

The reader who considers these reflections to be sufficient might proceed immediately to the next section. It is nevertheless illuminating to find them supported by Descartes's Latin writings from before 1630. In his correspondence with Beeckman the word occurs frequently. On 24 January 1619, Descartes inquires after his friend's health in a way that emphasizes the cognitive side: "You must believe that my concern is not just science alone but you yourself, not just ingenium, although it is the greatest part, but the whole man." In the next paragraph he says that he has been working not on an important (and otherwise unidentified) treatise that Beeckman had urged him to write but rather on drawing, military architecture, and Flemish, "things which without doubt your ingenium, occupied with higher things, will contemn." Here the sense again suggests the higher, intellectual faculties, although it is also possible that both occurrences include the wider spiritual aspects of human being as well, including character.

On 23 April 1619, Descartes writes, "For you truly are one who roused the slothful one, recalled an erudition that had almost lapsed from memory, and led the ingenium wandering from serious occupation back to better things." In the next paragraph he recalls the discoveries using the new mathematical compass that he had reported in a previous letter and says he is planning a treatise on the subject: "but now I have not worked for a

[21] For example, those whose brain matter was too soft could easily form perceptions but retain them only with difficulty, whereas those who had a very hard brain matter would typically be insensible to perceptions but could retain with ease those that managed to impress themselves.

month, because to be sure [my] ingenium was so exhausted by these discoveries that it no longer was sufficient for discovering those other things which I had hitherto resolved to seek. It will suffice, however, for preserving the memory of you perpetually." The "slothful one" that Beeckman had roused might in fact be (speaking grammatically) 'ingenium'; since the second passage allows for the exhaustion of 'ingenium', there is no reason why it could not be lazy as well. This certainly would not conflict with the second passage from the 24 January letter, in which Descartes had admitted to occupying his ingenium with relatively insignificant things.

On 29 April, Descartes writes asking Beeckman to consult Raymond Llull's Ars brevis for him and comments, "I have such confidence in your ingenium that I am certain you will easily see those things (if there are any) which are necessary to the intelligence of other things but otherwise omitted, which he [= a follower of Llull's with whom Descartes had conversed] calls 'keys'." Here the usage seems to emphasize that aspect of the cognitive abilities that we call ingenuity or shrewdness, the power of recognizing what is not readily apparent.

In these early letters ingenium is associated with intellect but implies a good deal more. It undertakes projects, it aims at discovery or invention, it remembers, its exercise requires effort, and it can be affected with peculiarities of character like sloth and physical or physiological states like exhaustion.^[22]

The only other Latin letter with an occurrence of 'ingenium' from before 1630 is conjecturally ascribed to 1628; it is Descartes's evaluation of the book Lettres du Sieur de Balzac.^[23] 'Ingenium' appears five times: attentive ingenia are said to be frustrated by the insubstantiality of many writers; in primitive times, when words were the sincere expression of one's mind, "there was in superior ingenia a certain divine power of eloquence, which flowing from zeal for truth and abundance of sense led primitive men out of the forests, imposed laws, founded cities, and the same had the power of persuading and simultaneously ruling"; Balzac makes arguments clear and simple enough to awaken trust in common people, yet "they are nonetheless so solid and true that the greater anyone's ingenium is, the more certainly he is convinced"; "if he decides to speak of himself, he does not fear contempt for laying open illnesses of body and the feebleness of nature nor envy for not dissembling the deserving merits of his ingenium";

[22] There are in fact only two other Latin letters extant from this period: a lengthy one concerning mathematical and physical matters (26 March 1619) and a one-paragraph message (20 April 1619), both addressed to Beeckman and neither of which uses ingenium.

[23] Balzac was a friend of Descartes's. It is conjectured that the letter was addressed to a friend of both, perhaps Jean Silhon. See Descartes: Correspondance, ed. Charles Adam and Gèr-ard Milhaud, 8 vols. (Paris: Félix Alcan [vols. l-2]/Presses Universitaires de France [vols. 3—8], 1936-1963), 1:30 n. 1.

and posterity will judge favorably "this candor and the ancient [i.e., like that of the ancients] character of an ingenium set above the vulgar." Even more clearly than in the letters of nearly a decade earlier, ingenium is as much a matter of general character, abilities, and judgment as of intelligence, and the intelligence described is as much practical as theoretical.

From these letters we see that ingenium is the greatest part of the human being; it engages in science, more generally in intellectual projects, and is the power by which we make discoveries; it can be qualified as being higher or lower, greater or lesser, slothful or industrious, which suggests that it constitutes at least part of what is called virtue, vice, and character. We might call it native intelligence, with the understanding that it is intelligence in all walks of life, including the intelligence of sensibility as well as of intellect; but even this probably restricts ingenium too much to the cognitive realm, and therefore it would probably be better to speak of the native (i.e., inborn) human endowment.^[24]

D. INGENIUM AND THE PRINCIPLES OF INNOVATION AND DISCOVERY

Descartes's Latin letters are not the only relevant source for his use of 'ingenium': there are also the notes of the "Cogitationes privatae." Indeed, ingenium, imagination, and mathematics are discussed in these private cogitations in a way that intimates the connection between them.

One note announces a fictive book, the Thesaurus mathematicus of Polybius the Cosmopolite, which will treat the means of solving all mathematical difficulties and in which "is demonstrated that nothing more can be done with regard to these by human ingenium"; it promises as well to relieve the tormenting labors of those who spend day and night becoming trapped in mathematical Gordian knots "and uselessly consume therein the oil of ingenium". (AT X 214). This ingenium that can become exhausted in mathematical labors is clearly in line with what we have previously seen. Another entry helps deepen the conception of ingenium, which we already know to be qualifiable in various ways.

For all ingenia determinate limits are prescribed that they cannot transcend. If some cannot use principles for discovery because of a defect of ingenium, they can nevertheless know the true reward of the sciences, which suffices them for carrying out true judgments in the estimation^[25] of things. (AT X 215)

[24] Norman Kemp Smith suggested translating 'ingenium' as 'total mind-body equipment', which captures the essence of the matter. See Kemp Smith, New Studies in the Philosophy of Descartes: Descartes as Pioneer (London: Macmillan, 1952), 15 l, 160.

[25] The term 'aestimatione' may implicitly refer to the internal sense vis aestimativa.

The first sentence asserts that ingenium is inevitably finite and limited. The second makes clear that it is not only limits due to the nature of inge-nium that Descartes has in mind but also those that have to do with the particular constitution of the individual's ingenium. The point, however, is that although defects of ingenium might make it impossible for someone to make discoveries directly from first principles, it does not affect the ability to make true judgments; apparently ingenium is the name for that power human beings have to assess and deal truly with whatever they meet in the course of their lives, regardless of their ability to reason from first principles.

The next note concerning ingenium, quoted already in chapter 2, is surprisingly clear about how far beyond the cognitive it goes.

There are certain parts in all ingenia that, when even lightly touched, excite strong affects: thus a boy with a strong spirit [forti animo], having been scolded, will not cry but get angry; another will cry. If it is said that many and great calamities have happened, we will be saddened; if it is added that some evil person was the cause, we will get angry. The passage from passion to passion [occurs] through neighboring ones; often, however, the passage from contraries is more robust, as when at a joyful party there is suddenly announced a sad event. (AT X 217)

Here ingenium has to do with the sensitive part of the soul in the amplest sense of the term: any part of the human being that is involved in a sensitive response is included. The full range of human affectivity, whether it is emotional, externally sensory, internally sensory, or rational, is embraced by ingenium. It might therefore be rightly conceived according to this note as the soul insofar as it is more than vegetative, that is, involved in more than the physical processes of constructing, maintaining, and reproducing the body. What Descartes is discussing in this note was of course treated many years later as passions of the soul. The affective, the sensitive, and the cognitive powers of ingenium are thus inborn and part of the nature of the individual.

What is at issue here is the individual native human endowment that makes the human being this person rather than that, yet still makes him or her a fully human being. One can have a limited or defective ingenium; one can be ingenious or industrious or slothful; one can be capable of both discovery and judgment, or just of judgment.

It is precisely because the fundamental powers of ingenium are common to all that it is capable of regulation. This aspect becomes clear by juxtaposing two other notes from the private cogitations:

As a youth, whenever ingenious discoveries were presented, I asked myself whether I could discover [them] for myself, even without having read the author: from which I gradually noticed that I was using fixed rules [certis regulis]. (AT X 214)

and

The sayings of the wise can be brought back [reduci] to a certain very few general rules. (AT X 217)

Inventions that were ingenious (ingeniosis inventis ), that showed the use of an energetic ingenium and were reinvented by the young Descartes simply from hearing of them without any explanatory gloss, led him little by little to recognize that this use of the ingenium proceeds according to certain rules; and he even gained the insight that the sayings of the wise, of those who know how to join science and virtue,^[26] can be led back to rules. What we have here, then, is an adumbration around 1620 of the field toward which the Regulae was directed: the proper use of the ingenium according to certain simple rules that are themselves inherent in ingenium. That is, the native human endowment by its very nature is capable of directing itself well if it recognizes the essential characteristics of its nature. Thus ingenium is also closely related to another theme found in both the "Cogitationes privatae" and the Regulae, that even without a conscious knowledge there exists within the soul a small number of principles, rules, sparks, seeds—as they are variously called—that are sufficient for discovery and judgment about all things.

It is almost just a corollary, then, that any theory of method, whether a method of invention for those blessed with a superb ingenium or simply a method of judging aright for those who have no more than the powers of ingenium common to all, would find its leading principle in the ingenium itself; and that such a theory would have not just a cognitive purpose, and certainly not just the goal of pure intellection, but also a practical purpose: the guidance of judgment in all things that are susceptible of judgment, including those things that the sensitive, responsive human spirit encounters in everyday living.

E. THE MATHETICS OF INGENIUM IN THE REGULAE

Ingenium, in a better than first approximation to Descartes's meaning, is the native endowment of the human being who is composed of body and soul (thus it would not be relevant to the soul that has been liberated from the body after death). All have this native endowment, but because of the particularities of their individual being, people would have a less or more retentive memory, a lesser or greater capability of imagining geo-

[26] At the beginning of the account of the Studium bonae mentis in his biography of Descartes, Baillet describes the Studium as "considerations on the desire we have to know, on the sciences, on the dispositions of the spirit for learning, on the order one must keep for acquiring wisdom [la sagesse ], that is, science with virtue, in joining the functions of the will with those of the understanding" (Baillet, Vie, 2:406; cited at AT X 191).

metrical figures, the need to exercise less or more attention to sense properly, and so on. However, the very fact that this native endowment is the result of the coexistence of a knowing power and a body, a coexistence with typifying characteristics, means that the native endowment of every human being can be employed similarly. Similarity does not guarantee equal success from person to person, but it does ensure that certain general principles or rules can be educed for the proper use of the native endowment. This native endowment, in particular its cognitively relevant aspects, would be most properly called ingenium.

What does this imply? In light of the later Descartes we are tempted to conclude that he is simply giving us the kind of division of the human spirit, the anatomy of the res cogitans, that is characteristic of the Meditations, where we find thinking anatomized into sensation, imagination, and pure thinking. But we should recall that in the Meditations the division of the soul comes about as a result of the division of ideas into different kinds: those that appear to come to us from an external world (adventitious ideas), those that we make (factitious ideas), and those that are innate. The ideas that occupy ingenium certainly may be of the first two kinds, as the definition of Rule 12 assures; and, as shall appear in the course of this analysis, ingenium can also work with ideas that might properly be called innate. Yet approaching the division of the soul by way of ideas is foreign to the Regulae .

Descartes uses 'idea' in the Regulae twenty-two times; except for one, all occurrences come in Rule 12 and after. 'Idea' is used in the Regulae not in the sense of the Meditations, however, but in a more restricted one. If we put aside the exception of Rule 4, it is always used to indicate particular contents of phantasia. Thus, in the parlance of the Meditations, 'idea' refers either to an adventitious or to a factitious idea but not to an innate idea proper to pure thinking (like the concept of triangle or the idea of God). 'Idea' in the Regulae can therefore be taken as synonymous with 'corporeal image' or 'corporeal figure' or, to use a term that Descartes employed in the early 1620s and that was the standard Scholastic term for the contents of the internal senses, 'phantasm'. At any rate, to overemphasize 'idea' in the Regulae would be a mistake, for it is merely a synonym for images within internal sense psychology.^[27]

[27] Roger Ariew and Marjorie Grene point out that in seventeenth-century literary usage 'idea' referred to images, usually those of sense; there was "a more obscure and ambiguous complex of philosophical definitions," the central one being the exemplars in the divine mind. See Ariew and Grene, "Ideas, in and before Descartes,"Journal of the History of Ideas 56, no. 1 (January 1995): 87-106; and also Stephen Gaukroger, "Descartes's Early Doctrine of Clear and Distinct Ideas," Journal of the History of Ideas 53, no. 4 (October-December 1992): 585-602. For the occurrences of 'idea' in the Regulae, see J.-R. Armogathe and J.-L Marion, Index des Regulae ad directionem ingenii de René Descartes, Lessico Intellettuale Europeo, no. 10, Corpus Cartesianum, no. 1 (Rome: Edizioni dell'Ateneo, 1976), s.v. 'idea'. The one usage in the Regulae that does not conform occurs in Rule 4, at AT X 376 1. 19. In the stratigraphic theory of composition, this is considered part of Rule 4-B, with which Descartes is supposed to have begun the Regulae in October or November 1619, that is, in the period leading up to his dreams of the night of 10-11 November 1619. This occurrence in Rule 4-B is odd, because it is the only one in the Regulae that does not have the sense 'corporeal image' but instead approaches the sense it has in the Meditations (in the Discourse both senses appear). Is this not a reason to doubt the very early dating that the stratigraphic theory attributes to 4-B?

'Ingenium' as Descartes specifically defines it in Rule 12 is not intrinsically concerned with the provenance of the image but rather with the ability of the knowing power to occupy itself with it, whether it has come from sense, memory, or the activity of the knowing power itself. The cognitive power's act of occupying itself with images as such is ingenium. In this respect it could be said to resemble what we call the free play of the imagination. However, it is important to keep in mind that this play of the imagination is the knowing power's play and thus that it always retains a cognitive purpose. The freedom of this play is the power of variation for the sake of finding something interestingly the same or different, that is, for the sake of discovery.

For example, the activity of constructing a geometrical proof would be largely in the domain of ingenium. In trying to prove that the three angle bisectors of a triangle intersect at a single point, we would ordinarily either just imagine a triangle with three angle bisectors, or, if our imaginative capacity were limited, we could draw a picture of a triangle with its angles all bisected. Then we would try to conceive how to go about the proof; in our imagination or on paper we would speculatively add new lines or follow any other strategy of modifying the figure that might suggest itself. Now clearly the drawing of a triangle involves our nerves, muscles, and limbs, as well as the apparatus of the external world, and as such it cannot be conceived as an act of ingenium alone, at least not in the strict sense of Descartes's definition. But the act of drawing is a direct consequence of the ingenial activity, so that especially given Rule 12's conception of phantasia as the originator of muscle motions, it is not fanciful to call it an act of ingenium. Moreover, insofar as the cognitive power is looking at a figure on paper with the intent of coming to a proof of the proposed theorem, the sensation involved is part of the cognitive power's occupying itself with the idea, and so it, in turn, may also be said to be an ingenial act.

As we have just characterized ingenium, it looks mathematical, or rather geometrical. As such, the psychophysiology of Rule 12 could be seen as an introduction to the figurative mathematical representation of problems that Descartes takes up in earnest in the second part of the Regulae, espe-

Fig. 7. Discrete elements are used to picture something enumerable by a counting number.

cially Rules 14 through 21. The art of mathematical representation taught there is without doubt ingenial activity. To recall the words of one of the "Cogitationes privatae," the imagination can use figures to conceive corporeal things. But is ingenial activity confined to the representation by "bare figures" advised in Rule 14, or is it wider still? One thing that is clear is that the representations mandated by that rule are not of physical bodies but rather of the terms of problems and that we learn not just how to introduce quantitative measure into the terms of problems but also how to use figures to present schematically the relationships implied in a problem and between its terms. As Rule 14 points out, we are not to use just any figures but

out of the innumerable different species of these, we are to use only those by which all the differences of habitudes [or relations] or proportions are most easily expressed. There are, however, strictly speaking two genera of things that are brought together for comparison with one another, multitudes and magnitudes; and so we have two genera of figures for proposing these things to our conception. For example, points [see fig. 7], by which is designated a triangular number, or the [family] tree which explicates someone's lineage

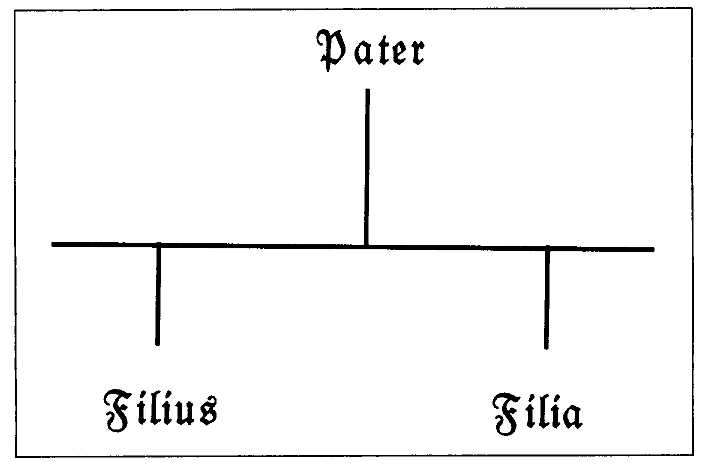
Fig. 8. Relationships between family members are pictured by a tree diagram.

[see fig. 8], etc., are figures for exhibiting a multitude [discrete quantity]; those, however, which are continuous and undivided, like the triangle, square, etc. [see fig. 9], explicate magnitudes [= continuous quantity]. (AT X 450—451)

It has been a commonplace in Descartes studies to assert that this is part and parcel of Descartes's method of applying mathematical or algebraic analysis to all problems. But this is a half-truth, and it describes the surface rather than the depths of Descartes's aim.

One applies a thing X to a thing Y either in the spirit of play or because one has the expectation that this application will be fruitful. A twentieth-century French philosopher might be willing to do the former, but it hardly seems credible as the basis for Descartes's early work. Why did Descartes believe that applying figures to problems of all kinds would be fruitful?

We have already seen elements of the answer in the preceding chapters. First, it was not just any mathematics that Descartes wished to apply, but the mathematics of proportional relations; and that relational mathematics was grounded in an ontological epistemology of analogy that implied similarity between different levels of being, a similarity that is in fact the ontological and epistemological ground of the applicability of mathematics and that gives ontological and epistemological priority to a mathematics of proportion. The very analogical structure of reality allowed for a

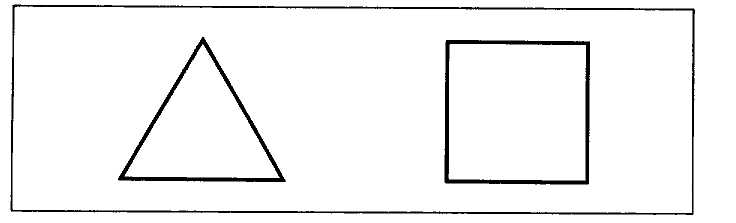
Fig. 9. Two-dimensional figures are used to picture different relationships.

certain flexibility in the application of mathematics, however; it is not the case that Descartes believed that there was a privileged mathematical representation of a problem or relation, but that there were alternative ways of presenting or approaching problems. The analogical structure of reality is warrant that there are many kinds and degrees of similarity, so that no one thing can be said to be a perfect representation—except the thing itself, which is not a representation at all, although a thing might stand for its own essence. As Descartes conceived these matters in the 1620s, however, the human mind does not understand things in themselves or in their essences but within the activity of figuration that he had begun exploring in the analogy notes of 1619-162 1.^[28]

This account immediately helps interpret the purpose of the second part of the Regulae . In the intended tripartite structure of the work, the first twelve rules were to (1) present the aim of a unified way to knowledge, (2) ground that knowledge in the two mental operations of intuition and deduction, (3) propose the division of questions in the sequential search for simple natures to be followed by a resurvey in order from the simplest things to the thing sought, and (4) sketch a psychological and even physiological basis for the right use of the native endowment. After the statement of the founding theory in the first twelve comes the explication in the twenty-four that follow. The second twelve rules were to deal with perfect problems, the third with imperfect problems. The second twelve rules, which teach how to present the scheme of relationships using lines and two-dimensional figures, serve two purposes: to train the reader (or Descartes the rememberer) not to ignore simpler things for the sake of the complex (perfect problems are easier to deal with than imperfect ones)

[28] I agree with Gãbe that before 1630 Descartes did not believe that human beings can know the essential natures of things per se; rather, one has a freedom of mind that allows one to approach things from many different perspectives. See Gãbe, Descartes' Selbstkritik, 84-92.

and to show in the most basic way how the ingenium can use marks and lines to aid in the solution of problems of proportion. One does not have to worry immediately about whether things really exist in the way they are represented; the question of existence is one for the physicist to solve (AT X 448), not the teacher of the new organon of the Regulae.

F. INGENIAL MATHEMATICS, OR THE ART OF MEMORY SUPPLANTED

One of the chief lessons to be drawn from the second part of the Regulae is always to simplify. For example, in Rule 14 we are told:

Finally it should be known that of the dimensions of continuous magnitude nothing is more distinctly conceived than length and width, and one should not attend to many [dimensions] simultaneously in the same figure when we are comparing two different ones with one another: because it is of the art that if we have more than two to compare with one another we run through these successively and attend to only two at any one time.
These things having been noted, it is easily gathered that: here propositions are no less to be abstracted from the figures of which Geometry treats, if the question is about these, than from any other matter; and for this use nothing is to be retained beyond rectilinear and rectangular surfaces, or straight lines, which we also call figures, because by means of these we could imagine a really extended subject no less than by means of surfaces, as has been said above; and finally by means of these same figures are to be exhibited sometimes continuous magnitudes, also sometimes a multitude or number; and nothing simpler for expressing all differences of habitude can be invented by human industry. (AT X 452)

At the outset of Rule 15, which follows immediately upon this paragraph, we are told that it is helpful to actually put images (species ) before our eyes. The unit, for example, can be represented as having length and breadth (a square), as having only length (a line), or simply as an element of a multitude (a point); "but however it be depicted and conceived, we always understand it to be a subject in every way extended and capable of infinite dimensions" (453). If we need to attend to two terms of a proposition simultaneously, "we exhibit them to the eye by means of a rectangle, whose two sides are the two proposed magnitudes"; if the two magnitudes are incommensurable, we use a simple rectangle, and if commensurable, we use a set of points or a rectangle composed of smaller unit rectangles so that their commensurability is evident. If we need to attend to just one magnitude, we present it either as a simple line or, if we will need to compare the line with a surface, as a rectangle, one side being the simple line and the other the unit length; or, if it is commensurable with the thing to which it is compared, by a set of points.

Everything propounded in the second part of the Regulae is for the sake of showing as simply as possible how problems with information sufficient for their solution can be attacked. None of the suggestions of Rules 14 and 15 about figuration and refiguration has to do with expressing the "nature' of the thing in question; they are only presentations or exhibitions of some aspect relevant to the problem (what Descartes calls 'dimension'). Therefore Descartes is not effecting an ontological reduction of the things in question to mathematics; that is, he is not arguing implicitly or explicitly that things are essentially, or essentially expressed, by figures, numbers, or extension. Quite the contrary: relations and aspects of things are expressible in this way.^[29] Moreover, whatever is not presently and immediately of concern in the problem does not need to be fully expressed but is to be kept in reserve by means of reminders, by marks rather than figures. This is a consequence of Descartes's behest that we never treat more than two things simultaneously.

Besides, because we said that not more than two different dimensions out of the innumerable ones which can be depicted in our phantasia are to be contemplated with one and the same intuitus, either of the eyes or of mind: it is of great value to retain all the others so that they can easily occur whenever need requires; for which end memory seems to have been instituted by nature. (AT X 454)

Since memory can be unreliable, and since we need to avoid diverting our attention, we make use of the invention of writing.

We shall commit nothing at all to memory, but turning a free and entire phantasia over to the present ideas we shall depict whatever was to be retained on paper; and this [is to be done] by means of the briefest notes [i.e., marks or symbols], so that after we have inspected the single things distinctly according to Rule 9 we can according to Rule 11 run through them all with a very rapid motion of cogitation and intuit simultaneously as many as possible. (AT X 455)

Presently we shall have to deal with issues such as the meaning of 'dimension', the problems that can and cannot be dealt with according to this procedure, the psychological act of running through things with a rapid motion of imaginative cogitation, and the significance of an intuition that can take place with respect both to the eyes and to the mind. For now we must note that Descartes is offering a technique of using the native faculties

[29] One thing to realize about these passages is that they are not concerned with the representation of things through figures but the exhibition of things and relations of things by means of other things—note that at AT X 453 11. l3-15 the figures are described as a subject, not as an idea of thought—and that the ways or dimensions in which they can be exhibited are infinite.

of the human being as simply and efficiently as possible in the working out of problems. The central faculty of this technique is imagination, that is, ingenium as the faculty of making and dealing with images or species in the phantasia and as the medium for translating those images in the mind into images and marks that appear on paper. The techniques are all accommodated to the strengths and weaknesses of ingenium. Too many aspects considered at once will overtax it, so it is necessary to keep the aspects to no more than two at any one time. We do not have to rely solely on the ability of our phantasia to retain the images it is working with, since we can draw appropriate, simple figures on paper to represent the relationships they bear to others. (Note that this is literally a re-presentation of a symbolized presentation of the relations of the terms of a problem!) This simplification of the work of the mind need not lead to neglect of the totality of what is at issue, for we have memory and, even more important, the aid to memory called writing. All we need do at any given moment, then, is to devote our immediate attention to the one or two relationships under present consideration and to remember that this is but a part of the problem; we do not have to actively remember the rest, since the marks that we make will enable us to find our place easily.

It is pertinent to recall Descartes's "Cogitationes privatae" entry about Schenckel's treatise on the art of memory. The medieval and early modern art of memory was constructed on a psychophysiological understanding of the mind and its functions. Depending on the physical constitution of the brain, on the relative dryness or moisture, heat or cold of its various parts, it was conceived as able to retain more or less easily the images conveyed to it by the senses and to impress more or less strongly those images in the corporeal memory so that they might be preserved. Vivid things are more easily remembered than ordinary ones, so the art counsels confecting striking images whenever possible (and as taught by Schenckel, it also provides mnemonically stimulating conventional images, like a bow for the letter C ) and keeping them well ordered by locating the images sequentially in a familiar and thus easily remembered place. In his comment on Schenckel, Descartes noted that he had thought of alternatives that eliminated the need for memory: generating phantasms from other phantasms, and using images and figures to stand for the relationships between the elements of a problem. The Regulae implements accordingly a program in which the use of and need for often unreliable memory is minimized, by keeping only one or two things active in imagination and relegating the rest to paper, with the sequence of steps to be taken determined by the principles of the first twelve rules. Of course Descartes is not teaching an art designed primarily to help us memorize things, but one that facilitates the solving of problems by an analysis into elements and the reassembly of these elements into the desired whole, a problem solving that can be re-

evoked and duplicated at any time and, unlike with things merely memorized, always with the full evidence of proof.

According to the psychophysiological hypothesis of Rule 12, Descartes, like Schenckel, is basing this "art," as he not infrequently calls it, on an understanding of the functions and physiology of the mind and brain. Rather than advise us to use vivid images of our own invention, however, he provides us with a stock of reliably and exactly reproducible images: not bows for C and scales for justice, but rectangles, lines, and points. This would seem to offer rather striking evidence that Descartes is in principle carrying out in the Regulae the advice that in 1619-1621 he had already given himself in the context of a solution he had devised to a problem of motion posed by Beeckman:

As I put down the foundations of this science, motion which is everywhere equal [i.e., uniform motion] will be represented by a line, or a rectangular surface, or a parallelogram, or a parallelepiped; that it increases from one cause, by a triangle; from two, by a pyramid, as above; from three, by other figures. (AT X 220)

And, as the note immediately following this remarks, "from these an infinity of questions can be solved.'

Indeed, in comparison with the "Cogitationes privatae," the Regulae effects a simplification. No longer will the problem solver need pyramids and other complicated three-dimensional figures, but only simple rectangles, lines, and arrays of points. The mathematical representation of things and problems has been reduced to a bare minimum.

But on the basis of what, and from what? We must remember that the mathematical technique introduced in the second part of the Regulae has a pedagogical purpose and so is maximally simple and that it rests on the identification of relevant aspects or dimensions of the problem at hand. We shall need to discuss where these dimensions come from and what they are before we can draw any definitive conclusions about the mathematical presentation of them; and, after all is said and done, the aim of problem solving must be to arrive at a rapid synthesis of all the elements into a whole that can, as it were, be intuited by a single act of mind. Moreover, it is not perfectly evident how this mathematical presentation can be translated into the solution of the so-called imperfect problems, where not everything is clearly distinguishable. But there is a piece of important evidence about the drift of Descartes's thinking around 1628, evidence that brings Descartes's techniques rather closer to a mathematized version of the classical art of memory, that allows a significant role to what we call secondary qualities, and, finally, that suggests that the rules of the second part of the Regulae were not written before late 1628.

The piece of evidence is an entry in the journal of Isaac Beeckman. In

October 1628, Descartes visited his friend whom he had not seen in nine years (and to whom it seems he had not even written since 1619!). In the course of the visit he revealed some of the mathematical and physical re-suits he had achieved in the intervening years. Beeckman recorded these in his Journal (see AT X 33 1-348). Under the heading "A Certain Specimen of Descartes's Algebra" he made an entry of particular interest.

He says also he invented a general Algebra, and for it he uses not the figures of bodies but only planes, because these are more easily insinuated into the mind; and so other things beyond Geometry are optimally expressed by these.
He conceives unity by a small rectangle; thus also he conceives a point. Even a line or a radix [= an unknown] he conceives by a parallelogram, conflated out of one side of this [unit] rectangle and [out] of the due length.^[30] A rectangle he conceives made out of so many radixes; a cube, made out of so many rectangles as the numbers indicate, reduced to oblong form; a biquadrate, in the same way, etc. Now he also explains all these things by lines, so that a represents a point, b a line, c a quadrangle, d a cube. In this way also f represented a cube made out of the multiplication of the quadrangle e by the number of the radix [see fig. 10].
With no less trouble he solves the same things by simple lines. . . .
In particular he of course conceives a cube by three dimensions, as others also do; but the biquadratic [which would be a four-dimensional figure] he conceives as if out of a simple cube, which is considered as wooden, there comes to be a stone cube; and so for the whole thing a dimension is added; and if another dimension is to be added, he considers the cube iron; then golden, etc., which happens not only in gravity, but also in colors and all other qualities. Thus cutting out of the wooden cube three rectangles, he also conceives finally that he is cutting a cube conflated of woodenness, iron-ness, etc., alone, so that the iron cube is drawn through [perducatur] into a wooden one in the same way that the simple cube [is drawn through] into rectangles oberved in every genus.^[31] (AT X 333-334)

Beeckman goes on to describe how one can solve equations using these techniques.

Setting aside inevitable obscurities, we can see that in the fall of 1628 Descartes was describing to Beeckman something akin to the techniques proposed in the second part of the Regulae , that is, the expression of all kinds of objects and relations, not just geometrical, by lines (in the third paragraph) and rectangular plane figures (in the first and second). But the fourth paragraph of Beeckman's entry describes something not to be

[30] That is, a line is represented by a rectangle that has as one side the line and the other the unit length.

[31] The concluding part of this last clause is garbled; the translation follows a suggestion of AT.

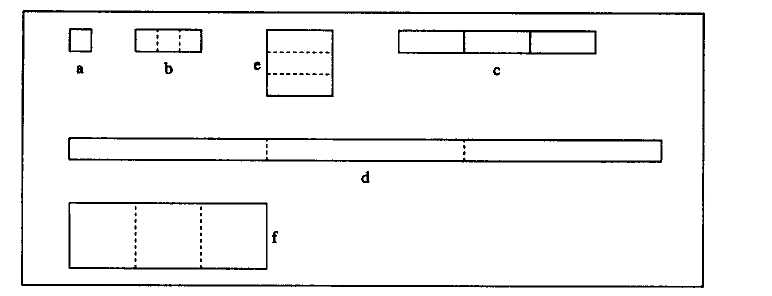
Fig. 10. The diagram that accompanies Beeckman's 28 October 1628 Journal entry.
All the elements of a problem are figured in two dimensions. The unit square is a;
three of them put together form b; three of those put together end to end make c,
whereas stacking three forms e; three of figure c make up d, while three of emake f.

found in the Regulae a technique that employs striking images not unreminiscent of those found in the second technique Descartes devised in response to the memory art of Schenckel, where he appealed to ascent on ladders, the hurling of spears, and the like, to help explicate the relations to one another of the elements of a series. A three-dimensional problem he conceives using a wooden cube, a four-dimensional one using stone, a five-dimensional using iron, and so on. But he uses not only gravity (perhaps the increasing specific weights of these materials is the significant comparative factor) but also colors and all other (secondary) qualities to differentiate problems.

Is this the direction in which Descartes intended to develop the third part of the Regulae ? Someone might object that the fourth paragraph of Beeckman's account presents a method so at odds with the others, not to mention with the Regulae , that this is implausible. Was Descartes, then, merely explaining to his friend a path he had formerly considered but had already rejected (and so perhaps Beeckman misunderstood this as part of Descartes's current algebra)? But this suggestion is highly implausible. Descartes was not in the habit of revealing even to friends anything he thought was imperfect, and unlike, say, a Kepler, he was not one to chronicle his missteps. Moreover, his introduction of cubes of different materials is not inconsistent with the method of representation in the Regulae if it is understood primarily as a ploy for keeping in mind, indeed embodying, all the dimensions of a problem. From Beeckman's description it seems that Descartes used these cubes to preserve multiple relations that could be

carved off as needed in the form of different cross sections, that is, rectangles, to which the kind of manipulations of lines and plane figures taught by the Regulae might be applied. The qualified cubes would thus be memory devices. What seems to have happened between the ingenious ideas of October 1628 and the last rules of the Regulae is that Descartes decided no longer to preserve all the dimensions in an actual geometrical figure, carving off those rectangular combinations of two dimensions as they were needed, but instead to use exclusively simple marks or notations on paper to help remember the dimensions not currently in use while actively concentrating on no more than two.

As Descartes conceived of his geometricized algebra before late 1628, then, it was an art of imagination (and thus of ingenium) even closer to the classical art of using striking images for remembering than is the technique of the Regulae. All experienceable qualities, not just the easily quantifiable ones that we call primary, were eligible for use in this earlier method, although when it came down to actual calculations the solids with secondary qualities were to yield up the information they stored by a method of sectioning that results in lines and rectangles. In addition, unlike the Regulae, which gives pride of place to manipulating lines, the October 1628 method appears to privilege plane figures.

Does the use of secondary qualities for memory images imply anything about Descartes's understanding of such qualities around 1628? What secondary qualities have in their favor is that they enable one to construct significant images beyond three dimensions; but perhaps just as one needs a three-dimensional object before one can have a colored or a weighty one, one would start the construction of the object using the three geometrical dimensions and only then add other qualities. Yet we must also note that as early as the note on Schenckel, Descartes did not believe that the use of particular kinds of images implied an ontological commitment, for there he remarked that the signification (by images such as hurled spears) might be either true or fictitious. This continues to be the case in the Regulae, where, in Rule 14, he says that the countless dimensions that are conceivable add nothing to the object, but "are understood in the same way whether they have a real foundation in the subjects themselves or have been excogitated out of the willed judgment [ex arbitrio ] of our mind" (AT X 448). 'Dimension' is thus not to be identified simply with 'geometric dimension'. The "Specimen of Descartes's Algebra" preserved in Beeckman's Journal vigorously asserts that this technique applies as much to representing dimensions geometrically as to representing them by means of color, specific gravity, hardness, or any other quality. None of these are meant to be true pictures of material or spatial reality as it is in itself, but as means to the expression of relations for the sake of solving problems. If colors or the different specific gravities of materials can mirror the pro-

portions or even just the order of real or possible relationships, then there is nothing to stand in the way of using them. Simplicity of expression and efficiency in contributing to solutions are the prime desiderata.

An example from Rule 12 helps confirm that this pragmatism about representative devices holds even in the Regulae. There Descartes proposes conceiving colors according to different patterns of lines and rectangles. Someone thinking of the later philosophy might see here a programmatic reduction of secondary to primary qualities. Although I would not deny that it can be construed as a step tending toward that end, his motives seem to be tactical rather than strategic. First of all, the Regulae reflects an awakening interest in anatomy and physiology, but Descartes's use of standard late sixteenth- and early seventeenth-century vocabulary and the lack of detail given in his psychophysiological hypothesis strongly suggest that he had done little more than read about these subjects and that he was trying to adapt what he had gleaned to his method of imaginative representation.^[32] In explaining the process of sense perception, he argues that the senses take on impressions in the same way as wax receives the impression from a seal; the senses then make an impression in the sensus communis, which in turn carries the impression into the phantasia; and finally—although here the example of the wax and seal becomes analogical rather than literal—the phantasia makes its impression on the knowing power. All of this he understands as taking place instantaneously and rigidly; the model he gives is the simultaneous motion of all the parts of a pen when the nib end is moved.

In this context he argues that the sensation of all qualities takes place by similar processes of impression; "thus the first opaque [surface] which is in the eye receives a figure impressed by the illumination endued with various colors; and the first membrane of the ears, nostrils, and tongue that is impervious to the object also thus borrows a new figure from sound, odor, and flavor" (AT X 412-413). Accustomed as we are to Descartes's only slightly later conception (as expressed at the outset of Le Monde, perhaps as early as 1630 and no later than 1633) of an instantaneous motion transmitted through space and along the nerves to the pineal gland, we feel the strong urge to read this as a first, clumsy way of putting that conception, but the interesting thing is that he does not state or apparently

[32] A firsthand knowledge of such things came later. In early 16310, Descartes tells Mersenne that he is studying chemistry and anatomy and learning things that are not in any book (15 April 1630, AT I 137). In late 1632, we find him writing to Mersenne that he is doing anatomical dissections (November/December 1632, AT I 263). His progress must have been prodigious, for he was invited to assume the chair in theory of medicine at the University of Bologna in 1633. See Vincenzo Busacchi, "La chiamata di Caresio alla cattedra eminente di teorica della medicina hello studio di Bologna nel 1633," Pagine di storia della medicina 11, no. 2 (1967): 9-13.

even intend this. The analogy to the motion of the whole pen does not imply that he is thinking of motion along the nerves. The nerves enter in only later, where they are identified as the medium of the active motive power of the body (AT X 414) rather than of the passive reception of impressions. The pen's motion appears simply to confirm that the impression on the sense organ can be transmitted whole and entire in an instant, not that the different parts of the impression are carried along different nerve paths (the Regulae gives no suggestion of this later conception). Descartes simply does not offer much information about the nerves and their modalities; this probably ought to lead one to conclude that he had not yet thought these things out in detail. But it is clear that he still thinks of colored light, sounds, odors, and flavors—not motions—as the agents effectively impressing themselves on the senses, a fact that is scarcely compatible with his having already arrived at a significant primary-secondary distinction.

In this context he goes on to suggest a way of expressing color by figures.

And this [i.e., the notion that the first membrane receives an impression from light, sound, etc.] greatly helps in conceiving all things, since nothing falls under the senses more easily than figure: for it is touched and seen. However, nothing false follows from this supposition any more than from some other, as is demonstrated from this, that the concept of figure is so common and simple as to be involved in every sensible thing. For example, suppose color is some force, you will nevertheless not deny that it is extended, and consequently figured. Therefore what incommodious thing follows if, taking care not to uselessly admit and rashly contrive any new entity, we do not even deny anything about color that pleases others but only abstract from everything else what has the nature of figure, and conceive the diversity that there is between white, blue, red, etc., as that between these or similar figures, etc. [see fig. 11]? The same can be said about all things, since it is certain that the infinite multitude of figures suffices to express all differences of sensible things. (AT X 413)

What appears to be happening is this: On the basis of the physical and physiological aspects of his hypothesis, it is plausible that all sensations make changes in the shape of the receptive membranes of the sense organs. This shape is immediately transmitted, apparently without deformation, along some unspecified route to the sensus communis, which can impress it on the phantasia, which in turn can (analogically) impress it on the knowing power. Whatever one thinks of the nature of sensation, it is undoubted (Descartes asserts) that the thing sensed has extension; this nature, extension, is simple and common to all sensibilia. And if we consider geometry, we see that the variety of figures is so rich that all differences between things can be expressed by them.

Fig. 11. Descartes's speculative example of how various colors might be represented by different geometric figures.

There are several levels in this argument. Descartes allows, as a proponent of analogical method must, that there are other suppositions possible for presenting the differences in colors (he remarks that other people might hold certain beliefs about color that his supposition does not deny, but also that nothing false follows from his any more than from some others; AT X 413). But physical things are extended, and so we are not to be surprised that extension and figure could be transmitted to and within our physiological apparatus. In any case, the figures of things transmitted in the physical and physiological processes will contribute something to the sensation/impression. Moreover, even if there is something fictional about the particular figurative representation we choose (say) for colors, nevertheless the differences in the figures can easily stand in for the differences between things. Perhaps some day we will even be fortunate enough to come upon the precise differences that distinguish them, or at least upon a system of figures that perfectly mirrors the system of relations between colors.

One might recall again a relevant note from the "Cogitationes privatae": "The cognition of natural things by human beings [occurs] solely through the similitude of those things that fall under sense: and indeed we judge that person to have more truly philosophized who will have more successfully assimilated the thing sought to what is cognized by sense" (AT X 218-219). In light of the psychophysiology of Rule 12, what falls under the senses in all cases is impressed figure, if nothing else (though we are not told we can conclude that this is all that can be impressed, and in fact the opposite is suggested). Therefore the one who reasons about natural things will use such figures and perhaps other sensible (and imaginable) things as well to philosophize more truly than one who does not.

It is curious that in some sense Descartes is trying in Rule 12 to take

advantage of both of his alternatives to the memory art of Schenckel. One was "natural," based on real causes: if the cause was identified, its corresponding image(s) or sequence of images in the mind could be reproduced at will. The other was a compromise between the artificial and the natural: a network of relationships might be analogically expressed through otherwise unrelated images (spears, ladders, stairs, and the like). On the one hand, Descartes in Rule 12 wants us to agree that the transmission of images from a thing to our senses to our knowing power is as he describes it and that the extendedness of the objects of sense is a real cause of the extension of the figuration in the organ's membrane; on the other hand, he is willing to be satisfied with analogy, that things are something like this, and with the thought that it is the differences of things and not their essence that are being expressed. Figures are simply marks that can bring these things and their interrelations to mind. He is still fundamentally appealing to the notion that things are related to one another by (not necessarily geometric or algebraic) analogy and proportion.

In the next chapters we will consider how the first part of the Regulae is also caught between the causal and the representative, between the literal and the analogical. But first it might be helpful to conclude with a speculative sketch of Descartes's progress in the use of imagination. In late 1618, the imagination was for Descartes the synthetic cognitive power able to recognize and construe proportions that are presented or revealed discursively, bit by bit (as in the progress of a song or the fits and starts of problem solving). His inclination to give cognitive primacy to imagination was undoubtedly encouraged by Beeckman, who believed that everything in the understanding of nature ought to be picturable^[33] —and thus began a shift to the paradigm (and analogy) of the visible and the manipulable. In the period 1619-162l, in part under the stimulus of his innovations in addressing the general theory of mathematical proportions, be elaborated an ontological epistemology of resemblance, according to which corporeal imagination could figure bodies, and bodies in turn could figure spiritual things. He believed that the chief instrument of discovery and of conceiving proportions was imagination and searched for ways to systematize and methodize it, especially its ability to move from image to image. Two possibilities he explored were that of generating a whole series of images by beginning with causes and that of expressing the relations of sequentialized objects by memory images that somehow mirror actual relations. When we become privy to his thoughts again after a seven-year hiatus, we see that he has universalized the geometrical figuration of relations as the foundation of a problem-solving method (his geometric algebra) but that he has not altogether abandoned nongeometrical images. Then, in the

[33] See van Berkel, Isaac Beeckman, chap. 7, and 317-319 (English summary).

final stage of the composition of the Regulae, after October 1628, he decides to abandon the use of secondary qualities as a part of his problem-solving armamentarium in favor of the marks and symbols of writing and to definitively set aside the use of figures of dimensions above two.

None of this had anything to do with the principal tenets of his later philosophy; for example, he was not motivated by any ontological imperative to reduce ordinary objects to pure extension. Rather, he was driven by the need to invent efficient devices for expressing and solving problems according to proportionality, whether or not those devices had anything directly to do with the way things exist in reality. Nevertheless, the working out of the details of the imaginative method, especially his nascent concern with the physical and physiological transmission of images, began to produce tensions that ultimately led to a breakdown in the theory. The place where those tensions become evident is in the first part of the Regulae, Rules 1 through 12, to which we now turn.