PART II
Imagination and the Regulae ad directionem ingenii

THREE
Ingenium and Figuration The Mathematics of the Regulae

Having discovered the importance of imagination in works from the years 1618-1621, we can now begin to ascertain what they contribute to an interpretation of the Regulae ad directionem ingenii.

The Regulae is unfinished. According to Rule 12, it was to have consisted of three parts with twelve rules each. The first, which is complete in the sense that there are twelve rules (rule headings) with discussion (rule commentary), lays down the basic principles of the method of properly ordering knowledge. The second, for which there are only six rules with commentary (13-18) and another three with just rule headings (19-21), was to have discussed problems that could be understood perfectly, even if the solution was not yet known (AT X 429). The third, sketchily planned but not executed, was to have treated problems not perfectly understood.

Interpretations of the Regulae usually emphasize several things: method, intuition and deduction, the unity of knowledge, simple natures, and the mathematization of thought. Very few emphasize the question of psychology,^[1] that is, the question of the powers of the soul that make intuitus and deductio possible and that allow the development of a method. From our earlier examination of Rule 12's account of the internal senses and its definition of ingenium as the power of treating images whether newly made or remembered, we recognize that the traditional rifle, which speaks of rules for the direction of the ingenium, is intimately tied to psychological matters.^[2] 'Ingenium' has, in English, typically been translated as 'mind', but

[1] Jean Laporte, Le Rationalisme de Descartes (Paris: Presses Universitaires de France, 1945), esp. 43-76, is an important exception, as is also Ferdinand Alquié, La Découverte métaphysique de l'homme chez Descartes, 2d ed. (Paris: Presses Universitaires de France, 1966).

[2] Of course, we cannot be certain what title, if any, the treatise bore in manuscript. In the French inventory of the posthumous papers of Descartes, the Regulae is given under item F: "Neuf cahiers, reliez ensemble, contenant partie d'un Traité des Regles utiles & claires pour la direction de l'esprit en la recherche de la verité." After examining the extant testimonies about the title, Marion argues that the first Latin edition of 1701, version A (Regulae ad directionem ingenii ), ought not to be completely authoritative. Just as crucial as the themes of rules and the direction of the spirit is the theme of the search for truth. He contends that the title of the French inventory is best; in the Latin of Pierre Borel, author of the Vitae Renati Cartesii (1656), it would read Regulae utiles et clarae ad ingenii directionem in veritatis inquisitione.

this is far too generic a concept to render even what Descartes expressly says about it. We might then well begin by asking, What is ingenium?

A. THE NATURE OF INGENIUM AND THE CONTEXT OF PHILOSOPHICAL PSYCHOLOGY

In English, the term is usually rendered as 'mind'; a revised version of a recent translation uses 'native intelligence'.^[3] The standard, hardly controversial, but also not very illuminating French rendering is esprit.^[4] In the few extant French letters before 1630, Descartes used 'esprit' in French wherever 'ingenium' might be expected in Latin. But Rule 12 makes it sufficiently clear that Descartes had in mind something rather more determinate than any of these terms conveys, Ingenium, as we have seen, is defined there as the action of the knowing power "when it at one moment forms new ideas in phantasia, at another applies itself to [or bears down on, concentrates on] those already made" (AT X 416). The formation of new ideas in phantasia, however, was defined a few lines earlier as imaginatio proper, and concentration on those already formed amounts to what was defined as remembering (reminisci ).^[5] Ingenium is therefore the general faculty of forming and acting upon images, which, because of the syn-

[3] Haldane and Ross typically use 'mind', and for the plural, 'mental powers'. CSM uses 'mind'; in Selected Philosophical Writings (1988), a one-volume selection of CSM, 'mind' has been changed to 'native intelligence', which, as we shall see, more accurately conveys an essential aspect of ingenium. In the present work, ingenium and ingenia will be left untranslated.

[4] The 1644 Latin translation of the Discourse on the Method authorized by Descartes renders esprit as ingenium, and the 1647 Frenching of the Meditations renders the few occurrences of ingenium as esprit.

[5] The Latin reads: "proprie autem ingenium appellatur, cum modo ideas in phantasia novas format, modo jam factis incumbit." The definitions of reminiscence and imagination/conception read: "si ad imaginationem solam ut diversis figuris indutam, dicitur reminisci; si ad eamdem ut novas fingat, dicitur imaginari vel concipere." The activity of imagining per se, that is, the application of the knowing power to the imaginative organ in order to shape or contrive new ideas, would seem to be exactly what the first modo clause of the ingenium definition describes. Similarly, the second modo clause appears to describe the application of the knowing power to imagination, insofar as it is already arrayed with various figures (with a strong sense of bearing down on the figures or ideas suggested by incumbit ).

onymy between 'imaginari' and 'concipere', would also mean the faculty of forming and acting upon what is conceived. It can be considered autonomous in that it does not directly depend for its contents on the external world but on the operations of the cognitive or knowing power in the organ phantasia. The very next paragraph of Rule 12 further emphasizes the unity of the power in question by arguing that memory, at least insofar as it is of corporeal things, is a power of imagination ("but the memory, at least that which is corporeal and similar to the recordation of beasts, is not at all distinct from imagination"); moreover, the same passage assigns to imagination the powers of moving (in addition to being moved by) intellect and of acting upon (in addition to being acted upon by) the senses.

The power of imagination/ingenium undergoes a rapid expansion of its psychophysiological competencies in these passages from Rule 12. In light of this and the definition of ingenium proper as imagination plus reminiscence, the Regulae ad directionem ingenii appears to be rules for the direction of the faculty of conceiving images, understood as a single, unified power.^[6]

Pressing too hard on synonymy and the exact wording of a text can lead to distortions in interpretation, of course. One could point out, for instance, that the language of the Regulae, even that of Rule 12 taken by itself, is not always consistent; at the very least there seems to be frequent terminological vacillation. For example, 'deductio', 'inductio', and 'enumeratio' are all used for what is arguably the same mental process.^[7] In Rule 12, 'intellectus' is sometimes used as an equivalent for 'vis cognoscens', the knowing power howsoever it manifests itself, but at other times in a strict sense of the knowing power acting on its own, apart from imagination. Again in Rule 12, the opposition of 'body' and 'spirit' is sometimes formulated alternatively as that of 'matter' and 'intellect'.

These terminological tensions, as we might call them, have not gone unnoticed individually, but their systematicity has been largely hidden from view by an almost total unawareness of the relevance of traditional philosophical psychology and the degree to which Descartes initially worked within its presuppositions. In the later works there are only hints and traces of this earlier concern. It is not so much that Descartes deliberately hid this from view, for instance by "sanitizing" the autobiographical account of his intellectual career in the Discourse. Descartes was under no obligation to describe every twist and turn of his philosophical education, especially not

[6] Wolfson remarks a tendency in early modern Scholasticism to reduce the number of internal senses, even to a single one. The example he gives is Eustace of St. Paul, an early seventeenth-century writer known to Descartes. Wolfson, 'Internal Senses in Latin, Arabic, and Hebrew Philosophic Texts,' 126; see also Etienne Gilson, Index scolastico-cartßsien (Paris: Alcan, 1913). S.V. 'imagination', pp. 137-139.

[7] But see chap. 4, Secs. D and E, below, for possible distinctions.

those paths that he had decided were impassable. (Moreover, the part of his philosophical apprenticeship that I am reconstructing here turns out to be at least consistent with most of what he says in the Discourse and elsewhere.) Nor is it the case that he ultimately rejected imagination as cognitively unimportant. Rather, after the Regulae he found it necessary to delimit its domain more carefully; yet what remained to it included nothing less than the whole of geometry and therefore also the substance of the physical world. But in comparison with the imagination of his earliest philosophical speculation, this was a very considerable restriction, for through principles of analogy its scope had formerly extended into the highest realms of spiritual truth.

It is a measure of the degree to which Descartes's writings shifted the philosophical horizon that we are scarcely aware of this development of his thought. That is, Descartes changed the terms and framework within which physiological, philosophical psychology was conceived and set an agenda radically different from the preceding tradition, which had drawn not just on Aristotle but on Plato and the Stoics as well. As a result it is easy to be insensible to the rich vocabulary and careful distinctions to be found in that tradition, a vocabulary and distinctions that are almost inevitably obscured in modern translations and interpretations.^[8] One need only compare English-language translations of Descartes's psychological terminology in the Regulae to the original Latin to recognize a conceptual flattening. 'Ingenium' is the outstanding example of this flattening. To render it as 'mind' or 'spirit' is to miss its specific character. Even the French 'esprit', which would seem to have Descartes's implicit authority, is far too approximate to come to terms with it.^[9]

The evidence of Rule 12 presented so far should make it compulsory that we look more deeply into the possibility that the universe of the Regulae is different from what we have thought. In beginning this investigation it is important to realize that although imagination and ingenium are points of focus, they lead into a different world of philosophical discourse. Moreover, what is at issue is not simply the Regulae or the early Descartes, so that those whose major concern is the "mature" philosophy might safely ignore these matters. Earlier we noted that Descartes justifies his use of

[8] As Descartes found it the vocabulary was almost exclusively Latin. By 1600, the traditional psychology had already been simplified and even vulgarized, and it did not survive long enough to be carried over fully into philosophy written in the vernacular languages. Indications of the remnants of this psychology in the seventeenth and the first half of the eighteenth century can be gleaned from John W. Yolton, Perceptual Acquaintance from Descartes to Reid (Minneapolis: University of Minnesota Press/Oxford: Basil Blackwell, 1984).

[9] The significance of ingenium has escaped even the philosophical subtlety and historical learning of Marion, who in his French translation and commentary uses esprit without cavil; nor is ingenium included in the index or in the list of Latin-French correspondences.

'idea', a term central to his later thought, by noting that philosophers use it "for signifying the forms of perceptions of the divine mind, although we recognize no phantasia in God" (AT VII 181; the French has "for signifying the forms of the conceptions of the divine understanding, although we do not recognize in God any fantasy or corporeal imagination" [AT IX 141]). If this is not enough to convince us of the relevance of these investigations of imagination for understanding Descartes as a whole, we need only remind ourselves once more that Descartes made the cogito , rendered into French as je pense and into English as 'I think', a vital part of the subsequent history of philosophy. By following the course of the Meditations, a thinker can presumably recognize her essence as res cogitans, the thing that engages in cogitatio—which in the Regulae is assimilated to imaginatio.^[10] We already recognize that in Scholastic psychology cogitatio is the activity of the vis cogitativa, which, along with imaginatio, is one of the internal senses, and that there was already in Avicenna and Averroês a tendency to assimilate the active functions of imagination to cogitativa. Is it not possible that if we do not take this into account, if we do not search out the ways in which a tradition may have shaped or at least affected Descartes's understanding of these matters, we run the risk of missing dimensions that are essential to the entire philosophy of Descartes?

B. THE MEANING OF 'INGENIUM'

In his commentary on the Discourse on the Method, Etienne Gilson distinguishes three senses of 'esprit' (having noted that the Latin equivalent is 'ingenium'): first, thought as substantial and personal—and, taken in its most general acceptation, as opposed to extension; second, memory and imagination, as distinct from reason in its proper sense (here Gilson refers to Rule 12); third, spirit as distinct from 'soul' (the latter term tends to include vegetative and motive powers and therefore might encourage the confusion of body and soul),^[11] But, as the definition of Rule 12 already suggests and as I hope will become clear from the remainder of this chapter, ingenium as used by Descartes in the period before 1630, though most closely resembling the second of the senses identified by Gilson, not only encompasses aspects of the others but also goes beyond them. Descartes's notion of 'ingenium' clearly takes on the personal and substantial aspect

[10] Cf. AT X 387 1. 12 with 388 1. 3. Giovanni Crapulli believes on the basis of the 1684 Dutch version N (which has "beweeging van denking" throughout) that "motion of imaginatio " should be emended to "motion of cogitatio. " See René Descartes, Regulae ad directionem ingenii, ed. Giovanni Crapulli, International Archives of the History of Ideas, no. 12 (The Hague: Martinus Nijhoff, 1966), 22. A, H, and AT all have imaginatio, however.

[11] René Descartes, Discours de la méthode, 5th ed., ed. Etienne Gilson (Paris: J. Vrin, 1976), 86.

indicated in Gilson's first sense of 'esprit', and if it does not really include the vegetative, it certainly includes the motive powers by virtue of phantasia's central control of the nerve and motor systems. This personal substantiality is understood as corporeal (and thus extended) as well as intellectual and spiritual: ingenium emphasizes the human person's endowment as a particular, corporeal-spiritual being, who because of those particularities has a somewhat greater or lesser aptitude for realizing the potentialities, especially cognitive ones, that are common to all human beings qua human. The notion therefore does not presume the radical dichotomy of thought and corporeality to be found in the later Descartes. Moreover, Descartes's ingenium is a cognitive power that is able to recognize the forms and relations of images and to manipulate them accordingly, so that it exercises functions of the Avicennan vis cogitativa and the Thomist particular reason.

In classical Latin, 'ingenium', a commonly used word derived from in -and gignere (to bear, produce, beget) and thus suggesting something inborn or innate, indicated in its most basic sense the sum of inborn faculties or powers. Of human beings it indicated the original power of inborn disposition, with also the more specific sense of a strong and firm soul. With regard to the intellect, it could be used generally of the powers of the mind and extended metonymically to the whole human being; used particularly, it could be synonymous with prudence, ingenuity, and the like, indicate single faculties of mind, or refer specifically to the faculties of invention or phantasia. It could be used of deficient or bad parts or characteristics of mind or soul; and, finally, it could occasionally be used of beasts and other natural things in the sense of their nature or faculties.^[12]

'Ingenium' is not uncommon in medieval Scholastics. For the most part it is not singled out for technical or specialized use (unlike 'ratio' or 'phantasia') but continues to convey the chief meanings of classical Latin usage. In Thomas Aquinas, for example, it can indicate ingenuity or cleverness, but also the sum of human powers or human intellectual powers; and in some formulations it suggests the properly human powers of knowing that therefore fall short of reaching the things of revelation.^[13]

The term does have a more systematic use in the works of Hugh of St. Victor (d. 1141), including the Didascalicon and his writings on meditation. In these works ingenium is paired with memoria as the two natural powers (naturae ; they are contrasted by Hugh to practice and discipline) that are necessary to prolonged study or meditation. Memoria enables human beings to retain what they have experienced and read, whereas inge-

[12] S.v. 'ingenium', Thesaurus linguae latinae, 25 vols. (Leipzig: B. G. Teubner, 1900-), vol. 7, pt. l, 1522-1535.

[13] See Petrus De Bergomo, ed., In opera Sancti Thomae Aquinatis Index seu Tabula Aurea (Paris: 1880; phototype ed. Alba-Rome: Editiones Paulinae, n.d.), 505.

nium is the natural aptitude for grasping or conceiving those things properly in the first place.^[14]

The word had a programmatic importance for Italian Renaissance humanists, as the human power of understanding and invention that in its flexibility and adaptability underlies the effective use of words and that contrasts with a reason (ratio) that deals with the eternal and thus transcends ail things specifically human.^[15] In the late sixteenth-century commentary on Aristotle's dialectics by the Jesuit cardinal Francisco de Toledo, a work that was certainly available to Descartes at the Collège Henri IV at La Flèche, 'ingenium' is used to indicate the highest rational powers of recognition (the fundamental modes of the syllogism, he says, depend on principles revealed by natural light from which the human ingenium is unable to dissent). The word is also not infrequent in the commentaries on Aristotle produced at the Jesuit University of Coimbra toward the end of the sixteenth century, and it even takes on a quasi-technical meaning in the one devoted to On Generation and Corruption. There 'ingenium' is equivalent to the embodied human spirit, the individual human being as a particularized corporeal manifestation of the species. Thus the term is broad enough to cover the peculiarities induced by individualization as well as the general nature and powers due to the species.^[16]

Ingeniurn takes up slightly more than a full two-column page in Rudolphus Goclenius's early seventeenth-century Lexicon philosophicum, which concisely summarizes the variety of learned acceptations of Latin and Greek philosophical terms.^[17] Goclenius starts with the key general and specific

[14] See book 3 of Hugh of St. Victor, The Didascalicon of Hugh of St. Victor: A Medieval Guide to the Arts, trans. Jerome Taylor (New York: Columbia University Press, 1961), esp. chaps. 7 and 8. The Didascalicon is perhaps the premier medieval treatise on the nature of science and method. Ingenium is prominent also in Hugh's "De modo dicendi et meditandi," in J.-P. Migne, ed., Patrologiae Cursus Completus, 2d ser. (Paris, 1854; known as Patrologiae Latinae ), 176: 875-880, esp. 877. The relationship of Hugh's work to Descartes and possible influences of this constellation of topics on Descartes's thinking deserve further investigation.

[15] See Ernesto Grassi, Heidegger and the Question of Renaissance Humanism: Four Studies, Medieval and Renaissance Texts and Studies, vol. 24 (Binghamton, N.Y: Center for Medieval and Early Renaissance Studies, 1983), 20, 73-76; and Hanna-Barbara Gerl, Einführung in die Philosophic der Renaissance (Darmstadt: Wissenschaftliche Buchgesellschaft, 1989), 154—163. Ingenium was fundamental to the invention of concetti or conceits in baroque aesthetics; see Joseph A. Mazzeo, Renaissance and Seventeenth-Century Studies (New York: Columbia University Press/London: Routledge & Kegan Paul, 1964), 29-43, and M. Fumaroli, ed., Critique et créa tion littéraires en France au xvii' siècle, Colloque International du Centre National de la Recherche Scientifique, no. 557, Paris, 4-6June 1974 (Paris: Editions du Centre National de la Recherche Scientifique, 1977).

[16] See Franciscus Toletus, Introductio in dialecticam Aristotelis (Venice, 1588), 163; Coimbran College of the Society of Jesus, In duos libros de Generatione et Corruptione Aristotelis, 2d ed. (Lyon, 1606), 485-489.

[17] S.v. 'ingenium' in Rudolphus Goclenius, Lexicon philosophicum quo tanquarn clave philosophiae fores aperiuntur (Frankfurt: M. Becker, 1613; photographic reprint Hildesheim: Georg Olms, 1964), 241-242.

uses: the most general is for the "inborn power and nature of any thing whatever"; the specific proper meaning indicates "the power of successfully and easily discovering and contriving in human beings, and the power of memory"; and the specific improper refers in analogical use to animals and in metonymic use to arts discovered through ingenium. His discussion makes several points important for our purposes. He remarks that

ingenium spoken most properly is the constitution of the rational faculty of the rational soul for understanding something or discovering or teaching. Or ingenium is the natural aptitude or faculty by which we teach, and through [which] we ourselves think, or discover something. The genus of ingenium is euphuia,^[18] more broadly indeed the latter is open to the former, since (generally it is the native goodness of soul or body) specifically it is the good constitution by nature of the rational soul now with respect to the true, now with respect to the good, nor is euphuia only of ingenium but also of natural judgment. Scheckius, Topic. at 39, agrees: "This in fact is euphuia, to be able to rightly elect the true and flee the false." But for Aristotle the part of ingenium is the natural facility for judging something.

Goclenius remarks further that a function of ingenium is eumatheia, "the right constitution for learning disciplines" and the habit of swiftly discovering middle terms, and he distinguishes it from sunesis, which is nevertheless affine to ingenium. After noting political, pneumatic (spiritual), and theological senses of an ingenium apart from judgment, he points out that Scaliger differs from those who subordinate judgment to ingenium and quotes the Jesuit Peter Molina, who said that "philosophy is the file of judgment, and the whetstone of ingenium," to show that memory is not necessary for good judgment. He concludes,

The variety of ingenium depends sometimes on the temperament of the body, sometimes on the various disposition of the mind, and the constitution of the organs, and of the auxiliary faculties, as of the phantasia (imaginatricis).
The distinctions of ingenium are various. For the ingenium is subtle, or thick, acute or obtuse. Perspicacious or less perspicacious, quick or slow, sharp or less sharp (because of which also sharpness [acrimonia] is attributed to judgment).

Thus ingenium has chiefly to do with the natural powers of things and, in human beings, with the natural powers associated with the rationality that differentiates them from animals, but that also includes the corporeal basis attendant on their being rational animals. It is associated with quickness of judgment and learning and the right constitution for learning in a

[18] This term and also the eumatheia and sunesis that Goclenius subsequently mentions appear in Aristotle's Nicomachean Ethics. Euphuia is 'natural gift', 'good natural parts', or 'cleverness' (e.g., at 1114b3-10); eumatheia is 'readiness in learning'; sunesis 'intelligence in practical judging'.

disciplined or scientific way; it is closely dependent on the disposition of the physical organs that aid the mind, especially the imagination.

The advantage of referring to Goclenius is that he reflects learned usage contemporary with Descartes's youth. 'Ingenium' was not just a word for philosophers' and theologians' treatises, however. We must recall that Latin was the language of instruction and communication at La Flèche, both inside and outside the classroom, and so Descartes would surely have picked up any colloquial meanings that the word had. It is interesting to note, then, that in assessing the performance of their pupils, the Jesuits used 'ingenium' as one of their categories, more or less synonymous with what we would today call "natural ability," "talent," or "aptitude." Thus René the schoolboy would have heard himself and his mates evaluated with respect to their ingenia in the following terms: mediocre, sufficiently acute, optimum, dull, very sharp, deficient in ingenium, does not lack ingenium, of moderate ingenium, somewhat acute, most perspicacious, lit-de apt for logic, of at most mediocre ingenium, minimally sharp, obtuse, not well constituted by ingenium, ingenious boy, has a good memory, less prompt ingenium, of sharpest ingenium and outstanding in memory, various and mutable ingenium, acute and subtle, stupid.^[19] The ingenium the instructors were assessing was an individuated capacity for learning, particular to each student.^[20] in which the premium was placed on quickness, penetration, and good memory.

C. DESCARTES AND INGENIUM

It is reasonable to think that the young Descartes would have been affected by, or at least aware of, the standard technical acceptations of philosophical terms common in his day, as well as the meanings of everyday language, even when he ultimately chose (as in the case of intuitus ; see AT X 369) to adapt terms to his own purposes. I wish to suggest, then, that 'ingenium' as used by Descartes, at least before 1630, lies on the semantic axis laid out by usage common in the late sixteenth and early seventeenth century, a usage that is in fact not far removed from that of classical times but that underwent developments in accord with the prevalent psycho-physiology. This axis would of course not necessitate that every occurrence of the term in Descartes bear the same meaning. But each occurrence

[19] All of these are taken from "report cards" kept at La Flèche; see Rochemonteix, Un Collège deJésuites aux XVII et XVIII siè, 4;205-206, 348-350.

[20] Given that the grade list Rochemonteix published evaluates 27 boys and considering that marks for ingenium were usually given in just one or two words, there is relatively little duplication from student to student. This would indicate that the instructor took some care to differentiate each case and thus confirms the essentially personal and individual character of ingenium.

should typically refer to inborn powers that are proper to human beings as such. More likely than not, the term will indicate intellectual or cognitive powers, often with at least some suggestion of the individualization or personalization of them due to the corporealization of spirit. 'Ingenium' therefore would be best understood in the first instance as particular corporealized spirit, that is, spirit that includes some of the peculiarities arising from this corporeal particularity.^[21] Putting aside for the most part the so-called vegetative powers (nutrition, reproduction, and the like), ingenium would be the native human endowment that gives rise to a human essence exhibiting personality and character. With emphasis placed on the cognitive side, it would be the embodied mind that has access to the fundamental principles of knowing (the natural light), and therefore the corresponding cognitive activity or knowing power would reflect both corporeality and spirituality. By virtue of ingenium, each human being would have all the peculiarities of his or her personal existence, but that personal existence would also include the powers and functions that are common to all human beings per se.

The reader who considers these reflections to be sufficient might proceed immediately to the next section. It is nevertheless illuminating to find them supported by Descartes's Latin writings from before 1630. In his correspondence with Beeckman the word occurs frequently. On 24 January 1619, Descartes inquires after his friend's health in a way that emphasizes the cognitive side: "You must believe that my concern is not just science alone but you yourself, not just ingenium, although it is the greatest part, but the whole man." In the next paragraph he says that he has been working not on an important (and otherwise unidentified) treatise that Beeckman had urged him to write but rather on drawing, military architecture, and Flemish, "things which without doubt your ingenium, occupied with higher things, will contemn." Here the sense again suggests the higher, intellectual faculties, although it is also possible that both occurrences include the wider spiritual aspects of human being as well, including character.

On 23 April 1619, Descartes writes, "For you truly are one who roused the slothful one, recalled an erudition that had almost lapsed from memory, and led the ingenium wandering from serious occupation back to better things." In the next paragraph he recalls the discoveries using the new mathematical compass that he had reported in a previous letter and says he is planning a treatise on the subject: "but now I have not worked for a

[21] For example, those whose brain matter was too soft could easily form perceptions but retain them only with difficulty, whereas those who had a very hard brain matter would typically be insensible to perceptions but could retain with ease those that managed to impress themselves.

month, because to be sure [my] ingenium was so exhausted by these discoveries that it no longer was sufficient for discovering those other things which I had hitherto resolved to seek. It will suffice, however, for preserving the memory of you perpetually." The "slothful one" that Beeckman had roused might in fact be (speaking grammatically) 'ingenium'; since the second passage allows for the exhaustion of 'ingenium', there is no reason why it could not be lazy as well. This certainly would not conflict with the second passage from the 24 January letter, in which Descartes had admitted to occupying his ingenium with relatively insignificant things.

On 29 April, Descartes writes asking Beeckman to consult Raymond Llull's Ars brevis for him and comments, "I have such confidence in your ingenium that I am certain you will easily see those things (if there are any) which are necessary to the intelligence of other things but otherwise omitted, which he [= a follower of Llull's with whom Descartes had conversed] calls 'keys'." Here the usage seems to emphasize that aspect of the cognitive abilities that we call ingenuity or shrewdness, the power of recognizing what is not readily apparent.

In these early letters ingenium is associated with intellect but implies a good deal more. It undertakes projects, it aims at discovery or invention, it remembers, its exercise requires effort, and it can be affected with peculiarities of character like sloth and physical or physiological states like exhaustion.^[22]

The only other Latin letter with an occurrence of 'ingenium' from before 1630 is conjecturally ascribed to 1628; it is Descartes's evaluation of the book Lettres du Sieur de Balzac.^[23] 'Ingenium' appears five times: attentive ingenia are said to be frustrated by the insubstantiality of many writers; in primitive times, when words were the sincere expression of one's mind, "there was in superior ingenia a certain divine power of eloquence, which flowing from zeal for truth and abundance of sense led primitive men out of the forests, imposed laws, founded cities, and the same had the power of persuading and simultaneously ruling"; Balzac makes arguments clear and simple enough to awaken trust in common people, yet "they are nonetheless so solid and true that the greater anyone's ingenium is, the more certainly he is convinced"; "if he decides to speak of himself, he does not fear contempt for laying open illnesses of body and the feebleness of nature nor envy for not dissembling the deserving merits of his ingenium";

[22] There are in fact only two other Latin letters extant from this period: a lengthy one concerning mathematical and physical matters (26 March 1619) and a one-paragraph message (20 April 1619), both addressed to Beeckman and neither of which uses ingenium.

[23] Balzac was a friend of Descartes's. It is conjectured that the letter was addressed to a friend of both, perhaps Jean Silhon. See Descartes: Correspondance, ed. Charles Adam and Gèr-ard Milhaud, 8 vols. (Paris: Félix Alcan [vols. l-2]/Presses Universitaires de France [vols. 3—8], 1936-1963), 1:30 n. 1.

and posterity will judge favorably "this candor and the ancient [i.e., like that of the ancients] character of an ingenium set above the vulgar." Even more clearly than in the letters of nearly a decade earlier, ingenium is as much a matter of general character, abilities, and judgment as of intelligence, and the intelligence described is as much practical as theoretical.

From these letters we see that ingenium is the greatest part of the human being; it engages in science, more generally in intellectual projects, and is the power by which we make discoveries; it can be qualified as being higher or lower, greater or lesser, slothful or industrious, which suggests that it constitutes at least part of what is called virtue, vice, and character. We might call it native intelligence, with the understanding that it is intelligence in all walks of life, including the intelligence of sensibility as well as of intellect; but even this probably restricts ingenium too much to the cognitive realm, and therefore it would probably be better to speak of the native (i.e., inborn) human endowment.^[24]

D. INGENIUM AND THE PRINCIPLES OF INNOVATION AND DISCOVERY

Descartes's Latin letters are not the only relevant source for his use of 'ingenium': there are also the notes of the "Cogitationes privatae." Indeed, ingenium, imagination, and mathematics are discussed in these private cogitations in a way that intimates the connection between them.

One note announces a fictive book, the Thesaurus mathematicus of Polybius the Cosmopolite, which will treat the means of solving all mathematical difficulties and in which "is demonstrated that nothing more can be done with regard to these by human ingenium"; it promises as well to relieve the tormenting labors of those who spend day and night becoming trapped in mathematical Gordian knots "and uselessly consume therein the oil of ingenium". (AT X 214). This ingenium that can become exhausted in mathematical labors is clearly in line with what we have previously seen. Another entry helps deepen the conception of ingenium, which we already know to be qualifiable in various ways.

For all ingenia determinate limits are prescribed that they cannot transcend. If some cannot use principles for discovery because of a defect of ingenium, they can nevertheless know the true reward of the sciences, which suffices them for carrying out true judgments in the estimation^[25] of things. (AT X 215)

[24] Norman Kemp Smith suggested translating 'ingenium' as 'total mind-body equipment', which captures the essence of the matter. See Kemp Smith, New Studies in the Philosophy of Descartes: Descartes as Pioneer (London: Macmillan, 1952), 15 l, 160.

[25] The term 'aestimatione' may implicitly refer to the internal sense vis aestimativa.

The first sentence asserts that ingenium is inevitably finite and limited. The second makes clear that it is not only limits due to the nature of inge-nium that Descartes has in mind but also those that have to do with the particular constitution of the individual's ingenium. The point, however, is that although defects of ingenium might make it impossible for someone to make discoveries directly from first principles, it does not affect the ability to make true judgments; apparently ingenium is the name for that power human beings have to assess and deal truly with whatever they meet in the course of their lives, regardless of their ability to reason from first principles.

The next note concerning ingenium, quoted already in chapter 2, is surprisingly clear about how far beyond the cognitive it goes.

There are certain parts in all ingenia that, when even lightly touched, excite strong affects: thus a boy with a strong spirit [forti animo], having been scolded, will not cry but get angry; another will cry. If it is said that many and great calamities have happened, we will be saddened; if it is added that some evil person was the cause, we will get angry. The passage from passion to passion [occurs] through neighboring ones; often, however, the passage from contraries is more robust, as when at a joyful party there is suddenly announced a sad event. (AT X 217)

Here ingenium has to do with the sensitive part of the soul in the amplest sense of the term: any part of the human being that is involved in a sensitive response is included. The full range of human affectivity, whether it is emotional, externally sensory, internally sensory, or rational, is embraced by ingenium. It might therefore be rightly conceived according to this note as the soul insofar as it is more than vegetative, that is, involved in more than the physical processes of constructing, maintaining, and reproducing the body. What Descartes is discussing in this note was of course treated many years later as passions of the soul. The affective, the sensitive, and the cognitive powers of ingenium are thus inborn and part of the nature of the individual.

What is at issue here is the individual native human endowment that makes the human being this person rather than that, yet still makes him or her a fully human being. One can have a limited or defective ingenium; one can be ingenious or industrious or slothful; one can be capable of both discovery and judgment, or just of judgment.

It is precisely because the fundamental powers of ingenium are common to all that it is capable of regulation. This aspect becomes clear by juxtaposing two other notes from the private cogitations:

As a youth, whenever ingenious discoveries were presented, I asked myself whether I could discover [them] for myself, even without having read the author: from which I gradually noticed that I was using fixed rules [certis regulis]. (AT X 214)

and

The sayings of the wise can be brought back [reduci] to a certain very few general rules. (AT X 217)

Inventions that were ingenious (ingeniosis inventis ), that showed the use of an energetic ingenium and were reinvented by the young Descartes simply from hearing of them without any explanatory gloss, led him little by little to recognize that this use of the ingenium proceeds according to certain rules; and he even gained the insight that the sayings of the wise, of those who know how to join science and virtue,^[26] can be led back to rules. What we have here, then, is an adumbration around 1620 of the field toward which the Regulae was directed: the proper use of the ingenium according to certain simple rules that are themselves inherent in ingenium. That is, the native human endowment by its very nature is capable of directing itself well if it recognizes the essential characteristics of its nature. Thus ingenium is also closely related to another theme found in both the "Cogitationes privatae" and the Regulae, that even without a conscious knowledge there exists within the soul a small number of principles, rules, sparks, seeds—as they are variously called—that are sufficient for discovery and judgment about all things.

It is almost just a corollary, then, that any theory of method, whether a method of invention for those blessed with a superb ingenium or simply a method of judging aright for those who have no more than the powers of ingenium common to all, would find its leading principle in the ingenium itself; and that such a theory would have not just a cognitive purpose, and certainly not just the goal of pure intellection, but also a practical purpose: the guidance of judgment in all things that are susceptible of judgment, including those things that the sensitive, responsive human spirit encounters in everyday living.

E. THE MATHETICS OF INGENIUM IN THE REGULAE

Ingenium, in a better than first approximation to Descartes's meaning, is the native endowment of the human being who is composed of body and soul (thus it would not be relevant to the soul that has been liberated from the body after death). All have this native endowment, but because of the particularities of their individual being, people would have a less or more retentive memory, a lesser or greater capability of imagining geo-

[26] At the beginning of the account of the Studium bonae mentis in his biography of Descartes, Baillet describes the Studium as "considerations on the desire we have to know, on the sciences, on the dispositions of the spirit for learning, on the order one must keep for acquiring wisdom [la sagesse ], that is, science with virtue, in joining the functions of the will with those of the understanding" (Baillet, Vie, 2:406; cited at AT X 191).

metrical figures, the need to exercise less or more attention to sense properly, and so on. However, the very fact that this native endowment is the result of the coexistence of a knowing power and a body, a coexistence with typifying characteristics, means that the native endowment of every human being can be employed similarly. Similarity does not guarantee equal success from person to person, but it does ensure that certain general principles or rules can be educed for the proper use of the native endowment. This native endowment, in particular its cognitively relevant aspects, would be most properly called ingenium.

What does this imply? In light of the later Descartes we are tempted to conclude that he is simply giving us the kind of division of the human spirit, the anatomy of the res cogitans, that is characteristic of the Meditations, where we find thinking anatomized into sensation, imagination, and pure thinking. But we should recall that in the Meditations the division of the soul comes about as a result of the division of ideas into different kinds: those that appear to come to us from an external world (adventitious ideas), those that we make (factitious ideas), and those that are innate. The ideas that occupy ingenium certainly may be of the first two kinds, as the definition of Rule 12 assures; and, as shall appear in the course of this analysis, ingenium can also work with ideas that might properly be called innate. Yet approaching the division of the soul by way of ideas is foreign to the Regulae .

Descartes uses 'idea' in the Regulae twenty-two times; except for one, all occurrences come in Rule 12 and after. 'Idea' is used in the Regulae not in the sense of the Meditations, however, but in a more restricted one. If we put aside the exception of Rule 4, it is always used to indicate particular contents of phantasia. Thus, in the parlance of the Meditations, 'idea' refers either to an adventitious or to a factitious idea but not to an innate idea proper to pure thinking (like the concept of triangle or the idea of God). 'Idea' in the Regulae can therefore be taken as synonymous with 'corporeal image' or 'corporeal figure' or, to use a term that Descartes employed in the early 1620s and that was the standard Scholastic term for the contents of the internal senses, 'phantasm'. At any rate, to overemphasize 'idea' in the Regulae would be a mistake, for it is merely a synonym for images within internal sense psychology.^[27]

[27] Roger Ariew and Marjorie Grene point out that in seventeenth-century literary usage 'idea' referred to images, usually those of sense; there was "a more obscure and ambiguous complex of philosophical definitions," the central one being the exemplars in the divine mind. See Ariew and Grene, "Ideas, in and before Descartes,"Journal of the History of Ideas 56, no. 1 (January 1995): 87-106; and also Stephen Gaukroger, "Descartes's Early Doctrine of Clear and Distinct Ideas," Journal of the History of Ideas 53, no. 4 (October-December 1992): 585-602. For the occurrences of 'idea' in the Regulae, see J.-R. Armogathe and J.-L Marion, Index des Regulae ad directionem ingenii de René Descartes, Lessico Intellettuale Europeo, no. 10, Corpus Cartesianum, no. 1 (Rome: Edizioni dell'Ateneo, 1976), s.v. 'idea'. The one usage in the Regulae that does not conform occurs in Rule 4, at AT X 376 1. 19. In the stratigraphic theory of composition, this is considered part of Rule 4-B, with which Descartes is supposed to have begun the Regulae in October or November 1619, that is, in the period leading up to his dreams of the night of 10-11 November 1619. This occurrence in Rule 4-B is odd, because it is the only one in the Regulae that does not have the sense 'corporeal image' but instead approaches the sense it has in the Meditations (in the Discourse both senses appear). Is this not a reason to doubt the very early dating that the stratigraphic theory attributes to 4-B?

'Ingenium' as Descartes specifically defines it in Rule 12 is not intrinsically concerned with the provenance of the image but rather with the ability of the knowing power to occupy itself with it, whether it has come from sense, memory, or the activity of the knowing power itself. The cognitive power's act of occupying itself with images as such is ingenium. In this respect it could be said to resemble what we call the free play of the imagination. However, it is important to keep in mind that this play of the imagination is the knowing power's play and thus that it always retains a cognitive purpose. The freedom of this play is the power of variation for the sake of finding something interestingly the same or different, that is, for the sake of discovery.

For example, the activity of constructing a geometrical proof would be largely in the domain of ingenium. In trying to prove that the three angle bisectors of a triangle intersect at a single point, we would ordinarily either just imagine a triangle with three angle bisectors, or, if our imaginative capacity were limited, we could draw a picture of a triangle with its angles all bisected. Then we would try to conceive how to go about the proof; in our imagination or on paper we would speculatively add new lines or follow any other strategy of modifying the figure that might suggest itself. Now clearly the drawing of a triangle involves our nerves, muscles, and limbs, as well as the apparatus of the external world, and as such it cannot be conceived as an act of ingenium alone, at least not in the strict sense of Descartes's definition. But the act of drawing is a direct consequence of the ingenial activity, so that especially given Rule 12's conception of phantasia as the originator of muscle motions, it is not fanciful to call it an act of ingenium. Moreover, insofar as the cognitive power is looking at a figure on paper with the intent of coming to a proof of the proposed theorem, the sensation involved is part of the cognitive power's occupying itself with the idea, and so it, in turn, may also be said to be an ingenial act.

As we have just characterized ingenium, it looks mathematical, or rather geometrical. As such, the psychophysiology of Rule 12 could be seen as an introduction to the figurative mathematical representation of problems that Descartes takes up in earnest in the second part of the Regulae, espe-

Fig. 7. Discrete elements are used to picture something enumerable by a counting number.

cially Rules 14 through 21. The art of mathematical representation taught there is without doubt ingenial activity. To recall the words of one of the "Cogitationes privatae," the imagination can use figures to conceive corporeal things. But is ingenial activity confined to the representation by "bare figures" advised in Rule 14, or is it wider still? One thing that is clear is that the representations mandated by that rule are not of physical bodies but rather of the terms of problems and that we learn not just how to introduce quantitative measure into the terms of problems but also how to use figures to present schematically the relationships implied in a problem and between its terms. As Rule 14 points out, we are not to use just any figures but

out of the innumerable different species of these, we are to use only those by which all the differences of habitudes [or relations] or proportions are most easily expressed. There are, however, strictly speaking two genera of things that are brought together for comparison with one another, multitudes and magnitudes; and so we have two genera of figures for proposing these things to our conception. For example, points [see fig. 7], by which is designated a triangular number, or the [family] tree which explicates someone's lineage

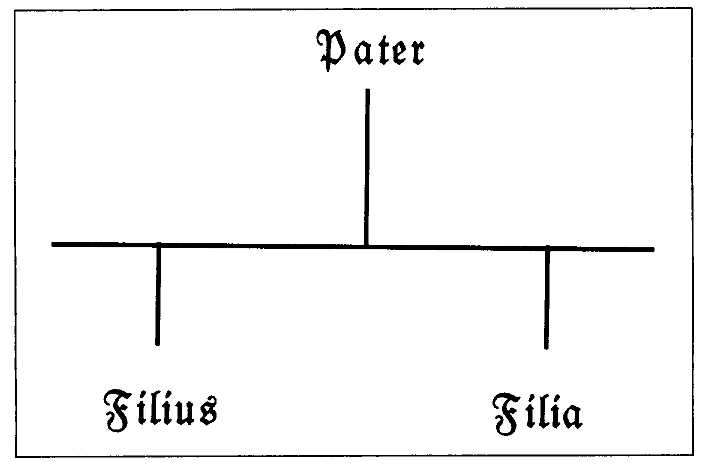
Fig. 8. Relationships between family members are pictured by a tree diagram.

[see fig. 8], etc., are figures for exhibiting a multitude [discrete quantity]; those, however, which are continuous and undivided, like the triangle, square, etc. [see fig. 9], explicate magnitudes [= continuous quantity]. (AT X 450—451)

It has been a commonplace in Descartes studies to assert that this is part and parcel of Descartes's method of applying mathematical or algebraic analysis to all problems. But this is a half-truth, and it describes the surface rather than the depths of Descartes's aim.

One applies a thing X to a thing Y either in the spirit of play or because one has the expectation that this application will be fruitful. A twentieth-century French philosopher might be willing to do the former, but it hardly seems credible as the basis for Descartes's early work. Why did Descartes believe that applying figures to problems of all kinds would be fruitful?

We have already seen elements of the answer in the preceding chapters. First, it was not just any mathematics that Descartes wished to apply, but the mathematics of proportional relations; and that relational mathematics was grounded in an ontological epistemology of analogy that implied similarity between different levels of being, a similarity that is in fact the ontological and epistemological ground of the applicability of mathematics and that gives ontological and epistemological priority to a mathematics of proportion. The very analogical structure of reality allowed for a

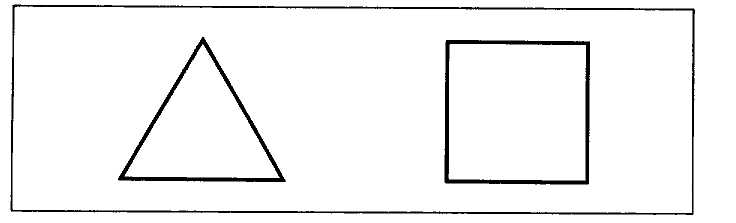
Fig. 9. Two-dimensional figures are used to picture different relationships.

certain flexibility in the application of mathematics, however; it is not the case that Descartes believed that there was a privileged mathematical representation of a problem or relation, but that there were alternative ways of presenting or approaching problems. The analogical structure of reality is warrant that there are many kinds and degrees of similarity, so that no one thing can be said to be a perfect representation—except the thing itself, which is not a representation at all, although a thing might stand for its own essence. As Descartes conceived these matters in the 1620s, however, the human mind does not understand things in themselves or in their essences but within the activity of figuration that he had begun exploring in the analogy notes of 1619-162 1.^[28]

This account immediately helps interpret the purpose of the second part of the Regulae . In the intended tripartite structure of the work, the first twelve rules were to (1) present the aim of a unified way to knowledge, (2) ground that knowledge in the two mental operations of intuition and deduction, (3) propose the division of questions in the sequential search for simple natures to be followed by a resurvey in order from the simplest things to the thing sought, and (4) sketch a psychological and even physiological basis for the right use of the native endowment. After the statement of the founding theory in the first twelve comes the explication in the twenty-four that follow. The second twelve rules were to deal with perfect problems, the third with imperfect problems. The second twelve rules, which teach how to present the scheme of relationships using lines and two-dimensional figures, serve two purposes: to train the reader (or Descartes the rememberer) not to ignore simpler things for the sake of the complex (perfect problems are easier to deal with than imperfect ones)

[28] I agree with Gãbe that before 1630 Descartes did not believe that human beings can know the essential natures of things per se; rather, one has a freedom of mind that allows one to approach things from many different perspectives. See Gãbe, Descartes' Selbstkritik, 84-92.

and to show in the most basic way how the ingenium can use marks and lines to aid in the solution of problems of proportion. One does not have to worry immediately about whether things really exist in the way they are represented; the question of existence is one for the physicist to solve (AT X 448), not the teacher of the new organon of the Regulae.

F. INGENIAL MATHEMATICS, OR THE ART OF MEMORY SUPPLANTED

One of the chief lessons to be drawn from the second part of the Regulae is always to simplify. For example, in Rule 14 we are told:

Finally it should be known that of the dimensions of continuous magnitude nothing is more distinctly conceived than length and width, and one should not attend to many [dimensions] simultaneously in the same figure when we are comparing two different ones with one another: because it is of the art that if we have more than two to compare with one another we run through these successively and attend to only two at any one time.
These things having been noted, it is easily gathered that: here propositions are no less to be abstracted from the figures of which Geometry treats, if the question is about these, than from any other matter; and for this use nothing is to be retained beyond rectilinear and rectangular surfaces, or straight lines, which we also call figures, because by means of these we could imagine a really extended subject no less than by means of surfaces, as has been said above; and finally by means of these same figures are to be exhibited sometimes continuous magnitudes, also sometimes a multitude or number; and nothing simpler for expressing all differences of habitude can be invented by human industry. (AT X 452)

At the outset of Rule 15, which follows immediately upon this paragraph, we are told that it is helpful to actually put images (species ) before our eyes. The unit, for example, can be represented as having length and breadth (a square), as having only length (a line), or simply as an element of a multitude (a point); "but however it be depicted and conceived, we always understand it to be a subject in every way extended and capable of infinite dimensions" (453). If we need to attend to two terms of a proposition simultaneously, "we exhibit them to the eye by means of a rectangle, whose two sides are the two proposed magnitudes"; if the two magnitudes are incommensurable, we use a simple rectangle, and if commensurable, we use a set of points or a rectangle composed of smaller unit rectangles so that their commensurability is evident. If we need to attend to just one magnitude, we present it either as a simple line or, if we will need to compare the line with a surface, as a rectangle, one side being the simple line and the other the unit length; or, if it is commensurable with the thing to which it is compared, by a set of points.

Everything propounded in the second part of the Regulae is for the sake of showing as simply as possible how problems with information sufficient for their solution can be attacked. None of the suggestions of Rules 14 and 15 about figuration and refiguration has to do with expressing the "nature' of the thing in question; they are only presentations or exhibitions of some aspect relevant to the problem (what Descartes calls 'dimension'). Therefore Descartes is not effecting an ontological reduction of the things in question to mathematics; that is, he is not arguing implicitly or explicitly that things are essentially, or essentially expressed, by figures, numbers, or extension. Quite the contrary: relations and aspects of things are expressible in this way.^[29] Moreover, whatever is not presently and immediately of concern in the problem does not need to be fully expressed but is to be kept in reserve by means of reminders, by marks rather than figures. This is a consequence of Descartes's behest that we never treat more than two things simultaneously.

Besides, because we said that not more than two different dimensions out of the innumerable ones which can be depicted in our phantasia are to be contemplated with one and the same intuitus, either of the eyes or of mind: it is of great value to retain all the others so that they can easily occur whenever need requires; for which end memory seems to have been instituted by nature. (AT X 454)

Since memory can be unreliable, and since we need to avoid diverting our attention, we make use of the invention of writing.

We shall commit nothing at all to memory, but turning a free and entire phantasia over to the present ideas we shall depict whatever was to be retained on paper; and this [is to be done] by means of the briefest notes [i.e., marks or symbols], so that after we have inspected the single things distinctly according to Rule 9 we can according to Rule 11 run through them all with a very rapid motion of cogitation and intuit simultaneously as many as possible. (AT X 455)

Presently we shall have to deal with issues such as the meaning of 'dimension', the problems that can and cannot be dealt with according to this procedure, the psychological act of running through things with a rapid motion of imaginative cogitation, and the significance of an intuition that can take place with respect both to the eyes and to the mind. For now we must note that Descartes is offering a technique of using the native faculties

[29] One thing to realize about these passages is that they are not concerned with the representation of things through figures but the exhibition of things and relations of things by means of other things—note that at AT X 453 11. l3-15 the figures are described as a subject, not as an idea of thought—and that the ways or dimensions in which they can be exhibited are infinite.

of the human being as simply and efficiently as possible in the working out of problems. The central faculty of this technique is imagination, that is, ingenium as the faculty of making and dealing with images or species in the phantasia and as the medium for translating those images in the mind into images and marks that appear on paper. The techniques are all accommodated to the strengths and weaknesses of ingenium. Too many aspects considered at once will overtax it, so it is necessary to keep the aspects to no more than two at any one time. We do not have to rely solely on the ability of our phantasia to retain the images it is working with, since we can draw appropriate, simple figures on paper to represent the relationships they bear to others. (Note that this is literally a re-presentation of a symbolized presentation of the relations of the terms of a problem!) This simplification of the work of the mind need not lead to neglect of the totality of what is at issue, for we have memory and, even more important, the aid to memory called writing. All we need do at any given moment, then, is to devote our immediate attention to the one or two relationships under present consideration and to remember that this is but a part of the problem; we do not have to actively remember the rest, since the marks that we make will enable us to find our place easily.

It is pertinent to recall Descartes's "Cogitationes privatae" entry about Schenckel's treatise on the art of memory. The medieval and early modern art of memory was constructed on a psychophysiological understanding of the mind and its functions. Depending on the physical constitution of the brain, on the relative dryness or moisture, heat or cold of its various parts, it was conceived as able to retain more or less easily the images conveyed to it by the senses and to impress more or less strongly those images in the corporeal memory so that they might be preserved. Vivid things are more easily remembered than ordinary ones, so the art counsels confecting striking images whenever possible (and as taught by Schenckel, it also provides mnemonically stimulating conventional images, like a bow for the letter C ) and keeping them well ordered by locating the images sequentially in a familiar and thus easily remembered place. In his comment on Schenckel, Descartes noted that he had thought of alternatives that eliminated the need for memory: generating phantasms from other phantasms, and using images and figures to stand for the relationships between the elements of a problem. The Regulae implements accordingly a program in which the use of and need for often unreliable memory is minimized, by keeping only one or two things active in imagination and relegating the rest to paper, with the sequence of steps to be taken determined by the principles of the first twelve rules. Of course Descartes is not teaching an art designed primarily to help us memorize things, but one that facilitates the solving of problems by an analysis into elements and the reassembly of these elements into the desired whole, a problem solving that can be re-

evoked and duplicated at any time and, unlike with things merely memorized, always with the full evidence of proof.

According to the psychophysiological hypothesis of Rule 12, Descartes, like Schenckel, is basing this "art," as he not infrequently calls it, on an understanding of the functions and physiology of the mind and brain. Rather than advise us to use vivid images of our own invention, however, he provides us with a stock of reliably and exactly reproducible images: not bows for C and scales for justice, but rectangles, lines, and points. This would seem to offer rather striking evidence that Descartes is in principle carrying out in the Regulae the advice that in 1619-1621 he had already given himself in the context of a solution he had devised to a problem of motion posed by Beeckman:

As I put down the foundations of this science, motion which is everywhere equal [i.e., uniform motion] will be represented by a line, or a rectangular surface, or a parallelogram, or a parallelepiped; that it increases from one cause, by a triangle; from two, by a pyramid, as above; from three, by other figures. (AT X 220)

And, as the note immediately following this remarks, "from these an infinity of questions can be solved.'

Indeed, in comparison with the "Cogitationes privatae," the Regulae effects a simplification. No longer will the problem solver need pyramids and other complicated three-dimensional figures, but only simple rectangles, lines, and arrays of points. The mathematical representation of things and problems has been reduced to a bare minimum.

But on the basis of what, and from what? We must remember that the mathematical technique introduced in the second part of the Regulae has a pedagogical purpose and so is maximally simple and that it rests on the identification of relevant aspects or dimensions of the problem at hand. We shall need to discuss where these dimensions come from and what they are before we can draw any definitive conclusions about the mathematical presentation of them; and, after all is said and done, the aim of problem solving must be to arrive at a rapid synthesis of all the elements into a whole that can, as it were, be intuited by a single act of mind. Moreover, it is not perfectly evident how this mathematical presentation can be translated into the solution of the so-called imperfect problems, where not everything is clearly distinguishable. But there is a piece of important evidence about the drift of Descartes's thinking around 1628, evidence that brings Descartes's techniques rather closer to a mathematized version of the classical art of memory, that allows a significant role to what we call secondary qualities, and, finally, that suggests that the rules of the second part of the Regulae were not written before late 1628.

The piece of evidence is an entry in the journal of Isaac Beeckman. In

October 1628, Descartes visited his friend whom he had not seen in nine years (and to whom it seems he had not even written since 1619!). In the course of the visit he revealed some of the mathematical and physical re-suits he had achieved in the intervening years. Beeckman recorded these in his Journal (see AT X 33 1-348). Under the heading "A Certain Specimen of Descartes's Algebra" he made an entry of particular interest.

He says also he invented a general Algebra, and for it he uses not the figures of bodies but only planes, because these are more easily insinuated into the mind; and so other things beyond Geometry are optimally expressed by these.
He conceives unity by a small rectangle; thus also he conceives a point. Even a line or a radix [= an unknown] he conceives by a parallelogram, conflated out of one side of this [unit] rectangle and [out] of the due length.^[30] A rectangle he conceives made out of so many radixes; a cube, made out of so many rectangles as the numbers indicate, reduced to oblong form; a biquadrate, in the same way, etc. Now he also explains all these things by lines, so that a represents a point, b a line, c a quadrangle, d a cube. In this way also f represented a cube made out of the multiplication of the quadrangle e by the number of the radix [see fig. 10].
With no less trouble he solves the same things by simple lines. . . .
In particular he of course conceives a cube by three dimensions, as others also do; but the biquadratic [which would be a four-dimensional figure] he conceives as if out of a simple cube, which is considered as wooden, there comes to be a stone cube; and so for the whole thing a dimension is added; and if another dimension is to be added, he considers the cube iron; then golden, etc., which happens not only in gravity, but also in colors and all other qualities. Thus cutting out of the wooden cube three rectangles, he also conceives finally that he is cutting a cube conflated of woodenness, iron-ness, etc., alone, so that the iron cube is drawn through [perducatur] into a wooden one in the same way that the simple cube [is drawn through] into rectangles oberved in every genus.^[31] (AT X 333-334)

Beeckman goes on to describe how one can solve equations using these techniques.

Setting aside inevitable obscurities, we can see that in the fall of 1628 Descartes was describing to Beeckman something akin to the techniques proposed in the second part of the Regulae , that is, the expression of all kinds of objects and relations, not just geometrical, by lines (in the third paragraph) and rectangular plane figures (in the first and second). But the fourth paragraph of Beeckman's entry describes something not to be

[30] That is, a line is represented by a rectangle that has as one side the line and the other the unit length.

[31] The concluding part of this last clause is garbled; the translation follows a suggestion of AT.

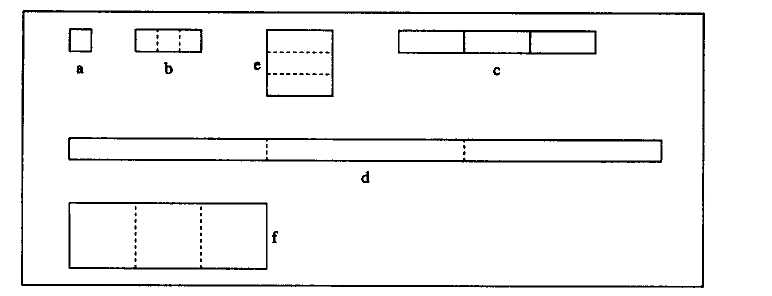
Fig. 10. The diagram that accompanies Beeckman's 28 October 1628 Journal entry.
All the elements of a problem are figured in two dimensions. The unit square is a;
three of them put together form b; three of those put together end to end make c,
whereas stacking three forms e; three of figure c make up d, while three of emake f.

found in the Regulae a technique that employs striking images not unreminiscent of those found in the second technique Descartes devised in response to the memory art of Schenckel, where he appealed to ascent on ladders, the hurling of spears, and the like, to help explicate the relations to one another of the elements of a series. A three-dimensional problem he conceives using a wooden cube, a four-dimensional one using stone, a five-dimensional using iron, and so on. But he uses not only gravity (perhaps the increasing specific weights of these materials is the significant comparative factor) but also colors and all other (secondary) qualities to differentiate problems.

Is this the direction in which Descartes intended to develop the third part of the Regulae ? Someone might object that the fourth paragraph of Beeckman's account presents a method so at odds with the others, not to mention with the Regulae , that this is implausible. Was Descartes, then, merely explaining to his friend a path he had formerly considered but had already rejected (and so perhaps Beeckman misunderstood this as part of Descartes's current algebra)? But this suggestion is highly implausible. Descartes was not in the habit of revealing even to friends anything he thought was imperfect, and unlike, say, a Kepler, he was not one to chronicle his missteps. Moreover, his introduction of cubes of different materials is not inconsistent with the method of representation in the Regulae if it is understood primarily as a ploy for keeping in mind, indeed embodying, all the dimensions of a problem. From Beeckman's description it seems that Descartes used these cubes to preserve multiple relations that could be

carved off as needed in the form of different cross sections, that is, rectangles, to which the kind of manipulations of lines and plane figures taught by the Regulae might be applied. The qualified cubes would thus be memory devices. What seems to have happened between the ingenious ideas of October 1628 and the last rules of the Regulae is that Descartes decided no longer to preserve all the dimensions in an actual geometrical figure, carving off those rectangular combinations of two dimensions as they were needed, but instead to use exclusively simple marks or notations on paper to help remember the dimensions not currently in use while actively concentrating on no more than two.

As Descartes conceived of his geometricized algebra before late 1628, then, it was an art of imagination (and thus of ingenium) even closer to the classical art of using striking images for remembering than is the technique of the Regulae. All experienceable qualities, not just the easily quantifiable ones that we call primary, were eligible for use in this earlier method, although when it came down to actual calculations the solids with secondary qualities were to yield up the information they stored by a method of sectioning that results in lines and rectangles. In addition, unlike the Regulae, which gives pride of place to manipulating lines, the October 1628 method appears to privilege plane figures.

Does the use of secondary qualities for memory images imply anything about Descartes's understanding of such qualities around 1628? What secondary qualities have in their favor is that they enable one to construct significant images beyond three dimensions; but perhaps just as one needs a three-dimensional object before one can have a colored or a weighty one, one would start the construction of the object using the three geometrical dimensions and only then add other qualities. Yet we must also note that as early as the note on Schenckel, Descartes did not believe that the use of particular kinds of images implied an ontological commitment, for there he remarked that the signification (by images such as hurled spears) might be either true or fictitious. This continues to be the case in the Regulae, where, in Rule 14, he says that the countless dimensions that are conceivable add nothing to the object, but "are understood in the same way whether they have a real foundation in the subjects themselves or have been excogitated out of the willed judgment [ex arbitrio ] of our mind" (AT X 448). 'Dimension' is thus not to be identified simply with 'geometric dimension'. The "Specimen of Descartes's Algebra" preserved in Beeckman's Journal vigorously asserts that this technique applies as much to representing dimensions geometrically as to representing them by means of color, specific gravity, hardness, or any other quality. None of these are meant to be true pictures of material or spatial reality as it is in itself, but as means to the expression of relations for the sake of solving problems. If colors or the different specific gravities of materials can mirror the pro-

portions or even just the order of real or possible relationships, then there is nothing to stand in the way of using them. Simplicity of expression and efficiency in contributing to solutions are the prime desiderata.

An example from Rule 12 helps confirm that this pragmatism about representative devices holds even in the Regulae. There Descartes proposes conceiving colors according to different patterns of lines and rectangles. Someone thinking of the later philosophy might see here a programmatic reduction of secondary to primary qualities. Although I would not deny that it can be construed as a step tending toward that end, his motives seem to be tactical rather than strategic. First of all, the Regulae reflects an awakening interest in anatomy and physiology, but Descartes's use of standard late sixteenth- and early seventeenth-century vocabulary and the lack of detail given in his psychophysiological hypothesis strongly suggest that he had done little more than read about these subjects and that he was trying to adapt what he had gleaned to his method of imaginative representation.^[32] In explaining the process of sense perception, he argues that the senses take on impressions in the same way as wax receives the impression from a seal; the senses then make an impression in the sensus communis, which in turn carries the impression into the phantasia; and finally—although here the example of the wax and seal becomes analogical rather than literal—the phantasia makes its impression on the knowing power. All of this he understands as taking place instantaneously and rigidly; the model he gives is the simultaneous motion of all the parts of a pen when the nib end is moved.

In this context he argues that the sensation of all qualities takes place by similar processes of impression; "thus the first opaque [surface] which is in the eye receives a figure impressed by the illumination endued with various colors; and the first membrane of the ears, nostrils, and tongue that is impervious to the object also thus borrows a new figure from sound, odor, and flavor" (AT X 412-413). Accustomed as we are to Descartes's only slightly later conception (as expressed at the outset of Le Monde, perhaps as early as 1630 and no later than 1633) of an instantaneous motion transmitted through space and along the nerves to the pineal gland, we feel the strong urge to read this as a first, clumsy way of putting that conception, but the interesting thing is that he does not state or apparently

[32] A firsthand knowledge of such things came later. In early 16310, Descartes tells Mersenne that he is studying chemistry and anatomy and learning things that are not in any book (15 April 1630, AT I 137). In late 1632, we find him writing to Mersenne that he is doing anatomical dissections (November/December 1632, AT I 263). His progress must have been prodigious, for he was invited to assume the chair in theory of medicine at the University of Bologna in 1633. See Vincenzo Busacchi, "La chiamata di Caresio alla cattedra eminente di teorica della medicina hello studio di Bologna nel 1633," Pagine di storia della medicina 11, no. 2 (1967): 9-13.

even intend this. The analogy to the motion of the whole pen does not imply that he is thinking of motion along the nerves. The nerves enter in only later, where they are identified as the medium of the active motive power of the body (AT X 414) rather than of the passive reception of impressions. The pen's motion appears simply to confirm that the impression on the sense organ can be transmitted whole and entire in an instant, not that the different parts of the impression are carried along different nerve paths (the Regulae gives no suggestion of this later conception). Descartes simply does not offer much information about the nerves and their modalities; this probably ought to lead one to conclude that he had not yet thought these things out in detail. But it is clear that he still thinks of colored light, sounds, odors, and flavors—not motions—as the agents effectively impressing themselves on the senses, a fact that is scarcely compatible with his having already arrived at a significant primary-secondary distinction.

In this context he goes on to suggest a way of expressing color by figures.

And this [i.e., the notion that the first membrane receives an impression from light, sound, etc.] greatly helps in conceiving all things, since nothing falls under the senses more easily than figure: for it is touched and seen. However, nothing false follows from this supposition any more than from some other, as is demonstrated from this, that the concept of figure is so common and simple as to be involved in every sensible thing. For example, suppose color is some force, you will nevertheless not deny that it is extended, and consequently figured. Therefore what incommodious thing follows if, taking care not to uselessly admit and rashly contrive any new entity, we do not even deny anything about color that pleases others but only abstract from everything else what has the nature of figure, and conceive the diversity that there is between white, blue, red, etc., as that between these or similar figures, etc. [see fig. 11]? The same can be said about all things, since it is certain that the infinite multitude of figures suffices to express all differences of sensible things. (AT X 413)

What appears to be happening is this: On the basis of the physical and physiological aspects of his hypothesis, it is plausible that all sensations make changes in the shape of the receptive membranes of the sense organs. This shape is immediately transmitted, apparently without deformation, along some unspecified route to the sensus communis, which can impress it on the phantasia, which in turn can (analogically) impress it on the knowing power. Whatever one thinks of the nature of sensation, it is undoubted (Descartes asserts) that the thing sensed has extension; this nature, extension, is simple and common to all sensibilia. And if we consider geometry, we see that the variety of figures is so rich that all differences between things can be expressed by them.

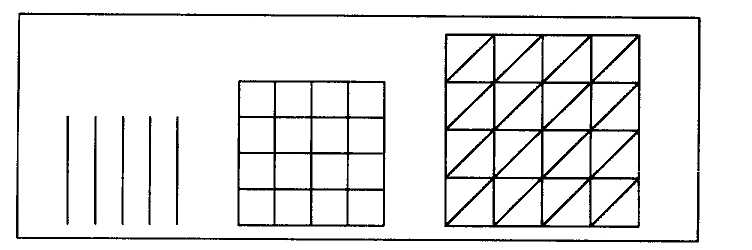
Fig. 11. Descartes's speculative example of how various colors might be represented by different geometric figures.

There are several levels in this argument. Descartes allows, as a proponent of analogical method must, that there are other suppositions possible for presenting the differences in colors (he remarks that other people might hold certain beliefs about color that his supposition does not deny, but also that nothing false follows from his any more than from some others; AT X 413). But physical things are extended, and so we are not to be surprised that extension and figure could be transmitted to and within our physiological apparatus. In any case, the figures of things transmitted in the physical and physiological processes will contribute something to the sensation/impression. Moreover, even if there is something fictional about the particular figurative representation we choose (say) for colors, nevertheless the differences in the figures can easily stand in for the differences between things. Perhaps some day we will even be fortunate enough to come upon the precise differences that distinguish them, or at least upon a system of figures that perfectly mirrors the system of relations between colors.

One might recall again a relevant note from the "Cogitationes privatae": "The cognition of natural things by human beings [occurs] solely through the similitude of those things that fall under sense: and indeed we judge that person to have more truly philosophized who will have more successfully assimilated the thing sought to what is cognized by sense" (AT X 218-219). In light of the psychophysiology of Rule 12, what falls under the senses in all cases is impressed figure, if nothing else (though we are not told we can conclude that this is all that can be impressed, and in fact the opposite is suggested). Therefore the one who reasons about natural things will use such figures and perhaps other sensible (and imaginable) things as well to philosophize more truly than one who does not.

It is curious that in some sense Descartes is trying in Rule 12 to take

advantage of both of his alternatives to the memory art of Schenckel. One was "natural," based on real causes: if the cause was identified, its corresponding image(s) or sequence of images in the mind could be reproduced at will. The other was a compromise between the artificial and the natural: a network of relationships might be analogically expressed through otherwise unrelated images (spears, ladders, stairs, and the like). On the one hand, Descartes in Rule 12 wants us to agree that the transmission of images from a thing to our senses to our knowing power is as he describes it and that the extendedness of the objects of sense is a real cause of the extension of the figuration in the organ's membrane; on the other hand, he is willing to be satisfied with analogy, that things are something like this, and with the thought that it is the differences of things and not their essence that are being expressed. Figures are simply marks that can bring these things and their interrelations to mind. He is still fundamentally appealing to the notion that things are related to one another by (not necessarily geometric or algebraic) analogy and proportion.

In the next chapters we will consider how the first part of the Regulae is also caught between the causal and the representative, between the literal and the analogical. But first it might be helpful to conclude with a speculative sketch of Descartes's progress in the use of imagination. In late 1618, the imagination was for Descartes the synthetic cognitive power able to recognize and construe proportions that are presented or revealed discursively, bit by bit (as in the progress of a song or the fits and starts of problem solving). His inclination to give cognitive primacy to imagination was undoubtedly encouraged by Beeckman, who believed that everything in the understanding of nature ought to be picturable^[33] —and thus began a shift to the paradigm (and analogy) of the visible and the manipulable. In the period 1619-162l, in part under the stimulus of his innovations in addressing the general theory of mathematical proportions, be elaborated an ontological epistemology of resemblance, according to which corporeal imagination could figure bodies, and bodies in turn could figure spiritual things. He believed that the chief instrument of discovery and of conceiving proportions was imagination and searched for ways to systematize and methodize it, especially its ability to move from image to image. Two possibilities he explored were that of generating a whole series of images by beginning with causes and that of expressing the relations of sequentialized objects by memory images that somehow mirror actual relations. When we become privy to his thoughts again after a seven-year hiatus, we see that he has universalized the geometrical figuration of relations as the foundation of a problem-solving method (his geometric algebra) but that he has not altogether abandoned nongeometrical images. Then, in the

[33] See van Berkel, Isaac Beeckman, chap. 7, and 317-319 (English summary).

final stage of the composition of the Regulae, after October 1628, he decides to abandon the use of secondary qualities as a part of his problem-solving armamentarium in favor of the marks and symbols of writing and to definitively set aside the use of figures of dimensions above two.

None of this had anything to do with the principal tenets of his later philosophy; for example, he was not motivated by any ontological imperative to reduce ordinary objects to pure extension. Rather, he was driven by the need to invent efficient devices for expressing and solving problems according to proportionality, whether or not those devices had anything directly to do with the way things exist in reality. Nevertheless, the working out of the details of the imaginative method, especially his nascent concern with the physical and physiological transmission of images, began to produce tensions that ultimately led to a breakdown in the theory. The place where those tensions become evident is in the first part of the Regulae, Rules 1 through 12, to which we now turn.

FOUR
Intuitus, Deductio, and Method The Psychological Foundations of Universal Mathesis

Let us speculate for a moment about what happens if the position of the earliest writings is driven toward logical limits. Its basic contention is that some things can be used to figure, conceive, and understand other things, ultimately because they are interrelated within a cosmic harmony. Two questions come immediately to mind: Are there things within this harmony that are privileged; that is, are there some things more fundamental or more worth knowing than others? And what is the nature of the relationship between figures and the bodies they image, and between bodies and the higher truths those bodies image?

A. SYMBOLS, ANALOGY, AND THE ONTOLOGY/ PSYCHOLOGY OF RESEMBLANCE

The answer to the second question looks fairly simple: the figure, whether we take this term literally or metaphorically, in some way represents or symbolizes the object conceived through it. The basic relationship would be one of representation or symbolization. This answer is minimally illuminating, however, because it is merely generic. As Descartes will point out at the beginning of Le Monde, words too represent thoughts or things, yet without any need of resemblance. They no more need to be like the thing than marks that we make on paper to keep track of the parts of a problem not currently under consideration need to be like the thing they stand for (AT XI 4). In asking about the relationship between figures and bodies we are not, however, asking how the letter a relates to a number, a line, or anything else, but rather how, for example, an oval stands in relation to an egg, a shade of blue to the sky, wind to spirit, and the like. With the egg's shape and the sky's color the kind of relationship seems obvious: we iden-

tify a feature of the object and portray it according to some schema, not, however, to isolate the feature and its schematic representation, which rather we take for granted, but instead to use these to get a better fix on the object in question and the relations within which it stands. One takes what amounts to a part, or a schematized part, of the object to get at the object's place in a network of relations. In an analogical universe, everything is expressive of other things, so the particular nature of any individual thing is not as important as its relationship to others.

Reminding ourselves of the earlier discussion of the symbol can help bring this into focus. Among the Greeks a symbolon was a part of a coin that had been split as the mark and seal of an agreement. Since coins in a money economy are the medium of exchange, they themselves participate in the nature of exchange or transaction and so are not mere physical objects. A transaction requires the performance by several parties; the partitioning of the coin mirrors this character. The completion of the transaction is imaged in the rejoining of the coin's parts into a whole. The network of relations created around the symbolon thus schematically displays features that are similar to that which it symbolizes, and the symbol and the symbolized share, each in its own plane, at least these features, and each of the two can be viewed in the perspective of the other. In the case of a contract, one can view the symbolon from the perspective of the plane of economic transactions, or the transaction from the plane of the divided symbolon.

In corporeal imagining, each aspect of the body in question is part of a whole. Viewing the body under the aspect of weight will evoke a different network of relationships and different results than will viewing it under the aspect of size or color or shape. If our interest is in the totality of being of that particular thing, we might imagine our cognitive goal to be bringing together all the parts or aspects for a full and clear conception of the thing, and we might want to call this representation proper of the thing. But this is a misleading way of approaching the questions of analogy in Descartes's early philosophy. In an analogical world, each thing is capable of representing many other things; moreover, conceiving a thing is achieved through the representation of aspects of the thing, rather than by a single image that is taken to be its paradigmatic, total representation. That is, there is no necessary implication that the end result will be a single (true) image that can be called the representation (or, using a later locution, the idea) of the thing. A representation is always a representation, one among the many possible needed to bring the thing in question into clear focus in one respect or another.

Imaginative cognition as conceived by the early Descartes is a partializing, discursive process. The body perceived is imaginatively brought into relationship with other things in certain respects (under an aspect, along

a certain axis). One might even try to bring these respects or aspects into relationship with one another (e.g., weight or shape could be related to density, or color to texture), but then one would have to decide whether these could be brought into a direct relationship or only an indirect one. Insofar as the origin of one's questioning is to conceive a body in its relationships, one might suspect that the relationship of aspect to aspect has to be conceived by way of a particular instance or instances. At any rate, what is essential to imaginative seeing within an analogical universe is that a characteristic of one thing can adumbrate an analogous characteristic in other kinds of things, and the relationships between things can be mirrored by other things. In this kind of universe such relationships and characteristics have a meaning relatively independent of any instance. A particular egg may be blue and oval, but the blueness and the ovalness suggest interconnections based on the nature of blueness and ovalness rather than on the nature of the egg, and their conjunction may be meaningful apart from any particular thing in which they appear together.

So much for corporeal imagination. Does intellectual imagination, which uses bodily things to figure higher, spiritual things, function similarly? How, for example, does wind figure spirit? The strategy of identifying features is not so clearly applicable, or one should say it is applicable only by stretching analogy even further. A body can be imaged in three dimensions by a geometrical solid (or by a two-dimensional figure projected onto a plane from a given vantage point), it has a color that can be seen, an odor that can be smelled, a hardness and texture that can be felt, and so on. We can conceive of each of these aspects guiding and focusing our imaginative attention. How does this translate into employing bodies to figure spiritual things? We cannot appeal to mathematics, because mathematics itself could be conceived as still within the limits of the corporeal insofar as it presupposes spatial extension.

It is not clear that Descartes gives us a concrete sample of intellectual figuring, unless we take his three dreams of 10-11 November 1619 as a revelation of Olympian or spiritual truths. Whatever the difficulties presented by the dreams, the account given by Baillet evidences a belief that lower or corporeal things can signify spiritual truths. In the narrative Descartes takes particular things as standing for higher ones (the Corpus poetarum, a collection of poetry, he interprets as science and wisdom joined together, the dictionary that appears he considers to be the sciences gathered into a whole, the melon that he is supposed to deliver to an acquaintance is taken for solitude, the wind that opposes him for a good or evil spirit). Yet it is also important that this "standing for" takes place within and depends on a narrative context. The dreams themselves, whose meaning Descartes begins interpreting while still dreaming the third dream, do not immediately reveal their significance any more than a body presented

to our senses is instantaneously understood in a clear conception. Just as we "interpret" the body by figuring it through aspects configured toward larger contexts linking individuals that share in the aspect in some way, so we interpret the dream by parts that are reciprocally configured to constitute, or at least to point toward, a larger, integrated context. That is, imagination, both corporeal and spiritual/intellectual, construes or constructs meaning as part of a narrative. Both show the power of interpretation at work.

This approach can help bring the imagination of the Compendium musicae, which is audial, into clearer conformity with the visual imagination of the "Cogitationes privatae." Each begins with things that are somehow presented or given (to hearing, to sensation in general, to protocognition); something is subsequently, yet almost immediately, detached from the given (proportions in sound, various qualities and quantities pertaining to bodies, aspects of possible signification in spiritual things), and through this detachment we try to conceive the entirety better. The process is discursive, and it involves a recognition of something that is already present but not—at least not initially—expressly or clearly noticed.

Still, a difference remains that is not unimportant for the later development of Descartes's conception of the uses of imagination. If you look at a body, you are in some sense instantaneously in possession of the whole that needs to be construed; likewise if you have an intimation of a higher truth. But a song is intrinsically extended through time, and one never has the whole immediately in one's possession—though it does make sense to say that there is such a thing as a whole song, appreciating which depends on a discursive account and therefore on memory. Memory is more obviously involved in the construal of music than in the construal of bodies and spiritual truths. More obviously, but perhaps not more essentially, since in vision the thing in question does not reveal the full extent of its relationships, which must be construed by an activity of mind. Interpretation in either case is arrived at through a discursive process, and, unless the chain of interpretation is at the last step abrogated by an immediate intuition of the whole truth, understanding requires recall of the whole chain. Whether that is done in the direct presence of a body or only through the memory of the object that we wish to understand (whether it is music, a body, or a spiritual thing) would seem to be of subordinate importance. As I have already noted and as shall be further confirmed presently, the Regulae attempts to give aids to replace memory, so that in the last analysis memory will be virtually overcome.

A discursive process of knowing, whether it is rational or imaginative, can come to a proper end only if there are self-evidencing truths, phenomena that reveal their meaning simply in terms of themselves; otherwise the discursion would be open-ended. If it were open-ended, there

might still be a possibility of knowledge if the entire cosmos were traversed and ultimately conceived (e.g., in a kind of circularity that avoided being vicious by encompassing everything). But from the beginning of his speculations about imaginative knowing Descartes assumed that knowledge is locally determinate. That is, knowledge is directed toward a given object (e.g., a falling cannonball) or class of objects (all falling things), and the process of discursion operates in a local logical space determined by the relationships between the imaged features and the object. (Here 'imaged features' is a first approximation to the simple natures of the Regulae, which will be examined in chapter 5.) One conceives the object not in remote relationship, for instance to an essence, but only in local relationship to the imageable feature that has struck one as relevant. Having conceived the given object and similar ones according to the degree to which they exhibit the isolated feature, one can use them and their relationships to conceive different, even higher, truths. To give an illustration (not found in Descartes), a lead ball might figure the gravity of matter and contrast with the lightness of a flame, which figures spirit. This process of coming to know is analogical but still more or less determinate; it works within the logical or imagistic space established by a discursivity that analyzes the relations present in or exhibited by the object, and thus it is, in a somewhat more extended sense of the term, still locally determinate. The philosopher or savant thus learns to discipline the imaginative leaps that the poet makes; guided by the spark of truth poetic imagination reveals, the philosopher fills in, item by item, through step-by-step imaginative discursion, the logical space that the poet typically overleaps.

This brings us back to our first question, whether in an analogical universe there are privileged truths. It might be argued, on the basis of the two-imaginations note, that two things are privileged: the bodies that are conceived by figures and the spiritual things that are figured by bodies. Because bodies are in one case the end and in the other the means, we have a kind of hierarchy: lowest of all are the figures, then come bodies, then spiritual things. It does not take too much imagination to see that there are traces of Plato's divided line here (Republic, bk. 6, 509D-511D). The line—which represents both powers of mind and the objects experienced by those powers, from the highest intelligence (nous) to phantasia, from Plato's Ideas to the images of things—is arrived at by dividing a line segment into two parts according to a given proportion and then dividing each of those parts again by the same proportion. In this line what holds together the divisions is the proportionality that obtains between the parts and the corresponding ability of each part of the line to serve as a more or less distant image of the other parts. The question can easily arise, What is the ultimate object of knowing? Is it the Ideas at the intelligible end of the line, or the proportionalities that make the line into a whole? Do we look to

the ultimate essences of things, or do we look to the proportionalities that underlie the imaging relationship between the parts of the ontological and psychological hierarchies represented on the line, an imaging relationship that acts according to proportions and gives rise to the resemblances between the different parts of the line? A similar question can be put to Descartes: Is it ultimately the highest things that we seek, the Olympian things, or is it an understanding of the analogical working of the entire cosmos?

On the one hand, we are inclined to answer that the spiritual things are privileged, are most worth knowing. Again citing Plato, in the intelligible part of the line, divided into the mathematicals (which are the foundations of discursive sciences) and the Ideas, it is the Ideas that are most worth knowing. But, on the other hand, what is most comprehensively true is the systematic relationships of all the parts of the line to one another, relationships that produce resemblances. Resemblance according to proportionality itself thereby gains an ontological status. Perhaps that is what is most worth knowing.

At this juncture there arises a difficulty. If there is a proportionality that governs the whole divided line, and proportionality is mathematical, but the mathematicals are not the very highest part of the line, how can proportionalized resemblances be most important of all? In addition, if we use a wooden triangle to envision the mathematics of a triangle, we are using something on the third level (physical things) as an image of something on the second (mathematicals); but if we imagine the outline of that wooden triangle, as we would in imaginative cognition, are we not descending to the fourth level, that of shadows or images of physical objects, rather than ascending to the second (even though an argument might be made that we are descending to the fourth for the sake of more easily conceiving pure, second-level mathematicals)?

Since my purpose is not to present an argument about Plato's line but rather to clarify the network of problems that Descartes was facing explicitly or implicitly, let us return the questioning to him. We come to understand things, not directly, but by way of intermediaries, by figures in the broadest sense of that term. This implies that we never (or at least rarely) conceive or understand things directly; we must, as it were, establish a distance from the thing—the corporeal object as sensed or the spiritual truth as intimated—by trying to "figure it out." We need some power or faculty that permits this. The one that Descartes identified in the two-imaginations note is imagination: not just corporeal, not just intellectual, but the combination of both, which together can figure out what presents itself to sense and what is present to intellect.

Let us turn again to intellect. If what we said earlier about needing an intermediary in order to understand is true, then intellect must perform its act of understanding by way of this intermediary, by way of a figuration

worked out by imagination. I believe that this is precisely the position held in the Regulae and that the tensions arising in that work are largely a result of Descartes's trying to erect on this basis a coherent and wide-ranging theory of the knowing powers and what is known. Given the speculations we have just undertaken, we might expect that certain problems will arise: for example, whether there are exceptions to intermediation (e.g., if at least some things are not images but fundamental realities, or if intellection can take place without using an image); how imagination in the lower, corporeal sense cooperates with intellect; whether there is a distinction between the higher, intellectual imagination and intellect pure and simple; whether the mathematics of proportionality has an absolutely privileged status or is simply a tool; and, above all, whether the activity of imagining, of figuring one thing in light of another, is separable from its objects. We in fact find all of these things at the heart of the Regulae —a confirmation that it is an attempt to work out the consequences of imaginative knowing in a comprehensive way.

B. THE PSYCHOPHYSIOLOGY OF UNIVERSAL MATHESIS

The psychology of Scholasticism underpins an understanding of scientific knowing that begins with the senses and ends in the abstraction from phantasms of an intelligible species, in accordance with which one can understand objects sensed or remembered and from which one might ultimately ascend to a knowledge of noncorporeal things: not just of the human spirit and God but also, more generally, of the forms or essences that are the natures of corporeal things and that when compounded with matter constitute substances. This psychological process supports a notion of science that gives privilege of place to what signifies the abstracta, the terms. Terms are combined in judgments and then detached from and reattached to one another in discursive reasoning, in particular by dint of syllogistic argument.

The doctrine of internal senses and the supporting physiology of external and internal sensation was at the center of this process of coming to know, and its peculiarities created both opportunities and problems. If all knowing begins in sensation and requires the intermediation of a phantasm, then a deeper knowledge of the corporeal workings of the external and internal sense organs and powers might well lead to improvements in knowing by capitalizing on their abilities and compensating for their limitations, and it might facilitate the ease and swiftness of discovering new truths. At the very least one might learn how to remove obstacles that an undisciplined or careless use of these faculties put in the way of knowing. Presumably such improvements could come about by various actions taken

in the everyday, corporeal world, for example by prescribing exercises or using medical or mechanical means.

Whether one could directly intervene to improve the working of the illumination of the phantasm by agent intellect (or the light of nature) would seem less likely. Light illuminates what it will; whether we see depends on the state of our bodies—this we might act to improve—and on whether we pay attention. Paying attention would seem to be in part a noncorporeal function that we might improve through practice and discipline. Yet this would train the will more than the intellect, for in the last analysis whether we see what we are looking toward, especially when it is not corporeal and seeing takes place in a metaphorical sense, is not finally up to us. If the light does not reveal something, then we cannot see it.

A further problem is how the physics of the world and the physiology of our bodies support scientific knowing. If, in particular, something in material things needs to be conveyed to the sense organs to provide us with a stimulus to knowing, then any limitations on the accuracy of the physical and physiological processes will adversely affect knowing. If, for example, no transparent medium can perfectly convey the sensible form of color to our eyes, or if the nerve processes can convey it to the cerebral centers of the internal senses only in diminished perfection, then there will be a limit in principle to how well the knowable that is in the sensible things (the form or essence) can be understood. This holds true even if it were in some sense proportionality that was conveyed in these processes. In fact, it might hold more critically, for a harmonious proportion can be destroyed by very small deviations in the component quantities.

If the process that brings the sensible forms to the brain is defective, perhaps there is nevertheless a possibility of at least schematically improving what can be derived from them. The biplanarity that allows human beings to see one thing in terms of another might be used to correct one image in the light of others. The use of mathematics, which has an exactitude exceeding that of the everyday world, might elucidate commonalities and counterbalance distortions. The power of recognizing proportion and analogy might by its very nature allow the human ingenium to correct slight, or even substantial, imperfections.

But this demands a kind of seeing that transcends the merely corporeal, that brings to the seeing more than is in the seen; it also raises problems about how the evidence that is implicit in corporeal things comes to light, how it is taken hold of in consciousness. Do we take hold of something that is in the objects or is immediately derived from them? How do we understand what is complex? How do we understand what is simple and know that it is simple? How do we forestall the problems that can arise because of defects in memory, even over the very short term? Can we

be sure that discursive reasoning, which moves from thing to thing, does not obscure the clarity of each individual step in the reasoning?

C. INTUITUS, DEDUCTIO, AND THE ACTIVITY OF COGITATION

The first two rules of Part I of the Regulae set out the basic premises. Rule 1 states that the aim of study is the direction of ingenium so that it can form true and solid judgments about everything that comes before it. Rejecting the Aristotelian-Scholastic division of the sciences according to subject matter, Descartes claims that "since all the sciences are nothing other than human wisdom [humana sapientia ], which always remains one and the same, however much it is applied to different subjects, and since it receives no greater distinction from these things than does the light of the Sun from the variety of the things it shines on, there is no need to confine ingenia to any limits" (AT X 360). Although he looks forward to pursuing sciences useful for the commodity of life and the pleasure of contemplating the truth, which are legitimate fruits of science, he points out that we often overlook small things that seem neither useful nor interesting but that are nevertheless essential to knowing other things and that "it is to be believed that all [sciences] are so interconnected that it is by far easier to learn them simultaneously joined than to separate a single one from the others." Thus one should "think only of increasing the natural light of reason, not in order to resolve this or that difficulty of the school but so that in the individual events of life the intellect might show forth to the will what ought to be chosen." In this way one will make more rapid progress than by pursuing particular studies (AT X 361).

Rule 2, developing the theme that our ordinary ways of pursuing knowledge are defective, argues that we often in effect diminish our knowledge by forming opinions about things that are too difficult. We should turn our attention only to those objects for which our ingenia appear sufficient to deliver certain and indubitable cognition; and so "we reject all those merely probable cognitions, and we hold that things are to be believed only if they are perfectly cognized and it is not possible to doubt them" (AT X 362). There are, Descartes insists, many more such cognitions than people think. The learned have by and large neglected them, despite the fact that they would "suffice for the certain demonstration of countless propositions which hitherto they have not been able to treat except probably."

In what at first may seem to be a partial recantation of the position just established, Descartes notes that there is hardly any question in the existing sciences that is not a matter of controversy. "Therefore about all things of which there are probable opinions in this way we seem unable to acquire a perfect science, because it is not permitted without temerity to

hope for more from ourselves than others have exhibited; so that if we do our reckoning well, only Arithmetic and Geometry remain, of the sciences already discovered, to which the observance of this rule leads us" (AT X 363). The accusation against the learned would thus become that they have neglected mathematics; but, as events will show, the recantation is more rhetorical than real, since a proper consideration of the basis of mathematical certainty opens up a new vista of knowing. He goes on to say that it is after all still better to exercise the ingenia of youth with uncertain opinions and move them to a spirit of emulating their masters than to leave them to their own devices. Those who are no longer under the tutelage of a master, however, and who wish to ascend to the heights of human cognition must follow the rule of not abusing leisure by pursuing difficult things and thus ultimately only adding to doubts. Easier things must not be neglected.

Arithmetic and geometry are "free from every vice of falsity and uncertainty" precisely because they are so easy. "To consider more diligently the reason why this is so it is to be noted first that we arrive at the cognition of things in two ways, namely, through experience or deduction." Experiences of things, however, are often fallacious, while deduction or "pure illation of one thing from another" never goes wrong for even the minimally rational mind—though the deduction can be missed if the mind overlooks it. Every deception of human beings is thus due solely to the fact "that certain little-understood experiences are supposed or judgments are set down rashly and without foundation." The greater certainty of mathematical disciplines arises because "these alone are engaged with objects so pure and simple that they suppose nothing at all that experience might render uncertain, but the whole consists in consequences to be deduced rationally. Thus they are the easiest and most perspicuous of all and have an object such as we require, since in those things it seems that, apart from inadvertence, the human being scarcely ever fails." The conclusion to be drawn is "not, however, that only Arithmetic and Geometry are to be studied, but only that those inquiring into the right road of truth ought to be occupied with no object about which they cannot have certainty equal to arithmetical and geometrical demonstrations" (AT X 366).

To summarize and elaborate: by the end of Rule 2, we have been told that there is a fundamental unity to knowledge, whether theoretical or practical; that this unity can be cultivated by increasing the natural light of reason; that there are two ways to knowledge, experience and deduction; that, as the pure deduction^[1] of one thing from another shows, the human mind is incapable of making a mistake where the object of knowledge is simple, although it is possible that we might overlook such simple things;

[1] That is rather different from its ordinary meaning I shall show presently.

and therefore that instead of pursuing complex and difficult problems, we should try first to notice and know the simple things, since only with them can we evade the uncertainties produced by fallacious experience.

When the mind is presented with simple things, it makes no mistakes in deduction. The advantage of mathematics is that it deals with simple objects not falsifiable by new experiences—they simply appear as they are and can always be experienced in an unfalsifiable simplicity. It is important to notice here that Descartes is not making deduction and mathematics the paradigm of science but rather using them as paradigmatic examples of how we can errorlessly arrive at truth when the simplicity of the object in question allows. Once we have simple things as our object, deduction— etymologically a leading of truth down or away from something given—will take care of itself because of the nature of the rational mind. There is no need for a new theory of logic or dialectic but rather for an acquaintance with simple things as simple.

Although experience, one of the two ways of knowing things, is often fallacious, there must be a kind that is not, or else deduction itself would be impossible, because deduction is based on an experience of one thing's truly following from another, and pointless, because deduction cannot yield truth without being given something true to begin with. The following rules thus quite logically concentrate on how we can arrive at the kind of truth that is most knowable because simplest, on the basis of which infallible deduction or illation becomes possible. The simple experience of simple things is not afflicted with uncertainty and so is the very basis of the certainty of deduction. This kind of experience is called intuitus.

Rule 3 introduces us to the Regulae's theory of intuitus and deductio. The first question to ask is how we should translate these words. 'Intuition' has (and had already at the beginning of the seventeenth century) collected a great deal of philosophical baggage not implied in Descartes, who explicitly states that he is not using the term in its philosophically accepted sense but rather in a way faithful to its simple Latin meaning. Intuitus is the past participle of the infinitive intueri, 'to look at, upon, or toward', in a more extended sense 'to regard, observe, contemplate, consider, attend to'; intuitus can be used as a noun meaning 'a look, view'. In translating Rule 3, I have used 'intuit-see' for intueri and 'intuitus-seeing' for intuitus.^[2]

[2] Later I shall on many occasions use ‘intuit’ for the verb, especially when there is no danger of suggesting a subjective, mysterious power of insight; another occasional alternative will be ‘clearly see’. I shall also loosen the rendering of intuitus from time to time, without, however, resorting to ‘intuition’. Neither Marion’s French (regarder and regard for the verb and noun, respectively) nor my English renderings bring out the connotations of the prefix in -, which intensifies the root sense of tuere and emphasizes the directedness toward or into an object. 'Insight' would seem to be the natural English equivalent, but it is used for other purposes and like 'intuition' suffers from a subjectivist connotation that weakens the sense of an intensive looking carefully aimed at its object. For a discussion of problems of translation, see Marion, Règles utiles et claims pour la direction de l'esprit en la recherche de la vérité, 295-302.

Deductio appears to be far less problematically rendered by 'deduction'. Yet there is a danger here as well. As we shall see, deductio must be understood first of all from the perspective of intuitus rather than from standard notions of syllogistic or other forms of logical deduction. Descartes has little more than scorn for the standard logic of his day (he saw it as useful for rhetorical purposes rather than for knowing; see AT X 406). I have therefore usually retained the Latin deductio rather than employ the too-familiar 'deduction'.^[3]

The rule heading immediately sets aside as objects of scientific inquiry all opinions, whether our own or others'; if science is to be acquired, we must investigate "what we can clearly and evidently intuit-see or certainly deduce" (quid clare & evidenter possimus intueri, vel certo deducere ; AT X 366). Reading ancient books is advisable "because it is an enormous benefit that we can exploit the labors of so many people," in part to learn about what has already been discovered, in part to learn about what remains to be thought in every discipline. But we run the risk of cultivating mere history rather than scientific knowing and of falling into the errors of our predecessors if we seek to know only what they said instead of the truth about things. In general their works are wrapped in controversy, and when they do relate something certain and evident they "never exhibit it without involving it in various obscurities, since they doubtless fear that the dignity of the discovery will be diminished by the simplicity of the reason, or because they begrudge us the open truth" (AT X 367). It is not enough even to commit to memory those things that are clearly true, like mathematical demonstrations, for the point is to know, not just to be able to recapitulate.^[4]

We must refrain from ever mixing the uncertain or probable with the certain. To this end we must acquaint ourselves with the only two "actions of our intellect through which we can arrive at the cognition of things without any fear of deception": intuitus scilicet & deductio, intuitus-seeing and deductio.^[5]

[3] Using deductio rather than 'deduction' helps keep English speakers from assuming too casually that what Descartes intends is fundamentally an accomplishment of logic. The verb form will sometimes be translated as 'lead down (from)' rather than 'deduce'.

[4] This can be taken as a negative adversion to the goals of the memory art, memorization rather than understanding.

[5] Version A of the Regulae has inductio rather than decluctio. Crapulli prefers deductio because it is attested both by version H and the Dutch translation of 1684 (version N). Since in the remainder of the rule Descartes discusses intuitus and deductio, this seems hardly controversial.

By intuitus I understand not the fluctuating faith of the senses or the fallacious judgment of a badly composing imagination; but the concept of a pure and attentive mind so easy and distinct that no doubt at all is left behind about what we understand; or, which is the same thing, the not doubtful concept of a pure and attentive mind, which arises from the light of reason alone, and is more certain than deductio itself, because it is simpler, although deductio cannot be badly done by human beings as we noted above. Thus everyone can intuit-see with respect to soul that it exists, that it thinks, that a triangle is bounded by only three lines and a globe by a single surface, and similar things that are far more numerous than most people consider, because they disdain turning their mind to things so simple. (AT X 368)

This intuitus is required not only for the kinds of propositions enunciated in the passage "but also for all discursive reasonings whatever" (sed etiam ad quoslibet discursus; AT X 369). Not only does it enable us to recognize that 2 + 2 = 4 and that 3 + 1 = 4 but also that both sums are equal to one another.

The other "mode of knowing" is deductio, by which, Descartes says,

we understand all that which is necessarily concluded from some other things known certainly. But it had to be done thus because many things are known certainly although they are not themselves evident, only they are [1] sometimes deduced from true and known principles through a continuous and in no way interrupted motion of cogitation perspicuously intuiting-seeing single things: [which happens in] no other way than that we know the extreme link of a long chain to be connected with the first, even if we do not contemplate with one and the same intuiting-seeing of the eyes everything intermediate on which this connection depends, [2] sometimes we shall have surveyed them successively, and still recall that the single ones adhere to their neighbors from the first to the last. Here therefore we distinguish the intuiting-seeing of the mind from certain deductio from this, that in the latter a motion or a certain succession is conceived, but not in the former; and furthermore because for the latter present evidence is not necessary, which is for intuiting-seeing, but rather it borrows in some way its certainty from memory. (AT X 369-370; the numbering is mine)

The chief advantages of rendering intuere and intuitus with terms that emphasize the act of seeing are two. First, the Latin words suggest a well-directed and careful attention of the kind specified in the alternative definitions Descartes gives. Each calls it the concept (easy and distinct in one case, not doubtful in the other) of a pure and attentive mind. (Later we shall probe the implications of this act of seeing's being called conceptum, insofar as the latter term suggests a kind of grasping.) Second, they can be used of both intellectual and visual attention. Descartes several times speaks of intuitus with respect to the eyes, and he constantly exploits the analogy between vision and knowledge (most extensively in Rule 9).

Even those who are favorably inclined to historical studies in philosophy may be suspicious of arguments from etymology. But Descartes points out that he is using 'intuitus' in a way different from the usual and makes a general admonition about his vocabulary: "I simply am not thinking about how each word has been employed [or usurped] in these recent times in the schools, because it would be most difficult to use these same words and take a completely different sense; but I only note what the individual words signify in Latin, so that, as often as proper ones are lacking, I transfer those which seem to me most apt to my own sense" (AT X 369). What Descartes is identifying by the term 'intuitus' is not a mysterious power but the principal effect in human ingenium of the light of reason, the natural light that according to Rule 1 is the unchanging source of all knowledge. It is not confined to those who have a special gift, but is inborn in, is part of the native endowment of, every human being who is minimally rational. It is that power that, when purely and attentively directed to at least relatively simple objects, reveals the truth. One quite simply sees or grasps the truth in such situations, and that simple seeing evokes the original Latin meaning of the term: one looks and sees.

If we took Descartes's general admonition at face value, we would probably want to refrain from calling to mind the way in which this and other terms were used by high and late Scholasticism. Yet for us who are unfamiliar with those usages it is helpful to consider them at least briefly. Intuitio (a word that Descartes does not use in the Regulae )^[6] and intueri almost invariably suggested an awareness of the immediate presence of an object that is being sensed or known. There is an intuition, therefore, involved in feeling the computer keyboard at one's fingertips, in noticing the limbs of the tree across the alley waving in the breeze, and in savoring the aroma of the morning's first coffee; but it will also (and especially) be present in the intuitive cognition of the immediate presence of God in the afterlife. One would not typically have an intuition of concepts, however. The concept was for the Scholastics the first act of the mind—the other two being judgment and discursive reasoning—but by that very fact, it was an intermediation between the knower and the thing known. Intuition is therefore a receptivity or apprehension of the mind that corresponds to the Thomist dictum that the first thing apprehended is being (even before conceptuality makes an appearance) and to the nominalist privileging as real the immediate impression of the object (in contrast to the artifactual character of the concept).

Intuitus, in contrast, had a technical meaning that was especially prominent in theories of contemplation, that is, of the ascent from cogitation to

[6] Therefore one must beware of casually taking this as a synonym of intuitus.

meditation to contemplation. The canonical medieval theory of this ascent is found in Hugh of St. Victor (d. 1141) and Richard of St. Victor (d. 1173), whose formulations created a framework that was authoritative well into the seventeenth century.^[7] In their writings intuitus and contuitus appear as names for the power of seeing unities through a manifold of evidence. Meditation is understood to be a discursive process that surveys the objects about which the mind is making inquiry and that carefully examines the variety of things that have been provided to cogitation by both sense and memory. Intuitus is the penetrating gaze by which the mind recognizes the truth of things in the light of reason. Without intuitus it would not be possible to achieve contemplatio, which is the gaze that steadily views that to which intuitus has penetrated.

Intuitus is also found in a somewhat different sense in late Scholastic manuals, like the Summa philosophiae quadripartita of Eustace of St. Paul (a work that Descartes knew), especially in the phrase simplex intuitus. Eustace defines the first act of the mind, which he initially calls conceptum, as "that by which the proposed things are apprehended in a simple intuitus";^[8] thereafter he uses the term 'simplex intuitus' for the mind's first act.

Descartes did not opt in the first instance for any of these uses of intuitus or intueri, although in a sense his understanding of intuitus adapts aspects of each. His notion of the immediacy of intuitus's evidence is analogous to the general Scholastic sense of immediate presence of the apprehended object through intuitio. The Victorines' Platonic framework of illumination parallels Descartes's conviction that intuitus is a clarified conception proceeding from the light of reason. And, like Eustace, he places intuitus at the root of cognition. One of course need not argue for the direct influence on him of any particular texts or theories—despite the fact that they would have been available at the Jesuit college at La Flèche— since these notions were staples of philosophical traditions that he would certainly have heard and read about. We need only claim that, whatever the provenance, Descartes came to think that there was a simple kind of apprehension of truth with precisely these characteristics: immediacy of present evidence; visibility or appearance in a fundamental, indubitable way to mind or eye (perhaps to other senses as well); and primordial or original simplicity among all the acts of the mind.

[7] S.v. "Meditation." Historisches Wörterbuch der Philosophie, ed. Joachim Ritter and Karlfried Gründer, vol. 5: L-Mn (Darmstadt: Wissenschaftliche Buchgesellschaft, 1980), 963; and Dictionnaire de spiritualité, ascétique et mystique: Doctrine et histoire, ed. Marcel Viller (Paris: Beauchesne, 1937-), 1:813.

[8] Eustachius a Sancto Paulo, Summa philosophiae quadripartita (Paris, 1609), 115. Frederick Van de Pitte explores Descartes's possible knowledge of Eustace in Van de Pitte, "Some of Descartes' Debts to Eustachius a Sancto Paulo," The Monist 71, no. 4 (October 1988): 487-497.

As we look more deeply into the Regulae, these characteristics will become more sharply defined. At this point, however, it is important to remark the degree to which the Regulae emphasizes the activity of mind. In his history of logic, Wilhelm Risse points out that the late sixteenth-and early seventeenth-century theorists strongly psychologized logic; that is, they emphasized the basis of logic in the activities of the mind. The Jesuits, who proposed rules and precepts that would give direction to the mind, were leaders in this trend, and Descartes's Regulae ad directionem ingenii was a continuation and development of it.^[9] Thus late Scholastic logicians took the established distinction between formal and material logic, the one culminating in syllogistic, the other in the analysis of the acts of the mind, and attributed primacy to the latter. Formal logic was no more than an abstraction from material logic.

Besides intuitus, Descartes's understandings of deductio, conceptum, and propositio all exhibit the primacy of mind's concrete actions. 'Conceptum' is not equivalent to 'abstract notion' but what is firmly grasped by means of a well-prepared and well-directed moment of seeing purely and attentively.^[10] That is, the object must first have everything extraneous or distracting cleared away, and the mind must take hold of it by means of a steady view within the context of inquiry.^[11] Indeed, the conceptum is clearly seen only so long as it is held clear of distractions, against a favorable background. Once the conceptum is acquired in this way, it becomes part of the stock of things clearly grasped that the ingenium will have at its command for future occasions.

The Descartes of the Regulae is constantly on the alert for ways in which people, especially the learned, mislead themselves (and others) with confused talk. When in the Second Part he teaches that one should whenever possible represent objects and relations by images, he is chiefly trying to forestall the intellect's unfortunate habit of thinking abstractly, apart from specific objects of thought. The concrete grasp of an object by a mind that is pure and attentive is the ultimate cognitive goal of the method (or art) of the Regulae. The model for this is presented in Rule 9, which advises the

[9] See Wilhelm Risse, Die Logik der Neuzeit, 2 vols. (Stuttgart-Bad Cannstatt Friedrich Frommann Verlag [Günther Holzboog], 1970), 2:14-47, esp. 30-31; and Risse, "Zur Vorgeschichte der cartesischen Methodenlehre," Archiv für Geschichte der Philosophie 45 (1963): 269-291, esp. 284-289; also Norman J. Wells, "Descartes' Idea and Its Sources," American Catholic Philosophical Quarterly 67, no. 4 (Autumn 1993): 513-535.

[10] Abstraction for Descartes involves isolating a term used analogically outside the context of any specific nature; see the discussion of 'limit' at AT X 418-419, which is treated in chap. 5, Sec. G.

[11] The context of inquiry is not emphasized here in Rule 3, but as the presentation of the method progresses through the rules it becomes evident that the conceptum of intuitus requires taking hold of the object in a perspective relevant to the problem. Intuitus is always oriented at the very least by the nature (aspect) under which an object is viewed.

reader to practice intuitus by imitating the craftsman, who is accustomed to making perfect distinctions between things and is capable of focusing on the smallest detail (AT X 401).

'Propositio', too, which we are inclined to take to mean a quasi-verbal entity, is another term that must be understood as an aspect of mental activity. Propositio is derived from proponere, to put out in front—here, before the mind. In Scholasticism, a proposition, which can of course be cast in verbal terms, was in the first instance an act of the mind, judgment, which sets before the mind a thought complete with respect to truth or falsity. We shall see that at crucial junctures Descartes uses the term not for a passive object of attention but for the product of the mind's work.

'Deductio', understood simply as logical deduction, fails to capture Descartes's understanding of this discursive act. Descartes's initial formulation—"all that which is concluded necessarily from certain other things known with certainty" (AT X 369)—is in fact misleading. The reader, inclined to think along the lines of syllogistic reasoning or Euclidean geometry, tends to overlook the very elementary sense in which a deductio leads or takes truth from one thing down to another in a motion of thought. The active sense is affirmed in Descartes's explanation of the distinction between deductio and intuitus: deductio is a motion of thought. The most basic justification for the distinction is not surprising: "many things are certainly known although they are not evident." The fact that we experience some truths as immediately evident while others appear only gradually makes it clear that there does exist a kind of knowledge mediated through progressive evidence. Deductio is this moving work of making and seeing the connections of one thing to others.

In standard Scholastic accounts, deductio is a form of discursive reasoning—thus proper to the third act of the mind—and depends on having multiple (at least two) propositiones formed by dint of the second act of the mind, judgment. From the Scholastic viewpoint, Descartes's account of intuitus and deductio appears confused, however, because it portrays intuitus as accomplishing judgments and even deductions, whereas deductio is at times reduced to intuitus. Immediately after defining intuitus Descartes gives four examples of truths it can know: "that it [the soul] exists, that it thinks, that a triangle is terminated by just three lines, a sphere by a single surface, and similar things," items far more numerous than people think because they disdain turning their minds to simple matters. Two paragraphs later he says that

indeed, this evidence and certitude by means of intuitus is required not just for single enunciations but also for any kind of discourse. For example, this consequence is drawn: 2 and 2 make the same as 3 and l; not only must it be intuited-seen that 2 and 2 make 4, and 3 and 1 also make 4, but, beyond

this, out of these two propositions the third is concluded necessarily. (AT X 369)

These examples show that intuitus compares and contrasts terms, something that in traditional logic should be an exercise of the second act of the mind, judgment, and it even conducts discursive reasoning (concluding that 2 + 2 = 3 + l), the third act.

It looks as if Descartes has indeed introduced a confusion. There appears to be an undeniable deduction involved in seeing that (a) 2 + 2 = 4, (b) 3 + 1 = 4, and then (c) 2 + 2 = 3 + l, yet Descartes calls these the result of intuitus. What the example shows, however, is that much intuiting-seeing involves a comparison between elements that can be, and in the process of discovery initially is , carried out sequentially, but that once the elements have been grasped is done in a single look. Once we know 2 + 2 and 3 + 1—that is, once we can instantly recognize each expression in its result—we can instantly recognize their equality.^[12] All seeing that is not the seeing of a simple thing (simple nature)^[13] is therefore an attempted seeing-as: is A the same as B, or different? The act presupposes an acquaintance with A and B and our ability to recognize without discursion whether the two things are the same or different. This intuitus is simultaneously an activity of seeing and an activity of discriminating, neither of which can be perfected without the other.

There is of course an ontological and epistemological problem not far beneath the surface: is the 4 that is recognized when we think '3 + 1' really composed out of sums or is it prior to any sum that yields it; and can we get beyond the act of composition, of summing, to recognize immediately the 4 that is arrived at by addition? What is really and ultimately simple, what is really complex, and how do we know the difference? As Jean-Luc Marion in particular has made clear, the Regulae does not have a definitive solution for this problem.^[14] In Rule 3 it is only touched upon. The chief aim there is to establish the need for two acts of mind, intuitus and deductio. The reason deductio is needed is precisely because we cannot or at least do not in every case reduce a temporal series of recognitions to a

[12] This is also the role of intuitus in the Victorines.

[13] Descartes does not mention the simples or simple natures at this point, however. For a discussion of the contemporary state of scholarship on the simple natures, see Jean-Luc Marion, "Cartesian Metaphysics and the Role of the Simple Natures," in The Cambridge Companion to Descartes, ed. John Cottingham, 115-139 (Cambridge: Cambridge University Press, 1992).

[14] But, he argues further, the theory of knowing it presents has an implicit, in Marion's words a gray, ontology, an ontology of the simple natures. It is one of the major unresolved tensions of the Regulae, and it was at least in part Descartes's effort to determine what might be simple in an absolute sense (especially in Rule 12) that led him to put aside the Regulae.

single seeing. Perhaps the greatest mathematician can immediately see the truth of the Pythagorean theorem, but even for her there will be innumerable other, more complex theorems the truth of which she can derive only by a tong, arduous process of discursive reasoning.

Near the end of Rule 3, Descartes acknowledges that the knowable cannot be neatly divided into what is properly approached only by intuitus and what is approached by deductio. Of course the very simplest knowings come through intuitus, the remotest conclusions through deductio, but "those propositions that are concluded immediately from first principles can be said to be known, under diverse consideration, in part through intuitus, in part through deductio" (AT X 370). Although this seems to muddy the distinction, looking back to the preceding characterization of deductio restores clarity about the underlying principle.

Deductio is described there (AT X 369-370) as knowledge not evident in itself that occurs in one of two ways. The first is "a continuous and in no way interrupted motion of cogitation intuiting-seeing single things perspicuously." In this manner we can know that the link at one extreme of a long chain is connected to the link at the other extreme without a single, all-encompassing regard of the whole or a stepwise viewing of each discrete connection. That is, we make an uninterrupted sweep of the chain's continuity, a sweep of thought that sees all the parts yet never comes to rest before reaching the end. This continuity is conceived as different from both simple seeing and step-by-step, term-by-term discursivity. We note the continuity surveyed by the uninterrupted motion of vision; we find no break in the motion of the mind. The second way of accomplishing deductio occurs when we note each connection individually, step by discrete step, and repeatedly resort to memory to recall that each successive link we check is connected one by one all the way back to the first. The importance of this distinction between two modes of deductio, both of them dynamic, the one being continuous, the other divided into discrete steps, will be discussed later.^[15] What both share is the understanding of deductio as a motion of cogitation—or even, as Rule 7 puts it (AT X 388 1. 3), a motion of imagination. The motion of cogitation either links discrete elements,

[15] In Sec. D of this chapter. The distinction is not unrelated to the difference between the two methods of imaginative knowledge presented in the Schenckel memory art note of the "Cogitationes privatae," one an evolution of phantasms according to cause, the other a preservation of proportional relationships in discrete images put together into a larger imaginative structure. To my knowledge, the fact that Descartes makes a distinction of principle in this passage of Rule 3 has not been appreciated in the extant secondary literature. Translations from Latin typically misrender the modo . . . modo . . . construction that introduces the distinction (AT X 369 1. 23, 370 1.2) as though the second modo were simply a repetition or explication of the first.

each regarded individually by intuitus, or in some way creates a continuously progressing vision that falls short of the immediate grasping of intuitus yet does not rest at any single point. (Intuitus must of course have a full and present evidence without any temporal progression from one thing to another.) Each of these motions "in some way borrows its certainty from memory," though the exact character of that borrowing depends on whether the motion is swift and continuous or slow and step-by-step. Deductio therefore always involves a motion of thought, whether it is prolonged or whether it is "immediate" in the sense of having no intermediate stages between the original thing conceived and the consequent. If one simply sees that 3 + 1 is identical to 4, one has experienced this by intuitus; if one takes 3, adds l, recognizes 4 and the equality, one is engaged in deductio.

In either case the mind is not passively receptive but actively involved in grasping the truth. Deductio's activity is more obvious in that it is a motion, but intuitus is no less an activity. For unless one is dealing with an object of absolute simplicity—what that might mean has by no means been made evident yet—the mind must clear away obstructions from the object so that it can be firmly grasped in the appropriate context. This clarity can have parts without being discursive, and so an object that can be surveyed by a discursive motion of thought might instead be held together by a single perspicuous act of the mind.

Rule 3 ends with a reiteration that these are the only two really certain ways to science, that "no more on the part of ingenium are to be admitted," and that all ways suspected of allowing error are to be rejected. This does not stand in the way of believing that divinely revealed things are "more certain than all cognition . . . since faith, all which is about obscure things, is not an action of ingenium but of will." Yet that which has some foundation in intellect can and should be discovered by one of the two ways, "as we perhaps will show in more detail some day" (AT X 370).

D. INTUITUS AND DEDUCTIO AS COGITATIO

In its dynamism the deductio of Rule 3 bears a resemblance to the imaginative process that Descartes had sketched for the perception of melodic and rhythmic unity in the Compendium rnusicae. They are not identical, of course, especially insofar as the imaginative conception in the Compendium functions by a projective, speculative synthesis (to the completion of the song), whereas deductio can never be hypothetical at any stage of its movement. But it is significant that in the Regulae Descartes returns to the issue of thought's movement and attempts to resolve doubts that it might cast on the certainty and truth of knowledge.

What is thought, that it is subject to motion? 'Think' is cogitare in Latin, 'thought' is cogitatio, two terms of crucial importance to Cartesian philosophy. What, then, is cogitatio? In the eleventh chapter of the tenth book of the Confessions, Augustine of Hippo gives his etymology of cogitare.

And how many things of this kind does my memory bear, which have already been discovered, and, as I said, are as it were placed ready to hand, which things we are said to have learned and to know: which if for a short interval of time I cease to recall, they sink back again and disperse as it were to remoter chambers, so that again they have to be thought out anew from there—for there is no other region for them—and gathered back together, that they might be known, that is, as collected from a certain dispersion, whence it is called cogitate. For cogo [= I gather together] and cogito are [to one another] as ago [= I do] and agito [= I exercise], facio [= I make] and factito [= I keep making, I practice]. But yet the rational soul lays proper claim to this word for itself, so what is collected, that is, gathered together, not just anywhere but in the rational soul, is now properly said to be cogitated.^[16]

The Latin philologist and grammarian Marcus Terentius Varro (116-27 B.C.) gave a somewhat different though not unrelated etymology. He understood the word cogito as co-agito, an intensive agitation or turning over of things by the mind.^[17] According to both of these traditional interpretations, cogitation is a repeated, intensive activity of the mind, an activity requiring mental effort and exertion.

The Regulae does not define 'cogitatio', but the overall impression of the word's occurrences is that it stands for any and all activities of the human mind, just as it did for Augustine. This of course includes intuitus and deductio but extends to any cognitively problematic activity (say, non-intuiting experience or nondeductive speculation) or to certain noncognitive activities as well (like fantasizing). The Regulae as a whole attempts to arrive at principles for regulating the activity of cogitation, principles based on these two fundamental cognitive actions, so that complex matters might be embraced completely and truthfully by the action and the motion or discursivity of thought.

Clearly the question of the continuity of cogitation's motion caused Descartes some difficulty. It is not simply that in the course of the Regulae he gives three names to what is arguably a single operation of discursive thought—deductio, enumeratio, and inductio —but that any thought requiring the passage of time calls on memory and thus introduces a cognitive gap through which uncertainty might creep. Rule 7, echoing the characterization of deductio given in Rule 3, promises the fulfillment of scien-

[16] Augustine, Confessions, trans. R. S. Pine-Coffin (Harmondsworth: Penguin Books, 1961), 218-219.

[17] S.v. cogito, Chariton T. Lewis and Charles Short, A Latin Dictionary (Oxford: At the Clarendon Press, 1879). Agito is the frequentative of ago .

tific knowing through "the continuous and in no way interrupted movement of cogitation" or "imagination" that leaves nothing out of account, a survey in motion that will be an aid "to the infirmity of memory." If I have come to know, by separate operations of mind, the proportions between A and B, between B and C, between C and D, and between D and E,

I do not see what it [the relation] is between A & E, nor can I precisely understand [it] from what is already known unless I remember all of them. For this reason I shall run through them continuously with a certain motion of imagination simultaneously intuiting-seeing individual things and transiting to some others, until I shall have learned to transit from the first to the last so quickly that, leaving almost no part to memory, I seem to intuit-see the whole thing at once; in this way, while memory is reinforced, the slowness also of ingenium is improved and its capacity extended by some reason [ratio]. (AT X 388)

In Rule 16, Descartes throws caution to the wind by claiming not merely that in this motion one seems to regard the whole thing at once but that by using the senses, the imagination, and the briefest mnemonic marks as efficiently as possible, "so that after we shall have inspected the single things distinctly in accordance with Rule 9, we might in accordance with Rule 11 run through them all by a motion of cogitation as fast as possible and intuit-see simultaneously as many as possible" (AT X 455; my emphasis).

There is no contradiction between the two passages, however. The goal of the Regulae is to improve the powers of ingenium; moreover, the ingenium of some people is able to do by intuitus what others have to do by laborious deductio. By working to improve the ingenium, the slower person can gradually approach the abilities of someone with more powerful inborn talents. Some things formerly known only by deductio can be recognized in a single intuitus; slower deductio will become faster; and things not previously known at all will be reached by the expanding operations of deductio.

This expansion of ingenium's power through exercise helps explain Descartes's introduction of a deductio-like power under the name 'enumeratio' or 'inductio' in Rule 7. It is required "because the other precepts help in resolving many questions, but only with the aid of enumeration can it happen that, to anything whatever to which we apply our soul, we will always render a true and certain judgment about it, and therefore nothing will entirely escape us, but we will appear to know something about all things" (AT X 388). The purpose is explained as follows:

There is therefore this enumeration, or induction, of all those things which are aspects of some proposed question, so diligent and accurate an examination [perquisitio] that from it we conclude certainly and evidently that nothing has been falsely overlooked by us: so that as often as we make use of it, if the sought thing is lacking to us, at least we will be wiser in this, that we

would perceive certainly that it could have been found in no way known by us; and, what is more, if as often happens we were able to survey all ways which give humans access to it, it would be permissible to assert boldly that cognition of it had been put above every capacity of human ingenium.
It is to be noted further that by 'sufficient enumeration' or 'induction' we understand only that out of which truth is concluded more certainly than through all other finds of proving [probandi genus], other than simple intuitus; as long as some cognition cannot be reduced to this [intuitus], since all the chains of syllogisms have been rejected there remains to us only this way, to which we must bring total faith. For whatever single thing we deduced immediately from others, if the illation was evident this thing has already been reduced to true intuitus. If however out of many and disjunct things we infer some one thing, often the capacity of our intellect is not such as to be able to grasp all this with a single intuitus; in which case the certitude of this operation must suffice. For which reason we cannot distinguish all the links of some longer chain with one intuitus of the eyes; but nevertheless, if we shall have seen the connection of the single ones with [their] neighbors, this suffices so that we might say we have also seen in what way the last is connected with the first. (AT X 388-389)

The effect of this passage is to begin a certain displacement of deductio proper. Rule 3 had already pointed out that the simple deductio of one thing from another is reducible to intuitus; the immediate illation of one thing from another, the immediate movement of thought, has in fact overcome movement with an instantaneous grasp. As the passages from Rule 7 and Rule 16 cited above suggest and as Rule 3 already allowed, an even longer chain can be reduced to instantaneity or to the semblance of it in a very rapid movement of thought.

At the end of the previous section I called attention to two senses in which deductio can be accomplished: either continuously or stepwise. In the long passage quoted above, the continuous kind so closely approximates intuitus that it shades off into it, is reduced to it, whereas the step-wise kind is evoked in the very chain image that had appeared in the second "sometimes' clause of the next to last paragraph of Rule 3 (AT X 370 11. 2-4).^[18] If the continuous and uninterrupted motion of cogitation leads effortlessly and certainly from one item to another, without the least hesitation and with the structure of the whole sequence clear at every step, then it can be called deductio in the full sense. It is an illation or inference that has proceeded without the least hesitation or doubt, and because of the unity of the process and the reduction of the need for memory, it begins to resemble or even to become intuitus. For the finite human being, who is usually engaged in the search for, rather than the possession

[18] That is, the second modo clause; the relevant passage is quoted in full in Sec. C, above. See also footnote 15, above.

of, truth, who starts in relative ignorance and stumbles many times along the way, this is knowledge in the full sense, which can be achieved only at the end of the search.

E. THE ART OF SOLVING PROBLEMS

We should pause briefly to note how this theory of intuitus-deductioenumeratio might have grown out of Descartes's physicomathematics. Anyone can grasp immediately (intuit-see) a line segment as a line segment. A young child might have to count the sides of a triangle the first time he encounters one—this is a step-by-step deductio—but soon he will grasp it all at once. If we ask the child whether a particular figure is continuous and closed, he can trace it with his finger—a continuous deductio—to see that there is no break. When we teach the now-older child geometry, we will show him how to construct a single mean proportional between two line lengths by adding the two to form a long segment, tracing a circle with that long segment as diameter, and then erecting a perpendicular segment from the point where they were joined to the circle's perimeter; this is again a step-by-step deductio. Perhaps he will mature mathematically to the point of being able to see these things immediately (intuitus) or at least in a continuous sweep of imaginative cogitation (continuous deductio). But if not, we can take a step toward immediacy by giving him Descartes's proportional compass and showing how it generates the mean proportion—indeed, multiple mean proportionals—in a continuous, uninterrupted motion that can be witnessed in fact and re-created in imagination. Any solvable problem of physicomathematics, perhaps any problem whatsoever, ought to be solvable in one of these ways. flour ingenium is overmatched by a problem, we will need to proceed stepwise and rely on memory and memory aids; if our ingenium is up to the task, we will see many aspects of the answer, perhaps the entire answer, in a glance. In between these extremes is continuously moving deductio: if we can find a way in which an answer can be generated by an uninterrupted, interlinked motion like those of the compass, a rotating line segment, a parabola sliding along a circle, or the like, we will have overcome some of the shortcomings of memory and achieved a kind of moving intuitus.

This is not solely a theory of how to do mathematics or physics, however. The Regulae attempts to sketch out a theory of how the dynamism of the mind can be adapted to the nature of questions or problems of all types. Mathematics affords us problems with relatively simple objects, so that the how and why of the employment of the ingenium is much more perspicuous than with more complex questions in remoter subject matters. Nevertheless, Descartes intends the lessons to be universally applicable. He is sketching out the logic of mathematical problems but also

exploring the logical-imaginative space within which all problems of all kinds play themselves out—one governed by the existence of intuitable elements that have determinate relationships to one another that can be traced out and even generated by the mind that observes the proportionalizing method of mathesis universalis.

The first desideratum in solving a problem is often not so much to proceed immediately to inferences as to gain a general notion of what the problem's relevant considerations are and how they fit together. In solving anything we first need to know the lay of the land. This general understanding of the problem is provisional; we either amplify it or modify it or reject it, depending on what eventuates.

If we are dealing with something complex, then it will take a long time to progress from the provisional notion to the detailed and perspicuous account. Having a general notion, a strategy for attacking the problem, is like having a map. If the map is good, it will help us see in principle how to reach our goal; but even a good map will not allow us to foresee every step of the way, and sometimes it will leave out relevant items. And, of course, sometimes maps contain errors. Accordingly, Rule 7 distinguishes different senses of 'enumeration': the complete enumeration (when not even the smallest thing in the chain is omitted, although reason proceeds stepwise rather than in an uninterrupted sweep), the distinct (when we have distinguished all the single parts from one another), and the sufficient.

What is especially curious about the last, in light of Descartes's mature position, is that the account in Rule 7 seems to allow incompleteness and indistinctness in the enumeration without invalidating it.

Again, at times this enumeration must be complete, at times distinct, sometimes neither is needed; and so it has been said only that it must be sufficient. For if I want to prove through enumeration how many kinds of entities are corporeal or in some way fall under sense, I will not assert that they are this many and no more, unless first I have known certainly that I have embraced everything by enumeration, and have distinguished the single things from one another [i.e., the enumeration is complete and distinct]. If indeed I want to show in the same way that the rational soul is not corporeal, it will not be necessary that the enumeration be complete, but it suffices if all bodies are simultaneously embraced in several collections so that I might show that the rational soul can be referred to none of these. If finally I want to exhibit through enumeration that the area of a circle is greater than the area of every other figure whose periphery is the same, it is not necessary to survey all figures, but it suffices to demonstrate this about certain ones in particular, so that through induction the same thing might also be concluded about all the others [i.e., all figures will have been treated in principle, but only a few will have been examined individually]. (AT X 390)

The examples of the rational soul and the circle show that to solve a problem you do not always need to enumerate distinctly or completely. For

certain purposes it may be enough to group quite different things in ways appropriate to the problem. I might be able to group together all corporeal things into certain sets—for example, nonhuman animal, vegetable, and mineral—whether or not the sets truly correspond to natural kinds, and show on their basis that the rational soul cannot be a member of any; the practice is commonplace in mathematics and logic, where, for example, it might be easier to prove a theorem by breaking it down into sets of cases that embrace all possibilities. These groupings can even display a certain arbitrariness (e.g., one might prove a theorem in arithmetic first for odd numbers and then for even). Of course one can be confident in the mathematical examples that the survey covers all relevant individuals, whereas in other cases there might be residual doubt about this (e.g., is the realm of corporeal things truly exhausted by the classes animal, vegetable, and mineral?).

The example of the circle as containing the largest area for a perimeter of a given length could perhaps be seen as appealing to mathematical induction, which allows a demonstration in a specific case to be extended in principle to all other cases. For example, to prove that the formula (n -2) × 180º gives the sum of the internal angles of an n -sided plane figure you could show (1) that if the formula holds for an n -sided figure it will also hold for a figure with n + 1 sides and (2) that it holds for the case n = 3, that is, for triangles; from (l) and (2) you can claim that it holds for all cases of n where n is greater than or equal to 3, without specifically examining any other case. But it would be anachronistic simply to assume that this is what Descartes had in mind. Rather, the example suggests that he is thinking of cases for which a few typical instances might be sufficient for recognizing the truth of a theorem. One might prove that a, say, regular octagon of a given perimeter has a lesser area than the circle of the same perimeter and note that doubling the number of sides increases the area in a way that does not exceed the area of the circle. If one can see as well a principle or a fact ensuring that further doublings will not increase the area at a sufficient rate to surpass the area of the circle, one need not distinguish and consider the intermediate cases or even make an explicit mathematical induction.

The secret to an induction of the kind Descartes proposes is that the cases be well ordered; although you do not inspect each and every one, you discover a principle in the actually examined cases that guarantees the validity of the conclusion. Rule 7 points out that well ordering, either by numerical sequence or according to partition classes, is crucial, because it often allows us to treat collectively things that could not be surveyed singly in the finite time given to human beings. Moreover, the order of enumeration does not have to be of a specific kind, "and it depends on the judgment of each person" (AT X 391). Descartes notes that if we wished to solve an anagram, we would not even need to follow the earlier rules; "it

will suffice to propose to yourself an order for examining the transposition of letters so that the same ones are never run through twice, and so that the multitude of them is, for example, distributed into certain classes so that it immediately appears in which there is greater hope of finding what is sought; for in this way it often will not take long but be only child's play" (AT X 391).

This passage, rather than marking a descent into triviality, not only reinforces the idea that there is no truth so elementary that it can be safely overlooked—in Rule 10, Descartes actually recommends exercising ingenium in games, puzzles, and crafts—but also shows that a recognition of truth does not require an absolute and total reduction of things to simplest parts. As we shall see in Rule 6, division into small parts is important, and even at times absolutely necessary, but only if the search for truth has been otherwise frustrated.

F. PRACTICING INTUITUS

Most of the remainder of the Regulae is dedicated to understanding and improving discursive reasoning. Rule 9, however, provides instruction about how one can improve the exercise of intuitus.

Rule 9: It is necessary to turn the whole sharpness of ingenium to the smallest things and the maximally easy things, and to remain in those things as long as needed, until we become accustomed to intuiting-seeing the truth distinctly and perspicuously.
Having set out the two operations of our intellect, intuitus and deductio, which alone, we said, are to be used in learning the sciences, we go on in this and the following proposition to explicate by what effort we can render [them] apter to exercising these things and simultaneously cultivating two principal faculties of ingenium, namely, perspicacity by distinctly intuiting single things and sagacity by skillfully deducing some things from others.
And, indeed, in what way one is to use intuitus of the mind we know by comparison with the same [intuitus] of the eyes. For whoever wants to look upon many objects simultaneously in the same intuitus will see nothing of them distinctly; and equally whoever is used to attending to many things simultaneously with a single act of cogitation is of confused ingenium. But those artisans who are practiced in the most minute labors and are accustomed to direct the sharpness of their eyes attentively to single points, acquire through use the capacity of perfectly distinguishing as many small and subtle things as one could wish; so also those who never distract cogitation with various objects simultaneously but who always occupy the whole [cogitation] with considering every simplest and easiest thing become perspicacious. (AT X 400-401)

It is to be noted that those who truly know distinguish the truth with equal facility whether they have educed it from a simple subject or from an

obscure one: for they comprehend each and every one [= truth] by a similar, single, and distinct act, once they have arrived at it; but the whole difference is in the way, which certainly ought to be longer if it leads from the first and maximally absolute principles to a more remote truth.
It is therefore proper that all become accustomed to embrace by cogitation simultaneously so few and so simple things that they never think they know something that is not intuited equally distinctly as that which they know most distinctly of all things. (AT X 401-402)

Descartes remarks that some people are born with a greater perspicacity than others but that practice can improve any ingenium. This is not done by turning to great and obscure things or to sublime philosophical arguments, because even the most "abstruse sciences are to be led down [deducendas ] only from easy things and more accessible ones" (AT X 402). He gives two examples: (l) If we wish to know whether a natural power can travel through space in an instant, it is a mistake to turn to difficult matters like magnetic force, the influence of the stars, or even the speed of light. Rather, one should turn to the question of the local motion of bodies, "because nothing in this whole subject matter [genus ] can be more sensible [i.e., more accessible to the senses]." Although the motion of an ordinary body proceeds from place to place and therefore is not instantaneous, an ordinary body can exhibit a type of instantaneous motion when it is moved as a whole: "for example, if I move one extremity of a stick, be it as long as one likes, I easily conceive that the power by which this end of the stick is moved necessarily also moves all the other parts of it in one and the same instant" (AT X 402). (2) In what way might one and the same simple cause produce simultaneous contrary effects? To answer this I should not think of medicines that drive out some bodily humors while retaining others or of the power of the moon to warm by its light as it cools by an occult quality, "but better that I shall intuit-see a balance scale, in which the same weight raises one pan in one and the same instant as it depresses the other, and similar things" (AT X 403).

The workings of the intuition of mind and eye are explained here using physical problems as examples, but that must not induce us into thinking that Descartes was illustrating only how to address corporeal problems. The entire context of Rule 9 takes as given the strict analogy between intuitus of the mind and intuitus of the senses, so that the latter can serve as a model for the former. This is entirely in the spirit of the principle of analogical resemblance of his earliest philosophy. Moreover, the rules of the second part of the Regulae show how imaginative aids can be used in solutions to any kind of problem; they show ways in which things can be "figured" concretely and further illustrate the biplanarity of intuitus.

In the "Cogitationes privatae," especially in the notes "Sensible things [are] apt for conceiving Olympian things" and "The cognition of natural

things by human beings [occurs] solely through the similitude of those things that fall under sense," corporeal things image things higher than the corporeal. In the present examples natural power and the possibility of its being instantaneously conveyed are illustrated by the humble (but perhaps not absolutely simple) example of a stick. The single example does not prove that any other natural power is instantaneously conveyed, but (putting twentieth-century physics to one side) it does show that such a power exists naturally. Similarly, the contrary motions of the two pans of a balance scale show that a single cause can have opposite effects. It is quite evident that Descartes is not proceeding by before-the-fact reasoning but rather showing that if we learn to grasp relatively simple, concrete things in the right ways we can immediately see truths of interest and relevance.

Suppose a Scholastic philosopher wanted to determine whether light traverses space over time or instead occupies the whole of the intervening space in an instant. He would proceed by searching for one or more middle terms that would connect the minor term, light, with the major term, instantaneity, and these middle terms would have to be abstract essences or qualities, just like the major and minor terms. Such a search would be close to hopeless. (l) If one conceives light by way of genus, say "natural power," one can show that light is instantaneous only if all natural powers are transmitted in an instant. A set of collapsing dominoes shows the contrary. (2) An alternative is to settle with exactitude the essence of light, in the hope that the essence will imply instantaneity. But essences cannot be discovered through middle terms (because they identify what the things in question simply are), so either (a) instantaneity must turn out to be the differentiating factor that makes light what it is (the instantaneous natural power) or (b) it will have to be an essential attribute that is derivable from the differentiating factor plus genus (suppose that there were a characteristic, informity, such that light was an informitive natural power, and everything informitive was instantaneous in effect) or (c) it is merely an accidental property of light. In cases (a) and (c) we would simply have to recognize light as instantaneous—in one case essentially, in the other accidentally—that is, no middle terms would be involved. In case (b) we would find ourselves back at the beginning: if we did not already know that all informitive things are instantaneous, we would have to search for middle terms to prove it, a task that would probably be more difficult than the original one. In order for the search to work at all, one simply must have an intuituslike power of recognizing things, even relatively complex things like pan balances, for what they are, what they do, and what they show.

Descartes abandons the search for essences in favor of the search for resemblances (at the outset of Rule 6; see chap. 5, Sec. B), and he thereby devises a method with many more expedients for addressing problems by putting intuitus at its heart. If Descartes had asked himself whether light

was instantaneously transmitted—and of course he did ask himself this question—he might in his search have proceeded like this: "How can I determine whether light is instantaneous? Well, I usually think of it as a natural power, but not the only one. Let me cogitate. . . . Perhaps I can enumerate different examples of natural power: light, gravity, impulsion. . . . This 'method' I am following here hardly seems comprehensive, it's just random. . . . But wait! I can approach this question from another, more concrete direction. I can imagine an instantaneous power in an elementary example, the motion of a rigid stick; when one end is pushed, the other moves at the same moment. So I know that at least one such natural power exists, because it occurs in a really existing natural thing. This will allow me to study light in a more focused way: I can analogize light to the stick, I can try to think of ways in which the action of the stick can be taken as a model for the action of light. Let's see. . . . Suppose that space were not void but a plenum, filled with matter, and that for any part of it to move the immediately adjacent part had to move, just as with the stick, and suppose that light is an action transmitted through this matter as medium, then. . . ."

This is, of course, not a solution, but just one or two steps on the way to a solution. Nevertheless, it promises to be a method much more flexible and rich in alternatives than is the abstract search for middle terms. To become knowledge these hypotheses and notions would have to be included in, first, a step-by-step deductio (a sufficient enumeration) and then perhaps into a continuous deductio approaching the status of intuitus, if my ingenium is powerful enough. The technique of analogical extrapolation from individual cases can lead to knowledge only if there is some basis for knowing not just (say) that the behaviors of sticks and light both exhibit natural powers but also that they have in them, or participate in, the characteristic "natural power" in the same relevant way. Rule 6 in fact presents a doctrine of natures conceived not as essences but as semblances that things participate in or contain in varying degrees.

But before we turn to this participation theory, we need to highlight Rule 9's special contributions to understanding the biplanarity of intuitus. One does not intuit things in the absence of context. The command "Intuit!" or "Intuit that balance scale!" would elicit the response "How?" "in what way?" Intuiting-seeing that the scale exists is different from intuiting-seeing that it is corporeal, which in turn differs from intuiting-seeing that the two pans move in opposite directions because of a single weight. The easy and distinct, the not doubtful concept of a pure and attentive mind (to use the idiom of Rule 3), requires that the object be cleared of extraneous considerations (e.g., in the case of Rule 9 the metal out of which the scale is made would be set aside) and that the mind be sharply focused and attentive. The clearing away of what is extraneous takes place in the

course of the search for truth, and the direction of focus is provided by the context of the problem.

Therefore, just as in the earliest philosophy, there is an object plane and an ocular or configuring (or figuring-out) plane. Intuitus is the hold that the mind gets on the object in light of what the context of the problem illuminates. The balance scale can be grasped in many ways: to name just a few, as simple machine, as material object, as existing being, as weighing device, as exhibitor of contrary effects by a single cause. Intuitus is therefore not grasping "the" idea of the scale; rather, the conceptum of intuitus is the particular, focused, active grasp of what has been presented to and prepared by the mind.

G. MATHESIS AND THE NECESSITY OF METHOD

As the "Cogitationes privatae" noted, every ingenium has limits that it cannot transcend, yet those who "cannot use principles for discovery because of a defect of ingenium can nevertheless know the true reward of the sciences, which suffices them for carrying out true judgments in the estimation of things" (AT X 215). Another private cogitation, which falls amid the notes about the powers of imagination and the capacity of sensible things to mirror Olympian things, remarks that "the sayings of the wise can be brought back [reduci ] to a certain very few general rules." A finite ingenium, whether considered under the aspect of its particular defects or from the perspective of the limits that are imposed on all human beings, is nevertheless capable of truly judging in the appraisal of things, and the very principles that are characteristic of all human ingenia are such that they can be made subject to a regulated use, that is, to method. Rule 3 has identified two ways native to ingenium, intuitus and deductio, and it is on the basis of these that the subsequent rules present a regulated use. Rule 4 quite consequently begins by announcing that "method is necessary to investigating the truth of things."

The predominating metaphors of Rule 4's first paragraph are blindness and aimless wandering: "Mortals are so much held by blind curiosity that often they lead down [deducant ]^[19] their ingenia along unknown ways without any reason of hope," as if someone overcome by greed for finding treasure should "perpetually wander the streets" looking for something mislaid by another traveler. Almost all chemists, many geometers, and no few philosophers proceed in this way. But it would be preferable never to think of searching for the truth of a thing than to proceed without method; "for it is most certain that through inordinate study of this kind and obscure meditations the natural light is confused and the ingenia are

[19] 'Deduction' would of course be completely unacceptable here.

blinded," just as eyes accustomed to darkness weaken so that they cannot bear the light of day.

What is method? "By method I understand sure and easy rules which anyone might observe exactly so that he never puts anything false for the true and, no endeavor of mind being uselessly squandered but rather always gradually increasing science, he arrives at the true cognition of all things of which he will be capable" (AT X 371-372).

According to the second paragraph of the rule, method will rightly teach how the proper use of mind's intuitus-seeing can prevent us from falling into error and how deductions are to be found so that we can come to the cognition of all things. It will also teach that nothing more is needed for the completeness of method than intuitus and deductio; that is, these two are both necessary and sufficient for method. Rule 4 is therefore a natural outgrowth of Rule 3. But the rule immediately moves to forestall a possible misconception about the direction the doctrine of method ought to take. The method of the Regulae will not teach how to perform intuitus-seeing or deductio, "because they are the simplest and the first of all, so that unless our intellect is already able to use them it would comprehend no precept at all of this method, however easy it might be" (AT X 372). Moreover, the operations of the mind that ordinary logic and dialectic teach are useless because they tend to impede and obscure the light of reason rather than add to it.

The next paragraph appears to begin with a justification for rejecting the classic logical-dialectical method in favor of the method of intuitus-deductio. Descartes says that since to give oneself over to studies without this true method is more harmful than helpful, he can easily persuade himself that the great minds of the past (called the majorii ingenii ) had already recognized it in some way, "by guidance of nature alone." Using a conceit that appeared in the "Cogitationes privatae" and that occurs three times here in Rule 4,^[20] Descartes announces that "the human mind has something divine, I know not what, in which are founded the first seeds of useful cogitations in a way that often produces spontaneous fruit, however neglected and suffocated it may have been by studies [that are] at cross-purposes" (AT X 373). As an example of the power of these first seeds, the rule adduces arithmetic and geometry, the latter in the form of the ancient geometric analysis, the former under the aspect of the still-developing

[20] Twice in 4-A (AT X 373 11. 8-9, "prima cogitationum utilium semina"; 374 ll. 7-8, "prima rationis humanae rudimenta") and once in 4-B (AT X 376 ll. 12-13, "prima quaedam veritatum semina humanis ingenijs a natura insita"). The count is raised to four if one includes a similar phrase in 4-A (AT X 373 ll. 19-20, "spontaneae fruges ex ingenitis hujus methodi principijs name"). Since Weber's stratigraphic theory of composition considers the repetition of ideas to be a mark of redundancy, then the supposedly later 4-A contains one of the very redundancies said to differentiate 4-B from the rest of the rule.

modem algebra. "These two are nothing other than the spontaneous fruit born from the congenital principles [ingenitis principijs ] of this method." They have flourished because of their very simple objects. Though all other sciences have had their advance blocked by greater impediments, "provided they are cultivated with the greatest care they will without doubt arrive at perfect maturity."

The next paragraph reflects on what this means for the project of the Regulae. "Indeed I have undertaken principally in this tractate to make this happen [i.e., the arrival at maturity of all sciences]." If he aimed at nothing more than solving inane problems like other logicians and geometers, his work would be as pointless as theirs. The discussion then turns to the purpose of the frequent references to figures and numbers that occur in the rest of the book.

From no other disciplines can be drawn examples so evident and so certain, but whoever will attentively have regard to my sense will easily perceive that I am thinking here of nothing less than the usual mathematics, but rather that I am setting out a certain other discipline, of which others are the integument [or covering] rather than the parts. For this [discipline] must contain the first rudiments of human reason and extend to eliciting the truth from any subject whatever; and, to speak freely, I persuade myself that this is greater than all other cognition that is humanly handed over to us, inasmuch as it is the fount of all the others. And I said 'integument' not because I want to cover over this doctrine and make it involved so as to keep away the vulgar [people], but rather to dress and ornament it so that it can be better accommodated to human ingenium. (AT X 374)

Some thirty years ago Jean-Paul Weber, the leading proponent of the thesis that the Regulae is a patchwork of inconsistent initiatives (the contradictions between which reveal the order of composition), claimed that these words mark the end of Rule 4-A, which he believes is the second draft of the rule. The last half, that is, the last two paragraphs, known as 4-B, he believes was the historical starting point for the entire Regulae and that it was composed in the weeks preceding Descartes's dreams of 10-11 November 1619. Before passing judgment on the possible coherence or inconsistency of 4-B with 4-A, then, it will be useful to reflect on where things stand at the end of 4-A and to compare how the two parts are formulated.

People ordinarily pursue knowledge randomly, and this random pursuit tends to blind the natural endowment of the seeds of truth. The leading, Aristotelian theory of scientific knowledge, embodied in dialectic and syllogistic logic, either confounds what is innate by trying to teach it or impedes the proper use of the inborn seeds of thought by presenting useless complications. Although the kind of success that cultivating the seeds can bring is most evident in mathematics, the object of the Regulae is neither to teach mathematics nor to drive off untutored readers with a smoke-

screen of figures and formulas. The goal is to bring about the perfection of all sciences whatsoever. Ordinary mathematics is introduced not for its own sake but as the only current example of how simple things can be certainly and evidently known by means of intuitus and deductio. Ordinary mathematics is but the outer vestment of the discipline that truly contains the first rudiments of human reason, and mathematics is an especially good source of examples because it is well accommodated to the ingenium of human beings.

Many themes of the cogitations of 1619-1621 are sounded here: that there are seeds of knowledge; that until now the sciences have been hidden; that only a small number of rules, not a complex science of logic and dialectic, are needed to guide the native cognitive endowment; that there are limits to human ingenium, but that each human being possesses what is needed to judge for him-or herself; and that the figures of mathematics can be used to show forth something else, something higher and more perfect than themselves. Descartes expresses through qualifications that he is dealing here in human things, in human knowledge, and that his standard is not divine knowing or being: the new discipline he is seeking is better than all other cognition humanly handed down to us, it contains the first rudiments of human reason, and the mathematical integument accommodates it to human ingenium.^[21] But what does it mean to be accommodated to the ingenium of human beings?

There is a fairly clear answer from our previous examination of imagination and ingenium. The ingenium as defined in Rule 12 is the generalized power of forming and manipulating images and of regarding images as images, that is, as figuring something else. The easiest thing for imaginative ingenium to do, the thing most accommodated to its nature in human beings, is to form simple geometrical figures to represent the proportions of relevant aspects of what is in question. Mathematics is not so much a discipline unto itself as the object most naturally suited to the human ingenium, which is able to figure things out much more readily by looking at a problem in particular respects than by trying to grasp essences and natures. The aim of the whole Regulae should accordingly be to show not how everything can be reduced to mathematics but rather how mathematics in its exquisitely simple work of making and examining images can be applied, and give crucial guidance, to the more comprehensive use of the ingenium. Ingenium is able to embrace all sciences by making figures that enable it to conceive the objects of those sciences. The

[21] Gäbe emphasizes the human limitation of Descartes's cognitive claims in the Regulae, as does also Josef Simon; see Gäbe, Descartes' Selbstkritik, and Simon, Wahrheit als Freiheit, pt. 2, chaps. 2 and 3. It is interesting here that, although the qualification of ingenium by humanum is not rare in the Regulae, ingenium occurs in the vast majority of cases without it. For a quick overview, consult the Index des " Regulae ad directionem ingenii. "

practice of mathematics, taken by analogy, will provide the humble model for using figuration and conceiving the nobler sciences. Thus figuration and conception is the discipline that contains and elaborates the seeds of all knowledge.

Part B of Rule 4 begins autobiographically.

When I first applied my rational spirit [animum] to Mathematical disciplines, I read through without pause most of those which are usually treated by their authors, and I cultivated chiefly Arithmetic and Geometry, because they were said to be the simplest, and as it were roads to the others. But in neither case did any writers by chance then fall into my hands who completely satisfied me: for I read many things in them about numbers, which when I performed the reasonings I experienced to be true; and about figures, they exhibited many things in a certain way to the eyes themselves, and they drew conclusions from certain consequences; but why these things were so, and in what way they were discovered, they did not appear to show sufficiently to the mind itself; and so I was not surprised if even most of those ingenious and erudite men either soon neglected these once-tasted arts as puerile and vain or on the contrary while learning [some things] from these were frightened away at the very border by seemingly very difficult and intricate things. For truly nothing is more inane than to treat of bare numbers and imaginary figures in such a way that we seem to want to find rest in the cognition of such trifles and to take pains with those superficial demonstrations, which most often are discovered more by accident than by art and pertain more to the eyes and the imagination than to intellect, so that we become unaccustomed in some way to using reason itself; and at the same time nothing is more intricate than by a mode of such testing to disentangle new difficulties involved with confused numbers. (AT X 374-375)

This passage (approximately one-fourth of the first paragraph of 4-B) is crucial not only because of its importance for determining whether the Regulae is a coherent work but also because of the clues it yields about Descartes's conception of the unity of his studies.

What does it accomplish? Despite its initial appearance of being an autobiographically narrative interloper in an otherwise discursive context, it is in fact strongly linked to what precedes. Rule 4 began as a reflection on the blind and errant ways on which human investigators set out and the relative good fortune of those who have not had their powers, their natural light, obscured by misguided experience. It spoke from the perspective of one who had already discovered the origin of all methodical inquiry, intuitus and deductio. It did not claim, however, that the origin and method were previously unknown; the existence in all human beings of inborn seeds of thinking and knowing led the author to persuade himself that, even when neglected or crossed, nature spontaneously leads some people to produce fruits of wisdom. Precisely at this point he first mentioned the

arithmetic and geometry of ancients and moderns as evidence of this thesis and as surety that, once more complicated objects have been approached with a deliberate application of method, the sciences of them will reach "perfect maturity." The account of 4-A therefore had three foci of development: the human search for truth, the seeds of method that can guide it, and the objects and disciplines that will be understood as a result. After Rule 3 had marked out two ways and two ways only of coming to the truth, Rule 4-A proceeded quite logically—for the young Descartes, who prefers thinking that is concrete—to the question of where and when they have been followed. The beginning narrative in Rule 4 was thus essentially the fruit of historical reflection on the hitherto largely abortive quests for truth and the reasons for their failures and any successes. Presumably the author of such a narrative was writing from the perspective of success in the quest for truth, and so it is understandable that he would include historical reflection on himself, that is, autobiography. Thus there is nothing very much surprising when the narrative turns to autobiographical considerations in 4-B.

This is a general justification of the beginning of 4-B, in terms of the rhetorical situation. What justifies its particulars? Consider: the last paragraph of 4-A made clear that it is not mathematics that the Regulae is intent on teaching, despite the fact that the work frequently adverts to examples of numbers and figures (as it had already done in Rule 3), but rather a discipline from which even the scientific subjects that are called mathematical ultimately derive their knowability and certainty, a discipline that is the ultimate discipline because it "contains the first rudiments of human reason and extends to eliciting the truth from any subject whatever." When Descartes wrote in the very last lines of 4-A that he calls mathematics the integument of this discipline not to hide it but to vest and ornament it "so that it can be better accommodated to human ingenium," he was not concluding his exposition but only setting the stage for an elaboration of (1) what in ordinary mathematics can be used to conceive this higher discipline, (2) what differentiates the higher discipline from ordinary mathematics, and (3) in what sense ordinary mathematics accommodates human ingenium to the higher discipline. Within the context of Rule 4, questions 1 and 2 receive provisional answers, while 3 awaits the further elaboration of how the regulation of the ingenium is to be undertaken in the succeeding rules. We already have seen, however, in what way Rules 12 through 21 can be said to present a doctrine that uses a simple mathematics of number and line in order to accommodate the pursuit of knowledge to the character of the human ingenium.

In 4-A, Descartes wrote that his first reading of mathematical authors concentrated on arithmetic and geometry "because they were said to be simplest and as it were ways to the other disciplines," But he did not find

them to be as he expected. Although by verifying the results he found that much of what they said was true, this did not satisfy him because they did not explain "why these things were so" or "in what way they were discovered." The reasons supporting the knowledge and the process of reaching it were left obscure. It was clear from the poor use these writers made of their discoveries that they did not really possess any clear method that had brought them to their results; it was as much chance as acumen. In addition, they acted as though the goal were to be satisfied with superficial demonstrations concerning bare numbers and imaginary figures, and their demonstrations appealed more to the eye and imagination than to the intellect. Obviously there is something more that Descartes expects of a process of knowing adapted to human ingenium. It is clear that he does not desire simply the application of mathematics for its own sake, but rather the science that uncovers and elaborates the unity of all knowing and that simultaneously is the ground of all application of knowledge.

In 4-B, Descartes points out that he reflected on a demand made by ancient thinkers: that one learn mathesis, the way of cognitive discipline, as a prerequisite to the study of wisdom, because it is the simplest and most necessary of all for preparing the ingenium.^[22] This reflection aroused a suspicion: that the ancients possessed the key to learning, a mathesis that was radically different from the mathematics and even the algebra of the current day. Here in 4-B, just as two paragraphs earlier in 4-A precisely at the point of discussing the works of predecessors, he adverts to the first seeds of knowledge, "certain first seeds of truth seated in human ingenium by nature." But here the reasoning has a different aim. In the earlier passage reflection on the divine seeds of knowing led to arithmetic and geometry as examples of how even neglect and miseducation cannot completely frustrate their effect, whereas here the ancients' treatment of mathematics as a preamble to wisdom spurs him to mention these seeds as leading not just to mathematics but also to fundamental knowledge of all kinds. The one who seeks wisdom can discover moral truths, just as the ancients discovered that virtue is to be preferred to pleasure and honesty to utility, and the other true ideas of philosophy and mathesis as well, all "with one and the same light of the mind." These are not mathematical ideas he is talking about but philosophical and mathetical ones.

Henceforth I shall use the term 'mathetical' to distinguish this fundamental philosophical character of mathesis from mathematics. Before explaining further its significance, we must note that Descartes does not say

[22] Marion traces the antecedents of this admonition. The ancients spoke of geometry rather than mathesis. A late sixteenth-century work that Descartes had certainly read, Clavius's book on the Elements of Euclid (1589; 2d ed. 1603), speaks of the need to know "the Mathematical sciences." Descartes's mathesis in fact radicalizes the admonition: learn not mathematics but the foundation of everything that is learnable.

he found the vestiges of this true mathesis in all past mathematicians—for example, he mentions Pappus and Diophantus but not Euclid—and he points out that in the recent past there have been "certain most ingenious men" who have tried to resuscitate it, although it needs to be relieved of "the multiplicity of numbers and the inexplicable figures under which it is buried."

The analysis of Pappus and Diophantus was a technique for solving geometrical and geometrically representable problems by taking both the known and the unknown as determinate and then, by means of relationships that are given or deducible, working out the unknowns.^[23] This is the discipline that Descartes calls a mathesis very different from the vulgar one of his age. It is not enough simply to foster problem solving by using the algebra of the mathematicians, however; for when this insight "recalled [him] from the particular studies of Arithmetic and Geometry to a certain general investigation of Mathesis," Descartes began to "inquire first of all precisely what everyone understands by this name" and why other sciences like astronomy, music, optics, mechanics, and many others are called parts of mathesis. He warns, however, that it is not enough simply to ask after the origin of the word. This calls to mind the caveat of Rule 3: look not to the meanings of the terms as usurped by the schools but to their simple Latin meanings, and then use the one most apt.

Descartes notes that 'mathesis' amounts to the same thing as 'disciplina', discipline, and by the criterion of simple meaning all methodically organized knowing has as much right to be called a discipline as does geometry. He then invokes the universal testimony of people, even those who possess a minimal rationality: all those who have reached school age easily distinguish the general matters that pertain to the fundamental discipline, mathesis, from what specifically belongs to other, particular disciplines. He arrives at the conclusion that everything in which order and measure are examined refers to mathesis and that the science that treats everything pertaining to order and measure in any manner and any matter whatsoever is to be called 'mathesis universalis', "because in this is contained all that on account of which the other mathematical sciences are called parts [of mathematics]." Of course, there are other, particular things for which this universal mathesis cannot account, but anything that in any way reflects order and measure is subject to it. As Descartes goes on to say in the second, concluding paragraph of 4-B,

But conscious of my weakness I decree that I will pertinaciously observe such order in the inquiring cognition of things that I will always proceed from the simplest and easiest things and never progress to others until it seems to me

[23] Jacob Klein, Greek Mathematical Thought and the Origin of Algebra, 126 -149; and Paul Tannery, La Géométrie grecque (Paris, 1887).

that nothing more to be wished for remains in these; wherefore I have cultivated till now this universal Mathesis insofar as was in my power so that 1 consider myself able to treat from the beginning somewhat profounder sciences with a not premature diligence. But before I turn to this, I want to collect into one and dispose in order everything I have perceived worthy of note with regard to these superior studies, partly so that one day I might easily recall such things from this book if the occasion demands, when memory is diminished by increasing age, partly so that now, memory being liberated from these same things, I can more freely shift my rational spirit [animum] to the others. (AT X 378-379)

Here is further evidence that the Regulae is paradoxically patterned on the art of memory, using various devices to minimize the need for that fickle power. Moreover, the chief autobiographical conceit of the paragraph, that the Regulae is a work of transition and an instrument for a memory that is always overburdened and in danger of failing, certainly adds to the impression that 4-B is in essential continuity with both the preceding three and a half rules and with Rules 12 through 21.^[24]

But the emphasis in the passage on the need for order in all studies and the orderliness of the Regulae itself—which is an orderly reflection on the fundamental principles of order—indicates that the Regulae participates in the very subject matter it is about: it is about order, and it is itself orderly. In this sense, the Regulae itself is more than a token for memory: in the sense identified earlier, it is itself a symbol of order, indicating the whole while also participating in it.

H. MATHEMATICS, IMAGINATION, AND MATHESIS

Chapter 1 introduced the medieval doctrine of the internal senses and argued that its durability was due not simply to the Aristotelianism of West-em Scholasticism but also to support from other traditions, especially medical theory. The understanding of the imagination as a power of sensibility dependent on localized brain functions and playing a significant role in cognition was therefore not specifically bound to the fate of Aristotelian

[24] It seems unlikely that this would accurately describe his situation in late 1619, though it seems more than apt for his intention to explore first philosophy at the urging of Cardinal Bérulle (perhaps in late 1627) and his actual execution of that intention during his first nine months in Holland (i.e., in 1629). One should note that Rule 4's autobiographical approach to the history of mathesis is not echoed in any of the notes from the period 1619-162l, apart from the narration of the dreams of 10-11 November 1619, which is an episode to be interpreted rather than a life to be narrated. The Studium bonae mentis, the only other early autobiographical piece, cannot antedate 2623, since according to Baillet's account it discusses events of that year, and it is possible that this no longer extant work was written years later. Once again the evidence points to a later rather than an earlier date for the composition of Rule 4.

or Scholastic tenets. The centrality of imagination was bolstered by the concurrence of other traditions that contributed theories of its importance. For example, the Stoics taught that the dominant power of reason, the hegemonikon, was located in the brain and there received the phantasiai from the external world. In the Neoplatonic Augustine, in contrast, memory was, along with intellect and will, a member of the highest triad of psychological powers, while corporeal imagination was part of the immediately subordinate triad of sensitive powers. Indeed any Neoplatonist is as likely as not to ascribe an important role to imagination. Although Neoplatonism is, "in general, inimicable to a constructive theory of fantasy," it

is capable at any time of taking a course which leads to the ennoblement of a mental capacity which its basic philosophy affected to despise. This paradoxical nature of Neoplatonic thought concerning phantasia and related powers can hardly be overemphasized: its idealism taught it to despise phantasies, its dualism found a place for them, its psychology, largely Aristotelian, taught it to study them, and its passion for the Timaeus led it to recognize them as God-given.^[25]

According to a recurrent Neoplatonic theme, the different levels of reality image or mirror one another, so that imagination can acquire a certain ontological and epistemological credibility and partially bridge the gap between the corporeal and spiritual realms.

With respect to mathematics, Descartes was not the first to ascribe a special role to imagination; indeed, already in late antiquity Neoplatonists interpreted the phantasia as providing the medium and matter for mathematical objects. In his monograph on the background to Descartes's use of the term 'mathesis universalis', Giovanni Crapulli traces the notion back to the Greek mathematician Euclid and the Neoplatonic philosopher Proclus (412-485). In the sixteenth century the content of a universal mathematics was discussed under various names, such as scientia communis, mathesis generalis or universalis, mathesis universa, and mathematica generalis. These names were intended to indicate the discipline common to all the mathematical sciences; the core of it was the Euclidean theory of proportion presented in the fifth book of the Elements of Geometry. Moreover, within these sixteenth-century discussions of mathesis universalis there was an influential strand of thought going back to ancient commentaries on Euclid that understood the medium or material of mathematics and mathematical objects to be the intelligible matter of phantasia. So, for example, in his commentary on Euclid's geometry, Proclus presented the notion of

[25] Murray Wright Bundy, The Theory of Imagination in Classical and Mediaeval Thought, University of Illinois Studies in Language and Literature, vol. 12, nos. 2-3 (Urbana: University of Illinois Press, 1927), 146.

kinesis phantastike (imaginative motion) as underlying the mental activity of the geometer; elsewhere he described the phantasia as a "form-giving intellection of the intelligibles."^[26]

This doctrine of the imaginative basis of mathematics gained renewed topicality in the sixteenth century, especially through Alessandro Piccolo-mini's Commentarium de certitudine mathematicarum disciplinarum. In his discussion of the common science (scientia communis) he argued that the mathematical sciences were considered by the ancients as intermediate sciences both because they were neither entirely intellectual nor entirely immersed in matter, and also because of their efficient cause, the phantasia: "a certain power of soul that holds an intermediate place between sense and intellect," which Piccolomini, following Proclus and others, identified with Aristotelian intellectus passivus (nous pathetikos), passive or potential intellect. The things of mathematics "are not at all sensibles in the subject [= substance] nor things inwardly liberated from it: those mathematical figures are found rather in phantasia itself, garbed nevertheless on the occasion by quantities found in sensible matter." The phantasized quantity (quantum phantasiatum ) did not constitute the matter of any particular kind of mathematics; rather, "one thing of great weight is to be noted, that when we have shown the phantasized quantity to be the matter or subject of mathematicians, this is said to be the subject not of geometry or arithmetic, which two are the first genera of mathematics, but of a certain faculty common to geometry and arithmetic." Piccolomini understood this quantum phantasiatum and its underlying faculty of mind as clarifying what other authors had "improperly" called intelligible material; according to him, it was not so much intelligible as imaginative.^[27]

In the Ethics of Geometry, a reflection on the different significance of construction in ancient and modern mathematics (with Euclid and Descartes the protagonists), David Lachterman suggests that Proclus's elevation of imagination makes him the first modern mathematician. His influence, in combination with an affinity for imagination among early modern algebraists that was encouraged by their adaptation of techniques from the arts of memory taught by Llull, Petrus Ramus, and Giordano Bruno, decisively shaped modern mathematics. Lachterman considers, in particular, the use of diagrams in ancient and early modern mathematics within the context of an ontological dilemma posed by imageability. He

[26] Discussed by Lachterman, Ethics of Geometry, 89-90. The quote, given by Lachterman, is from the Commentary on the Republic, 1.235.18.

[27] See the account of Piccolomini in Giovanni Crapulli, Mathesis Universalis: Genesi di un'idea nel XVI secolo, Lessico Intellecttuale Europeo, no. 2 (Rome: Edizioni dell'Ateneo, 1969), 36-38. According to Crapulli (p. 41), Piccolomini was regarded by most of his contemporaries and immediate successors as a mathematician of eminence.

interprets Aristotle, in comparison to Neoplatonists, as more sharply separating the knowledge of mathematics from imagination, in that the process of abstraction makes the image transparent to intellection so that the latter can know unchangeable, universal essences.^[28] In following Proclus rather than Aristotle, modern thinking betrays a practical rather than a theoretical orientation toward mathematics. "Simply stated, radically modern thinking about imagination takes its bearing from the phenomenon of productive arts, including especially those arts adept at fashioning internal mental images and then embodying these elsewhere, by design"; Descartes, in particular, is one of these radically modern thinkers, and his mathematics is a paradigm of the modern approach.^[29]

To settle these issues would require not only broaching the controversies between ancients and moderns but also—and more to the point—set-fling the nature and source of mathematics and mathematical thinking. Both tasks are beyond the scope of this book. The point in raising them here is different: first, to show, however sketchily, that imagination was traditionally and perhaps inextricably bound up with the early modern understanding of mathematics and mathesis universalis; second, to make clear that universal mathematics, far from being merely a mathematician's concern, inevitably raises questions about the means by which things are knowable and about what ontological status the things known have. Even if Descartes had intended to confine his interests strictly to mathematics, the context of the subject matter would have forced him to move into metaphysical territory.

Yet it is probably incorrect to deduce that Descartes merely stumbled onto this territory. For from the sixth rule onward Descartes recurs more and more insistently not merely to the faculties by which we know and to the processes and method of knowing but also to the status of the things that are known and to the question of whether they can be known apart from concrete imaginings. It is not just the psychology of imagination that

[28] The discussion is in Lachterman, Ethics of Geometry, 76-90. Lachterman's inclination is to discount the importance in mathematics of the phantasm per se, because this transparency makes it invisible; the mind transcends the phantasm and proceeds to unchangeable. universal essences. He considers the noetic status of phantasms to be the key difference between ancient and modem mathematics. Ancients gave priority to the purely theoretical, whereas the modem orientation is more practical. I am not entirely persuaded by Lachterman's effort to distinguish Aristotle from Descartes on the issue of phantasms, however, not only because I interpret Descartes as attempting to think through some of the aporiai about phantasms left by Aristotle and Aristotelians but also because I believe that Lachterman understates the essentiality and indefeasibility of phantasms in Aristotle's theory of knowledge. Nevertheless. we can only regret that he is not alive to enlighten us further on this and many other things.

[29] Lachterman, Ethics of Geometry, 82, 86.

is important, then, but also the ontological underpinnings of this psychology and its associated epistemology—or, to use a name truer to the teachings of the Regulae, the ontological underpinnings of its way of mathesis.

Where this ontological concern first emerges with consummate clarity is in the doctrine of natures. Where Descartes begins the exploration of this doctrine is in Rule 6, a rule that he calls the secret of the whole art.

FIVE
Order, Natures, and Series The Topology of Imagination

Rule 4 left us in the following situation. To actualize the fundamental unity of all science we need not just the two ways of knowing, intuitus and deductio, but also a methodical way of approaching and acquiring knowledge. Descartes vaunts himself as the first not so much to realize that there is such a method (for he finds traces of it in predecessors) as to explicate and publicize it. Rule 4 told how he came to this discovery and explained (l) that this method of mathesis is a discipline for which the hitherto most certain of sciences, the mathematical, are like vestments, (2) that it is the source of what is perspicuous and easy in ordinary mathematics, (3) that the mathematicians of his day who cultivate algebra are attempting to resuscitate the mathetical art of analysis that the ancients knew, and (4) that this mathesis is the science of everything having to do with order and measure. The art of analysis of the ancients took both what was known and what was sought in a problem as given and used the codetermination of the parts to arrive at an exact determination of the unknown.^[1] In general, the values that are possible for any one of a set of factors are at least partially determined and delimited by the structure of relationships that hold between them all.

If we recall that the Regulae was projected to consist of three parts, the latter two being devoted to perfect and imperfect problems, respectively, we begin to see more clearly how in principle the account of the method was to be laid out. After Part I set down the basics of the doctrine, Part II would show how the codetermination of factors could be used to discover unique solutions for unknowns, and Part III would deal with situations

[1] See chap. 4, Sec. G, above.

where the givens are insufficient to determine a solution.^[2] We see that the lines and rectangles that Descartes introduced in Rules 15 through 21 are meant to create a kind of calculus, an algebra using figures rather than numbers, to instantiate the dimensions of a problem. The theory of proportions that Descartes had been working on at least since 1619 received its ultimate methodological expression in this geometric calculus.

What harm is there, then, in saying that this science, this universal mathesis, is mathematics, that the Regulae creates a new, more general type of mathematics to deal with problems of all kinds at a high level of abstraction, and thus that the Regulae culminates in the doctrine of the universal applicability of mathematics? After all, the Regulae in essence teaches how mathematical problems can be presented through a system of equations that can be turned into geometry; these equations, whether in one or several unknowns, and whatever their degree, are solvable precisely insofar as the various terms are codetermined by their relationships to one another.

One difficulty with this conception is that it might simply be an anachronism deriving from the long tradition of historiography of science that credits Descartes with inventing modern analytic geometry. What that tradition tends to minimize is that Descartes's approach was motivated by geometrical considerations more than by what we consider algebra.^[3] But this orientation to geometry, on my interpretation, is due not so much to an essentially backward-looking (and, from a twentieth-century viewpoint, atavistic) notion of geometry's preeminence over arithmetic (and thus also over algebra) as it is to the method of imaginative cognition that Descartes had been cultivating at least since 1618, a method that gives primacy to the formation and use of images. What the Regulae is attempting to pro-

[2] Rule 8 presents the distinction between the parts somewhat differently, however: it promises that the second part will deal with composite natures that are deduced from the simplest natures, and the third with composite natures "that presuppose other things also, which we experience to be composite on the part of the thing" (AT X 399).

[3] It is unclear at what stage in his career Descartes began using—and apparently invented—a modem power notation for representing polynomials. Milhaud dates Descartes's first use of a modern notation to around 1620; see Milhaud, Descartes savant, 86. P.J. Fededco places Descartes's invention of modern notation close to 1630; see Federico, Descartes on Polyhedra: A Study of the "De Solidorum Elementis," Sources in the History of Mathematics and Physical Sciences, vol. 4 (New York: Springer Verlag, 1982), 30-32. From Beeckman's journal entries of late 1628, it is clear that Descartes was still using the older cossic notation (it is, of course, conceivable that Descartes used cossic formulas to make things easier for Beeckman) and was solving what we consider to be algebraic problems by geometrical methods close in spirit to those of the Regulae. For more general considerations on the relation between algebra and geometry in Descartes, see Timothy Lenoir, "Descartes and the Geometrization of Thought: The Methodological Background of Descartes' 'Géométrie,'" Historia Mathematica 6 (1979): 355-379; and Pierre Costabel, "La mathématique de Descartes antérieure à la 'Géométrie,'" in Démarches originales de Descartes savant (Paris: J. Vrin, 1982), 27-37.

vide, I claim, is a supporting theory of the nature of human cognition that explains why and how imagination can play the central role in human knowing.

A. THE AIM OF MATHETICAL KNOWING

Let us remind ourselves of the ambition for imagination in the period 1619—1621: corporeal imagination would use figures to image bodies, while intellectual imagination would use bodies to image spiritual truths, the two standing in an analogical relationship to one another. What happens in the Regulae, indeed in the very heart of Rule 4, is that the direction of ingenium takes ultimate aim at human wisdom, the origins of which are the first seeds of truth that 4-B says led the ancients to prefer honesty to utility and virtue to pleasure and, more generally, to acknowledge true ideas of mathesis (disciplina) and philosophy. It is the native endowment of human beings that makes ail this possible, and what Descartes seems to be offering in this work, which intends to sum up what he has learned before he goes on to profounder studies (AT X 379), is a distillation of the simple truths governing all cognition into a small number of rules that henceforth can be used by anyone to judge of the truth in any matter whatsoever. This doctrine governing knowing is based on the premise of the intuitus of simple things and the deductio from these of truths that cannot be known immediately: everything that can be known leads back ultimately to the distinct and easy concept of a pure and attentive mind, and what cannot be so led back cannot properly be known.

This way of knowing is truly universal in scope, since even just the rudiments of it led the ancients to true ideas of mathesis and philosophy (Philosophiae etiam & Matheseos veras ideas agnoverint ; AT X 376 11. 18—19).^[4] What this means is that the first seeds of knowledge enable us, if we look with a pure and attentive mind, to recognize certain objects, like what is virtuous and what is honest, and to see how they stand with respect to other objects, like pleasure and utility.^[5] But immediately after noting these fundamental

[4] This is the only occurrence of 'idea' before Rule 12, and the only one in the Regulae where the word seems to mean something other than "corporeal image." This is a small piece of evidence that, contrary to the Weber thesis, Descartes may have worked on 4-B much later than 1619.

[5] This implies that the recognition of terms is prior to the recognition of propositional truths. Despite the fact that the Regulae frequently relates its teachings to the cognition of propositiones, the basis of the proposition is the mental grasp of a relatively simple object. What words go with any particular grasp is indifferent, but as soon as one compares one thing with another, one arrives at a judgment, which is the basis for all verbal propositions. One must recall again Descartes's penchant for looking to the original meaning of terms: 'propositio' ultimately derives from what is proposed to (propositus ), put before, the mind; as any Scholastic thinker would have noted, the linguistic proposition ultimately derives from the receptivity and acts of the mind.

principles understood mathetically by the ancients, Descartes turns the discussion toward a mathesis conceived along mathematical lines. Whatever else they might have been, Pappus and Diophantus were recognized, not chiefly as wise men, first philosophers, or teachers of ethics, but as mathematicians. And even though order and measure are so broad as to encompass more than strictly mathematical things, the context of the last part of 4-B is dominated by the presence of the traditionally mathematical disciplines. It is quite understandable that most people have interpreted the Regulae as applying a kind of conventionally conceived higher mathematics to all problems. It is important to recognize, however, that in the fundamental intention of the work and in the very notion of mathesis something even higher is implied that the work itself at crucial points falls short of—especially as the universal basis laid down in the first part is gradually steered toward becoming a problem-solving technique.

Yet even at its most technical, the Regulae stays in close contact with cognitive imagination; in fact, it is precisely where the doctrine becomes most mathematical, in the last of the extant rules, that Descartes insists on using images formed both in phantasia and "on paper" (in the external world) to assist the intellect, which otherwise is in danger of error through overlooking relevant considerations. We should recall once more the two imaginations of the "Cogitationes privatae": the corporeal one uses figures to conceive bodies, and the intellectual one uses bodies to figure spiritual truths. The Regulae gives primacy to the corporeal imagination and conceives the intellect as for the most part dependent on mathetical images, yet essentially different from the corporeal imagination because it, the intellect, is spiritual.^[6] The independence of faculties as conceived by the Scholastics is displaced by a more unitary notion of mind. Properly speaking, according to Rule 12, it is now the vis cognoscens or, in a broad sense, intellect that uses figures to conceive things even at the lower level; the operation of the vis cognoscens in phantasia is what imagination in the precise sense is. And, as will be remarked in Rule 8 and reiterated thereafter, body or the corporeal comes into consideration not as existing in the world

[6] One of the "Cogitationes privatae" sheds light on what differentiates this from the earliest position. "For God to separate light from darkness, in Genesis is to separate the good angels from the bad, because a privation cannot be separated from [its] habit: for which reason it cannot be understood literally. Pure intelligence is God" (AT X 218; the order of the concluding sentence, "Intelligentia pura est Deus," decidedly identifies pure intelligence with God). The implication is twofold: the image used in Genesis conveys something of the truth, but it requires analogical understanding; moreover, since only God is pure intelligence, human beings are not, and so the highest truths must in some way be accommodated to their lesser capacities. The intellect of the Regulae seems in many passages to be a pure form of spirit, but its continuing dependence on images and its involvement with the body suggest there is at least a remnant of the impure analogical intelligence described in the Genesis note.

but only insofar as it is conceived, or touched, by the mind. This is the realm of pure phantasms.

What we are likely witnessing in the Regulae is a transformation from the earliest conception of imagination, its aspects, its powers, and its objects, a transformation that is probably implicit in the logic of any cognitive method that prominently features imagination. The notes of 1619-1621 reflected a native realism about bodies: there was no sign that they were being thought of with the proviso "bodies only insofar as they are conceived by the mind," and in fact Descartes presumed to know that there was one active power in things, and that in bodies this was corporeal form. The forms of things in the world were somehow grasped by us, and those forms in turn could be used to grasp higher things. Imagination was the power that enabled us to get a tighter grasp than mere gawking would; it allowed us to draw back from the immediacy of the given so that we might use figuration to better conceive things. Yet this distance loosened the connection between sensation and knowing, it opened up a space where the imagination could function but simultaneously introduced the possibility of going astray because of chance, arbitrariness, and the ineffective use of this power. The imagination is in need of direction, and what pro-rides that direction are the seeds of knowledge given to every ingenium and the small number of rules it is possible to prescribe therefrom. As the private cogitation on Schenckel's art of memory suggested, two ways of approaching the truth open up: proceeding from phantasms to cause and back and forming a phantasm common to each of a group of phantasms, that is, finding the idea or eidos of the group (AT X 230). Either of these ways, or both taken together, would provide guidance for the otherwise unstable, labile imagination. The first method is a way that leads to the real and the causes of things; the second is a way that can proceed along either real or fictive lines so long as order is maintained. But this quite naturally opens up a new problem, for how can we know that a method allowing fictions will ultimately lead to the real and true? Moreover, what is the nature of the real, of the cause, that produces phantasms? Is it itself something that shares in the nature of the phantasm, or is it external to that realm? Does the activity of the mind parallel the activity of the world, or are mind's activity and mind itself something other than the world?

The Regulae can be understood, I think, as an attempt to work out these problems and questions, an attempt that still maintains a basic confidence in the powers of imagination. But certain qualifications and limitations have inevitably worked their way in. Intellect, which in the early notes exercised the higher kind of imagination that is proper to the poets, namely, using corporeal things to figure spiritual things, is now the agent proper in all cognitively relevant acts, from sensation to pure intellection. Bodies are no longer considered per se but as they are touched by the mind.

Although Descartes credits the ancients with recognizing philosophical and ethical truths through the rudiments of mathesis, there is otherwise no mention of how the intellect uses bodies, or ideas of bodies, to figure spiritual—both moral and intellectual—truths. If the primary motif of the early notes was cognitive and spiritual ascent by way of both corporeal and intellectual imagination, the dominant motif of the Regulae is the intellect working on problems that are "beneath' it. It is of course true that even in the early notebooks Descartes was a mathematical and physical problem solver, but then he stood in the first glow of enthusiasm for a technique that promised to carry its practitioner to the highest heights, to which otherwise only the poets easily ascended; whereas now that the technique is being worked out in detail, the heights may be appearing in the guise of the simple, that is, simple objects simply grasped by a pure and attentive mind. The high imaginative leaps of the poet are being implicitly condemned as unmethodical and replaced with the step-by-step ascent of the order-loving philosopher.

B. SERIATION AND THE NATURALNESS OF SIMPLICITY

Rule 4 announced that every examination of order and method properly refers to universal mathesis; Rule 5 announces that the whole method consists in proper ordering and that the two rules that follow will clarify how this order is to be discovered and how it is possible to avoid error. The emphasis on order is not at all surprising, since it is an elaboration of what is implicit in the doctrines of intuitus and deductio. If we are to use these properly (that is to say, if we are to proceed methodically) we must know when they are in order. We cannot inspect or intuit just anything: the problem is that most people are trying to understand a blooming, buzzing confusion, the everyday world, whereas inspection is possible only where we have separated out the confusions and have arrived at something easy; and only once we have recognized these easy things can we reverse direction and begin deductio, proceeding from the simplest to the most complex. This orderly procedure is what Rules 6 and 7 teach. But, as one would expect from what has preceded, this orderly procedure should involve learning both how to put the mind into a pure and attentive state and what the mind is recognizing when it is in that state: that is, there are two subjects under consideration, the activities and powers of mind and the proper objects of those activities. Rule 6 in fact emphasizes the proper object of cognition, under the rubric of simplicity, which makes that object well adapted to the limits of ingenium.

The heading of Rule 6 reads: "In order to distinguish the simplest from involved things and to follow through in order, it is required to observe, in

every series of things in which we directly deduce [or lead down] certain truths one from another, what is maximally simple and in what way all the others are more, or less, or equally, removed from it." The commentary begins by saying that this rule "contains the chief secret of the art, nor is any other more useful in this whole treatise." The reason is expressed in the next clause.

For it advises that all things can be disposed [i.e., set out] according to certain series, not indeed insofar as they are referred to a certain genus of entity, as philosophers divide these things into their categories, but insofar as some can be known from others, such that as often as some difficulty occurs we can immediately notice whether certain ones are prior to others, and which ones, and in what order to survey [them]. (AT X 381)

The secret to the art is thus the disposal of things into series according to a cognitive order of dependency. What is rejected is Aristotelian-Scholastic practice: identifying things according to genus and differentiating character (which two make up the identification of the species) and classifying all the ways in which things exist according to the categories of substance, quality, quantity, place, relation, and so on, that is, according to the order of being rather than of knowing. In addition, as will become clear from the sequel, Descartes is also rejecting the resort to abstract universals, the "terms" of the dialecticians and logicians, in favor of a special kind of particularity. It appears, then, that the secret of mathesis is the proper ordering of certain kinds of things; universal mathesis is the science of the proper order of what is known.

But how can cognition and the cogitation that arrives at cognition exhibit proper order? The answer is implicit in what has preceded. Simple objects are the things most easily knowable of all, and as such they are the origin of knowing: they are first in the order of knowing. One can call them the origin of knowing in two senses. First, there is nothing more knowable than simples; they are perfectly tailored to the nature and capacity of the human mind. Second, from simples we can arrive at other, more complex truths; the place of complex things in the order of knowing depends on how remote they are from the simple firsts. How do we know that we have hit upon a simple? By the fact that it is so easy and distinct that it leaves no doubt in a pure and attentive mind. That is all well and good, but it does not give any guidance about how to put our minds in such a state or any criterion for distinguishing a complex from a simple thing. How do we manage to avoid the aimless wanderings that most of our predecessors have fallen into among the welter of a complicated world?

In the very next paragraph Descartes begins to address this question. "In order however that this might come about rightly, all things, in the sense according to which they can be useful to our proposal, where we do

not look at the solitary natures of them, but rather compare them to one another so that some might be known from others, can be called either absolute or respective." He proceeds to define what he means by 'absolute': "I call absolute whatever contains in itself the pure and simple nature which is in question, like everything that is considered as independent, cause, simple, universal, one, equal, similar, direct [or straight], or other things of this kind; and I call this first thing the most simple and most easy inasmuch as we use it in resolving questions." The 'respective', in turn,

is what participates [in] the very same nature, or at least something from it [= from the nature in question], according to which it [= the respective thing] can be referred to the absolute, and deduced from it [= the absolute] through a certain series; but beyond this it involves certain other things in its conception, which I call respects: such things are whatever is called dependent, effect, composite, particular, many, unequal, dissimilar, oblique, etc. Which respective things are the more removed from absolute things by this, that they contain more respects of this kind subordinated one to another; all which things, we will be advised by this rule, are to be distinguished, and the natural nexus of these among themselves and the natural order are so to be observed that from the last we might by transiting all the others reach to that which is maximally absolute. (AT X 382)

The crucial notions here are a nature, one or more things that contain or participate (in) this nature, and an act of comparison. Comparison is of course implicit in a way of cogitation according to resemblance, whether in comparing images to bodies, bodies to higher things, or any orderable or measurable things to others of the same kind. Comparison operates according to biplanarity. Either one compares two things alongside one another (in the first plane) with respect to some characteristic (which defines the second plane) or one thing is seen with respect to the characteristic.

It is probably not possible to give a seamless, totally consistent account of the absolute, the respective, the simple, and natures, and it is likely that one of the chief causes of Descartes's leaving the Regulae unfinished was the intrinsic difficulty of explaining them. Yet a careful examination of Rule 6 in comparison with other parts of the Regulae allows us to illuminate the key elements.

Descartes's account of the absolute and the respective is not in the first instance about natures (and certainly not about essences) but about what contains or participates them. One has a thing in mind, and one views it in terms of a nature, "the pure and simple nature that is in question." For example, a king might be viewed in terms of independence. It would seem right to affirm that a king, if anyone, is independent. But the method of Rule 6 requires comparison. So now one takes into view not just a king but

also an earl, a knight, a yeoman, and a serf. The resulting relationships to independence have become more complex and articulated. The serf participates least in independence, because he seems close to a slave; one must beware of simply asserting that he participates to degree zero, however, precisely because we have now conceived of another individual who participates in less than he. (Furthermore, one might go on to compare a domestic slave, a slave who works in the stables, another who works in the fields, and a fourth who labors in a mine). The yeoman clearly has more independence than the serf, the knight more than the yeoman, the earl more than the knight, up to the king, who, if his power is not qualified by anything or anyone higher, not merely participates in the nature but wholly contains it. In this series the king is absolute—and that is true even if he is not fully independent in an "absolute" sense. Absoluteness as Descartes defines it is a property of standing at the head of a series with respect to a nature by virtue of wholly containing it or perhaps just participaring it more than any other member of the series.

A fine line etched in a flat marble slab, a railroad track crossing a plain, the path of a beam of light, a bricklayer's plumb line: all participate to varying degrees in straightness, extension, and length. Perhaps none wholly contains the nature straightness (each probably deviates from perfect straightness to some degree); each seems to contain wholly extension in length, and for that matter extension in the other two dimensions as well (the etched line may be just 0.01 mm in width and 0.005 mm in depth, but that is still existence in three dimensions). As we saw in chapter 3, Sec. F (with reference to AT X 453), Descartes conceives actual images as having the three spatial dimensions of length, width, and depth. That is, even a line drawn on paper or a line imagined in phantasia has three-dimensionality (see Rule 14, esp. AT X 446). But the power vis cognoscens is such that we can reliably focus on just one aspect, one nature, at a time.

It is not properly the natures that are absolute or respective but the "things" (res) that contain or participate a nature, or, as Descartes qualifies further in the definition of 'respective', participate "at least something from the nature" according to which it can be referred and compared to the absolute thing that stands at the head of the series and perhaps even wholly contains the nature. Thus it is contained and participating natures that are the foundation of comparison: the absolute things that wholly contain the natures serve as standards from which the respective things are judged to be more or less removed or distant. The respective things, in their turn, can be compared to one another as more, or less, or equally participating a nature. Each group of things can consequently be put into a series—serialized or seriated—according to this comparison in light of their differential participation of a specified nature. Moreover, the absolute

in each such series is the simplest and easiest insofar as it facilitates the solution of problems.^[7]

'Absolute' and 'respective' are therefore pragmatic rather than ontological terms, that is, relative to the practice of comparison for the sake of problem solving. At least for the time being, Descartes is not addressing the question of whether all things can be ontologically reduced to a few simple natures (like thinking and extension). It is not even clear that he is allotting ontological or even epistemological primacy to 'independence', 'cause', 'simplicity', 'universality', 'oneness', 'equality', 'similarity', 'straightness', and the anonymous 'others of this sort'. The passage that privileges these categories in determining the absolute can be read as saying not that these are absolutes but that they are marks or criteria that a thing exhibiting a relation to a nature (other than these) actually contains the nature and thus can be called 'absolute'. For example, the rigid stick and the pair of scales adduced at the end of Rule 9 simply contain, respectively, "immediately conducted natural power" and "natural power simultaneously producing contrary effects"; the former contains unity and cause in a simple manner, the latter cause and equality (of opposites). This interpretation is consistent with Descartes's initial emphasis on the things rather than on the natures the things exhibit. Thus because a king is the cause of the authority of his vassals, he may be called the "most simple and easiest" thing in the series with respect to authority. In comparison to the king's prime minister, the king's authority is undivided (unitary or one); again this is a mark that the king stands in the absolute position.

These reflections lead to a question: is it the natures that are simple and pure, or the things exhibiting them? Recall that in the definition of intuitus it was the grasp or concept that was characterized as easy and the mind as pure. Both the thing and the nature need to be grasped; perhaps the nature is nothing more than a determinate way of grasping (or a determinate focus of attention to) a thing. It is possible that both natures and the things that participate them can be simple and pure, although in the development of the theory of natures that takes place later in Rule 6, and even more in Rules 8 and 12, purity and simplicity come to be seen as

[7] This last characterization in terms of a thing's problem-solving efficacy pushes the serializer to find something absolute not just for a particular series but for all series of the same kind. Thus a wooden ruler might serve as the "absolute" meter for one type of measurement (say, the layout of a practice track), whereas a standard meter made of precious metal preserved in a vacuum at constant temperature would supersede the wooden ruler in an amplified series and be even more effective for setting the standard of scientific measurement (though obviously one uses it to measure only occasionally, for example to establish standard meter lengths for the bureaus of standards of different countries). Most effective of all might be a new absolute defined in terms of a certain number of wavelengths of a certain kind of atom (which is how the standard meter is currently defined).

most properly ascribed to natures. The latter two rules much more directly address ontological questions about natures and manifest multiple tensions and strains. As I shall show, the natures led Descartes away from the resemblance doctrine of his early years; initially conceived as a support for that doctrine, the natures gradually undermined the notion of cognition by resemblance and analogy when the natures were conceived in a radically foundationalist way.

In Rule 6 the place where the development of the account of natures begins is not so much in the definition of 'absolute' as in that of 'respective'. A thing is respective not just when it participates a nature in less than the absolute way but also by involving respects that are connected to one another in a hierarchical way. Besides the participating thing, there is "whatever is called dependent, effect, composite, particular, many, unequal, dissimilar, oblique, etc." This list is in perfect parallel with the previous paragraph's listing of the characteristics that make a thing absolute; each term is the privative or negative correlate of the corresponding member of the first list. The logic appears to be this: A thing we call dependent, or effect, or composite, and so on, is to be understood ultimately as being in relation to the positive form of the characteristic, that is, the independent, the cause, the simple. A thing that in its being grasped (in suo conceptu )^[8] involves dependence, say, a king's vassal, is at a certain remove from the king. If we call to mind that the vassal in turn has his own vassals, we view him not simply in direct regard of independence but, for instance, also as the cause of the powers of his vassals, and this might remind us that his being a vassal toward the king means he is an effect as well.

Descartes emphasizes that 'absolute' and 'relative' are not themselves absolute terms.

And so the secret of the whole art consists in this, that in everything we diligently direct ourselves to that which is maximally absolute. For some things are, under one consideration, more absolute than others, but looked at otherwise they are more respective: as the universal is more absolute than the particular, because it has a simpler nature, but all the same it can be called more respective, because that it exists depends on individuals, etc. (AT X 382)

Moreover, he goes on, things are more or less absolute depending on where they stand: thus if we are looking to (respiciamus ) individuals the species is absolute, but if we are looking to the genus it is respective; likewise

among measurable things extension is something absolute, but among extensions it is length, etc. And finally, so that it might be better understood

[8] This is the fourth-declension noun conceptus, not the second-declension conceptum ; the former is the act of conceiving, collecting, or gathering (here, in the mind).

that we are looking here at the series of things to be known, and not the nature of each one, we have deliberately counted cause and equal among the absolute, although their nature is really respective: for even among Philosophers cause and effect are correlative; here, however, if we inquire which is the effect, it is necessary to know the cause first, and not the contrary. Equals also correspond one to another, but things that are unequal we do not recognize except by comparison to equals, and not the contrary, etc. (AT X 382-383)

These qualifications are baffling unless we keep constantly before our minds—precisely as Descartes admonishes us—that the end is not to understand natures per se, much less things as having unique and essential natures, but to know things according to series, as they exhibit a certain nature or look from the perspective of the inquiry.

'Nature' is in effect used in a threefold sense in Rule 6. First, it is synonymous with Aristotelian-Scholastic 'essence'; but Rule 6 at the outset discounts the value of pursuing natures in this sense, although it does not go so far as to deny that such natures exist. Descartes's assertion that the natures 'cause' and 'equal' are really respective suggests that he attributes a certain reality to at least some natures. Second, it means an aspect or characteristic in view of which a thing can be determinately viewed and grasped, the sense that is most basic to the method explained by Rule 6. Third, it means a restricted class of natures in the second sense, the few natures that are knowable in independence from all other natures, as the second annotation to the rule explains.

It is to be noted second that, strictly speaking, few are the pure and simple natures, the ones it is granted to intuit first and per se, not dependent on any others but either in the experiences themselves or by a certain light situated in us; and these things, we say, are to be diligently attended to: for they are the same ones that in every single series we call maximally simple. All the others, however, can be perceived in no other way than if they are led down [deducantur] out of these, and this either immediately and proximately, or not unless through two or three or more different conclusions; the number of which also is to be noted, so that we might recognize whether these are removed from the first and maximally simple proposition by many or by fewer degrees. Indeed of such a nature is the contexture of consequences everywhere, out of which are born those series of things to be inquired about, to which [series] every question is to be brought back [reducenda], so that it might be examined by a sure method. Because, however, it is not easy to survey all together, and furthermore because they are not so much to be retained by memory as distinguished by a certain acumen of ingenium, some [means] is to be inquired after of forming the ingenia so that they [= ingenia] immediately heed them, as often as there will be need; I have experienced that for this there is really nothing apter than if we become accus-

tomed to reflect with a certain sagacity on each minimum thing out of those that we have already perceived previously. (AT X 383-384)

It would be premature to assume that Descartes had in mind with this third sense of 'nature' the reduction of all things to either extension or thinking, although that is a direction in which it might be taken. How few are the natures of this kind? Descartes does not say, but only our knowledge of the later Descartes will make us assume they are just two; the tenor of the passage suggests a relatively but not minimally small number. Moreover, as we shall see shortly, Rules 8 and 12 allow at least three types of natures, those that are corporeal, those that are intellectual or spiritual, and those that can be either (i.e., exhibited by either corporeal or intellectual things).

What Descartes seems to be aiming at here is building in the methodical investigator a broad and deep experience of natures as points of reference, so that when a problem appears she will be provided with every possible way of approaching it under diverse considerations (they are therefore like topics in the classical, rhetorical sense). We are given assurance that there are simple and pure natures in an ultimate sense, but we do not necessarily have to resort to them in addressing particular problems (though they have the advantage that they are to be found as maximally simple in every—presumably complete—series we might encounter).^[9] A familiarity with such basic natures and their interconnection with others will keep a problem solver from being stumped if she cannot solve a problem expressed in its original terms. For example, in an example provided by Rule 9,^[10] if one is trying to determine at what speed light travels one might recall that it is a natural power, and this in turn might induce one to think of simple, concrete examples of the propagation of natural forces, some temporal, others instantaneous. Here the pure and simple nature, or at least the surrogate for it, is 'natural power', which certainly does constitute a perspective under which many series can be perceived.

But has not Descartes changed the way in which problems are to be solved by shifting from seeing things in the perspective of natures to seeing natures in the perspective of other natures? Does this not displace thinking in terms of concrete things with thinking in terms of the terms? The answer is that a shift may be under way but it is not accomplished. Rather, the Regulae appears to be at the threshold of such a shift. The

[9] Clearly Descartes means not that any one or two of these natures appear in every series, but that, given any arbitrary series, the way to at least one nature will glimmer in the distance (in the last analysis, so to speak).

[10] In the discussion of perspicacity, which is the habit of an ingenium practiced in the division of things into parts and their seriation.

interconnection of natures and the existence of some that are either experienced by themselves or known by themselves through a certain light of nature is not the center of gravity of the method of the Regulae . That center is instead the comparison of things according to their degrees of resemblance to one another, with the principle of resemblance taking the name 'nature'. The method of noting resemblances does not depend on an ontological reduction to fundamental natures. So, for example, one is not limited to using the method of figuration only for solving corporeal problems, because it is the proportional interconnection of things and natures that is at issue, and the concrete, proportionalizing figurations that the Regulae employs are perfectly suited to representing such interconnections, that is, the proportional involvement and intrication of natures, whatever those natures might be. To conceive the Regulae as counseling the direct, purely intellectual thinking of natures would be to fall back into the Scholastic methods that Descartes has rejected.

Later, when in the first half of Rule 12 Descartes suggests representing colors by geometrical figures, he is not effecting the ontological reduction of color to extension (or to motion and extension) but implying that colors are invariably involved with the nature extension. Color itself is a nature in the sense of the Regulae —for example, natural objects participate in colors, and one can serialize objects according to their hues. Although the conveyance of the impression of color to the senses and the mind involves extension, color is not simply replaceable by extension or by a mode of it, since, as Descartes notes, someone blind from birth cannot know color. What he does hope to establish in Rule 12, however, is that the variety of geometrical figures is ample enough so that the patterns of the interrelationships that hold among colors can be accurately represented by the pattern of differences between the representing figures.

What Descartes's method in the Regulae proposes is not to come at concepts abstractly, as is the common Scholastic practice in the quaestio, wherein we would define and distinguish so that we might deduce, but rather to think of the individuals, the instantiations that participate wholly or in part in these natures, and to arrive at an intuitus of the nature by relating (distinguishing and assimilating) individuals to one another in a series. Descartes's method is thus directed toward the classification of individuals, or, to put it more accurately and less misleadingly, toward the viewing of individuals under particular aspects. 'Individuals' here can be taken in a broad sense, limited only to whatever directly appears to the mind as an object. Under this definition it would not be the case that the simple natures themselves are individuals, since they are perceived only as participated in by individuals. Descartes's understanding of the act of the mind, grounded in comparison, or rather seeing a thing along an axis ultimately pointing toward maximally simple natures, involves not irreducible

elements but the grasp (concept) of a thing in light of an aspect it participates or contains. The simplest proposition is thus derived by grasping a thing with a pure and attentive mind in light of a purified aspect or nature; this kind of grasp is intuitus of the most elementary (though not to say elemental) kind.^[11] Intuitus takes place at more developed levels as well, of course, since every deductio is ultimately based in intuitus; simple intuitus is seeing something in its most unelaborated form, simply as it most fundamentally shows itself easily and distinctly within the network of appearances. The object need not be ontologically simple, only phenom-enologically: it must stand out sharply, by virtue of careful preparation (using series), from its aspectual background. Therefore some people might well be able to grasp the Pythagorean theorem in a single intuitus rather than in a complex series of aspects reduced to other aspects.

As has already been remarked several times, we must take Descartes's admonition about his use of Latin words seriously. It should cause us to hesitate whenever we are inclined to take terms in a conventional way. So, for example, the word conceptum, which appears in both definitions of intuitus, should not without further ado be assimilated to 'concept'. Concipere, of which conceptum is the past participle, means most basically 'to take hold of'; as I have already pointed out, it is used in both the Compendium musicae and the Regulae (Rule 12) as a synonym of imaginari. Since intuitus is presented as an act of the mind, the primary sense of the definition should be something like "the hold that the pure and attentive mind has taken on its object." Similarly, to stand in a series is to be proposed (propositum ) to the mind's view in a certain way, and thus every element in the series, including the simplest, is a propositio, and underlying every proposition as statement is a propositio as act of the mind.

What Descartes presents here as a method of inquiry is thus grounded in the very structure and nature of the mind's acts. When the mind presents itself, or is presented with, an individual object, it already has it in its grasp along an axis. Only if we are faced literally with blooming, buzzing confusion do we fall short of this state. But usually we are already presented with more: the identification of this individual as shaped thus and so, of a certain color, of a certain kind. That is, we are presented with various aspects or axes along which to see the thing, some quite definite, others rather vague. If it is definite, then we have already (implicitly) placed

[11] Further light is shed on what is involved in the simple intuitus of natures by Rule 12's account of universals. We are told there that 'limit' is not properly a nature, even though it seems to be more general than terms like 'shape', because it is conflated out of different realms, for example, limit with respect to space and limit with respect to time (AT X 418-419). This means that the ultimate criterion of whether one is dealing with a real (much less simple) nature is whether it is unequivocally instantiated in things and also that not every universal is a nature. See also footnote 36, below.

the individual in a specific location along the relevant axis; if vague, then we can, by applying industry, seek a precise location along the axis. The axis and the indefiniteness, or even the axis and unexplicitated definiteness, present us with the task of precise location: that is, we are faced with something to inquire after, a quaestio, which can be resolved if we identify sufficient determining factors and also represent to ourselves, if need be by the method of geometrical instantiation, the order and the definite proportions that hold between those factors, the natures or aspects.

C. SERIATION AND GEOMETRIC INSTANTIATION

The evocation of the least things in our past experience at the end of the second annotation to Rule 6 leads quite naturally to the third annotation, which sounds a recurrent theme of the Regulae by inviting us to practice our powers first not with complex but with fairly simple matters.

Third and finally, it is to be noted that the beginning of studies is not to be made with the investigation of more difficult things; but, before we gird ourselves for certain determinate questions it is needful previously to collect spontaneously, without any choosing, obvious truths, and tentatively thereafter to see whether certain others can be deduced from them, and in turn others from these, and so forth. This having been done, one must attentively reflect on the discovered truths, and must diligently think why we were able to find some earlier and more easily than others, and which ones these are; so that from this we will judge, when we set upon some determinate question, which other things to be discovered it will help to attend to first. (AT X 384)

The first annotation brought our attention to natures and the degree to which things participate in them; the second points out that these differences in participation give rise to series leading up from the given objects to the maximally simple natures and back; this third annotation finally gives us an easy, "bootstrapping" method for familiarizing ourselves with degrees of participation in series by advising us to turn first to the easiest kinds of problems. This is accessible to anyone and everyone who possesses reason in the least degree, regardless of previous experience. You do not even need to exercise prudent choice; just take the first obvious truth that comes by and see where it leads, then look back over the whole sequence of one thing's being related to another to gain insight into how problems are solved. This provides not only knowledge of the form of argument but, even more important, the material out of which problems are made. After all, in familiarizing ourselves with the dependency between certain truths and others we are acquainting ourselves with series that lead back or point to natures. Any particular practice exercise may not necessarily lead us all the way back to maximally simple natures, but it is these

to which the whole method refers and on which its efficacy depends. In the last analysis these practice exercises teach us how to maneuver within the cognitive realm laid out on their basis.

The example Rule 6 gives of choosing a simple truth and seeing where it leads is the relations between the members of the series of numbers 3, 6, 12, 24, 48, and so on. We notice, for example, that 6 is double 3 and inquire what the double of 6 is, namely, 12, and so on; from this we deduce that the proportion between each successive pairing (between 3 and 6, between 6 and 12, between 12 and 24) is the same and thus that the whole series constitutes a continuing proportion. Descartes grants that this seems a bit childish, but that is simply because these things are consummately perspicuous. "By reflecting attentively on this I understand with what reason [or ratio, ratione ] all questions that can be proposed about the proportions or habitudes of things are involved, and in what order they ought to be inquired after: which one thing embraces the sum of the whole science of pure Mathematics [totius scientiae purae Mathematicae summam ]" (AT X 384-385). This is a remarkable claim, that all of pure mathematics derives from these simple reflections; it evinces the power and ambition of the proportionalizing method he is proposing.

The rest of the rule explores further what is involved in this simple numerical series and shows how the ease or difficulty of discovering the different members and their relations to one another depends on the particular way in which a problem is posed. For example, given 3 and 6 it is easy to find 12, but if you were given 3 and 12 and asked to find the mean proportional (the number between 3 and 12 such that 3/x = x /12) the problem would be more difficult; and even more difficult would be to find two mean proportionals between 3 and 24 (numbers x and y such that 3/x = x/y = y /24). Of course, since we already have the series in hand, these are artificial rather than real problems, but if we change the given numbers to, say, l0 and 150, we recognize that it is not at all obvious what the mean proportionals are and that it would take some at least minimal intellectual agility to find them. (The formulas I have given in parentheses in the previous two sentences greatly facilitate the exact solution of the problem; such formulas are not given in the Regulae, and one might reflect that our ability to reduce the problems to such simple equations is precisely the sort of thing that Descartes was trying to cultivate.) But if we conclude that just adding to the number of proportionals to be found makes the problem increasingly difficult, we will be wrong; for if we are asked to find three mean proportionals, we might notice that this problem can be reduced to simpler ones: namely, first find the mean proportional between the two extremes, say 3 and 48 (this is 12, since 3/12=12/48), then find the mean proportionals between this number and each of the extremes (6 is the mean proportional between 3 and 12, 24 is the mean between 12 and 48).

These discoveries about this particular series of numbers depend on the fact that each member of the series is derived from 3 by successive doubling; the series is 3, 2 × 3, 2 × (2 × 3), 2 × (2 × 2 × 3), and so on, or, using algebraic notation and a generalized formula, the nth member of this series is given by the formula 2^n-1 × 3 (again, Descartes does not give such a formula here). Putting this into the framework of the entire Rule 6, we can say the following: in this series, the absolute member is the first, in that it contains wholly and purely the fundamental nature, 3, that gives rise to the whole series, and all the other members are respective, relative to this.^[12] Of course, the series is determined not just by the number 3 but also by the way in which all the other members participate in 3, that is, according to the formula 2^n-1 × 3 (according to the common nature 'double'; the common natures will be explained in Sec. D, below). Thus the secret of the whole art, Rule 6, teaches that the key to solving problems is twofold: (1) finding the ultimate perspective, the nature, involved in a thing; and (2) analyzing the determinate relationship of this thing to similar things. All problems always involve at least one given aspect or nature and the relation of at least one thing to that nature.

Thus Descartes in Rule 6 gives not just a method of problem solving but a philosophical theory of what a problem is. The rule is key to understanding why Descartes insisted that his art or method was different from the Scholastic method predicated on terms and concepts: rather than seek the essence and the attributes of a thing, it fosters noting what is given, remarking similarities, differences, and resemblances, and identifying axes or aspects under which the given can be viewed. Having mastered the simple but powerful mathematics of proportion we can thereafter address any problem and either solve it or come to the realization that with our current resources it is unsolvable.

Indeed, one might consider the entire Regulae as a treatise on what constitutes a problem. The medieval notion of quaestio is redefined: no longer is it a question that has arisen because of controversy, because of a conflict of interpretations, which is resolved by attending to the necessary conceptual distinctions for the matter at hand or the thing in view. In Descartes's eyes these are disputes over words. He urges instead attending to the object presented to the mind and the possible aspects under which it can be grasped, estimating the relation of the object to other objects having the same aspect so that its relative or proportional distance from the pure and whole participation in that aspect can be more or less precisely deter-

[12] Note that the simplest element might not always appear among the given members of the series, for example, if the series had a more complicated formula (though it would not need to be very much more complicated; e.g., the one determined by the formula [2 × 3]-1).

mined, and then determining the interrelations of these objects with respect to different aspects; if a sufficiently well-developed network of relationships is established, all the relevant degrees of interparticipation can be reckoned; if not, either more work remains to be done or the problem is unsolvable.

D. IMAGINABILITY OF SERIATION, IMAGINABILITY OF INTELLECT

Things participate in certain natures to varying degrees, and the human ingenium can easily ascertain whether two things participate equally, or one more and the other less. This ability to compare participation is the psychological foundation of order and, when a unit of comparison can be ascertained, measure. All relationships of order and measure can be simply represented by figures. Where order is in question the figures can be either discrete or continuous (e.g., a collection of three points to represent the third position versus a line segment three units in length); where measure is in question it is often necessary to use a continuous representation, unless all the measures involved are commensurable (i.e., expressible either in whole numbers or in rational fractions).

In Rules 12 through 14, Descartes brings to a focus the use of imagination in cognition. This use observes the powers and limits of human ingenium raised in the first part, and it develops imagination into a universal instrument of knowing.

Rule 12 lays down both a schema of the faculty psychophysiology of cognition and a theory of natures. In accordance with the preliminary discussion in Rule 8, the natures are divided into those that are maximally simple and those that are complex or composite (AT X 399). The simple natures cannot be false; only in natures composed by the intellect can there be falsity. In Rule 8 the maximally simple natures are divided into the spiritual, the corporeal, and those pertaining to either of these; Rule 12 calls them intellectual, or material, or common to both (AT X 419).^[13] But Descartes quickly sets aside the question of how things actually exist in favor of how they appear to the mind.

For if, for example, we consider some extended and figured body, we even say that, from the perspective of the thing, it is something one and simple;

[13] These divisions appear to be, in the language of Rule 7, enumerations that are sufficient rather than complete or distinct. An ontologically curious philosopher would eventually wonder whether the terms 'corporeal', 'intellectual', 'common', and so forth, refer to genuinely simple natures or simply to abstract generalizations, like the term 'limit' (as explained at AT X 418-419). See footnote 11, above.

and indeed, in this sense, it cannot be said to be composed out of corporeal nature, extension, and figure,^[14] because these parts never existed each distinct from the others; but from the perspective of our intellect, we call the composite something [composed] out of these three natures, because we understood the single things separately before we could judge these three in one and discover them simultaneously in the same subject. For this reason, since here we are not treating of things except insofar as they are perceived by the intellect, we call only those simple the cognition of which is so perspicuous and distinct that they cannot be divided into several things more distinctly known by the mind: such are figure, extension, motion, etc.; all the rest, however, we conceive as in some way composed of these. (AT X 418)

Once again a pragmatic epistemological aim rather than an ontological one governs the discussion. It is not so much that the natures are being treated as fictional as that their mode of existence in the thing is allowed to be different from their mode in the mind. That they certainly are con-rained or participated by things is not in question. The principle of the division of natures into intellectual, material, and common classes shows this.

Those things, which with respect to our intellect are called simple, are either purely intellectual, or purely material, or common. Purely intellectual are those that are known by the intellect through a certain inborn light, and without the aid of any corporeal image: for it is certain that there are some such things, nor can any corporeal idea be feigned that would represent to us what cognition is, what doubt, what ignorance, likewise what is the action of will that it is granted to call volition, and similar things; all which we nevertheless truly know, and so easily that for this it suffices that we be participators in reason. Purely material are those which are not known unless they are in bodies: as are figure, extension, motion, etc. Finally, those are to be called 'common' that sometimes are attributed to corporeal things, sometimes to spirits without distinction, like existence, unity, duration, and similar things. To this also are to be referred those common notions which are like a certain chain conjoining other simple natures to one another, and by the evidence of which is supported whatever we conclude by discursive reasoning. Viz., these: those things that are the same as a third are the same as one another; likewise, what [two things] cannot be related in the same way to a third thing also have some difference between them, etc. And even these common ones can be known either by pure intellect, or by the same [intellect] intuiting the images of material things. (AT X 419-420)

Descartes also includes among the simple natures negation and privations of the positive natures. Abstractions like 'limit', which we derive by abstract-

[14] Note how Descartes distinguishes these as though they were three maximally simple natures. In the later philosophy, extension would be the foundation of the other two.

ing from different simple natures (in cases of shape, duration, motion, and the like), are not numbered among those natures.

The crisis in Descartes's thinking posed by his development of the natures doctrine will be taken up in the next two chapters. For now we shall consider only that the natures of Rule 12 are sufficient to ground the universality of imagination as a problem-solving instrument. This is true despite the fact that the intellect recognizes the purely intellectual natures by an innate light without representing them in images.

Of course Descartes leaves no doubt that there can be pure intellectual knowledge, but the examples he gives have some curious features. All of them are actions or passions of the mind or soul: knowledge, doubt, ignorance (a passion), volition. None of the natures involved is a direct object of cognition, however: willing would be recognized as such in the act of willing something else, and similarly for the others. All of these acts can have as their object an image or a body. Moreover, the fact that a certain nature can be recognized by intellect alone does not imply that imagination cannot be of assistance in addressing questions about intellectual things, especially since Descartes's problem solving in the Regulae is not a matter of determining essences. For example, a kind of order should be possible even with respect to knowing and willing: after all, the Regulae itself is an attempt to discover and encourage order in knowing. One might order volitions according to objects. One might ascertain that a certain order or proportion exists between willing and knowing in even purely intellectual acts, and this order and proportion could be represented schematically by discrete or continuous figures. Representing one act of will as participating in understanding more than another, or adjudging that one act of will is more intense than another, does not require ontologically reducing something purely intellectual to corporeal form. That a volition in itself is noncorporeal and as such has no similarity to the images of the corporeal realm is one thing; that my participating in willing is so-and-so intense and relates to another act of will in a certain proportion is quite another, having to do with the interrelations of things and natures. Recall that the common natures include the "common notions" that are like a "chain conjoining other simple natures to one another, and by the evidence of which is supported whatever we conclude by discursive reasoning." All discursive reasoning, even that about intellectual natures, thus has recourse to common natures, which can be instantiated by either intellectual or corporeal things. That there are natures common to both spirit and corporeal things means that there are ways of at least indirectly representing spirit through corporeal symbols. The "existence, unity, duration, and the like" of a spiritual thing can be represented by a parallel and proportionate corporeal instantiation of "existence, unity, duration, and the like."

E. SOLVING PROBLEMS BY PROPORTION

"All human science consists in this one thing, that we distinctly see in what way these simple natures simultaneously concur for the composition of other things" (AT X 427). The common error in encountering any problem is to suppose that there is involved some kind of previously unknown entity; the particular temptation to which the educated succumb is to substitute their learned conceptions and learned vocabularies, which are really unintelligible both to themselves and to others, for what they have experienced.

But whoever cogitates that nothing in [for example] a magnet can be known that does not consist of certain simple natures, known through themselves, is not uncertain about what to do: first to collect diligently all experience that it is possible to have about this stone, out of which then he tries to lead down [or deduce] what mixture of simple natures is necessary for producing those effects that he has experienced in the magnet; once these are discovered, he can boldly assert that he has experienced the true nature of the magnet insofar as it could be discovered by a human being and from the given experiences. (AT X 427)

The key is to ascertain what natures might be involved and how they can be combined, the chief device for which is the determination of orderly relations between things and natures noted by the ingenium's powers of comparison, serialization, and proportionalization.

Rule 12 ends with a remark that prepares the way for the rules of the second part. It says that everything will be divided either into simple propositions or questions (problems).

As for simple propositions, we treat no other precepts than those which prepare the power of knowing [vim cognoscendi]^[15] for intuiting any object whatever more distinctly and scrutinizing it more sagaciously, because these must occur spontaneously, nor can they be inquired after; which we have embraced in the twelve preceding precepts, and in which we believe we have exhibited all things that we judge can render the use of reason somewhat easier. (AT X 428-429)

What involves a simple nature simply cannot be investigated, it is simply seen. But when there is any interconnection or relation not clearly seen there is a question or problem of proportion to be resolved. Like the Scholastics, Descartes proposes to address quaestiones. The logic of addressing them, however, is not dialectical and verbal, that is, dependent on past texts

[15] Note the similarity to, but also difference from, Rule 12's 'vis cognoscens' (for which the form here would be 'vim cognoscentem'). The variations in terminology add further weight to the contention that Descartes's thinking was in flux.

and authorities, but the serializing and proportionalizing logic of the interconnection of natures—mathesis universalis.

Descartes divides questions or problems into two kinds, those that are perfectly understood, to be treated in Rules 13 through 24, and those that are not, to which the projected Rules 25 through 36 were to be dedicated. The reason for this division is pedagogical: the last twelve rules would have presupposed acquaintance with the preceding dozen, and "we teach those earlier with which also we think we should first be occupied in order to cultivate the ingenia" (AT X 429). The perfectly understood problems of Rules 13 through 24 require that we perceive three things: "by what signs that which is being sought can be known, when it presents itself; what it is, precisely, from which we must deduce it; and in what way it is to be proved that these things so depend on each other that one can by no reason [ratio ] be changed, leaving the other unchanged" (AT X 429). This is a case of learning how to discover a conclusion not by deducing one thing from a single simple thing, "but one thing depending on many implicate things simultaneously, evolved so artfully that it requires no greater capacity of ingenium than for making the simplest illation' (429). This is shown most easily by using examples from arithmetic and geometry, which are useful for the practice needed to acquire the technique.

Rules 13 and 14 lay the groundwork for the treatment of questions or problems, and as such they are both an extension of what precedes and an anticipation of what is to come. Descartes begins by distinguishing what he is doing from the practice of Scholastic logicians. We are not to search for the middle term connecting two extremes but rather (in echo of the last paragraph of Rule 12) to recognize that in every problem there is something unknown, that this unknown must be designated in a determinate way, and that this designation must be made in terms of what is already known.

This is precisely what we teach children in algebraic problem solving today. "A truck sets out from city A for city B at 1 P.M. It arrives in city B at 3:30 P.M. The truck averages 45 miles per hour. How far apart are cities A and B?" There is something unknown, the distance between A and B; we designate this by x . This designation has to be put in relation to things that are known, the time oft. ravel (2.5 hours) and the average velocity (45 miles/hour), by means of an equation: x = 2.5 hours × 45 miles/hour = 112.5 miles. This kind of problem reflects the progressive complication that marks the division of the Regulae into three major parts. In comparison with the simplest things—for example, noticing that the truck is moving, that it is moving faster than a car, that cities A and B are different but still both cities—this problem is complicated. But in conformity with Rule 12's criterion (AT X 429), the answer is perfectly knowable in terms

of the given because all the proportions are interrelated in a way that allows a unique solution (in contrast to problems in which the information is inadequate—for instance, what the speed of the truck was at precisely 2:00 P.M.—or the interrelations determine no solution or multiple solutions). In conformity with Rule 8's distinction between the second part, treating of natures deduced from simple and evident natures, and the third, treating of natures that presuppose natures composite in reality (AT X 399), these types of problems involve natures so perspicuously interrelated (space, time, motion) that a further knowledge of natures, one that can be acquired only through the experience of compositions accomplished in reality, is not necessary.^[16]

What seems quite simple to us was not yet a permanent acquisition of mathematics around 1630; Descartes of course was one of the first to insist on the need to name unknowns and to manipulate them mathematically as though they were ordinary numbers. Even this is to put a modern spin on things, for the extant part of the rules does not explicitly deal in equations, and, given the kind of geometric rather than arithmetical representation and manipulation it presents, we cannot simply assert that it is teaching the elementary algebra of problem solving. Rather, it is the elementary art of problem solving, which is the largest part of what Rule 4 calls mathesis universalis.

The remainder of Rule 13 gives instruction in what we should do as we begin to approach a problem, in the initiating heuristic of problem solving. We are told that if the problem is, for instance, about the nature of the magnet, we already possess the meanings of the terms 'nature' and 'magnet' and thus have a preliminary determination of how to proceed. In another case we might be asked what is inferable of the nature of the magnet from the experiments published in William Gilbert's De magnete (1600), whether they be true or false; in yet another we might be given specific data about the size and weighting of strings and asked to determine whatever we can about the nature of sound. Descartes grants that these specific problems are imperfect, in that we cannot be sure at the outset that we have everything needed to solve them, but nevertheless they can give an idea of how we begin a "reduction" to a perfect problem by trying to enumerate the simplest parts or natures. Descartes promises further that in his explanations "it will appear also in what way this rule can be observed, so that the well-understood difficulty be abstracted from every

[16] Such problems of real complexity—presumably Descartes is thinking of natures no less complex than color, which Rule 12 grants can be known only through real-life encounters—require a background experience that goes far beyond what is accessible by a certain inborn light of reason (the distinction is made in this way in Rule 6, AT X 383). Only natures known to us in the latter way axe suitable for the most perspicuous kinds of problems and thus treated in the second part of the Regulae.

superfluous concept, and so far reduced so that we will not think [= cogitate] of busying ourselves more widely with this or that subject but only in general concerning certain magnitudes to be compared/composed^[17] with one another" (AT X 431).

Rule 13 reminds us that Rules 5 and 6 had advised taking difficulties back to simple things, and Rule 7 dividing them, "so that afterwards ail may be comprehended simultaneously by a sufficient enumeration' (AT X 432). If there are many experiments concerning the magnet, I must run through them separately, one after another; if the question is about sound, I will compare first strings A and B, then A and C, and so forth, with the aim of comprehending the enumerated whole. Descartes remarks that one needs to resort to Rules 5 through 7 only, using pure intellect with respect to the terms of each proposition, before going on to Rules 14 through 24, and he promises to explain how this should be done in the never-written third part of the Regulae .

The pure intellect must do its work before the rules explicitly applying spatial figuration can be used effectively. Why? Because only intellect has the power of making the distinctions necessary for the "abstraction [of a question] from ail superfluous concepts,' and distinctions are an exercise of the power of negation.^[18] In the initial formulation of a problem the given data and terms are treated as abstract units of comparison; their specific content is not appropriated until the actual solution process begins in accordance with Rules 14 through 24. Thus, although this distinction making is a work of the intellect alone, it is not the work of an intellect dealing with only noncorporeai objects; quite the contrary. The power to cognize and recognize differences is fundamentally that of intellect, in whatever ideational or imaginal form the differences appear.

Thus it is the intellect that initiates a question by setting up its fundamental terms. Once the question has been set in this manner "it is to be seen precisely in what its difficulty consists, so that this thing, abstracted from everything else, might more easily be solved" (AT X 437). "Here, therefore, we say only this to be worthwhile, to review in order ail those things that are given in the proposition,^[19] rejecting those that we see manifestly do not contribute to the thing [ad rem non facere aperte ], retaining the necessary ones, and sending the doubtful back for a more diligent examination" (AT X 438).

[17] A has componendas, H comparandas ; the difference is not of great importance, as comparison is the way ingenium has of analyzing the composed things it experiences, and it is in accordance with its comparative understanding of series leading to natures that it learns how things are composed.

[18] See the next section, below, for this point as it is raised in Rule 14's discussion of the different ways in which the term 'extension' is to be taken.

[19] Quite clearly, 'proposition' (propositio ) must be understood here as "what is proposed or set forth to the mind."

These are the concluding words of Rule 13. At this point, if the problem has not resolved itself, the work of imagination must begin. As the Rule 14 heading puts it, "this same [question] is to be transferred to the real extension of bodies, and the whole proposed to the imagination through bare figures: for thus it will be perceived far more distinctly by the intellect" (AT X 438).

It would be mistaken to minimize this as counsel that applies only to problems concerning corporeal things, for it is presented not as a special case of problem solving but as the appropriate way of taking further any problem that has not been solved already by the simplifying and distinguishing work of Rule 13. What makes this method of mathesis universal is precisely (1) the proportionality of things' participating in natures and (2) the enumerable interconnections of one nature with others, both of which can be perspicuously represented in bare figures.

This is exactly the point made by the first paragraph of the commentary to Rule 14.

So that, however, we might also use imagination as an aid, it is to be noted that whenever one unknown thing is deduced from some other already known, not for all that is some new genus of entity discovered but rather this whole cognition is only extended thus, that we perceive the thing inquired after to participate thus or so [in] the nature of those which were given in the proposition. For example, if someone is blind from birth, it is not to be hoped that we can ever by any argument bring about that he perceive the true ideas of colors such as we have with sound senses; but if someone has at some time seen the primary colors, although never the intermediate and mixed ones, it can happen that he might form images also of those that he has not seen from the similitude of others through a certain leading-down [deduction]. In the same way, if in the magnet is some genus of entity to which our intellect has hitherto perceived nothing similar, it is not to be hoped that we will ever know that through discursive reasoning; but it will be necessary to be instructed either by some new sense or by the divine mind; but whatever in this matter can be discharged by human ingenium, we shall believe ourselves to have gained, if we perceive most distinctly that mixture of already noted entities or natures that produces the same effect that appears in the magnet. (AT X 438-439)

The following paragraphs explain as concisely as possible that when we know something it happens by means of the proportionalizing comparison of one thing to another, according to their differential participation in a nature or common idea/appearance (except in the case of the intuitus of a single thing). That comparison, to become perspicuous, requires an equalization (setting equal) by proportions—today we understand this as setting up an equation—and all comparison, insofar as it involves differences of degree with respect to a nature, can be brought back to differences in magnitudes that are easily depictable in the imagination.

And indeed all these entities already noted, such as are extension, figure, motion, and the like, enumerating which is not in place here, are known through the same idea in diverse subjects, and we do not imagine the figure of a crown differently if it is silver than if it is gold; and this common idea is transferred from one subject to another in no other way than through simple comparison, through which we affirm that what is sought is, according to this or that, similar, or the same, or equal to some given: so that in all ratiocination we know the truth precisely only through comparison. For example, in this: all A is B, all B is C ; therefore all A is C ; the sought-for and the given are compared to one another, namely, A and C, according to the fact that each is B, etc. But because, as we have already often warned, the forms of syllogisms help not at all in perceiving the truth of things, it will profit the reader if, these things being outright rejected, he conceive all cognition whatever that is not had through the simple and pure intuitus of one solitary thing to be had through the comparison of two or several to one another. And indeed almost the whole industry of human reason consists in this operation's being prepared; for when it is open and simple there is not need of the assistance of art for intuiting the truth which is had thereby but only of the light of nature.
And it is to be noted that comparisons are said to be simple and open only when the sought-for and the given participate [in] some nature equally; all the rest, however, require preparation for no other reason than that the common nature is not equally in each, but according to certain other habitudes [or relations] or proportions in which it is involved; and the preeminent part of human industry is to be located in nothing other than reducing these proportions so that equality between the sought-for and something that is known is seen clearly.
It is to be noted consequently that nothing can be reduced to such equality unless it receive more or less, and that all this is comprehended through the word 'magnitude': so that after the terms of the difficulty are abstracted from every subject according to the preceding rule, we understand ourselves to attend successively only to magnitudes in general. (AT X 439-440)

One can hardly exaggerate the importance of this passage, for it not only illuminates what follows but articulates the foundation of the method in the first twelve rules as well. It is comparison that is essential to knowing, and knowledge by means of comparison is a judgment of either similarity, or sameness (i.e., identity), or equality; and this judgment is made in light of a given that is viewed in a particular way (secundum hoc vel illud, according to this or that). The kind of ordered and proportionalized seriation envisioned in Rule 6 is possible and truthful only on such a basis. Two things that participate in one nature participate in it in a similar, an identical, or an equal degree. If identical, then the two things are either one and the same or at most different instances of the same thing, and they will occupy the same rung in the series; if merely equal, they are different things that nevertheless are on the same rung with respect to the particular nature in

question (with respect to other aspects, however, they will differ); if similar, then they participate in the same nature in different ways or degrees. Often we can easily see that one is more or less participant than another, but this becomes perfected knowledge only once we have ascertained this relation precisely, that is, only once we have discovered the proportion of participation. Whether the participation is equal or proportional, however, this relation participates in quantity, and because of this it can be expressed in magnitudes. This holds true whether we are dealing with a corporeal nature, a mixed or common nature, or a purely intellectual nature. With respect to the relation of participation in natures, there is no essential difference among these types, and even the relations of purely intellectual things can be expressed through corporeal magnitude. This knowledge by proportionalization is truly a mathesis universalis.

Descartes says that all knowledge that requires two or more things is comparative; thus deductio and enumeratio are embraced by this category. The only exception is the simple and pure intuitus of a solitary thing. Yet within the framework of the Regulae it is not clear whether we can ever have such intuitus. The only candidate for it is a nature, or rather a simple nature/thing. Do we ever have intuitus of pure extension? As we shall see shortly, Descartes says in Rule 14 that there cannot be extension without an extended thing. So the question becomes, Can we have intuitus of a particular extended thing? But then we would appear to have at least two things: the particular instantiation and also the simple nature in light of which we are viewing the thing (which, presumably, we could also view in light of figure, motion, or other natures).^[20] This may in fact impart some clarity, retrospectively, to the point of calling the highest thing in a series constituted according to Rule 6 'absolute'. It is absolute by virtue of wholly containing the nature in question, rather than merely participating in it to some degree (see AT X 381 11. 22-23 and 382 11. 3-6). Any extended thing wholly contains the nature extension (there still can be a differentiation based on the quantity of the extension). Even a finely drawn line is extended in three dimensions and thus contains extension wholly. It also participates differentially in linearity or in curvature; the straightest one we are able to draw would serve as the absolute member of the series 'linearity'. In an important sense, the full character of the (simple) nature itself becomes purely and simply apparent only if it is seen in its preeminent instance or instances, and those instances are seen as preeminent only in comparison to instances that participate in the nature to a lesser degree.

[20] Once again, our impressions of the later Descartes mislead us. We have become accustomed to thinking that a pure inspection by the mind of a simple idea in and by itself is not only possible but the very stuff of Descartes's thought, to the point that we tend to overlook evidence to the contrary.

Therefore even the simple nature cannot be seen as simple except in contrast to other things; and without a full-blown innatism, the likes of which the Descartes of the Regulae does not seem willing to countenance,^[21] one would have to rely on something like habit, thus on memory, for a series-less evocation of the simple natures. The only way that one might be able to escape this paradox without abandoning the framework of the Regulae would be to argue that pure and simple intuitus is properly interpreted as the careful and penetrating viewing of a single thing actually present to consciousness in its most crucial or essential aspect.^[22] That perhaps does not fully eliminate the possible taint of plurality, although it would appear to take an important step toward the kind of inspectio mentis that divides the world into two mutually exclusive simple substances, res cogitans and res extensa, and identifies every particular thing as an instance or a modalization of one or the other.

Only one additional point is needed to make the doctrine of the rules that follow almost a mere consequence of the foregoing discussion: the role of imagination, to which Rule 14 immediately turns.

So that indeed we now also imagine something and do not make use of pure intellect but of the help of species depicted in phantasia: it is to be noted finally, that nothing is said about magnitudes in general that cannot be referred also to any in particular.^[23] From which it is easily concluded that it will be not a little helpful if we transfer those things that we understand about magnitudes in general to that species of magnitude that, among all, is drawn most easily and distinctly in our imagination: indeed that this is the real extension of a body abstracted from every thing other than that it is figured follows from what was said at Rule 12, where we conceived phantasia itself with existent ideas in it to be nothing other than a true body, real, extended, and figured. Which thing is also evident per se, since in no other subject are all differences of proportion more distinctly exhibited; for although one thing can be said to be more or less white than another, likewise one sound more or less sharp, and similaxly for other things, we nevertheless cannot exactly define whether such excess consists in a duple or triple, etc., proportion unless through a certain

[21] In supposition six of Rule 12 we are advised that falsity can be avoided by resorting solely to what we have actually experienced (AT X 422-423). The inborn seeds of knowledge that the Regulae counts on are not sufficient to generate a priori all knowable things.

[22] In the Principles (I 52-53, AT VIIIA 25) we know a substance through an attribute only, never in itself. Thus the mature philosophy retains the biplanarity characteristic of the early period.

[23] Although the parallelism of "de magnitudinibus in genere" with "ad quamlibet in specie" suggests this translation, there is also a parallel to "speciebus in phantasia" in the first part of the sentence, so that this could be rendered: "nothing is said about magnitudes in general that cannot also be referred to any in an image." But this does not affect the interpretation.

analogy to the extension of figured body. Therefore let it stay settled and fixed that perfectly determined questions contain scarcely any difficulty beyond that which consists in evolving proportions into equalities; and all that in which precisely such a difficulty is discovered can easily, and must, be separated from every other subject, and then transferred to extension and figures, about which things alone we now will treat up to Rule 25, every other cogitation being omitted. (AT X 440-441)

This passage makes the truly remarkable statement that it is in phantasia that the differences of proportion are more distinctly evident than anywhere else; as we shall see from the next section of Rule 14, this implies as well that intellect is incapable of recognizing proportions in any distinct way without the aid of imagination. Nor, to emphasize it once more, is this procedure being restricted to the treatment of questions about corporeal and corporeal/intellectual natures. It is a perfectly general procedure, for any problem whatsoever. Even the transfer of degree of participation in natures to line lengths is presented as an example of what this procedure allows, not as its essence, since many other kinds of figuration are possible and permissible, depending on the problem.

The doctrine of natures or common ideas, whatever their provenance, is the foundation of the cognitively effective application of phantasia. Degree of participation or containment can, indeed must, always be compared using magnitudes. Since proportions can be maintained at any arbitrary scale, one can take any magnitude one pleases and call it the whole or, in cases of measure, the unit; all the relations of other things to this magnitude can be expressed proportionally using larger or smaller magnitudes. Moreover, once one has led the participation down to magnitudes one does not have to keep in mind the natures themselves. One can solve (equalize) degrees of participation while completely prescinding from the special character of the nature not expressed in magnitudes. Only at the end of the equalization process, when one has determined the magnitude that corresponds to the unknown thing by treating it as though it were known—what we would call "solving equations in unknowns"—does one need to remind oneself what the nature is, just as in physics one can solve equations using techniques of pure mathematics while ignoring the units in question until the end, when one has to remind oneself that they are centimeters, or joules, or kilogram-meters per second squared.

These foundational principles of the imaginative problem-solving technique are elaborated at the end of Rule 14 (after an intervening discussion of different ways in which extension is imagined and understood; see Sec. G, below).

Here therefore we turn to the extended object, considering nothing else in it but the extension itself and abstaining by industry [or on purpose] from the word 'quantity', for there are certain philosophers so subtle that they

have distinguished that also from extension; but we suppose all questions so deduced that nothing else is sought for than a certain extension that is to be known, by its being compared with a certain other known extension. (AT X 447)

This will be accomplished by reducing involved proportions, all expressed extensionally, to a single one that is equal to the unknown; this can be done no matter how many differences of proportion there are. The crux of the matter is figuring out ways of presenting these differences and "reducing" their relationships so they are visible to the eye and the imagination. "And therefore it will be sufficient to our institution if in this extension we consider all those things that can assist the exposition of the differences of proportion, of which there occur only three, namely, dimension, unit, and figure" (AT X 447).

Dimension and unit have to do chiefly with what is measurable; figure, with both the measurable and the orderable. Rule 5 had asserted that the method was a matter of ordering and arranging things, Rule 6 that the participation of things in natures could be used to produce orderly and even measurable series. This part of Rule 14 shows how this order can be imaged and develops an understanding of measure as derivative from a certain type of order. Measuring requires a unit of measure; a unit of measure must measure something, a dimension; a dimension is a particular way of grasping the things in question. It is either a nature or naturelike—even if it turns out that it does not actually exist!

By 'dimension' we understand nothing other than the mode and reason according to which some subject is considered to be measurable: so that not only length, width, and depth are dimensions of body, but also gravity is a dimension according to which subjects are weighed, speed is a dimension of motion, and infinite others of the same kind. For division itself into several equal parts, whether it is real or only intellectual, is properly a dimension according to which we number a thing; and that mode that makes the number, is properly said to be a species of dimension, although there is some diversity in the signification of the name. For if we consider the parts in an order toward the whole, then we are said to number; if contrariwise we view the whole as distributed into parts, we are measuring it: e.g., we measure centuries by years, days, hours, and moments; if however we number the moments, hours, days, and years, we will finally fill up centuries.
From these things it appears that there can be infinitely many different dimensions in the same subject, and that these add on nothing at all to the things measured out [rebus dimensis], but are understood in the same way whether they have a real foundation in the subjects themselves or have been excogitated from a willed judgment [ex arbitrio] of our mind. For the gravity of body, or the speed of motion, or the division of a century into years and days is something real; not, however, the division of days into hours and moments, etc. All these things nevertheless relate to one another in the same

way if they are considered only under the reason of dimension, as is to be done here and in the mathematical disciplines; for it pertains more to the physicists to examine whether the foundation of these is real. (AT X 447-448)

Descartes points out that although length, width, and depth have a real basis in corporeal things, the three are arbitrarily distinguished.

Here we do not consider these any more than infinite others that are either feigned by intellect or have a foundation in things: as in the triangle, if we want to measure it perfectly, three items on the part of the thing are to be known, namely, either three sides, or two sides and one angle, or two angles and the area, etc.; similarly in the trapezium five, six in the tetrahedron, etc.; all of which can be called dimensions. So, however, that we choose here those by which our imagination will be maximally helped, we will never attend to more than one or two simultaneously depicted in our phantasia, even if we understand that in the proposed thing about which we are busying ourselves there exist as many others as we could wish; for [the essence] of the art is to distinguish these into as many as possible so that we turn simultaneously only to as few as possible but nevertheless to all in succession. (AT X 449)

The notion of dimension established here, Descartes argues, is not the geometer's arbitrary one of the three spatial dimensions length, width, and depth. These correspond to something real in things, he agrees, but they are not simply given by nature; rather, they involve an identification by intellect of a mode or aspect of a thing that is measurable according to some conceivable division. To take the measure of a triangle we need to know at least three elements "on the part of the thing"—three sides, or two sides and one angle, or two angles and the area, and so on. In a trapezium we need five elements (even though it has four sides), in a tetrahedron (a solid with four faces) we need six: "which all can be called dimensions" (AT X 449). Although both the trapezium and the triangle are plane figures existing in two spatial dimensions, the perfect determination requires five and three question-dimensions, respectively; the three-dimensional tetrahedron requires six dimensions.^[24] As is typical of the Regulae, it is not a question of determining or defining the essences of these things. Indeed, their essences in the Scholastic sense are taken for granted, and one's in-

[24] A trapezium is a quadrilateral with no parallel sides; one could determine it precisely by (to give one example) specifying the length of a first side (this is the first factor or dimension), the angles at which the two sides come off the ends of that first (two more dimensions), and the lengths of those two sides (another two, making five in all). A tetrahedron is a solid with four triangular faces; one could determine it by specifying first one of the triangles as a base (this requires three dimensions) and then the apex at which the other three faces meet (by taking one of the sides of the base triangle as an axis and giving three coordinates that would take you from one of its end points to the position of the apex point; this gives three more dimensions).

terest instead is how to construct them unambiguously—more generally, how to get dimensions that codetermine one another and thus allow the solution of the question at hand.

What one needs to solve a question depends on what the question asks for. Moreover, Descartes as always urges us to adapt ourselves to the capabilities of our ingenia. To repeat the admonition of Rule 14:

So, however, that we choose here those [dimensions] by which our imagination will be maximally helped, we will never attend to more than one or two simultaneously depicted in our phantasia, even if we understand that in the proposed thing about which we are busying ourselves there exist as many others as we could wish; for [the essence] of the art is to distinguish these into as many as possible so that we turn simultaneously only to as few as possible but nevertheless to all in succession. (AT X 449)

To summarize the process of Rules 13 and 14: In setting up the problem one uses intellect to enumerate and distinguish all the relevant aspects, terms, and divisions of the thing in question. Then one expresses in easily imaginable, figurate form the proportional relations that are determinately given, and one treats what is unknown as though it were known—known, that is, in relation to the proportional participation in natures of other things or their aspects.^[25] The figures—chiefly line segments, but also discrete magnitudes and two-dimensional figures where appropriate—will then become the objects of manipulation as one tries to equalize the various proportions, with the aim of expressing the designated unknowns in terms of what is known. To keep this all manageable for an ingenium that has difficulty attending to more than two things at a time, one will use marks and symbols to keep track of the problem—a technique that will generate symbolic equations.

But at this point Descartes is envisioning more than the development of modern algebraic problem solving. What counts most for him is the universal relevance of proportional participation in natures, a participation that is expressible in its most perspicuous form not by algebra, which is symbols without content, but by figures, which visibly embody actual proportions. For every algebraic manipulation one can perform on an equation there is, more important, a quite precise, imaginably executable geometric construction corresponding to it. (In fact, it is only in the later mathematics of the Geometry that there emerges an independence, or rather

[25] For example, in a physics problem concerning the weight, density, hardness, and size of minerals, there will be proportional relations between the different aspects (e.g., weight might be equal to length times width times height times density, and hardness might be a function of density). These proportions "reduce" each nature to others, not in the sense of ontologically eliminating it but in the sense of expressing interconnections. The science of the Regulae is not the reductive science of the Discourse.

quasi-independence, of algebraic manipulation from geometric representation; nevertheless, the Geometry is in principle still about how to discover and execute exact geometric constructions by following the pattern of manipulations indicated in algebraic equations.) The marks and symbols are especially helpful in the sorting out of the elements of a problem, for representing in a contentless but mnemonically useful way the line segments and other figures that embody the proportions. The sorting-out process is what the ancient geometers called analysis: taking the unknowns as known and schematically working out what would be true if they were known; and then, provided one reaches the point of having reduced the problem to terms that are known or constructible, the reverse process of synthesis, of the actual construction (or deduction, a leading down ) of the solution, can be carried out.

In comparison to the ancients, Descartes simplifies the analytic phase by making it more accessible to human ingenium. The ancient geometers had worked with complicated figures requiring a sophisticated geometrical insight, and each stage of analysis required finding an executable next step that was usually dependent on multiple considerations (e.g., one might need to add several new lines to an already complicated figure). Descartes uses the identification of relevant dimensions, the simple figurate representation of proportions one at a time, and the symbols and marks of "algebraic equations" to reduce the analysis to a progressive linear sequence requiring attention to no more than two things at once. What is more, the algebraic equations, by containing direct symbolic references to the original givens and unknowns of the problem (x ⁴ = a² + 2bc - c³ directly involves the x, the a, the b, and the c ), allow one, if the analysis is successful, to construct the unknown proportion step-by-step (multiply the line a by itself, add to this result the line that is twice the product of b and c ; subtract line c multiplied by itself and by itself again; then take the fourth root of this result, and you get the desired, previously unknown x ). This entire process, then, is simply an iterated and reiterated application of intuitus and deductio to the image forms of the problem, arrayed in a sequence and manner that makes everything as clear and as imaginable as possible.

The decisive advantage of this kind of deductio over the deduction from axioms and postulates of ordinary logic and dialectic is its perfect reversibility and reciprocity: if y is the product of f and g, it is also true that f can be obtained from y and g by division (i.e., by a proportion, y/g ), and likewise g can be obtained as y/f The terms of dialectic, however, are not in general reversible. "All human beings are animals" does not justify the conclusion that all animals are human beings but only the weak and relatively indeterminate "Some animals are human beings." From this latter assertion no further conclusion is possible without the addition of a new

universal premise telling us something about either animals or human beings. Descartes's problem solving, by contrast, uses universal mathesis to reason about nothing other than particularly represented relations, so that the presence of nothing but particulars does not prevent a solution. On the contrary, it is what makes a single determinate solution possible.

In the concluding remarks to Rule 14, Descartes notes that in choosing among figures for expressing the relations in problems "it is necessary to know that all relations that there can be between entities of the same genus are to be referred to two headings: namely, to order or to measure" (AT X 451). As to order, the whole Regulae has been directed toward showing the nature and consequences of order and the search for it. Originally finding out an order can take a great deal of work (though some orderliness is intrinsically simple), but once an order is discovered there is no difficulty in knowing it by following Rule 7's advice of running through a sequence of the parts that have been distinctly separated from one another,

because, to wit, in this genus of relations one part is referred to others out of themselves alone, but not by means of a third, as happens in measurings, about the evolving of which we are alone here treating. For I recognize what is the order between A and B without considering anything beyond each extreme; I do not, however, know what the proportion of magnitude is between two and three unless it is considered by some third thing, namely, by the unity which is the common measure of each. (AT X 451)

Continuous magnitude can always be reduced, at least in part, to a multitude (a line of length 7.333 . . . can be approximately represented by 7 points or, if one takes. 1 as the unit, 73, etc.), which means that problems of measure can, by means of the unit of measure, be translated into problems of order.^[26] To represent dimensions by continuous magnitude we should not use anything more than length and width; that is, we should not attend to more than two dimensions simultaneously. In conclusion, he points out a consequence: that even problems concerning mathematical entities (like geometrical figures) are to be treated according to this method.

Here propositions are to be no less abstracted from those figures that geometers treat, if the question is about them, than from any other matter whatever; and for this purpose none are to be retained beyond rectilinear and rectangular surfaces, or right lines, which also we are calling figures,

[26] I do not see that one in fact gains much fundamentally from this procedure, since it does not eliminate the unit (which is a third thing interposing itself between the two things to be compared) but rather leaves it implicit. Nevertheless, it perhaps gives a more imaginable precision: two lines, one of length 71/3, the other of length pi, leave considerable work to the imagination in fixing the exact proportion, whereas putting 73 tenth-units next to 31 makes the proportion somewhat more determinately, though approximately, evident.

since by means of these we imagine a truly extended subject no less than by means of surface, as was said above; and finally by means of the same figures both continuous magnitudes and also multitude or number are to be exhibited; and nothing simpler for the exposition of all differences of relation can be invented by human endeavor. (AT X 452)

Thus, far from applying ordinary mathematics to all things, Descartes is advising the application of mathesis universalis, the science of concretely imaged proportional relations, even to arithmetic and geometry. A mathematician will therefore identify relevant aspects or natures in any strictly mathematical problem, proportionalize the givens, then perform an imaginative process of continued proportionalization to solve for an unknown. If this process is different from the ordinary methods of mathematical proof, so be it.

The rules following—15 through 18 have both headings and explications, 19 through 21 only headings—are virtually contained in Rule 14. Rule 15 shows how to use a point or line or square to stand for the unit and then how to extend these to represent measures that are commensurable with the unit or to construct a rectangle to exhibit to the eyes two measures in relation to one another. Rule 16 advises the use of concise marks to keep track of the problem as a whole; Rule 17 advises surveying all the parts of the problem on the same basis of instantiated proportions, whether they be known or unknown. Rule 18 shows how to add and subtract line segments from one another and explains the principle underlying multiplication and division using lines and rectangles. Crucial to the effectiveness of the procedure is the ability to translate a measure from a line segment into a rectangle and from a rectangle into a segment, so that it is never necessary to exceed two spatial dimensions (in ancient mathematics, the multiplication of two numbers was conceived by constructing a rectangle with sides of those lengths; multiplication by a third number required the construction of a solid; multiplication by a fourth number thus presented nearly insuperable problems of conception, since it would have required entering a fourth spatial dimension).^[27] Rule 19 (heading only) says that in solving a problem we need to find as many magnitudes (line lengths, rectangles, numbers) as there are unknown terms by using operations on the unknowns as if they were known (in modern algebraic terms, we look for equations setting x, y, z, and any other unknowns equal to some formula that contains only known values). Rule 20 (heading only) promises to tell how to carry out the operations of multiplication and division

[27] Descartes's technique of reducing a plane figure to a line represents an advance over the mathematical adaptation of the memory art he had explained to Beeckman in October 1628; see chap. 3, Sec. E above.

(which had been put off until this point because of their greater technical difficulty). And Rule 21, the last extant heading, urges that many equations be reduced to a single one. At this point the Regulae breaks off.

F. THE SCIENCE OF ORDER AND MEASURE AND THE PARADOXES OF SIMPLE NATURES

Was the Regulae abandoned, or did Descartes simply leave it incomplete? Are there tensions and conflicts between it and the later philosophy, or is the later philosophy simply a continuation of what was laid down in its rules?

With each question cases can be made for either alternative. Consider the possible significance of the fact that the break in the Regulae occurs at Rule 21 and that none of Rules 19 through 21 consists of more than a heading. All three have to do with forming equations on the basis of figurate and symbolic representations and the operations of addition, subtraction, multiplication, and division discussed in the preceding rules. The last substantive remark made in the commentary under Rule 18 says that in order to reduce any rectangle to a line segment one must be able to construct on a given line a rectangle equal (in area) to a given rectangle. The rationale is this: The product of a length a multiplied by a length b can be represented by the area of a rectangle with sides of length a and b . If one wants to multiply this product by another number, one needs to convert ab into a line length and then construct a new rectangle with sides of length ab and c , the area of which will be abc . One could construct a cube with dimensions a, b, and c, but then in order to perform a new multiplication one would have to reduce the cube's volume to an area or a line; but a cube in any case requires attention to three measures at once (length, width, and height), contrary to the advice of the Regulae to keep comparisons to two items at a time. Thus any geometric technique of multiplying is going to require the reduction of a higher-dimension figure to a figure of the next lower dimension.

If a and b are integers or rational numbers, the construction of a line segment equal in length to their product is relatively simple—one can just reckon up the total number of units or fractional parts and then build up the product line piece by piece—but if one of the numbers is irrational, this will not be possible. Nor will any arithmetic or algebraic techniques (algorithms) give the result exactly, for they work by approximation. The desired line length could be obtained by identifying a general technique of geometric construction, however. Given a rectangle of area ab, if one can construct a second rectangle of equal area on a line segment having unit length, the two sides adjacent to this unit segment obviously will both

have length ab. So the ability to construct on a given unit line a rectangle equal in area to another given rectangle amounts to being able to construct a line whose length represents the product of two numbers.

The general technique is conceptually simple; actually constructing such a line or rectangle is quite another matter.^[28] But does this Regulae method really serve Descartes's larger and ultimate goals? The Geometry of 1637, one of the three essays that followed the Discourse on the Method, gives some insight into this question. On the one hand, the Geometry can be conceived as Descartes's further elaboration of the correspondence between line lengths and symbolic algebra, with the algebra subordinate insofar as it is an easily manipulable symbolic form for expressing proportions that are ultimately to be translated into geometric constructions. On the other hand, it can be seen as a rejection of the method of applying straight lines and rectangles in favor of a general technique of solving for proportions by the generation of complex curves. The Geometry works as resolutely in two dimensions as does the Regulae, but its favored tools are straight lines and curves derived from the motions of straight lines and lower-dimensioned curves by continuous and rigorously mechanical processes. The antecedent of this aspect of the Geometry is Descartes's study around 1620 of the properties of new kinds of tools for geometric construction, like the proportional compass, the operation of which could be used to trace out curves by virtue of the mechanical linkage of its segments. The later geometry of Descartes puts a greater premium on the generative process and its continuity, and it systematically explores the possibilities of generating complex curves that correspond to algebraic equations. This is a dynamic geometry, in contrast to the more static and episodic character of the mathematics in the extant Regulae, where one always stops to compare just one line to another, then performs one or more simple manipulations, then compares the result to one of the original lines or yet another, and so on. The Geometry 's geometry proceeds continuously and dynamically, not step-by-step.

The context of the mathematics of the Geometry is the scientific understanding of extension and matter that Descartes developed for Le Monde, a work begun about 1630, after the abandonment or presumed abandonment of the Regulae. How that work is predicated on a more continuous and dynamic, but also more restricted, power of imagination will be revealed in the next chapter. Before we can proceed to that, we must con-

[28] If you know exactly how long the unit length should be, relative to the lengths a and b, it is easy to construct the line of length ab. Form a first fight triangle with legs of length 1 and a, then draw a line of length b parallel to the side of length i and construct a second triangle on length b similar to the first triangle by drawing parallels to the other two sides. The other leg of the second triangle (parallel to the side a of the first triangle) will have length ab. When a and b are rational numbers it is always possible to construct a line of unit length, but when they are both irrational the whole trick is to construct such a unit length exactly.

clude the discussion of the Regulae by raising some of the major unresolved problems to which it led. They will be presented under two headings: the paradox of the natures doctrine in the context of science, especially in matters of physiology and physics, and the interaction of intellect and imagination. Imagination, it turns out, figures centrally in both.

Rule 6 introduced the natures in the phrase "pure and simple natures," but what they amount to in the first instance are aspects common to many things (à la Rule 14) that are participated to varying degrees. This differential participation gives rise to an order from the least to the most; the things that most participate in—or, better, wholly contain—the nature in question are called 'absolute'. But even in the course of Rule 6 there begins to appear the thornier question of the participation of natures in one another. Rule 8 and, even more, Rule 12 go on to address not just the powers of mind but also the objects of those powers, the natures. The natures are divided in Rule 8 into the spiritual, the corporeal, and the spiritual/corporeal; in Rule 12, into the intellectual, the material, and the common. Both rules distinguish simple natures from complex ones; the latter are either originally experienced as such, that is, as complex, or are composed by the intellect. Falsity exists only in the composite natures put together by intellect.

The second part of Rule 12 in fact offers a presuppositional account of natures, in much the same way that the first part presents an account of the psychophysiology of the internal senses that, like the hypotheses of the astronomers, is intended to make things clearer without a final assurance of truth. The presuppositional account goes as follows. First, the way that natures exist in reality is said to probably differ from how they appear in knowledge, since, for example, real bodies, which are single and simple as things, are understood as somehow put together out of diverse natures. Second, there are three classes of nature, intellectual, material, and common, the last including the common notions of mathematics and reason (e.g., if two things are equal to a third thing, they are equal to one another). Third, any simple nature is evident, known in itself, so that having the slightest grasp of it is to have it complete. Fourth, the simple natures are conjoined either necessarily or contingently; in the first case separating them makes it impossible to conceive the components distinctly. Fifth, the only things we can understand are these simple natures and a certain mixture or composition of them. Sixth, the composite natures are either known as such through experience or are made up by intellect. Seventh, the composites we make come about through impulse, through conjecture, or through deduction (AT X 418-425).

Marion has argued at length that the simple natures of Descartes are inscribed against a background of Aristotelian ontology and epistemology and that in the doctrine of them is contained what he calls the "gray

ontology" of the Regulae, that is, an inexplicit ontological framework that subsequently evolved into the philosophy of Descartes's maturity.^[29] Marion is certainly right to put such weight on the natures for Descartes's future thought. Descartes sought from them ontological support for the method of the Regulae, and the partially developed theory of natures offered there raises themes and suggests positions of the later philosophy without set-fling them.

In the Regulae, Descartes appears to be quite content with the possible discrepancy between natures in existent things and natures in our knowledge that the first of the seven presuppositions allows. Even on the epis-temological level he displays a remarkable casualness about the natures. Although they are to provide the foundations for all knowing, Descartes does not insist on a perfect reductio to them. He is perfectly happy to get on with the task of problem solving by means of pragmatic and heuristic expedients, the most basic of which is the discovery of series with absolutes that are less than absolutely absolute.

In fact this casualness is not unique to the Regulae but is a recurrent trait in all Descartes's writings, a casualness grounded in a conviction, first, that human nature—human ingenium—is constituted so that it can know and learn and, second, that the foundations of knowing are not infinitely or even greatly remote from our capabilities but only a short distance beneath the surface (often buried under the debris of philosophical maleducation). To use an image of the Discourse, most people build on sand, and this is especially unfortunate because one need not dig deep to hit clay or rock. Or to change to a visual metaphor: one can reach the truth relatively easily by looking carefully and clearing away what is extraneous; once one has done this it is easy to see things, and once one sees them one has them. One might recall in addition the recurrent motif of Descartes's writings that says one must once in one's life undertake an examination of one's mind and opinions to find the truth and combine this with the fact that he acknowledges having recognized this need early in his own life yet postponed the examination for nearly a decade (AT VI 10 16-17, 22; VII 17). That it needs to be done but once in one's life indicates that, unlike ancient theoria and medieval contemplatio, the ultimate truths do not open up a way of life that is a continuous gazing on truth, but that once truths are seen they can be used to guide all the concerns and solve all the problems that life presents. Real truth is secure and may be relied on; given God's veracity, it does not even have to be recalled in its full and present evidence but only remembered as having in the past been known. Yet the atheist can recognize the truth just as well as the believer in the moment of evidence; this confirms that truth's foundations are in essential har-

[29] See Marion, Sur L'Ontologie grise de Descartes, esp. 131-148, 185-190.

money with the careful but nonfoundational use of one's knowing powers. Therefore one can know, live, and act in the light of the truth even when one has not looked to the source of the illumination, and one does not need in every case of knowing to look deep beneath the surface of things.

The Regulae appears to be written in this double confidence, that the foundations are shallow but still secure and that the good use of ingenium does not in most cases require going down to the foundations. The hypothetical mode of all of Rule 12, combined with the relative simplicity of the physical and physiological language and themes posited there (and elsewhere, for example Rule 8, which discusses the anaclastic line of optics in physical terms that are more Scholastic than Cartesian),^[30] tends to confirm that the Regulae precedes the deeper investigations of physics, metaphysics, and foundational epistemology that we regard as genuinely Cartesian. But this would be perfectly consistent with an essential continuity of this work with the ontological epistemology of resemblance, which is more coherentist than foundationalist and expresses a confidence that higher truths are adumbrated even in the least things. A Descartes working at the Regulae with this confidence would see the fundamental cognitive task as one of progressive clarification.

Yet it is doubtless right that the question of what in the last analysis we see when we see and what we know when we know induced Descartes to put a term or end point to seeing and to call them natures. His first impulse, one expressed in the main project of the Regulae, was to treat them as the aspects of things; his second impulse, which appears in the obviously incomplete sections of Rules 8 and 12, was to conceive them as a kind of object (or res, thing) capable of participating in other natures just as ordinary things do. At the limit of this participative process stood the ultimate simple natures, which need no further phenomenological or causal support. Descartes's treatment of them is hesitant, however; he does not push the simple natures to their logical and ontological extremes, but instead takes them in several directions not entirely consistent with one another.

The mathetical approach of Rules 13 through 21 is oriented to practical problem solving and an imaginative mathematics of participation in

[30] See AT X 394. The anaclastic line is the curve of a lens that would focus all parallel rays of light to a single point. Although the Regulae 's discussion of optical matters suggests that Descartes had already achieved no little mathematical sophistication in optical theory, his physical theory of light is still markedly traditional. A sign of this is his use of diaphanum. CSM is certainly wrong in rendering totum diaphanum as 'the entire transparent body' and explaining it in a note as 'the very fluid 'subtle matter' which Descartes took to be the medium of the transmission of light' (CSM 1:29), for diaphanum is simply the Latin term for the transparent medium that, according to Aristotle, must be actualized by light for the proper sensible, color, to be conveyed to the eye.

natures that gives rise to measuring the degree of participation. It has a pragmatic conception of natures, understood as dimensions, which can be either fictional or real. The idea of reductio presented is not ontological but proportional, which means simply that proportions allow us to express one thing in determinate, reversible relations to others by way of various dimensions. So, for example, the reflection of a light ray can be analyzed as a relation between lines standing for the ray and a line standing for the reflecting surface; the proportions between the lines can be expressed by angles; and the natural forces involved can be put in terms of the angles and lines. The source of error in this process is the intellect, when it overlooks what the concrete presentation of the problem contains. Nevertheless, intellect still has the fundamental problem-solving task of sorting out the different nature-dimensions in the givens of the problem and determining what is relevant—which also means leaving aside the irrelevant, although no criterion for this distinction is given.

Rule 6 presents an object-centered approach oriented by a participation in natures that gives rise to an ordering, serializing activity. It establishes a wobbly foundation for the later mathetical rules, which presuppose the in-genial activity of comparing one thing to another in light of natures that are the starting point of Rule 6. The serializing is chiefly of the things that participate in natures rather than of the natures themselves. The things rather than the natures are in the first instance treated as absolute or respective. The second annotation of the rule begins to broach the question of the participation of natures in one another without clarifying whether this participation is of a different kind.

Rule 12 (and Rule 8) attempts to probe what Rule 6 presupposes: the character of the physical processes and of the psycho-organic apparatus that convey the appearances of things to mind, and also the very natures that are increasingly conceived as the ultimate objects of the psychological activities. But Rule 12 proceeds by presupposition. In the psychophysical part it presumes that the impressions of things are conveyed by physical processes that are wholly reliable and preserve the semblances of things intact (one might surmise that he expects the physicist to confirm this in short order), and it adapts a long-established internal senses doctrine to a modified but still traditional physiology in a manner that shows no particular acquaintance with concrete anatomical studies^[31] He identifies the real source of imagination as the vis cognoscens acting in the organ phan-

[31] Descartes probably did not begin studying anatomy at first hand until sometime in 1629; see Dennis L. Sepper, "Descartes and the Eclipse of Imagination, 1618-1630," Journal of the History of Philosophy 27, no. 3 (July 1989): 379-4o3; and Sepper, "Ingenium, Memory Art, and the Unity of Imaginative Knowing in the Early Descartes," in Essays on the Philosophy and Science of Rtné Descartes, ed. Stephen Voss, 142-161 (New York: Oxford University Press, 1993). See also chap. 3, footnote 32, above.

tasia—as much will-like as intellectlike, since it is an intentional application of the knowing force—and places thinking's center of gravity there; yet he allows a certain degree of autonomy to a pure intellect that he scarcely even begins to articulate.

In the natures part of Rule 12 he countenances a possible discrepancy between how things in the world and things in the mind participate in natures, yet he postulates a foundationalist ontology of epistemological natures that has to be ultimately consistent with the being of real things if it is to be cognitively effective. He says that natures must be composable and distinguishes between necessary and contingent composition, but he does not clarify necessity in any deeper sense than the mind's inability to distinctly separate the necessarily composed natures. In this schematics of natures as necessary or contingent, falling into the three classes of the purely material, the purely intellectual, and the either material or intellectual, he begins to evolve a higher-order vocabulary for talking about natures that suggests there are higher-level or transcendental simple natures, the character of which is left obscure. Finally, the theory of the composition of natures that our intellect performs, according to either impulse, conjecture, or deduction, begins to address what might provide a foundation for the cognitive activity of imagination, although Descartes's presentation is a mixed bag of problematic assertions (AT X 424). (1) He tells us that impulse can lead to either truth or error: it is never a source of error when it comes from on high (although this stands outside the scope of method), rarely when from our free will, almost always when it is due to an indisposition of phantasia (like jaundice). (2) By conjecture we compose what is merely probable; this does not deceive us so long as we do not assert it to be true. (3) Deductio remains as the sole way of composing things so that we can be certain of their truth, precisely by using intuitus in a progression that reveals the necessity of the conjunctions of natures. Descartes appears to have found the themes of his maturity and the germ of his approach to them in this quick sketch, but the compression and problematic coherence suggest that he had not yet thought them through.

G. COMPARATIVE INTELLECT AND CONCRETE IMAGINATION

Intuitus, of course, is the easy and distinct conceptum of a pure and attentive mind. Yet the thing-oriented intuitus of the early rules as well as the mathetical intuitus of the final rules begin to intimate that natures might be the easy and distinct things grasped by the pure and attentive mind. Consonant with the biplanar consciousness of Descartes's philosophy, in-tuitus is the well-prepared seeing of a thing with respect to a nature. Natures are thus in the first instance a modality of the grasping-seeing of a

thing, an indirect object, so to speak. Can natures in turn become the direct objects of intuitus? If they can, they would resemble the ideas of the later Cartesian philosophy.

There are reasons provided in Rule 14 to think that Descartes did not intend such an outcome, that he in fact intended something quite different. The relevant passage is the long discussion of the mutual assistance of intellect and imagination in conceiving the various senses of extensio, 'extension'. He introduces the passage by saying that the mathetical rules are indeed useful in the mathematical sciences, but that

the utility is so great for attaining to higher wisdom that I am not afraid to say that this part of our method was discovered not on account of mathematical problems but more that these things are to be learned almost solely for the sake of cultivating it. And I suppose nothing from these disciplines except perhaps certain things that are known through themselves and obvious to everyone; hut the knowledge of them as it is usually presented by others, even if it is corrupted by no manifest errors, is nevertheless obscured by oblique and badly conceived principles that we will try to emend here and there in the things that follow.
By 'extension' we understand all that has length, width, and depth, not asking whether it is a true body or only space; nor does it appear to require greater explication, for nothing at all is more easily perceived by our imagination. Nevertheless, because often the learned use such acute distinctions that they dissipate the natural light and discover shadows even in those things that are never unknown [even] to peasants: they are to be advised that here by 'extension' is designated not a distinct something, separated from its own subject, nor do we acknowledge in the universe philosophical entities of this kind, which do not truly fall under imagination. For even if someone could persuade himself, e.g., that it would not be contradictory, if whatever is extended in the nature of things were reduced to nothing, that extension itself existed per se alone, he nevertheless will not be using a corporeal idea for this conception but only badly judging intellect. Which he will confess him-serf, if he reflects attentively to that image itself of extension that he will try to feign there in his phantasia: for he will notice that he does not perceive it destitute of every subject, but imagines it completely otherwise than he judges; so that those abstract entities (whatever intellect should believe about the truth of the thing) nonetheless never are formed in phantasia separate from subjects. (AT X 442-443)

It is the intellect, not the imagination, that is responsible for error. The passage discusses extension in particular, but its conclusion applies to all thinking directed toward an image, all thinking that requires or involves phantasms. The intellect, not the imagination, tends to mislead us because it often looks away from the phantasm when the conclusion it tries to draw concerns the phantasm. In its desire to make subtle distinctions the

intellect dupes itself; it overlooks the fact that it is trying to separate the inseparable^[32]

These reflections about what a word is taken to mean versus what even the most unlearned peasant knows about the thing the word designates lead to a discussion of the various senses in which imagination and intellect take things in different contexts of meaning.

Since henceforth we shall be doing nothing without the assistance of imagination, it is worth the effort to distinguish carefully through which ideas the individual significations of words are to be proposed to our intellect. For which purpose we propose to consider these three forms of speaking: "extension occupies place," "body has extension," and "extension is not body."
Among which things the first shows in what way 'extension' is taken for that which is extended; for I plainly conceive the same thing by saying: "extension occupies place," as by saying: "the extended occupies place." Nevertheless, it is not on that account the case that to avoid ambiguity it is better to use the word '[the] extended': for it would not signify so distinctly that which we conceive, namely, that some subject occupies a place because it is extended; and someone could interpret [it] as "the extended is a subject occupying place," no differently than if I should say: "the animated occupies place." Which reasoning explicates why here we shall say that we are dealing with extension rather than with the extended, even if we think it should be conceived no differently than the extended.
Now we come to these words: "body has extension," where 'extension' we understand to signify something other than 'body'; we nevertheless do not form two distinct ideas in our phantasia, one of body, the other of extension, but only a single one of extended body; and it is no different on the part of the thing than if I should say: "body is [the] extended"; or rather: "the extended is extended." Which thing is peculiar to those entities that are [= exist] only in another, and cannot ever be conceived without a subject; and it happens otherwise in those things that are really distinguished by means of subjects^[33] for if I should say, e.g.: "Peter has riches," the idea of Peter is plainly different from that of riches; likewise, if I should say: "Paul is riches," I imagine something completely different than if I should say, "riches are riches." Many, not distinguishing this difference, falsely opine that extension contains something distinct from what is extended, just as the riches of Paul are other than Paul.
Finally, if it is said: "extension is not body," then the word 'extension' is

[32] Abstractions and distinctions of reason therefore can easily turn out to be false when they concern concrete objects or images. The implications of this could be considerable, especially in the search for truly fundamental simple natures.

[33] CSM translates "illis, quae a subjectis realiter distinguuntur" as "entities which are really distinguishable from their subjects" (CSM 1:60), hut the examples are not of things that are distinguishable from their subjects (Peter, Paul, and riches) but of two subjects that are distinguishable.

taken far differently than above; and in this signification no peculiar [= particular] idea in phantasia corresponds to it, but this entire statement is accomplished by pure intellect, which alone has the faculty of separating this kind of abstract entity. Which thing is the occasion of error to many, who, not noticing that extension taken in this way cannot be comprehended by imagination, represent it to themselves through a true idea [veram ideam]; since such an idea necessarily involves the conception of body, if they should say extension so conceived is not body, they are imprudently implicated in this, that "the same thing is simultaneously body and not body." And it is of great moment to distinguish statements in which names of this kind: extension, figure, number, surface, line, point, unity, etc., have so strict a signification that they exclude something from which they are truly not distinct, as when it is said: "extension, or figure, is not body"; "number is not numbered thing"; "surface is the limit of body, line of surface, point of line"; "unity is not quantity," etc. All which similar propositions are to be completely removed from the imagination in order to be true; for which reason we shall not be dealing with them in the following.
And it is to be diligently noted that in all other propositions in which these words, although they retain the same signification and are said in the same mode abstracted from subjects, nevertheless exclude or negate nothing from which they are not really distinguished, we can and must use the help of imagination: because then, even if the intellect precisely attends to only that which is designated by the word, imagination nevertheless must feign a true idea of the thing so that, whenever use demands, the same intellect can turn to its other conditions not expressed by the word and not ever imprudently judge that they have been excluded. So if the question is about number, we shall imagine some subject measurable by means of many units, to the sole multitude of which the intellect can indeed turn in the present moment, yet we shall take care that from this subsequently it not conclude something, in which the numbered thing is supposed to have been excluded from our power of conception: as those do who attribute to numbers wonderful mysteries and unadulterated nonsense, to which they certainly would not lend so much faith if they did not conceive number to be distinct from the numbered things. Likewise, if we are dealing with figure, we will think we are dealing with an extended subject according to what is conceived by this reason only [sub hac tantum ratione concepto], that it is figured; if with body, we will think we are dealing with the same thing, as so long, so wide, and so deep; if with surface, we conceive the same as long and wide, depth being disregarded, not negated; if with line, as long only; if with a point, the same with everything else omitted except that it is an entity. (AT X 443-446)

This extended passage is motivated in the first place by the need to explain how terms in linguistic propositions are to be conceived by the mind, in particular in what ways the imagination can conceive them. As corollary, it also indicates a role of pure intellect, the functioning of which Descartes had in Rule 12 promised to describe. The particular context in which the passage appears is the preceding statement that all the proportions that

can be detected ought to be expressed in extension and figuration, so that it appears to be the appropriate place for an explanation of 'extension'; yet the points made are not restricted to this notion alone but are applicable by analogy to distinctions of other terms as well.

The passage, in brief, says the following: Every word or form of signification has a "true (imaginative) idea" associated with it, and in almost all cases it is appropriate and necessary to portray this idea in phantasia. A statement that has two terms (e.g., "body is extended") does not necessarily require that two things be imagined, however, because certain natures are such that they are always and everywhere implicated with others. In such cases we should form one image or idea, and by a difference in focus, by a different concentration or grasp—that is, by a different concept —the intellect can now direct itself to this or that aspect of the one image. In other cases, when there is not this implication of natures in the two terms (e.g., "Peter has riches"), it is necessary to form two ideas. But there is a class of cases where meaning or signification is intended in so restricted a sense that it is inappropriate to form an image because the statement would be contradictory if it directly intended the image. In these cases it is pure intellect alone that makes the judgment truthfully. To put this latter point differently, when we say that extension is not body, we are referring precisely not to either extension or body but to the distinction between the two, which (because both the subject and the predicate actually involve extension) no image can directly present and which only the intellect can grasp securely.^[34]

For the second time in the Regulae the role, or at least one of the functions, of the pure intellect is explained (the first was in Rule 13, where pure intellect was assigned the task of setting up the initial terms of a problem). It might appear on first glance that it demonstrates the power of the intellect to rise above imagination. But the tenor of the passage is at odds with this conclusion. It rules out, in general, philosophical entities that do not fall under the imagination, that is, abstract entities that are entirely separated from a subject, from something in which they inhere. When there is something imaginable or portrayable in imagination, the intellect does wrong, and risks error, by trying to judge on its own. In prescinding or turning away from the true image the intellect tends to overlook what is actually included in the idea; it is as though the intellect can easily "forget" when it is not presented with an image, or with some other kind of concrete object. Moreover, the kind of case in which the passage allows

[34] Descartes does not so much forbid one to imagine anything in this case as consider the imagined things an indirect object that must be looked away from in order for the intended negation to be true; or, more precisely, it is to its own way of taking and not taking images that the intellect must directly attend, not to the images themselves.

knowing by pure intellect is a very limited, negative knowledge. All the examples given involve privation or negation (note that "surface is a limit of body" and the like involve the privative notion of limit). Some insight into the issue can be gained from the statement that, in the case of "extension is not body," pure intellect alone "has the faculty of separating this kind of abstract entities." It is only in such an abstract realm, in the abstract, indirect taking of things, that these statements are true.

Behind this assertion is probably the thesis of Aristotelian-Scholastic philosophy that a faculty cannot judge of forms in a way that exceeds its proper powers. Vision can perceive white, it can even distinguish white from black, blue, red, and so forth, but it cannot judge that a white thing is sweet; for this there is required the common sense. Common sense and the other internal senses can judge of such particular differences but not of the genera or forms; for this one needs intellect. Yet intellect does not operate without a phantasm; that is, thought is intellect busying itself about a phantasm in order to grasp what that phantasm stands for by means of the form actively abstracted in intellect.^[35]

Rule 14 agrees insofar as it is the intellect that is properly said to understand by attending to the true ideas in phantasia. One is able in phantasia to make separate images when the proposition in question allows it; when the proposition is about different aspects of an inextricable whole, then the differential attention of intellect alone can track the difference. But when intellect goes it alone, it is not capable of making positive judgments truthfully; rather, it is only able to note differences by way of severely restricting the meanings of terms and abstracting them from all images.^[36] This would seem to be connected with the intellect's capacity of noting simple natures: when properly prepared it can recognize them in things, and it can recognize the difference between such natures, but it cannot define their essences. Properly prepared intellect can only experience simple natures; there is no deeper sense in which they can be said to be "known" by intellect. But this is to reinforce that intellect's function is to enable us to distinguish and recognize, to grasp similarities and differences. In comparison to some other traditional notions of intellect this

[35] In this respect, Descartes arrives at a similar conclusion, in that he denies that one can ever come into possession of a nature or an abstraction without the direct—or, in the case of negations, indirect—presence of a phantasm.

[36] This helps throw light on the point Descartes made in Rule 12 (AT X 418—419) about limit not being a simpler nature than the things from which it is abstracted. Although he was willing to allow that the negations of simple natures are themselves simple natures for methodological convenience, limit is an act of negation or privation that can be applied indifferently to this or that nature. Limitation is a fundamental act of intellect rather than a simple nature that appears in itself.

seems not very powerful, but it nevertheless is, precisely because it allows a freedom from the brute force of the given taken as an undifferentiated whole, or as a whole differentiated only by corporeal processes (as in functions of the brain and nerves). Whatever is presented to us we can compare or contrast with other things not immediately present, things we can call up from memory or produce by the recombinative powers of imagination—that is, of the knowing force acting in phantasia. Intellect allows us to articulate thoughts directed to things, but when left to itself it is mute and inarticulate. In saying that "extension is not body" intellect is in effect judging that its way of attending to things is differentiated; that is, this judgment is not about the thing but about the intellect's way of acting.

This leaves a problem, however: can all these things be said of the intellect when it recognizes what is entirely noncorporeal, for instance, what willing or ignorance is, or that my being implies God's? The answer, I think, is twofold. One part has to do with our expectations of Descartes. Insofar as we judge from our knowledge of what he wrote later, we want to find anticipations of it earlier. There is nothing wrong with this; indeed it is probably a necessary prejudgment that induces us to read the noncanoni-cai works of any major author. But we must avoid the pitfalls of an excessively teleological reading, that is, assuming that the later positions are present in nuce in the earlier or that they were an inevitable outcome. Although the Descartes of the Regulae has set out on the way of ideas, it is not by the way of doubting, a via negativa, but by the via positiva of knowing. Although he understands intellect to be as different from body as blood is from bone (AT X 415), this is not yet the basis of a truly dualistic metaphysics. Although the intellect is what knows in the proper sense, the activity of pure intellect that he describes in Rules 13 and 14 is only a momentary step back from the imaginative realm, and nowhere does he state or even suggest that dealing with problems involving perfectly intellectual or spiritual natures is substantially different from dealing with other natures, especially since there are similarities and analogies that he is willing to countenance between the spirit and the body.

The second part of the twofold answer about the incorporeal has to do with what we have learned about intellect's acting on its own. It acts proximately and for the most part in conjunction with phantasia. It can abstract from phantasia, but then it risks error; what it can truthfully achieve in prescinding from the corporeal is an awareness of its own way of attending to and grasping the corporeal. When it truthfully judges that "extension is not body," it is not attending to the corporeal ideas but rather to its way of attending to ideas, and in this sense such a judgment is still related to the corporeal; it is a potential involvement with the corporeal rather than an actual involvement. For example, intellect would not truthfully be judging

that extension is not body if it made such a judgment having never experienced the extended realm or not recalling what kind of experience the judgment is about.

But then it is clear that intellect can attend to its own activity with images (what Descartes refers to as its reflex contemplation of itself; AT X 422-423): its knowing, not knowing, doubting, willing, to name the four that Descartes explicitly mentions (AT X 419). Most of this attention to self will be related to, if not about, activity in the body (which includes sensation, imagination, and locomotion). The question then becomes: is it possible for intellect to attend to itself in complete abstraction from the body and imagination? For the Meditations, the answer would seem to be a decisive yes,^[37] but the answer for the Regulae is less clear-cut. It is evident that there is a "depth dimension" to intellect attending to itself, for the case of Socrates, who by doubting that he knows anything comes to know that he doubts, implies that there is an intrication of natures in the purely intellectual realm (AT X 421). Even more suggestive are Descartes's assertions that I can know that because I exist, God exists and that because I understand, I have a mind distinct from body (AT X 421-422). They lead us to suspect that Descartes had already worked out the arguments of the Meditations. Yet important elements are missing. The argument for God's existence requires a distinction between the formal and objective reality of ideas, of which there is no trace in the Regulae , and the Meditations' radical distinction of thinking and extension is present in the Regulae in at most attentuated form. Since God as the foundation of our personal being is a very old theme in Christian thought—not to mention the contrast of body and soul—with a particularly pertinent form of it in the arguments of Augustine,^[38] the notion that our existence implies God's is not in itself distinctive or remarkable. If the method of the Regulae is any indication, Descartes probably thought that such truths were potentially evident by intu-itus. By not confronting the questions of existence the Regulae prescinds from these matters, and it leaves open where, how, and at what level natures are implicated in one another.

Descartes justifies Rule 14's lengthy discussion of intellectual and imaginative approaches to extension by expressing his fear that it is not sufficiently long to prevent people from falling into error, "so preoccupied are the ingenia of mortals" (AT X 446). The practitioners of geometry and arithmetic ordinarily think they are dealing with numbers abstracted from all subjects, lines that have no width, surfaces that have no depth, and so on, all things that he has shown to be false. Rather than go on with such a critique, he turns in the rules that follow to a positive account of how objects should be conceived, that is, imagined.

[37] Chapter 7 will give us some reasons to be less certain of this, however.

[38] For example, in book l0 of the Confessions.

The method of the Regulae is calculated to explicate how we can understand things through the aspects they display. It is a rationalization of the coherentist psychology of resemblance characteristic of his earliest thought. But it is also the beginning of the reification as natures of the aspects under which things appear. What a nature is, is ambiguous: it is an aspect, a way of taking a thing, but it is also ontologically ambiguous and appears to take on an increasingly independent existence. The evolution of the natures doctrine did not have solely ontological consequences, of course, for "natures" is also the answer to the question, "What is (most) knowable?" As the natures underwent a change in conception, so too did the faculties of imagining and knowing.

H. THINKING IMAGINATION BEYOND THE REGULAE

Thinking, as the young Descartes conceived it, was an activity, one that was constantly challenged to respond to the changing deliverances of the sensitive faculties. (Consider, for example, the Compendium musicae's dynamic, imaginative way of conceiving a song out of the individual notes.) In the Regulae this activity was conceived as having two major cognitive forms, intuitus and deductio. Discursive reasoning is described many times as a movement of cogitation, once even as a movement of imagination. Since neither intuitus nor simple deductio can be taught, the rules were designed to call attention to them and how they might be practiced and honed and to regulate those activities of cogitation requiring a complex movement of thought from one thing to another.

Intuitus might seem to be perfectly passive, but in fact it is defined as a grasping-beholding by a pure and attentive mind. The mind and its object must be purified and prepared, attention must be carefully directed, and the mind must take hold of its object. Because of this activity Descartes did not need to make the distinction of the Fourth Meditation between the intellect that perceives ideas (without assent or dissent) and the will that makes judgments. The mind or, more significant because of the implications of its name, the vis cognoscens, knowing force, brings a significant component of will into knowing and implicitly makes it more activity than receptivity.

The vis cognoscens can act on its own, but the greatest part of its activity is in and through phantasia. Accordingly, the model for knowing that the Regulae presents is a thinking through images: the distinct and easy grasp of the aspects they present, and the knowing power wending its way among images—noting, comparing, forming, and transforming them—in order to arrive at the truth of any question.

In the accounts of cogitation and imagination given in the Meditations, there is a difference of no little significance. Although imagination is men-

tioned as part of thinking in the Second Meditation, in the Sixth it is excluded from the essence of the thinking thing; and in the Third Meditation thinking is apparently transformed from the active grasping, comparing, and moving of thoughts into the more passive perception of ideas that are in oneself or one's mind innately. One perceives ideas, one has them. Imagination itself thereby becomes just another way of having ideas. Imagining is simply contemplating the shape or image of a corporeal thing (AT VII 28); when the mind imagines it turns toward its associated human body and looks at something in the body that conforms to an idea understood by the mind or perceived by the senses (AT VII 73). Rule 12 had defined imagination as an activity, as the application of the vis cognoscens to the phantasia in order to form new figures. Where has the activity of thinking and imagining gone?

As we shall see in the following chapters, the activity of thinking (and the activity of imagining) did not disappear in the later Descartes but was obscured by the static implications of thinking and imagining understood as the perceiving of ideas. In depicting these activities the later Descartes's vocabulary displaces a psychology of faculties with a unitary power (the mind) standing opposite and viewing a relatively fixed object. This new psychology nevertheless falsifies the genuine logic of the Meditations, which, as the long philosophical and theological tradition of meditation would lead one to expect, requires a highly active, discursive process of thinking through which one is able to perceive certain unities and finally arrive at a contemplative state.

The vocabulary and psychology of the Regulae are closer to the truth than the Meditations. Yet one must also concede that the psychological logic of the Regulae, with its division of the act of discursive knowing into parts, favored the reduction of knowing to the simple mental having of elemental ideas, and by undermining memory the Regulae left the way open to a static intellectualism devoid of concreteness. This, I contend, was contrary to Descartes's deepest intentions, whether we look to 1628 or 1641.

The having and manipulating of images becomes, in the later Descartes, a source of uncertainty. In important respects the later philosophy deprives imagination of cognitive force. Yet in the later Descartes the very activity of meditating is modeled on imaginative discursiveness, and imagination retains cognitive relevance precisely as a dynamic, productive activity. This occurs first and foremost in his mathematics and physics, beginning with Le Monde . So it is to Le Monde that we turn in order to begin locating the traces of imagination in the later Descartes.