Chapter Four—
Symbols—An Analysis
The preceding chapter has brought us to a crucial juncture in assessing the merits of the Computational Theory of Mind. The criticisms raised by Searle and Sayre point to some potentially serious problems for computationalism. But the exact nature and force of the problems cannot be judged without first undertaking an analysis of the notion of symbol, which figures prominently both in the claims made by computationalists and in the criticisms leveled by their opponents. In particular, we must ask what it is to be a symbol and how symbols may be said to have syntactic and semantic properties. This chapter will present answers to these questions, and will offer a rich set of terminology for talking about symbols, syntax, and semantics.
The terminology makes two important kinds of distinctions. First, the ordinary usage of the word 'symbol' as a sortal term is ambiguous. Sometimes the word is used precisely to denote utterances or inscriptions that have semantic interpretations—things that syrnbolize something. But in other contexts the word is used to denote things which do not have semantic properties: there are purely formal symbol games, for example, in which the tokens have syntactic but not semantic properties, and there are even symbols such as letters on eyecharts which have neither syntactic nor semantic properties. To distinguish these different senses of the word 'symbol', three sortal terms will be developed. The term 'marker' will be used to capture the road usage of 'symbol' which includes letters on eyecharts. To be a marker is just to be a token of a conventional type, and does not have any necessary semantic or syntactic consequences. The
term 'signifier' will be used to denote markers that have semantic interpretations. An object is a signifier just insofar as it is a token of a marker type which has an interpretation. The term 'counter' will be used to pick out markers on the basis of their syntactic features within some language game. To be a counter is to be a token of a marker type which has a particular set of conventionally determined syntactic properties in a particular language game.
The terminology developed in this chapter will also reflect a second, and equally important, distinction. For there are several different senses in which an object may be said to be a marker, a counter, or a signifier. For example, if we say that a marker token "has an interpretation," we might mean one of four things: (1) that there is a linguistic convention that associates the marker's type with that interpretation, (2) that the author of the marker meant it to have that interpretation, (3) that someone who apprehended the marker took it to have that interpretation, or merely (4) that there is an interpretation scheme available in principle that associates that marker's type with that interpretation. The terminology developed in this chapter disambiguates expressions like 'is a signifier' or 'has semantic properties' by offering different locutional schemas for each of the four legs of the ambiguity. In the four cases above, for example, the marker token would be said, respectively, to be (1) interpretable (under convention C) as signifying X , (2) intended (by its author S) as signifying X , (3) interpreted (by some Y) as signifying X , and (4) interpretable-in-principle as signifying X . These locutions point to four modalities under which an object may be said to have properties dependent upon conventions or intentions, and these modalities also apply to the sortals 'marker' and 'counter', as well as 'signifier', in ways that will be made clearer in the course of the chapter. The result is a terminology that reflects four different ways in which an object may be said to be a marker (a symbol in the barest sense), four ways a marker may be said to take on syntactic properties, and four ways it may be said to take on semantic properties. The remainder of this chapter will be devoted to a more detailed development of these distinctions.
4.1—
Symbols: Semantics, Syntax, and Tokening a Type
It should come as no surprise that the word 'symbol' is used in widely differing ways by writers with different research interests. When a linguist studying the development of the set of graphemic characters used
to represent English words speaks of the graphemes as "symbols," he will very likely mean something different from what a Jungian psychologist means when he expresses an interest in finding out what "symbols" are important to a patient. But even if we restrict our attention to the linguistic notion of symbol that is relevant to the analysis of natural, technical, and computer languages, there are still ambiguities that need to be unraveled.
First, the word 'symbol' is sometimes used precisely to indicate objects that symbolize something else. An object is a symbol in this sense just in case it has a semantic interpretation . This usage of the word 'symbol' is found quite frequently in discussions of computation and the philosophy of mind. Fodor, for example, uses the word 'symbol' in this way in the introduction to RePresentations, where he repeatedly glosses the word 'symbol' with the phrase "semantically interpreted object[s]" (Fodor 1981: 22, 23, 30) and claims that the objects of propositional attitudes "are symbols . . . and that this fact accounts for their intensionality and semanticity" (ibid., 24). Haugeland likewise uses the word 'symbol' in this way when he writes, "Sometimes we say that the tokens in a certain formal system mean something—that is, they are 'signs,' or 'symbols,' or 'expressions' which 'stand for,' or 'represent,' or 'say' something" (Haugeland 1981: 21-22).
But not all writers who discuss the tokens employed in formal systems follow Haugeland's practice of applying the word 'symbol' only to objects having semantic interpretations. Pylyshyn, for example, distinguishes between "a system of formal symbols (data structures, expressions)" and a scheme of interpretation "for interpreting these symbols" (Pylyshyn 1984: 116). Here Pylyshyn uses the word 'symbol' in a way which clearly and explicitly does not have semantic overtones, since the "symbols" of which he speaks are purely "formal" and are only imbued with meaning through the additional imposition of a scheme of interpretation. Logicians interested in formal systems likewise use the word 'symbol' to denote the characters and expressions employed in those systems, even though by definition semantics falls outside of the purview of formal systems.
Such a practice is also justified by ordinary usage: it is quite acceptable, for example, to use the word 'symbol' to refer to graphemic characters such as letters, numerals, punctuation marks, and even to such characters as those employed in musical notation. To merit the application of this use of the word 'symbol', an object need not have any semantic interpretation. For example, individual letters employed in
inscriptions in a natural language seldom have semantic values, and yet there is nothing strange about referring to them individually as symbols.
Here it might seem tempting to follow Haugeland's terminological practice and to contrast "symbols" (things with interpretations) with "formal tokens"—or, alternatively, to join Pylyshyn in using the expression 'formal symbols' when referring to such entities as character strings without reference to their semantic properties. But to do so would be to risk running afoul of a further distinction. For the word 'formal' has weaker and stronger uses. In its weaker use, it means "not semantic"; in its stronger use, it means "syntactic." This distinction is important because entities such as letters and phonemes fall into types quite independently of their syntactic properties . The same set of letter types, for example, is employed in the written forms of most of the European languages, and the same letters take on different syntactic properties in different languages. Now if letter types were determined by the syntactic positions that their tokens could occupy in a symbol game, then symbol games with different syntactic rules would, by definition, have to be construed as employing different symbol types. For example, given that the spelling rules of English and French allow different combinations of letters to occur, one would have to say that English and French employ different letters. But surely such a conclusion would be misguided: there is good reason to say that written French and written English employ the same symbol types (i.e., the same letter types), but that symbols of the same types take on different syntactic properties when used in inscriptions in different languages. It is surely more natural, for example, to say that the letter y can stand alone as a word in French but not in English than to say that French and English have distinct symbol types which happen to look alike, just because the English y can occur only within a larger word while the French y can occur alone. Or, to take a different example, it seems natural to say that base-2 notation and base-10 notation both employ the numerals zero and one, even though those numerals take on different combinatorial properties in the two systems. (This is trivially true, since the digits 0 and 1 can be combined in base-10 notation with digits that are not employed in base-2 notation.)
We thus stand in need of three separate sortal terms to play the different roles played by the ordinary term 'symbol'. First, we need a term that designates objects like letters and numerals quite apart from any considerations about what syntactic or semantic properties they might take on in a particular context. Second, we need a term that designates objects just insofar as they are assigned a semantic interpretation. Finally,
we need a term that designates objects just insofar as they are of a particular syntactic type.
4.2—
Markers, Signifiers, Counters
I propose to use three existing words in new and technical ways in order to supply the necessary sortal terms. I propose to use the word 'marker' to replace the term 'symbol' in its broadest sense, the usage that can be applied to letters and numerals and carries no syntactic or semantic connotations. There are marker types (e.g., the letter P ) and marker tokens (a particular inscription of the letter P ). Marker types such as letter types and numeral types are a particular class of conventionally established types. And so an object is a marker token just insofar as it is a token of such a conventional type . Sometimes markers are used in such a fashion that they carry semantic values. The complex marker type 'dog', for example, has a conventional interpretation in English, but does not have one in French. Insofar as an object is a marker that carries a semantic value, it will be called a signifier . Finally, markers can be employed in symbol games in such a fashion that they have syntactic properties. The lower-case letters, for example, take on no syntactic properties when they are used on an eyechart, but take on one set of syntactic properties when used as proposition letters in the propositional calculus, and take on a different set of syntactic properties when used as variable letters in the predicate calculus. The syntactic rules of a symbol game serve to partition the markers employed in that game according to the syntactic positions they can occupy. These syntactic types will be called counter types, and a marker will be said to be a counter just insofar as it takes on syntactic properties within a symbol game .
These three sortal terms—'marker', 'signifier', and 'counter'—will play a significant role in the discussion of the nature of symbols and symbolic representation that is to follow. Although this book does not undertake to develop a thoroughgoing semiotics, it will prove helpful to undertake a brief discussion of each of these three terms.
4.3—
Markers
The first and most basic of the three sortal terms is 'marker'. Thus far the development of the term 'marker' has consisted of the citation of a few paradigm examples (letters, numerals, characters employed in musical notation) and a negative claim to the effect that being a marker has
nothing to do with syntax or semantics. To come to a better understanding of markers, it will be useful to employ a thought experiment.
4.3.1—
The "Text from Tanganyika" Experiment
Suppose that the noted Victorian-age explorer and linguist Sir Richard Francis Burton, while traversing central Africa in search of the source of the Nile, comes upon a lost city. There he finds a clay tablet on which there are inscriptions of unknown origin and meaning. One line of the script reads as follows:
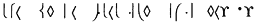
What assumptions can Burton reasonably make about the inscription? First, he can probably proceed upon the assumption that what he has come upon is an inscription in a written language, which he dubs "Tanganyikan." He can assume that, like other written languages, Tanganyikan will employ symbols, that it will have a syntactic structure, and that at least some of the symbols will be used meaningfully. At this point, however, he most emphatically does not know what any of the symbols mean. Nor does he even know what symbolic units are meaningful . What he encounters may be a phonetically based script like that used in written English, in which case few if any of the individual characters will be meaningful. On the other hand, it might be an ideographic notation like that employed in written Chinese, in which case individual ideogram types are correlated with specific interpretations. Or it might be like Egyptian or Coptic script, in which characters can function as ideograms in some contexts and function as indications of phonemes in others. (If English were to be represented in a similar way, for example, we might have a character
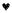
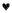
Now there is a great deal that Burton can do without an interpretation scheme for this writing. Notably, he can begin by making a list of the atomic characters employed, and on the basis of this he can do such things as compare them with characters used in other African languages to see if Tanganyikan may be related to any of these. For example, if the writing found at Timbuktu contains a character
and that Tanganyikan is related to Timbuktuni. And he can do all of this without knowing anything about the syntax or semantics of Tanganyikan. Indeed, even if it turns out that what he has found are a child's handwriting exercises or an ancient eyechart—in which case what he sees does not have either syntactic structure or semantic interpretation—his conclusions about the character type need not be imperiled. And the reason for this is that the characters themselves can be understood as falling into types quite independently of the linguistic uses to which they are put.
Once Burton has made this observation, he begins to realize that it is not only atomic graphemic character types that can be studied apart from their syntactic and semantic properties. On the one hand, strings of characters that function together can be treated as a single unit, and hence Burton can make some guesses about what sequences of characters make up words.[1] On the other hand, graphemic characters are not the only tokens whose membership in a type can be understood apart from syntax and semantics. The very same kind of analysis can be applied to nonvisual units, such as phonemes, Morse code units, or ASCII units in computer storage locations. If, for example, Burton had a tape recording of someone speaking Tanganyikan, he might undertake a very similar analysis of the phonemes employed in the language, even without knowing where the breaks between words fall or what anything in the language means. Or, if he were in a position to intercept an electronically transmitted message such as a transmission in Morse code, he might be able to figure out the basic units (e.g., dots and dashes) and how they were instantiated in a telegraph wire or through modulations of radio waves. In light of these realizations, of course, he would come to realize that he could no longer employ the term 'character' to cover all of the relevant cases, and would be in search of a suitably neutral term: for example, the term 'marker.'
4.3.2—
What Is Essential to the Notion of a Marker?
If 'marker' is to serve as a generic term for phonemes, graphemes, units of Morse code, and other such entities, it is worth asking just what is involved in being an entity of one of these kinds. And the best way of answering is by making a series of observations.
(1) Markers are tokens of types . The type-token distinction is applicable to all markers—to letters, numerals, Morse code units, ASCII code units, phonemes, and so on.
(2) Marker types are conventional . To say that a graphite squiggle on
a sheet of paper is a letter P is to say that it is a token of a particular type that is employed by particular linguistic communities. To say that it is a rho is to say that it is a token of a different particular type employed by a different community. And to claim that a particular squiggle is a P is not the same thing as to claim that it is a rho, even if it is the case that an object has the right shape to count as a P if and only if it has the right shape to count as a rho. This is because the claim that the squiggle is a P (or a rho) makes reference to more than the shape of the object: it makes reference to specific conventions of a specific linguistic community as well. Likewise, the claim that the squiggle is a P (or a rho) is not equivalent to a claim about its shape—for example, that it is composed of a vertical line on the left and a half-oval attached to the right side of the upper half of the line.
When I say that marker types are conventional, what I mean is merely that marker types are established by the beliefs and practices of language users. In particular, I wish to emphasize that marker types are not natural kinds . To be sure, sounds and squiggles may also fall into natural kinds on the basis of physical patterns present in them, such as their waveforms or their shapes: a sound wave is a sine wave at 440 kHz just because of its physical characteristics, and an inscribed rectangle is a rectangle just because of the distribution of graphite on paper. But when we say that an object is a marker—for example, an inscription of the letter P or an utterance of the word 'woodchuck'—we are not picking it out just by its sound or its shape, but by the way it fits into established linguistic practices in some community of language users. To determine what marker types an object falls into, we need to know more than what patterns are present in the object: we need to know what marker types there are as well, and what kinds of objects can count as tokens of those types. And to answer those questions, we need to know what linguistic communities there are and what shared understandings and practices members of those communities have about using sounds and inscriptions communicatively. An object can only be a P-token if there is a letter type P , and there can only be a letter type P if there is some community of language users who have a set of shared beliefs and practices to the effect that there is a marker type whose tokens are shaped in certain ways and may be employed in certain activities. So when I say that marker types are conventional, I mean that the existence of the type is determined by the beliefs and practices of language users.
(3) The conventions that establish marker types involve criteria gov -
erning what can count as tokens of those types . So while the assertion that a squiggle is a rho involves more than claims about its shape, it does entail things about the shape of the squiggle as well. The letter type rho is established by the conventions employed by writers of Greek, but part of what is involved in those conventions is a set of criteria governing what a squiggle has to look like in order to count as a rho.
(4) The criteria governing what can count as a token of a marker type pick out a set of (physically instantiable) patterns such that objects having those patterns are suitable to count as tokens of that type . In the case of letters, numerals, and other graphemes, the patterns are two-dimensional visible spatial patterns. In the case of phonemes, they are acoustic patterns distinguishable by the human auditory system. In the case of Morse code and computer data storage they are abstract patterns made up, respectively, of dots and dashes or binary units which can be instantiated in various ways in different media. One can also have complex marker types that are formed from arrangements of simple marker types: written words, for example, are complex markers composed of sequences of atomic markers (letters).
(5) The criteria for a marker type may be flexible and open-ended, and need not be subject to formulation in terms of a rule . This is clearest in the case of graphemic symbols. As Douglas Hofstadter (1985) has argued, letter types seem to permit an indefinite number of stylistic variations. A reader who has not foreseen these can nonetheless quickly recognize them as such when presented with them. It is by no means clear that one could provide a rule (e.g., in the form of a computer program) that could, for example, distinguish all of those patterns that a person could recognize as stylistic variants of the letter P from those patterns which a person would not recognize as such.
(6) Marker types are often found in groups or clusters that are employed in the same symbol games . Thus we speak of different sets of graphemic characters such as "the letters," "the numbers," "the punctuation symbols," and so on.
(7) Criteria for marker types may overlap, both within groups and across groups . Thus the same squiggles that count as letter o's can count as zeroes and omicrons as well. And indeed, as anyone who has had trouble reading another person's handwriting knows, handwritten letters are often interpretable in a number of different ways.
(8) Language users possess a repertoire of marker types, which can be used in various ways . Mathematicians, for example, are in the busi-
ness of developing new symbol games. In doing so, they commonly employ existing marker types such as letters and numerals whose origins may be traced to various linguistic communities. Mathematicians use existing marker types, but put them to new uses in new symbol games. Similarly, one can use one's knowledge of phonemes and the rules for combining them into words in one's language in order to coin a new word if one is needed.
(9) Marker types can be added to or deleted from an individual's repertoire . That is, a person can learn marker types and also forget them.
(10) Marker types can be added or deleted from the repertoire of a linguistic group . New words (complex markers) are coined, new atomic markers are invented (as in the case of the integration sign used in the calculus or the missionary St. Cyril's invention of the Cyrillic alphabet) and imported (as in the case of Europe's adoption of the Arabic numerals). Markers also disappear from usage. Many of the complex markers (Middle English words) one finds in Chaucer's writings, for example, are no longer in use; and the Old English letter thorn has survived only in the guise of a y on the signs of anglophilic innkeepers.[2]
(11) The boundaries of a "linguistic group" and the extent to which conventions are shared within a group are highly flexible . In the case of natural languages, for example, there are often significant differences in dialect and idiolect which involve differences in the conventions for pronunciation, inscription, and so on. It is not always fully clear when one should say that one is faced with separate linguistic groups and when one is faced with a variety of practices within a single group. Moreover, there may be groups within groups: all topologists may observe certain notational practices, but topologists who work in a particular topological specialty (e.g., surgery theory) may all observe an additional set of practices not shared by other topologists, and an individual mathematician who has developed his own techniques for a particular problem may be the only person employing his new conventions. Similarly, an individual may find the need for a new word in a natural language and may therefore choose a phonetic sequence (a complex marker type) that is not currently used in his language and then employ it as a marker type. The new marker type is conventional in the sense that it is established by a human convention and not simply by a natural pattern, even though the convention that establishes it is not (yet) a convention of English, but merely a convention within some individual's idiolect. (Of course, it can become a convention of English; new words are introduced into languages, and they all start out as someone's idiosyncrasies.)
4.4—
Signifiers
While the conventions that establish marker types function independently of the particular uses to which the markers are put in actual practice, it is nonetheless part of the nature of markers that they can be used meaningfully. So while there is nothing, for example, about the marker type consisting of the sequence of letters d-o-g that binds it to a particular meaning, the marker type—just by virtue of being a marker type—is the sort of thing that can be associated with a meaning in such a fashion that its tokens can count as carrying or expressing that meaning. And within a linguistic community—such as the community of English speakers—there are conventions that set up an association between marker types and meanings. When we speak of something as a meaningful word in a natural language such as English, for example, we refer to it as a token of a marker type (be it typified phonetically, graphemically, or both) that is associated with a meaning by English semantic conventions, and we pick it out both by its marker type and by the associated meaning.[3] (Hence we can distinguish between different words with the same spelling but different meanings, and vice versa.) Similarly, when we speak of a written number, we refer to a marker string and to its associated meaning. The marker string 1-1-0-1 can be used in the representation of various numbers: thirteen in base-2 notation, thirty-seven in base-3 notation, and so on. In the technical terminology introduced in this chapter, insofar as an object is a marker that is associated with a meaning, it may be called a signifier .
It will prove useful to think of symbols as things that can be examined at several different levels of analysis . Thus the inscription
dog
can be seen at several levels. First, it can be examined at what might be called the "marker level," at which it is a sequence of letters from the Roman alphabet, and also a complex marker employed in English. The atomic marker types are established by the conventions of a linguistic community, and the complex type is licensed for use in English by similar conventions. But the above inscription may also be examined at a second or "signifier level." At the signifier level, the inscription is a token of a signifier type employed in English. That signifier type is established by a linguistic convention that associates a complex marker type with a meaning.
The conventionality of signifier types is again a matter of there being
certain shared understandings and practices within a linguistic community. Individual inscriptions of the word 'dog' mean dog because they are tokens of a particular signifier type employed in English. That signifier type exists by virtue of a convention: in this case, a shared understanding among speakers of English that tokens of the complex marker type d-o-g can be used to express the meaning dog, and a shared practice of using tokens of that complex marker type to express that meaning.
There are thus at least two levels of conventionality involved in being a signifier token. First, anything that is a signifier must also be a marker, and marker types are established by conventions. Second, signifier types are established by conventions that associate marker types with interpretations. The first kind of conventionality appears at the marker level, the second connects the marker level to the signifier level. It is by virtue of marker conventions that objects bearing patterns can count as markers, and it is by virtue of signifier conventions that markers can count as signifiers.
4.5—
Counters
Markers can, of course, take on syntactic as well as semantic properties. But like semantic properties, syntactic properties are extrinsic to the marker type. That is, there is nothing about the marker type P that implies anything about the syntactic properties of P -tokens. P 's can be used in symbol games without syntactic rules—for example, on eyecharts. They can also be used in games that have syntactic rules, such as written English, written French, algebraic topology, and predicate logic. Just what syntactic properties a P -token can take on depends on what symbol game it is used in, what syntactic categories are involved in that symbol game, and which syntactic slots can be occupied by P -tokens.
Now all of this implies that there is more to syntax than marker order—that the syntactic properties of a marker token are intimately connected with the role it plays in larger linguistic activities, and are not just a matter of the marker's combinatorial properties. One could, of course, use the word 'syntax' so broadly as to include all arrangements of markers—or, indeed, to include all arrangements of objects, since all objects can, in principle, serve as markers. But the word 'syntax' has some paradigm uses in which it is applied to specifically linguistic structures, and there is arguably a great deal about linguistic structure that falls under the rubric of syntax that goes beyond combinatorial features. There is, for example, a sense in which we should say that a sentence has a syn-
tactic structure while the order found in other entities (e.g., the sequence of cars in a traffic jam, the sequence of philosophy courses taken by an undergraduate major) is not plausibly regarded as syntactic.
Let us briefly inquire as to how the syntactic structure of a string of markers is dependent upon the symbol game in which it is employed. Consider, for example, the marker string
Fad
What is the syntactic structure of this sequence of markers? The answer depends entirely upon the symbol game that is operative. If the letters appear on a line of an eyechart, one would be inclined to say that the string of markers has no syntactic structure: there is an order to the markers, to be sure, but it is not a syntactic order. But if the markers make up the English word 'fad' with a capitalized f , the story is quite different. It has both internal syntactic structure, since spelling rules can plausibly be called "syntactic" (even if spelling is not the kind of syntax that comes most quickly to mind). It also has external or relational syntactic properties, since the word 'fad' is of a grammatical type that can occupy certain slots in English sentence structure, but not others. For example, sentence (1) is grammatically permissible in English, while sentence (2) is not:
(1) The hula hoop was a fad.
(2) * The hula hoop fad was.
The string F-a-d could also be used as an expression in the predicate calculus, with F being a predicate letter and a and d its arguments. Here once again the string would have both internal and relational syntactic properties, but very different ones from the previous case. The difference, of course, lies in the fact that the same marker string can be used in several different language games, but those games have different syntactic rules, and the role that the markers play in the different games is correspondingly different. Moreover, the kinds of syntactic categories in terms of which one can analyze a marker string are closely related to kinds of symbol games. Natural languages have nouns, verbs, adjectives, and so on. Some natural languages also have syntactic features that others do not: articles, plural suffixes, case indicators, privative prefixes, and so on. (Greek has all of these features; Chinese has none of them.) Technical languages may have very different categories: predicate logic, for example, has no nouns or verbs but does have quantifiers, predicate letters,
variable letters, and connectives, while the propositional calculus has only sentence letters and connectives.
When we are interested precisely in the syntactic role that a marker or marker string plays in a particular symbol game, it is useful to be able to refer to it precisely as an object of a type distinguished by its syntactic role in that symbol game (as a predicate letter, for example, or as a count noun). Each symbol game has some set of syntactic categories. (It may be the empty set, as in the case of the eyechart.) These are established by the conventions governing the symbol game—that is, the set of beliefs and practices, shared by those who have mastered the game, that govern how symbols may be combined within the game. These conventions also govern what markers and marker strings can be employed in the symbol game, and which syntactic slots they may occupy.
Sometimes, as in the case of the predicate calculus or the Fortran programming language, the stock of markers is set up from the very beginning to fall into categories such that one can tell from the marker type itself what syntactic roles it can play. In the predicate calculus, capital letters can be predicate letters but not variables, while lower-case letters can be variables but not predicate letters. In Fortran, variables with names beginning with the letter i can only store integer values, while variables with names beginning with the letter n can only store floating-point values. But other symbol games are more complicated. In English, the marker string h-o-u-s-e can be used either as a verb or as a noun, and one cannot tell just from the string of symbols which it will be in a given instance. The language has conventions establishing both 'house' the noun and 'house' the verb; and there is no reason that the marker string could not be used as an adjective as well. Likewise, in the computer language Pascal, virtually any string of ASCII characters can be used as a the name for a variable that can store any kind of value. One simply has to specify elsewhere what kind of variable it is, and that will have consequences for its syntactic properties. (A variable that stores a boolean value, for example, cannot appear immediately before a slash indicating division.)
The word 'counter', as it is being developed here, will be used to indicate a marker as it takes on particular syntactic properties in a specific language game. Thus, for example, 'house' the noun and 'house' the verb are of separate counter types; for while they employ the same marker string, they have different syntactic properties in English. When we are attending specifically to syntax, we may say that we are working at the counter level. Like the marker and signifier levels, the counter level has
its uses. Notably, the study of formal systems, for example, takes place almost exclusively at the counter level, since it brackets semantics and treats differences in what markers are employed as "notational variants." Likewise, much of computer science is devoted to work at the counter level.
4.6—
The Relationship of the Marker, Signifier, and Counter Levels
Since marker types are independent of the syntactic and semantic properties that their tokens can take on in different symbol games, while counter and signifier types presuppose the existence of marker types, there is a hierarchic relationship between the marker level and the signifier and counter levels. Analyzing a complex of sounds or squiggles as counters presupposes dividing them into markers, and so both the counter and signifier levels are dependent upon the marker level.
There is not, however, any absolute dependence between the counter and signifier levels. One can, for example, assign interpretations to marker types without situating them within a syntactically structured symbol game, and one can concoct "purely formal systems" for which there is no interpretation scheme. This does not mean, however, that syntax and semantics are absolutely independent, either. The semantic values of some marker complexes, such as sentences, are dependent upon the syntactic structure of the complexes as well as the interpretations of the signifying terms. Such structures are subject to compositional analysis . But there is no absolute dependence of either the counter or the signifier level upon the other in the way that both are dependent upon the marker level.
The marker level is similarly related to lower levels of analysis. An entity's ability to count as a marker, after all, depends not only upon conventions but upon the fact that it bears a physically instantiated pattern satisfying the criterion for its type. One might see such patterns as abstract physical features that are literally present in objects, and one might thus speak of a "pattern level" which is connected to the marker level above it by marker conventions and to other physical descriptions below it by various kinds of abstraction. These abstractions bracket those features of an object that are not relevant to its having a pattern, rendering it suitable to count as a token of a marker type. We might represent the resulting structure of levels of analysis graphically as in Figure 5, with the nodes representing the objects appearing at a level and the arrows
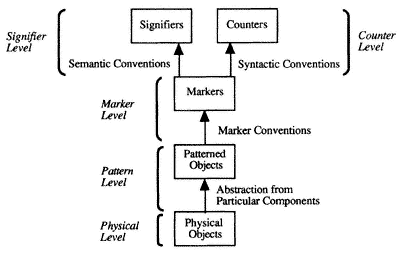
Figure 5
between nodes representing what relates the objects appearing at one level to those appearing at the next.
Now it is important to note that the sortal terms 'marker', 'signifier', and 'counter' designate conventional rather than natural kinds, and that they can pick out the same objects under different aspects. Indeed, any object that is a signifier or a counter must also be a marker, and objects that are markers may very well be signifiers and counters as well. The need for the sortal terms arises not because there are three mutually exclusive classes of particulars, but because there are different sorts of questions about symbols that call for classifications based on different features. (There are, for example, questions about orthography, syntax, and semantics.) The distinction between markers, signifiers, and counters is also useful for discussing certain aspects of language, such as ambiguity, homonymy, homophony, and certain kinds of performance errors. One kind of ambiguity occurs, for example, when one has marker strings that admit of multiple semantic interpretations. Homonymy occurs when a single graphemic marker string is associated by different signifier conventions with two or more meanings. Homophony occurs when a single auditory marker string is associated with multiple meanings. Performance errors such as slips of the tongue, malapropisms, and spoonerisms are ways of producing a marker token that is not compatible with the semantic interpretation that one intended one's utterance to have.
The different sortal terms also license different kinds of inferences about the objects they pick out. From the fact that an object is a counter in some language game, it follows that it is a marker and that it has syntactic properties. Nothing follows, however, about whether it has semantic properties. Similarly, if an object is a signifier, it follows that it is a marker and that it has semantic properties; but nothing follows about whether it is used in a syntactically structured symbol game. And from the fact that an object is a marker, nothing follows about whether it has either syntactic or semantic properties.
4.7—
Four Modalities of Conventional Being
This concludes the first part of the disambiguation of the notion of symbol —the separation of 'symbol' into three separate sortal terms. But there is also a need for a second disambiguation, a disambiguation of the senses in which a thing can be said to "be" a symbol. And the ambiguity that is of concern here is reflected in the technical terms 'marker', 'signifier', and 'counter', as well as the original term 'symbol'. I intend to present a case that, because each of these categories is convention-dependent, there are four ways in which an object can be said to be a token of one of the types, corresponding to four ways it can be related to human conventions and intentions. Once again, the distinctions are best motivated by a series of thought experiments.
4.7.1—
Case 1—The Optometrist
A man named Jones goes to an optometrist for an eye examination. The examination involves a test which requires the patient to look through a device containing a number of movable lenses. The device is pointed at an eyechart, and is so positioned that just one character on the chart can be seen through the eyepiece. The examination begins with the device being pointed at the single character on the uppermost line of the chart, in this case a letter P . Jones looks into the eyepiece and sees the following image:
P
The optometrist asks Jones, "What letter do you see?" Jones responds, "The letter P ." For purposes of this example, assume that Jones has correctly identified the character. One of the things that Jones has accomplished is the successful identification of a physical particular as a token
of a particular conventionally sanctioned marker type. To do this, Jones need not impute any syntactic or semantic properties to the marker token he sees. Indeed, if the doctor were to ask Jones "What does that symbol mean?" or "What is its truth value?" or "What are its syntactic properties?" Jones would likely perceive the questions as very queer indeed. Letters on eyecharts simply do not have syntactic or semantic properties. Moreover, it would be possible for Jones to learn to identify the symbol correctly even if he had never used the Roman letters in the representation of meaningful discourse, much as he might learn to distinguish Chinese ideograms without learning their meanings or the syntactic rules for Chinese—and even without learning that the ideograms were used by the Chinese as a form of writing. Even with such a poverty of competence with written language, Jones could still be said to have recognized and identified what he saw as a token of the type P .
4.7.2—
Case 2—The Bilingual Optometrist
Yet if we adjust the circumstances in the right ways, it quickly becomes more difficult to characterize what Jones has and has not accomplished. Suppose that Jones goes to a second optometrist, Dr. Onassis. Dr. Onassis lives and works in a Greek neighborhood and has a number of clients who speak and read only Greek, and so he has two sets of eyecharts—one with Greek letters, one with English letters. When Jones looks through the eyepiece of Dr. Onassis's instrument, he sees the following pattern:
P
Dr. Onassis asks Jones, "What letter do you see?" And Jones responds, "The letter P ." At this, however, Dr. Onassis casts Jones a very puzzled look. He then looks at the eyechart and laughs. "Oh, I see," he says. "I made a mistake, and put up the Greek eyechart instead of the English one, and then I was puzzled, because the English chart begins with the letter Q and does not even contain a letter P . What you see, by the way, isn't a P but a rho."
This example differs from the first in that our natural intuitions about what Jones has and has not accomplished no longer serve us as well as they did in the first case. Indeed, they may tend to lead people towards two opposite extremes. To continue the story: Jones, upon being told that what he is looking at is not a P at all, becomes quite indignant. "Of course it's a P ," he says. "I know what a P looks like, and I can see this one as
plain as day, and it's a P if ever I've seen one!" This, however, is taken by the doctor as a challenge to his professional competence. "Look here," he says, "I made this chart myself, so I know darned well what the letters are. I made it for my Greek patients, and meant this symbol to be a rho, so a rho is what it is!"
Jones and the doctor are each partially correct in their claims, and each is partially mistaken as well. The most important thing to see, however, is that they are both making the implicit assumption that there is just one univocal meaning to the locutional schema 'is a P ' (or 'is a rho'), while in fact there are several ways a particular may be said to be a token of a conventional type. The necessary distinctions are easily missed, however, because the same English locution can be used to express each of the several ways. Yet the distinctions may be formulated out of fairly ordinary English locutions, and are easily mastered if one attends to the nature of the situation rather than the form of the ordinary locutions.
4.7.3—
Interpretability
First, consider Jones's line of reasoning: Jones is a competent user of the letters employed in the representation of English. (Here they will be called "the Roman letters.") The pattern he sees meets the spatial criteria for counting as a token of the marker type P . Under the conventions governing the Roman letters, the pattern Jones sees can count as a P , and cannot count as a token of any of the other marker types which form the set of Roman letters. There is thus a sense of "being a P " which does apply to the mark on the eyechart.
Notice, however, that the exposition of how the character Jones sees can be said to be a P has required an appeal to several things in addition to the mark and the marker type—notably, it has required an appeal to (a ) a community which employs a certain set of marker types which includes P , and (b ) conventions within that community which govern what can count as a token of that marker type. The sense of "being a P " that is operative here, then, turns out to be more complex than is suggested by the locution used to express it. To put it differently, the predicate indicated by this usage of the locutional schema 'is a P ' is more complex than one might assume. To spell out entirely the sense in which Jones might be right in saying that what he sees is a P , one would have to say something like the following: "This mark t has a pattern pi which is a member of the set P of patterns suitable for tokening the marker type T employed by linguistic community L ."
We may capture and codify this sense of "being a symbol" by coining the technical expression 'is interpretable as a token of type T ' (e.g., 'is interpretable as a rho'). The rules for the application of this predicate may be articulated as follows:
(M1) An object X may be said to be interpretable as a token of marker type T iff
(1) there is some linguistic community L which employs marker type T ,
(2) the conventions in L which govern what can count as a token of type T allow any object having any pattern piÎP :{p1 , . . . , p n } to be suitable to count as a token of type T ,
(3) X has a pattern p j , and
(4) pjÎp .
This sense of "being a P " points to a relationship between (1) a physical particular, (2) a pattern present in that particular, (3) a convention linking that pattern to a marker type, and (4) a linguistic community using that marker type and employing that convention. An object X related in such a fashion to a marker type T will be said to be interpretable as a (marker) token of type T (under convention C) (for linguistic group L) . The parentheses are used here to separate a short form of the new technical term—'interpretable as a token of type T '—from its complete form. In many cases it will prove unnecessary to allude specifically to a convention or a linguistic group, and so the shortened locution 'interpretable as a token of type T ' can purchase some measure of simplicity with little cost in terms of exactitude. The items in parentheses, however, are not optional —any claim that a physical pattern is interpretable as a token of a marker type involves at least implicit reference to a convention and to a linguistic community, even if these are not specified.
It is, of course, quite possible for a single object X to be interpretable as a token of a number of different marker types {T 1, . . . , Tn }. In each of the optometrist examples, the object Jones sees is interpretable under the conventions for Roman letters as a P and interpretable under the conventions for Greek letters as a rho. It may be subject to interpretation as a token of other marker types as well. There is no inconsistency in saying that a mark is interpretable as a token of a variety of different types. Such illusion of an inconsistency as there may be is quickly dispelled if one looks at the long way of describing interpretability. If one says "X
is interpretable as a token of type T " and "X is interpretable as a token of type U ," the long versions of the two statements will always reveal additional differences which will explain how it is that X is multiply interpretable. These will be differences in what linguistic community's conventions are involved (as in the case of the bilingual optometrist), or differences in the particular conventions of a single community which are operative in the different cases (as in the case of the numeral zero and the letter o in our community), or differences in what pattern in each particular mark is relevant to its interpretability as a marker of that type.[4]
4.7.4—
Intentional Tokening and Authoring Intentions
If Jones has something of a point, the doctor does as well. The doctor's line of argument is that he drew the eyechart himself, and as a consequence he is in a special position to say what the characters are. Indeed, he might go so far as to say that he is in a position to stipulate what they are. The mark on the chart was, after all, made with the intention that it be a token of a particular marker type—in this case that it be a token of the Greek letter rho. There is thus a sense in which it seems right to say that the doctor inscribed a rho. And in this sense it would not be correct to say that he inscribed a P , because he did not intend it to be a P .
Hence, in distinction with the interpretability of a particular object X as a token of type T , one may also develop another technical locution:
(M2) An object X may be said to have been intended (by S) as a token of marker type T iff
(1) there is some linguistic community L that employs marker type T ,
(2) there is a language user S who is a member of L (or is otherwise able to employ the conventions in L governing marker type T ),
(3) S inscribed, uttered, or otherwise "authored" X , and
(4) S intended what he authored to count as a token of type T by virtue of conventions in L governing marker type T .
Several clarifications and caveats are immediately in order. First, the term 'intended' is meant very broadly here. Notably, it need not imply that the author of the mark must have a conscious, linguistically formulated characterization of what he is doing in producing the marker.
When someone writes a sentence without any explicit awareness of making marks with a pen, he would, according to this usage, "intend" his marks to be letters of particular types.[5] This use of 'intend' is also meant to allow a great deal of latitude in how direct a causal chain there is between the intention of the author of the marker and its ultimate production. Notably, it is intended to be broad enough to cover at least some instances of the printing of stored representations of text by a computer. The explanation of how the marks on a printed page—a page of a book, for example—are said to count as letters (and how conglomerations of them are to count as words, sentences, statements, and arguments) will need to appeal in part to the intentions of the author. (It may also need to appeal to the intentions of the various engineers and programmers who designed the hardware, software, and coding schemes which mediate the process which begins with the author's striking keys on a keyboard and ends with the production of a printed page.)
A second clarification which needs to be made is this: the author of a marker token may intend it to be a token of more than one type. Within the story about the bilingual optometrist, one should say that the mark which Jones saw was interpretable as a P and interpretable as a rho, but that it was intended as a rho and not intended as a P . In devising the two scenarios used in this thought experiment, however, the visible pattern that was chosen—namely,
P
—was deliberately chosen precisely for its susceptibility to multiple interpretations. One could devise more complex enterprises which turn upon such ambiguities, such as acrostics which make sense in two languages, or which make sense in one language vertically and another horizontally. (In spoken language, puns might well fall into this category. Take for example the case of Lewis Carroll's "We called him the Tortoise because he taught us, " which works in British but not American English because the expressions 'tortoise' and 'taught us' sound the same in British English, but different in American English.)
From these two clarifications a third emerges—namely, that there is room for some very different ways of intending an utterance or inscription to count as a token of more than one type. Here are a few exampies: (1) In devising the P /rho example, the intention was to find an inscription that could clearly count as a token of either of two marker types which might be presumed to be familiar to those likely to read these pages. (2) In legal, political, and diplomatic enterprises, it is often deemed
prudent to choose what one says or writes so that it has multiple interpretations—in particular, so that it has one natural interpretation that is likely to appeal to the hearer or reader, and another more exacting interpretation which can be offered as what was "really meant" at a later date. (For example, promising "no new taxes" does not, strictly speaking, involve promising that existing taxes will not be raised by 10 percent or even 1000 percent.) This kind of intentional ambiguity is most important on the semantic level, but could occur at the level of marker interpretability as well. (3) A slightly different form of ambiguity is present when what is said or written is intended to be interpretable in more than one way, all of which are intended to be understood by the hearer or reader, who then chooses which leg of the ambiguity to treat as operative. An expression of interest in doing business together in the future, for example, can be treated as an opening move in negotiations to do business or as a mere expression of good will. Properly used and properly understood, such ambiguous expressions can allow two parties to explore one another's interests without risk of "losing face." (This practice is reportedly expected by Japanese in business dealings to a degree seldom appreciated by American businessmen.)
4.7.5—
Actual Interpretation
In addition to the interpretability of a marker token and its intended interpretation, one may identify two additional relationships between a particular marker token and a marker type. The first of these is (actual) interpretation of the figure as a marker of some particular type. In both of the optometrist examples, Jones interprets the figure he sees as a letter of a familiar type—he identifies each as a P -token. One might want to say there is a sense in which he was right in so identifying each (because each is interpretable under English conventions as a P ) or that there is a sense in which he was wrong in his identification of the second figure (because its author intended it to be a rho and did not intend it to be a P ). But neither of these facts alters one fact about what Jones did: namely, he placed an interpretation upon a figure he saw; he interpreted it as or took it to be a P -token.
Once again, the new terminology has hidden references to marker types, conventions governing what can count as tokens of the types, and linguistic communities which use the types. To interpret a figure as a token of type T is to be familiar with marker type T employed by some linguistic community L , which in turn involves understanding (not nec-
essarily perfectly) how to apply the criteria for interpretability as a token of that type (though the "understanding" does not necessarily involve the ability to form or consciously articulate a rule for what can and cannot count as a P , but is better understood as a kind of competence ).
This notion of actual interpretation may once again be expressed by a more technical definition:
(M3) An object X may be said to have been interpreted (by H) as a token of marker type T iff
(1) there is some linguistic community L which employs marker type T ,
(2) there is a language user H who is a member of L (or is otherwise able to employ the conventions in L governing marker type T ),
(3) H saw, heard, or otherwise apprehended X , and
(4) H construed X as a token of type T .
Now it is important to see the distinction between authoring intentions and mere interpretations. For while authoring intentions do, in a sense, involve interpretation, the author of a marker's intention is not "just another interpretation." There is a significant difference between Dr. Onassis's original interpretation of the figure on his eyechart—the one that was involved in its authoring—and Jones's interpretation of it, and this leads to our strong intuition that there is a sense in which the figure "is a rho" and "is not a P ." The difference between intended interpretation, or authoring interpretation, and other interpretations of the same figure also applies to Dr. Onassis's own later interpretations of what he has inscribed. The author of a marker token is certainly likely to be in a unique epistemic position with regard to what the token was meant to be, even long after he has brought it into being, and hence he is usually accorded unique authority in clarifying any ambiguities which might be spotted. But the reason for this is precisely that he is believed to know better than anyone else what he intended to write or utter, and it is what he intended that determines "what it is" in one sense—namely, in the sense captured by the technical locution 'intended to be a token of type T .' (Note, for example, that the author's [current] interpretation of his words and actions is not accorded the same respect if its fidelity to his original intent is in question—if he is a defendant in a libel suit, for example, or if he has suffered a loss of memory.)[6]
4.7.6—
Interpretability-in-Principle
There is one way of "being a symbol" that is yet to be discussed. It is most easily developed for signifiers—and will be shortly—but can be developed for markers as well, albeit with less intuitive appeal. Again let us perform a thought experiment. Assume that there is a sandstone cliff in the Grand Canyon that bears certain dark patterns against a lighter background. Let us assume, moreover, that there are no actual orthographic conventions, past or present, by virtue of which these patterns would be interpretable as marker tokens. The patterns are not now interpretable as marker tokens. But consider the future. It could be the case that some future culture will develop an orthography whose conventions will be such that the patterns on the sandstone cliff would then be interpretable as markers in that orthography. It could even be that members of that culture would naturally perceive the cliff as bearing a meaningful message in their language. Let us call this scenario "Future A ." Now of course it could also be the case that such a culture will not arise—that it will never be the case that there is a culture anywhere that will employ conventions by virtue of which the patterns on the cliff face would be rendered interpretable as marker tokens. Call this scenario "Future B ."
Now it would seem to make some sense to say that the patterns on the cliff face are already suitable to count as markers, given the existence of the right sorts of conventions. It seems right to say that, if only the right sorts of conventions were adopted—for example, the conventions that are eventually adopted in Future A but not in Future B —those patterns would then be interpretable as markers. To put it slightly differently, we might say that, while those patterns are not in fact interpretable (under any actual conventions) as markers, they are nonetheless interpretable-in-principle as markers under conventions that could be (or could have been) adopted, and their being so interpretable-in-principle is independent of which future—A or B —actually comes about.
This notion of interpretability-in-principle can be developed more exactly as follows:
(M4) An object X may be said to be interpretable-in-principle as a token of a marker type T iff
(1) a linguistic community could, in principle, employ conventions governing a marker type T such that any object having any pattern piÎP :{p1 , . . . , pn } would be suitable to count as a token of type T ,
(2) X has a pattern p j , and
(3) pjÎp .
That is, for any object X one might consider, if X has some pattern that could, in principle, be used as the criterion for a marker type, then X is interpretable-in-principle as a marker. (One could, for example, establish a convention whereby spherical objects could count as markers of a particular type, and hence globes, oranges, and planets are interpretable-in-principle as markers.)
Now it should be immediately evident that this notion of interpretability-in-principle is extremely permissive. For while the range of patterns that human beings can easily employ for marker types is rather limited, and the range of patterns they do in fact employ is more limited still, this is more a consequence of the nature of our bodies than of the nature of markers. The patterns we use for markers are chosen for the ease with which we can perceive and implement them. Thus until very recently marker types were confined largely to those distinguished by patterns that could be easily seen or heard. With the aid of instruments, however, humans can deal with markers that are distinguished by patterns of voltage levels in a wire or across a field of circuits, or by patterns of magnetic activity, or by various other kinds of patterns. And there is no reason why a being with very different powers and senses could not use very different sorts of things as markers. (To take an extreme example: an all-powerful God might use configurations of stars as criteria for marker types employed in storing messages for very large angels, and use patterns of electron activity in a single atom as criteria for marker types used to send messages to very small angels.) As a consequence, it would seem that everything whatsoever is interpretable-in-principle as a marker token.
4.7.7—
The Four Modalities
The expression 'is a marker' has been replaced by four locutional schemas that have been given technical definitions:
—'is interpretable (under convention C of linguistic group L ) as a marker of type M '
—'was intended (by its author S ) as a marker of type M '
—'was interpreted (by some H ) as a marker of type M '
—'is interpretable-in-principle as a marker'
To these four locutional schemas correspond what might be called four modalities of conventional being, or four ways in which an object can be related to a conventionally established type (though in the case of interpretability-in-principle, the conventions and the type need not be actual). These four modalities can be applied not only to markers, but to other conventionally established types as well, as we shall see presently. These locutional schemes, moreover, are intended to capture and distinguish four different senses in which one might speak of an object "being" a marker (e.g., a letter or a Morse code dot) or "being" of one of the other conventionally established types. These different senses are, to some extent, already operative in ordinary and technical uses of the word 'symbol', but existing terminology is not subtle enough to distinguish the different senses.
4.8—
Four Ways of Being a Signifier
Just as it is important to distinguish four senses of "being a marker," it is likewise important to distinguish four different senses in which a marker may be said to "have" or "bear" semantic properties, and hence four ways in which a marker may be said to be a signifier. In order to clarify these four senses, we shall employ another thought experiment. The great detective Sherlock Holmes has been called in to solve a murder case. The victim, a wealthy but unpleasant lawyer, has been poisoned. Before dying, however, he managed to write a single word on a piece of paper. The inscription is
PAIN
Inspector Lestrade of Scotland Yard has concluded that the deceased was merely expressing the excruciating agony that preceded his death. Holmes, however, makes further investigations and discovers that the victim's French housekeeper is also his sole heir. It occurs to Holmes that 'pain' is the French word for bread, and upon inquiring he discovers that the housekeeper did indeed do the baking for the household. Perhaps, reasons Holmes, the deceased was poisoned by way of the bread, and has tried to indicate both the means by which the poison was conveyed and the identity of his murderess by writing the French word for bread.
Which was inscribed on the dead lawyer's stationery—the English word 'pain' (meaning a particular kind of sensation) or the French word 'pain' (meaning bread)? To put it differently, what does the inscription mean —pain or bread? It should immediately be evident that this ques-
tion is very much like the question about the figure on the bilingual optometrist's eyechart. First, there is a sense in which what is on the paper is interpretable (under English conventions) as meaning pain . In this very same sense the mark on the paper is interpretable (under French conventions) as meaning bread . That is, the sequence of Roman letters on the stationery is used by English speakers to carry one meaning and used by French speakers to carry a different meaning.
Yet there is also a sense in which the inscription can be said to mean one thing and not the other, provided that one assumes that the victim intended what he wrote to mean one thing rather than the other. If Holmes's hypothesis is correct, for example, the lawyer meant to write the French word for bread and did not mean to write the English word for pain. Assuming that this was the case, there is a sense in which the inscription can be said to mean bread but not to mean pain.
This distinction between two ways a marker token can be related to a meaning should seem familiar, as it parallels the first two ways an object could be said to "be" a marker token—namely, interpretability and intended (or authoring ) interpretation .
(S1) An object X may be said to be interpretable as signifying (meaning, referring to) Y iff
(1) X is interpretable as a marker of some type T employed by linguistic group L , and
(2) there is a convention among members of L that markers of type T may be used to signify (mean, refer to) Y .
(S2) An object X may be said to be intended (by S) to signify (mean, refer to) Y iff
(1) X was produced by some language user S ,
(2) S intended X to be a marker of some type T ,
(3) S believed that there are conventions whereby T -tokens may be used to signify Y, and
(4) S intended X to signify Y by virtue of being a T -token.
Two observations should perhaps be noted about these definitions. First, neither of them is intended to correspond precisely to what is meant by the vernacular usage of the words 'meaning' or 'reference'. Indeed, the whole enterprise of specifying new terms such as these is necessary only because ordinary usage is ambiguous and imprecise. In as-
suming that the inscription meant pain, Lestrade was probably (implicitly) assuming both that the inscription was interpretable under English conventions as carrying the meaning pain and that the deceased had intended the inscription to mean pain. But his assumption would be implicit in that he has probably never made the distinction under discussion. It is only when someone like Holmes notices that the ordinary assumptions do not always hold that distinctions can be made, and at such a point it is of little interest to the specialist (be he detective or philosopher) to argue about whether interpretability or authoring intention or the combination of the two best captures the "real" (i.e., the vernacular, precritical) use of the term 'meaning' (or 'reference'). It is the new, more refined terms that are needed. The determination of vernacular usage may be left to the descriptive linguist.
Yet there is most definitely no intention here to imply that ordinary usage is irrelevant in the pursuit of philosophy. Attention to ordinary usage can often be of great help in solving philosophical problems, especially when those problems are themselves caused by an impoverished understanding of language on the part of the philosopher. The point here is that language points to the phenomena to be studied, and sometimes it points too vaguely and indistinctly to serve the purposes of the theorist. When this happens, terminology must be refined to capture distinctions the specialist needs but the ordinary person does not. The enterprise is far more risky when the process proceeds in the opposite direction—that is, when ordinary terms are extended instead of refined . The application of the terms 'symbol' and 'representation' to the contents of intentional states is a case in point. (This entire book is an examination of what has gone wrong in the extension of such ordinary terms as 'symbol' and 'representation'.)
The second observation about these definitions is that the definition of authoring intention allows for the possibility that the speaker is wildly idiosyncratic in his use of language. If, for example, Jones believes that the word 'cat' is used to refer to newspapers, and utters "The cat is on the mat" to express the belief that the newspaper is on the mat, we may nonetheless say that Jones intended to signify the newspaper. In particular, he uttered a token of the marker type 'cat', which he believed could be used to signify newspapers, and intended to signify the newspaper by uttering the word 'cat'. Of course, there is no convention of English that allows the word 'cat' to be used to signify newspapers. (Utterances of 'cat' are not interpretable, under English conventions, as signifying newspapers.) But Jones nonetheless intended to refer to the newspaper by
uttering the word 'cat'. And of course there could be subgroups of English speakers who employ semantic conventions that are not conventions of English, but only of a dialect of English (as, for example, some Baltimoreans refer to street vendors as "Arabs" [pronounced ay -rabz], or Bostonians refer to submarine sandwiches as "grinders"). And indeed one might even wish to speak of idiolects in terms of the special semantic conventions of a linguistic subgroup consisting of one member, in which case Jones correctly believes that there is a convention licensing the use of 'cat' to refer to newspapers, but incorrectly believes that it is a convention of English rather than of his own idiolect. One might wish to use the term 'convention' in such a case because there are beliefs and practices that can govern how a marker may be used. These beliefs and practices are, in principle, public and shareable, even though in fact only one person possesses them. (Because they are essentially public, and the fact that they are possessed by only one person is merely incidental, Wittgenstein's concerns about a private language do not arise here.)
Third, it should be noted that the semantic features to which these definitions are relevant are meaning and reference. The truth value of a signifier is undetermined by the relationships between the token, linguistic conventions, and the intentions of its speaker or inscriber. (There are some exceptions, such as analytic truths, but here the interest is in a general characterization of ways objects can be said to have semantic properties.)
In addition to interpretability (under conventions employed by some linguistic group) and intended interpretation, one may distinguish two additional ways in which a thing may be said to carry a semantic value. These correspond to the two remaining ways that a figure could be said to count as a marker token: namely, actual interpretation (by someone apprehending the signifier) and interpretability-in-principle . Regardless of what the deceased lawyer intended his inscription to mean, it is nonetheless the case that it was interpreted by Lestrade as meaning pain and interpreted by Holmes as meaning bread. These actual acrs of interpretation are, indeed, independent of whether the lawyer intended his inscription to mean anything at all —they would be unaltered if, for example, he had been scribbling random letters. The notion of actual interpretation may be defined for signifiers as follows:
(S3) An object X may be said to have been interpreted (by H) as signifying (meaning, referring to) Y iff
(1) some language user H apprehended Y ,
(2) H interpreted X as a token of some marker type T ,
(3) H believed there to be a linguistic convention C licensing the use of T -tokens to signify Y , and
(4) H construed X as signifying Y by virtue of being a T -token.
Finally, it is notorious that any symbol structure (i.e., any marker, simple or complex) can be used to bear any semantic interpretation whatsoever. Haugeland, for example, writes of a set of numerical inscriptions he supplies as examples in Mind Design that "formally, these numerals and signs are just neutral marks (tokens), and many other (unfamiliar) interpretations are possible (as if the outputs were in a code)" (Haugeland 1981: 25). And Pylyshyn writes of symbols in computers,
Even when it is difficult to think of a coherent interpretation different from the one the programmer had in mind, such alternatives are, in principle, always possible. (There is an exotic result in model theory, the Lowenheim-Skolem theorem, which guarantees that such programs can always be coherently interpreted as referring to integers and to arithmetic relations over them.) (Pylyshyn 1984: 44)
In the terminology developed in this chapter, what this means is that there is nothing about markers that places intrinsic limits upon what interpretations they may be assigned, and so it is possible for there to be conventions which assign any interpretation one likes to any marker type one likes. Now there are two different ways in which we might wish to formulate this insight. One way of formulating it would be to say that, for any marker type T and any interpretation Y , it is possible for there to be a semantic convention to the effect that Y -tokens are interpretable as signifying T . In terms of a technical definition:
(S4) An object X may be said to be interpretable-in-principle as signifying Y iff
(1) X is interpretable-in-principle as a token of some marker type T, and
(2) there could be a linguistic community L that employed a linguistic convention C such that T -tokens would be interpretable as signifying Y under convention C .
That is, to say of some X and some Y that "X is interpretable-in-principle as signifying Y " is to say (1) that one could, in principle, have a marker convention whereby X would be interpretable as a marker of some type
T , and (2) that one could, in principle, have a semantic convention C whereby T -tokens would be interpretable as signifying Y .
One might, however, wish to characterize semantic interpretabilityin-principle in a different manner. All that is necessary for an object X to be interpretable-in-principle as signifying Y is the availability of an interpretation scheme that maps X 's marker type onto Y . And all that this requires is that X be interpretable-in-principle as a marker, and that there be a mapping available from a set of marker types to a set of interpretations that takes X 's marker type onto Y . In terms of a technical definition:
(S4* ) An object X may be said to be interpretable-in-principle as signifying Y iff
(1) X is interpretable-in-principle as a token of some marker type T ,
(2) there is a mapping M available from a set of marker types including T to a set of interpretations including Y , and
(3) M(T) = Y .
Definitions (S4) and (S4* ) are extensionally equivalent for real and counterfactual cases. Under either definition, for any object X and any interpretation Y that one might specify,[7]X is interpretable-in-principle as signifying Y . First, we have already seen that every object is interpretable-in-principle as a marker token of some type T . Now, according to definition (S4), all that is additionally necessary for X to be interpretable-in-principle as signifying Y is that one could, in principle, have a convention licensing T -tokens as signifying Y . But one could, in principle, have such a convention for any type T and any Y . Similarly, according to definition (S4* ), what is necessary for X to be interpretable-in-principle as signifying Y (over and above X 's being interpretable-in-principle as a marker of some type T ) is the availability of a mapping M from marker types to interpretations such that Y is the image of T under M . Such a mapping is merely an abstract relation between two sets, however, and there is such a mapping, for any type T and any Y , that maps T onto Y . So both (S4) and (S4* ) license the conclusion that every object is interpretable-in-principle as signifying anything whatsoever. This conclusion may seem bland in and of itself, but it is important to distinguish this sense of "having a meaning" or "having a referent" from
other, more robust senses. It is all the more important to do so since computationalists seem at times to be interested in this sort of "having a meaning," but do not always make it adequately clear what role (if any) it plays in their accounts of semantics and intentionality for cognitive states.
4.9—
Four Modalities for Counters
The four conventional modalities are also applicable to counters. Returning to the optometrist examples, suppose that the optometrist's instrument is adjusted so that Jones can see more than one symbol at a time. Suppose, moreover, that what he sees is the following image:
p & q
Jones has just come from his logic class, and so, when asked what he sees, says "p and q ." The optometrist, however, is ignorant of the conventions of logic. To him, this is just a line of three characters: the letter p , an ampersand, and the letter q . As the doctor sees it, the symbols on the eyechart are not related to one another syntactically, because the "eyechart game" does not bare any syntactic rules .
Once again, both Jones and the doctor are partially right, and in much the same ways they were each partially right in the original examples. Jones has a point in that the figures he sees are interpretable as markers of familiar types (and are in this case intended to be of the types that Jones guesses), and he is furthermore right in seeing that they are arranged in a fashion that is interpretable, under the conventions he has been taught for the propositional calculus, as having a certain syntactic form in the propositional calculus. Yet the optometrist has a point as well: the chart at which Jones is looking was designed as an eyechart. (We may, if we like, assume once again that the doctor drew the chart himself, and knows quite well what he meant to draw.) It was not intended to contain formulas in the notation employed in propositional logic, and the fact that some symbols in the eyechart are interpretable as forming such a formula is quite accidental. Similarly, if a diagonal sequence of letters should be interpretable as a sentence in Martian, that fact would be quite accidental. When the author of the eyechart drew it, Martian language played no role in his activity, and neither did the propositional calculus. To use terminology developed earlier, syntactic relationships did not form part of the authoring intention with which the

Figure 6
chart was created, and so the symbols in question would not rightly be said to have been intended to have a particular syntactic form.
It is, of course, possible that someone should devise an eyechart or some other display of symbols with more than one symbol game in mind. Someone who believed in subliminal suggestion, for example, might devise a display of symbols so that parts of it were interpretable under standard English conventions in a fashion that was not supposed to be consciously recognized by the reader. Thus a greedy optometrist might try to sell extra pairs of glasses by designing his eyechart like that shown in figure 6. In this case, the figures on the chart can be interpreted in two ways: (1) as characters on an eyechart, and (2) as letters forming English words that make up the sentence "Buy an extra pair now." As they are employed in the "eyechart game," the markers on the display do not enter into syntactic relationships, because syntactic relationships are always relative to a system with syntactic rules, and the "eyechart game" has no syntactic rules. As markers used in the formation of an English sentence token, however, they are counters having syntactic properties, because the English language does have syntactic rules. In this example, moreover, the markers on the chart are not only (a ) interpretable as syntactically unstructured tokens in the eyechart game and (b ) interpretable as syntactically structured tokens in a written English sentence, they are also (c ) intended as syntactically unstructured tokens in the eyechart game and (d ) intended as syntactically structured tokens in a written English sentence. Both "games" are intended by the author of the chart in this case—unlike the earlier case, in which the optometrist did not intend the line of symbols p-&-q to count as a formula structured by the rules of propositional logic, even though the line of symbols was nonetheless interpretable as such.
In that example, moreover, the line of symbols was also interpreted (by Jones) as a formula in propositional calculus notation, and was interpreted in such a fashion that Jones imputed to it a certain syntactic structure that is provided for by propositional logic. This interpretation is not affected in the least by the fact that the eyechart was not designed with it in mind, or even by the fact that the author of the chart was unfamiliar with propositional logic. Finally, as in the case of markers and signifiers, there is infinite latitude in the ways a display of markers could, in principle, be interpreted as counters of various sorts, because any given marker type can be employed in an indefinite number of systems characterizable by syntactic rules. For any arrangement of markers, one could, as Haugeland says, "imagine any number of (strange and boring) games in which they would be perfectly legal moves" (Haugeland 1981: 25).
It is now possible to provide definitions for the four ways of being a counter. These definitions will not be employed directly in the argumentation that follows, but are provided for the sake of exactitude and balance in the development of semiotic terminology. They may safely be skimmed over by the reader who is not interested in the definitions for their own sake, but only in their contribution to the main line of argument.
(C1) An object X may be said to be interpretable as a counter of type C iff
(1) X is interpretable as a marker of type T ,
(2) the marker type T is employed in some language game G practiced by a linguistic community L ,
(3) G is subject to syntactic analysis,
(4) there is a class C of markers employed in G sharing some set F of syntactic properties, and
(5) the conventions of G are such that tokens of type T fall under class C .
(C2) An object X may be said to be intended (by S) as a counter of type C iff
(1) there is a language user S who is able to apply the conventions of a language game G ,
(2) the marker type T is employed in G ,
(3) G is subject to syntactic analysis,
(4) there is a class C of markers employed in G sharing some set F of syntactic properties,
(5) the conventions of G are such that tokens of type T fall under class C ,
(6) S intended X to be a marker of type T ,
(7) S intended X to count as a move in an instance of language game G , and
(8) S intended X to fall under class C .
(C3) An object X may be said to be interpreted (by H) as a counter of type C iff
(1) some language user H apprehended X ,
(2) H interpreted X as a token of type T ,
(3) H is able to apply the conventions of language game G ,
(4) the marker type T is employed in G ,
(5) G is subject to syntactic analysis,
(6) there is a class C of markers employed in G sharing some set F of syntactic properties,
(7) the conventions of G are such that tokens of type T fall under class C ,
(8) H interpreted X as counting as a move in an instance of G , and
(9) H interpreted X as falling under class C in game G .
(C4) An object X may be said to be interpretable-in-principle as a counter of type C iff
(1) X is interpretable-in-principle as a token of marker type T ,
(2) there could be a language game G employing markers of type T ,
(3) that game G would be subject to syntactic analysis,
(4) these conventions would be such that there would be a class C of markers employed in G sharing some set F of syntactic properties, and
(5) the conventions of G would be such that tokens of type T would fall under class C .
4.10—
The Nature and Scope of This Semiotic Analysis
The preceding sections of this chapter have been devoted to the development of an analysis of symbols and their semantic and syntactic properties. In the ensuing chapters this analysis will be applied towards an assessment of CTM's claims about the nature of cognition. Before proceeding to that assessment, however, it is important to clarify the nature and status of the semiotic analysis that has been presented here.
The new terminology is intended to resolve perilous ambiguities in the uses of (a ) the word 'symbol' and (b ) expressions used to predicate semantic and syntactic properties of symbols (for example, 'refers to', 'means', 'is a count noun'). For purposes of careful semiotic analysis, the technical terms are meant to replace the ordinary locutions rather than to supplement them. Thus the sortal terms 'marker', 'signifier', and 'counter' do not name different species of symbol, nor do they signify different objects than those designated by the word 'symbol'. Rather, these terms serve collectively as a disambiguation of the word 'symbol' as it is applied to discursive signs, and each sortal term is designed to correspond to one usage of the word 'symbol'.
Similarly, the modalities of interpretability (under a convention), authoring intention, actual interpretation, and interpretability-in-principle have been referred to as "ways of being" a marker, signifier, or counter. But this does not mean that there is such a thing as just being a marker, signifier, or counter, and—over and above that—additional properties of being interpretable as one, being intended as one, and so on. For there is no such thing as simply being a symbol. Symbol is not a natural but a conventional kind, and to say that something "is a symbol" (a marker) is to relate it in some way to the conventions that establish marker types.
But there are several ways in which an object can be related to such conventions: it can be interpretable as a token of a type by virtue of meeting the criteria for that type, it can be intended by its author as being of that type, it can be interpreted as being of that type, or it can simply be such that one could have a convention that would establish a type such that this object would be interpretable as a token of that type. The case is much the same for semantics and syntax: there is no such thing as a marker simply being meaningful or simply referring to an object. To say that a marker has a meaning, or that it refers to something, is to say something about interpretation and interpretive conventions. We can say that
the marker is of such a type that it is interpretable, under English semantic conventions, as referring to Lincoln. We can say that its author intended it to refer to Lincoln, or that someone who apprehended it construed it as referring to Lincoln. And we can say that one could, in principle, have a convention whereby it would be interpretable as referring to Lincoln. But there is no additional question of whether a symbol just plain refers to Lincoln. Expressions such as 'refers to Lincoln', 'is a marker', 'is a P ', or 'is an utterance of the word dog ' are ambiguous. The process of disambiguation consists of substituting the four expressions, 'is interpretable as', 'was intended as', 'was interpreted as', and 'is interpretable-in-principle as' for 'is'.
So, for example, if someone asks of an inscription, "What kind of symbol is that?" we should proceed by supplying four kinds of information: (1) We should provide a specification of how it is interpretable as a marker token by virtue of meeting the criteria for various marker types. For example, we might point out that it is interpretable under English conventions as a P or under Greek conventions as a rho. (2) If the mark was in fact inscribed by someone, we should say what kind of marker it was intended to be: for example, that it was intended as a P , or that it was intended as a rho, or that it was intended precisely to meet the criteria for both P and rho. (3) If someone has interpreted the inscription as a marker token, we should say who did the interpreting and what they took it to be. We might say, for example, that Jones took the symbol to be a P , while Mrs. Mavrophilipos took it to be a rho. (4) We should point to the fact that such a mark might be used in all kinds of ways—namely, that one could, for example, develop new marker conventions whereby that mark might count as a token of some new type.
Similarly, if someone asks what an inscription means, a full response would involve the following: (1) A list of the meanings that the inscription could be used to bear under the semantic conventions of various linguistic groups. (For example, English speakers use the marker string p-a-i-n to mean pain while French speakers use it to mean bread.) (2) A specification of what the author of the inscription intended it to mean. (The deceased lawyer in the thought experiment, for example, might have used it to mean bread, while I, the author of the example, intended precisely that it be interpretable as meaning either bread or pain.) (3) A specification of how anyone who apprehended the symbol interpreted it. (For example, Lestrade took it to mean pain and Holmes took it to mean bread.) (4) A reference to the fact that one could, in principle, use markers of that type to refer to anything whatsoever.
And similarly for counters, if one were to inquire as to the syntactic properties of an inscription such as 'p & q', a complete answer would require four kinds of information: (1) A list of ways that string could be interpreted as bearing a syntactic structure in different symbol games. (It could be a series of syntactically unrelated markers on an eyechart, for example, or a conjunction in the sentential calculus.) (2) A specification of how the inscription was intended by its author. (For example, the optometrist intended those markers as items on an eyechart, and did not intend them to bear any syntactic relation to one another.) (3) A specification of how such persons as apprehended the symbols took them to be syntactically arranged. (Say, Jones took them to constitute a propositional calculus formula of the form 'p and q', while Mrs. Mavrophilipos took them to just be individual letters.) Finally, (4) an allusion to the fact that one could devise any number of symbol games with quite a variety of syntactic structures such that this inscription would be interpretable as being of the syntactic types licensed by the rules of those games.
Now there are other uses of the term 'symbol'—for example, those employed in Jungian psychology and cultural anthropology. Similarly, there are other senses in which a marker might be said to "mean something." Holmes's companion Dr. Watson might, for example, inquire of Holmes, "What does the deceased attorney's inscription mean?" and Holmes might reply, "What it means, Watson, is that the housekeeper is a murderess." In this case, Watson's query, "What does it mean?" amounts to asking "What conclusions about this case can we draw from it?" and Holmes's answer supplies the relevant conclusion.
Yet it is important to emphasize that there is no general sense of "being a symbol" or "meaning such-and-such" over and above those captured by our technical terms. For suppose that someone were to ask what the first mark on the eyechart was, and we told him about how it was interpretable under various conventions, how it was intended by the doctor who drew it, how it was interpreted by various people who saw it, and pointed out, finally, that one could develop all sorts of conventions that could apply to marks with that shape. Suppose, however, that our questioner was not satisfied with this, but insisted upon asking for more. Suppose he said, "I don't want to hear what conventional types it meets the criteria for, or how it was intended, or how anyone construed it, or how it could, in principle, be interpreted. I just want to know what kind of symbol it is ." Suppose that it was clear from the way that he spoke that he thought that there was just some kind of brute fact about
an object that consisted in its being a marker of a particular type, quite apart from how it met the criteria for conventionally sanctioned types, how it was intended, and so on. How would we construe such a question?
There are, I think, two basic possibilities. The first is that the questioner is just confused, and does not realize that the relevant uses of the expression 'is a symbol' have effectively been replaced by our technical terminology. If this is the case, he would seem to be suffering from a misunderstanding of what is meant when we say that something is a rho, or a P , or a token of some other marker type. He is much like the person who misunderstands the use of the word 'healthy' when it is applied to food and demands of us that we tell him what "makes vitamin C healthy" without telling him how it contributes to the health of a body.
The second possibility is that the questioner has some special use of the expression 'is a symbol' in mind. He might, for example, be asking for an answer cast in the vocabulary of some particular psychological or anthropological tradition. (We might, for example, respond to a query about something on the wall of an Irish church in the following fashion: "This is the Celtic cross, a fine example of syncretic symbolism. In it one finds the Christian cross, the symbol of salvation through the death of Christ, cojoined with the Druidic circle, symbolizing the sun, the source of life and light.") Or he might have some more novel use of words in mind. He might, for example, just use the word 'symbol' in a way that did not make appeals to conventions. Allen Newell, for example, apparently identifies symbols with the physical patterns that distinguish them. Newell writes, "A physical symbols system is a set of entities, called symbols, which are physical patterns that can occur as components of another type of entity called an expression (or symbol structure)" (Newell and Simon [1975] 1981: 40, emphasis added). In another place, Newell (1986: 33) speaks of symbols systems as involving a physical medium and writes that "the symbols are patterns in that medium."
I shall discuss the proper interpretation of Newell's usage at length in chapter 5, but the basic point I wish to make may be summarized as follows: In characterizing symbols in this way, Newell is using the word 'symbol' differently from the way it is normally used in English, not unlike the way someone might just use the word 'healthy' to mean "full of vitamins." (By the same token, one could use the word 'symbol' to designate all and only objects that have odors pleasing to dogs. Why one should wish to abuse a perfectly good word in such a fashion, however, is quite another matter.) This kind of idiosyncratic use of words may be confusing, but it need not be pernicious so long as the writer (a ) does
not draw inferences that are based upon a confusion between his idiosyncratic usage of the word and its normal meaning (e.g., inferring that food that is healthyv [i.e., full of vitamins] must be healthy [i.e., conducive to health]), and (b ) makes his own usage of the word adequately clear that his readers are not drawn into such faulty inferences. Thus there is nothing troublesome about using the word 'charm' to denote a property of quarks because (a ) physicists have an independent specification of the meaning of 'charm' as applied to quarks, and (b ) no one is likely to mistakenly infer that quarks would be pleasant guests at a soirée.
Similarly, it is possible to use words such as 'means' and 'refers to' in novel ways. One could, for example, become so enamored of causal theories of reference that one began to use sentences like "The word 'dog' refers to dogs" to mean something like "Tokens of 'dog' stand in causal relation R to dogs." This would, of course, be an enterprise involving linguistic novelty: the locutional schema 'refers to' is not generally used by English speakers to report causal relationships per se. But the idiosyncratic usage of the locutional schema might be an efficient way of expressing something that is important and for which there is no more elegant means of expression. So long as the writer makes his usage of words clear and does not make illicit inferences based on nonoperative meanings of words, his idiosyncrasy need not be construed as being pernicious. But if, for example, someone uses 'refers to' to mean "is larger than," he cannot draw an inference like that below from (A) to (B) just by virtue of the meanings of the sentences
(A) The title 'Great Emancipator' refers to Abraham Lincoln.
(B) Abraham Lincoln is also known as the Great Emancipator.
If one used such a novel definition to try to show that one could derive "X is known as Y " from "X is greater than Y ," one would be arguing fallaciously.
Nor can the inference from (A) to (B) be drawn by virtue of the meanings of the sentences if one just defines 'refers to' in causal terms. That is, if one uses (A) to mean "Tokens of 'Great Emancipator' stand in causal relation R to Abraham Lincoln," one cannot infer from (A) that Abraham Lincoln is also known as the Great Emancipator. One might, however, be able to infer (B) from the conjunction of the two claims (A* ): "Tokens of 'Great Emancipator' stand in causal relation R to Lincoln" and (C): "For every signifier token M and every object N , if M stands in causal relation R to N , then M refers (in the ordinary sense) to N ." But
(A* ) and (C) jointly entail (B) only because (A* ) and (C) jointly entail (A), and (A) entails (B). (A* ) alone does not entail (A), however, even if there is a causal relation R that always in fact holds between signifiers and their referents.
4.11—
The Form of Ascriptions of Intentional and Semantic Properties
One of the motivations for undertaking this analysis of symbols was an objection to CTM that was suggested in chapter 3. This objection, called the Conceptual Dependence Objection, involved two important claims about ascriptions of semantic and intentional properties. The first claim was that terms used in ascriptions of semantic and intentional properties are ambiguous: ascriptions of semantic and intentional properties to symbols and ascriptions of semantic and intentional properties to mental states have different logical forms and indeed involve attributions of different properties. The second claim was that ascriptions of semantic and intentional properties to symbols are conceptually dependent upon attributions of cognitive states. In Aristotelian terms, the homonymy of semantic and intentional terms is an example of homonymy pros hen, and the focal meaning of the terms is that which applies to cognitive states. These claims were offered only provisionally in chapter 3, however, and a major reason for undertaking this analysis of the nature of symbols was to provide resources for investigating the claims.
I shall argue in the next chapter that the analysis that has been offered here bears out both claims. For present purposes, I shall confine myself to commenting on the logical form of ascriptions of semiotic properties to symbols. We have discovered that the surface form of ascriptions of semantic values and intentionality to symbols is misleading. When we say, for example, "(Inscription) I refers to X ," it looks as though the verb phrase 'refers to' expresses a two-place predicate with arguments I and X . This way of reading the sentence, however, is wrong in two respects. First, the locutional schema 'refers to' is ambiguous, and may be used to express four very different propositions. More perspicuous expressions of these propositions are supplied by our technical terminology:
(1) I is interpretable (under convention C of linguistic group L ) as referring to X .
(2) I was intended (by its author A ) to refer to X .
(3) I was interpreted (by some reader R ) as referring to X .
(4) I is interpretable-in-principle as referring to X .
Second, on none of these interpretations does 'refers to' turn out to be a two-place predicate linking a symbol and its referent. The first interpretation, an attribution of semantic interpretability, involves implicit reference to a linguistic community and the semantic conventions of that community. The second interpretation, an attribution of semantic authoring intention, involves implicit reference to the cognitive states (namely, the authoring intentions) of the author of the symbol. The third interpretation, an attribution of actual semantic interpretation, involves implicit reference to the cognitive states of an individual who apprehends I . Finally, if we look at the definition of interpretability-in-principle, we see that the fourth interpretation involves implicit reference as well, either to the availability of a mapping that takes I 's marker type onto an interpretation, or to possible conventions. What has been said of ascriptions of reference may be said of ascriptions of meaning and intentionality as well. In each case, there are four ways of interpreting such ascriptions, and these involve covert reference to intentions and conventions in just the same ways as ascriptions of reference to symbols involve it.
4.12—
Summary
This chapter has developed a set of terminology for dealing with attributions of syntactic and semantic properties to symbols. The terminology involves the disambiguation of the term 'symbol' into three sortal terms—'marker', 'signifier', and 'counter'—and a distinction between four ways in which an object may be said to be a symbol (a marker) and to have syntactic or semantic properties. The analysis has already produced a significant conclusion: once we have rendered ascriptions of semantic properties to markers more perspicuous by employing the terminology that has been developed here, it becomes apparent that the logical forms of these expressions involve complex relations with conventions and intentions.
This analysis provides the basis for an investigation of the claims of CTM. The next chapter will investigate the implications of this analysis for the nature of semantic attributions to minds and to symbols in computers. The one that follows it will examine an objection to the analysis
presented in this chapter and articulate an alternative reading of the semiotic vocabulary as employed by advocates of CTM. Afterwards, we shall examine the implications of this analysis for CTM's representational account of the nature of cognitive states and its attempt to vindicate intentional psychology by claiming that cognitive processes are computations over mental representations.