APPENDIX

Bust of Mary Somerville, by Chantrey, currently located in the library of the Royal Society in London. Somerville died in 1872, at the age of 92, after an active career as a scientific writer. During her lifetime women were not eligible for membership, but the Royal Society did recognize her achievements. In 1832, sixty-four subscribers, headed by the Duke of Sussex, pledged funds to have this bust made and placed in the Royal Society. In 1922, it was decided that in consequence of legislation enacted since the war of 1914–1918 women were eligible for election. The first two women Fellows were elected at the close of the war of 1939–1945. Copyright © The Royal Society. Reproduced by permission.
An English Translation of Sections 1, 2, and 3 of Book One from the First (1687) Edition of Newton's Mathematical Principles of Natural Philosophy
In the first edition of the Principia , Newton advised his readers to concentrate on the first three sections of Book One and then to select topics of interest from Book Three. This advice remained unchanged in the two revised editions published during his lifetime and has guided my selection of text for translation. I have selected the first edition for translation, although it is the third and final edition on which most base their study of Newton's dynamics. I maintain, however, that such a study should begin not with the third edition and its many additions and revisions, but rather with the first edition and its relatively straightforward presentation. In the first edition, Newton clearly explicates his analysis with a single method applied consistently to several problems. Until the reader understands Newton's original method and his unpublished restructuring, Newton's additions to the much revised third edition distract rather than enrich the reader.
This Appendix contains a translation into English of the first three sections of Book One of the first Latin edition of the Principia . The translation of Newton's text from the Latin into English requires the skills of a classical linguist, a mathematician or physicist, and a historian of science; a combination rarely found in one individual. This translation was produced by combining the talents of a classical scholar and a physicist turned historian of science: Mary Ann Rossi and myself. She produced a first draft of a section, which I then read and commented upon, and we both discussed and revised the translation. My challenge was to produce a text that made mathematical and physical sense, and the challenge for her was to produce a text true to the Latin text. When successful, the translation conveys Newton's mathematical and physical intentions while remaining faithful to the Latin. The occasionally awkward language of the translation
must be weighed against the virtue of a translation that is relatively free from the translator's bias.
Nevertheless, a faithful translation does not overcome all obstacles to a clear rendering of Newton's intentions. In Problems 1, 2, and 3 in On Motion , for example, Newton writes corpus gyrat (a body orbits). These same problems appear in the Principia as Propositions 7, 10, and 11 where Newton writes gyretur corpus (let a body be orbited) for the first two and revolvatur corpus (let a body be revolved) for the third. The former ("a body orbits") does not imply an external agent responsible for the motion, while the latter ("let a body be orbited") might be so construed.[1] No supporting evidence suggests, however, that Newton intended this change in the Latin to imply a change in physical doctrine. On the contrary, in Definition 8 Newton states that he considers "forces not physically, but only mathematically. Hence, let the reader beware lest, because of words of this kind [attraction or impulse], they should think either that I am defining . . . a physical cause or reason, or that I am attributing forces truly and physically to centers (which are mathematical points)." Still, Newton is consistent in his revision of the voice of the verb in all three problems while leaving the remainder of the text unchanged. Most translations of this text translate both forms as "a body orbits." Given our self-imposed constraints to follow the Latin text as closely as possible, we have made the distinction. So let the reader beware.[2]
The only liberty taken with the Latin original was to modify the format of the text in order to clarify each part of a proposition. For example, in the solution of the Kepler problem in Proposition 11, the description of the diagram is differentiated from the details of the demonstration by separating each into its own paragraph; the paragraph containing the demonstration in turn is separated into a series of logical steps by inserting a number of line breaks; and the conclusion is set forth in yet another paragraph. Newton presents all of the text (description, demonstration, and conclusion) in a single paragraph. I find, however, that there must be room for the eye and the mind to rest if the entire proposition is to be read with ease and so I have introduced the separations.
The following is an English translation, without commentary, of the first three sections of Book One of the 1687 edition of the Principia .[3] Section 1 contains the lemmas that provide a formal defense of the limiting procedures that Newton employs in the sections that follow. Section 2 contains the basic paradigm for the solution of direct problems, and examples of such solutions. Section 3 opens with the solution to the direct problem of elliptical/focal planetary motion (Proposition 11) and concludes with what Newton may have intended as the solution to the inverse problem (Proposition 17). The reader may wish to begin, however, by selecting topics of interest, such as the demonstration of Kepler's law of equal areas in
equal times (Theorem 1 in On Motion and Proposition 1 in the Principia ), or the derivation of the basic paradigm for the solution of direct problems (Theorem 3 in On Motion and Proposition 6 in the Principia ), or perhaps the solution to the Kepler problem (Problem 3 in On Motion and Proposition 11 in the Principia ). The content of these propositions in the 1687 Principia has changed very slightly from their presentation in On Motion , and the reader can refer to the detailed commentaries earlier in this book if questions arise. If there are questions on a lemma or proposition in the Principia , then the reader can use the following list to locate relevant earlier commentaries:
|

Preface to the Reader
Since the Ancients (as Pappus tells us ) regarded Mechanics to be of the greatest [significance ] in the investigation of Natural things, and moderns, having rejected substantial forms and occult qualities, have undertaken to adapt the Phenomena of Nature to Mathematical laws, it seemed good to me to cultivate Mathematics in this Treatise, insofar as it relates to Philosophy. The Ancients really considered Mechanics twofold: as Rational, which proceeds accurately by Demonstrations, and Practical. All the manual arts belong to practical mechanics, from which the name mechanics was taken. But since artificers are not used to laboring with accuracy, it happens that Mechanics as a whole is distinguished from Geometry in this way: anything done accurately is referred to Geometry; anything done less accurately, to mechanics. The errors, however, are not of the art, but of the artificers. The one who works less accurately is a more imperfect mechanic, and the one who can work most accurately, this one would be the most perfect mechanic of all. For the descriptions of straight lines and circles, on which Geometry is founded, belongs to Mechanics. Geometry does not teach the drawing of these lines, but requires it. For it requires that the beginner learn to describe these [lines] accurately before he reaches the threshold of Geometry; then it teaches how problems may be solved through these operations. To describe straight lines and circles are problems, but not geometric ones. The solution of these is required from Mechanics; the use of the solutions is taught in Geometry. And Geometry prides itself that from so few principles brought from without, it accomplishes so many things. Therefore Geometry is founded on mechanical practice and is nothing else than that part of universal Mechanics that proposes and demonstrates the art of measuring accurately. But since the manual arts are chiefly employed in the moving of bodies, it happens that Geometry commonly refers to their magnitude, and Mechanics to their motion. In this sense rational Mechanics will be the science of motions that result from any forces whatso -
ever, and also of the forces required to produce any motions, accurately proposed and demonstrated. This part of Mechanics had been cultivated by the ancients among the five powers pertaining to manual arts, and they considered gravity (since it was not a manual power) hardly other than among the weights to be moved by those powers. But I consider philosophy rather than the arts, and I write concerning not manual, but natural powers, and consider chiefly those things that relate to gravity, levity, elastic force, the resistance of fluids, and similar forces, whether attractive or impulsive; and therefore I offer this work as the mathematical principles of philosophy. For the whole burden of philosophy seems to consist in this: from the phenomena of motions to investigate the forces of nature, and then from these forces to demonstrate the other phenomena; and to this end I directed the general propositions in the first and second books. In the third book I have set forth an example of this subject in the explication of the system of the world. For there, through propositions demonstrated mathematically in the first books, are derived from the celestial phenomena the forces of gravity by which bodies tend toward the sun and the individual planets. Then from these forces, through additional mathematical propositions, are deduced the motions of planets, comets, the moon, and the sea. I wish we could derive other phenomena of nature by the same kind of reasoning from mechanical principles. For I am induced to suspect for many reasons that they may all depend upon certain forces by which the particles of bodies, by some causes so far unknown, are either mutually impelled toward one another and cohere in regular figures, or are repelled and recede from one another. Since these forces are unknown, philosophers have up to now examined nature in vain. But I hope that the principles set down here will shed some light either on this method of philosophy or on some truer method .
The most intelligent and universally erudite Mr. Edmund Halley worked zealously in the publishing of this work. He assisted me not only in correcting the printing errors and preparing the geometrical figures, but he was also the source of my undertaking to publish them. For when he had received from me my demonstrations of the figure of the celestial orbits, he did not desist from urging me to communicate these to the Royal Society, who afterward, by their kind encouragement and requests, led me to think of publishing them. But after I had begun to consider the inequalities of the lunar motions, then I had also undertaken to attempt some other matters relating to the laws and measures of gravity and of other forces: [e.g., ] the figures that would be described by bodies attracted according to given laws; the motions of several bodies among themselves; the motions of bodies in resisting mediums; the forces, densities, and motions of mediums; the orbits of the comets, and other such matters. I thought that publication must be deferred to another time so that I might research these matters and might publish them together. What relates to the lunar motions (being incomplete) I have put all together in the corollaries of Proposition 66, to avoid being obliged to propose and distinctly demonstrate the several things contained there in a method more expansive than the subject deserved and
interrupt the series of the other propositions. Some things, found out after the rest, I chose to insert in places less suitable, rather than to change the number of the propositions and the citations. I earnestly entreat that everything be read honestly, and that the defects, in matters so difficult, be not so much refuted, as investigated by the Readers' new efforts, and be kindly made complete .
On this Work of Mathematical Physics
Of the Most Outstanding Man Most Learned Isaac Newton
an egregious distinction of our time and race.
Behold, for you, the pattern of the celestial globe,
the scales of divine mass, the computations of Jupiter,
which laws, while composing the beginnings of things,
the Creator did not wish to defile,
and fixed the foundations of the eternal work.
The inmost spaces of the conquered heaven lie open,
nor is the force obscured that rotates the farthest orbs.
The sun, residing on his throne, commands all things to tend toward
him
by inclination and descent, nor does he allow the sidereal paths to
be moved
through the vast void by a straight path,
but he attracts them to himself as center, in unmoved orbits.
Now lies open the veering path of the comet, once a source of
dread,
nor are we now astonished at the phenomena of the bearded stars.
From this work we learn at last the reason that the silvery moon
advances with steps unequal,
As if she scorned to suit her pace to numbers, to this day unknown
to any astronomer;
Why the seasons return and the hours move forward.
We learn too with what forces roaming Cynthia impels the ebbing
sea,
now, with waves subdued, it leaves the seaweed behind, and bares the
sands, esteemed by sailors; and now, in alternate turns, crashing on
the highest shores.
Questions that tormented the minds of ancient scholars so often,
And even now trouble our scholars in vain with raucous strife,
We see clearly, learning routing the cloud of ignorance.
And now in no gloominess does error aggravate doubts for those
Whom the brilliance of sublime genius has allowed to penetrate
The homes of the gods and to scale the heights of heaven.
Arise, Mortals, cast off earthly cares;
And from this [book] distinguish the powers of a heaven-born mind,
Removed, far and wide, from the life of the herds.
The person who through written tablets ordered the repression
Of murder, theft, and adultery, and crimes of perjured guile,
Or the one who gave to roving peoples cities with walls,
Was a founder; or the one who blessed the peoples with Ceres' gift
And who pressed from grapes the mitigation of cares;
Or the one who showed how to meld sounds inscribed on a reed of
the Nile;
And thus to reveal voices to the eyes, did lighten the human lot:
Offsetting thus the miseries of life with some felicity.
But now we are admitted to the banquet of the gods; we are allowed
To deal with the laws of the celestial globe; and now
Those things enclosed and hidden in the blind earth lie revealed;
As are the unchanging order of things; and what past centuries
Of earth's long history have concealed.
Now celebrate in songs with me,
You who delight in enjoying heavenly nectar,
NEWTON, who has set forth such things, unlocking the treasures of
hidden truth,
NEWTON, dear to the muses,
So richly through his mind has Phoebus cast
The radiance of his own divinity.
Nearer to the gods no mortal may approach.
EDMUND HALLEY
On the Motion of Bodies Book One
Section 1
On the method of first and last ratios, with the help of which the following [lemmas ] are proved .
Lemma 1
Quantities, as well as ratios of quantities, that constantly tend to equality in a given time, and in that way are able to approach each other more closely than for any given difference, come ultimately to be equal .
If you deny it, let their ultimate difference be D . They are therefore unable to approach nearer to equality than for the given difference D ; contrary to hypothesis.
Lemma 2
If in any figure AacE comprised of the straight lines Aa and AE and the curve acE, there should be inscribed any number of parallelograms Ab, Bc, Cd, etc. [generated] by equal bases AB, BC, CD, etc., and sides Bb, Cc, Dd, etc., parallel to the side Aa of the figure, and [if ] the parallelograms aKbl, bLcm, cMdn, etc., should be completed, and then the width of these parallelograms should be diminished, and the number should be increased indefinitely: [then] I assert that the last ratios that the inscribed figure AKbLcMdD, the circumscribed AalbmcndoE, and the curvilinear AabcdE, are equal ratios . [See fig. A.1.]
For the difference of the inscribed and circumscribed figures is the sum of the parallelograms Kl + Lm + Mn + Do , that is (because the bases of all are equal), the rectangle beneath the base Kb of one, and the sum Aa of their heights, and that is the rectangle ABla . But this rectangle, because
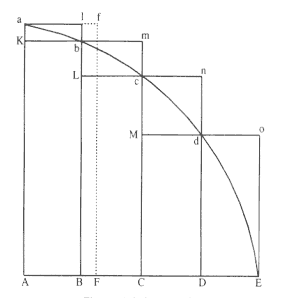
Figure A.1
Lemma 2.
its width AB is diminished indefinitely, comes to be less than any given [area]. Therefore, by Lemma 1, the inscribed and circumscribed figures, and even more by far the intermediary curvilinear figure come ultimately to be equal. Which was to be proven.
Lemma 3
The same last ratios are also of equality when sides AB,BC,CD, etc., of the parallelograms are unequal, and all are diminshed indefinitely .
For let AF be equal to the maximum width, and let the parallelogram FAaf be completed. This will be greater than the difference of the inscribed and circumscribed figures, but with its width AF diminished indefinitely, it will come to be less than any given rectangle.
Corollary 1 . Hence the ultimate sum of the vanishing rectangles coincides in every part with the curvilinear figure.
Corollary 2 . And the rectilinear figure, which is comprised of the chords of the vanishing arcs ab, bc, cd , etc., ultimately coincides much more with the curvilinear figure.
Corollary 3 . So too the rectilinear figure, which is circumscribed by the tangents of the same arcs.
Corollary 4 . And consequently these ultimate figures (with respect to their perimeters acE ) are not rectilinear, but the curvilinear limits of rectilinear [figures].
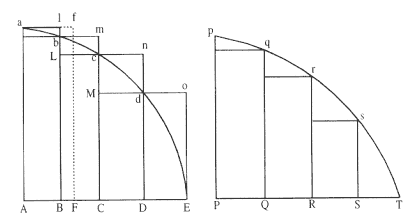
Figure A.2
Lemma 4.
Lemma 4
If in two figures AacE and PprT there should be inscribed (as above ) two series of parallelograms, and if the number of both should be the same, and when the widths are diminished indefinitely, the last ratios of parallelograms in one figure should be individually the same as the parallelograms in the other figure; [then ] I assert that the two figures AacE and PprT are in the same ratio to one another . [See fig. A.2.]
For as the individual parallelograms are to each other, so (by compounding) does the total sum come to be one to the other, and so, too, figure to figure, the former figure, of course, being (by Lemma 3) to the former sum, and the latter figure to the latter sum in a ratio of equality.
Corollary . Hence if two quantities of any kind are divided in any way into the same number of parts, and, when their number is increased and their size diminished indefinitely, those parts maintain a given ratio to one another, the first to the first, the second to the second, and the rest to the rest in their sequence; [then] their totals will be to each other in that same given ratio. For if the parallelograms in the figures of this lemma should be assumed as parts of each other, [then] the sums of the parts will always be as the sums of the parallelograms; and consequently, when the number of parts and parallelograms is increased, and the size diminished indefinitely, [they will be] in the last ratio of parallelogram to parallelogram, that is (by hypothesis) in the last ratio of part to part.
Lemma 5
[In ] similar figures, all sides which correspond to each other mutually, curvilinear as well as rectilinear, are proportional, and their areas are in the doubled ratio of their sides .
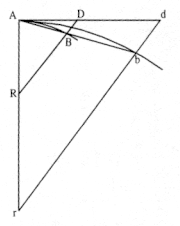
Figure A.3
Lemma 6.
Lemma 6
If any arc AB given in position should be subtended by the chord AB, and [if ] at some point A in the middle of its continuous curvature, it should be touched by the straight line AD extended in either direction; then [if ] points A and B should approach each other and coalesce; I assert that the angle BAD [generated ] by the chord and tangent, would be diminished indefinitely and would ultimately vanish . [See fig. A.3.]
For extend AB to b , and AD to d , and, with points A and B coalescing, with no part AB of Ab lying any longer within the curve, it is clear that this straight line Ab will either coincide with the tangent Ad , or will be drawn between the tangent and the curve. But the latter case is contrary to the nature of curvature, and therefore the prior case obtains. Which was to be proven.
Lemma 7
With the same suppositions, I assert that the last ratio of the arc, chord, and tangent to each other is the ratio of equality. (See the figures of Lemmas 6 and 8 .) [See fig. A.4.]
For extend AB and AD to b and d , and parallel to the secant BD , draw bd . And let the arc Ab be similar to the arc AB . And, the points A and B coalescing, the angle dAb , by the lemma above, would vanish; and thus the straight lines Ab and Ad and the intervening arc Ab will coincide, and accordingly they will be equal. Hence the straight lines AB and AD , which are always proportional to these, and the intervening arc AB , will have the last ratio of equality. Which was to be proven.
Corollary 1 . Hence if through B parallel to the tangent there should be
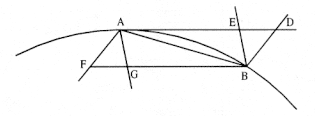
Figure A.4
Lemma 7.
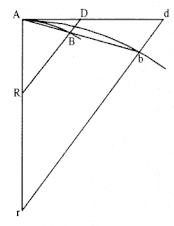
Figure A.5
Lemma 8.
drawn BF perpetually cutting at F any straight line AF passing through A , this will ultimately have the ratio of equality to the vanishing arc AB , since, when the parallelogram AFBD is completed, it always has the ratio of equality to AD .
Corollary 2 . And if through B and A several straight lines BE, BD, AF , and AG are constructed, intersecting the tangent AD and its parallel BF , the last ratio of all the lines AD, AE, BF, Bg , and the chord and arc AB to each other will be the ratio of equality.
Corollary 3 . And accordingly all these lines in any discussion about last ratios can be used mutually in place of each other.
Lemma 8
If the given straight lines AR and BR constitute with the arc AB, its chord AB, and the tangent AD the three triangles ARB, ARB, and ARD; and then [if ] the points A and B approach each other; I assert that the ultimate forms of the vanishing triangles is one of similarity, and the last ratio, of equality . [See fig. A.5.]
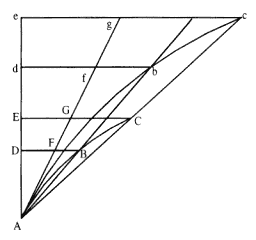
Figure A.6
Lemma 9.
For let AB, AD , and AR be extended to b, d , and r . Draw rbd parallel to RD , and construct arc Ab similar to arc AB . As the points A and B coalesce, the angle bAd vanishes, and accordingly the three triangles rAb, rAb , and rAd will coincide; and on that account they are similar and equal. And hence [triangles] RAB, RAB , and RAD , always similar and proportional to these [triangles], will come to be ultimately similar and equal to each other. Which was to be proven.
Corollary . And hence those triangles can mutually be used in place of each other in every proof of last ratios.
Lemma 9
If the straight line AE and the curve AC given in position mutually intersect at the given angle A; and [if ] BD and EC should be applied as ordinates to that straight line at any given angle, meeting the curve at B and C; and [if] the points B and C approach point A; [then ] I assert that the areas of triangles ADB and AEC will be ultimately to each other in the doubled ratio of the sides . [See fig. A.6.]
For in AD extended take Ad and Ae proportional to AD and AE , and erect the ordinates db and ec parallel and proportional to the ordinates DB and EC . Extend AC to c , and construct the curve Abc similar to ABC , and let each curve be touched at A by the straight line Ag , and let the ordinates be cut by it at F, G, f , and g . Then let the points B and C coalesce with the point A , and with the angle cAg vanishing, the curvilinear areas Abd and Ace will coincide with the rectilinear [areas] Afd and Age ; and thus, by Lemma 5, they will be in the doubled ratio of the sides Ad and Ae .
But always proportional to these areas are the areas ABD and ACE , and to these sides, the sides AD and AE . Therefore also the areas ABD and ACE are ultimately in the doubled ratio of the sides AD and AE . Which was to be proven.
Lemma 10
Spaces which a body describes at the urging of any standard force are, at the very start of motion, in the doubled ratio of the times . [See fig. A.6.]
Let the times be expressed by the lines AD and AE , and the velocities generated by the ordinates DB and EC ; and the first spaces described by these velocities will be as the first areas ABD and ACE described by these ordinates: that is, at the very beginning of motion (by Lemma 9) in the doubled ratio of the times AD and AE . As was to be proven.
Corollary 1 . And hence it is easily concluded that in proportional times similar parts of similar figures of bodies describing deviations that are generated when equal forces are applied to the bodies similarly in those same parts, and that are measured by the positions of the figures to which the bodies would arrive in the same proportional times without those same forces, [these deviations] are as nearly as possible the squares of the times in which they are generated.
Corollary 2 . But deviations that are generated by proportional forces similarly applied are as the forces and the squares of the times conjointly.
Lemma 11
The vanishing subtense of an angle of contact is ultimately in the doubled ratio of the subtense of the conterminous arc . [See fig. A.7.]
Case 1 . Let AB be the arc, AD its tangent, BD the subtense of the angle of contact perpendicular to the tangent, and AB the subtense of the arc. Perpendicular to the latter subtense AB and to the tangent AD , erect AG and BG , meeting at G ; then let the points D,B , and G approach the points d, b , and g ; and let J be the intersection of the lines BG and AG , ultimately occurring when the points D and B approach up to A . It is obvious that the distance GJ can be less than any assigned one.
Now (from the nature of circles passing through points ABG and Abg ) AB 2 is equal to AG × BD , and AB2 is equal to Ag × bd , and hence the ratio Ab2 to Ab2 is composed of the ratios AG to Ag and BD to bd . But since JG can be assumed less than any assigned length, it can be arranged that the ratio AG to Ag differs from the ratio of equality less than for any assigned difference, and thus as the ratio AB2 to Ab2 differs from the ratio BD to bd less than for any assigned difference. By Lemma 1 there is, therefore, the last ratio AB 2 to Ab2 equal to the last ratio BD to bd . Which was to be proven.
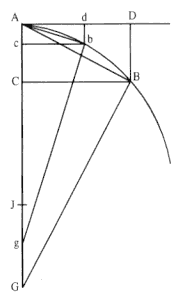
Figure A.7
Lemma 11.
Case 2 . Now let BD be inclined to AD at any given angle, and there will always be the same last ratio as before and hence also the same AB 2 to Ab2 , as was to be proven.
Case 3 . Moreover, although the angle D may not be given, the angles D and d will always verge toward equality and approach nearer to each other than for any assigned difference, and hence, by Lemma 1, will ultimately be equal, and accordingly, the lines BD , bd will be in the same ratio to each other as before. Which was to be proven.
Corollary 1 . From this, since the tangents AD and Ad , the arcs AB and Ab , and their sines BC and bc are made ultimately equal to the chords AB and ab ; their squares will also be ultimately as the substenses BD and bd .
Corollary 2 . The [area of the] rectilinear triangles ADB and adb are ultimately in the tripled ratio of the sides AD and ad , and in the three-halves ratio of the sides DB and db , since the definition [of area] is in the compounded ratio of the sides AD and DB , Ad and db . Thus also the triangles ABC and Abc are ultimately in the tripled ratio of the sides BC and bc .
Corollary 3 . And since DB and db are ultimately parallel and in the doubled ratio of their [sides] AD and AD , the ultimate curvilinear areas ADB and Adb (from the nature of a parabola) will be two-thirds of the rectilinear triangles ADB and Adb , and the segments AB and Ab one-third of the same triangles. And hence these areas and these segments will be in the tripled ratio both of the tangents AD and Ad and of their chords and arcs AB and Ab .
Scholium
As for the rest, we suppose in all these things that the angle of contact is neither infinitely greater than the angles of contact which circles contain with their tangents nor infinitely less than these same [angles]; that is, the curvature at point A is neither infinitely small nor infinitely large, but the interval AJ is of finite magnitude. For DB can be taken proportional to AD3 , in which case no circle can be constructed through point A between the tangent AD and the curve AB , and hence the angle of contact will be infinitely less than the circular ones. And by a similar argument if DB is made successively proportional to AD4 , AD5 , AD6 , AD 7 , etc., there will be a series of angles of contact continuing to infinity, any succeeding one of which is infinitely smaller than the preceding one. And if DB is made successively proportional to AD 2 , AD3/2 , AD4/3 , AD5/4 , AD6/5 , AD7/6 , etc., there will be another series of infinite angles of contact, the first of which is of the same class as the circular ones, the second infinitely greater than it, and any succeeding one infinitely greater than the preceding one. But also between any two of these angles can be inserted a series of intermediate angles proceeding either way to infinity, of which any succeeding one will be infinitely greater than the preceding one. For example, between the terms AD2 and AD3 may be inserted the sequence AD13/16 , AD11/5 , AD9/4 , AD7/3 , AD5/2 , AD8/3 , AD11/4 , AD14/5 , AD17/6 , etc. And again there can be inserted between any pairs of angles in this sequence a new series of intermediate angles differing from one another by infinite intervals. And nature knows no limit.
What has been demonstrated about curved lines and the areas they contain may easily be applied to the curved surfaces and contents of solids. Indeed I have placed these lemmas first in order to avoid the tedium of deducing complicated proofs ad absurdum in the manner of ancient geometers. For proofs are rendered more compact by the method of indivisibles. But since the hypothesis of indivisibles is rather difficult, and moreover that method is considered less geometric, I have preferred to reduce proofs of the following matters to the last sums and ratios of vanishing quantities and the first ones of nascent quantities, that is, to the limits of these sums and ratios, and to place proofs of those limits first as concisely as I could. For the same is accomplished by these [proofs] as by the method of indivisibles, and when the principles have been proven, we shall employ them more safely. Hence in what follows, if I ever consider quantities as consisting of particles, or if for straight line segments I use minute curved ones, [then] I want it understood that these are not indivisibles, but vanishing divisibles, not the sums and ratios of definite parts, but the limits of such sums and ratios; and that the force of proofs must always be referred to the method of the preceding lemmas.
There is an objection, rather futile, that there is no ultimate proportion
of vanishing quantities, since, before they have vanished, there is no last, and when they have vanished, there is none. But also by that same argument it can be contended that there is no ultimate velocity of a body proceeding to a certain position. For before the body reaches the position, there is no ultimate [velocity], and when it has reached it, there is no velocity. And the response is easy. For the ultimate velocity, is to be understood that with which the body moves, not before it reaches the last position and motion ceases, nor afterward, but at the moment when it reaches it, that is, that very velocity at which the body reaches the ultimate position and at which motion ceases. And likewise by the last ratio of vanishing quantities must be understood the ratio of quantities not before they vanish, nor afterward, but at which they vanish. Correspondingly, moreover, the first ratio of nascent quantities is the ratio at which they come into being. And their first and last sum is that at which they begin or cease to be (or to be increased or diminished). There exists a limit which their velocity can attain at the end of motion, but not exceed. This is the ultimate velocity. And there is an equal ratio of all quantities and proportions beginning and ceasing. Since this limit is certain and determined, the problem to determine it is truly a geometrical one. Indeed all things geometrical are legitimately employed in determining and demonstrating other geometrical matters.
It can also be argued that if the last ratios of vanishing quantities are given, the ultimate magnitudes will also be given; and thus every quantity will consist of indivisibles, contrary to what Euclid demonstrated on incommensurables in his tenth book of Elements . But really this objection is based on a false hypothesis. Those last ratios with which quantities disappear are not true ratios of ultimate quantities, but limits toward which ratios of quantities decreasing without limit are always approaching, and which they can follow more closely, for any given distance, but can never exceed, nor reach before the quantities diminish into infinity. The matter may be understood more clearly in infinitely large terms. If two quantities of a given distance are increased to infinity, the last ratio of these will be given, that is, the ratio of equality, and yet the ultimate or maximal quantities will not be given, that is, their ratio. Therefore in the following, if ever, intending an easy mental picture of things, I speak of the smallest quantities possible either as vanishing or as ultimate, [then] be careful not to understand quantities determined in magnitude, but consider them always diminished without end.
Section 2
Of the invention of centripetal forces .
Proposition 1—
Theorem 1
The areas that bodies driven in orbits describe with radii having been constructed to a stationary center of forces, lie in stationary planes and are proportional to the times . [See fig. A.8.]
Let the time be divided into equal parts, and in the first part of the time let a body by its innate force describe the straight line AB . The same body would then, if nothing impeded it, proceed directly to c in the second part of the time, describing the line Bc equal to the same AB (by Law 1), so that, when the radii AS , BS , and cS were drawn to the center, areas ASB and BSc would be made equal.
Now when the body comes to B , let the centripetal force act with one great impulse, and let it make the body deflect from the straight line Bc and proceed along the straight line BC . Parallel to the same BS , let cC be extended, meeting BC at C , and when the second interval of time is finished, the body (by Corollary 1 of the Laws) will be found at C , in the same plane with the triangle ASB . Join S and C and the triangle SBC which, because of the parallels SB and Cc , will be equal to the triangle SBc and hence also to the triangle SAB .
By a similar argument, if the centripetal force should act successively at C , D , E , etc., making the body in separate moments of time describe the separate straight lines CD , DE , EF , etc., then these will lie in the same plane, and the triangle SCD will be equal to the triangle SBC , SDE to SCD , SEF to SDE . In equal times, therefore, equal areas are described in a stationary plane; and in combining, whatever are the sums of areas SADS and SAFS among themselves, they are as the times of descriptions.
Now let the number of triangles be increased and their width be diminished indefinitely, and their ultimate perimeter ADF (by the fourth corollary of the third lemma) will be a curved line; hence the centripetal force by which a body is perpetually drawn away from the tangent of this curve, will act uninterruptedly; but whatever areas SADS and SAFS described which are always proportional to the times of the descriptions, will be proportional to the same times in this case. Which was to be proven.
Corollary 1 . In nonresisting media, if the areas are not proportional to the times, [then] the forces are not directed along the path of the radii.
Corollary 2 . In all media, if the description of the areas is accelerated, [then] the forces are not directed along the path of the radii, but in consequence deviate from there.
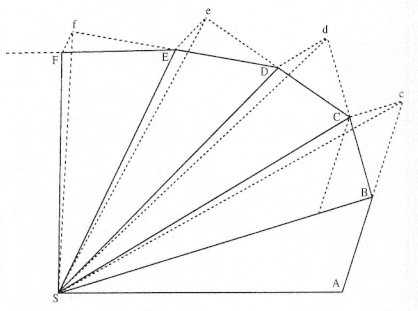
Figure A.8
Proposition 1.
Proposition 2—
Theorem 2
Every body that, when it is moved along some curved line with a radius having been constructed to a point [that is ] either stationary or advancing uniformly in a rectilinear motion, describes areas proportional to the times around that point, is urged on by a centripetal force being directed to the same point .
Case 1 . For, every body which is moved in a curved line is diverted from the rectilinear path by some force acting on it (by Law 1). Moreover, that force by which the body is diverted from the rectilinear path and is made to describe in equal times around a stationary point S the smallest equal triangles possible SAB , SBC , SCD , etc.; [such a force] acts at position B along a line parallel to cC (by Elements , I, 40, and Law 2): that is, along line BS ; and at position C along a line parallel to dD : that is, along line CS , etc. It acts, therefore, always along lines being directed to that stationary point S . Which was to be proven.
Case 2 . And by the fifth Corollary of the Laws, it is just the same whether the surface on which the body describes the curvilinear figure remains at rest, or whether the same surface is moved uniformly along a straight line, together with the body, the figure described, and its point S .
Scholium
A body can be urged by a centripetal force compounded of several forces. In this case the sense of the proposition is that the force which is compounded of all, is directed to the point S . Further, if any force acts along a line perpendicular to the described surface area, this will make the body deflect from the plane of its motion, but it will neither increase nor decrease the quantity of the described surface area, and, moreover, it must be neglected in the compounding of forces.
Proposition 3—
Theorem 3
Every body that, with a radius having been constructed to the center of another arbitrarily moving body, describes areas proportional to the times around that center, is urged by a force compounded of the centripetal force being directed toward the other body, and of the whole accelerative force by which the other body is urged .
For (by Corollary 6 of the Laws) if any body is urged along parallel lines by a new force which is made equal and opposite to that by which the other body is urged the first body will continue to describe the same areas around the other body as before; but the force by which the other body was being urged will now be canceled by the force equal and opposite to it, and moreover (by Law 1) that other body will either remain at rest or will be moved uniformly in a straight line, and the first body, at the urging of the difference of forces, will proceed to describe areas proportional to the times around the other body. The difference of forces, therefore (by Theorem 2), is directed to that other body as the center. Which was to be proven.
Corollary 1 . Hence if one body, with a radius having been constructed to another body, describes areas proportional to the times, and [if] from the total force (whether single or compounded of several forces, according to the second corollary of the laws) by which the first body is urged [there] is subtracted the whole accelerating force by which the other body is urged (by the same corollary of the laws); [then] the whole remaining force by which the first body is urged will be directed toward the other body as center.
Corollary 2 . And if those areas are as closely as possible proportional to the times, [then] the remaining force will be directed as closely as possible to the other body.
Corollary 3 . And conversely, if the remaining force is directed as closely as possible to the other body, [then] those areas will be as closely as possible proportional to the times.
Corollary 4 . If a body [A ] with a radius having been constructed to another body [B ] describes areas which, when compared with the times, are greatly unequal, and [if] that other body [B ] either remains at rest or is moved uniformly in a straight line, [then] the action of centripetal force being directed to that other body [B ] is either nothing or is mixed and compounded with the very powerful actions of other forces; and the entire force, compounded of all, if the forces are several, is directed to another center [C ] (whether stationary or moving), around which there is an equal description of areas. The same obtains when the other body [B ] moves with any motion whatever, if only there is assumed a centripetal force which remains after subtracting every force acting on that other body [B ].
Scholium
Since the equable description of the areas is an indication of the center toward which is directed that force by which a body is most affected, while that body is kept in its orbit by the force being directed to the center; and [since] every circular motion is correctly said to be made around that center, by whose force the body is drawn away from the rectilinear motion and is kept in orbit; [then] why should we not use in what follows the equable description of areas as an indication of the center around which every circular motion [i.e., general curved motion] is performed in free space?
Proposition 4—
Theorem 4
For bodies that describe different circles with equable motion, the centripetal forces are directed toward the centers of those circles, and are to one another as the squares of the arcs described in the same time divided by the radii of the circles . [See fig. A.9.]
Let the bodies B and b orbiting on the circumferences of circles BD and bd describe in the same time the arcs BD and bd . Since by their innate force alone they would describe the tangent lines BC and bc equal to these arcs, it is clear that the centripetal forces are those that perpetually draw bodies back from the tangents toward the circumferences of the circles, and hence these are to each other in the first ratio of the nascent intervals CD and cd ; they tend, in fact, toward the centers of circles by Theorem 2 because the areas described by the radii are set proportional to the times.
Let figure tkb be similar to figure DCB , and then, by Lemma 5, the line segment CD will be to the line segment kt as the arc BD to the arc bt ; and also, by Lemma 11, the nascent segment tk is to the nascent segment dc as
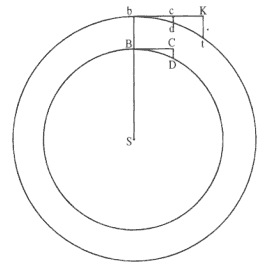
Figure A.9
Proposition 4.
bt2 to bd2 , and, in like manner, the nascent line segment DC is to the nascent line segment dc as BD × bt to bd 2 , or, what is the same thing, as BD × bt / Sb to bd2 / Sb , and thus (from equal ratios bt /Sb and BD / SB ) as BD 2 / SB to bd 2 / Sb . Which was to be proven.
Corollary 1 . Hence the centripetal forces are as the squares of the velocities divided by the radii of the circles.
Corollary 2 . And reciprocally as the squares of the periodic times divided by the radii, so are these forces to each other. That is (if I may speak as a geometer) these forces are in a ratio compounded of the doubled ratio of the velocities directly and in a simple ratio of the radii inversely; also in a ratio compounded of a simple ratio of the radii directly and of the squared ratio of the periodic times inversely.
Corollary 3 . From this, if the periodic times are equal, both the centripetal forces and the velocities will be as the radii, and conversely.
Corollary 4 . If the squares of the periodic times are as the radii, [then] the centripetal forces are equal, and the velocities in the halved ratio of the radii, and conversely.
Corollary 5 . If the squares of the periodic times are as squares of the radii, [then] the centripetal forces are reciprocally as the radii, and the velocities equal, and conversely.
Corollary 6 . If the squares of the periodic times are as the cubes of the radii, [then] the centripetal forces are reciprocally as the squares of the radii; but the velocities are in the halved ratio of the radii, and conversely.
Corollary 7 . [In the cases] in which bodies describe similar parts of any similar shapes whatsoever having centers similarly placed; all of these same [statements] about times, velocities, and forces follow from the demonstration of the preceding [corollaries] applied to these very cases.
Scholium
The case of the sixth corollary holds true in celestial bodies (as our compatriots Wren, Hooke, and Halley have also concluded independently), and for this reason I have decided to explain more fully in what follows those [questions] that concern centripetal force decreasing in the doubled ratio of the distances from the centers.
Further, with the help of the preceding demonstration, the proportion of a centripetal force to any known force, such as that of gravity, is also determined. For, in the time a body traverses the arc BC , that [centripetal] force, which at the very beginning of its motion is equal to the square of the arc BD divided by the diameter of the circle, impels [the body] through the space CD ; [and since] every body with the same force continued always in the same region, would describe spaces in the doubled ratio of the times; [then], in the time a revolving body describes any given arc, that [centripetal] force will bring it about that the same body progressing in a straight line describes a space [S ] equal to the square of that arc applied to the diameter of the circle; and thus [that centripetal force] is to the force of gravity as that space [S ] is to the space which [the body] describes in falling heavily in the same time. And by propositions of this kind, Huygens in his outstanding tract on the oscillating clock, compared the force of gravity with centrifugal forces of revolving [bodies].
The preceding [statements] can also be demonstrated in this way. In any circle let a polygon of any number of sides be described. And if a body, in moving at a given velocity along the sides of the polygon, is reflected from the circle at each angle of the polygon, the force with which it impinges on the circle at each reflection will be as its velocity. And thus the sum of the forces in a given time will be as that velocity and number of reflections conjointly: that is, (if the species of the polygon is given) as the [product of the] length described in that given time and that length divided by the radius of the circle: that is, as the square of that length divided by the radius. Thus, if the polygon, with its sides diminished infinitely, coincides with the circle, then the sum of the forces in a given time will be as the square of the arc in a given time is divided by the radius. This is the force by which the body urges the circle, and equal to this is the opposite force by which the circle continuously repels the body toward the center.
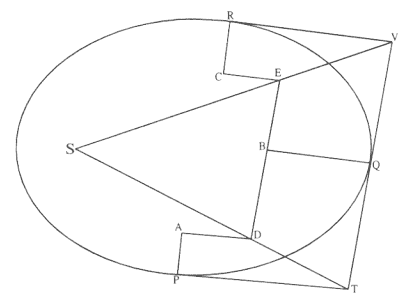
Figure A.10
Proposition 5.
Proposition 5—
Problem 1
Given, in any places, a velocity by which a body describes a given figure by forces directed to any common center, to find that center . [See fig. A.10.]
Let three straight lines PT, TQV , and VR , meeting at T and V , touch the figure described at the same number of points, P, Q , and R Let PA, QB , and RC be erected perpendicular to the tangents, and inversely proportional to the velocities of the body at the points P, Q , and R , from which they are erected: that is, as PA is to QB so is the velocity at Q to the velocity at P , and QB is to RC as the velocity at R is to the velocity at Q . Through the ends of the perpendiculars, A, B , and C , let AD, DBE , and EC be constructed at right angles, meeting at D and E . And TD and VE , when drawn, will meet at the required center S .
For since the body at P and Q , with radii constructed to the center, describes areas proportional to the times, and since those areas described are at the same time as the velocities at P and Q constructed respectively on the perpendiculars dropped from the center to tangents PT and QT , those perpendiculars will be as the velocities reciprocally, and thus as the perpendiculars AP and BQ directly, that is, as perpendiculars dropped from point D to the tangents. Hence it is easily understood that points S, D , and T are in a straight line. And by a similar argument points S, E , and V are also in a straight line; and accordingly center S is found at the meeting of straight lines TD and VE . Which was to be proven.
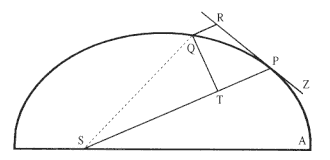
Figure A.11
Proposition 6.
Proposition 6—
Theorem 5
If a body P by revolving around the center S, should describe any curved line APQ, and if the straight line ZPR should touch that curve at any point P, and if to this tangent from any other point Q of the curve , QR should be drawn parallel to the distance SP, and if QT should be dropped perpendicular to the distance SP; [then ] I assert that the centripetal force would be reciprocally as the solid SP2 × QT2 / QR, provided that the quantity of that solid that ultimately occurs when the points P and Q coalesce is always taken . [See fig. A.11.]
In the indefinitely small figure QRPT the nascent line segment QR is, given the time, as the centripetal force (by Law 2), and, given the force, as the square of the time (by Lemma 10); and hence, when neither is given, as the centripetal force and the square of the time conjointly; and hence the centripetal force is as the line segment QR directly, and the square of the time inversely. The time, however, is as the area SPQ , or its double SP × QT , that is, as SP and QT conjointly, and hence the centripetal force is as QR directly and SP2 into QT2 inversely, that is, as SP2 × QT2 / QR inversely. Which was to be proven.
Corollary . Hence if any figure is given, and on it a point toward which a centripetal force is directed, it is possible for the law of centripetal force to be found which will make a body orbit on the perimeter of that figure. Specifically the solid SP2 × QT2 / QR reciprocally proportional to this force must be computed. We shall give examples of this procedure in the following problems.
Proposition 7—
Problem 2
Let a body be orbited on the circumference of a circle; there is required the law of centripetal force being directed to some given point on the circumference . [See fig. A.12.]
Let SQPA be the circumference of a circle, S the center of centripetal force, P a body carried on the circumference, and Q a nearby position into
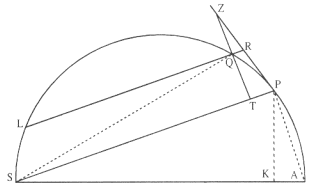
Figure A.12
Proposition 7.
which it will be moved. To the diameter SA and to the straight line SP drop the perpendiculars PK and QT , and through Q draw LR parallel to SP , reaching the circle at L and the tangent PR at R , and let TQ and PR come together at Z .
Because of the similarity of the triangles ZQR, ZTP , and SPA , there will be RP 2 (that is, QR × LR ) to QT2 as SA2 to SP2 . Therefore (QR × LR ) × (SP2 / SA2 ) = QT2 . Multiply these equals by SP2 / QR , and, with points P and Q coalescing, let SP be written in place of LR .
Thus SP5 /SA2 will be made equal to QT2 × SP2 / QR . Therefore the centripetal force is reciprocally as SP5 / SA 2 , that is (because SA 2 is given), as the fifth power of the distance SP (by the corollary of Theorem 5). Which was to be found.
Proposition 8—
Problem 3
Let a body be moved on a circle PQA: for this effect there is required the law of centripetal force being directed to a point at such a distance that all lines PS and RS constructed to it can be considered as parallels . [See fig. A.13.]
From the center of circle C let radius CA be drawn cutting those parallels perpendicularly at M and N , and let CP be joined. Because the triangles CPM and TPZ , that is, TPQ (by Lemma 8), are similar, there is CP2 to PM2 as PQ2 , that is, PR2 (by Lemma 7) to QT2 , and from the nature of the circle, the rectangle QR × (RN + QN ) is equal to the square of PR . But as the points P and Q coalesce, RN + QN becomes equal to 2PM . Therefore there is CP2 to PM2 as QR × 2PM to QT2 , and hence QT2 / QR = 2PM3 / CP2 and so QT2 × SP2 / QR = 2PM3 × SP2 / CP 2 . Therefore (by the corollary to Theorem 5) the centripetal force is reciprocally as 2PM3 × SP2 / CP 2 , that is (after the determinate ratio 2SP2 / CP 2 is neglected), reciprocally as PM3 . Which was to be done.
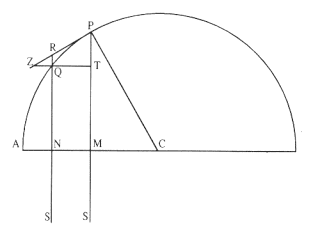
Figure A.13
Proposition 8.
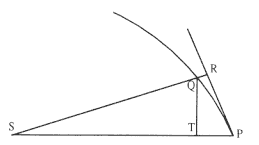
Figure A.14
Proposition 9.
Scholium
And by a similar argument a body will be moved on an ellipse, or also on a hyperbola or a parabola, by a centripetal force which is reciprocally as the cube of its ordinate being directed to a center of forces extremely far away.
Proposition 9—
Problem 4
Let a body be orbited on a spiral PQS intersecting all the radii SP, SQ, etc., at a given angle; there is required the law of centripetal force being directed to the center of the spiral . [See Fig. A.14.]
Let there be given the indefinitely small angle PSQ , and, because all the angles have been given, the figure SPQRT will be given in species. The ratio QT /RQ is therefore given, and there is QT2 / QR as QT , that is, as SP .
Now let the angle PSQ be changed in whatever manner, and the straight
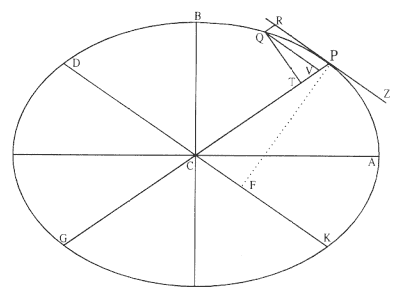
Figure A.15
Proposition 10.
line QR subtending the angle of contact QPR will be changed (by Lemma 11) in the doubled ratio of PR or QT . Therefore QT2 / QR will remain the same as before, that is, as SP .
For this reason, QT2 × SP2 / QR is as SP3 , that is (by the corollary of Theorem 5), the centripetal force is [reciprocally] as the cube of the distance SP . Which was to be done.
Lemma 12
All parallellograms described around a given ellipse are equal to each other. Understand the same for parallelograms described in a hyperbola around its diameters .
This is evident from Conics .
Proposition 10—
Problem 5
Let a body be orbited on an ellipse; there is required the law of centripetal force being directed to the center of the ellipse . [See fig. A.15.]
Let CA and CB be the semi-axes of the ellipse; GP and DK conjugate diameters; PF and QT perpendiculars to these diameters; QV ordinate to the diameter GP ;
and if parallelogram QVRP should be completed, there will be (from the Conics ) PV × VG to QV2 as PC2 to CD2 ,
and (because of similar triangles QVT and PCF ) QV2 is to QT2 as PC2 to PF2 ,
and on combining these ratios PV × VG to QT2 as PC2 to CD2 to CD2 and PC2 to PF2 ,
that is, VG to QT2 / PV as PC2 to CD2 × PF2 / PC 2 .
Write QR in place of PV , and (by Lemma 12) BC × CA in place of CD × PF , and in addition (with the points P and Q coalescing) 2PC in place of VG , and, when the ends and middles are multiplied into each other, there will result QT2 × PC2 / QR = 2BC2 × CA2 / PC .
The centripetal force is therefore reciprocally as 2BC2 × CA2 / PC (by the corollary to Theorem 5), that is (because 2BC 2 × CA2 is given), as 1/PC , that is, directly as the distance PC . Which was to be found.
Corollary 1 . And therefore, conversely, if the force is as the distance, the body will be moved on an ellipse having its center at the center of forces, or perhaps on the circle into which the ellipse can degenerate.
Corollary 2 . And there will be equal periodic times of revolutions made in all figures around the same center. For those times in the same ellipses are equal by Corollaries 3 and 7 of Proposition 4; but in ellipses having a common major axis, they are in turn as the total areas of the ellipses directly, and as parts of the areas described inversely in the same time; that is, as the minor axes directly, and the velocities of bodies on the principal vertices inversely, that is, as the axes directly to it, and the ordinates to the other axes inversely, and accordingly (because of the equality of the direct and inverse ratios) in the ratio of equality.
Scholium
If the ellipse, with the center going to infinity, should be turned into a parabola, a body will be moved on this parabola, and the force, now being directed to an infinitely distant center, will turn out equable. This is Galileo's theorem. And if the parabolic conic section, with the inclination of the plane to the conic section having been changed, should be turned into a hyperbola, the body will be moved on its perimeter, with the centripetal force changed into a centrifugal one.
Section 3
Of the motion of bodies in eccentric conic sections .
Proposition 11—
Problem 6
Let a body be revolved on an ellipse; there is required the law of centripetal force being directed to a focus of the ellipse . [See fig. A.16.]
Let S be a focus of the ellipse above. Let SP be drawn cutting not only the diameter of the ellipse DK at E , but also the ordinate QV in X , and let the parallelogram QXPR be completed.
It is clear the EP is equal to the semi-major axis AC , seeing that, when from the other focus H of the ellipse the line HI has been drawn parallel to CE (because CS and CH are equal), ES and EI would be equal, and hence EP would be half the sum of PS and PI , that is (because HI and PR are parallel, and the angles IPR and HPZ are equal), of PS and PH which are conjointly equal to the total axis 2AC .
Let the perpendicular QT be dropped to SP , and, after calling the principal latus rectum (or 2BC2 / AC ) of the ellipse L ,
there will be L × QR to L × PV as QR to PV , that is, as PE (or AC ) to PC ;
and L × PV to GV × VP as L to GV ;
and GV × VP to QV2 as CP2 to CD2 ;
and (by Lemma 8) QV2 to QX2 , is, with points P and Q coalescing, a ratio of equality;
and QX2 or QV2 is to QT2 as EP2 to PF2 , that is, as CA2 to PF2 , or (by Lemma 12) as CD2 to CB2 .
And when all these ratios are combined,
L × QR becomes to QT2 as (AC to PC ) × (L to GV ) × (CP2 to CD2 ) × (CD2 to CB2 )
that is, as AC × L (or 2CB2 ) × CP2 becomes to PC × GV × CB2 ,
that is, as 2PC to GV .
But with the points Q and P coalescing, 2PC and GV are equal. Therefore the proportionals of these, L × QR and QT 2 , are also equal. Let these equals be multiplied by SP2 / QR , and L × SP2 will be made equal to SP2 × QT2 / QR .
Therefore (by the corollary of Theorem 5) the centripetal force is reciprocally as L × SP2 , that is, reciprocally in the doubled ratio of the distance SP . Which was to be found.
With the same brevity with which we transferred the fifth Problem to the parabola and the hyperbola, it would be possible to do the same here;
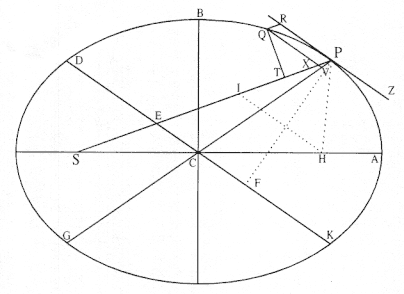
Figure A.16
Proposition 11.
but because of the dignity of the problem and its use in what follows, it will be no trouble to corroborate the other cases by [separate] proof.
Proposition 12—
Problem 7
Let a body be moved on a hyperbola; there is required the law of centripetal force being directed to a focus of the figure . [See fig. A.17.]
Let CA and CB be semi-axes of the hyperbola; PG and KD conjugate diameters; PF and QT perpendiculars to the diameters; and QV ordinate to the diameter GP . Let SP be drawn cutting both the diameter DK at E and the ordinate QV at X , and let the parallelogram QRPX be completed.
It is clear that EP is equal to the transverse semi-major axis AC , seeing that, when from the other focus H of the hyperbola the line HI has been drawn parallel to CE (because CS and CH are equal), ES and EI would be equal, and hence EP would be the half-difference of PS and PI , that is (because HI and PR are parallel, and the angles IPR and HPZ are equal), of PS and PH , whose difference is equal to the total axis 2AC .
Let the perpendicular QT be dropped to SP , and, after calling the principal latus rectum (or 2BC2 / AC ) of the hyperbola L ,
there will be L × QR to L × PV as QR to PV ; that is, as PE (or AC ) to PC ;
and L × PV to GV × VP as L to GV ;
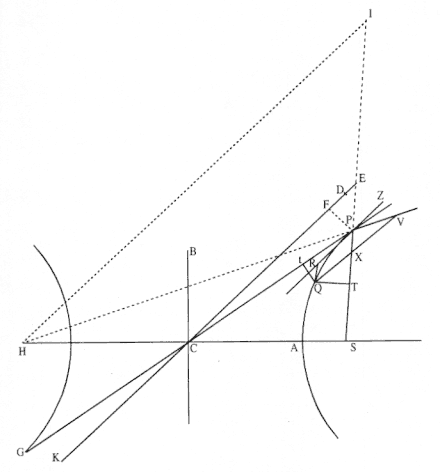
Figure A.17
Proposition 12.
and GV × VP to QV2 as CP2 to CD2 ;
and (by Lemma 8) QV2 to QX2 , becomes, with points P and Q coalescing, a ratio of equality;
and QX2 or QV2 is to QT2 as EP2 to PF2 , that is, as CA2 to PF2 , or (by Lemma 12) as CD2 to CB2 .
And when all these ratios are combined,
L × QR becomes to QT2 as (AC to PC ) × (L to GV ) × (CP2 to CD2 ) × (CD2 to CB2 ),
that is, as AC × L (or 2 CB2 ) × PC2 becomes to PC × GV × CB2 ,
that is, as 2PC to GV .
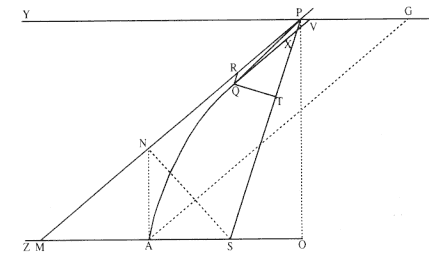
Figure A.18
Lemma 14.
But with points Q and P coalescing, 2PC and GV are equal. Therefore the proportionals to these, L × QR and QT2 , are also equal. Let these equals be multiplied by SP2 / QR , and L × SP2 will be made equal to SP2 × QT2 / QR .
Therefore (by the corollary of Theorem 5) the centripetal force is reciprocally as L × SP2 , that is, reciprocally in the doubled ratio of the distance SP . Which was to be found.
In the same manner it is proven that a body, with this centripetal force changed to centrifugal, will be moved in a conjugate hyperbola.
Lemma 13
The latus rectum of a parabola pertaining to any vertex is quadruple the distance of that vertex from the focus of the figure .
This is evident from the Conics .
Lemma 14
A perpendicular which is dropped from the focus of a parabola to its tangent is a mean proportional between the distances of the focus from the point of contact and from the principal vertex of the figure . [See fig. A.18.]
For let APQ be the parabola, S its focus, A the principal vertex, P the point of contact, PO the ordinate to the principal diameter, PM a tangent meeting the principal diameter at M , and SN a perpendicular line from the focus to the tangent. Let AN be joined, and, because MS and SP, MN and NP, MA and AO are equals, straight lines AN and OP will be parallel,
Figure A.19
Proposition 13.
and hence the triangle SAN will have a right angle at A and likewise for the equal triangles SMN and SPN . Therefore PS is to SN as SN to SA . Which was to be proven.
Corollary 1. PS2 is to SN2 as PS is to SA .
Corollary 2 . And, because SA is given, SN2 is as PS .
Corollary 3 . And the meeting of any tangent PM with the straight line SN , which is perpendicular from the focus to it, falls on the straight line AN , which touches the parabola on the principal vertex.
Proposition 13—
Problem 8
Let a body be moved on the perimeter of a parabola; there is required the law of centripetal force being directed to the focus of this figure . [See fig. A.19.]
Let the construction of Lemma 14 remain, and let P be the body on the perimeter of the parabola, and then, from the position Q to which the body next moves, draw QR parallel to SP and QT perpendicular, and also QV parallel to the tangent and meeting both the diameter YPG at V and the distance SP at X .
Now because triangles PXV and MSP are similar, and the sides SM and SP of one are equal, the sides PX or QR and PV of the other are equal. But, from the Conics , the square of the ordinate QV is equal to the rectangle [generated] by the latus rectum and the segment PV of the diameter, that is (by Lemma 13), equal to the rectangle 4PS × PV or 4PS × QR ; and, with points P and Q coalescing, the ratio QV to QX (by Lemma 8) is one of equality.
Therefore in this case QX 2 is equal to the rectangle 4PS × QR . But (because angles QXT, MPS , and PMO are equal), QX2 is to QT2 as PS2 to SN2 , that is (by Corollary 1, Lemma 14), as PS to AS , that is, as 4PS × QR to 4AS × QR , and therefore (by Proposition 9, Book 5 Elements ), QT2 and 4AS × QR are equal.
Let these equals be multiplied by SP2 / QR and SP2 × QT2 / QR will become equal to SP2 × 4AS ; and therefore (by the corollary of Theorem 5) the centripetal force is reciprocally as SP2 × 4AS , that is, because 4AS is given, reciprocally in the doubled ratio of the distance SP . Which was to be found.
Corollary 1 . From the last three propositions it follows that if any body P should depart from position P along any straight line PR , with any velocity, and is at the same time acted upon by a centripetal force that is reciprocally proportional to the square of the distance from the center, this body will be moved in one of the sections of conics having a focus at the center of forces; and conversely.
Corollary 2 . And if the velocity with which the body departs from its position P should be such that the line element PR could be described in some minimal particle of time, and the centripetal force should be able to move the same body through the space QR in the same time; this body will be moved in some conic section whose latus rectum is that quantity QT2 / QR , which would ultimately result when the line segments PR and QR are diminished infinitely. I place the circle [in the same category] with the ellipse in these corollaries, but I exclude the case where the body descends straight to the center.
Proposition 14—
Theorem 6
If several bodies should be revolved around a common center, and [if ] the centripetal force should decrease in the doubled ratio of the distances from the center, [then ] I say that the latera recta of orbits are in the doubled ratio of the areas that bodies describe by radii constructed to the center in the same time .
For (by Corollary 2, Problem 8) the latus rectum L is equal to the quantity QT2 / QR , which would ultimately result when points P and Q coalesce. But the very small line QR , given the time, is as the generating centripetal force, that is (by hypothesis), reciprocally as SP 2 . Therefore QT2 / QR is as QT2 × SP2 ; that is, the latus rectum L in the doubled ratio of the area QT × SP . Which was to be proven.
Corollary . Hence the total area of the ellipse, and, proportional to it, the rectangle [generated] by the axes, is in the ratio compounded of the halved ratio of the latus rectum and the whole ratio of the periodic time.
Proposition 15—
Theorem 7
With the same suppositions, I say that the periodic times in ellipses are in the three-halved ratio of the transverse axes .
For the minor axis is the mean proportional between the major axis (which I call transverse) and the latus rectum , and therefore the rectangle [generated] by the axes is in a ratio compounded of the halved ratio of the latus rectum and the three-halved ratio of the transverse axis. But this rectangle, by the corollary of the sixth theorem, is in a ratio compounded of the halved ratio of the latus rectum and the whole ratio of the periodic time. Let the halved ratio of the latus rectum be taken away from each side and there will remain the three-halved ratio of the transverse axis equal to the ratio of the periodic time. Which was to be proven.
Corollary . The periodic times in ellipses, therefore, are the same as in circles whose diameters are equal to the major axes of ellipses.
Proposition 16—
Theorem 8
With the same suppositions, and with straight lines drawn to bodies that touch the orbits in the same places, and with perpendiculars dropped to these tangents from a common focus, I say that the velocities of the bodies are in a ratio compounded of the ratio of perpendiculars inversely, and the half ratio of the latera recta directly . [See fig. A.20.]
From the focus S to the tangent PR drop the perpendicular SY , and the velocity of the body P will be reciprocally in the halved ratio of the quantity SY2 / L . For that velocity is as the smallest possible arc PQ described in a given particle of time, that is (by Lemma 7), as the tangent PR , that is (because PR is proportional to QT as SP to SY ), as (SP × QT ) / SY , or as SY reciprocally and SP × QT directly; and there is SP × QT as the area described in a given time, that is (by Theorem 6), in the halved ratio of the latus rectum . Which was to be proven.
Corollary 1 . The latera recta are in a ratio compounded of the doubled ratio of the perpendiculars and the doubled ratio of the velocities.
Corollary 2 . The velocities of bodies at the greatest and smallest distances from the common focus are in a ratio compounded of the ratio of distances inversely and the halved ratio of the latera recta directly. For the perpendiculars are now those very distances.
Corollary 3 . Thus the velocity in a conic section, at the smallest distance from the focus, is to the velocity in a circle at the same distance from the center, in the halved ratio of the latus rectum to that distance doubled.
Corollary 4 . The velocities of bodies orbiting on ellipses at mean distances from the common focus are the same as those of bodies orbiting
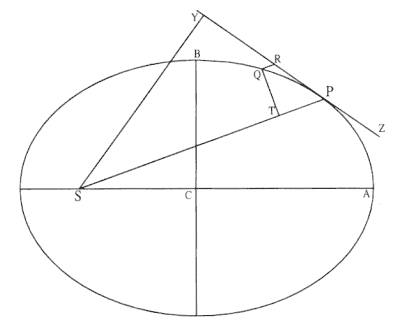
Figure A.20
Proposition 16.
on circles at the same distances, that is (by Corollary 6, Theorem 4), reciprocally in the halved ratio of the distances. For the perpendiculars are now [equal to] the semi-minor axes, and these are as the mean proportionals between the distances and the latera recta . Let this ratio be compound inversely with the halved ratio of the latera recta directly, and it will become the half ratio of the distances inversely.
Corollary 5 . In the same [figure] or in equal figures, or even in unequal figures, whose latera recta are equal, the velocity of a body is reciprocally as the perpendicular dropped from the focus to the tangent.
Corollary 6 . In a parabola the velocity is reciprocally in the halved ratio of the distance of the body from the focus of the figure; in the ellipse it is less than in this ratio, in the hyperbola greater. For (by Corollary 2, Lemma 14) the perpendicular dropped from the focus to the tangent of a parabola is in the halved ratio of the distance.
Corollary 7 . In a parabola the velocity is everywhere to the velocity of a body orbiting on a circle at the same distance in the halved ratio of the number 2 to unity; in the ellipse it is less than in this ratio, in the hyperbola greater. For by the second corollary of this [proposition], the velocity on the vertex of a parabola is in this ratio, and by the sixth corollary of
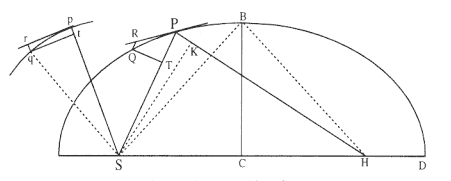
Figure A.21
Proposition 17.
this [proposition] and of the fourth theorem, the same proportion is preserved at all distances. Hence also in a parabola the velocity everywhere is equal to the velocity of a body revolving in a circle at half the distance; in the ellipse it is less, in the hyperbola greater.
Corollary 8 . The velocity of [a body] orbiting on any conic section is to the velocity of [a body] orbiting on a circle at a distance of half of the latus rectum of the section, as that distance to the perpendicular dropped from the focus to the tangent of the section. It is evident by the fifth corollary.
Corollary 9 . From this (by Corollary 6, Theorem 4) since the velocity of [a body] orbiting on this circle is to the velocity of [a body] orbiting in any other circle reciprocally in the halved ratio of the distances, similarly the velocity of [a body] orbiting on a conic section will become to the velocity of [a body] orbiting on a circle at the same distance, as the mean proportional between that common distance and half the latus rectum of the section to the perpendicular dropped from the common focus to the tangent of the section.
Proposition 17—
Problem 9
Supposing that the centripetal force be made reciprocally proportional to the square of the distance from its center, and that the absolute quantity of that force is known; there is required a line which a body will describe, when leaving from a given position with a given velocity along a given straight line . [See fig. A.21.]
Let the centripetal force being directed to point S be that which makes body p orbit in any given orbit pq , and let the velocity of this [body] at position p be known. Let the body P be released from the position P with a given velocity along line PR , and soon after let it deflect under the compulsion of the centripetal force into the conic section PQ . The straight line PR , therefore, will touch this at P .
In the same way let another straight line pr touch the orbit pq at p , and if from S perpendiculars are understood to be dropped to those tangents, there will be (by Corollary 1, [Proposition 16], Theorem 8) the latus rectum of the conic section to the latus rectum of the given orbit in a ratio compounded of the doubled ratio of the perpendiculars and the doubled ratio of the velocities, and therefore [the latus rectum of the conic section] is given. Let that be L .
In addition the focus S of the conic section is given. Let angle RPH be the complement of angle RPS to two right angles, and there will be given in position the line PH in which the other focus H is located. After the perpendicular SK has been dropped to PH , and the conjugate semi-axis BC has been erected, there is

To each side let 2KP x PH + L x (SP + PH ) - SP2 - PH2 be added and there will come L x (SP + PH ) = 2SP x PH + 2KP x PH , or, SP + PH to PH as 2SP + 2KP to L .
Hence PH is given in length as well as position.
Specifically, if the velocity of the body at P should be such that the latus rectum L would be less than (2SP + 2KP ), [then] PH will lie on the same part of the tangent PR with the line PS ; and thus the figure will be an ellipse, and it will be given both from the given foci S and H and from the [given] principal axis (SP + PH ).
But if the velocity of the body is so great that the latus rectum L is equal to (2SP + 2KP ), [then] the length of PH will be infinite, and as a result the figure will be a parabola having its axis SH parallel to the line PK , and from this it will be given.
But if the body is released from its position P with an even greater velocity, [then] the length PH must be taken on the other side of the tangent, and thus, with the tangent proceeding between the foci, the figure will be a hyperbola having its principal axis equal to the difference of the lines SP and PH , and from this it will be given. Which was to be found.
Corollary 1 . Hence in every conic section, given the principal vertex D , the latus rectum L , and the focus S ; the other focus H is given by taking DH to DS as the latus rectum is to the difference between the latus rectum and 4DS . For the proportion SP + PH to PH as 2SP to L , in the case of this corollary it would be DS + DH to DH as 4DS to L , and, by dividing, DS to DH as 4DS – L to L .
Corollary 2 . From there if the velocity of a body is given at its principal vertex D , the orbit will be found expeditiously, to be sure by taking its latus rectum to twice the distance DS in the doubled ratio of this given velocity to the velocity of the body revolving on a circle at the distance DS (by Corollary 3, Theorem 8), and then DH to DS as the latus rectum to the difference between the latus rectum and 4DS .
Corollary 3 . Hence even if a body should be moved on any conic section, and should be disturbed from its orbit by any impulse, the orbit can be ascertained in which it would afterward continue its course. For by combining the particular motion of the body with that motion which the impulse alone would generate, there will be obtained the motion with which the body, from the given place of the impulse, will depart from its position along a given straight line.
Corollary 4 . And if that body, pressed by some outside force, is continually perturbed, its course will become known as nearly as possible by collecting the changes which that force induces at certain points and by estimating from an analogy of the sequence the continual changes at intermediate positions.