Uniform Circular Motion:
The Polygonal Approximation

As his first wave of mathematical creativity came to a close early in 1665, other interests began to claim Newton's attention. Among them was his study of dynamics founded on the works of Galileo and Descartes. His first investigations into this subject were concerned with collisions and appear in his bound notebook, the Waste Book . The only date among the dynamical entries in the Waste Book was the marginalia, "Jan. 20th 1664" (1665 new style),^[3] which appeared in a section devoted to problems of collisions between two perfectly inelastic bodies.^[4] In this section, Newton developed and refined the concepts and axioms of motion that Descartes had set out

in 1644. In particular, Newton's statement of Descartes's concept of linear inertia originally appeared in Newton's Waste Book as follows:

Every thing doth naturally persevere in that state in which it is unlesse it bee interrupted by some externall cause, hence . . . A body once moved will always keepe the same celerity [speed ], quantity, and determination [instantaneous direction ] of its motion.^[5]

This Cartesian view that uniform rectilinear motion is the natural isolated state is crucial to Newton's dynamics, and an enlarged version of the statement appeared some twenty years later as the first law of motion in the Principia .

Newton extended the dynamics of intermittent colliding bodies to his analysis of bodies subject to a continuous force. He determined the nature of the force directed toward the center of a circle that will move the body uniformly around the circle (i.e., the solution to the direct problem of uniform circular motion). Newton envisioned a ball in uniform circular motion about a given center, and he sought information concerning the nature of the force impressed upon the ball. In a later work he demonstrated that force was directly proportional to the square of the speed and inversely proportional to the radius of the circle. In the section on uniform circular motion that first appears in the Waste Book , however, he did not explicitly obtain that result. The relationship he did obtain compared the magnitude of the change in motion produced by a sum of impulsive forces to the magnitude of the orbital motion. It is not the type of problem that would concern a contemporary physicist. Newton's analysis, however, and not the specific problem, is of interest.

In this analysis the circular path is approximated by a polygonal path of n sides (shown in fig. 3.1 as an octagon), where the number of sides of the polygon will ultimately increase without limit. The ball is envisioned to collide elastically (i.e., the speed or magnitude of the velocity does not change) with the circle or with the circumscribed polygon. At each collision, an impulsive force, directed toward the center of the circle, acts on the ball; between collisions no force acts on the ball and it moves with uniform rectilinear motion. The impulsive force acts for an extremely short time and produces a change in what Newton called the "quantity of motion in a body." He calculated the sum of the magnitudes of these changes in the quantity of motion, which he called "the force of all the reflections," and compared that sum to the quantity of motion of the body's constant orbital motion, which he called "the force of the body's motion." As the number of sides of the polygon was increased, the polygonal path approached a circular path, and the ratio of "the force of all the reflections" and "the force of the body's motion" was found to approach the value of 2p .

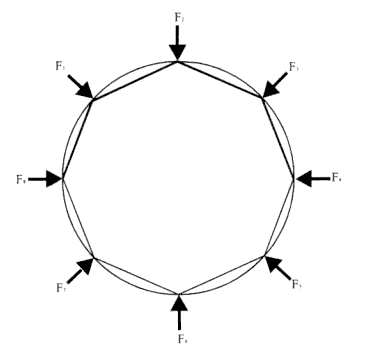
Figure 3.1
A circular path is approximated by an octagon. An impulsive force
F  acts on the body at each intersection of the circle and octagon.

To the modern eye, Newton's demonstration may seem insufficient because he did not calculate the mathematical structure of the force, directed toward the center of the circle, that is required to maintain uniform circular motion. Moreover, the modern reader will find that Newton's terminology is at variance with current usage. In modern terminology, the change in motion that Newton calculated at each collision is the magnitude of the change in the linear momentum Dmv . In the terms used in a modern textbook, this quantity Dmv is equal to the product of the force F and the small time of collision dt , where the product F × dt is defined as the impulse I . The magnitude of the vector linear momentum mv does not change at an elastic collision, only its direction. Hence, there is a finite change in the vector linear momentum Dmv provided by the impulsive force. There is no explicit use of such a modern vector resolution in Newton's text, but it resides implicitly in his analysis. One must not judge the value of the text from the viewpoint of modern expectations. Newton was exploring the phenomenon of uniform circular motion, and the techniques he developed in that exploration served him as a springboard for further analysis. The methods of analysis found in this early text provided a basis to continue into the more mature considerations to follow.

The text of Newton's analysis, which was written in English, is found on the first pages of the Waste Book and is dated about 1665.^[6] Because of the complicated but polished nature of the text, it has been argued that this passage may not represent Newton's first written thoughts on the subject of circular motion, even though it appears first in the book. He may have worked out the demonstration on loose sheets, revised it, and then transcribed it onto the blank first page.^[7] Newton makes an opening formal statement of the result he intends to demonstrate, and then he gives his detailed demonstration or proof of that opening statement. Below is this opening statement, simply intended to set forth the problem and solution. It will be followed by a detailed mathematical demonstration.