Subsurface Thermal Energy Estimates

The most widely applied estimates for thermal energy in magmatic systems underlying volcanic fields are based on the volume and age of the most recent volcanism associated with these systems. As discussed in Chapter 1, Smith and Shaw

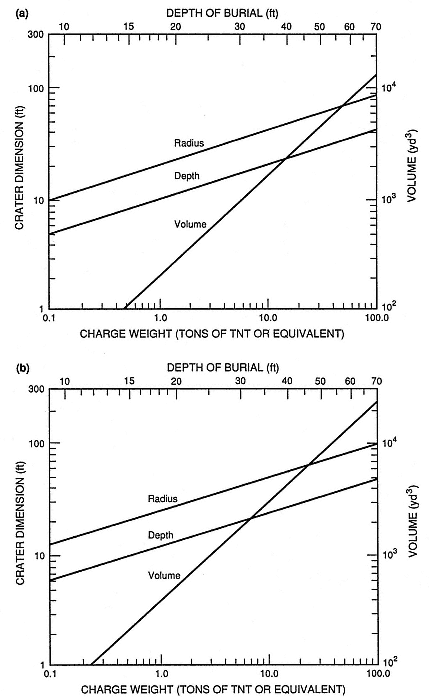
Fig. 2.4
Scaling crater dimensions and depth of burial to the explosive energy
equivalent of TNT. English units have been used for dimensions to preserve
the original logarithmic scale. For reference, TNT releases about
4.6 MJ/kg of energy, which is about four times the enthalpy released
by cooling 1 kg of magma from 1473 to 273 K. For optimum thermal
conversion efficiencies of 10% (see Fig. 1.21), a ton of erupted magma is
roughly equivalent to 0.025 tons of TNT. Comparison of the plots for
explosions in (a) dry rock and (b) soil indicates that larger craters
typically form in soils.
(Adapted from Johnson, 1971.)

(1975; 1979), have used this approach in estimating thermal energies of magmatic systems. Volumes are inferred from caldera size, vent distribution, seismic shadows, fracture patterns, topographic uplift, geophysical anomalies, and estimates of silicic ejecta volume. If a volcano produces chemically evolved (nonbasaltic) products—especially those spanning andesite through dacitic and rhyolitic compositions—it is very likely that magma has formed a crustal magma chamber and has differentiated on its path to the surface. Because differentiation is a time-dependent process, evolved compositions can indicate prolonged residence in the crust, during which a significant amount of heat flowed from the magma into crustal rocks. The larger the magma chamber, the larger is the thermal resource, which is a measure of the amount of economically useful energy.

The thermal resource (H_tr ) of a magmatic heat source is proportional to the volume of rock (V_tr ) that exceeds the minimum temperature for economic heat extraction (q_tr )

Table 2.2 summarizes the parameters of Eq. (2-6), which outlines aspects of modeling heat flow from a crustal magma body such as the silicic caldera depicted in Fig. 2.5. The general nature of the function for V_tr in Eq. (2-6) is based on the solution of heat flow in and around the magma body—a calculation that is discussed later in this chapter.

Because numerous petrologic experiments have shown that magma-chamber temperatures range from about 900 to 1200°C, depending upon their composition, it is possible to use heat content data (Bacon, 1977) and magma-chamber volume to calculate thermal energy. Smith and Shaw (1975) based their conclusions about magma-chamber volumes on models of magma and heat transport in the earth's crust, observations of exhumed intrusive bodies, petrologic constraints on the production of evolved magmas, and geophysical studies of active igneous systems. Smith et al . (1978) and Shaw (1985) extended this approach to the study of volume-periodicity relationships for a wide variety of volcanoes; their results, along with those of Crisp (1984) and Wadge (1984), support the basic premise that extruded volumes as well as caldera areas and other geophysical measurements can be related to magma-chamber volumes. For silicic eruptions, conservative estimates of magma-

chamber volume are ~10 times greater than those for the dense-rock equivalent (DRE) volume of silicic products erupted. For composite cones (discussed in Chapter 7), this ratio of intrusive to extrusive volumes may range from <2 to >10. In the case of basaltic volcanoes, the relationship is uncertain because these volcanoes may not have high-level crustal magma reservoirs.

Pyroclastic Rock Volumes

Pyroclastic rock volumes provide the simplest method of estimating magma-chamber volumes for eruptions of evolved magmas in many localities. Several methods can be used to calculate the volumes of pyroclastic products. Froggatt's (1982) comparison of three types of volume estimations is based on (1) mathematical models of aerial dispersal, (2) field measurements of area and volume vs thickness, and (3) measurements of crystal-to-glass ratios.

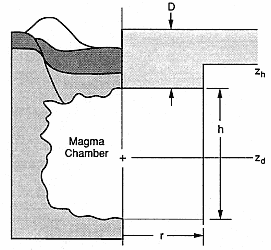
Fig. 2.5
Heat flow from a magma body beneath a silicic
caldera is modeled for situations in which the
rock is unsaturated. In such areas, the thermal
resource might be exploited by using the hot
dry rock (HDR) technology described later in
this chapter (Rowley, 1982). The light shading
denotes country rock, and the dark shading
represents caldera fill and outflow rocks
(mostly volcanic).

The first of these volume estimation methods is predicated on the general assumption that pyroclastic deposits exponentially decrease in thickness with distance from the vent if there is no significant ponding of the deposit in topographically low areas (Froggatt, 1982; Pyle, 1989). Measurements of maximum thickness (L_i ) and distance over which the deposit thickness halves (r_h ) are sufficient to characterize the volume of a deposit of circular isopach distribution.

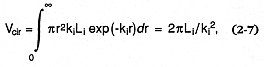
where k_i = [ln (2)]/r_h . For deposits of elliptical distribution, one may assume a constant eccentricity (e_e ) given by e_e = (1-b_e )^1/2 , where b_e = r_y /r_x . For this case, r_h is measured along both the major and minor axes of the ellipse to give r_x and r_y , respectively, and k_i = [ln (2)]/r_y . The volume integral reflects this ratio:

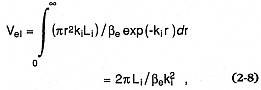
The second method requires many field measurements of thickness for logarithmic plots of isopach area or volume vs thickness. These plots make it possible to extrapolate volumes of deposits for which minimum thicknesses are not exposed in the field area. For each isopach, a minimum volume is found by multiplying its thickness by its mapped area. A sum for all isopachs gives the total volume. Froggatt (1982) found that plots of log-volume vs log thickness were superior for extrapolations.

The third method was proposed by Walker (1980) to estimate eruptive volumes when a significant proportion of ash (<2-mm diameter) has been carried great distances from the vent and therefore cannot be measured in the field. This method is based on the assumptions that all crystals, being

denser than glass, fall out near the vent and that large pumices show average magmatic ratios for glass to crystals. It is possible to calculate the proportion of vitric ash missing from the deposit by measuring the crystal abundance in both ash and pumices and then determining the difference in enrichment. Walker (1981) suggested, however, that this third method may overestimate the deposit volume.

By recalculating the volumes of volcanic products, including tephra and lavas, to DRE (V_dre@ 0.6 V for tephra and V_dre@ V for lavas) and by assuming that they represent some fraction of the magma-chamber volume (for example, 0.1 for silicic volcanic fields), it is possible to obtain a measurement of the thermal resource described in Eq. (2-6). For instance, Fig. 2.6 depicts a young, silicic pyroclastic deposit for which V = 1.0 km³ . The thermal resource (H_tr ) of the magma chamber (volume = 6.5 km³ ) is shown as a function of the kinetic energy of the eruption that emplaced the deposit. Assuming a conservative 1% recovery of the thermal resource, the potential electrical energy resource for this system is estimated by tapping 250°C fluids from the associated hydrothermal or hot dry rock system (discussed later). About 850 kJ/kg is available from the saturated vapor produced; if one allows for a conservative 14% turbine cycle efficiency for saturated vapor cooled to 50°C, then wells producing ~600 tons/hour would generate ~19 MWe (see Appendix D).

Heat-Flow Calculation

There is one important limitation of the simple thermal resource estimation described above: the volcanic products must be erupted from a crustal magma chamber that is sufficiently young to retain much of its initial heat. This limitation has been studied in detail by Smith and Shaw (1975; 1979) and applied to numerous volcanic fields where the volume and age of underlying magma chambers have been estimated from both geomorphological constraints (for example, caldera size, vent distribution, and volume of silicic pyroclastic deposits) and geophysical anomalies. Thus, for the 1.0-km³ pyroclastic deposit shown in Fig. 2.6, one can apply the cooling calculations of Smith and Shaw (1975) as shown in Fig. 1.5. Assuming that (1) the pyroclastic deposit age reflects the time over which the magma chamber has cooled from solidus temperatures, and (2) the deposit represents about one-tenth of the magma-chamber volume, then it follows that the deposit would have to be younger than ~10,000 yr for exploitable temperatures to exist in and around the magma chamber. This estimate is conservative even if the magma chamber has cooled as a result of hydrothermal convection in roof rocks above the magma chamber. If cooling were solely conductive, the age limit could be extended to nearly 20,000 yr.

In making a detailed estimation of thermal resource (H_tr ), the thermal resource volume function (V_tr ) of Eq. (2-6) can be modeled by heat flow calculations. A first-order model assumes heat flow by conduction only, which requires solution of Fick's second law of diffusion:

for which H = the heat content or enthalpy (which is directly proportional to temperature) and k_t = the rock thermal diffusion coefficient, which can be directionally and spatially dependent. Equation (2-9) can be conveniently solved with an explicit numerical procedure (Appendix E) for a variety of geometric, initial temperature, and diffusivity conditions. An approximation for convective transport is included in the numerical procedure to better estimate heat flow in areas where hydrothermal convection is important. The procedure, given in FORTRAN in Appendix E, can be adapted for personal computers. It solves thermal diffusion in two dimensions for a variety of rocks, geologic structures, and effective x and y diffusion coefficients. The problem

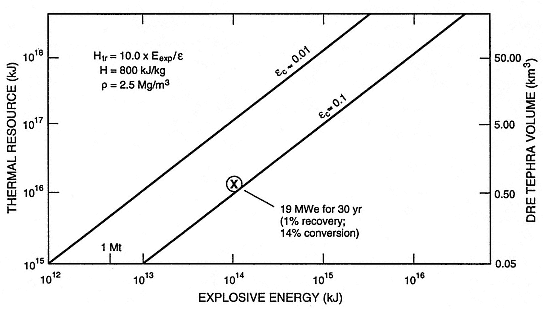
Fig. 2.6
Thermal resource (total heat contained in a magma body) and tephra volume are related to explosive
energy [1 Megaton (Mt) equivalent] by the conversion efficiency (e_c ) of the magma's thermal
energy to explosive energy (kinetic) during an eruption. For this plot, it is assumed that
the tephra volume of an eruption represents 10% of the magma body volume (Smith, 1979),
the magma density (r ) = 2.5 × 10³  kg/m³ , and the magma body is young enough to have a heat
content (H) = 800 kJ/kg. This example (X) depicts a volcano that recently erupted a 1.0-km³
pyroclastic deposit (at 0.65 km³  DRE) with an explosive energy equivalent of about 24 Mt
(e_c  = 0.077), which represents a magma chamber with a thermal resource (H_tr ) of 1.3 × 10¹⁶  kJ.
Assuming about 1% of the magma chamber's thermal resource can be exploited with ~14%
conversion to electrical energy, a geothermal plant could produce
nearly 19 MWe for 30 yr by either hydrothermal or hot dry rock methods.

for this calculation is set up in a manner similar to that outlined in Eq. (2-6). The results of this calculation give a two-dimensional representation of V_tr for any time after formation of a magma chamber. One should be cautious when using this routine to model measured geothermal gradients; the case described here is considered mathematically ill-posed because solutions may not be unique.

Figure 2.7 shows results of the above heat flow calculation for a cooling, subvolcanic pluton 2.5 km wide and 4 km below the surface. The results are compared for 100 and 200 ka of cooling, with and without a convective zone above the magma chamber. At an age of 100 ka, the two-dimensional thermal resource volume (V_tr ) within the calculated area ranges from 2 to 9 km² (the latter value is for the model with convection). This result is based on a volume of rock with temperatures above 150°C within 3 km of the surface. From Fig. 2.7b, one can see from thermal gradients that V_tr would be slightly greater after 200 ka of heat flow. Although the convection model produces a higher near-surface thermal gradient than the nonconvective model does, the gradient can not be reliably projected to greater depths. Such modeled or measured geothermal gradients are an significant initial step in evaluating the geothermal potential of an area. Figure 2.8 plots several general types of thermal gradients and their general relationship to geothermal potential.

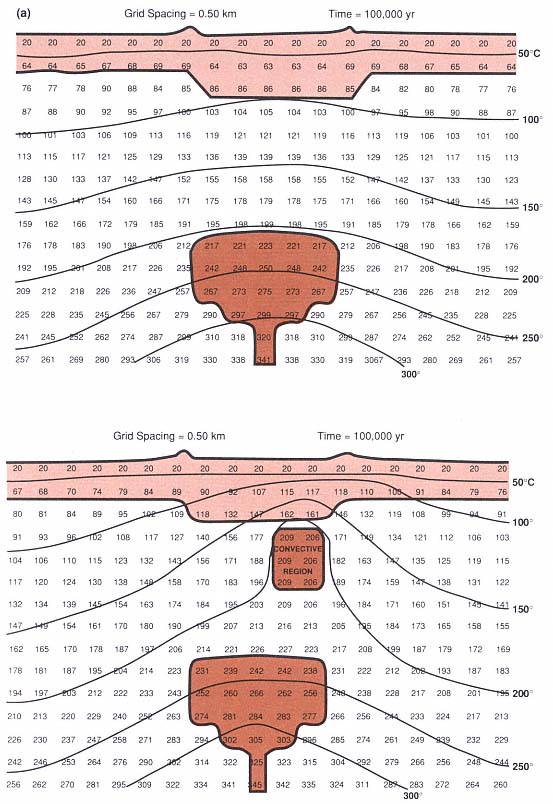
Fig. 2.7
(a) Results of heat flow calculation for a 2.5-km-wide magma body (dark shading) at a depth
of 4.0 km below a caldera filled and surrounded by volcanic rocks (light shading). This problem is
similar to that outlined in Fig. 2.5. The top plot depicts purely conductive heat flow;
the bottom plot includes the effects of a convective region (dark shading) below one side of
the caldera. The numbers in the grid show rock temperatures (°C) and temperature contours
after 100,000 yr of cooling.

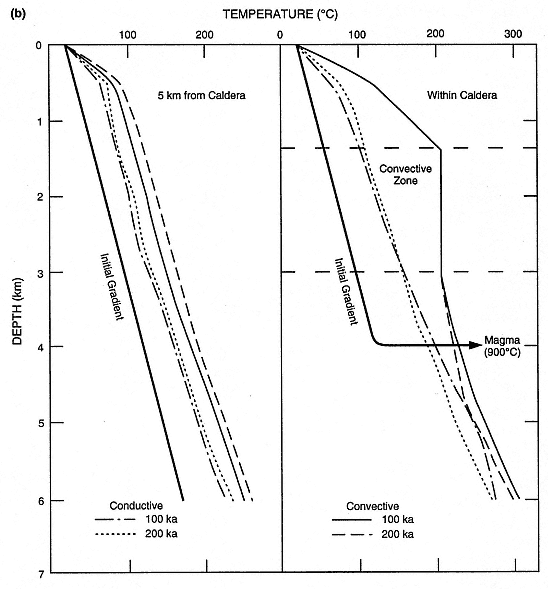
Fig. 2.7
 (b) Plots of calculated thermal gradients at 100 and 200 ka of
cooling compare conductive and convective gradients for locations 5 km from the caldera
and within the caldera itself. Note the high gradient for convective heat flow in the upper 1.0 km;
if projected to greater depths, this gradient would give false predictions of maximum temperatures.

Hot Dry Rock Geothermal Energy

Most of the geothermal heat associated with volcanic fields is contained in rocks some distance from zones of formation and fracture permeability. For example, the Valles caldera in New Mexico has an estimated resource base of 8,425 × 10¹⁸ J (Smith and Shaw, 1975); of that resource base, the hydrothermal component is ~90 × 10¹⁸ J. This component represents a great deal of energy, but it is only ~1% of the entire resource base (Brook et al ., 1978). In most geothermal systems associated with volcanic fields, ~95% of the thermal resource is hot dry rock; exceptions are geothermal systems in carbonate rocks where the permeability is high.

The world's very substantive hot dry rock resource can be developed if attempts to create man-made hydrothermal circulation systems are successful. The basic concept involves drilling a hole into a thermal anomaly, fracturing the rock by stimulation techniques, and drilling a second hole into the fractured rock adjacent to the first well (Smith et al ., 1975). Water is circulated down one well, percolates through the mass of hot, fractured rock, and is extracted at high temperatures from the second well. Hot dry rock experiments have been studied in several countries, but the most extensive experiments are being conducted at Fenton Hill, just outside the west rim of the Valles caldera in New Mexico. These experiments were successful with a circulation loop through fractured rock at a depth of 3 km, where the bottomhole temperature is 197°C; present experiments are testing a similar loop at a depth of 5 km in rocks with a temperature of ~320°C. New concepts being explored will develop this source of alternate energy, which is referred to as heat mining (Armstead and Tester, 1987).

If a conventional hydrothermal well penetrates high-temperature zones with no fluids, an attempt should be made to open existing pathways or create new fractures by using stimulation techniques such as pressurizing the well with pumped fluids. If this procedure does not work, a hot dry rock system can be realistically considered: the first well will have provided a great body of data about the geology and thermal regime that can be used to design a manmade geothermal system.