1—
Nucleonics

The neutron was a frustrating object in the laboratory. It went everywhere, refusing obedience to the electric and magnetic fields to which other particles submitted; it provoked a wide—indeed, too wide—range of nuclear transformations; and it was dangerous to living things. The danger, as we know, inspired the Laboratory to invent neutron therapy and caused all large-cyclotron laboratories to surround their machines with a protective barrier, usually of water. Most of the neutrons entering the water quickly slowed to thermal velocities by sharing their energy in collisions with hydrogen atoms and either died in their bath or emerged relatively harmless into the experimental space. The promiscuity of neutrons—their easy union with most nuclei—usually increases as their velocity diminishes, as Fermi had found; in order to explore nuclear responses to their wanton behavior, it was very desirable to work with neutrons of uniform speed. Interest in making homogeneous or "monochromatic" beams of neutrons grew strongly in 1936, when Bohr offered his liquid-drop model of the nucleus in explanation of the anomalously high absorption by certain substances of bombarding particles of particular energies. To study his idea further—to find the energies of particle beams with which various nuclei "resonated"—required control of the beam velocity. And just here the chargeless neutron, the most promising tool for probing resonances, eluded the will of the experimenter.

Although neither the cyclotron nor its keepers at Berkeley were temperamentally adapted to the careful study of resonances, control of neutron beams was of central interest there. Shortly after Fermi's discovery of the power of slow neutrons, several members of the Laboratory discussed production of a roughly monochromatic neutron flux by interrupting the deuteron beam to the

cyclotron's beryllium target. The general idea, according to Alvarez's reference to it in 1938, was to shut off the radio frequency potential intermittently and to turn on an amplifier attached to a neutron detector when the accelerating potential cut out. The only neutrons counted by the chamber would be those created in the beryllium during the deuteron bursts (radio frequency on) with such velocities that they could reach the detector during its live time (radio frequency off). The idea was temporarily dropped when the Laboratory learned of a rough-and-ready adaptation of an old technique to the new purpose. Physicists at Columbia ran the output from a Rn-Be source through paraffin and then into a chopper consisting of two disks, each made in alternate sections of duraluminum and cadmium, which are, respectively, transparent and opaque to slow neutrons. When the disks spin around the same axis, only slow neutrons that passed through a transparent section in the first disk with a speed that brought them to a similar section in the second could reach the detector.^[3]

The urgency of the study of resonance absorption—"the point of greatest interest today in nuclear physics," to quote British opinion in the fall of 1938—reopened the matter. The neutron chopper did not give monochromatic rays, among other reasons because fast neutrons could pass right through the disks. Two new solutions to the problem were offered that same fall, one by Alvarez, who developed the scheme discussed in the Laboratory in 1935, and the other by a group around G.P. Thomson at Imperial College, London. By then both parties had been working at their projects for some time.^[4] A team at the University of Utrecht may

[3] Alvarez, PR, 54 (15 Oct 1938), 609; Dunning et al., PR, 48 (1935), 704, letter of 7 Oct; Lawrence to Pegram (Columbia), 24 Oct 1935 (4/8), reporting a trial by Stern, then visiting Berkeley, to measure velocities of slow neutrons. The final report of the Columbia experiments by the junior member chiefly involved is Fink, PR, 50 (1936), 738–47, rec'd 13 Aug.

[4] Nature, 142 (17 Sep 1938), suppl., 520, report of a discussion on nuclear physics at the British Association for the Advancement of Science, 18 Aug 1938, led by Bohr, quote. Alvarez first presented his method in public at the APS meeting in San Diego, 22–24 June 1938, abstract in PR, 54 (1938), 235; the British group, in the persons of P.B. Moon and C.D. Ellis, gave first notice at the BAAS meeting just mentioned and first results on absorption in Fertel et al., Nature, 142 (5 Nov 1938), 829, letter of 10 Oct.

also have hit on a solution independently, although their first published description of their method was prompted by a preliminary report of Alvarez's.^[5]

The machines built by Thomson and by Alvarez highlight typical features of British and California approaches to instrumentation. The Imperial College group used as source Oliphant's version of the Cockcroft-Walton machine, capable of 150 to 250 kV; Alvarez used the 37-inch cyclotron, then delivering deuterons at 8 MeV. Alvarez interrupted his deuteron beam by suppressing the current at the plates of the rf tubes supplying the accelerating potential; the method required considerable electrical power and some electronics and yielded long deuteron bursts (4 msec) that were not very well defined. The British modulated the current through the discharge tube that created the deuterium ions by amplifying the current from a photocell activated by a light beam interrupted by a tuning fork or rotating shutter; it required little power and gave bursts of about 0.5 msec.

Both parties sent the neutrons from the beryllium target through a standard paraffin "howitzer" (fig. 9.1) and into a cadmium-lined pipe to remove stray particles (cadmium has an extraordinary appetite for slow neutrons); and both employed as primary detector the by then standard BF₃ ionization chamber activated by alpha particles from the reaction B¹⁰ (n,a )Li⁷ . Alvarez fed the output from his chamber into an amplifier regulated by an elaborate electronic timing circuit to process pulses only during a short time after each deuteron burst; by setting the time in accordance with the distance from the beryllium to the detector, he could arrange that only neutrons of (or, rather, around) a selected velocity would be counted. The British continuously applied the output of their chamber and fed the result to an oscilloscope, which indicated the times of the deuteron bursts as well as the times of the associated chamber pulses. A motion picture of the oscilloscope traces preserved them for analysis. The Dutch competition planned to work much in the British manner, obtaining their neutrons from a d-d reacton in a HT tube, modulating the accelerating potential, and synchronizing the detecting amplifier

[5] Milatz and Ter Horst, Physica, 5 (Aug 1938), 796.

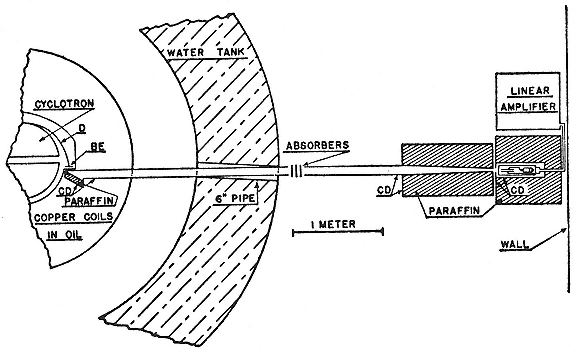
Fig. 9.1
Alvarez's setup for collimating and detecting fast neutron beams. The beam arising from deuterons on
beryllium runs through a cadmium-lined pipe in the cyclotron's water shield. The cadmium takes out slow
neutrons. Alvarez, PR, 54  (1938), 613.

and oscilloscope with the modulator. They criticized Alvarez's method for permitting the detection of only one neutron velocity at a time.^[6]

This property made Alvarez's instrument what might be called a monochromator: although its chamber received an inhomogeneous beam, the amplifier insured that only neutrons of the selected velocity were counted. Did this mean that the experimenter could consider that he had a homogeneous beam? A deep question that, or perhaps only a matter of words: it called forth expression of a philosophy of science, a very rare, and perhaps unique utterance from the Laboratory in the 1930s. "On the operational viewpoint," Alvarez wrote, in reference to the then widely accepted teachings of Percy Bridgman, "one is justified in asserting that the beam is composed solely of thermal neutrons." The British had no need for Bridgman's philosophy. Their instrument was a velocity spectrometer: the intervals between the chamber pulses and the associated deuteron bursts showed the velocity distribution among the slow neutrons reaching the detector. Their cumbersome method of oscilloscope recording and analysis worked only for small fluxes, however. They ordinarily counted about 25 neutrons a minute. Alvarez's Berkeley rate was 1,000/min.^[7]

The definitive form of the neutron velocity spectrometer was made by R.F. Bacher and his students at Cornell. It followed the British by modulating the deuteron source and Alvarez by measuring timed neutrons through a system that split the signal from the BF₃ detector, routing one half to a continuously active amplifier and the other to one alive only when neutrons of the velocity of interest arrived. They obtained very nice records of resonance that confirmed consequences of Bohr's nuclear theory as calculated by Bethe. And—a matter that proved more important to the common man—they measured neutron absorption in the isotopes of uranium. Their design was further perfected at Illinois and at

[6] Alvarez, PR, 54 (1938), 235, and ibid., 609–17, rec'd 20 Aug 1938; Fertel et al., Nature, 142 (5 Nov 1938), 829, and PRS, A175 (1940), 316–31; Milatz and Ter Horst, Physica, 5 (1938), 796.

[7] Alvarez, PR, 54 (1938), 609–10; Fertel et al., PRS, A175 (1940), 322. On the popularity of Bridgman, Schweber, HSPS, 17:1 (1986), 61–7.

Stanford in 1941. By then the British team had long since retired into the scientific war against Germany.^[8]

Alvarez continued with neutronics in collaboration with a refugee from Germany's war against science, Felix Bloch, who had joined the physics department at Stanford in 1934. Their experiment—the exact determination of the magnetic moment of the neutron—was a perfect matching of skills, interests, and ambitions. Bloch had given its theory in 1936, after a visit to Heisenberg that convinced him that Stanford's deepest and quickest route to a place in nuclear physics was via an experimental program in neutronics. He discussed the measurement at the periodic joint Stanford-Berkeley physics seminar and interested Laslett and Alvarez, who mentioned it as a possible application of his monochromator.^[9] The business did not seem overly promising, however, since earlier attempts to detect magnetic behavior in the neutron had failed and the very concept of a magnetic moment of an uncharged particle smacked of oxymoron. There seemed no other explanation, however, of the results obtained by Otto Stern and his associates O.R. Frisch and Immanuel Estermann with their hydrogen beams in Hamburg.

According to classical theory, the ratio between the magnetic moment µ and the angular momentum p of a spinning sphere of charge e and mass M is µ/p =e /2Mc . One might expect therefore that in quantum theory the magnetic moment of an elementary charged particle with angular momentum sh /2p , where s is its spin quantum number, would be µ=(eh /4pmc )s . But in the case of the electron, spectra required both µ_e =eh /4pMc and s = 1/2; a contradiction supressed by introducing a numerical factor g into the relationship, µ/p =g_ee /2mc , and setting g_e = 2. The Dirac theory of the relativistic spinning electron produced spontaneously, among many other marvels, the value g_e =2. It was therefore assumed that if the theory applied to protons, s_p =1/2, g_p =2, and the relevant magneton, let us call it µ₀ , would be smaller than µ_e in the ratio of the masses of the electron and proton, m/M . But in 1933 Stern and his associates announced that the proton

[8] Baker and Bacher, PR, 59 (1941), 332–48, rec'd 30 Dec 1940; Bethe, "History" [1960], 3; Haworth and Gilette, PR , 69 (1946), 254; Fryer, PR , 70 (1946), 235–44.

[9] Chodorow et al, Bloch , vii; Alvarez, PR, 54 (1938), 609.

moment, µ_p , amounted to around 5µ₀ . A quick measurement on the heavy water sent by Lewis showed that the moment of the deuteron was smaller than the proton's, although its spin was twice as great. By 1936, owing to further work by Stern in Pittsburgh, where he set up after the Nazis closed his institute, and by Rabi, who greatly improved the technique, the magnetic moments of proton and deuteron were established at between 2.5 and 3.0 µ₀ and around 0.8 µ₀ respectively.^[10]

The obvious way to square the numbers was to assume that their difference measured the moment of the neutron. Since the deuteron was known to have a spin of 1 and since indirect evidence made the neutron's spin 1/2, it appeared that the spin, and hence the moment, of the deuteron's constituents added together, whence µ_n » –2µ₀ , the minus sign signifying the relationship between spin and moment characteristic of the electron. But how to explain that µ_n does not equal zero? Following a suggestion made by G.C. Wick, who drew on Fermi's theory of beta decay, Bloch and other theorists supposed that the neutron spends some of its time dissolved into an electron and a proton and that in this state "it" can interact with a magnet and so show a moment. Since µ_e» 2000µ₀ , the neutron need not spend much of its time in pieces in order to show an average moment of –2µ₀ . Since Fermi's theory treats protons and neutrons on the same footing, the excess moment of the proton was supposed to arise from its temporary disaggregation into a positron and a neutron. Since by the symmetry of the theory, this excess should be equal and opposite to the apparent neutron moment, µ_p + µ_n » µ₀ , which came close to the deuteron moment.

All this was, of course, only inference, an effete proceeding necessary, perhaps, in astrophysics, but unmanly with objects produced by the billions in the laboratory. Bethe supposed that knowledge of the neutron moment would continue to come exclusively from such indirect arguments: "the magnetic moment of the neutron is hardly accessible to direct measurement." Bloch thought otherwise and offered a calculation of the effects of µ_n on

[10] Rigden, HSPS, 13:2 (1983), 339–53; Bethe and Bacher, RMP, 8 (Apr 1936), 91–2, give µ_p =2.9µ₀ and µ_d =0.85µ₀ from the latest experiments of Rabi's group.

the scattering of very slow neutrons. The calculation suggested that µ_n might be deduced by scattering slow neutrons from magnetic atoms and by passing them through thin magnetized plates. (Slow neutrons are required in order that their wavelength have about the same size as the atoms scattering them.) Since the total transmission through the plates should depend upon their relative magnetization, Bloch hoped that with such a setup he could obtain a direct indication of the existence of the neutron's suppositious moment.^[11]

Bloch set something going. Bethe and Livingston organized an experiment at Cornell that showed a 2 percent difference in transmission through plates with parallel and antiparallel magnetism and calculated that the result was not incompatible with Bloch's theory and µ_n = –2µ₀ . Julian Schwinger then published a long calculation treating neutron scattering by Dirac theory that predicted a larger effect in the transmission experiment than Bloch had computed. In commenting on a draft of Schwinger's paper, Bethe, fresh from his try at µ_n , reaffirmed his view that direct measurements were not likely soon to improve upon subtraction of µ_p from µ_d : "It will be a long time before the direct determination will give the neutron moment to anywhere near this accuracy," which he reckoned at 0.15 µ₀ .^[12] Next, Rabi proposed a refinement in his method of spin flipping that J.R. Dunning and his students at Columbia immediately adapted to Bloch's transmission experiment.^[13] They showed that the transmission of neutrons through a thin magnetized plate increases with the magnetization and thickness of the plate and with the slowness of the neutrons and that Rabi's method could partially unpolarize the partially polarized beam emerging from the first plate (fig. 9.2b).

[11] Bloch, PR, 50 (1936), 259–60, and Inst. Henri Poincaré, Ann., 8:1 (1938), 70; Bethe and Bacher, RMP, 8 (Apr 1936), 91, 205–6; Rigden, HSPS, 13:2 (1983), 253–4.

[12] Hoffmann, Livington, and Bethe, PR, 51 (1937), 214–5, rec'd 3 Dec 1936; Schwinger, PR, 51 (1937), 544–52; Bethe, "Comments to Schwinger," 15 Jan 37 (HAB, 14/22/976).

[13] Rabi, PR, 51 (1937), 652–4, rec'd 1 Mar. Frisch, von Halban, and Koch, Nature, 139 (1937), 756, and PR, 53 (1938), 720, and Bloch, in a letter to Frisch, 12 Jan 39 (Frisch P), and in Alvarez and Bloch, PR, 57 (1940), 112, claimed to have invented a similar apparatus independent of Rabi.

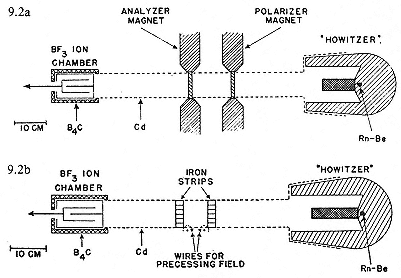
Fig. 9.2
Methods for detecting the nuclear moment of the neutron: 9.2a, Bloch's;
9.2b, Rabi's. In both cases fast neutrons from alpha particles on beryllium
shoot from a paraffin howitzer and into a cadmiumcoated pipe. In the first
case, the polarization of the neutrons is changed by passing through
magnetized iron; in the second case, by traversing a precessing magnetic
field. Powers, PR, 54  (1938), 834, 836.

Then, with the help of further calculations by Schwinger, they deduced from the amount of transmission with and without spin flipping that µ_n is negative and lies between 1 and 3 µ₀ . No revelation that; and, because they could not determine with any accuracy the strength and variation of the magnetic field causing the flips, they could say no more. "Further refinements are in progress."^[14]

While Dunning's associates were flipping neutrons Rabi's way, a group at Copenhagen led by Frisch, who had settled into Bohr's institute in 1934, independently suggested the use of a depolarized field in an experiment of Bloch's type. They worked with small fields and smaller effects; they could count only about 100 transmitted neutrons/minute from their weak Rn-Be source; they

[14] Powers, Carroll, and Dunning, PR, 51 (1937), 1112–3, letter of 18 May; Powers et al., PR, 52 (1937), 38–9, letter of 19 June.

learned nothing more than that a value of µ_n = –2µ₀ was not incompatible with their experiments, and they gave up. "It would be hopeless to discuss these results any further and to try and enclose the magnetic moment of the neutron between definite limits."^[15] Meanwhile Bloch, who did not agree that Schwinger's calculation came closer to reality than his, had proposed to Laslett that he try to find effects of µ_n by scattering off nickel and iron. Laslett went to work at about the same time the Cornell group did; unlike them, he found no positive results, nothing that would permit any useful quantitative statement about µ_n . Bloch himself tried to detect something useful in the scattering of neutrons (obtained from d-d synthesis) on cobalt. But in the fall of 1937 many, perhaps most, nuclear physicists shared the "pessimism about the moment of the neutron"—the belief that experimental difficulties of direct determination of µ_n would not soon be overcome—expressed by Bloch's friend Egon Bretscher.^[16]

In June 1938 Bloch and Rabi, then visiting Stanford, went to Berkeley to watch Alvarez demonstrate his neutron monochromator (plate 9.1). Bloch returned to Stanford, to have a try at µ_n with a Rn-Be source; but he did no better than others, and came to think that useful quantitative results could only be obtained "when an intense neutron source is available that will make it possible to use monochromatic neutrons."^[17] In September, he and another émigré, Hans Staub, decided to build a high-tension apparatus for the purpose by exploiting a disused 170 kV x-ray outfit and the d-d reaction; but before they had finished, as Staub tells the tale, Bloch "quite unexpectedly [!] got the apparatus" to work with Alvarez and the Berkeley cyclotron. Was the surprise

[15] Frisch, von Halban, and Koch, Nature, 139 (1937), 756, letter of 7 Apr, and ibid., 1021, letter of 12 May; PR, 53 (1938), 721–3. Frisch et al. used the remanent field in their magnetized plates, some 10 kG; the Columbia group (Powers, PR, 54 (1938), 832–3) required fields almost twice as large to produce any noticeable magnetic scattering, as did Alvarez and Bloch, PR, 57 (1940), 112, who accordingly doubted that the results of Frisch et al. were "significant."

[16] Bloch, PR, 51 (1937), 994; Livingston to Lawrence, 2 Dec 1936, and Lawrence to Livingston, 15 Dec 1936 (12/12); Laslett and Hurst, PR, 52 (15 Nov 37), 1035–9, rec'd 24 Aug; Bloch to Bretscher, 1 Sep 37 (Mrs. Bretscher).

[17] Cooksey to Lawrence, 17 June 38 (4/21); Alvarez and Bloch, PR, 57 (1940), 112, and Bloch to Frisch, 12 Jan 39 (Frisch P); Bloch, Inst. Henri Poincaré, Ann., 8:1 (1938), 78.

Lawrence's willingness to allow a lengthy bit of physics to tie up the machine? Alvarez and Bloch began to work together in the late fall of 1938. The final report of the Columbia measurements (µ_n is "probably" around –2 ± 0.5µ₀ ), published about that time, gave them an easy mark to better. It is doubtful that the news that Frisch planned another go, with the enthusiastic support of Bohr, would have caused Alvarez and Bloch any anxiety.^[18] They had the barren field of exact neutron magnetonics to themselves.

Their great advantage over earlier investigators was the neutron flux from the 37-inch cyclotron. Whereas the Columbia and Copenhagen groups had counted a few million neutrons, Alvarez and Bloch counted two hundred million in their year of experimenting. The hundredfold increase in beam allowed them to detect and correct many subtle instrumental effects that menaced their measurement; although for their definitive value of µ_n they counted only four million neutrons, a number readily obtainable from a good Rn-Be source, they needed the previous two hundred million, which could have been obtained only from an accelerator. The final experimental design is shown schematically in figure 9.3.

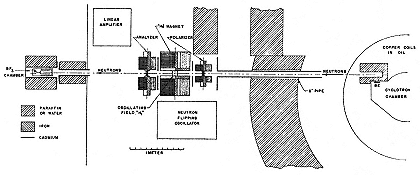
Fig. 9.3
Alvarez and Bloch's definitive experimental setup. Compare fig. 9.1. Alvarez
and Bloch, PR, 57  (1940), 116.

Neutrons from a beryllium target, struck by deuterons and slowed down by passage through paraffin, ran down a cadmium-lined tube stuck through the water shielding around the cyclotron. The

[18] Staub in Chodorow et al., Bloch , 194–5; Powers, PR, 54 (1938), 827–8, rec'd 22 Sep; Frisch to Meitner, 19 Sep 1938 (Frisch P).

paraffin so successfully removed unwanted fast neutrons that it proved unnecessary to use Alvarez's modulated beam as originally intended; and the cadmium swallowed slow neutrons so effectively that the entire arrangement introduced a strong collimated beam consisting primarily of slow neutrons to the thin piece of iron that, when magnetized, acted as a polarizer. The design profited perhaps from the contemporaneous work of Aebersold on the collimation of neutron beams for therapy.

The partially polarized neutrons entered the flip space, where they felt two magnetic fields: a constant one, H₀ , to provide direction for the orientation of the magnetic moments, and an oscillating field, H₁ , to incite the flips. The analyzer consisted of a second piece of iron in a second powerful electromagnet. The detector was the standard BF₃ chamber. The electromagnets at either end were borrowed, one from a colleague who used it for Zeeman spectroscopy, the other from Shell Development Company; the coil energizing the field H₀ had been cannibalized from the 11-inch cyclotron and the solenoid that made H₁ was wound from flat copper strips through which the neutrons passed in entering and leaving the flip region. The currents energizing H₀ and H ₁ were kept regular by tapping them from the cyclotron's automatically stabilized supply.^[19]

A measurement consisted of reading the number of neutrons registering in the detector as H ₀ swept through the value H _n that maximized the number of flips. (This occurs when f_n , the frequency of the oscillating field, equals the frequency with which the neutron moments process around H₀ .) The underlying concept: with H ₁ off and polarizer and analyzer magnetized in parallel, a certain flux of neutrons will be counted; with H₁ on, a fraction of the neutrons will have their moments reversed, somewhat fewer than before will pass the analyzer, and a smaller flux will register. When this reaches a minimum, resonance obtains and µ_n comes immediately from the value of the precessional frequency: µ_n = f_nh /2H_n . Or, rather, it comes immediately after the values of f_n and H_n have been determined. Alvarez and Bloch invented a method of measuring these quantities that allowed greater

[19] Alvarez and Bloch, PR, 57 (1940), 116–8, rec'd 30 Oct 39.

accuracy than standard methods would have given. Write µ_n = g_n µ₀ , g_n being the value of the neutron moment in nuclear magnetons. From the resonance condition of the experiment, f_n = 2H_ng_n µ₀ /h . But from the resonance of protons in the cyclotron, f_p = eH_p /2pMc , we have f_p = 2H_p µ₀ /h ; hence g_n = (f _n /f_p )(H_p /H _n ). The measurement reduces to finding the ratios of frequencies and fields, which was not difficult, and requires no knowledge of the values of the absolute constants. In effect, the cyclotron supplies the values of e/Mc .^[20]

The counting itself was done electronically via a clever circuitry that monitored the unsteady neutron output of the cyclotron. (At best the cyclotron ion beam could be held constant to 1 percent; Alvarez and Bloch worked to an accuracy of a tenth of a percent.) The circuit divided the counting time into intervals of a few seconds during which the flipping fields were alternately on and off. When off, the amplified output of the BF₃ chamber was routed to one of a pair of counters; when on, to the other; comparison of the two allowed correction for fluctuations in the initial beam strength. After making this correction, Alvarez and Bloch got the nice sharp dip of resonance indicated by figure 9.4. With the values of frequency and field thus implied, they obtained g _n = –1.935, which they judged to be good to about 1 percent.^[21] At the time the latest Columbia values for µ_p and µ_d were 2.785µ₀ and 0.855µ₀ respectively, both to an accuracy of 0.7 percent. Consequently, to within experimental error the old relation, µ_d = µ_p + µ_n , still held, although it seemed very unlikely that the intrinsic moments of the constituents should not be altered to some extent by their combination. It was primarily to achieve these measures and amplify their effects that Bloch and his co-workers undertook to build a cyclotron at Stanford. His subsequent

[20] Cf. Norman Ramsey in Trower, Discovering Alvarez (1987), 30–1.

[21] Alvarez and Bloch, PR, 57 (1940), 120–1, quoting an error of ±0.02µ₀ , which they later raised to ±0.03µ₀ without explanation (PR, 57 (15 Nov 1940), 352). This did better than Bloch hoped for in January 1939, when, after Bohr told him about Frisch's latest try, Bloch responded with his and Alvarez's first results (between –1.9 and –2.3 µ₀ ), and anticipated an eventual accuracy of 2 percent. Bloch to Frisch, 12 Jan 39 (Frisch P). Six months later they had fixed on the average, –2.1 µ₀ ; Lawrence to Smyth, 12 June 1939 (16/32).

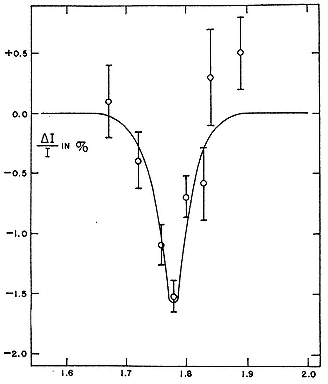
Fig. 9.4
Alvarez and Bloch's definitive measurement. The abscissa is
the current energizing H₀  in arbitrary units; the ordinate, the
fractional change (in percentage) of the intensity of the
neutron beam under the influence of the field. Alvarez and
Bloch, PR, 57  (1940), 120.

development of a technique for precise measurement of nuclear magnetic moments, and the work he did with it, brought Bloch the Nobel prize for physics for 1952, a handsome payoff for his switch to experimental neutronics sixteen years earlier.^[22]

[22] Alvarez and Bloch, PR, 57 (1940), 121–2; Rigden, HSPS, 13:2 (1983), 367; Bloch, Nicodemus, and Staub, PR , 74 (1948), 1025–45. Alvarez and Bloch's result was high, and Rabi's low, but both within the estimated error; with more precise measurements after the war, the additivity of the moments failed to hold by 0.0223µ₀ .