Chapter XIII
Quantum Beauty
Schrödinger's Equation
The News
From March 1926 on, Erwin Schrödinger published a series of memoirs on a new theory of quantization based on his famous equation. In a conception derived from de Broglie's, stationary states were identified with stationary modes of electron waves in atoms. The corresponding calculations required none of Göttingen's transcendent algebra; they rested on a mathematical technique well known to anyone versed in the classical theory of waves. Within this new framework Schrödinger could very quickly and simply solve many of the standard problems of quantum theory. Surprisingly, the results appeared identical with those given by matrix mechanics, whenever comparison could be made.[72]
Dirac's first reaction to this spectacular invention was essentially negative. A wave theory of matter, he thought, had to be just as inconsistent as the wave theory of light. Moreover, there was no need for a new quantum mechanics, since there already was one, the foundation of which he did not question. A letter from Heisenberg of May 1926 changed his opinion. It explained how the Schrödinger equation could be used as a tool to derive matrices satisfying the fundamental equations of quantum mechanics. One just had to solve this equation (the time-independent version,
[72] Schrödinger 1926a, 1926b, 1926d, 1926e.
which was the only one available at that time) for eigenfunctions yn with the energies En ,
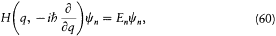
and form the matrix
associated with the quantum variable g (q, p ) according to the rule
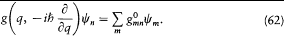
While such a development is possible only if the functions yn span the space of y -functions (that is, if the condition of "completion" is met for the original wave equation), Heisenberg, unencumbered by this type of consideration, immediately proceeded to prove his assertion.[73]
First of all, the matrix associated with the product xy of any two quantum variables is the product of the matrices respectively associated with x and y . This is a trivial result for the modern reader since the equation (62) just says that 
is the matrix representation of an operator in the base of the yn 's. In this scheme the relation
immediately follows from (62) and
Finally, the time dependence of matrices introduced ad hoc in equation (61) warrants, as usual, the result that
The above consideration is so simple that one may wonder why the Schrödinger equation was not derived from the original quantum mechanics before it was inferred from de Broglie's notion of matter waves. At
[73] Heisenberg to Dirac, 26 May 1926, AHQP. Dirac's first reaction to wave mechanics is inferred from Heisenberg's comment in this letter: "I quite agree with your criticism of Schrödinger's paper with regard to a wave-theory of matter. This theory must be inconsistent, so just like the wave-theory of light." The connection between matrix and wave mechanics was simultaneously discovered by several theoreticians, among whom were Pauli (letter to Jordan of 12 Apr. 1926, PB , no. 131) and Schrödinger 1926c. Unlike Pauli and Heisenberg, Schrodinger noted the role of the condition of completion.
Göttingen, theoreticians had been for some time inhibited by Heisenberg's doctrine of observability, which confined quantum mechanics to the methods of matrix algebra. In early 1926 Born, Wiener, and Lanczos attempted to remove this restriction, and would probably have reached the Schrödinger equation (they came very close to it) if only there had been enough time before Schrödinger's publication. On the other side of the Channel, Dirac would have been in the best position to discover the new wave equation since his conception of q -numbers was not bound to any specific representation. For instance, he could have noticed that a differential operator made a good representation of the momentum quantum variable. However, he did not, because his intellectual adventure remained restricted by the analogy with the method of uniformizing variables, as we just saw.
The Crop
In compensation for not having found it, both Heisenberg and Dirac made faster progress in exploiting the Schrödinger equation than did Schrödinger himself. In his letter to Dirac, Heisenberg announced that he already knew how to solve the helium atom. Within the three following months Dirac reached no less important results. As usual, he put a touch of relativity in the new equation, that is to say, he extended the substitution
to
This gives instead of equation (60) the so-called "time-dependent Schrödinger equation"
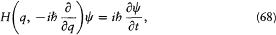
which Schrödinger obtained at the same time through less straightforward means.[74]
[74] Heisenberg to Dirac, 26 May 1926, and Heisenberg 1926a, 1926b; Dirac 1926f, 661-663. Schrödinger had only an a posteriori justification for this form of the time-dependent equation: it led to the correct dispersion formula. He had earlier used another equation,
[]The stationary solutions leading to the energy spectrum are the ones for which
Consequently, they evolve in time according to
The functions yn , now directly engender Heisenberg's time-dependent matrix according to a rule similar to (62):
Dirac published this most adequate presentation of the relation of Schrödinger's equation to his quantum mechanics in the first part of a paper entitled "On the theory of quantum mechanics." In the second part he gave his argument about the impossibility of action-angle variables for several indistinguishable particles, together with a reference to Heisenberg's observability principle:
In Heisenberg's matrix mechanics it is assumed that the elements of the matrices that represent the dynamical variables determine the frequencies and intensities of the components of the radiation emitted. The theory thus enables one to calculate just those quantities that are of physical importance, and gives no information about quantities such as orbital frequencies that one can never hope to measure experimentally. We should expect this very satisfactory characteristic to persist in all future development of the theory.[75]
Along the same line, Dirac argued that for a pair of (noninteracting) electrons a single wave function had to be associated with a given pair of individual stationary states m and n , in order that no distinction could be made between the transitions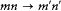 
and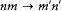 
. Accordingly, the simplest type of wave function for the compound system had to be
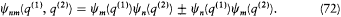
In general, Dirac took the wave function of a system of identical particles to be a totally symmetrical or antisymmetrical function of the positions of the particles. The symmetrical case led to the Bose-Einstein statistics, while the antisymmetrical one led to Pauli's exclusion principle and to the Fermi gas, according to procedures that have now become standard.
[75] Dirac 1926f, 666-667.
Up to that point, Dirac's recourse to the Schrödinger equation was simply a new way to achieve a specific matrix representation of his q -numbers. In a subsequent paper on the Compton effect he noted: "The wave equation is used merely as a mathematical help for the calculation of the matrix elements, which are then interpreted in accordance with the assumptions of matrix mechanics." The last part of "On the theory of quantum mechanics" contained, however, a first departure from this limited viewpoint. There Dirac considered the case of a time-dependent Hamiltonian, more specifically the one corresponding to an atom subjected to an electromagnetic field. He calculated the function y through a now standard perturbative method, the first step being the development of the wave function in terms of the stationary solutions of the unperturbed Schrödinger equation:
0
Then he interpreted the squared modulus |cn |2 as the number of atoms to be found in the stationary state n , when a large assembly of atoms is subjected to the perturbation. "We take |cn |2 instead of any function of cn ," he commented, "because . . . this makes the total number of atoms remain constant." Indeed, the hermiticity of the Hamiltonian operator implies the constancy of S n |cn |2 .[76]
With this rule Dirac derived Einstein's B coefficients for induced atomic transitions. Quantum mechanics, once equipped with Schrödinger's equation, was now able to say something about radiation processes (although not yet anything about spontaneous emission). The procedure leading to this progress once again had some resemblance to Eddington's principle of identification. A new equation, the time-dependent Schrödinger equation, was first introduced by formal considerations; then a permanence property, the conservation of the norm Sn |cn |2 of the wave function, oriented the discussion of the physical meaning of the solutions.
Transformations
After this quick and rich crop of fundamental results, Dirac pondered about the general interpretation of quantum mechanics. There were basically two ways to draw observable information from the fundamental
[76] Dirac 1926g, note added in proof (to compare with Gordon's approach), 507; Dirac 1926f, 674. Dirac sent this paper for publication in late August 1926, that is, a month after Born gave a talk at the Kapitza club (29 July 1926) on "collisions in wave mechanics," with the same interpretation of |c n | (see further on pp. 334-335). The absence of any reference to Born's considerations in Dirac's paper suggests that he reached his conclusions independently.
equations of quantum mechanics. One could either construct matrices that would then be interpreted à la Heisenberg, or one could try to guess a direct interpretation of Schrödinger's y . As we just saw, Dirac initially favored the first approach, although with his interpretation of the c 's he already had started using the second.
Partial Interpretations
In the last semester of 1926, Dirac became aware of several new points of contact between theory and observation, derived either from the matrix camp or from the wave camp. Originally, Schrödinger regarded the y -function as describing some substantial oscillation within the atom. He quickly realized, however, that this "heuristic viewpoint" could not be taken too literally, since for a quantum system involving more than one particle, the oscillations no longer occurred in the ordinary physical space but in the 3n -dimensional configuration space associated with the n particles. In his fourth installment of wave mechanics, completed in June 1926, he therefore reinterpreted the wave function in the following way:
|y |2 is a kind of weight-function in the configuration space of the system. The wave-mechanical configuration of the system is a superposition of many—strictly speaking, of all —onfigurations allowed in the mechanics of a point. . .. For the ones who like paradoxes, the system can be said to occupy all kinematically conceivable positions at the same time, but not "in the same degree."[77]
Nevertheless, Schrödinger still regarded the fluctuation of the electric density (in ordinary space) calculated through y as real, certainly more real than the one attached to the corpuscular picture. There was in his opinion more truth in the continuous evolution of the y than in the quantum leaps of the matrix theory.[78]
In the same month, Max Born compromised between particles and waves. His purpose was to give a quantum-mechanical treatment of collisions between atoms and particles. As we saw in part B (p. 253), after the Bothe and Geiger experiment disproving the BKS theory he had tried with Jordan to come back to Einstein's and Slater's original idea of a wave guiding light quanta. Born had given up this attempt for about a year when he decided to use it as a heuristic analogy for the wave-mechan-
[77] Schrodinger 1926e, 135.
ical collision problem. Just as free light quanta were guided by a plane monochromatic "ghost" wave, the free asymptotic motion of colliding particles had to be represented by a plane monochromatic Schrödinger wave; the distribution of scattering angles was obtained by developing the scattered wave in terms of such plane waves:
After some hesitation Born decided that |a (k)|2 (not |a (k)|) would give the scattering probability in the direction of k. In a slight generalization, if y is developed in a basis of stationary states yn according to
then |cn |2 determined the relative probability of the state n (Born used the word Háufigkeit , which refers to the statistical conception of probability), as in Dirac's perturbation theory. Accordingly, quantum mechanics gave no deterministic prediction of an observable quantity, the scattering angle. Born believed this feature to be fixed and central, in conformity with his earlier intuition that the world was essentially a kind of lattice (see part B, p. 196): "I myself am inclined to give up determinism in the atomic world." For the consolation of deterministic thinkers he then introduced the notion of statistical determinism: "The motion of particles is ruled by probability laws, but the probability itself propagates in accordance with the causal laws."[79]
In a letter to Heisenberg of 19 October 1926, Pauli combined Born's idea of a probability wave with Schrödinger's "weight functions" in configuration space: the expression
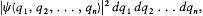
he wrote, had to give the probability for the system to be found in the configuration q 1 , q2 , . . ., qn (actually within a little volume dq1dq2 . . . dq n ). Closer to Born's collision case, one could also build a probability density
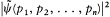
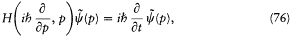
[79] Born 1926a, 867 for the first quotation; Born 1926b, 804 for the reference to Einstein's Gespensterfeld , 827 for the second quotation. See Konno 1978.
[80] Pauli to Heisenberg, 19 Oct. 1926, PB , no. 143.
for which
Pauli further remarked that Born's scattering probabilities were intimately connected with a special matrix already introduced in the Born-Heisenberg-Jordan paper. Up to a proportionality coefficient they were the matrix elements of the interaction potential with respect to the stationary states of the unperturbed Hamiltonian. This suggested a deep-lying connection between Heisenberg's original interpretation of matrices and the new probabilistic interpretation of Schrödinger's waves.
During the following month Heisenberg made some progress in clarifying the connection. His motivation was to show that Schrödinger's continuum theory was unsuited for giving a correct intuitive understanding of the internal energy fluctuations taking place when two atoms are interacting. Suppose two identical atoms originally in the stationary states m and n to be weakly coupled. A resonant interaction takes place, which according to Heisenberg corresponds to discontinuous exchanges of the energy values Em and En between the two atoms. In this view the energy of one of the atoms can take only the values Em and En , whereas in Schrödinger's view it can take all intermediate values given by the continuous y -evolution.[81]
There was a way, Heisenberg argued, to decide between the two conceptions. Matrix mechanics could certainly not give the energy H1 of one of the atoms as a function of time, but it was nonetheless able to determine the probability for this energy to take a given value. One just had to assume that, for any dynamic variable, the diagonal elements of the corresponding matrix gave its average value in the various stationary states of the global system; according to this rule, one could derive the average value of any function of H1 , for example the moments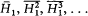 
and therefore the probability distribution of H 1 . The result read
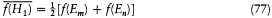
in conformity with Heisenberg's intuition of discontinuous switches.
Moreover, the probability distribution of H1 was explicitly given by the squared moduli of the elements of a matrix S that had been introduced in the three-men paper and related the matrices g of the dynamic variables of the unperturbed system (no coupling between the two atoms) to the
[81] Heisenberg 1926c.
matrices G of the corresponding variables of the perturbed system according to
There is no need here to give the details of Heisenberg's argument, since they will result from Dirac's much more general investigation of relations of the above type.
The Formal Apparatus
When he set out to elaborate his own interpretation of quantum mechanics, Dirac was aware of Schrödinger's fourth memoir, had heard Born speak on collisions at the Kapitza club (on 29 July 1926), and had seen the manuscript of Heisenberg's fluctuation paper. He was dissatisfied with the multiplicity of partial, disconnected, and sometimes contradictory interpretations. But he saw an important advance in Heisenberg's considerations, for they indicated how to derive probability distributions from the original matrix formulation of quantum mechanics.[82]
However, Heisenberg had limited his interpretative inquiry to simple examples, a result of his search for an intuitive understanding of quantum mechanics. Dirac, following his Eddingtonian bent, returned to his fundamental equations of quantum mechanics and formulated the preliminary interpretative problem very generally: as the search for c -numbers connected with the q -numbers satisfying these equations. Since the action-angle variables could no longer help in this problem, one needed to consider all matrix systems capable of representing the q -numbers, without including the restriction that action variables should be diagonal. Even Heisenberg's limitation to a diagonal (total) energy matrix had to be avoided, since it introduced a premature interpretative element.
The fundamental equations read
(in order to present the equations more compactly, they will be written for the case of one degree of freedom, even though the discussion will refer to the general case). Dirac first noticed that one goes from one matrix
[82] Dirac 1927a, 621. Dirac's transformation theory is discussed in Jammer 1966, 300-305, and Kragh 1990, 38-42.
representation of these equations to another through a transformation of the type
Interestingly, Dirac had learned much earlier from Göttingen's theoreticians that a relation of this type existed between any two sets of canonical coordinates (in Heisenberg's representation). But at that time he believed the remark to be of no practical use, for it had no obvious classical counterpart.[83] In late 1926 he was completely freed from the inhibitory effects of his desire to maintain a close classical analogy, and regarded instead the form (80) of transformation as most essential.
Representations are likely to be of physical interest, Dirac went on, only if they make a given set x of dynamic variables diagonal. The set is said to be complete if there is only one representation for which it is diagonal. Dirac found it convenient to represent the transformations from one representation to another by symbols x '/x' ) with c -number values, wherein x ' and x' represent the diagonal elements of two complete sets and x. In this notation the equation (80) becomes
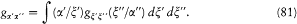
(to the mathematicians' horror, gx'x" was not to be regarded as the same function of x'x" as g x 'x " is of x 'x ").
Although this type of formula seems to be limited to the case of continuous spectra, Dirac took it to also cover discrete and mixed spectra, assuming the integral to represent a sum in the discrete case. The continuous case itself called for a few mathematical tricks. First of all, in order to be able to write the transformation (x '/x ") corresponding to the identity (b = 1), Dirac introduced the now famous "d -function," some kind of limit of sharply peaked functions such that
for any (regular) function f . Then the choice
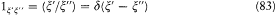
makes (81) an identity, as required. As usual, Dirac did not worry about a rigorous mathematical construction (Laurent Schwarz's distributions later provided such a construction). To him as to his precursor Heaviside,
[83] Dirac 1926a, 564-565: "These formulae do not appear to be of great practical value."
it was sufficient that the symbolic manipulations of the d -function did not lead to contradictions.[84]
The next easier matrix after the identity is the one representing x in its own scheme. It must be a diagonal matrix with elements x ', which leads to the expression
assuming the d -function to generalize Kronecker's symbol dij in the continuous case. Dirac further showed that the matrix hx 'x " when h is canonically conjugate to x is given by
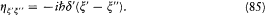
The proof required a few d -gymnastics performed on the commutator
[x , h ]:[85]
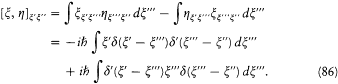
Performing an integration by part on the last integral gives
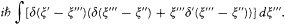
The second term of this integral cancels the first integral in (86), while the first provides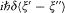 
, that is, 
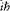times the identity matrix, which completes the proof.
On the basis of the general transformation formula Dirac could calculate the matrices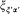 
and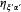 
in a representation where the rows refer to x and the columns to a :
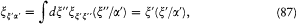
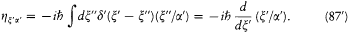
[84] Heaviside introduced discontinuous functions like "Heaviside's step function" (which he designated as Q), and also its time derivative, that is, a d -function (which he designated as pQ , with p = d/dt ), to help the solution of hnear inhomogeneous differential equations, for instance in Heaviside 1893, 133 of the Dover reprint (1950). Dirac had used d -functions in several anterior publications, but without a specific notation.
[85] Dirac's multiplications of singular distributions can be justified from the modern point of view, because they occur only within convolutions.
More generally, any function g(x , h ) expressible as a sum of products of and h allowed the mixed representation:
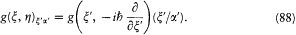
In order to prove this identity, it is sufficient to show that when it holds for f and g , it also holds for f + g and fg . The first part of the latter assertion being trivial, we are left with the second one:
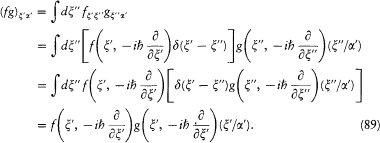
The identity (88) played a central role in Dirac's transformation theory. As a first outstanding application of it, let us choose g to be the Hamiltonian H,x the position coordinates, and x a complete set of dynamic variables commuting with H :
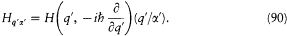
Using a relation similar to (87), we also have
and, therefore,
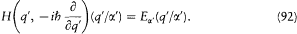
In this way Dirac could have discovered the Schrödinger equation before Schrödinger, if only he had earlier exploited the freedom of representation of his fundamental equations. At least he was able to realize a posteriori that Schrödinger's y was nothing but the transformation from a scheme in which the position variables are diagonal to one in which the energy is diagonal. It further appears that there are as many equations
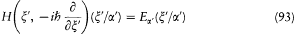
as there are choices of x , since the above deduction is not limited to the case of position coordinates.
Finally, the Dirac-Schrödinger evolution for a transformation (x '/a '), when x is a constant of the motion (a = 0),
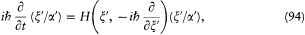
follows from the fundamental equation
This is easily proved by calculating the matrix elements of the two members of this equation in the a -scheme:[86]
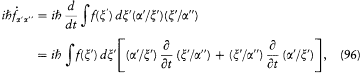
while
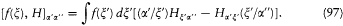
The function f and the values of a ' and a " being arbitrary, the expressions are identical if and only if
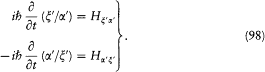
These two equations are equivalent in any Hermitian scheme for which
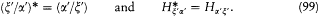
Combined with the identity (88), they lead to the time-dependent Schrödinger equation (94), as stated.
The formal apparatus of quantum mechanics was now thoroughly unified, Schrödinger's equation being harmoniously blended with the fundamental equations ruling q -numbers. According to Dirac's own criteria, the whole theory was impressively beautiful, for it displayed a transformation apparatus as elegant and powerful as those of relativity or Hamiltonian dynamics.
[86] The following proof differs slightly from Dirac's.
Dirac was now ready to attack the interpretation problem proper. He started with the following words:
To obtain physical results from the matrix theory, the only assumption one needs make is that the diagonal elements of a matrix, whose rows and columns refer to the x 's say, representing a constant of integration, g say, of the dynamical system, determine the average values of the function g (x , h ) over the whole of h space for each particular set of numerical values for the x 's in the same way in which they certainly would in the limiting case of large quantum numbers.[87]
There is an unfortunate obscurity in what Dirac meant by the "limiting case" here. The following is a very plausible interpretation.
As a first remark, the term "constant of integration" in the above extract is misleading. Dirac just means that he is considering a dynamic variable at a given instant of time , as made clear by an earlier footnote in the paper. If so, the matrix element gz 'z ' is independent of the choice of the Hamiltonian H . Its interpretation is obtained by exploiting this independence and provisionally considering the Hamiltonian to commute with all the x 's. Then gz 'z ' represents the time average of g, according to Heisenberg's previous interpretation of matrices, or from a comparison with the high quantum-number limit in the Bohr-Sommerfeld theory; besides, the conjugate variables h are, in the Bohr-Sommerfeld theory, phases (or "angles" in the action-angle formulation) varying linearly in time, so that the time-averaging is here identical with an h -averaging. In the general case for which H and x do not necessarily commute, it is therefore natural to assume that gz 'z ' represents the average of g when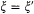 
and h is uniformly spread.
Very cleverly, Dirac deduced a complete interpretation of the quantum formalism from this seemingly limited assumption. His magic wand was the identity
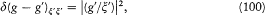
which simply results, for any complete set g of dynamic variables, from
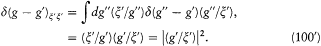
The function d (g - g' ) is nonzero only for g ~ g' . Therefore its "h -average" for x = x ' is nothing but the fraction of the h -space for which g = g' when
[87] Dirac 1927a, 637.
x = x '. In other words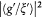 
is the relative probability that g = g' knowing that x = x . According to Dirac, this answered all the questions "to which the quantum theory [could] give a definitive answer." These questions, he added, were "probably the only ones to which the physicist could give an answer."[88]
Welcome To Copenhagen
Dirac completed his transformation theory in December 1926 in Copenhagen, where he was treated like a hero. There he learned that Pascual Jordan had formulated a similar theory, though from a different point of view. Instead of studying transformations from one matrix representation of the fundamental equations to another, Jordan examined transformations from one canonical pair, say (x , h ), to another, say (a , b ), in a given representation. His theory was similar to Dirac's insofar as it led to unitary operators b generating the canonical transformations according to
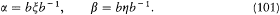
Superficially, this point of view might have seemed closer to the transformation theory of classical dynamics, which also related canonical pairs. In reality Jordan departed much more from the classical model than did Dirac: he defined canonical conjugation not by commutation rules transposed from the Poisson algebra but by broader axioms at the quantum level. For instance, anticommuting variables like the spin operators Sx , Sy were conjugate in Jordan's sense.[89]
Dirac could not be sympathetic to such a wild deviation from classical canons. Later he even rejected some interesting products of Jordan's conception like the notion of anticommuting quantized fields.[90] One might wonder, however, why he did not view transformations as relating canonical pairs, since this was, after all, the conception that dominated his own work before the advent of Schrödinger's equation. The reason might well have been psychological: to somebody who had just discovered that his dear uniformizing variables failed to solve the problem of atoms with more than one electron, other canonical transformations had little chance to stand at the foreground of a fundamental exposition of quantum mechanics. That Jordan somehow succeeded in adopting this conception did not persuade Dirac to change his position. In his first lectures on quantum
[88] Ibid., 641.
[89] Jordan 1927a, 1927b; Dirac compares the two approaches in Dirac to Jordan, 24 Dec. 1926, AHQP.
[90] See Darrigol 1986.
mechanics he did try to lay out his competitor's theory, but he quickly returned to his own, which he found simpler and more elegant.[91]
There is one feature of Dirac's original transformation theory that is likely to surprise the modern quantum physicist: the notion of state vector is completely absent. It was in fact introduced later by Weyl and von Neumann, and subsequently adopted by Dirac himself. In 1939 Dirac even split his original transformation symbol (x '/a ') into two pieces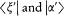 
, the "bra" and the "ket" vectors.[92] The mathematical superiority of the introduction of state vectors is obvious, since it allows—albeit not without difficulty—an explicit construction of mathematical entities (rigged Hilbert spaces) that justify Dirac's symbolic manipulations. There was also a more physical advantage to the notion of state vector: it placed the superposition principle in the foreground, which pleased Bohr, who set wave-particle duality at the core of complementarity. Perhaps modern-day interpreters of quantum mechanics should nevertheless remember that there exists a formulation of quantum mechanics without state vectors, and with transition amplitudes (transformations) only.
In this original conception Dirac had nothing to call the state of a system, except the old (q, p ) configuration. This state of affairs conditioned his conclusion to "The physical interpretation of the quantum dynamics":
It may be mentioned that the present theory suggests a point of view for regarding quantum phenomena rather different from the usual ones. One can suppose that the initial state of a system determines definitively the state of the system at any subsequent time. If, however, one describes the state of the system at an arbitrary time by giving numerical values to the coordinates and momenta, then one cannot actually set up a one-one correspondence between the values of these coordinates and momenta initially and their values at a subsequent time. All the same one can obtain a good deal of information (of the nature of averages) about the values at the subsequent time considered as functions of the initial values. The notion of probabilities does not enter into the ultimate description of mechanical processes; only when one is given some information that involves a probability (e.g . that all points in h -space are equally probable for representing the system) can one deduce results that involve probabilities.[93]
Such a view was still too conservative to please Copenhagen authorities. Once again Dirac was charged with having overplayed the classical anal-
[91] Dirac [1927c].
[92] Dirac 1939b. The Principles (Dirac 1930), already in the first edition, introduced the state vectors before the transformations.
[93] Dirac 1927a, 641.
ogy. Nevertheless, the success of the transformation theory was immediate, with respect to both interpretation and application of quantum mechanics. From the transformation connecting two conjugate variables,
Heisenberg deduced the uncertainty relations; and he showed that the re-suiting limitations in the definition of conjugate quantities exactly corresponded to the concrete limitations of double measurement processes. On the more practical side, the transformation theory gave a general method of quantizing everything, since, contrary to Heisenberg's original matrix mechanics, it was completely independent of the nature of the dynamic system under consideration. Dirac's radiation theory, published in early 1927, was the first of a long list of spectacular successes resulting from this method.[94]
As Dirac would have said, Nature was being seduced by mathematical beauty. The transformation theory equaled the aesthetic qualities that he had earlier contemplated in classical theories. In the fall of 1927 Dirac explained this to his first students in quantum mechanics:
The quantum theory has now reached a form . . . in which it is as beautiful, and in certain respects more beautiful than the classical theory. This has been brought about by the fact that the new quantum theory requires very few changes from the classical theory, these changes being of a fundamental nature, so that many of the features of the classical theory to which it owes its attractiveness can be taken over unchanged into the quantum theory.[95]
Summary and Conclusions
In March 1926 Schrödinger published the first of a series of memoirs in which he tried to reduce atomic theory to a mechanics of matter waves la de Broglie. Dirac's first reaction was negative, for he already had placed his hopes in another quantum mechanics. Yet, taking a suggestion of Heisenberg, he promptly exploited the Schrödinger equation, if only as a "mathematical help in calculating matrix elements." In the summer of 1926 he thus reached some of the basic notions of modern quantum
[94] 1927b. Equations (87) and (88) for x = q and a = p give together a differential equation leading to equation (102). Dirac 1927b. On subsequent applications of transformation theory see Kragh 1990 and Darrigol 1984, 1986.
[95] Dirac 1927c, introduction.
mechanics. Most important, in the name of Heisenberg's principle of observability he introduced symmetrical and antisymmetrical wave functions of the configuration of a set of identical particles, and proceeded to connect respective symmetry classes with Bose's statistics on the one hand, and Pauli's exclusion principle on the other. This provided the general basis both for quantum statistics and for the calculation of properties of atoms with several electrons (but Heisenberg was the one who first solved the helium atom within the new mechanics).
In another important innovation, Dirac presented a method for treating time-dependent perturbations; with it he could derive general expressions for Einstein's transition probabilities. In this case he gave the Schrödinger waves a more direct interpretation (not via Heisenberg's matrices), as a means to calculate the (statistical) probability of the system to be in a given stationary state. Characteristically, he presented this interpretation as being suggested by an invariance property (the invariance of the norm of the wave function).
In the summer of 1926 there were several other contributions to the interpretation of the two or three distinct quantum formalisms that had arisen, proposed both by Schrödinger and by the Göttingen group. Schrödinger, retreating somewhat from his original mechanistic conception of matter waves, now regarded the wave function as a (nonstatistical) sort of "weight function" in the configuration space of the system. While treating the problem of particle scattering, Born related the (outgoing) wave function to the scattering probability. Pauli, blending Schrödinger's notion of a weight function with Born's statistical conception, interpreted the squared modulus of the wave function as giving the probability for the system to be found in a specified configuration, and he vaguely suggested a connection between these probabilities and the transition probabilities of Heisenberg's theory. Finally, Heisenberg made the latter connection entirely explicit within the context of a suggestive example, the energy fluctuation of an atom when coupled with an identical atom (quantum-mechanical resonance): the relevant probability was obtained by taking the squared modulus of the elements of the unitary matrix connecting the stationary states of the coupled system to those of the uncoupled system.
In the fall of 1926 Dirac decided to bring some order to this proliferation of partial interpretations. In accordance with Eddingtonian methodology, and in contrast with Heisenberg, he did not start from specific physical examples but explored instead the transformation properties of the fundamental equations of his quantum mechanics (still the ones he had devised in the fall of 1925). He was now in a position to fully exploit the freedom
of representation of q -numbers inherent in his conception of quantum algebra. Dropping Heisenberg's restriction to a matrix scheme in which the energy matrix is diagonal, he studied the general set of bilinear transformations mutually connecting all possible matrix schemes and proved by symbolic means that Schrödinger's wave function was just a particular case of transformation. This showed that both matrix mechanics and wave mechanics were implicitly contained in his fundamental equations.
For the interpretation of his general formalism, the only assumption Dirac made was that there existed a limited "correspondence" with classical theory. Through an extremely ingenious argument based on transformation properties, he could show that this assumption was sufficient to derive a general interpretation of matrices and transformations. The standard question Dirac's theory could answer, in the simple case of one degree of freedom, was: What is, for a given value of a dynamic coordinate q , the relative probability of the values which a given dynamic quantity can take if the conjugate coordinate p is uniformly distributed? Dirac believed this was the only type of question physicists could answer. In this sense his interpretation was a statistical one; influenced, however, by the classical analogy, he still imagined the state of the system to be represented (at a given time) by definite coordinates q and p . In this view, the theory of transformations just implied that it was fundamentally impossible to predict unambiguously the state of the system at a subsequent time.
Bohr and Heisenberg soon persuaded Dirac to give up the "fiction" of a definite p and q . Accordingly, in his later presentations of quantum mechanics Dirac abandoned the notion of a (q, p ) state, and adopted the formal notion of "state vector" proposed by the Göttingen mathematicians (Weyl and yon Neumann).
A transformation theory partly and formally similar to Dirac's was simultaneously invented by Jordan in Göttingen. In general, Jordan tended to build quantum mechanics on autonomous axioms, without reference to classical theory. As a result, his notion of canonical conjugation, in contrast with Dirac's, did not necessarily correspond to the classical one. However, his idea of a transformation was in some respects closer to the classical idea of canonical transformation than Dirac's was. In this case, Dirac distanced himself from the classical analogy, presumably because his early attempts to adapt canonical transformations in quantum mechanics had become stagnant in the spring of 1926. At any rate, Dirac's transformation theory was more elegant than Jordan's; it was easier to apply (at least in its creator's hands), and as a result of the classical analogy it involved a more restrictive concept of canonical conjugation. These virtues
explain to a large extent the "miracles" Dirac subsequently performed in the contexts of radiation theory and relativistic quantum mechanics.
That Dirac's success owed much to the classical analogy was obvious and explicit. It remains to be seen to what extent his use of analogies was related to the correspondence principle. Dirac discovered the connection between Poisson brackets and commutators by examining Kramers and Heisenberg's procedure of symbolic translation, which itself derived from a sharpening of the correspondence principle. And his use of classical mechanics as a template for the construction of the new theory can be seen as a mathematical version of Bohr's continual appeal to formal analogies between classical and quantum theory. In this sense Dirac fulfilled Bohr's old prophecy of a "rational generalization" of the classical theory.
However, some essential aspects of Dirac's method were foreign to Bohr's strategy of correspondence. For instance, the way Dirac connected the algebra of Poisson brackets with the algebra of commutators was more similar to the mathematicians' notion of isomorphism than to the formal or symbolic analogies cultivated in Copenhagen. Further, in his approach to the transformation theory Dirac was inspired by another type of classical analogy, one in which he tended to imitate the relativistic strategy of theory building. As we saw, he first developed, at an abstract level, the transformation properties of his fundamental equations and then used these properties in identifying the physical content of the formalism. Since to him this was the royal road to fundamental theories, his greatest satisfaction as a theoretical physicist was obtained in the creation of the transformation theory. More generally, he relished the thought that quantum mechanics, in its genesis and expression, could compete in beauty with the greatest classical monuments, Hamiltonian mechanics and general relativity.